Low resistance, large dimension entrance to the inner cavity of BK channels determined by changing side-chain volume

Abstract

Large-conductance Ca²⁺- and voltage-activated K⁺ (BK) channels have the largest conductance (250–300 pS) of all K⁺-selective channels. Yet, the contributions of the various parts of the ion conduction pathway to the conductance are not known. Here, we examine the contribution of the entrance to the inner cavity to the large conductance. Residues at E321/E324 on each of the four α subunits encircle the entrance to the inner cavity. To determine if 321/324 is accessible from the inner conduction pathway, we measured single-channel current amplitudes before and after exposure and wash of thiol reagents to the intracellular side of E321C and E324C channels. MPA⁻ increased currents and MTSET⁺ decreased currents, with no difference between positions 321 and 324, indicating that side chains at 321/324 are accessible from the inner conduction pathway and have equivalent effects on conductance. For neutral amino acids, decreasing the size of the entrance to the inner cavity by substituting large side-chain amino acids at 321/324 decreased outward single-channel conductance, whereas increasing the size of the entrance with smaller side-chain substitutions had little effect. Reductions in outward conductance were negated by high [K⁺]_i. Substitutions had little effect on inward conductance. Fitting plots of conductance versus side-chain volume with a model consisting of one variable and one fixed resistor in series indicated an effective diameter and length of the entrance to the inner cavity for wild-type channels of 17.7 and 5.6 Å, respectively, with the resistance of the entrance ∼7% of the total resistance of the conduction pathway. The estimated dimensions are consistent with the structure of MthK, an archaeal homologue to BK channels. Our observations suggest that BK channels have a low resistance, large entrance to the inner cavity, with the entrance being as large as necessary to not limit current, but not much larger.

INTRODUCTION

Ion channels are membrane-spanning proteins that play key roles in physiological processes by controlling the flux of ions through cell membranes to generate electrical activity (Hille, 2001). The outward movement of K⁺ down its electrochemical gradient through K⁺ channels is a major factor in determining resting membrane potential and in controlling excitability of nerve and muscle cells. One family of voltage-dependent K⁺ channels is the large-conductance Ca²⁺- and voltage-activated K⁺ (BK) channels (Marty, 1981; Pallotta et al., 1981; Latorre et al., 1982; Adelman et al., 1992; Butler et al., 1993; Cox et al., 1997; Magleby, 2003; Lee and Cui, 2010). The synergistic activation of BK channels by voltage and intracellular Ca²⁺ places BK channels in negative feedback loops to control the firing patterns of neurons, transmitter release, insulin secretion, and smooth muscle contraction (Robitaille et al., 1993; Brenner et al., 2000; Berkefeld et al., 2010; Houamed et al., 2010). Defects in BK channel function can lead to epilepsy, paroxysmal movement disorder, and chronic hypertension (Brenner et al., 2000; Sausbier et al., 2004, 2005; Du et al., 2005; Laumonnier et al., 2006).

In addition to their feedback role, BK channels are of special interest because they have the highest conductance (250–300 pS) of all K⁺-selective channels, being 10–20 times greater than that of most other K⁺ channels (Hille, 2001). In spite of these large differences, both large- and small-conductance channels in the BK-containing family of K⁺ channels have common architectural features, with a central ion-permeation pathway formed by four α subunits with a narrowed selectivity filter region near the extracellular side that is highly conserved, and a cavity on the intracellular side leading to the selectivity filter (Heginbotham et al., 1994; Doyle et al., 1998; Jiang et al., 2002a, 2003; Kuo et al., 2003; Long et al., 2005, 2007; Wang and Sigworth, 2009).

Some factors contributing to the large conductance of BK channels have been identified. A ring of eight negative charges formed by E321 and E324 on each of the four subunits at the entrance to the inner cavity of BK channels doubles the outward single-channel current amplitude, i_out, by an electrostatic attraction of K⁺ to the entrance (Brelidze et al., 2003; Nimigean et al., 2003). This doubling of conductance would not be sufficient to account for the 10–20 times greater conductance of BK channels compared with other K⁺ channels. A ring of four negative charges in the shallow extracellular cavity of BK channels also increases the outward conductance (Haug et al., 2004), but most K⁺ channels of smaller conductance have the extracellular ring of negative charge, so the extracellular ring is unlikely to be responsible for the higher conductance of BK channels. Li and Aldrich (2004) found that large quaternary ammonium molecules have faster blocking and unblocking rates for BK channels than for other K⁺ channels, and suggested that BK channels have a larger inner mouth and inner cavity than other K⁺ channels, which could contribute to their high conductance. Consistent with this possibility, reducing the diffusion coefficient of K⁺ and the effective volume of the inner conduction pathway of BK channels with sugars reduces conductance (Brelidze and Magleby, 2005).

Although a large inner cavity may facilitate the passage of K⁺ through the inner cavity to reach the selectivity filter, the inner cavity might also have an opposite effect on conductance if the inner cavity is too big. Theoretical considerations suggest that increasing the mean diameter of the inner cavity might decrease the conductance, as widening a hypothetical inner cavity of KcsA increased the volume of water, which then screened the attractive charges of the P-loop backbone, leading to less attraction of K⁺ to the selectivity filter and decreased conductance (Furini et al., 2007).

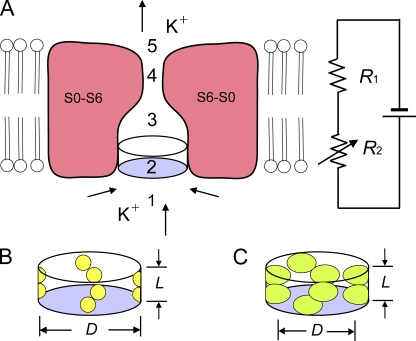
The purpose of our study is to determine the resistance and dimensions of the entrance to the inner cavity of BK channels to examine to what extent the entrance contributes to the high conductance of the channel. The experimental approach is depicted in Fig. 1, which presents a hypothetical midsection through a BK channel showing the membrane-spanning portions of two of the four α subunits that form the central conducting pore, where the membrane-spanning regions of the α subunits are formed from segments S0–S6 (Adelman et al., 1992; Butler et al., 1993; Meera et al., 1997). Not included in the diagram is the large intracellular gating ring of the channel, which is comprised of eight RCK domains (regulators of the conductance of K⁺), two per subunit (Jiang et al., 2002a,b; Wang and Sigworth, 2009; Wu et al., 2010).

Figure 1.

Schematic drawing of the ion conduction pathway of a BK channel and its representation by a two-resistor model. (A) Schematic side view of a section through the transmembrane segments (S0–S6) of a BK channel, with the front and back subunits removed. Arrows show direction of K⁺ movement for outward currents. The two-resistor model is depicted to the right. Not depicted are the intracellular gating ring with a large square central pore that is 20 Å on a side (Wu et al., 2010) and the side portals (Zhang et al., 2009) between the gating ring and the transmembrane portion of the channel. For outward current, K⁺ diffuses from the cytoplasm through the central pore of the gating ring and through the side portals (1) to the entrance to the inner cavity, through the entrance (2), through the inner cavity (3), through the selectivity filter (4), and through the shallow extracellular cavity (5) to the extracellular solution. For the two-resistor model, R₂ is a variable resistor representing the resistance of the entrance to the inner cavity (2), and R₁ is a fixed resistor representing the resistance of the remaining segments (1+3+4+5) of the ion conduction pathway. (B and C) Schematic diagrams of the entrance to the inner cavity for small (B) and large (C) side-chain substitutions at positions 321/324. The effective diameter (D) and length (L) of the entrance to the inner cavity are indicated. Increasing the volume of the side chains at positions 321/324 decreases the effective diameter, increasing the resistance of R₂.

The outward movement of K⁺ through an open BK channel would involve the diffusion of K⁺ from the cytoplasm (Fig. 1 A, part 1) to reach the entrance to the inner cavity (part 2). This diffusion would occur through (not depicted) a large square central opening in the gating ring, 20 Å on a side (Wu et al., 2010), and also through four side portals between the gating ring and the transmembrane part of the channel, which are large enough to allow access of the N terminus of auxiliary β2 subunits (when present) to the central cavity (Zhang et al., 2009). After passing through the entrance to the inner cavity (Fig. 1 A, part 2), the K⁺ would diffuse through the remainder of the inner cavity (part 3) and through the selectivity filter (part 4), and then exit to the extracellular solution through the shallow outer cavity (part 5). If a large entrance to the inner cavity is required for the large conductance of BK channels, decreasing the size of the entrance to the inner cavity by replacing smaller side-chain amino acids at the entrance (Fig. 1 B, yellow spheres) with larger side-chain amino acids (Fig. 1 C, green ellipsoids) should decrease i_out by reducing the outward movement of K⁺. On the other hand, if a large entrance is not required for the large single-channel conductance, decreasing the size of the entrance moderate amounts should have little effect on i_out.

We find that mutated residues E321C and E324C at the entrance to the inner cavity are accessible from the intracellular side of the ion conduction pathway, as indicated by changes in i_out after the application and wash of thiol reagents. The size of the entrance to the inner cavity is then varied by replacing E321/E324 with neutral amino acids with different-sized side chains. Increasing side-chain volume decreases i_out, whereas decreasing side-chain volume has little effect on i_out. Increasing K⁺_i from 0.15 to 2.5 M greatly reduces the effects of changes in side-chain volume on i_out. Changes in side-chain volume have little or no effect on inward single-channel current amplitudes, i_in. The above observations suggest that increased side-chain volume is limiting conductance by limiting diffusion of K⁺ into the inner cavity.

By analyzing plots of single-channel conductance versus side-chain volume with a model consisting of a fixed and variable resistor in series, we estimate that the resistance of the entrance to the inner cavity is ∼7% of the resistance of the entire ion conduction pathway including the selectivity filter. Hence, the effective resistance of the entrance to the inner cavity is small compared with the total resistance of the channel. We estimate the entrance to the inner cavity for wild-type (wt) channels to have an effective diameter of 17.7 Å and length of 5.6 Å, consistent with the idea that a large entrance contributes to the large conductance of BK channels, as making the entrance smaller reduces conductance.

MATERIALS AND METHODS

The α subunit of BK channels (mSlo1) used was initially cloned by Pallanck and Ganetzky (1994), modified for expression by Merck research laboratories by removing all 5′ noncoding sequences up to the second potential translation initiation site AUG (1–940), and provided by Merck (sequence available from GenBank/EMBL/DDBJ under accession no. U09383). The residue numbering in our study reflects this modification. Mutations were made using the QuikChange Site-Directed mutagenesis kit (Agilent Technologies) and checked by sequencing. The mutated sites E321/E324 can be identified by the sequence: 316ASYVPEIIELIGNRK330. The cRNAs were made with the mMessage mMachine kit (Invitrogen). Each oocyte was injected with 0.5–2 ng cRNA and then incubated at room temperature in Barth’s saline (88 mM NaCl, 1 mM KCl, 2.4 mM NaHCO₃, 0.3 mM CaNO₃, 0.41 mM CaCl₂, 0.82 mM MgSO₄, 15 mM HEPES, pH 7.6, and 12 µg/ml tetracycline) for 2–5 d before recording. Animal protocols were approved by the Animal Care and Use Committee at the University of Miami Miller School of Medicine and are in accordance with National Research Council guidelines for the care and use of laboratory animals.

Thiol reagents were purchased from Toronto Research Chemicals. The other chemicals were purchased from Sigma-Aldrich. The typical extracellular (pipette solution) and intracellular solutions contained 150 mM KCl and 5 mM TES buffer. In some experiments, where indicated, the intracellular K⁺ was increased to 2.5 M with KCl. For experiments at negative potentials, 100 µM Ca²⁺ was typically added to the intracellular solution to increase open probability. This low concentration of Ca²⁺ does not change single-channel conductance (Zhang et al., 2006). The pH of the solutions was adjusted to 7.0. Solutions were changed using a custom microchamber perfusion system (Barrett et al., 1982).

Thiol reagents maleimido proprionic acid (MPA), maleimido butyryl biocytin (MBB), and 2-(trimethylammonium) ethyl methanethiosulfonate bromide (MTSET) were dissolved in deionized water at 100 mM and stored at −20°C. During experiments, MTSET aliquots were thawed and stored on ice before diluting to 100 µM in 150 mM KCl and 5 mM TES, pH 7.0. The diluted MTSET solution was freshly made just before application and discarded 10 min later. MPA and MBB stock solutions were diluted to 100 nM in 150 mM KCl and 5 mM TES, pH 7.0. The diluted MPA and MBB solutions were stable at room temperature and used throughout the day. Thiol reagents were applied to the intracellular side of inside-out patches for 5 min, with the membrane potential held at +20 mV. To remove the unbound thiol reagents, the inside-out patch was washed with 150 mM KCl and 5 mM TES, pH 7.0, for 2 min with continuous flow. Single-channel currents were recorded after washing away the unbound thiol reagents.

Standard inside-out patch clamp techniques were used to record single-channel currents (Hamill et al., 1981; Brelidze et al., 2003). BK channels were identified by their characteristic response to both voltage and Ca²⁺ (Barrett et al., 1982) before changing to the experimental solutions described above. Single-channel currents were sampled with pClamp9 at 200 kHz and filtered to 5 kHz (−3 dB). These data were analyzed to determine i_out or i_in, as appropriate, which were then plotted as single-channel current amplitude versus voltage (i-V plots). i_out was measured as the distance between the peaks of all-point histograms of the single-channel currents, as described in Brelidze and Magleby (2004). The initial bin width for the all-points histograms was typically 0.2 pA, after which the histograms were further processed with a moving bin averaging of typically nine bins to smooth the response. Because of the low channel activity associated with the negative potentials used to obtain i_in, there were insufficient openings to apply all-point histograms. Consequently, i_in was measured by the difference between dashed lines placed visually at the open and closed current levels. Conductance was calculated by dividing i_out or i_in by the driving force, defined as the holding membrane potential minus the reversal potential for K⁺.

Plotted symbols are the means for data obtained from three to five patches for each mutation. The error bars, often not visible because they are less than the size of the plotted symbols, indicate the SEM. Current amplitudes for different mutations were compared with the Student’s t test, with P ≤ 0.05 indicating a significant difference. Experiments were at room temperature: 23–25°C.

RESULTS AND DISCUSSION

Residues at positions 321 and 324 contribute to the ion conduction pathway on the intracellular side of the selectivity filter

Sequence alignment of BK channels with MthK, a large conductance archaeal channel whose crystal structure is known (Jiang et al., 2002a,b), suggests that residues E321 and E324 in BK channels are located at the entrance to the inner cavity (Brelidze et al., 2003; Nimigean et al., 2003). To examine if the side chains for residues at positions 321/324 are accessible from the ion conduction pathway, we examined whether thiol reagents (Karlin and Bartels, 1966) could attach to cysteine side chains from the mutations E321C and E324C. To test for attachment, we measured outward single-channel current amplitude, i_out, before and after treatment and wash with thiol reagents. Thiol reagents attached to side chains in the conduction pathway might be expected to alter i_out. Three charged membrane-impermeable thiol reagents were examined: MPA⁻, MBB⁻, and MTSET⁺.

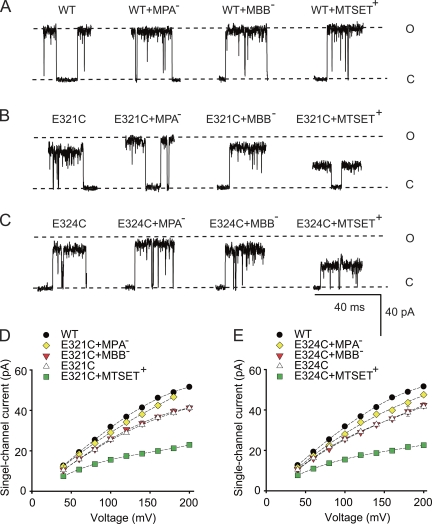
Treating wt BK channels with MPA⁻, MBB⁻, or MTSET⁺ did not change i_out (Fig. 2 A). Thus, the cysteines of wt BK channels are either not accessible to intracellular thiol reagents or thiol binding to native cysteines does not alter i_out, consistent with previous observations of no effect of intracellular thiol reagents on i_out for native BK channels (Wang et al., 1997). In contrast, the treatment of E321C channels with MPA⁻ increased i_out compared with E321C alone (Fig. 2, B and D). This observation suggests that MPA⁻ specifically binds to the cysteine at position 321 because, as described above, MPA⁻ application to wt BK channels had no effect. The increased i_out with MPA⁻ treatment likely arises because the negative charge on MPA⁻ bound to E321C increases the local K⁺ concentration in the inner cavity of the E321C channels (Brelidze et al., 2003; Nimigean et al., 2003).

Figure 2.

Residues E321C/E324C at the entrance to the inner cavity are accessible to the intracellular solution. (A–C) Representative records of outward currents through single BK channels held at +180 mV before and after applications of thiol reagents to wt and mutated channels. The dashed lines show the open and closed current levels of wt channels. Current levels after intracellular application of MPA⁻, MBB⁻, or MTSET⁺ to wt channels followed by thorough washing (A) were unchanged, whereas application and wash to E321C (B) or E324C (C) channels changed single-channel current levels after treatment with MPA⁻ or MTSET⁺. (D and E) Plots of i_out versus voltage for the indicated treatments for E321C (D) and E324C (E) channels. Treatment and wash of the thiol agents to wt channels had no effect on i_out and are not plotted. In this and subsequent plots, the dashed lines are cubic spline fits, and the absence of visible error bars indicates that the SEM is less than the symbol size. Data are from three to five different oocytes for each plotted symbol. Positions E321C and E324C are both accessible to the ion conduction pathway from the intracellular side with equivalent effects of thiol reagents at these positions on i_out. 150 mM K⁺_i.

In contrast to MPA⁻ treatment, which increased i_out, treatment with MBB⁻ had little effect on i_out (Fig. 2, B and D). To test whether MBB⁻ was bound, MPA⁻ was applied to E321C channels previously treated with MBB⁻. There was no effect on i_out (not depicted), indicating that MBB⁻ was bound to E321C, preventing the binding of MPA⁻. Why is there no effect of bound MBB⁻? Although both MPA⁻ and MBB⁻ are negatively charged, MBB⁻ (mol wt, 537) is much larger than MPA⁻ (mol wt, 169). The lack of effect of bound MBB⁻ on i_out could reflect two opposing effects: the attraction of K⁺ to the inner cavity by the negative charge on MBB⁻, and partial blocking of the conduction pathway as a result of the very large size of MBB⁻, which could restrict the flow of K⁺.

We next examined the effect of attaching positively charged MTSET⁺ to E321C. MTSET⁺ decreased i_out (Fig. 2, B and D). The reduced current could arise from a decreased concentration of K⁺ at the inner cavity from electrostatic repulsion of K⁺ and also from a reduction in the size of the entrance to the inner cavity as a result of the large size of MTSET⁺ (mol wt, 278).

Analogous experiments were performed for E324C channels with the same findings as for the E321C channels (Fig. 2, C and E). These observations suggest that the side chains of residues at positions 321 and 324 are accessible from the conduction pathway from the intracellular side, and that the side chains at these two positions have equivalent effects on conductance. The change in i_out after thiol treatment would be consistent with location of the side chains of residues 321 and 324 in the conduction pathway, as Kurata et al. (2004) found that introducing negative charged residues to pore-facing residues altered the conductance in Kir6.2 channels, whereas substitutions with residues facing away from the pore did not. Even if the side chains at positions 321 and 324 were partially buried, changing side-chain volume might still be expected to displace parts of the channel into the conduction pathway, reducing the size of the entrance. Consequently, changing the side-chain volume of residues 321 and 324 would be expected to change the size of the entrance to the inner cavity, either directly or indirectly by displacement (Fig. 1, B and C).

Decreasing the size of the entrance to the inner cavity with larger hydrophobic side chains decreases i_out

If a large entrance to the inner cavity is necessary for the large conductance of BK channels, decreasing the size of the entrance should decrease i_out. To test this hypothesis, we substituted neutral amino acids with different-sized side chains at positions 321 and 324 and measured i_out. Neutral amino acids were used because charge could obscure the effects of side-chain size on conductance (Fig. 2) and also change the effective access resistance (Andersen, 1983; Aguilella-Arzo et al., 2005). Table I lists the increase in side-chain volume compared with glycine for the substituted amino acids. Because the degree of hydrophobicity of the substituted amino acids might also be expected to have effects on conductance, the amino acids in Table I are divided into hydrophobic and uncharged hydrophilic groups based on the classification in Lodish (2008). Additional hydrophobicity scales will be considered later.

Table I.

Increase in side-chain volume compared to glycine

Amino acid	Å3
Hydrophobic amino acids
Alanine (A)	28.5
Valine (V)	79.9
Leucine (L)	106.6
Phenylalanine (F)	129.8
Tyrosine (Y)	133.5
Tryptophan (W)	167.7
Hydrophilic uncharged amino acids
Serine (S)	28.9
Threonine (T)	56.0
Asparagine (N)	57.6
Glutamine (Q)	83.8
wt amino acid at E321/E324
Glutamate (E)	78.3

Values indicate the increase in side-chain volume compared to the side-chain volume of glycine, calculated from the volume of the indicated amino acid minus the volume of glycine. Amino acid volumes are from Creighton (1984).

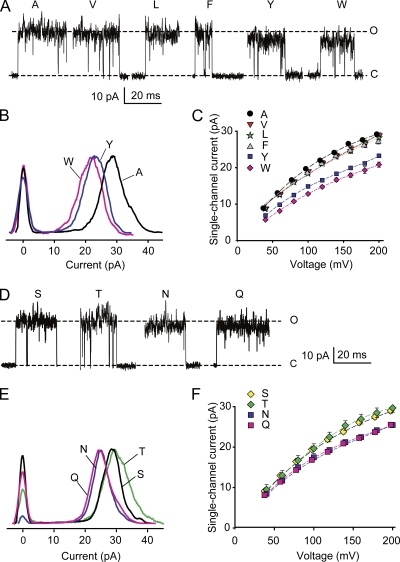
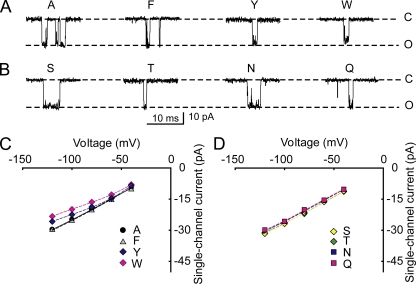
Representative single-channel currents for substitutions of hydrophobic amino acids at positions 321 and 324 are shown in Fig. 3 A, where a reduction in i_out occurs as side-chain volume increases. The average i_out for each substitution was determined from the distance between the most frequent current levels in all-points histograms (Fig. 3 B), and the mean current at each voltage obtained from three to five different channels was plotted for the examined range of voltages in Fig. 3 C. Substitution with alanine gave the largest i_out of the hydrophobic substitutions. Substitution with valine, leucine, or phenylalanine gave a small but typically insignificant decrease in i_out compared with alanine (typically, P > 0.1; n = 3–5 for all voltages), whereas substitution with the amino acids tyrosine and tryptophan, with their progressively larger side chains, led to significant reductions in i_out (P < 0.001; n = 3–5 at all voltages; Fig. 3, A–C).

Figure 3.

Increasing side-chain volume at the entrance to the inner cavity reduces i_out for both hydrophobic and uncharged hydrophilic amino acids. (A) Representative single-channel currents at +200 mV for substitution of the indicated hydrophobic amino acids at positions 321/324. Dashed lines show the mean open and closed current levels of E321A/E324A channels. Larger side-chain amino acids at positions 321/324 decrease i_out. (B) Representative all-points histograms for currents like those in A for the indicated amino acid substitutions. The values on the ordinate are proportional to the frequency of observations of the current levels indicated on the abscissa. The distributions centered on 0 pA indicate the current fluctuation around the closed level, and the distributions to the right indicate the current fluctuations around the open levels. Histograms are scaled so that the peak frequencies of the open current levels are the same. The larger amino acid side chains of tyrosine and tryptophan shift the entire distributions to lower current levels compared with alanine. The excess open-channel noise compared with wt channels (Fig. 2 A) suggests that the substitutions destabilize the open state. (C) Plots of i_out versus voltage indicate that the reduction of i_out for the larger side chains occurs over the range of examined voltages. Substituting valine, leucine, or phenylalanine for alanine had little effect on i_out, whereas substituting tyrosine or tryptophan with their larger side chains reduced i_out. (D–F) Same as A–C, except for substitutions of hydrophilic uncharged amino acids. Dashed lines in D are for serine substitution. Asparagine and glutamine with their larger side chains decrease single-channel current compared with serine and threonine with their smaller side chains. For i-V plots in this and Fig. 4, some symbols have been shifted laterally 2.5 mV to avoid overlap. 150 mM K⁺_i.

Although the hydrophobic amino acid substitutions increased the open-channel noise compared with wt channels (compare Fig. 3 A to Fig. 2 A), the all-points histograms indicated that the entire distributions of open-channel current amplitudes for tyrosine and tryptophan substitutions were shifted left to lower current amplitudes when compared with distributions for alanine substitutions (Fig. 3 B); valine, leucine, and phenylalanine were similar to alanine and not depicted. Therefore, over the range of the noisy open-channel current amplitude distributions, the single-channel conductance for hydrophobic amino acids was in this order: alanine ∼ (valine, leucine, phenylalanine) > tyrosine > tryptophan.

For phenylalanine substitutions in two of the four channels examined, there were two closely spaced open-channel current levels (not depicted) rather than the dominant open-channel current level in Fig. 3 A. Nevertheless, both current levels were still greater than for channels with tyrosine or tryptophan substitutions. The mean of the two current levels (when present) for phenylalanine substitutions was used when averaging data for the plot in Fig. 3 C.

Decreasing the size of the entrance to the inner cavity with larger hydrophilic uncharged side chains decreases i_out

Representative single-channel currents for substitutions of hydrophilic uncharged amino acids at positions 321 and 324 are shown in Fig. 3 D, where a reduction in i_out occurred for substitutions with asparagine and glutamine, with their larger side chains compared with serine. The average i_out for each substitution was determined from all-points histograms (Fig. 3 E), and the mean current at each voltage obtained from three to five different channels was plotted for the examined range of voltages (Fig. 3 F). Asparagine and glutamine substitutions gave significantly reduced i_out at all voltages (Fig. 3, D–F) when compared with serine and threonine (P < 0.01; n = 3–5 at each voltage), suggesting that large side chains reduce i_out. However, a comparison of the side-chain volumes (Table I) and current amplitudes (Fig. 3, D–F) suggests that there is not a strict relationship between side-chain volume and current for hydrophilic amino acids: threonine and asparagine have similar volumes but different conductances, and asparagine and glutamine have different volumes and similar conductances. Hence, other factors such as the structures of side chains, as well as their volumes, can influence the movement of K⁺ through the entrance to the inner cavity.

Increasing K⁺_i from 150 mM to 2.5 M negates the effect of side-chain volume on i_out

In the previous sections it was found that substituting hydrophobic or hydrophilic uncharged amino acids with large side chains at the entrance to the inner cavity can decrease i_out. If this decrease arises because side chains with large volume physically limit the diffusion of K⁺ ions from the bulk intracellular solution into the inner cavity, then increasing K⁺_i from 150 mM to 2.5 M would be expected to reduce or eliminate the effect of side-chain volume on i_out. This is the case because a greatly increased K⁺_i would be available to diffuse into the inner cavity, compensating for the smaller entrance. Alternatively, if the substituted amino acids allosterically altered the selectivity filter in some way to reduce the movement of K⁺ through the filter, increasing K⁺_i might not necessarily be expected to reverse the effects of the substitutions.

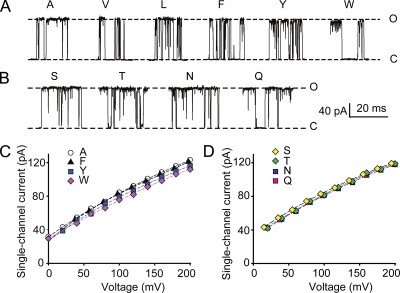
Fig. 4 (A–D) shows that 2.5 M K⁺_i eliminated the effect of increased side-chain volume on reducing i_out for all of the examined hydrophobic (A and C) and hydrophilic (B and D) amino acids except for tryptophan, which still reduced i_out a small (9%) but significant (P < 0.05) amount compared with the larger 30% reduction with 150 mM K⁺_i in Fig. 3 (A–C). These observations are consistent with increased side-chain volume reducing conductance by decreasing the size of the entrance and not from indirect effects.

Figure 4.

Increasing side-chain volume has little effect on i_out in the presence of 2.5 M K⁺_i. (A and B) Representative records of outward currents through single channels at +200 mV with 2.5 M of intracellular K⁺ for hydrophobic (A) and uncharged hydrophilic (B) amino acid substitutions at positions 321/324. The dashed lines show current levels with alanine substitutions. (C and D) Plots of i_out in the presence of high 2.5-M K⁺_i versus voltage for hydrophobic (C) and uncharged hydrophilic (D) amino acid substitutions. Plots for valine and leucine substitution superimposed the plots for alanine substitution in C and are not shown. High K⁺_i negates the effect of side-chain volume on i_out (compare with Fig. 3 with 150 mM K⁺_i), as would be expected if larger side chains reduce the size of the entrance to the inner cavity.

Increasing side-chain volume decreases i_in less than i_out

The experiments in the previous sections examined the effect of side-chain volume on i_out by making the intracellular side of the membrane positive to electrostatically push K⁺ out through the channel. To test the effect of side-chain volume on inward single-channel current amplitudes, i_in, the intracellular side of the membrane, was made negative to attract K⁺ inward through the channel. Replacing alanine with larger side-chain hydrophobic amino acids reduced i_in a maximum of 18% for the largest side-chain tryptophan (Fig. 5, A and C) compared with a 30% reduction for i_out (Fig. 3, A–C). Replacing serine with larger side-chain uncharged hydrophilic amino acids had no effect on i_in (Fig. 5, B and D) compared with an ∼13% reduction on i_out (Fig. 3, D and E). A larger reduction of i_out compared with i_in with increasing side-chain volume is consistent with larger side-chain volumes reducing the size of the entrance to the inner cavity. For outward currents, decreasing the size of the entrance to the inner cavity could directly limit how much diffusing K⁺ would enter the entrance to the inner cavity (be captured) to be driven through the channel by voltage. In contrast, for inward currents, decreasing the size of entrance to the inner cavity (now the exit) could lead to an increased concentration of K⁺ in the inner cavity, increasing the probability of K⁺ exiting to the intracellular solution, compensating to some extent for the smaller exit size.

Figure 5.

Increasing side-chain volume has little or no effect on i_in. (A and B) Representative records of inward single-channel currents at −100 mV for the indicated amino acid substitutions. Dashed lines are the current levels with alanine substitution (A) and serine substitution (B). (C and D) Plots of i_in versus voltage for hydrophobic (C) and uncharged hydrophilic (D) amino acid substitutions. Side-chain volume has less of an effect on i_in compared with i_out (compare with Fig. 3). The reduced effect of side-chain volume on i_in is consistent with larger side chains reducing the size of the entrance to the inner cavity. 150 mM K⁺_i.

Larger side-chain volumes decrease single-channel conductance for different scales of hydrophobicity

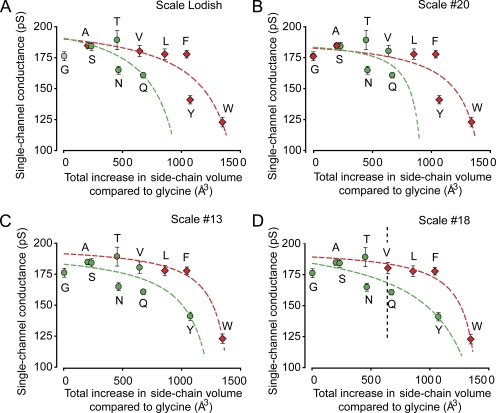
Fig. 6 plots mean single-channel conductance for outward currents versus the total increase in side-chain volume compared with glycine at the entrance to the inner cavity for the 11 examined amino acid substitutions at positions 321/324, including the special amino acid glycine. Because the current–voltage plots deviate from linearity (Fig. 3, C and F), the mean single-channel conductance over the examined range of voltage was plotted for each substitution. The total increase in side-chain volume on the abscissa is eight times the volume in Table I because substitution occurs at positions 321 and 324 on each of the four subunits. The data are plotted using four representative scales out of over 100 classifying amino acid hydrophobicity (Lodish, 2008; Mant et al., 2009), where red and green symbols in Fig. 6 represent hydrophobic and hydrophilic amino acids, respectively, as defined by the different scales. Independent of the hydrophobicity scale used, single-channel conductance decreased with increasing side-chain volume at the entrance to the inner cavity. The decrease occurred progressively faster as side-chain volume increased.

Figure 6.

Decreasing the size of the entrance to the inner cavity decreases single-channel conductance for the four indicated scales of hydrophobicity in a manner consistent with a two-resistor model. (A–D) Plots of single-channel conductance versus total increase in side-chain volume for the indicated amino acid substitutions at positions 321/324 on each of the four subunits. The total increase in side-chain volume compared with glycine is 8w_X ų, where w_X is the increased side-chain volume from Table I for a single amino acid. The different scales of hydrophobicity used for classifications are: (A) Lodish (2008), (B) Scale #20, (C) Scale #13, and (D) Scale #18 from Mant et al. (2009), with the dividing line between hydrophobic and hydrophilic on the Mant et al. scales based on our assessment of the scale data. The data points are plotted at the same positions in each panel, with the differences among the panels being the classification of one or more of the amino acids into hydrophobic (red) or uncharged hydrophilic (green) data. Glycine is considered a special amino acid in the Lodish (2008) classification where it is plotted as gray. The dashed lines indicate predicted changes in single-channel conductance obtained by fitting the hydrophobic (red) or hydrophilic (green) data with Eqs. A1–A4 describing the two-resistor model (Fig. 1). Fitted parameters are in Table II. 150 mM K⁺_i. The vertical dashed line in D indicates the volume that would be occupied by the side chains of glutamate at E321/E324 in wt channels.

Resistance and dimensions of the entrance to the inner cavity of BK channels

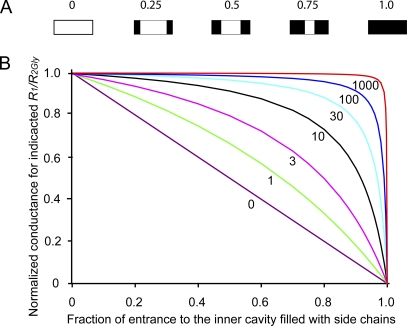
This section uses equations derived in the Appendix for a two-resistor model to fit the data in Fig. 6 to obtain estimates of the resistance and effective dimensions of the entrance to the inner cavity of BK channels. The flow of K⁺ through the ion conduction pathway of a BK channel is assumed to be described by two resistors in series: R₁ is a fixed resistor, and R₂ is a variable resistor (Fig. 1 A). R₁ arises from the sum of the resistance for all parts of the conduction pathway except the entrance to the inner cavity. R₂ arises from the resistance of the entrance to the inner cavity. Increasing side-chain volume in the entrance (Fig. 1, B and C) increases R₂. Fig. 7 A depicts idealized side views of the entrance to the inner cavity being filled with progressively larger side chains (black). For this idealization, the conductance of the entrance, g₂, would decrease linearly with increasing side-chain volume, whereas the resistance of the entrance, R₂, would increase superlinearly, as 1/g₂. Such a two-resistor model predicts characteristic plots of single-channel conductance versus increased side-chain volume (Fig. 7 B and Appendix), with the shape of each plot depending on the ratio of R₁/R_2Gly, where R_2Gly is the resistance of the empty entrance to the inner cavity, as is the case for glycine substitutions at positions 321/324.

Figure 7.

The two-resistor model for the conduction pathway of BK channels (Fig. 1 and Appendix) predicts characteristic plots of normalized single-channel conductance versus side-chain volume in the entrance to the inner cavity. (A) Schematic side views through the midsection of an idealized entrance to the inner cavity for side chains occupying from 0 to 1.0 of the fractional volume of the entrance. (B) Plots of theoretical normalized single-channel conductance versus side-chain volume as a fraction of the entrance to the inner cavity filled with side chains. The label on each line indicates the ratio of R₁/R_2Gly. R_2Gly is the resistance of the entrance to the inner cavity when it is empty. Each R₁/R_2Gly ratio results in a unique curve as side-chain volume increases. The theoretical plots in Fig. 7 B with R₁/R_2Gly ratios in the range of 10–20 appear consistent with the experimental data in Fig. 6. Theoretical plots calculated with Eq. A5.

For the theoretical case where the fixed resistor R₁ = 0, giving an R₁/R_2Gly ratio of 0, all of the resistance in the conduction pathway would be in R₂, and there would be an inverse linear relationship between total conductance (equal to g₂ in this case) and side-chain volume (Fig. 7 B, purple straight line labeled 0). If R₁ is >0, total conductance no longer decreases linearly with increasing side-chain volume, with the deviation from linearity increasing as the R₁/R_2Gly ratio increases. For ratios >10, increasing side-chain volume had limited effect on conductance until the entrance to the inner cavity was almost filled with side chains, after which the conductance fell rapidly toward 0 (Fig. 7 B) as side-chain volume approached the volume of the entrance (Fig. 7 A, right).

A comparison of the theoretical curves for the two-resistor model (Fig. 7 B) to the single-channel data (Fig. 6) suggests that the two-resistor model may be consistent with the experimental data for R₁/R_2Gly ratios of ∼10. To test this possibility, estimates of the parameters for the two-resistor model were obtained separately for hydrophobic and hydrophilic amino acid substitutions for each of the four different hydrophobicity scales in Fig. 6. This was done by fitting the conductance versus increased side-chain volume data with Eqs. A1–A4. The red and green dashed lines, which approximate the trend in the experimental data, are the best-fitting solutions for hydrophobic and hydrophilic amino acids, respectively. R₁/R_2Gly ratios for each of the eight sets of data are in Table II together with estimates of R₁, R_2Gly, and the effective volume, length, and diameter of the entrance to the inner cavity (assuming K⁺ is a point charge) with glycine substitutions (calculated as described in Appendix). The parameters in Table II for hydrophobic and hydrophilic substitutions were not significantly different (P > 0.05). Nevertheless, it can be argued that the best estimates of the parameters would be those obtained when fitting data over the widest range of side-chain volumes, as was typically the case for fitting the hydrophobic amino acids. Consequently, further discussion will center on the mean estimates in Table II for fitting the hydrophobic data for the four different hydrophobic scales. Additional support for using the mean values for the hydrophobic scales is that simultaneous fitting of the hydrophilic and hydrophobic data gave parameter estimates within a few percentages of those for mean hydrophobic values alone (not depicted).

Table II.

Parameters for a two-resistor model^a of the conduction pathway of E321G/E324G BK channels, unless indicated

Parameterb	gT	R1	R2	R1/R2	W	L	D	Wwtc	Dwtc
	pS	GΩ	GΩ		Å3	Å	Å	Å3	Å
Hydrophilic amino acids
Scale Lodishd	189	4.86	0.440	11.0	980	5.20	15.5	354	9.3
Scale #13d	182	5.13	0.369	13.9	1,308	5.49	17.4	682	12.6
Scale #18d	185	4.71	0.690	6.8	1,503	8.05	15.4	877	11.8
Scale #20d	185	5.08	0.315	16.1	1,126	4.72	17.4	500	11.6
Meane	186	4.95	0.454	12.0	1,229	5.86	16.4	603	11.3
SEM (n = 4)	1	0.10	0.083	2.0	113	0.75	0.6	114	0.7
Hydrophobic amino acids
Scale Lodishd	189	4.87	0.432	11.3	1,540	6.45	17.4	913	13.4
Scale #13d	197	4.74	0.316	15.0	1,481	5.41	18.7	854	14.2
Scale #18d	192	4.88	0.316	15.5	1,487	5.42	18.7	861	14.2
Scale #20d	181	5.21	0.289	18.0	1,485	5.18	19.1	859	14.5
Meane	190	4.92	0.338	14.9	1,498	5.62	18.5	872	14.1
SEM (n = 4)	3	0.10	0.032	1.4	14	0.29	0.4	13	0.2

^aTwo-resistor model with R₁ as a fixed resistor and R₂ as a variable resistor (Fig. 1).

^bFormal definitions and equations for estimating the parameters by separately fitting data in Fig. 6 for amino acid substitutions classified as uncharged hydrophilic or hydrophobic are in the Appendix. g_T is single-channel conductance, R₁ is resistance of all parts of the conduction pathway, except the entrance to the inner cavity, and R₂ is the resistance of the entrance to the inner cavity. W, L, and D are the calculated effective volume, length, and diameter of the entrance to the inner cavity. Values are for E321G/E324G channels unless indicated as for wt channels. All resistances and dimensions calculated assuming K⁺ is a point charge without volume or waters of hydration.

^cW_wt and D_wt are the calculated volume and diameter of the entrance to the inner cavity obtained for hypothetical neutral amino acids with the same volume as wt glutamate at positions 321/324. The calculated value of L_wt is the same as L.

^dThe different hydrophobicity scales are from Lodish (2008) and Mant et al. (2009).

^eMean values for the four different hydrophobicity scales above.

When the entrance to the inner cavity was empty, as defined to be the case for glycine substitutions with their small side chains of −H, R₁ was 4.92 ± 0.10 GΩ and R_2Gly was 0.338 ± 0.032 GΩ (mean hydrophobic values; Table II) for a total resistance of 5.26 GΩ (190 pS). The R₁/R_2Gly ratio from these mean values was 14.6, and from the mean of the individual ratios it was 14.9 ± 1.4 (Table II). Hence, the majority (93%) of the total resistance in the conduction pathway with an empty entrance to the inner cavity is in R₁, with R₂ contributing only 7% of the resistance.

For tryptophan substitution, an R₁/R_2Trp ratio of 1.52 was calculated from 4.92/3.24 GΩ, where R_2Trp = 3.24 GΩ = 0.338 GΩ/(1−(8 × 167.7 ų/1498 ų)) from Eq. A11 (in Appendix), with R₁ (4.92 GΩ), R_2Gly (0.338 GΩ), and W_Gly (1498 ų) from the mean values in Table II for hydrophobic amino acid substitutions, and w_Trp (167.7 ų) from Table I. Thus, with the largest substituted amino acid tryptophan, 40% of the total resistance to the movement of K⁺ is distributed to R_2Trp, compared with 7% with glycine substitutions.

Assuming that K⁺ is a point charge, the calculated effective length of the entrance to the inner cavity with either glycine or tryptophan substitutions was 5.62 Å (Table II; Eqs. A8–A11 in Appendix). With the same point charge assumption, the calculated effective diameter of the entrance for glycine substitutions was 18.5 Å (Table II) and for tryptophan substitutions was 5.95 Å (Eqs. A8–A11 in Appendix). Assuming a hydrated diameter for K⁺ in the range of 3.6 to 6.6 Å (see Appendix), the calculated effective diameter of the entrance to the inner cavity for glycine substitutions would be in the range of 22.1–25.1 Å (18.5 + 3.6–6.6 Å; see Appendix), and for tryptophan substitutions it would be in the range of 9.6–12.6 Å (5.95 + 3.6–6.6 Å).

The vertical dashed line in Fig. 6 D indicates the volume that would be occupied by the side chains of glutamate at E321/E324 for wt BK channels. Based on the side-chain volume of glutamate and the mean hydrophobic parameters for glycine substitution, the calculated dimensions of the entrance to the inner cavity for wt BK channels assuming that K⁺ is a point charge gives an effective diameter of 14.1 Å and a length of 5.62 Å (Table II). Assuming a hydrated diameter for K⁺ in the range of 3.6–6.6 Å, the effective diameter of the entrance for wt BK channels would be in the range of 17.7–20.7 Å (14.1 + 3.6–6.6 Å). Because of the complex geometry of the ion conduction pathway leading up to the entrance to the inner cavity, with a large square-shaped central pore in the gating ring of 20 Å on a side (Wu et al., 2010), four side portals between the gating ring and the transmembrane portion of the channel leading to the entrance (Zhang et al., 2009), and the likely case that the entrance to the inner cavity transitions smoothly into the inner cavity itself (see Fig. 8 A for MthK), no corrections for hydrated radius have been applied to the estimates of the length of the entrance.

Figure 8.

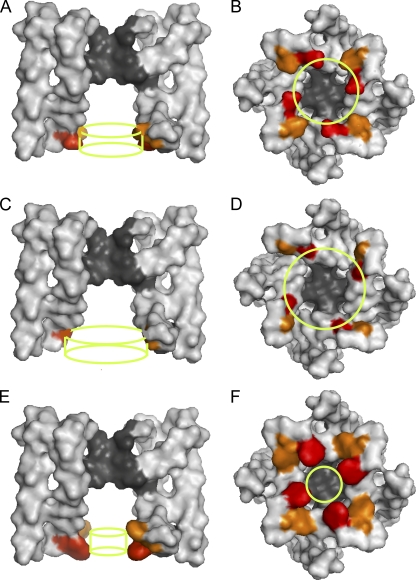
The predicted effective dimensions of the entrance to the inner cavity with the two-resistor model are consistent with the crystal structure of MthK. (A) Molecular surface of a side view (extracellular at top) of the membrane-spanning portions of MthK, with front and back subunits removed, as generated with Pymol software and Protein Data Bank accession number 1LNQ (Jiang et al., 2002b). The wt glutamates at positions E92 (red) and a computer mutation glutamate at E95 (orange) are indicated by color. The green cylinder indicates the calculated effective dimensions of the entrance to the inner cavity for wt BK channels (E321/E324). The cylinder diameter is 17.7 Å (14.1 Å from Table II plus 3.6 Å for the hydrated diameter of K⁺), with a length of 5.62 Å. (B) Same as A, except for a bottom view looking out from the intracellular side with all four subunits. (C and D) Same as A and B, but for glycine substituted at positions E92/E95 in the structure of MthK. The green cylinders indicate the calculated effective dimensions of the entrance to the inner cavity for BK channels with glycine substitutions (E321G/E324G). The cylinder diameter is 22.1 Å (18.5 plus 3.6 Å for the hydrated diameter of K⁺), with a length of 5.6 Å. (E and F) Same as above, except with tryptophan substitutions at positions E92/E95 in the crystal structure of MthK. The green cylinders indicate the calculated effective dimensions of the entrance to the inner cavity for BK channels with tryptophan substations (E321W/E324W). The cylinder diameter is 9.6 Å (5.95 plus 3.6 Å for the hydrated diameter of K⁺), with a length of 5.62 Å. The predicted effective dimensions of the entrance to the inner cavity for wt and mutated BK channels are generally consistent with the crystal structure of wt and computer-mutated MthK channels.

The calculated dimensions of the inner cavity for BK channels are consistent with the crystal structure of MthK channels

It is of interest to compare the calculated dimensions of the entrance to the inner cavity for BK channels to the crystal structure of MthK, an archaeal large-conductance Ca²⁺-activated K⁺ channel (Jiang et al., 2002a,b). For these comparisons, we have retained the glutamate at E92 in wt MthK and added a computer-generated mutation, L95E, to MthK to match the spacing of the glutamate residues E321/E324 in wt BK channels. With this mutation, the side chains at positions 92/95 in the structure of MthK appear accessible from the conduction pathway to be consistent with the accessibility experiments for BK channels in Fig. 2, which suggest that E321/E324 is accessible from the conduction pathway. Fig. 8 A shows the molecular surface (extracellular at top) of a side view of the mutated MthK, with front and back subunits removed. The wt glutamate at position E92 (Fig. 8 A, red) and computer-substituted glutamate at position E95 (orange) are indicated by color. Fig. 8 B presents a bottom view looking out from the intracellular side, with all four subunits present. The green cylinder superimposed on each view indicates the calculated effective dimensions of the entrance to the inner cavity for wt BK channels, with a diameter of 17.7 Å (14.1 Å from Table II plus 3.6 Å for the hydrated diameter of K⁺) and a length of 5.62 Å. Fig. 8 (C and D) presents views of MthK that have been computer mutated to have glycines at positions 92/95, and Fig. 8 (E and F) presents views for tryptophan at positions 92/95. The green cylinders are the calculated effective dimensions of the entrance to the inner cavity for BK channels with glycine (Fig. 8, C and D) or tryptophan (E and F) substitutions (dimensions in legend to Fig. 8).

The calculated effective dimensions for BK channels for the indicated amino acid substitutions appear generally consistent with the structure of MthK for computer-generated amino acid substitutions. To the extent that BK and MthK channels have similar entrance structure, this general agreement lends support to the analysis. Nevertheless, these comparisons also indicate that the calculated dimensions for BK are only effective dimensions because the entrance to the inner cavity of BK, based on comparison to MthK, would be more complex than an idealized cylinder. For example, in addition to contributing to the structures defining the entrance to the inner cavity, the examined side chains may also contribute to the structures forming the four side-portal pathways to the entrance located between the membrane-spanning portions of the channel and the cytoplasmic gating ring. (See Fig. 1 in Zhang et al., 2009, for a cartoon of the side-portal pathways.)

The entrance to the inner cavity of wt BK channels is sufficiently large to not limit single-channel conductance

Having estimated the effective entrance to the inner cavity of wt BK channels (Fig. 8, A and B), the next question is whether the entrance is large enough to not limit single-channel conductance. If the effect of the negative charge on the glutamate side chains in wt BK channels at E321/E324 is ignored for the moment, it can be seen from Fig. 6 D (vertical dashed line) that side chains with the volume of (hypothetically neutral) glutamates would be small enough to have little effect on the single-channel conductance. This is the case because making the entrance larger by substituting smaller side chains gave only small increases in conductance, whereas making the entrance smaller by substituting larger side chains gave large decreases in single-channel conductance. Hence, an entrance the size of that in the wt channels, but without the ring of negative charge, would be large enough to have little effect on limiting single-channel conductance. It will be argued in a later section that this conclusion would still be valid when the ring of negative charge that is present in wt BK channels is taken into account.

Consistent with a conclusion of an entrance sufficiently large to not limit conductance, Brelidze et al. (2003) found that replacing the larger negatively charged glutamates in wt channels with smaller negatively charged aspartates (E321D/E324D) to preserve the ring of negative charge had little effect on the conductance. Also consistent with a large entrance are the observations of Li and Aldrich (2004). They found that the large molecule tetrabutylammonium applied intracellularly had much faster blocking and unblocking rates in BK channels than in smaller conductance K⁺ channels, and suggested that a large inner mouth and cavity could contribute to the large conductance of BK channels. Consistent with their blocking experiments, our estimates of an effective entrance diameter for wt BK channels of 17.7–20.7 Å would allow tetrabutylammonium (with nonhydrated dimensions of ∼10 × 7.4 Å) to readily enter the inner cavity of BK channels. Further indirect support for a large entrance and large inner cavity for BK channels comes from calculations based on the crystal structure of MthK, suggesting that the resistance for a K⁺ ion diffusing through the inner cavity of MthK to the selectivity filter is low (Jiang et al., 2002b). Similar to BK channels, Contreras et al. (2010) presented experimental data and theoretical calculations suggesting that the majority of the voltage drop in CNG channels is across the selectivity filter rather than across the inner cavity.

The contribution of the resistance of the entrance to the inner cavity toward the considerably lower conductance of other K⁺ channels could be determined using methods similar to those used in this study for BK channels. Such experiments could provide insight into whether differences in conductance between different K⁺ channels arise from differences in the resistance of the entrance to the inner cavity or in other parts of the conduction pathway.

The ring of negative charge doubles single-channel conductance by decreasing both R₁ and R₂

Nimigean et al. (2003) and Brelidze et al. (2003) found that the ring of negative charge at the entrance to the inner cavity doubles the single-channel conductance of wt BK channels because of the electrostatic attraction of K⁺. What is the mechanism of action of the increased K⁺? One possibility is that the increased K⁺ reduces the resistance of the entrance (part 2 represented by R₂ in Fig. 1) sufficiently to double the overall conductance. To explore this possibility, we first calculated the theoretical values for R₁ and R₂ with 150 mM K⁺ for a channel with hypothetical side-chain volumes the same as for glutamate in wt channels, but without negative charge. The hypothetical resistance of R₂ for such a channel would be: R_{2Hypothetical} = 0.581 GΩ = 0.338 GΩ/(1−(8 × 78.3 /1498 ų)), calculated with Eq. A11 and values in Tables I and II (hydrophobic mean values). The total resistance for this hypothetical channel would then be: 5.50 GΩ = R₁ + R_{2Hypothetical} = 4.92 GΩ + 0.581 GΩ, with R₁ from Table II (hydrophobic mean).

Restoring the charge to the entrance by replacing the hypothetical neural side chains with charged wt side chains to obtain E321/E234 channels would then increase the effective K⁺_i at the entrance to 500 mM through electrostatic attraction of K⁺ from the intracellular solution (Brelidze et al., 2003). This threefold increase in K⁺ for wt channels would then be expected to decrease the resistance of R₂ for wt channels to approximately one third of its value compared with 150 mM K⁺ because of the approximately threefold decreased resistivity of the solution.

If the assumption is made that the electrostatically increased K⁺ only reduces R₂, with no effect on R₁, then the total resistance of the wt channel would be 5.11 GΩ, calculated from: 5.11 GΩ = R₁ + R₂ = 4.92 GΩ + 0.581/3 GΩ. A reduction in the total resistance from 5.50 to 5.11 GΩ would increase single-channel currents by ∼7% ((5.50−5.11)/5.50), rather than the doubling that is observed with the ring of negative charge. Even in the unlikely case that the extra K⁺ attracted by the ring of negative charge in wt channels decreased R₂ to 0 Ω, the single-channel currents would increase by only 11% ((5.50−4.92)/5.50) rather than doubling. Hence, reductions of R₂, however great, are not sufficient to double the current.

Consequently, to double the current, the increased K⁺ attracted by the ring of negative charge in wt channels would also need to reduce R₁. The required decrease in R₁ can be calculated as follows. Doubling the current with the ring of negative charge requires decreasing the total channel resistance to half, from 5.50 to 2.75 GΩ. For half the total resistance, 2.75 GΩ = R₁ + R₂ = 4.92 /x + 0.581/3 GΩ. Solving for x to obtain the reduction in R₁ gives: x = 1.92, R₁ = 2.56 GΩ, and R₂ = 0.194 GΩ. Thus, based on the above reasoning, the increased K⁺ attracted by the ring of negative charge would decrease R₁ to ∼50% and R₂ to ∼33% of their values when compared with the values in the absence of the ring of negative charge, with an estimated R₁/R₂ ratio for wt channels of 13.2. Hence, as is the case in the absence of the ring of negative charge (Table II), the resistance of the entrance to the inner cavity in the presence of the ring of negative charge remains small (∼7%) compared with the total resistance of the conduction pathway.

The reduction in R₁ to half of its value by the increased K⁺ attracted by the ring of negative charge could arise from a decreased resistance in parts 1 and 3 of the conduction pathway in Fig. 1 and from a decreased effective resistance of the selectivity filter (part 4). It might be expected from the anticipated geometry that the resistance of parts 1 and 3 of the conduction pathway would be low, just as the resistance of the entrance to the inner cavity is low. Therefore, decreasing the resistance of these segments with the increased K⁺ attracted by the ring of negative charge would be expected to increase single-channel currents, but not sufficiently to double the current. Thus, a major effect of the increased K⁺ attracted by the ring of negative charge in doubling the conductance would be to decrease the apparent resistance of the selectivity filter (Fig. 1, part 4), perhaps through an increased forward rate of K⁺ into the selectivity filter from mass action as a result of the increased K⁺ in the inner cavity. On this basis, limitations in the speed of transfer of K⁺ from the intracellular cavity (Fig. 1, part 3) into the selectivity filter (part 4) would be a major contributor to the apparent resistance of the total conduction pathway for BK channels.

APPENDIX

Estimating the resistance and dimensions of the entrance to the inner cavity

As diagramed in Fig. 1, the passage of K⁺ through the BK channel was modeled with two resistors in series: a variable resistor R₂ that represents the resistance of the entrance to the inner cavity with different-sized side chains, and a fixed resistor R₁ that includes the sum of the resistance of all the remaining segments of the ion conduction pathway. Equations are derived in this section to estimate R₁ and R₂, and also the effective diameter and length of the entrance to the inner cavity from experimental plots of single-channel conductance versus total increase in side-chain volume compared with glycine.

The (total) single-channel resistance R_T is given by the sum of R₁ and R₂, and is related to conductance by

$$R_{\text{T}}=R_{\text{1}}+R_{\text{2}}=\text{1}/g_{\text{T}}=\left(\text{1}/g_{\text{1}}\right)+\left(\text{1}/g_{\text{2}}\right),$$ (A1)

where g_T is (total) single-channel conductance and g₁ and g₂ are the conductances associated with R₁ and R₂, respectively. For the idealized case depicted in Fig. 7 A, where the side chains reduce the volume of the entrance to the inner cavity by decreasing the diameter while spanning the length of the inner cavity,

$$g_{\text{2X}}=g_{\text{2Gly}}\left(\text{1}-F_{\text{X}}\right),$$ (A2)

where g_2X is the conductance of the entrance to the inner cavity with eight substitutions of amino acid X (two on each of the four subunits at positions E321X/E324X), g_2Gly is the conductance of the empty entrance to the inner cavity with glycine substitutions at positions 321/324 (the entrance is considered empty with glycine substitutions), and Fx is the fractional volume of the entrance to the inner cavity occupied by the side chains of amino acid X. Eq. A2 assumes that the conductance of the entrance to the inner cavity decreases linearly as substituted side-chain volume increases. Fx is given by

$$F_{\text{X}}=\text{8}{w}_{\text{X}}/W_{\text{Gly}},$$ (A3)

where w_X is the increase in the side-chain volume of amino acid X compared with glycine (Table I), 8w_X is the total increase in side-chain volume at the entrance to the inner cavity when each of the eight glycines at the entrance is replaced by substitution with amino acid X, and W_Gly is the volume of the empty entrance to the inner cavity with glycine substitutions. W_Gly, g_2Gly, and R_2Gly thus represent the volume, conductance, and resistance of the entrance to the inner cavity when it is empty. When 8w_X = W_Gly, the entrance to the inner cavity is entirely filled with the side chains of the substituted amino acid X, so that g_2X = 0 and R_2X = ∞.

Substitution of Eq. A2 into Eq. A1 with rearrangement gives

$$g_{\text{TX}}=\frac{1}{\frac{1}{g_1}+\frac{1}{g_{\text{2Gly}}(1-F_{\text{X}})}},$$ (A4)

where g_TX is the single-channel conductance with amino acid X substitution. Normalizing the single-channel conductance with amino acid X substitutions to the single-channel conductance with glycine substitutions gives g_TXnor = g_TX/g_TGly, and expressing g₁ and g_2Gly in terms of resistance gives

$$g_{\text{TXnor}}=\frac{\frac{R_1}{R_{\text{2Gly}}}+1}{\frac{R_1}{R_{\text{2Gly}}}+\frac{1}{(1-F_{\text{X}})}}.$$ (A5)

Eq. A5 is used to calculate the theoretical curves for plots of g_TXnor versus the fraction of the entrance to the inner cavity filled with side chains (Fig. 7 B). A different curve is obtained for each R₁/R_2Gly ratio. For the specific case of R₁ = 0 (g₁ = ∞), Eq. A4 reduces to Eq. A2, so that both g_2X and g_TX are equal and decrease linearly as Fx increases, approaching 0 as F_X approaches 1 (Fig. 7 B, purple straight line for R₁/R_2Gly = 0). When R₁ > 0, g_2X still decreases linearly with increasing side-chain volume, but the overall decrease in conductance assumes characteristic shapes depending on the R₁/R_2Gly ratio, as shown in Fig. 7 B for the indicated ratios.

R₁, R_2Gly, and W_Gly are estimated from experimental data by fitting plots of single-channel conductance versus total increased side-chain volume compared with glycine (Fig. 6) with simultaneous Eqs. A1–A4. The length L_Gly and diameter D_Gly of the empty entrance to the inner cavity are related to W_Gly, the volume of the empty entrance with

$$W_{\text{Gly}}=L_{\text{Gly}}\pi D_{\text{Gly}}^2/\text{4},$$ (A6)

and the resistance R_2Gly of the empty entrance is related to L_Gly and D_Gly with

$$R_{\text{2Gly}}=\rho L_{\text{Gly}}/(\pi D_{\text{Gly}}^2/\text{4}),$$ (A7)

where ρ is the resistivity of the solution (Hille, 2001). For a 150-mM KCl solution in which both K⁺ and Cl⁻ carry current, the value of ρ is 80 Ω · cm (Hille, 2001). For BK channels, Cl⁻ does not carry current through the channel (Blatz and Magleby, 1984). Consequently, if Cl⁻ enters the inner cavity, it must exit the same way it entered, so there would be no net flux of Cl⁻ into the inner cavity and no contribution of Cl⁻ to current flow. With half as many ions to carry current, ρ might be expected to double to 160 Ω · cm, which is the value used in the calculations. Solving for L_Gly and D_Gly in Eqs. A6 and A7 gives

$$L_{\text{Gly}}=\sqrt{R_{\text{2Gly}}{W}_{\text{Gly}}/\rho }$$ (A8)

$$D_{Gly}=2\sqrt{W_{\text{Gly}}/\left(\pi L_{\text{Gly}}\right)}.$$ (A9)

Hence, Eqs. A8 and A9 allow unique values of D_Gly and L_Gly to be found using values of R_2Gly and W_Gly obtained from fitting the data in Fig. 6.

Given R_2Gly and W_Gly, the volume of the entrance to the inner cavity with amino acid X substitutions, W_X, can be calculated from

$$W_{\text{X}}=W_{\text{Gly}}-\text{8}{w}_{\text{X}},$$ (A10)

and R_2X can be calculated with Eqs. A1–A3 to obtain

$$R_{\text{2X}}=R_{\text{2Gly}}/\left(\text{1}-\text{8}{w}_{\text{X}}/W_{\text{Gly}}\right).$$ (A11)

W_X and R_2X can then be used with Eqs. A8 and A9 with subscript Gly in the equations replaced by subscript X to calculate the effective length and diameter of the entrance to the inner cavity for amino acid X substitutions. It can be shown by substitution of Eqs. A10 and A11 into Eq. A8 that the effective length L_X for any amino acid X substitution is the same as L_Gly for glycine substitution. In contrast, the effective diameter decreases as the volume of the side chain for amino acid X increases.

Correcting for the hydrated diameter of K⁺

The above equations assume that K⁺ is a point charge with no volume and no waters of hydration. K⁺ itself has a diameter of 2.66 Å, and this diameter is increased by the waters of hydration. Experimental and molecular dynamics estimates of the number of waters of hydration for K⁺ range from ∼3 to 7.6 (Enderby, 1995; Hille, 2001), with as many as eight in crystal structures (Zhou et al., 2001). Estimates of the effective hydrated diameter for K⁺ typically range from 3.6 to 6.6 Å (Enderby, 1995; Hille, 2001; Kiriukhin and Collins, 2002; Tansel et al., 2006). Table II presents calculated effective diameters of the entrance to the inner cavity assuming K⁺ is a point charge and that the entrance is cylindrical. The data were presented in this manner because of uncertainty in the effective hydrated diameter of K⁺ at the entrance to the inner cavity. To obtain estimates of the effective physical diameter of the entrance to the inner cavity, the entrance diameters calculated with the above equations and listed in Table II need to be increased by the hydrated diameter of K⁺, similar to increasing the capture radius calculated assuming a point charge by the hydrated radius of K⁺ (Andersen, 1983).

The effective diameters for the entrances to the inner cavity in Fig. 8 (green cylinders) were calculated using a 3.6-Å dimension for the hydrated diameter of K⁺. Using a 6.6-Å estimate would increase the calculated effective diameters by 3 Å, which would still be generally consistent with the structure of MthK.

Effective dimensions for the entrance to the inner cavity

All estimated dimensions for the entrance to the inner cavity must be viewed as effective dimensions because the structure of the entrance to the inner cavity for MthK channels (Fig. 8), and presumably for BK channels, deviates from an idealized cylindrical structure. In addition, four side portals lead to the entrance for both MthK (Fig. 8) and BK (Zhang et al., 2009). These side portals could increase the effective diameter of the entrance compared with the narrowest physical diameter by allowing K⁺ to enter the entrance from the four sides. In addition, the substituted side chains will not necessarily change the entrance volume as depicted in the idealized cartoons in Fig. 7 A, as assumed for deriving the equations.