Metapopulation dynamics of rabies and the efficacy of vaccination

Abstract

Spatial structure in a host population results in heterogeneity in transmission dynamics. We used a Bayesian framework to evaluate competing metapopulation models of rabies transmission among domestic dog populations in villages in Tanzania. A proximate indicator of disease, medical records of animal-bite injuries, is used to infer the occurrence (presence/absence) of suspected rabid dog cases in one month intervals. State-space models were used to explore the implications of different levels of reporting probability on model parameter estimates. We find evidence for a relatively high rate of infection of these populations from neighbouring districts or from other species distributed throughout the study area, rather than from adjacent wildlife protected areas, suggesting wildlife is unlikely to be implicated in the long-term persistence of rabies. Stochastic simulation of our highest ranked models in vaccinated and hypothetical unvaccinated populations indicated that pulsed vaccination campaigns occurring from 2002 to 2007 reduced rabies occurrence by 57.3 per cent in vaccinated villages in the 1 year following each pulse, and that a similar regional campaign would deliver an 80.9 per cent reduction in occurrence. This work demonstrates how a relatively coarse, proximate sentinel of rabies infection is useful for making inferences about spatial disease dynamics and the efficacy of control measures.

1. Introduction

Rabies exerts a major public health and economic burden: it is responsible for 55 000 deaths worldwide (predominantly in Africa and Asia), and expenditure on treatment and control exceeds US$500 million per annum [1,2]. Although effective post-exposure prophylaxis exists, it is expensive, often scarce, and must be administered shortly after exposure to be effective, and therefore such treatment is problematic in developing countries. Yet, rabies is a pathogen that can be effectively controlled or eliminated by vaccinating hosts [3]. Rabies virus is a multi-host pathogen that infects a wide range of mammals [4] and is therefore also an important threat to animal populations of conservation concern [5–7]. A single rabies epidemic can eliminate a large proportion of a population [8,9]. Our interest in rabies control is, therefore, motivated by both human health and conservation concerns.

Epidemiological models are frequently used to estimate basic parameters [10], evaluate alternative control strategies [11–14] and set levels for control measures such as vaccination [3,9,15], culling [16] or quarantine/isolation [17]. However, many applications of epidemiological models to disease control apply to human or agricultural systems where detailed information about movement, transmission, and host populations is available (e.g. [16,18–20]). This quantity and quality of epidemiological data are usually unavailable for diseases in developing regions where formal monitoring, reporting and diagnosis can be ineffectual or absent [2].

Limited availability of epidemiological data can be addressed in two ways. First, theoretical or general models can be used to explore the relative efficacy of different control strategies, and to devise approximate rules for setting control targets (e.g. [3,14,21,22]). For instance, one frequently used approximation of the proportion of a population that must be vaccinated to reduce the basic reproductive number, R₀, below 1 is 1 − 1/R₀ [10]. The second approach is to collect epidemiological data, which is often difficult and costly. This approach is typically applied to the development of non-spatial models (e.g. [15,23,24]) because spatial models require the estimation of more parameters and, therefore, require more extensive data collection. Also, although valuable, detailed individual-level epidemiological data (e.g. diagnostic tissue testing, sequence data and case histories) often cannot be collected retrospectively or over large areas.

Disease dynamics and the efficacy of control measures are, however, influenced by the spatial distribution of the host populations and interventions. Spatial structuring of the host population resulting from social organization or a patchy physical environment violates the assumption of many simple models that the population is well mixed. Metapopulation models explicitly model this spatial structure as a system of loosely coupled discrete populations or patches with different rates for within- and between-patch transmission [25–28]. Disease persistence in the metapopulation is profoundly influenced by these spatial dynamics [29,30]. Thus, the promise of spatially explicit epidemiological models is that, because they are locale-specific and capture some of the spatial dynamics of transmission, they allow us to maximize the efficacy of control designs and, therefore, the deployment of limited control resources.

Our focus is the control of rabies in a multi-host African ecosystem (Serengeti District (SD), Tanzania) in which domestic dogs are thought to be the disease reservoir [31] and are, therefore, the target of control measures (vaccination). This study presents methods for using an existing, indirect measure of disease occurrence (medical records of animal-bite injuries) to parametrize and evaluate competing spatially explicit models of disease occurrence and transmission among dogs at a regional scale, and to quantify the efficacy of a control programme. Although insights into the transmission dynamics of rabies in domestic dogs have been presented previously [23,32], the spatial dynamics at a more regional scale are still poorly understood, yet important because control measures are often targeted at these larger scales. We also evaluate evidence for three hypothesized sources of infection of the domestic dog population because of their importance to maintaining a disease-free state: infected domestic dogs from neighbouring (unmodelled) districts, interactions with wildlife originating from neighbouring wildlife protected areas and inter-species transmission with other hosts (domesticated and wild) occurring throughout the district.

2. Methods

(a). Assessing the occurrence of rabies

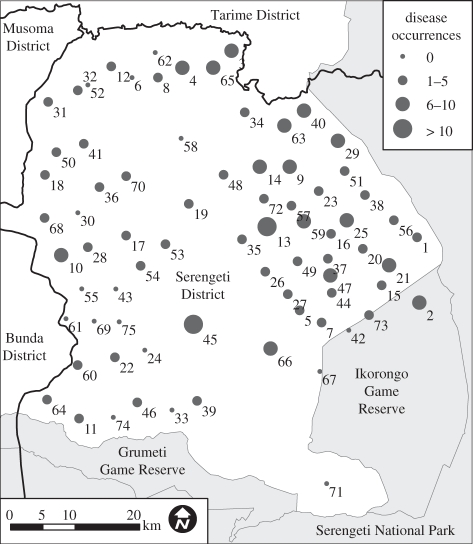
This study took place in SD, northern Tanzania, which borders wildlife protected areas to the south and east (Serengeti National Park and the Ikorongo and Grumeti Game Reserves), and other inhabited districts to the north and west (Bunda, Musoma and Tarime Districts). SD consists of 75 villages (figure 1 and electronic supplementary material, table A.1) and is inhabited by approximately 174 400 people (Population and Housing Census of Tanzania 2002) in primarily agro-pastoralist communities that use domestic dogs for guarding households and livestock.

Figure 1.

The total number of occurrences of rabies observed (2002–2007) among the 75 villages in Serengeti District, Tanzania, whereby an occurrence is defined as the presence of at least one suspected rabid dog in a village in a one month period. The district is bordered by wildlife protected areas (grey) to the south and east, and other inhabited districts (white) to the north and west. Black lines depict district boundaries. Village names (indexed by the village ID numbers shown) are included in the electronic supplementary material, table A.1.

Medical records of patients reporting with animal-bite injuries were collected from local hospitals and medical dispensaries and were used to identify bites from suspected rabid dogs [32–35]. Most records indicate the bite date, biting animal and village from which a patient reported. There are also several other ways in which medical records may misrepresent actual cases of rabies in domestic dogs: not all rabid dogs bite humans, bite victims do not always report to hospital and possible misidentification of whether an animal was rabid, and records generally do not indicate whether patients were reporting because of bites by the same dog, if this is known. We interpreted bite records conservatively, therefore, and explicitly modelled the effects of uncertainty in detection using a state-space modelling framework.

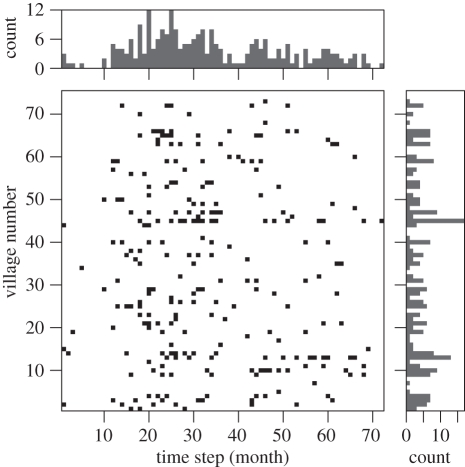
We summarized the occurrence (presence or absence) of exposures by suspected rabid dogs in one month intervals in each village over a 6 year period (2002–2007). A one month interval was used because some medical records can only be dated to the month in which they occur and, given the incubation period averages 22.3 days [32], a transmission event in one month is likely to result in an infectious case the following month. The justification for a presence–absence representation is that most of the time (89%) an occurrence reflects just one or two bite records in that month. Furthermore, as a single infectious dog can bite several people (30% of rabid dogs that bite people bite at least two people and 3% bite five or more), multiple bite records may often only correspond to a single infectious dog. Although an occurrence may sometimes correspond to the presence of more than one infectious dog in that month, the number of infectious dogs in any one month period is likely to be low. We identified 243 monthly occurrences of rabies among all 75 villages and across all 72 months (figure 2).

Figure 2.

Graphical depiction of rabies occurrence (black squares) among the 75 villages in Serengeti District, Tanzania, over a 6 year period (2002–2007). Villages are ordered alphabetically (y-axis), and occurrence is quantified in one month intervals (x-axis). The histograms (top and right subplots) summarize the pattern of occurrence among villages and time periods, respectively.

(b). Dog demography and vaccination history

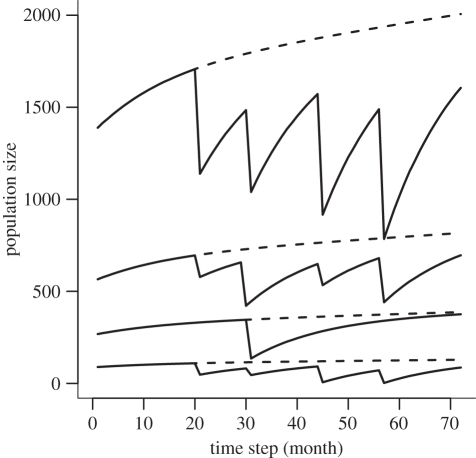
The initial number of susceptible dogs in each village in January 2002 was estimated based on the human population size and the average number of dogs per household in this region [31,36], and the numbers of dogs vaccinated. The number of susceptible dogs in subsequent months (figure 3) was modelled as a function of the birth and death rate, the number of dogs vaccinated during vaccination campaigns and the rate at which vaccination coverage wanes (see [32] for details).

Figure 3.

The estimated population size of susceptible dogs (solid lines) in four representative villages from 2002 to 2007. Declines in population numbers result from vaccination of dogs, and increases result from both population growth and the waning of vaccination. Included are villages with the smallest, largest and two intermediate dog populations. The dashed line represents the estimated population of susceptible dogs in the absence of vaccination.

Following an initial vaccination campaign in 2000 that resulted in low (35–40%) and patchy coverage, subsequent campaigns targeted villages within 10 km of the wildlife protected areas (figure 1) and increased coverage levels to between 40 and 80 per cent [32]. Specifically, there were four vaccination campaigns: August 2003 (4179 dogs, 33 villages), June/July 2004 (12 975 dogs, 67 villages), August/September 2005 (7998 dogs, 39 villages) and August/September 2006 (8030 dogs, 36 villages).

(c). Modelling disease dynamics

Rabies infections are characterized by an incubation period when the animal is infected but not infectious and exhibits no clinical signs, and an invariably fatal infectious period where the animal displays the clinical signs of rabies and can transmit the virus in its saliva to uninfected animals. In domestic dogs in this region, the mean duration of the incubation and infectious periods are 22.3 (95% CI: 20.0–25.0 days) and 3.1 days (95% CI: 2.9–3.4 days), respectively [32]. We assume, therefore, that transmission from a village with infectious animals results in incubating animals in the same one month time step (t), which become infectious animals in the next time step (t + 1).

We define H as the matrix of observed occupancy in each village and time step, which is a function of the unobserved, true occupancy matrix, I, and the probability of detection of an occurrence (ρ):

2.1

If disease was present, it was observed with probability ρ, but if disease was absent, it could not have been observed. If reporting is perfect (ρ = 1), then H = I. The probability of detecting infectious dogs based on medical records is influenced by a complex interaction among human social and educational factors, dog behaviour and record quality. Our detection parameter, ρ, encapsulates all of this uncertainty in the simplest possible (one parameter) data model as we have no quantitative basis for developing a more complex model.

The probability of transmission of infection depends on the number of contacts between infectious and susceptible individuals. We hypothesize that contact rates among dogs scale with the dog population size (S) of each village, which we approximate using the susceptible dog population estimate described above, and the distance (d) between villages. Larger populations of dogs may be more likely to receive infection because they represent larger infection targets: there is a greater probability that an infectious dog will encounter a susceptible dog. Larger villages may also be more likely to both receive and transmit infection as they are local centres of human activity (e.g. markets) that could increase contact rates among dogs from different villages. Although an occurrence usually corresponds to a single infectious dog, it is plausible that occurrences in larger dog populations are sometimes characterized by more than one case simply because larger populations are associated with larger outbreaks. More infectious cases would result in increased risk of transmission. We test the hypotheses, therefore, that transmission is negatively associated with distance between villages, that larger populations of dogs are more likely to encounter infectious animals and acquire infection and that larger populations of dogs are more likely to transmit infection.

The infectious state, I, of the ith village at time t is modelled using an exponential distribution:

2.2

where c is the hazard rate. The full transmission model is

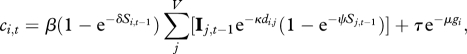2.3

where V is the total number of villages, d_i,j is the Euclidean distance between the centres of ith and jth villages (km) and S is the number of dogs in the village receiving (S_i,t) or transmitting (S_j,t) infection. Transmission is conditional on the village transmitting infection having infectious dogs (I_{j,t − 1} = 1). The parameters κ, δ and ψ determine the relative contribution of the distance between villages and the size of the receiving and transmitting village to the probability of acquiring infection. Infections from outside the system are modelled using τe^−μg_i, where τ is proportional to the rate of infection, and μ scales τ as a function of distance to the source of infection (g). Thus, for each village, there is a fixed risk of infection from external sources and, when there is infection present within the system, an additional risk of acquiring infection that depends upon the distances to the villages with infectious dogs, and the dog population sizes of villages transmitting and receiving infection.

We identify three competing models. Model 1 includes only the distance component:

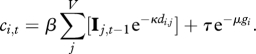2.4

Model 2 includes the distance and size of the receiving village components:

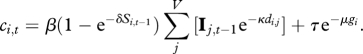2.5

Model 3 is the full model (equation (2.3)). We also fit a reference model (model 0) where β is the only parameter (c_i,t = β) to gauge the performance of the three competing models. The implication of the reference model is that all infection arises randomly, with no inter-village transmission and no population size effects.

There are three hypothesized sources of external infections: spill-over infections from species that occur throughout SD indicated by randomly distributed infections (‘R’), wildlife protected areas (‘P’) to the east and south, or the inhabited adjacent districts (‘D’) to the north and west (figure 1). For source R, μ = 0, and τ represents the rate at which a village acquires infection from an external source per time step. For sources P and D, g_i represents the distance to the protected area boundary or nearest adjacent district boundary, respectively (km). In these models, μ was allowed to vary as a free parameter, and τ was calculated deterministically so that the overall rate of external infection among all villages remained constant. For all sources, we evaluated rates of external infections of two, six and 10 infections per year, which we consider to span the range of low to high estimates of the true rate of external infection. This rate is difficult to estimate empirically; therefore, we selected three rates that allow us to make a qualitative assessment of the impact of different rates of external infection on model dynamics.

Models were fit using WinBUGS [37] using uninformative prior distributions (β ∼ U(−4, 0), κ ∼ U(0, 0.5), μ ∼ U(0, 0.7), δ ∼ U(−8, − 2), ψ ∼ U(−8, − 2)). For β, δ and ψ , the prior distributions were log-transformed so that the posterior distribution was approximately normally distributed, which facilitates the estimation of the effective number of parameters (pD) for model comparison. We generated 37 500 samples from the posterior distributions of all parameters using three chains, a burn-in period of 200 samples and a conservative thinning rate of 1 : 50 to ensure the resulting 750 samples were not autocorrelated. Chain convergence was quantified using the R̂ statistic (values close to 1.0 indicate convergence). Models were ranked using deviance information criteria (DIC) [38]. Model validation was based on 1000 stochastic simulations of the highest ranked models using the mean estimated parameter values for each model. For each simulation, the frequencies of occurrences of rabies in each village over the 6 year period were ranked in ascending order, and these ranked distributions were used to quantify the expected mean and 95% CI, which was compared with the observed data. We use state-space models to evaluate how reporting error influences parameter estimation in the highest ranked models (processing time constraints prevented us from running all models as state-space models). The transmission component of the models remained the same, but we evaluate reporting probabilities of ρ = 0.6 and ρ = 0.8.

We use 1000 stochastic simulations of each of the four highest ranked models to quantify the efficacy of pulsed SD vaccination campaigns that occurred from 2002 to 2007 [32]. Using the mean parameter values for each model, occurrence of rabies was quantified in three scenarios: unvaccinated populations, vaccinated populations with a continuing external infection source and vaccinated populations with an external infection source that ends six months after the first set of vaccinations. The last scenario corresponds to hypothesized vaccination at a regional scale that eliminates cross-district transmission, or that reduces the incidence of rabies in other species that could then infect dogs. For the unvaccinated population scenario, the number of susceptible dogs was estimated based on the vaccination history and demographic parameters (figure 3). The difference in overall disease occurrence (the total number of months in which disease is observed) between the vaccinated and unvaccinated population simulations is a measure of the expected efficacy of vaccination. We measured efficacy among the villages targeted for vaccination in the 12 month period following a vaccination campaign, and over the entire district from the first month in which vaccination occurred until the end of the study period. Simulations were initialized by randomly assigning infections to three villages in the first time step, then running the simulation over a 72 month burn-in period with constant population sizes (these data were discarded) before recording simulated occurrence over the following 72 month period in which population sizes varied as described above. These simulations were performed in R [39].

3. Results

We obtained good chain convergence for all models (R̂ < 1.1 for all variables in all models). Sampling the prior distributions for β, δ and ψ on a log-transformed scale was essential for obtaining reasonable estimates of the effective number of parameters (pD).

Of the 28 models tested (table 1), the highest ranked model included a probability of transmission that was a function of both inter-village distance and the number of dogs in the village receiving infection, and where the probability of acquiring an external infection declined as a function of distance to neighbouring districts. However, three other models performed similarly well (ΔDIC < 2 relative to the top model) and therefore also warrant consideration. We infer from these four models that there is strong support for the role of village distances and the size of the village receiving infection in driving transmission dynamics (components of all four top-ranked models), but weaker support for the role of the size of the village transmitting infection (a component only of the models ranked third and fourth).

Table 1.

Summary of competing patch-occupancy models, the number of parameters in the model, the effective number of parameters (pD) and the difference in the deviance information criteria value (ΔDIC) relative to the highest ranked model (DIC = 1839).

model	source	rate	parameters (free/fixed)	pD	ΔDIC
2	D	10	5 (3, 2)	3.32	0
3	D	10	6 (4, 2)	3.67	0.69
2	R	10	4 (3, 1)	2.44	0.71
3	R	10	5 (4, 1)	2.67	1.22
2	P	10	5 (3, 2)	3.08	3.95
3	P	10	6 (4, 2)	3.33	4.50
2	D	6	5 (3, 2)	3.29	11.4
3	D	6	6 (4, 2)	3.53	11.9
2	R	6	4 (3, 1)	2.44	13.5
3	R	6	5 (4, 1)	2.66	14.0
2	P	6	5 (3, 2)	3.23	16.4
3	P	6	6 (4, 2)	3.56	17.1
2	D	2	5 (3, 2)	3.32	45.1
3	D	2	6 (4, 2)	3.58	45.6
2	R	2	4 (3, 1)	2.31	48.2
3	R	2	5 (4, 1)	2.65	48.9
2	P	2	5 (3, 2)	3.16	50.1
3	P	2	6 (4, 2)	3.60	51.1
1	R	10	3 (2, 1)	1.88	61.8
1	D	10	4 (2, 2)	2.96	62.9
1	P	10	4 (2, 2)	2.84	66.9
1	D	6	4 (2, 2)	2.90	78.2
1	R	6	3 (2, 1)	1.91	78.4
1	P	6	4 (2, 2)	2.71	81.8
1	D	2	4 (2, 2)	2.86	114.0
1	R	2	3 (2, 1)	1.95	116.0
1	P	2	4 (2, 2)	2.81	118.2
0	R	0	1 (1, 0)	0.97	123.2

Overall, there was most support for the district source of external infection (table 1), especially at the lowest rate of infection (2 per year). At the higher rates of infection, the district and random-source models of external infection performed similarly: although the district model had a lower DIC value in five out of six comparisons (models 1–3, for rates 6 and 10 per year), the difference was generally less than 2. We found only weak support for the wildlife protected area source models, which consistently ranked lower than the other source models for each model and rate combination.

There was also strongest support for the highest rate of external infection (table 1). On average, 10 external infections per year would account for 24.7 per cent (60 of 243 over the 6 year study period) of all observed occurrences (we reiterate that occurrence is not a direct measure of incidence). However, the inferences regarding the source of external infection and the important components of transmission dynamics were consistent among the three external infection rates (table 1).

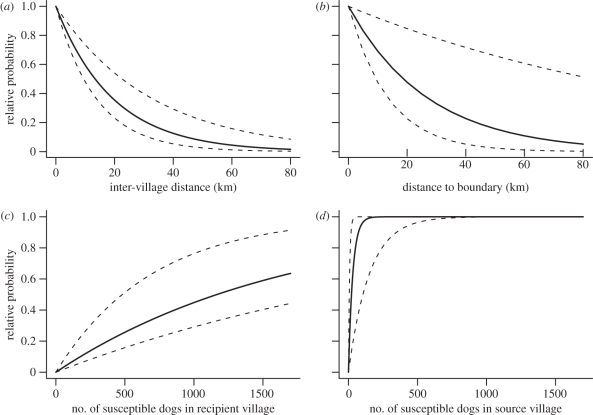
Although the highest ranked models have different structures and, therefore, do not all share the same set of parameters, there was high consistency in parameter values among these models (table 2 and the electronic supplementary material, table A.2). The implications of the parameter values on the probability of transmission are shown in figure 4. Although this figure is based on the parameter values of the most complex model, which ranked second, it is representative for all four top-ranked models. For all models, the probability of transmission is negatively associated with the distance between villages and positively associated with the population size of dogs in the village receiving transmission. The probability of acquiring external infection declines with distance from the district boundary in the district-source models. Finally, the population size of dogs in the village transmitting infection is important only for small populations, whereby very small populations (less than 150 dogs) have a lower probability of transmission. Validation based on stochastic simulations indicate that, of the 75 villages, all but 3, 3, 1 and 2 villages in the four highest ranked models, respectively, fell within the 95% CI of the expected values (electronic supplementary material, figure A.1). These exceptions exceeded the upper 95% CI by a count of one occupancy in all cases.

Table 2.

Estimated mean parameter values and 95% CI for the four highest ranked rabies disease transmission models. (A dash represents a model in which that parameter was omitted. The full table is provided in the electronic supplementary material, table A.2.)

model	infection source	β × 10−1 (95% CI)	κ × 10−2 (95% CI)	δ × 10−3 (95% CI)	ψ × 10−1 (95% CI)	μ×10−1 (95% CI)
2	R	2.11 (0.923, 4.31)	5.28 (2.89, 7.75)	0.608	—	—
2	D	2.14 (0.936, 4.46)	5.23 (3.06, 7.76)	0.603 (0.344, 1.47)	—	0.365 (0.0858, 0.734)
3	R	2.15 (0.889, 4.55)	5.25 (2.90, 7.72)	0.607 (0.343, 1.63)	0.319 (0.0604, 1.21)	—
3	D	2.19 (0.884, 4.31)	5.16 (2.88, 7.55)	0.591 (0.346, 1.50)	0.334 (0.0607, 1.28)	0.369 (0.0826, 0.743)

Figure 4.

The relative probability of transmission between villages is negatively associated with (a) distance between villages and (b) distance to neighbouring districts, and positively associated with the population size of dogs in the village (c) receiving and (d) transmitting infection (table 2). The mean (solid lines) and 95% CI (dashed lines) are based on parameter estimates for κ, μ, δ and ψ (table 2) for the most complex model (ranked second), but are representative of all the models because of the consistency in parameter estimates among models.

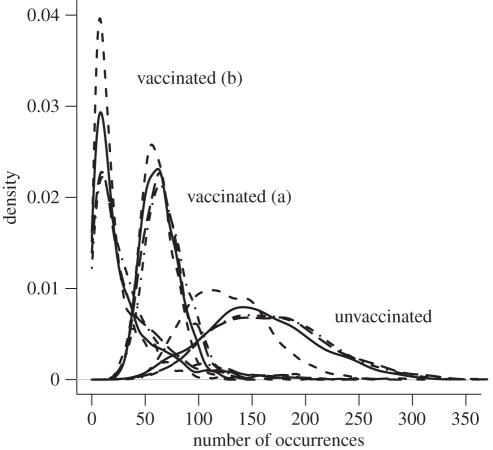
Within the set of villages that were targeted for vaccination (all but five of the 75 villages in SD) and in the 12 month period following a vaccination campaign, vaccination reduced the occurrence of rabies by 57.3 per cent (59.0, 51.9, 60.0 and 58.1% for the four highest ranked models, respectively) relative to the occurrence predicted if no vaccination had occurred (figure 5). Under the alternative assumption that regional-scale vaccination occurred (thereby eliminating the external infection source after six months), vaccination reduced the occurrence of rabies by 80.9 per cent (81.7, 83.9, 79.0 and 78.9%, respectively) relative to the unvaccinated population. Vaccination also reduced the variance in the size of outbreaks (for instance, the standard deviation in the count of occurrences was reduced from 51.4, 38.6, 54.8 and 51.7 to 17.4, 16.0, 19.1 and 19.4, respectively, for each of the four highest ranked models). Over the entire district, and including all months following the first vaccination campaign, vaccination reduced the occurrence of rabies by 50.0 per cent (51.0, 44.9, 52.6 and 51.5%, respectively), and assuming regional-scale vaccination, the occurrence of rabies was reduced by 81.7 per cent (82.2, 84.1, 80.3 and 80.3%, respectively).

Figure 5.

Frequency of disease occurrence based on 1000 stochastic simulations of the four highest ranking models (different line styles) among the 75 villages in Serengeti District. To quantify vaccination efficacy, rabies occurrence was quantified in unvaccinated populations, vaccinated populations with a continuing external infection source (a) and vaccinated populations with an external infection source that ends six months after the first set of vaccinations (b). Occurrence was summed among villages targeted for vaccination (all but five of the 75 villages) for the 12 month period following a vaccination campaign in each village. Solid line, model 1; short dashed line, model 2; large dashed line, model 3; dashed-dotted line, model 4.

Explicitly assuming that the reporting probability is only 60 or 80 per cent relative to perfect reporting (100%) resulted in a marginal increase in the estimates of all parameters (electronic supplementary material, figure A.2 and table A.3). This corresponds to a reduction in the spatial transmission kernel (a reduced probability of transmission over longer inter-village distances), and an increase in the probability of a village receiving infection as population size increases, for all four top-ranked models. For the models with the neighbouring district source of infection, there was a decrease in the spatial transmission kernel from that source. Finally, there was also a reduced effect of population size on the probability of transmission from a source village in model 3 (the full model).

4. Discussion

This work demonstrates that a relatively coarse, proximate sentinel (i.e. medical records of animal-bite injuries) of rabies infection can be used to make inferences about spatial transmission dynamics of rabies and the efficacy of control measures. This has important practical implications for identifying drivers of disease transmission, and the design and assessment of control protocols when only limited, indirect epidemiological and demographic data are available. Medical bite records are widely available in Tanzania (and many other countries), and therefore, if they are sufficient to make useful epidemiological inferences, then much progress could be made using information that is already available without necessarily prioritizing further investment in the acquisition of expensive surveillance data.

Although there are several examples of the application of epidemiological models to rabies control problems in Africa (e.g. [15,23,24]), none of them are spatially explicit. While non-spatial models provide approximate rules for control measure targets (e.g. the proportion of a population that must be vaccinated to reduce R₀ below 1 is 1 − 1/R₀), the efficacy of controls in a specific context (such as SD) is influenced by the spatial distribution of the host population, of other host populations and of control measures. The promise of spatially explicit models is the potential to maximize the efficacy of controls in a specific circumstance, thereby optimizing the deployment of limited intervention resources. Moreover, these models provide novel insights into the importance of local population size and coupling, and proximity to wildlife host species on disease dynamics. Developing a detailed, more mechanistic understanding of disease dynamics also provides new opportunities for understanding how disease dynamics in different regional contexts may differ.

Spatially explicit models can also provide insight into drivers of regional-scale transmission dynamics. A subjective interpretation of the spatial distribution of rabies occurrences (figure 1), which is highest near the wildlife protected areas, might conclude that infection of the domestic dog reservoir from wildlife in these protected areas was implicated in long-term disease persistence. However, our models demonstrate that, once inter-village transmission dynamics are accounted for, there is only weak evidence of a link between the protected areas and infection of dogs. There is stronger evidence that the source of infection is the inhabited neighbouring districts, or that a source of infection is distributed randomly throughout the district. Both of these hypotheses are plausible and consistent with previous studies in this region that indicate domestic dogs are the reservoir for rabies [23,31]. Inter-district infection could result from movement of infected domestic dogs, either on foot or in vehicles. Randomly distributed within-district infection could result from inter-specific transmission between several species, e.g. Lembo et al. [31] report rabies in domestic cats and eight wild carnivore species in that region.

However, it is not clear to what extent other wild and domestic species contribute to disease persistence. Our models indicate that the rate of external infection in the SD dog population may be quite high, although this rate includes transmission from domestic dogs in adjacent districts and is therefore not specific to wildlife. An external infection rate of 10 occupancies per year would, on average, account for 60 of the 243 occupancies observed (24.7%), implying that inter-village transmissions are only four times more common than transmissions from external sources. Lembo et al. [31] estimate that dog to dog transmissions are approximately eight times as common as transmissions between dogs and other carnivores; therefore, occasional infection of the dog population from wildlife is plausible. If vaccination reduces the reservoir dog population below the critical threshold required for endemic rabies to persist, then this should also eliminate rabies outbreaks in other species and remove one source of infection of the dog population. Improving our understanding of inter-species transmission rates is a priority for future work.

Some infection events could result from rare, long incubation periods in some cases of rabies. While the mean incubation period is typically 22.3 days (95% CI: 20–25 days) [32], incubation periods of months or years are possible, although rare, in mammalian hosts [4]. Our model does not allow for a low frequency of long incubation periods, and this could account for some of the observed occupancies (figure 2), implying the frequency of transmission events between villages or from the external source may be overestimated in our models.

Assessing the efficacy of vaccination is not straightforward because disease transmission is a stochastic process that can result in highly variable spatial and temporal patterns of occurrence. Field observations of occurrence before and after vaccination provides an important measure of the realized efficacy, but this measure is based on only a single realization of a stochastic process and therefore may not be a good representation of the efficacy that would be expected in general. Our approach, using stochastic simulations of the vaccinated population and a hypothetical, unvaccinated population, provides an estimate of the expected efficacy resulting from the pulsed vaccination campaigns that took place between 2002–2007. This measure of expected efficacy may be more relevant when planning future interventions as it describes the expected mean reduction in occurrence resulting from the vaccination campaigns.

Although we found that the four vaccination campaigns between 2002 and 2007 resulted in a 57.3 per cent (or 80.9% assuming a regional-scale vaccination programme) decrease in our measure of occurrence, it is important to recognize that the reduction in incidence will be greater than this. Mean outbreak size is positively associated with the number of susceptible dogs [32]; therefore, occurrence in the unvaccinated populations is likely to correspond to a larger number of infectious dogs than occurrence in the vaccinated populations. This nonlinear relationship between our measure of occurrence and outbreak size implies that the estimate of the efficacy of the vaccination campaigns would be higher if we were able to monitor incidence at the individual animal level. For instance, Cleaveland et al. [34] estimate that vaccination campaigns in SD in the decade prior to this study reduced the incidence of rabies by approximately 90 per cent based on the incidence of bites of humans by suspected rabid dogs.

These models suggest a potentially complex relationship between vaccination coverage levels and the reduction in disease occurrence. As expected, we found strong evidence that the population size of dogs was an important predictor of the probability of transmission: smaller populations were less likely to acquire infection, and this effect was approximately linear. However, we also found support for a strong reduction in the probability of transmission in small populations (fewer than 150 dogs), indicating a possible threshold beyond which vaccination may have increasing benefits. A possible explanation of this effect is that the density of susceptible dogs may become so low in these highly vaccinated populations that fade-out of the disease becomes increasingly likely. Alternatively, this effect could result from human social factors that might vary as a function of population size. Understanding this effect warrants further investigation as it has the potential to be exploited to improve disease management.

The most ambitious zoonotic disease control programmes aim to achieve disease eradication at regional scales. Although we have used our four highest ranked models to quantify the efficacy of the pulsed vaccination campaigns (2002–2007), there is clearly scope to apply them to optimize the design of vaccination programmes in metapopulations [40], to design responses to subsequent disease outbreaks in disease-free populations, and to predict what the large-scale implications of intervention actions might be. The application of metapopulation models to inform management decisions has the potential to increase both the efficacy and cost-effectiveness of control and eradication programmes.

State-space models provided a rigorous method for quantifying the effect of measurement error on parameter estimates and model inferences. Because processing times were considerable, we evaluated the influence of measurement error only on the highest ranked models and suggest this approach provided a reasonable trade-off between expediency and confidence in inferences. Metapopulation models provide a powerful framework for investigating disease dynamics in spatially structured populations, and for evaluating the efficacy of control strategies. This work demonstrates that these powerful models can be developed based on proximate measures of disease occurrence when more specific and detailed epidemiological data are unavailable.