The cardiac output from blood pressure algorithms trial*

Abstract

Objective

The value of different algorithms that estimate cardiac output (CO) by analysis of a peripheral arterial blood pressure (ABP) waveform has not been definitively identified. In this investigation, we developed a testing data set containing a large number of radial ABP waveform segments and contemporaneous reference CO by thermodilution measurements, collected in an intensive care unit (ICU) patient population during routine clinical operations. We employed this data set to evaluate a set of investigational algorithms, and to establish a public resource for the meaningful comparison of alternative CO-from-ABP algorithms.

Design

A retrospective comparative analysis of eight investigational CO-from-ABP algorithms using the Multiparameter Intelligent Monitoring in Intensive Care II database.

Setting

Mixed medical/surgical ICU of a university hospital.

Patients

A total of 120 cases.

Interventions

None.

Measurements

CO estimated by eight investigational CO-from-ABP algorithms, and CO_TD as a reference.

Main Results

All investigational methods were significantly better than mean arterial pressure (MAP) at estimating direction changes in CO_TD. Only the formula proposed by Liljestrand and Zander in 1928 was a significantly better quantitative estimator of CO_TD compared with MAP (95% limits-of-agreement with CO_TD: –1.76/+1.41 L/min versus –2.20/+1.82 L/min, respectively; p < 0.001, per the Kolmogorov-Smirnov test). The Liljestrand method was even more accurate when applied to the cleanest ABP waveforms. Other investigational algorithms were not significantly superior to MAP as quantitative estimators of CO.

Conclusions

Based on ABP data recorded during routine intensive care unit (ICU) operations, the Liljestrand and Zander method is a better estimator of CO_TD than MAP alone. Our attempts to fully replicate commercially-available methods were unsuccessful, and these methods could not be evaluated. However, the data set is publicly and freely available, and developers and vendors of CO-from-ABP algorithms are invited to test their methods using these data.

Cardiac output (CO) is a cardinal parameter of cardiovascular state, and a fundamental determinant of global oxygen delivery. Historically, routine clinical measurement of CO has been limited to critically-ill patients, often with invasive indicator-dilution methods such as thermodilution (CO_TD). Alternative CO measurement strategies have not replaced indicator-dilution methods in critical care, and outside the intensive care unit, imprecise metrics (e.g., blood pressure, urine output, mental status, etc.) are used to assess CO and circulatory adequacy.

For more than a century (1), the premise that relative changes in CO could be estimated by analysis of the arterial blood pressure (ABP) waveform has captured the attention of many investigators. Today, peripheral ABP is routinely available in intensive care unit (ICU) patients, and noninvasive devices exist to measure peripheral ABP in noncritically-ill populations (2,3). Tracking changes in CO continuously via ABP waveform analysis, without the risks of central catheterization, may be valuable both within and beyond the ICU setting: such a “vital sign” might be a sensitive and specific indicator of circulatory pathology and useful in optimizing therapies such as volume resuscitation and catecholamine infusions. Today, several commercially-available methods offer competing algorithms that derive CO from the ABP waveform (4–6). Other algorithms have been proposed in the medical literature but not incorporated into commercial products (7–13). There are major challenges that each of these algorithms must confront to accurately estimate global blood flow from a peripheral blood pressure waveform. For instance, the relationship between arterial pressure and volume (i.e., compliance) varies from person to person, and for any given individual, compliance also varies as a nonlinear function of ABP and adrenergic state. Furthermore, the pressure pulse represents the superposition of antegrade waves that drive forward flow as well as retrograde reflected waves that retard forward flow. To date, the relative capability of the various algorithms is difficult to ascertain, because published evaluations are performed in different sets of patients with different physiologic ranges and different pathologies, making direct comparisons between studies problematic.

In this investigation, we used a subset of the Multiparameter Intelligent Monitoring in Intensive Care II (MIMIC II) database (14) containing radial artery waveform data and contemporaneous reference CO_TD measurements to evaluate eight CO-from-ABP algorithms previously described in the literature. The test data were collected in an ICU patient population during routine clinical operation and contain “real-world” (e.g., not artificially pristine) ICU physiologic data that can be fairly applied to any number of disparate CO-from-ABP algorithms, establishing a resource for their meaningful comparison. Furthermore, we are making this data set publicly available to support the evaluation and further development of CO-from-ABP techniques (available at http://www.physionet.org/physiotools/cardiac-output/). The MIMIC II CO_TD/ABP data set is in this sense an analog of the public access arrhythmia databases that have played an indispensable role in the development, refinement, and— ultimately—widespread acceptance of automated algorithms for electrocardiogram analysis (15).

MATERIALS AND METHODS

Database Development

Our CO_TD/ABP data set was extracted from the MIMIC II database (14). The MIMIC II database includes physiologic and wide-ranging clinical data from over 2,500 ICU patients (medical ICU, critical care unit, and surgical ICU) hospitalized at the Beth Israel Deaconess Medical Center, Boston, USA between 2001 and 2005. Radial ABP waveform data from the M1006B invasive pressure module and CO_TD data (temporally resolved to the nearest minute) were originally sourced from Philips CMS bedside patient monitors (Philips Medical Systems, Andover, MA), so both shared the same electronic time reference. Waveforms were sampled at 125 Hz with 8 bit resolution. The patients’ gender and age were input by the nursing staff as part of routine clinical operations, using the Philips CareVue system, and these archived data were another component of the MIMIC II database. Additional details about the MIMIC II database are available in (14). The data were collected and analyzed with institutional approval by the local IRB.

We identified and extracted MIMIC II cases with CO_TD measurements and one-minute-long segments of radial ABP waveform that immediately preceded the CO_TD measurement (up to and including the time of the CO_TD measurement). All algorithms used in our analyses were implemented in Matlab (Math-works, Natick, MA). These algorithms, and the MIMIC II CO_TD/ABP data set, have been contributed to PhysioToolkit (16) and are available for free public use (http://www.physionet.org/physiotools/cardiac-output/).

ABP Signal Processing

Within each minute-long ABP segment, individual heart beats were identified using a Matlab (Math-works, Natick, MA) implementation of an algorithm by Zong (17). The waveform quality of each ABP pulse was assessed automatically using a signal abnormality index (SAI) algorithm (18). A set of features from each ABP pulse was computed, including the peak (systolic blood pressure, [SBP]), trough (diastolic blood pressure [DBP]), mean arterial pressure (MAP) and pulse pressure (SBP minus DBP); see Figure 1. Each ABP pulse's average of negative slopes was computed, providing a metric of spiky, nonphysiologic noise in the ABP pulse waveform. After computing the preceding features for an ABP pulse, the SAI algorithm checked that all were within normal limits (18). The SAI also checked that the features’ variations from one ABP pulse to the next were within normal limits. The SAI algorithm reported a binary ‘normal’ or ‘abnormal’ rating for each ABP pulse, depending if all the normality criteria were met (18). Any abnormal beat was excluded from further analysis. If a given minute-long ABP segment contained more than 40% of abnormal beats, the entire segment (and its corresponding CO_TD) was excluded from further analysis.

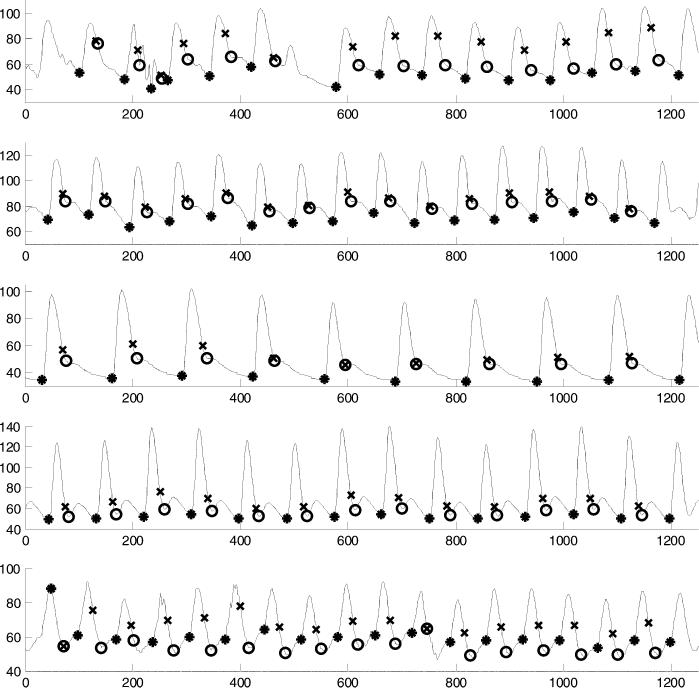
Figure 1.

Five examples of arterial blood pressure waveforms and their key features as identified by our automated algorithms. The horizontal axis is sample number, with 125 samples = one second. Onset point of each beat is indicated by an asterisk “_*”; end of systole, estimated by 0.3 · √beat_period, is indicated by “X”; end of systole, estimated by the ‘lowest nonnegative slope’ method, is indicated by a “0”.

In addition, we estimated the duration of each entire beat and its systolic interval. There is no single widely accepted method to identify the systolic interval in a peripheral ABP pulse (in contrast to a central ABP pulse, the dicrotic notch—if present—in a peripheral ABP pulse does not indicate closure of the aortic valve). Therefore, we chose two alternative criteria to identify the end of systole. First, we computed a heuristic estimate of systolic duration, (0.3 ·√beat_period), originally suggested as an approximation of the QT interval (19). Second, we identified the point after SBP with the lowest nonnegative slope, as shown in Figure 1. In practice, this method located the trough of the dicrotic notch, or any relative plateau which persisted for two or more ABP samples.

Investigational CO-from-ABP Algorithms

The investigational algorithms are summarized in Table 1. Most algorithms predict stroke volume, and CO is taken as the product of median stroke volume and median heart rate over the one-minute window. Many of the algorithms were initially intended for a central aortic ABP waveform; in this investigation, we explored their application to a peripheral radial ABP.

Table 1.

Investigational CO-from-ABP algorithms

	(CO = Stroke Volume × HR)
Pulse pressure (7)	Stroke volume = k × (SBP – DBP)
Liljestrand (8)	$\text{Stroke volume}=\frac{k\times (SBP-DBP)}{(SBP+DBP)}$
Systolic area (9, 10)	Stroke volume = k × ∫Systole ABP(t)dt
Systolic area with Kouchoukos correction (11)	$\text{Stroke volume}=k\times \left(1+\frac{Duratio{n}_{Systole}}{Duratio{n}_{Diastole}}\right)\times {\int }_{Systole}ABP\left(t\right)dt$
Diastolic decaya	Solves for beat-to-beat peripheral vascular resistance, fitting a monoexponential curve to each ABP pulse's peak of systole and trough of diastole, where: PDiastolic = PSystole × e–k × time/PVR
Herd (22)	Stroke volume = k × (MAP – DBP)
Corrected impedance (23)	Stroke volume = k × (163 + HR – 0.48 · MAP) × ∫SystoleABP(t)dt
AC power (root-mean-square)	$\text{Stroke volume}=k\times \sqrt{\frac{1}{T}{\int }_T{(ABP\left(t\right)-MAP)}^{2}dt}\text{where: T}=\text{duration of heart beat}$

^aAdopted from Circ Res 1976; 39:15–24.

CO, cardiac output; ABP, arterial blood pressure; HR, heart rate; SBP, systolic blood pressure; DBP, diastolic blood pressure; MAP, mean arterial pressure; AC, alternating current.

MAP is positively but imperfectly correlated with CO. Of course, variable degrees of systemic vasoconstriction or dilation (which affect peripheral vascular resistance [PVR]), as well as variable venous pressure, make MAP an unreliable predictor of CO. ABP waveform analysis assumes that other features in the waveform are less affected by confounders such as PVR, and are thus more reliable correlates of CO. MAP serves as our control method against which eight investigational CO-from-ABP methods are compared.

(A) Pulse Pressure

In 1904, Erlanger and Hooker suggested that the pulse pressure is a surrogate of stroke volume (7). This notion naturally arises from a basic Windkessel model of the arterial tree, in which the arterial system is considered a single elastic tank, with flow exiting through a distal resistive element. Assuming that cardiac ejection is near-instantaneous, then the product of pulse pressure and heart rate is a predictor of CO.

(B) Liljestrand and Zander

The compliance of the arterial tree varies with blood pressure. The Liljestrand algorithm accounts for the dependence of arterial compliance on arterial pressure by scaling its CO estimate to the reciprocal of MAP (8).

(C) Systolic Area

A number of methods treat the arterial tree as a long viscoelastic tube, a “transmission line” model. Within a transmission line, pressure gradients accelerate or decelerate flow. By assuming that retrograde (reflected) pressure waves are negligible during systole, it is possible to estimate the pressure gradient and the forward flow from an ABP waveform. Specifically, stroke volume is proportional to the area under the systolic portion of the ABP pulse (9, 10).

(D) Kouchoukos Correction

A potential source of error is the assumption that cardiac ejection is so rapid that no blood flows out of the arterial tree during systole (“run-off”). Kouchoukos proposed a simple correction factor, related to the ratio of systolic-to-diastolic duration (11); this was a variation of an earlier method proposed by Warner (12).

(E) Diastolic Decay

Bourgeois developed an algorithm to quantify systolic run-off (13). This method leads to an estimation of PVR (CO can then computed from MAP/PVR, assuming venous pressure is negligible). Bourgeois’ method is based on a constant compliance Windkessel model. In such an idealized model, a mono-exponential diastolic decay (due to the arterial run-off) is expected in the ABP pulse waveform, and that diastolic curve changes solely as a function of PVR (20). Our diastolic decay method adapts the original Bourgeois method to the radial ABP (and thus its performance is likely to be degraded significantly due to the loss of the dicrotic notch). We fit a monoexponential curve to just two points of each ABP pulse, taking the peak of systole as the onset of a mono-exponential decay, and the trough of diastole as its end (21).

(F) Herd

Systolic blood pressure may be prone to amplification due to early reflected waves. Herd et al proposed an empirical method, the difference between mean and diastolic pressure, as a predictor of stroke volume that would be less confounded by this effect (22).

(G) Corrected Impedance

Wesseling's Corrected Impedance method provides an empirical correction to the systolic area-under-the-ABP curve approach, to account for some of the sources of error described above (23).

(H) AC Power

Reportedly the commercial LiDCO Plus PulseCO method of pulse power analysis (LiDCO Ltd., London, England) makes use of the power of the ABP signal, deriving the “beat power factor (r.m.s.—root mean square) which is proportional to the nominal stroke volume ejected into the aorta” (4). This method also entails additional processing steps that are not comprehensively described; therefore we could not independently replicate their methodology. Rather we assessed how well the stroke volume could be estimated with just the computed ABP waveform root-mean-square, which is one component of the LiDCO Plus PulseCO method.

We attempted to evaluate two additional methods that are distributed commercially, Modelflow (Finapres Medical Systems, Amsterdam, The Netherlands) and PiCCO (PULSION Medical Systems, Munich, Germany), by developing new software routines that were consistent with published details about these algorithms. However, the results of our implementations were unsatisfactory and we decided to exclude these algorithms from our trial. This is considered further in the Discussion section.

Calibration

We applied the investigational algorithms described above (and summarized in Table 1) to the data of subjects who had at least two paired measurements of CO_TD and a contemporaneous, minute-long segment of ABP waveform of sufficient quality. Each algorithm was calibrated to each patient, using two different methods. First, the “best-possible calibration factor” was computed, C1 (Fig. 2). C1 was selected to minimize the root-mean-square of the differences of each pairing of CO_TD and CO-from-ABP. It provides the best accuracy that could be obtained with a single calibration factor. Next, each algorithm was calibrated to each patient using a different methodology, C2 (Fig. 2). C2 was calculated only from the first pairing of the CO estimate and CO_TD. C2 describes an algorithm's lower limits of performance, if caregivers rely on just one initial pairing of CO_TD and CO-from-ABP to calibrate the algorithm. All investigational algorithms were compared against MAP as predictors of CO. MAP was calibrated exactly like other algorithms, i.e., C1 and C2.

Figure 2.

We studied two methods of calibrating the algorithms for a subject. In C1 the “best-possible calibration factor” was computed, minimizing the root-mean-square of the difference of each pairing of cardiac output thermadilution (CO_TD) (stem plots) and the corresponding CO-from-arterial blood pressure estimations (black line). In C2, the first pairing of the CO-from-arterial blood pressure estimate (gray line) and CO_TD was used to establish the calibration factor, which was then used for all subsequent CO estimation.

Statistical Analysis

Each paired CO-from-ABP and CO_TD had an identifiable “error” (their difference). The distribution of errors for each investigational algorithm was computed, for both the C1 and C2 calibration methods. From these error distributions, 95% limits-of-agreement were computed for each CO-from-ABP algorithm, per Bland-Altman methodology (24).

We tested if the error distribution for an investigational algorithm was statistically different from the error distribution of “calibrated MAP” (using the C1 data), using the Kolmogorov-Smirnov test (in Matlab). The Kolmogorov-Smirnov test can detect if one error distribution has a significantly wider limits-of-agreement. We did not apply statistical methods such as the Student's t test, repeated measures analysis of variance, or mixed-effects models, because these assess if the means of the distributions are different. Because we calibrated the investigational methods to the reference method, the means of these error distributions were expected to be near-zero, i.e., minimal measurement biases, so these tests would be nonsignificant.

For each subject, we also computed the root-mean-square of the CO-from-ABP versus CO_TD errors. This yielded a number that measures the width of the error distribution, for a given subject and a given algorithm. Grouping all the r.m.s. values for a given algorithm, we applied a paired Student's t test versus calibrated MAP. This statistical methodology is quite conservative, treating repeated observations in a given subject as only one datum (one r.m.s. value).

Finally, we computed the frequency with which directional changes (i.e., increase or decrease) of each CO-from-ABP algorithm agreed with CO_TD. To avoid analysis of trivial changes in CO_TD we identified the single largest magnitude percent change in each patient record (increase or decrease) and computed the incidence of algorithm/CO_TD directional agreement. We tested if each algorithm was significantly different from the performance of “calibrated MAP” using McNemar's test.

RESULTS

Table 2 shows the characteristics of the 120 subjects analyzed. Typical of an ICU population, the subjects were older (age 69 yrs ± 12 Sd), 67% were male. The average length of stay in the ICU was slightly over 2 days with an average of ten CO_TD measurements per patient. On average, each subjects’ CO_TD varied by ±46%, PVR varied by ±50%, and MAP varied by ±32%.

Table 2.

Characteristics and physiologic variation of the study population

	Units	Mean ± sd	N
Study population
Age	yr	69 ± 12	120
Stay duration	day	2.3 ± 2.2	120
COTD measurements per patient		10 ± 8	120
COTD range per patient	L/min	2.3 ± 1.2	120
Mean arterial pressure range per patient	mm Hg	24 ± 10	120
Peripheral vascular resistance range per patient	mm Hg-s/ml	0.5 ± 0.3	120
Pooled data
COTD	L/min	5 ± 2	1164
Mean arterial pressure	mm Hg	75 ± 10	1164
Heart rate	bpm	88 ± 17	1164
Peripheral vascular resistance	mm Hg·s/ml	1 ± 0.4	1164

CO_TD, cardiac output thermadilution.

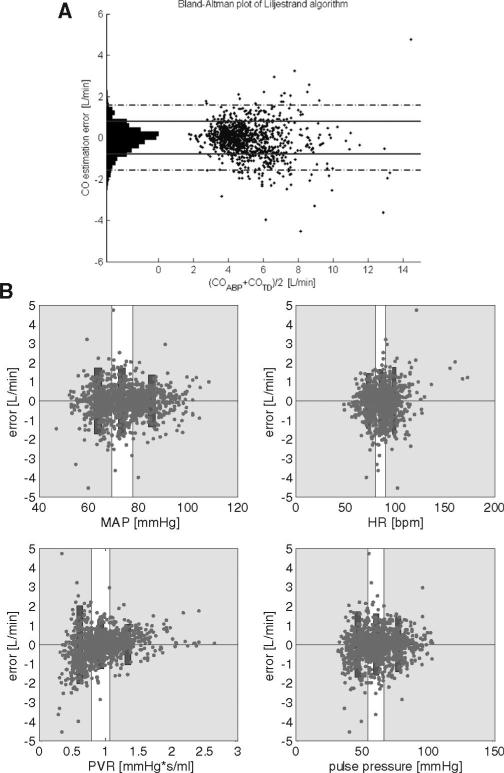
We excluded 13.7% of the available minute-long ABP data segments (and their paired CO_TD measurements) which did not pass our data quality criteria (those segments contained more than 40% of abnormal ABP pulses). Table 3, tabulates the 95% limits-of-agreement for eight of our investigational algorithms using both the C1 and C2 calibration methods. The Liljestrand algorithm performed the best, and was statistically superior to calibrated MAP by the Kolmogorov-Smirnov test. Figure 3 plots the differences (“errors”) between the Liljestrand method and CO_TD, and subplots in Figure 3 show error plotted as a function of various physiologic parameters. One notable trend is that the Liljestrand error grew larger as PVR lessened.

Table 3.

Agreement between thermodilution CO and investigational CO-from-ABP algorithms

Investigational Predictors of COTD	“Best Possible Single Calibration” (C1) 95% Limits Agreement (±L/min)	KS Test vs. Mean Arterial Pressure (p)	“First Pairing Calibration” (C2) 95% Limits Agreement (±L/min)	% Agreement of Directional Δ's vs. COTD
Liljestrand	–1.76/+1.41	0.0001	–2.81/+2.04	78b
Corrected impedance	–1.91/+1.57a	<0.01	–3.39/+2.28	78b
Pulse pressure	–2.07/+1.73	>0.05	–3.05/+2.76	74b
Systolic area	–2.07/+1.73c	>0.05	–2.85/+3.05	77b
Systolic area with Kouchoukos correction	–2.08/+1.71	>0.05	–3.20/+2.89	78b
AC power (root-mean-square)	–2.09/+1.73	>0.05	–3.12/+2.78	79b
Diastolic decay	–2.23/+1.77	>0.05	–3.22/+2.57	78b
Mean arterial pressure	–2.20/+1.82	–	–3.19/+3.42	56
Herd	–2.66/+1.89	>0.05	–3.65/+3.16	78b

CO, cardiac output; ABP, arterial blood pressure; COTD, CO thermadilution; KS, Kolmogorov-Smirnov; AC, alternating current.

Figure 3.

A, Bland-Altman plot comparing cardiac output (CO) estimated by the algorithm (Liljestrand, using the C1 calibration methodology) with CO thermadilution (CO_TD). 95% limits-of-agreement for this algorithm and the other investigational algorithm are summarized in Table 3. B, Liljestrand algorithm estimation error as a function of several variables. Bins of equal sample sizes are illustrated. Rectangular bars represent 95% limits-of-agreement for each bin. For example, as shown, CO estimation error decreases as peripheral vascular resistance (PVR) increases. MAP, mean arterial pressure; HR, heart rate.

In 79 cases the largest magnitude change in CO_TD was an increase (ranging from +5% to +192%, with an average of +65%), and in 29 cases the largest magnitude change was a decrease (ranging from –10% to –56%, with an average of –32%). For these largest magnitude changes, all eight of the reported algorithms showed similar frequencies of directional agreement with CO_TD, and all were significantly different from calibrated MAP. See Table 3.

The results in Table 3 and Figure 3 are exclusive of the minute-long ABP segments with >40% abnormal beats. After recomputing the Liljestrand 95% limits-of-agreement for all data segments (i.e., regardless of data quality) the Liljestrand limits-of-agreement grew to –1.88/+1.57 L/min. By contrast, applying more stringent ABP quality criteria (analyzing minute-long ABP waveform segments with no more than 5% of abnormal beats), the limits-of-agreement were reduced to –1.48/+1.29 L/min, although this more stringent ABP quality criteria excluded 40% of the available ABP data segments.

Some of the algorithms required determining the end-of-systole in a radial ABP pulse. The results in Table 3 were all based on our heuristic method 0.3 ·√beat_period. For select algorithms, superscripts in Table 3 report the results for an alternative method of identifying the end-of-systole (the “lowest nonnegative slope” method), which trended toward worse results.

Grouping all the subjects’ r.m.s. error values for each algorithm and for calibrated MAP, we compared the algorithms’ distributions versus calibrated MAP, using the paired Student's t test. This statistical methodology was more conservative, treating repeated observations in a given subject as only one datum (one r.m.s. value). We found that the Liljestrand method was again significantly better than calibrated MAP (p < 0.01). The Herd method yielded p = 0.04. The other p values were greater than 0.05.

DISCUSSION

In 1983, Wesseling pointed out that the ability to monitor CO continuously by analyzing the ABP waveform could provide “an early warning signal if cardiac output would rise or fall suddenly, to adjust drug rates and infusion rates [...] to sense bleeding [...] to get a true mean cardiac output under arrhythmias, etc (23).” Yet the optimal method and clinical applicability of ABP waveform analysis have not been definitively identified. Perhaps this is in part because these algorithms haven't been adequately evaluated in a comparative manner (25).

In this investigation, we found that all eight of the investigational algorithms were superior to MAP as directional, qualitative indicators of major changes in CO_TD. Although the methods offer similar information about major directional changes in CO_TD (i.e., about 78%), they can differ drastically in magnitude. Only the Liljestrand method was a superior quantitative predictor of CO than calibrated MAP, which is essential for meaningful interpretation of directional changes. The Liljestrand predictor may be a useful parameter for intelligent monitoring algorithms when a patient's radial ABP is measured, providing more information than MAP alone. As quantitative predictors of CO, the other investigational algorithms failed to surpass calibrated MAP, including several algorithms that we developed which incorporated publically-disclosed aspects of the Modelflow, PulseCO, and PiCCO methodologies. We conclude that it is difficult to satisfactorily implement proprietary methods. As we were unable to independently evaluate these proprietary algorithms, it underscores the need for a fair method for publicly comparing competing CO-from-ABP methodologies.

Such evaluation could be enabled by one or more publicly available testing databases. In the 1970s, this laboratory made the Beth Israel Hospital-Massachusetts Institute of Technology Arrhythmia database publicly available (15). That database, together with other public access databases, e.g., the European ST-T database, promoted the development of automated electrocardiogram (ECG) interpretation algorithms. Thirty years later, computerized ECG arrhythmia analysis has evolved so that it is now standard in bedside monitors and even automated defibrillators.

The Database

Academic and commercial developers can freely access and download the MIMIC II CO_TD/ABP data set (www.physionet.org/physiotools/cardiac-output/), apply their algorithms, and report their results. This database contains a large number of radial ABP waveforms and paired measurements of CO_TD (over 1000 paired data points from over 100 patients), archived during routine clinical operations. We observe that the typical record shows distinct intervals of relative stability and other intervals of dynamic physiologic change, as in the example in Figure 4. The range of physiologic states in the overall database is summarized in Table 2. The data quality in this data set—motion artifacts, incidence of dampened catheters, etc.—is consistent with routine practice, rather than idealized research conditions. To our knowledge, there is presently no comparable public database. The performance of a novel algorithm, including breakdown conditions or generally unsatisfactory performances, can be identified using this testing database. Furthermore, direct comparisons of different algorithms using a common testing database should breed healthy competition, and promote clear, iterative improvements. Finally, credible evaluation using a standard database may encourage adoption of innovative methods by caregivers, particularly when some methods are proprietary and not fully disclosed to the public. The usefulness of ancillary algorithms for CO estimation (e.g., generalized transfer functions to estimate central aortic pressure, or ABP dampening detectors) can likewise be tested.

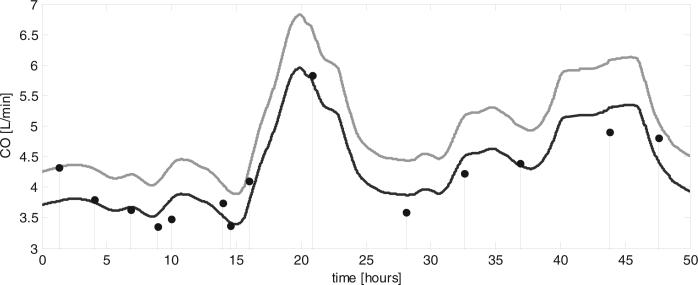
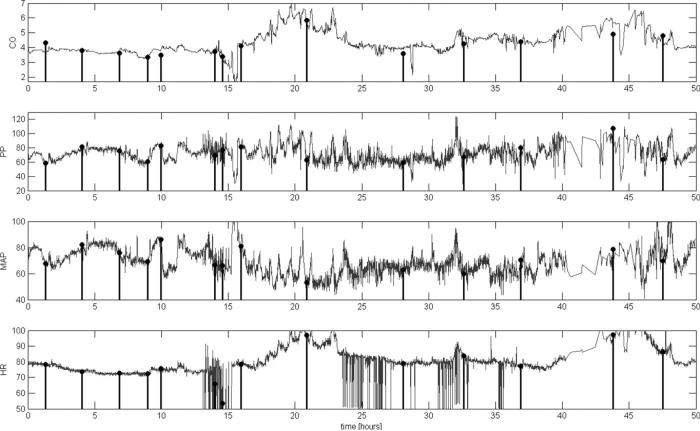
Figure 4.

Example of continuous cardiac output (CO)-from-arterial blood pressure (ABP) estimated by the Liljestrand algorithm (gray line) versus episodic thermodilution CO measurements (stem plots) for a subject over a 50-hr time interval, using a single calibration factor (C1, see text for details). Pulse pressure (PP), mean arterial pressure (MAP) and heart rate (HR) through this same temporal window, as computed by our algorithm, are also shown (gray lines) with stem plots illustrating their values each time CO thermadilution (CO_TD) was measured. C1 calibration minimizes the root-mean-square of the difference of each pairing of CO_TD and the corresponding CO-from-ABP estimations. C2 calibration uses the first pairing of the CO-from-ABP estimate and CO_TD only. For each investigational algorithm, the distribution of errors versus CO_TD was compared with the distribution of errors of ‘calibrated MAP’ using the Kolmogorov-Smirnov test. *Significantly different from calibrated MAP (p < 0.001) per McNemar's test. ^#When using the alternative “lowest nonnegative slope” method to estimate the systolic interval, the lower/upper limits are –1.94/+1.54 L/min. Results in Table 3 employ 0.3 ·√beat_period to estimate systolic interval. ^##When using the alternative “lowest nonnegative slope” method to estimate the systolic interval, the lower/upper limits are –2.40/+1.97 L/min.

Because this CO_TD/ABP data set contains “real-world” ICU data, collected during routine operations, the reference CO measurements were single CO_TD determinations. This reflects our ICU's clinical practice, even though it is an imperfect CO reference method (26,27). As for quality control of the ABP signals, the ICU protocol calls for rezeroing and the flush test at least once per shift, although there was no explicit mechanism for us to assess protocol compliance. Despite these limitations, however, this large data set offers a fair basis for the relative comparisons of different CO-from-ABP algorithms. Even if there are random errors in some of the CO_TD measurements and random artifacts in some ABP waveforms, a superior algorithm should, on average, prove to be a better predictor of CO_TD than an inferior CO-from-ABP algorithm, given a data set of this size. (Such sources of error tend to be carefully minimized during controlled clinical trials, and so such trials may or may not be applicable to routine clinical conditions). Arguably, the fact that these are “real-world” data (e.g., real-world incidence of improper transducer zeroing, damping, etc.) enhances the validity of such relative comparisons, since these measurements reflect the actual conditions under which any useful algorithm must operate. On the other hand, this data set is problematic for evaluating the absolute accuracy of a given algorithm; the use of single CO_TD measurement, an imperfect reference method, will widen the overall limits-of-agreement, because the investigational algorithm and the CO reference will differ due to error in both the CO algorithm and in CO_TD.

If and when future investigators collect additional data sets (perhaps using alternative CO reference methods as in (28), or ABP measured from other anatomical locations such as the femoral artery), these data sets can also be freely posted on PhysioNet for public access, permitting further standardized comparisons of different CO estimators. We suggest that it is beneficial to make available the largest volume of data for the widest range of populations and physiologic states, rather than idealized, smaller data sets.

Investigational Algorithms

We report results from eight CO-from-ABP algorithms, many of which were originally intended for use with a central ABP waveform. One finding in this trial was the superiority of the CO-from-ABP algorithm described in 1928 by Liljestrand and Zander, which is a modestly but significantly superior estimator of CO_TD than MAP alone (95% limits-of-agreement with CO_TD are 0.85 L/min smaller). To the extent that CO_TD is a useful parameter to monitor, the Liljestrand algorithm may enhance standard vital signs. Also, compared with MAP, the Liljestrand method offers additional (although imperfect) directional information about major changes in CO_TD, 78% versus 56%, respectively. Many of the other algorithms offered very similar directional agreement with CO_TD, although failed to track CO_TD changes quantitatively (relative to MAP). We speculate that one reason why the algorithms do not exceed 79% agreement with these major changes in CO_TD is because of noisy or artifactual measurements in either ABP or CO_TD, which skew these results. The former might be addressed in the future with improved preprocessing of the ABP waveform. One exemplary case of CO estimated continuously by the Liljestrand algorithm versus CO_TD measured episodically is illustrated in Figure 4.

The performance of the Liljestrand method is notable because the ABP data were collected during routine ICU clinical operations, during which some degree of motion artifact, catheter damping, improperly calibrated transducers, etc. are inevitable. We employed lenient ABP quality criteria (analyzing all data with ≤40% abnormal ABP pulses), which only excluded 13.7% of the noisiest minute-long ABP waveform segments. We found that the 95% limits-of-agreement between the Liljestrand CO estimates and CO_TD are a function of ABP waveform quality: as the ABP quality criteria are made increasingly stringent, the limits-of-agreement grow tighter, although more data are excluded. Note that we did not explicitly exclude dampened ABP waveforms, aside from requiring that the pulse pressure was >20 mm Hg. Waveform damping (due to air bubbles, thrombus, partial lumen occlusion, etc.) can subtly reduce the measured pulse pressure and so is a potentially serious source of error for the Liljestrand algorithm, which contains pulse pressure in its numerator). If an automated algorithm were able to detect or exclude slightly dampened ABP waveforms, or if the clinical staff took special care to avoid dampened intra-arterial measurements, it is likely that the Liljestrand method, or indeed any of the investigational methods in Table 1, would prove even more accurate.

Presently, the best known CO-from-ABP algorithms are the commercially-available methods, such as PiCCO, Modelflow, and LiDCO Plus PulseCO (4–6), which are procedurally more complex than the simple formulas in Table 1. We attempted to implement algorithms based on limited published descriptions of the commercial systems. We examined the pulse power (r.m.s.), which is reportedly one component of the LiDCO Plus PulseCO method (4); the results are provided in Table 3. In addition, we developed operational algorithms that were consistent with certain published details of the Modelflow and PiCCO methods. To test the Modelflow method, we developed a nonlinear three element model consistent with (6). To test the PiCCO method, we implemented an algorithm that uses mathematical formulas reported in (29), to estimate arterial compliance as a nonlinear function of ABP and a calibration factor, and subsequently, to estimate CO as a function of ABP and arterial compliance. The references described certain details about the methods, but not numerous additional details that are necessary for functional signal processing software. Because these commercial methods are not “open source” we had to rely extensively on our own software engineering judgments to produce functional data processing software, consistent with what we thought the commercial products might do. The performance of our algorithms, however, was not significantly better than calibrated MAP in terms of both 95% limits-of-agreement, and frequency of directional agreement with CO_TD for major changes in CO_TD.We therefore chose to exclude these algorithms from our study, in case they might be misconstrued as relating to the actual commercial algorithms, rather than our own unsuccessful software development efforts. Our software implementations are available for review on the Physionet website. We conclude that it is very difficult to satisfactorily implement proprietary methods and independently evaluate their capabilities.

Ideally, vendors would make the source code for their methods available for public inspection, to bring unreliable methods to light and accelerate acceptance of rigorous algorithms. However, this is simply not standard practice for commercial biomedical algorithms. Because most commercial algorithms will remain proverbial “black-boxes” to the user community, and because it is challenging to evaluate these algorithms independently, publicly and freely available testing databases are all the more essential. Indeed, testing proprietary ECG arrhythmia detection algorithms using standard testing databases is a mandatory step in obtaining United States Food and Drug Administration approval (15). The clinical community might want to demand similar comparative evaluation of other types of diagnostic algorithms, such as CO-from-ABP algorithms, before relying on these methods for patient care. The MIMIC II CO_TD/ABP data set is now publicly and freely available as a first step toward providing such a database. We invite developers and vendors of CO-from-ABP algorithms to test their methods and report their performance on the MIMIC II CO_TD/ABP data set. Our best performing algorithm, the Liljestrand method, may be a useful basis for comparison.

The modest performance of most of the investigational algorithms requires discussion. As noted in the Introduction, it is a theoretical challenge to rigorously estimate global blood flow from a peripheral pressure measurement, because of arterial compliance changes, superposition of antegrade and retrograde pressure waves, and other factors. In this investigation, furthermore, additional factors may have contributed to the poor performances, including: use of real-world ABP waveform data rather than pristine research data (discussed above); use of radial ABP waveforms rather than central ABP waveforms; one-time calibration rather than repeated recalibration; and inclusion of all subjects regardless of cardiac valve function.

Most of the investigational algorithms were originally intended for use with a central ABP waveform, where the systolic interval of the ABP may have relatively fewer retrograde components (i.e., reflected waves). The PiCCO method has been applied primarily to femoral ABP (e.g., 5). Yet measurement of a radial ABP is a common clinical practice, and algorithms which perform suitably using a radial ABP may prove more valuable because radial ABP is more often available, and because noninvasive devices exist to measure distal extremity ABP. Therefore we feel that investigation of these algorithms applied to a radial ABP is warranted. There is precedent for applying an algorithm intended for a central ABP on a peripheral BP (6,28). Indeed, we discovered that the Liljestrand method performs well when applied to radial ABP.

Many pulse contour methods prescribe recalibration after each new reference CO measurement, although we did not use this methodology in our investigation. More frequent calibrations will certainly improve accuracy, not only because this accounts for dynamic changes in arterial compliance, but because each CO_TD is, on average, a good predictor of the subsequent CO_TD. Yet this does not reveal the key question: when the patient's cardiovascular state is changing but CO_TD is unknown—and this is precisely when continuous CO-from-ABP could prove useful—how accurate is the algorithm? Taking a new measurement of CO_TD (for recalibration) defeats the need for CO to be independently estimated via waveform analysis. Thus, in this study, we compared how well each algorithm can estimate CO using just a single calibration factor. The calibration methods in this study included C1, the “best possible calibration” (a retrospective construct, in which one optimal calibration factor that minimizes the overall estimation error is employed); and C2, in which only the first pairing of CO-from-ABP and CO_TD are employed for calibration, and subsequent pairings are examined for accuracy. Presumably, real-world performances (making some use of recalibration) will lie somewhere between the ideal of the C1 calibration method and the imprecision of the C2 method.

We did not exclude subjects based on heart valve function. Rather, we trusted that the ICU staff would only measure CO_TD in appropriate patients (e.g., without significant tricuspid regurgitation), and that the ideal CO-from-ABP algorithm would tolerate some aortic valve dysfunction. When we studied the subset of cases with documented normal tricuspid and aortic valve function, we did not find improvement in any of the algorithms’ performances. Echocardiograms were available in 56 subjects, and normal cardiac valve function was found in 64% of them (36 subjects). For all eight investigational algorithms, the 95% limits-of-agreement with CO_TD were no better in this subset of 36 subjects with documented normal valve function.

CONCLUSION

All of the investigational algorithms were superior to MAP as directional, qualitative indicators of major changes in CO_TD. However, only the Liljestrand method was superior to calibrated MAP as a quantitative predictor of CO (which is essential for meaningful interpretation of directional changes). The Liljestrand predictor may be a useful parameter for intelligent monitoring algorithms when a patient's radial ABP is measured, providing more information than MAP alone. In this study, we developed complex algorithms that incorporated publicly-disclosed details of two commercial CO-from-ABP methods but their performances were unsatisfactory and we excluded these methods from study. We conclude that it is very difficult to satisfactorily implement proprietary methods and independently evaluate their capabilities. Since our testing data set is publicly and freely available, investigators and vendors of CO-from-ABP algorithms are invited to test their methods using these data, offering a fair basis for comparison of different CO-from-ABP algorithms under real-world clinical conditions. The clinical community might expect vendors to publically report how well their algorithms perform in public testing databases before relying on the algorithms for patient care, and the MIMIC II CO_TD/ABP data set is a first step toward such a public resource.