A “midinfrared” scenario for cuprate superconductivity

Abstract

I conjecture that the mechanism of superconductivity in the cuprates is a saving, due to the improved screening resulting from Cooper pair formation, of the part of the Coulomb energy associated with long wavelengths and midinfrared frequencies. This scenario is shown to provide a plausible explanation of the trend of transition temperature with layering structure in the Ca-spaced compounds and to predict a spectacularly large decrease in the electron-energy-loss spectroscopy cross-section in the midinfrared region on transition to the superconducting state, as well as less spectacular but still surprisingly large changes in the optical behavior. Existing experimental results appear to be consistent with this picture.

Despite 12 years of intensive experimental and theoretical research on the high-temperature (cuprate) superconductors, the question “What is the mechanism of superconductivity in these materials?” still lacks an answer that commands even majority, let alone universal, support. What most theoretical papers in the literature seem to understand by “mechanism” is a model: i.e., a specification of an effective Hamiltonian that describes the low-energy behavior of the normal phase, augmented by some further effective interaction that is responsible for the onset of Cooper pairing; a given model is usually regarded as satisfactory (at least by its authors!) if it can (i) generate a gap equation that in favorable circumstances has a nontrivial solution up to temperatures of ∼150 K, and (ii) replicate the major low-energy experimental properties of the normal and superconducting states of the cuprates.

In this paper, I radically reinterpret the starting question. Indeed, I quite explicitly and deliberately eschew any model of the normal state or of the pairing interaction and make only a set of very generic assumptions about the cuprates (A.1–4 of Section 3) that I believe to be supportable directly from experiment; this leads me to a very generic Hamiltonian (Eq. 3.2.1), of which the bulk of the “models” explored in the literature are special cases. Assuming that (as confirmed subsequently), superconductivity results in a saving of interconduction-electron Coulomb energy, I then ask: In what regions of q and ω does the saving take place? and point out that differential electron-energy-loss spectroscopy (EELS) experiments provide, in principle, a direct answer to this question. The main topic of this paper is my conjectured answer to the question, which I call the “midinfrared” (MIR) scenario: The saving of Coulomb energy takes place primarily at midinfrared ω(≈0.1–2 eV) (1 eV = 1.602 × 10⁻¹⁹ J) and small q(≲0.3 Å⁻¹). The physics underlying this rather surprising conclusion is that Cooper pair formation essentially modifies the bare density response function; in the small-q regime, this can lead to an improvement in the screening and thus a decrease in Coulomb energy. I show that the MIR scenario makes some spectacular and testable (but until now untested) predictions about the changes induced by the onset of superconductivity in the EELS cross-section and some less spectacular but nontrivial predictions about those in the optical spectra; I also show that the scenario gives a natural explanation of the dependence of T_c in the Ca-spaced cuprates on the c-axis layering structure.

The plan of the paper is as follows. In section 2, I very briefly review those experimental properties of the cuprates on which I shall be relying and summarize my notation. In section 3, I present a set of very general assumptions (A.1–4) about superconductivity in the cuprates, which can effectively be summarized as stating that it can be understood as a consequence of the three principal forms of energy associated with the conduction electrons in the CuO₂ planes, namely kinetic, lattice potential, and (screened) interconduction-electron Coulomb interaction; this is quantified in the very general Hamiltonian (Eq. 3.2.1). I then (subsection 3), for simplicity only make two further assumptions (B.1–2) that reduce the Hamiltonian to the simpler and more manageable, but still generic, form (Eq. 3.3.2) and list other assumptions that I will make subsequently. Section 4 is devoted to a general discussion of the interconduction-electron Coulomb interaction, including its relation to the optical and EELS data, and to the precise formulation (subsection 4) of the MIR scenario. Section 5 is the heart of the paper: I derive from the scenario exact and approximate predictions for the differential optical and EELS behavior and for the trends of T_c with layering structure in the Ca-spaced materials and as far as possible compare them with experiment (subsection 6). In section 6, I briefly discuss the implications of the scenario and some of the (many) questions that it does not (yet) answer; section 7 is a brief conclusion.

It goes without saying that every individual ingredient in the MIR scenario (importance of midinfrared peak, dominance of small q, overscreening, interplane interactions, etc.) has been previously explored in the literature, in most cases by several authors independently, to the extent that any attempt at a bibliography seems pointless. However, in most cases one or more of these considerations has been investigated in isolation, and typically in the context of some specific model; I am unaware of any reference in the existing literature where they have been integrated so as to give model-independent conclusions and predictions. This is the point of the present paper.

A brief presentation of the general philosophy of the MIR scenario has been given in ref. 1 and some of the predictions, in particular for T_c as a function of layering structure, are found elsewhere (2). I intend to give elsewhere an extended discussion, which will be to a large extent independent of the validity or not of the scenario, of the optical and EELS properties of the cuprates; I also hope to discuss elsewhere alternative explanations for the dependence of T_c on layering structure, including the case of the non-Ca-spaced materials.

2. Some Relevant Experimental Facts About the Cuprates: Notation

Most of the statements made in this section are noncontroversial, and, in most cases, the supporting evidence can be found in refs. 3 or 4, so I shall not give detailed references.

2.1. Composition and Structure.

A typical cuprate has the formula XA_n−1(CuO₂)_n, where n is a positive integer, A is either an alkaline earth, a rare earth, Y, or (in rare cases) La, and X is a collection of atoms, in general in nonstoichiometric proportions, which includes O and possibly also Cu and/or A. There are n CuO₂ planes per formula unit, which for n > 1 are spaced ∼3.5 Å apart by the element A; the different “multilayers” (groups of n layers) are separated by the group X (the so-called “charge reservoir”), and their (center-to-center) separation is typically ∼6–15 Å. A “homologous series” is a set of compounds with the same X and A but differing in the value of n; note that, for reasons of valency (compare below), such a series is interesting in the present context only if A is an alkaline earth.

2.2. Phase Diagram.

For any given compound, we can always define a “reference” composition such that, with the normal rules of valency, the outer shells of the planar Cu and O atoms are, respectively, 3d⁹(Cu⁺⁺) and 2p⁶(O⁻⁻); where such a composition is chemically and metallurgically stable, as in the case of La₂CuO₄ and YBa₂Cu₃O₆ [respectively, (La₂O₂)(CuO₂) and (Ba₂CuO₂)Y(CuO₂)₂ in our notation], the system is invariably a Mott insulator, and we can use it as a reference zero for the “number of free carriers per CuO₂ unit,” which we denote by p and which we can reasonably infer, for any given compound and doping level, from chemical considerations. With this definition, there is considerable evidence (5–8) that the phase diagram in the T_c-p plane is at least qualitatively universal for any superconducting cuprate and, in particular, that the maximum value of the superconducting transition temperature T_c(p) always occurs for a value of p close to 0.18.

2.3. Normal-State Properties.

The following two properties, which will be essential to the discussion of this paper, appear to be generic to all cuprates, whether or not they exhibit superconductivity. (i) Anisotropy of the electromagnetic properties: a typical cuprate has a d.c. resistivity anisotropy ρ_c/ρ_ab ≈ 10²–10⁵(for notation, see subsection f); the same ratio holds, at least up to an order of magnitude, for frequencies up to several electron volts. (ii) Midinfrared (MIR) peak: If, rather than representing the optical data in terms of the real and imaginary parts of the (ab-plane, transverse, q → 0) dielectric constant ɛ_⊥(ω), one plots the “loss function” L(ω) = −Im ɛ_⊥⁻¹(ω), there is always a broad peak extending from a lower cutoff at ≈0.1 eV to a (somewhat material-dependent) upper cutoff at ∼1–2 eV. This peak is also reflected in the electron-energy-loss-spectroscopy (EELS) data and will be discussed in more detail in section 4.2. I stress that, in this paper, I take the “MIR peak” as an input datum and make no claim to explain it.

2.4. Superconducting-State Properties.

The property of most direct interest for the discussion of this paper is the T = 0 superconducting condensation energy E_cond per CuO₂ unit. For this quantity, I shall rely principally on the differential-calorimetry measurements of Loram and coworkers (see, e.g., ref. 9) and will in particular use, for approximate estimates, the fact that, at optimal doping (i.e., p such that T_c(p) = max) E_cond is in almost every case approximated within a factor of ≈2 by the Bardeen-Cooper-Schrieffer-like formula E_cond ≅ 1.5 N(0) T_c², where N(0) is approximately material-independent and of order 1 eV⁻¹/CuO₂ unit/spin; a useful mnemonic is that the condensation energy of Tl-2201 is of order 1 K/CuO₂ unit. (actually 1.4 K).

2.5. Systematics of T_c.

The primary determinant of T_c appears to be the number p of carriers per CuO₂ unit; as already noted, for any given compound, T_c(p) appears to peak around p = 0.18. However, even for the same p, T_c can vary very considerably from compound to compound. Generally speaking, for given p, T_c appears to be increased by compression (at least up to ≈20 GPa) but to be decreased by “buckling” of the CuO₂ planes, by in-plane disorder (e.g., chemical substitution for the in-plane Cus), and probably (though the evidence is less clear-cut) also by disorder in the atoms close to but not in the planes.

A further determinant of T_c that will be very important below is the layer multiplicity n (i.e., the number of CuO₂ planes per formula unit). Contrary to a widespread belief, it is not in general true that T_c increases with n—this is true (or, more accurately, demonstrated to be true) only when the “spacer” element is Ca. A particularly striking exhibit in this respect is the two bilayer homologues of LSCO: when the element A is Ca, La_2−xSr_xO₂A(CuO₂)₂ is a superconductor, with a T_c^max of ≈58 K, considerably greater than that of LSCO itself, whereas, when A is Sr, it is not superconducting at all (10, 11), even when doped right through the optimal region of p. Indeed at the time of writing there exists to my knowledge no clear example of a bilayer cuprate spaced entirely with either Sr or Ba that displays superconductivity for any p.

2.6. Notation.

I use the conventional notation a and b for axes parallel to the CuO₂ planes and c for the perpendicular axis. Unless explicitly otherwise noted, vectors are always two-dimensional and lie in the ab plane. I denote by d, d_int and d̄, respectively, the intramultilayer spacing (≈3.5 Å), the intermultilayer (center-to-center) distance (≈6–15 Å), and the average interlayer spacing (≡d_int for n = 1); the side of the (approximately square) CuO₂ unit is denoted a. I will also refer from time to time to a wave vector q_o, which defines, to an order of magnitude only, the “scale” of the normal-state in-plane behavior; for particular models of this behavior, q_o might be, for example, the Fermi wave vector q_F(≈1 Å⁻¹), the reciprocal lattice vector Q ≡ 2π/a (≈1.8 Å⁻¹), or something else, but the important qualitative point is that, for just about any realistic assumptionsb, we have q_od_int ≫ 1 and q_od ≳ 3–4; I shall thus treat the quantity q_od as “large.”

Some miscellaneous notation: Quantities evaluated in the (notional) normal groundstate and the superconducting groundstate will be denoted by subscripts n and s, respectively,c and ΔA will denote the difference A_s − A_n. The notation δ⁽ⁿ⁾A, on the other hand, will denote the difference (per CuO₂ unit) between the value of the quantity A in the n-plane and single-plane members of an “ideal” homologous series. A homologous series (or part of it) is said to be ideal if, for the given levels of per-plane doping, etc., the relevant “bare” single-plane properties, and in particular the quantity K(qω) introduced in section 4.1, are (i) for n > 1 independent of plane and (ii) independent of n; a tentative identification of two such (part-) series is made in section 5.6. The notation N(0) represents, generically, the order of magnitude of the average number of free carriers of one spin per CuO₂ unit divided by a “typical” energy associated with them; as above, it will be taken to be material-independent at optimal doping and equal to ≈1 eV⁻¹. Finally, for brevity, I refer to the two homologous series (TlBa₂O_3−δ) Ca_n−1(CuO₂)_n and (Tl₂Ba₂O_4−δ)Ca_n−1 (CuO₂)_n as the “1 − Tl” and “2 − Tl” series, respectively.

3. Theoretical Prejudices

3.1. Introduction.

The complexity of the cuprate materials is such that any attempt at understanding their behavior has to start with a number of simplifying assumptions. In most theoretical papers in the literature, these assumptions are implicit, being buried, for example, in the choice of some “model Hamiltonian” such as the two-dimensional (2D) Hubbard or t-J model. Because the whole philosophy of the present paper is to avoid commitment to any such specific model, in this section I shall try to make my assumptions as explicit as possible. Apart from the fundamental “MIR scenario” itself, which is the hypothesis to be tested, I distinguish two kinds of assumptions: those labeled A, which are essential to the general argument of the paper and which I believe to be both plausible on rather general grounds (hence “prejudices”) and also to one degree or another supported by experiment, and those I label B, which, while I believe also plausible, are made solely so to (i) keep this paper within a manageable length and/or (ii) permit precise quantitative predictions; the consequences of relaxation of the various type-B assumptions will be briefly discussed in section 5.5.

3.2 Essential Assumptions.

My first two assumptions are shared by ≈99% of the theoretical literature and thus are probably not in need of detailed justification.

(A.1) Core-conduction electron separation.

(A.2) Dominance of CuO₂ planes.

My third assumption is again a very common though not universal one and may be justified by the lack (12) of a substantial isotope effect in the higher-T_c cuprates:

(A.3) Irrelevance of ionic motion, at least in the first instance.

Finally, I assume

(A.4) Two-dimensionality: For purposes of analyzing the mechanism of superconductivity, we may neglect intermultilayer tunnelling. (Obviously, we would need to take it into account as a “weak” after-effect to stabilize true long-range order). For the justification of this assumption, see ref. 1.

On the basis of assumptions A.1–4, we can write down a generic Hamiltonian for the discussion of superconductivity in the cuprates. It refers explicitly only to the conduction electrons and reads

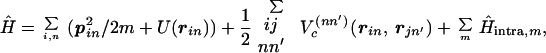3.2.1

where r_in is the (2D) in-plane coordinate of the ith electron in the nth CuO₂ plane, and p_in is the corresponding conjugate momentum. U(r_in) is the (local) potential energy of the conduction electrons in the periodic field of the lattice. The term Ĥ_intra,m, which will be left unspecified except that it is assumed invariant under lattice translations, describes the effects of tunnelling between the different layers of the mth multilayer; it trivially vanishes for the single-plane case. The term V_c^(nn′) is the interconduction electron Coulomb interaction as screened by the core electrons: Note that, in general, it is finite even when n and n′ are in different multilayers. We note that Eq. 3.2.1 is invariant under lattice translations in the ab-plane.

Two features of the Hamiltonian (Eq. 3.2.1) need emphasis. First, it is very generic indeed, including as special cases the vast majority of model Hamiltonians that have been used in the existing theoretical literature (with the exception, of course, of those papers that attribute a significant role to phonons and/or to intermultilayer tunnelling). Secondly, in so far as it is valid at all, it is complete; supplementation of Eq. 3.2.1 with terms supposedly describing (e.g.) spin fluctuations, excitons, or “anyons” is not only superfluous but actually illegitimate. Insofar as these or other phenomenological concepts are in fact valid descriptions of the low-energy behavior, they must in principle be derivable from Eq. 3.2.1, not added to it!

3.3. Nonessential (Simplifying) Assumptions.

The Hamiltonian (Eq. 3.2.1), while very generic, is rather messy to work with, in particular because the screened Coulomb potential V_c^(nn′)(ṟ_in, ṟ_jn′) may have a complicated dependence on its arguments and indeed in principle may even be frequency-dependent. I therefore make, at this stage, an important simplifying assumption, the consequences of relaxing which will be discussed in section 5.5.

(B.1) The screened interconduction electron Coulomb interaction V_c^(nn′)(ṟ_in, ṟ_jn′) may be approximated by the form [where ṟ^(3D) is a 3D vector; see below]:

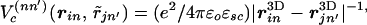3.3.1

where ɛ_sc is a real, positive, frequency-independent number, greater than or equal to unity.

A second approximation that permits appreciable simplification is that the quantity d_int is so large that intermultilayer Coulomb interactions may be neglected:

(B.2) In the Coulomb term in Eq. 3.2.1, the sum over n and n′ may be restricted to the case where n and n′ lie in the same multilayer.

Given assumption B.2, the Hamiltonian (Eq. 3.2.1) reduces to a sum of independent terms Ĥ_m, referring to different multilayers m; by B.1, the form of Ĥ_m is

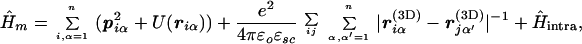3.3.2

where α = 1 … n labels the different layers within the multilayer. In the bulk of this paper, I shall discuss the simplified single-multilayer Hamiltonian (Eq. 3.3.2). Note that, in it, r_iα^(3D) − r_jα^(3D) ≡ (α − α′)dẑ + r_iα − r_jα′ (ẑ ≡ unit vector in c direction).

For ease of reference, it is convenient to list here the other B-type assumptions that will be made below (for the notation, see the relevant sections). I emphasize again that, while plausible (see below), those assumptions, like B.1–2, are in no way essential to my argument and that the consequences of relaxing them will be discussed in section 5.5.

(B.3) The matrix χ̂^(o)(q, ω) of Eq. 4.1.2 may be approximated by its diagonal part.

(B.4) An expansion of quantities δ⁽ⁿ⁾A to lowest order in δ⁽ⁿ⁾T_c/T_c⁽¹⁾ (or a related quantity) is legitimate.

(B.5) The q-dependence of the quantities (a) K_o(qω) and (b) η(qω) (section 5.1) may be neglected in the regime qd ≲ 1.

(B.6) An expansion of quantities ΔA to lowest order in η(ω) is legitimate.

(B.7) The quantity K_o(ω)/dɛ_sc (≡ζ) may be treated as large compared with unity.

4. The Coulomb Interaction: General Considerations

4.1. Introduction.

In this section I shall consider (except in subsection 2, paragraph 3) the special case of Eq. 3.3.2 corresponding to a single-plane cuprate; that is, I shall set n = 1 and discard the term Ĥ_intra. Then, when written in terms of the Fourier transform ρ̂_q of the conduction electron density, the Hamiltonian (3.3) takes the form

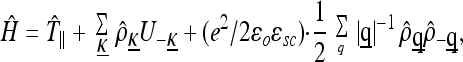4.1.1

where T̂_∥ is the in-plane kinetic energy, the sum over κ runs over vectors of the reciprocal lattice, and the U_κ̱ are fixed numbers. Note that the last (“Coulomb”) term, unlike the second, is invariant against arbitrary translations in the plane.

Let us consider the complete density response function χ(r, r′: t − t′) ≡ −δρ(rt)/δU_ext(r′t′) (see, e.g., ref. 13, section 4.1, where it is called the “unscreened” response.). Its Fourier transform may be written in the form of a matrix χ_nn′(qω) ≡ χ̂(qω), where q + κ̱_n and q̱ + κ̱_n′are, respectively, the Fourier variables corresponding to r and r′. Now, suppose that we write down the diagrammatic series for χ̂ and remove all diagrams that can be cut into two by cutting a single line of wave vector q̱ + κ̱_n (where κ̱_n is any reciprocal lattice vector including zero), thereby defining the bare response χ_nn′^(o)(q̱, ω). Then the relation between the matrices χ̂ and χ̂^(o) is

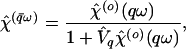4.1.2

where the matrix V̂_q has elements (V̂_q)_nn′ ≡ (e²/2ɛ_oɛ_sc|q̱ + κ̱_n|)δ_nn′. It is important to note that Eq. 4.1.2 is not an approximation; rather, it is effectively a definition of χ̂^(o).

I shall now, for the sake of an uncluttered presentation only, make assumption B.3; that is, I shall approximate χ_nn′^(o), by its diagonal terms. The rationale for this approximation is discussed in appendix A, which is published as supplemental material on the PNAS web site, www.pnas.org. Note that, to the extent that the concept of a “band structure” is applicable, assumption B.3 in no way precludes χ_o from having appreciable contributions from interband transitions and/or from Umklapp processes in the lowest occupied band(s).

It is useful to introduce the quantity

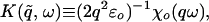4.1.3

which is, apart from a factor of ½ω⁻², the (longitudinal) current response function per plane. As such, it is by definition (see section 2.6) “universal” (i.e., n-independent) for an ideal homologous series, but it is convenient to express it in terms of the nonuniversal quantity ɛ_∥(qω), the 3D longitudinal dielectric constant of the cuprates in question:

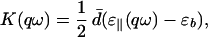4.1.4

where ɛ_b is the “background” (core) contribution to ɛ(ω) (see next subsection).

To conclude this introduction, I write down a general expression for the expectation value, at zero temperature, of the total Coulomb energy V_c in the Hamiltonian (Eq. 4.1.1). This result, which is exact given B.3, relies only on the fluctuation–dissipation theorem and hence is applicable to any state that is stable against development of charge density waves, including the notional normal groundstate:

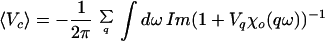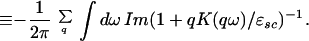4.1.5

It can be generalized to finite T by multiplying the integral by (1 − exp − βω) (β ≡ 1/k_BT) and allowing K to be also a function of T. Eq. 4.1.5 is the basis of all of our subsequent work.

4.2. Optics, EELS, and the Coulomb Energy.

An excellent overall source for the relevant optical properties of the cuprates is ref. 14 and 15; see also ref. 16. I intend to give elsewhere a general discussion of these and the EELS (17, 18) properties; here I confine myself to the truly essential points and will have to make some statements without explicit justification.

First, it is essential to bear in mind that the optical and EELS experiments correspond to quite different wavelength regimes. To the best of my knowledge, in all existing optical experiments, the in-plane wave vector q of the light in the medium has been either zero or at least ≪d_int⁻¹; by contrast, in the EELS experiments, one has always had qd_int ≳ 1 and usually qd_int ≫ 1 (though not necessarily qd ≫ 1). Thus, there is no a priori reason for the data to coincide.

What the (ab-plane polarized) optical experiments measure (usually after appropriate Kramers-Kronig manipulation) is the complex, ab-plane, transverse, q → 0 dielectric constant ɛ_⊥(ω); in the normal phase, at least, this should coincide with ɛ_∥(ω), so I shall drop the subscript from now on. Now the simplest possible ansatz for ɛ(ω) in an n-layer cuprate would represent it as the sum of a term ɛ_c⁽ⁿ⁾(ω) − 1 ≡ (2n/d̄) lim_q→o K(qω), which is the contribution of the CuO₂ planes (compare Eq. 4.1.4) and a background (core) term ɛ_b⁽ⁿ⁾ = 1 + (ɛ_b⁽¹⁾ − 1)(1 + na/d_int⁽¹⁾)⁻¹, where ɛ_b⁽¹⁾ may be series-specific and the last factor allows for the “dilution” of the charge reservoir material in a multilayer system. [Strictly speaking, this ansatz implicitly assumes that the polarizability of the spacer element A is negligible (compare section 5.5)]. The existing data (14–16) do appear consistent with this ansatz, at least qualitatively, in the MIR region, with a value of ɛ_b⁽¹⁾, which is real and frequency-independent up to at least ≈3.5 eV and typically ≈5–6 and a K(ω) (≡lim_q→o K(qω)), whose real part is negative for all relevant ω and that is small above ≈1.5 eV [and whose phase is probably, though not certainly, fairly constant for ω ≲ 1 eV (compare Fig. 4 of ref. 16)]. It should be emphasized that the quantity ɛ_sc, which controls the in-plane screening, can be identified with ɛ_b only under specific assumptions, which I prefer not to make; however, it can be shown (unpublished work) that ɛ_sc ≤ ɛ_b. The principal qualitative conclusion I want to draw from the (normal-state) optical data is that the quantity ζ ≡ |K(ω)|/dɛ_sc is likely to be fairly large compared to unity over most of the MIR frequency region.

In the case of EELS, I shall discuss here only the very simplest case: namely, high-energy transmission EELS from a single-plane cuprate with momentum transfer q in the ab-plane (for a more complete discussion, see ref. 19); moreover, I shall assume the limit qd_int ≫ 1. Then, apart from a straightforwardly calculable system-independent geometrical factor (G.F.), the absolute EELS cross-section σ(qω) is proportional to q⁻⁴ Im χ_tot(qω), where χ_tot is the response of the total charge density, including that associated with the cores. Fortunately this complication yields only a (possibly material-independent) overall factor (unpublished work), so we obtain

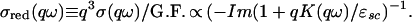4.2.1

Comparing Eq. 4.2.1 with Eq. 4.1.5, we see that, for any given material, the (reduced) EELS cross-section is a direct measure of the Coulomb energy locked up in the region (q, ω); this is true in both the normal and the superconducting states, and thus, differential EELS measurements can provide a direct experimental answer (1) to the question “where is the energy saved?” (Needless to say, this observation is quite independent of the validity or not of the MIR scenario.)

Although it is necessary to generalize Eq. 4.2.1 somewhat (unpublished work) before applying it to the existing MIR EELS experiments (17, 18) (which are all on bilayer materials), we can draw from these experiments two important qualitative conclusions: (i) For all q ≲ 0.5 Å⁻¹, the main region <3.5 eV where the Coulomb energy is locked up is the MIR one, and (ii) in this region of q, the function K_n(qω) is only weakly dependent on qd thereby justifying approximation B.5a.

4.3. How To Save Coulomb Energy by Pairing: “Weak-Coupling” and “Overscreened” Regimes.

In the present subsection, which is purely motivational in nature, I shall assume (i) that superconductivity in the system considered is due to formation of Cooper pairs, and (ii) that the energy saving driving such formation is, at least primarily, of the Coulomb term V_c (the last term in 4.1.1). Since I am quite deliberately eschewing the use of any specific microscopic model, the ensuing considerations are rather qualitative, but I believe none the less persuasive for that.

Excluding for the moment the case of small q and midinfrared ω, which is rather special and will be discussed in detail in section 5.2, let us tentatively assume that the (complex) quantity χ_no(qω) is not too sharply peaked as a function of ω. Then we can deduce from the compressibility sum rule that |χ_no(qω)| will be of the order of the static bare susceptibility χ_no(q), which in turn is of order of the uniform neutral (2D) compressibility χ_no. Let us then, noting that V_qχ_no is a decreasing function of q, define a 2D “Thomas-Fermi” wave vector q_TF by the prescription that V(q_TF) = χ_no⁻¹. To obtain an order of magnitude for q_TF, we take for χ_no the value appropriate to a noninteracting band picture, namely m*/πℏ²; then we have q_TF = 2(m*/m)ɛ_sc⁻¹a_o⁻¹ (a_o = Bohr radius). The important qualitative point is that, irrespective of the details, q_TF is to a first approximation independent of the carrier density and of the general order of q_o.

The physical significance of the characteristic vector q_TF is that it separates, in a qualitative sense, two regimes of q in which a modification Δχ_o(qω) of χ_o, e.g., by Cooper pair formation, may have qualitatively different effects on 〈V_c〉. In the “weak-coupling” regime q ≫ q_TF, we can expand the denominator of Eq. 4.1.5, and it is then clear that to decrease 〈V_c〉 we need to decrease the quantity ∫ Im χ_o(qω) dω ≡ S_o(q). Now in a simple Bardeen-Cooper-Schrieffer-type model we have by the standard “Hartree-Fock-Gor’kov” decoupling

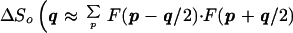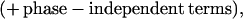4.3.1

where F(p) is the pair wave function (order parameter); and, while Eq. 4.3.1 may not be quantitatively true in a more general model, it seems generally plausible that to reduce the contribution to 〈V_c〉 from this region, we need F(p) to change sign as a function of p̃ over some region ≈q_o, as indeed seems to be indicated by experiment (20).

By contrast, in the “overscreened” limit q ≪ q_TF, we see from Eq. 4.1.5 that what is required in order to decrease 〈V_c〉 is a decrease in the quantity −Im[χ_o(qω)]⁻¹ (or, equivalently, −Im[K(q̃ω)]⁻¹), something which is (or may be) perfectly compatible with an increase in the quantity S_o(q). Thus, even though the order parameter does not change sign within this (small) range of q, we can get a net saving of Coulomb energy: The main effect of pair formation in this region is to increase the effectiveness of the screening and thus to reduce the preexisting repulsion. This is the crucial point of this paper.

4.4. The “Mid-Infrared Scenario.”

The fundamental hypothesis explored in this paper is that the driving force leading to superconductivity in the cuprates is the saving of Coulomb energy and that a substantial fraction of this saving comes from regions of “small” q(≪q_o). Once this is granted, then the next question is: Where in frequency ω is the energy saved? To answer this, we simply apply the “Willie Sutton principle”e: You can’t take it away if it’s not there in the first place! Directly from the normal-state EELS (and optical) data (section 4.2), we see that, in the normal phase, there is essentially no Coulomb energy locked up below ≈0.1 eV while a very substantial amount is locked up in the midinfrared peak (0.1 eV ≲ ω ≲ 2 eV); for the upper limit, compare the remark at the end of section (4.2). Substantial energy is also locked up at energies >3.5 eV, but the data here are rather material-specific, and I shall provisionally assume that this region is not directly relevant to superconductivity. Thus, the MIR scenario is defined as the hypothesis that superconductivity in the cuprates is driven primarily by a saving of Coulomb energy in the “over-screened” regime of q(q ≤ q_o) and in the MIR region of frequency.

It should be mentioned that the viability of the MIR scenario for any given material requires (at least) both effective two-dimensionality and a broad (as well as strong) MIR peak. The first requirement is rather obvious from a comparison of Eq. 4.1.5 with the corresponding 3D formula, in which (1 + qK)⁻¹ is replaced by ɛ⁻¹, so that the q-integral is weighted down in the small-q region relative to the 2D case by a factor of q²; the second is less obvious [it follows from a consideration of the various sum rules obeyed by χ(qω)] and is discussed elsewhere (unpublished work).

5. Predictions of the MIR Scenario

5.1. General Formula for the Saving of Coulomb Energy.

In the bulk of this section, I consider a multilayer cuprate described by the Hamiltonian (Eq. 3.3.2) with the intramultilayer tunnelling term H_intra set equal to zero (but see subsection 7); this case will be tentatively identified with the Ca-spaced cuprates (see below). I shall furthermore assume that the n-layer system in question belongs to an “ideal homologous (part)-series” in the sense of section 2.6. Then the appropriate generalization of Eq. 4.1.5 is (per CuO₂ unit)

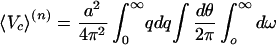5.1.1

In Eq. 5.1.1, the angular integration is over directions in the ab-plane, the quantity K(qω) is, by the “ideality” condition, independent of n, and the quantity f_i(q) (i = 1 … n) is the ith eigenvalue of the matrix f_αα′(q) ≡ exp − qd|α − α′|, which expresses the α-dependence of the Fourier transform of the inter- (and intra-) layer Coulomb potential V_c ≈ |r_α^(3D) − r_α′^(3D)|⁻¹. I note for further reference that, in the limit qd → ∞, all f_i(q) tend to unity while, for qd → 0, one eigenvalue (which I shall label the “optical” one) tends to n while all of the rest (the “acoustic” branches) are proportional to q. It should be emphasized that Eq. 5.1.1, which will form the basis of all of our work in subsections 1–4, is very generic; it requires only assumptions A.1–4 and B.1–3 and is otherwise completely independent of any microscopic model.

We shall be most interested in the quantity δ⁽ⁿ⁾Δ 〈V_c〉: that is, the change in the expectation value of the Coulomb energy of the nth member of the series on passing from the normal to the superconducting groundstate, measured with respect to the corresponding quantity for the single-layer case (for notation, compare section 2.6). It is convenient to define the (complex) quantity η⁽ⁿ⁾(qω) ≡ ΔK⁽ⁿ⁾(qω)/K_o(qω), where here and subsequently, in order to avoid confusion with the multiplicity label n, I denote the normal-state value of K(qω) as K_o rather than K_n; by the “ideal homologous” assumption, K(qω) is independent of the layer multiplicity n. We will see below that the quantity |η⁽ⁿ⁾(qω)| is unlikely to much exceed 0.1 for any q or ω, so it should be legitimate to expand to lowest order in η (assumption B.5). Thus, we get, recalling that δ⁽ⁿ⁾A is always defined per CuO₂ unit,

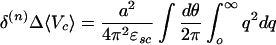5.1.2

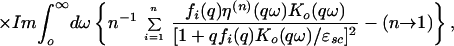where it should be noticed that, in the second term, η⁽ⁿ⁾ is replaced by η⁽¹⁾, as well as f_i(q) by 1.

Let us consider the differential condensation energy δ⁽ⁿ⁾E_cond ≡ δ⁽ⁿ⁾ΔE (compare section 2.6 for notation) as a functional of n and of the function η(qω) for small values of q(q ≲ d⁻¹ ≪ q_o). There is an explicit dependence through the difference in Eq. 5.1.2 between f_i(q) and 1 and the difference between η⁽ⁿ⁾ and η⁽¹⁾ in this region and an implicit dependence via the one-particle terms and also in general via the large-q terms in Eq. 5.1.2 (since the pair-formation process does not, in general, permit η(q, ω) to be varied independently for different q). It is convenient to lump the implicit terms in δ⁽ⁿ⁾Δ 〈V_c〉 in with the one-particle terms and to define a quantity δ̄⁽ⁿ⁾Δ〈V_c〉, which is the explicit contribution only. For an arbitrary dependence of η⁽ⁿ⁾ on n, this procedure is somewhat ambiguous, so let us at this stage make assumption B.4 in the form δη⁽ⁿ⁾/η⁽¹⁾ ≪ 1; then the expression for δ̄⁽ⁿ⁾Δ〈V_c〉 is unambiguous and is

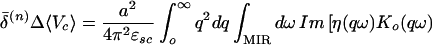5.1.3

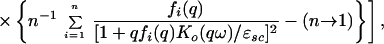where η(qω) may to the accuracy of approximation B.4 be taken to be independent of n. In Eq. 5.1.3, I have taken advantage of the fact that the integral is now non-negligible only at small q to replace the angular integral ∫ dθ/2π by unity (since, for q → 0, K must be isotropic in the ab-plane, at least to the extent that the crystal is tetragonal) and to restrict the frequency integral to the MIR region (compare section 4.4).

Although Eq. 5.1.3 already allows us to make some nontrivial predictions (see subsection 3), we can get a lot further if we know a little about the behavior of the functions K_o(qω) and η(qω), and I now turn to this subject.

5.2. Effect of Superconducting Transition on K(qω).

We already saw in section 4.2 that it should be a reasonably good approximation to take the normal-state response function K_o(qω) in the region q ≪ q_o to be (i) independent of q (assumption B.5a) and (ii) large in absolute magnitude compared to dɛ_sc over most of the relevant frequency range (assumption B.7), and I shall make these assumptions in what follows. It remains to discuss the relative change η(qω) of the (complex) quantity K(qω), which is generated by the formation of Cooper pairs, and in particular to justify assumption B.5b.

While the T = 0 Cooper pair “radius” ξ_o is difficult to obtain quantitatively from the available experimental data, all reasonable estimates at optimal doping give ξ_o ≫ d; thus, in the following, I shall mean by “the limit q → 0,” q ≪ q_o (and thus possibly q ≲ d⁻¹) but q ≫ ξ⁻¹ (it is not, in fact, entirely clear that this premise is necessary for my argument, but I include it for completeness).

With this understanding, what can we plausibly say about the q-dependence of η(qω) in the limit q → 0 without invoking a detailed microscopic model of the normal state or of the process of pair formation? Any behavior (such as that implicitly assumed in ref. 1, in retrospect unjustifiably), which is divergent as q → 0 would require subtle cancellations to avoid violation of the sum rules, and it seems very unlikely that its effects would have been missed in the optical data. As to the possibility that η(qω) tends to zero as q → 0, there is no obvious reason (such as, e.g., a conservation law) for such behavior, and a study of the formal diagrammatic series for K_o(qω) (see, e.g., ref. 21) suggests no obvious way other than a pathological cancellation in which it could occur. Thus, I believe it is reasonable to make assumption B.5b; that is, to take η(qω) = η(ω) in the region of q and ω of interest. It is worth emphasizing that assumption B.5b, while perhaps rather less firmly based than the rest of B.3–7, is (i) directly testable by experiment and (ii) in no way essential to the general structure of the MIR scenario; it is required only to the extent that we wish to use the latter to make exact quantitative predictions, as we shall in subsections 3 and 4.

In appendix B (published as supplemental material on the PNAS web site, www.pnas.org) it is shown that, with the above approximations, the expression 5.1.3 takes, for n not too large and up to terms of relative order ζ⁻¹ ≡ ɛ_scd/|K|, the simple form

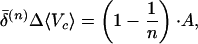5.2.1

where the quantity A is independent of n to within the very small correction β_n given in Eq. B.5 and given by the formula

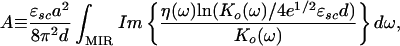5.2.2

where it should be borne in mind that the logarithm is itself a complex quantity. Although Eq. 5.2.1 is less exact then Eq. 5.1.3, its simplicity makes it extremely useful for generating approximate predictions.

5.3. Predicted Minimum Value of η(ω).

Consider the application of Eq. 5.1.3 to (e.g.) the n = 2 and n = 1 members of an ideal, homologous (part)-series as defined in section 2.6, e.g., plausibly, the compounds Tl-2201 and Tl-2212 (see section 5.6). The stability of the n = 1 superconducting groundstate implies that the differential condensation energy δ⁽²⁾E_cont ≡ −δ⁽²⁾Δ〈H〉_T=0 is bounded above by the negative of the right-hand side of this equation, and we thus obtain a prediction for the quantity η(qω) in the form of a lower limit on the negative of the right-hand side of Eq. 5.1.3. This prediction, which depends on assumptions A.1–4 and B.1–4 but is independent of B.5–7, can in principle be tested directly in EELS experiments (though see below).

A more practically useful inequality results if we can make the approximations B.5–7 and thus replace the right-hand side of Eq. 5.1.3 by that of Eq. 5.2.1. Then we have for η(ω) ≡ ΔK_o(ω)/K_o(ω) the prediction

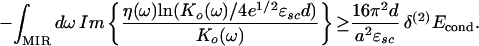5.3.1

This prediction can in principle be tested in either EELS or optical experiments. To obtain a crude order of magnitude for the minimum predicted value of |η| in the MIR region, we estimate the integral of K_o⁻¹ over this region as of the order of d/2 times that of the optical loss function: that is, ≈40 meV; we also take ɛ_sc ≈ 1 (see section 6), set the mean value of the logarithm to be of order 2, and take δ⁽²⁾E_cond ≈ 2(δ⁽²⁾T_c/T_c⁽¹⁾)E_cond⁽¹⁾. This then gives for Tl-2201 (or equally for Tl-2212) the estimate |η|_min ≈ 12%, a value much larger than that (≈10⁻³) obtained from the standard BCS order of magnitude estimate η(ω) ≈ (k_BT_c/ℏω)².

5.4. Predicted Systematics of T_c in the Ca-Spaced Cuprates.

To the extent that approximation B.4 is valid, the Hellman-Feynman theorem assures us that the differential condensation energy δ⁽ⁿ⁾E_cont should be simply proportional to the quantity δ̄⁽ⁿ⁾〈V_c〉 and thus by Eq. 5.2.1 to 1 − 1/n. While the existing data on E_cond does not allow reliable direct tests of this prediction, it is consistent with B.4 to linearize the relation E_cond ∝ T_c² in δ⁽ⁿ⁾T_c (compare above). Thus, we obtain, for any ideal homologous series in which intramultilayer tunnelling is negligible, the simple result

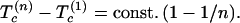5.4.1

The prediction (Eq. 5.4.1), while striking, is in fact not peculiar to the MIR scenario (compare, in particular, ref. 22 and 23); I hope to discuss alternative explanations elsewhere.

5.5. Effect of Relaxing Non-Essential Assumptions.

It is clear that the effect of relaxing assumptions B.4–7, provided only that (i) the asymptotic independence for q → 0 of K_o and η on q assumed in B.4 is not affected and (ii) the quantity ζ is not actually smaller than unity, is quantitative rather than qualitative: The general pattern of the results is not affected, but we can no longer make simple exact predictions such as Eqs. 5.2.1 and 5.4.1. (However, in the first case, we can still get a useful inequality based on Eq. 5.1.2).

The effect of relaxing assumption B.3 is examined in appendix A: The large-q contributions to 〈V_c〉 may be substantially affected, but, while this formally changes Eq. 5.1.2, the effect drops out in Eq. 5.1.3 and thus in all subsequent results. Regarding the small-q terms that are the main focus of this paper, the effect is simply to replace the function K_o(ω) by an “effective” quantity K̃_o(ω), which has much the same properties. This does not affect the predictions for EELS (since these involve no assumptions about the specific form of K), but compounds the complications in relating the EELS and optical properties that arise from relaxation of B.1–2 (see below).

Relaxation of B.2 in general affects both the discussion of the EELS experiments in section 4.2 and the results of this section. In the former case, the effect of allowing for a finite value of (qd_int)⁻¹ is to replace the expression for the EELS cross-section in the relevant geometry by a more complicated expression, which for q → 0 is simply proportional to the optical loss function L(ω). Since this latter quantity is likely to peak at a somewhat lower value of frequency than L_ps(ω) ≡ −Im(ɛ_∥(ω) − ɛ)⁻¹, this effect may account for at least part of the shift of the EELS peak to higher frequencies with increasing q observed (17 and 18) in existing experiments (unpublished work). Regarding the considerations of the present section, one might at first sight think that any contribution to the Coulomb energy from intermultilayer interactions would be suppressed relative to the intramultilayer contributions by a factor of at least d/d_int. However, this argument is not entirely waterproof because of the possibility (see below) that the relevant values of ɛ_sc differ by a similar factor, and one cannot absolutely exclude the possibility that even in the single-plane case intermultilayer Coulomb interactions make a substantial contribution to the condensation energy. However, to a first approximation, one might expect to be able simply to lump this contribution in with the other (in-plane) contributions to 〈V_c〉⁽¹⁾, so that the considerations of this section should not be qualitatively affected.

The most problematic of our nonessential assumptions is B.1. Even if the dielectric properties of the CuO₂ planes themselves are simple, the dielectric constant associated with the background (ionic cores), even if approximately independent of frequency in the MIR region, is likely to be material- and position-dependent and quite likely anisotropic. In these circumstances, the quantity ɛ_sc is likely to be unequal to ɛ_b, q-dependent (though hopefully not seriously so for qd ≲ 1), and, most seriously, different for intra- and interplane interactions. As regards the last point, the simplest reasonable approximation would seem to be to take one value of ɛ_sc, say ɛ_sc^(opt) ≈ ɛ_b ≈ 4–5, for the single optical eigenvalue (i = n) and a different value, ɛ_sc^(ac), for the n − 1 acoustic ones; on the grounds that ɛ_sc^(ac) is principally sensitive to the Ca⁺⁺ spacers, and that these are likely to be very unpolarizable, I take ɛ_sc^(ac) to be close to unity. It is clear that this modification affects the equations of the present section at most to relative order (lnζ)⁻¹, but it will become important in our discussion of the implications of the MIR scenario in section 6.

5.6. Experimental Predictions: Comparison with Experiment.

(a) EELS and optics.

The most spectacular prediction of the MIR scenario is a decrease, of the order of 0.1 ɛ_sc⁻¹, in the EELS cross-section in the MIR region on going from the normal to the superconducting groundstate (and hence, at least plausibly, on cooling from T > T_c to T ≪ T_c). To the best of my knowledge, existing EELS data do not permit a test of this prediction; however, experiments that should do so are currently in progressf in Groningen [though in a “reflection” geometry, so that further analysis (unpublished work) beyond that of section 4.2 is needed]. Since it is difficult to think of a good reason why ɛ_sc^(ac) should be very different from unity, a reliable experimental upper bound substantially <10% on the change of the (transmission) spectrum, coupled with a direct verification of our estimate for δ⁽²⁾E_cond, would cast serious doubt on the MIR hypothesis, and one less than, say, 1% would definitively refute it.

The predicted changes in the optical spectra are (or at least may be) much less spectacularg. To see why, let us use Eq. 4.1.4 and make for illustration the simplest possible assumption: namely, that the phase of the complex quantity K(ω) is independent of frequency in both the normal and superconducting phases [and, in fact, that η(ω) is real]. Then we have for the change ΔR ≡ R_s(T = 0) − R_n of the reflectance (at normal incidence) on the onset of superconductivity the simple relation

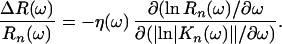5.6.1

Since η(ω) is likely to be largest where |K_n(ω)| is smallest, i.e., in the region of the reflectance minimum and above, it is clear that ΔR/R may be an order of magnitude smaller than η. Thus the value of ΔR(ω)/R_n(ω) reported (for T/T_c ≥ 0.75 and for unpolarized light at 45° incidence) by Holcomb et al. (24) [which are ≤0.8%, (see, especially, fig. 18 in ref. 24) seem consistent with the MIR scenario, both in order of magnitude and, as discussed elsewhere (unpublished work), in their frequency dependence.

(b) Systematics of T_c.

The principal problem in comparing the prediction (Eq. 5.4.1) with experiment is that it is strictly valid only for an “ideal homologous series” as defined in section 2.6, and this concept is one that may well exist only in the fevered imagination of the theorist! Since a serious discussion of the degree of “universality” of in-plane behavior, both within and between series, would be a paper in itself, I shall simply state that I believe it to be a reasonable act of faith (which is not obviously contradicted by any experiment known to me) that, whatever may be the case as regards other compounds,h the n = 1, 2, 3 members (at least) of the 2-Tl and Hg series indeed form, at least approximately, an ideal homologous (part)-series. If so, then the prediction of Eq. 5.4.1 is that, in each of these series, the ratio (T_c⁽³⁾ − T_c⁽²⁾)/(T_c⁽²⁾ − T_c⁽¹⁾) is 1/3. In view of the approximations made in deriving this formula (in particular, B.4, the experimental ratios (25, 26) of ≈0.33 for 2-Tl and ≈0.28 for Hg may be regarded as in satisfactory agreement with the MIR scenario.

5.7. The Dogs That Did Nothing in the Night Time.

An appealing feature of the MIR scenario is that it suggests a natural explanation of the fact that (to my knowledge) there exists no bilayer cuprate spaced entirely with either Sr or Ba, which is known to be superconducting for any p. Unfortunately, space precludes a discussion here; a very brief sketch of the argument (which is connected with the effects of Ĥ_intra in Eq. 3.3.2) is given in ref. 1, and I hope to give a more extended discussion elsewhere.

6. Discussion

The astute reader will not have failed to note that, while the general, motivational discussion of section 4 refers to a single-plane cuprate, the considerations of section 5 refer exclusively to the case n > 1. However, as I shall now show, they enable us to draw some useful conclusions about single-plane effects in a cuprate (such as, hopefully, Tl-2201 or Hg-1201), which is the n = 1 member of an ideal homologous series, and by extension more generally about single-plane cuprates. The following discussion assumes that the MIR scenario is indeed the correct explanation of the trend of T_c(n) in such (Ca-spaced) cuprates.

Let us compare the contributions to Δ〈V_c〉 from “small” q, say for definiteness q < 2d ≅ 0.6 Å⁻¹, in the n = 1 and n = 2 members of the series. According to Eqs. 5.1.1 and 5.2.1 and the considerations of section 5.6, the ratio of the n = 1 contribution to the difference of the n = 2 and n = 1 contribution is approximately (2ɛ_sc^(opt)/ɛ_sc^(ac)) [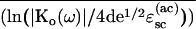]⁻¹, where the bar indicates an appropriate average. Now, we have seen that ɛ_sc^(opt) is plausibly of the order of ɛ_b, i.e., ≈4–5, while ɛ_sc^(ac) is likely to be little different from 1; and, while it is difficult to make a completely trustworthy quantitative estimate of the averaged logarithm, it seems unlikely to be very much >2. Thus, we conclude that the ratio is at least ≈4, and this then implies that it is, at least, not obviously inconsistent to assume that even in a single-plane cuprate, a large fraction of the superconducting condensation energy comes from the region of small q—the full-blown MIR scenario. Needless to say, this hypothesis does not exclude the possibility that the “large-q” (q ≳ q_o) contributions play an essential role in, e.g., tipping the balance between d-wave and s-wave symmetry. Should the hypothesis be confirmed by further experiment, it would appear prima facie to have serious implications for those theories of cuprate superconductivity (e.g., those based on the simple Hubbard or t-J model), which do not explicitly build in the effects of the long-wavelength part of the Coulomb interaction.

It is clear that, while the predictions of the MIR scenario appear to be consistent with current experiment, further experimental tests are highly desirable. While the “make-or-break” testi is the differential EELS behavior, further optical data along the general lines of ref. 24 also would be informative. In a different direction (and independently of the specific MIR scenario), I believe it should be a high priority to establish under exactly what circumstances, and to what degree, the “single-plane” behavior of the multilayer cuprates is universal; this would help us to judge whether the agreement, at present relatively modest, between the prediction (Eq. 5.4.1) and experiment is significant. On the theoretical front, two developments that are urgently needed are the derivation of an explicit gap equation within the MIR scenario (note that here the standard Eliashberg technique is almost certainly inadequate!) and some account of the origin of the normal-state MIR peak, which plays such a crucial role in it. In addition, detailed calculations of the differential optical and Raman properties are a high priority; I hope to report on these developments elsewhere.

7. Conclusion

In this paper, I have attempted to derive, directly from the experimental data and without relying on any microscopic model, some rather generic conclusions about the mechanism of superconductivity in the cuprates. Needless to say, even if the considerations advanced here should turn out to be brilliantly confirmed by future experiment, they do not add up to a “theory” of cuprate superconductivity but only, as has been repeatedly stressed, to a scenario for it. One may ask whether this scenario has at present any status better than that of an inspired guess, and to attempt an answer, let me rearrange the logical order of some of the considerations of this paper, as follows:

The systematic increase of T_c with n in the Ca-spaced cuprates is a major puzzle. Given only the assumption that the effects of Ĥ_intra are negligible at MIR frequencies (on which, see ref. 1), the interplane Coulomb interaction must make a contribution to this dependence, and the only question is whether it is responsible for all or most of the observed effect. If so, then, because the interplane interaction falls off as exp − qd, it follows inexorably that the difference in condensation energy between (e.g.) Tl-2201 and Tl2212 arises wholly or mainly from effects associated with small q, q ≲ d⁻¹ ≪ q_o. This then implies a lower limit on the quantity |η(qω)| in this region, and this in turn a lower limit on the effects that arise even in a single-plane cuprate from this small-q regime. Finally, the Willie Sutton principle then implies that the frequency region in which the saving primarily occurs must be the MIR (or possibly higher), so that we reach the full MIR scenario.

ABBREVIATIONS

EELS

electron-energy-loss spectroscopy

MIR

midinfrared

2D

two-dimensional