AN EFFICIENT HIGHER-ORDER FAST MULTIPOLE BOUNDARY ELEMENT SOLUTION FOR POISSON-BOLTZMANN BASED MOLECULAR ELECTROSTATICS

Abstract

In order to compute polarization energy of biomolecules, we describe a boundary element approach to solving the linearized Poisson-Boltzmann equation. Our approach combines several important features including the derivative boundary formulation of the problem and a smooth approximation of the molecular surface based on the algebraic spline molecular surface. State of the art software for numerical linear algebra and the kernel independent fast multipole method is used for both simplicity and efficiency of our implementation. We perform a variety of computational experiments, testing our method on a number of actual proteins involved in molecular docking and demonstrating the effectiveness of our solver for computing molecular polarization energy.

1. Introduction

Models of molecular potential energy are often used in biology to understand the structure-function relationships of proteins. Computation of molecular binding affinities and molecular dynamics [28, 57, 58] involves repeated evaluation of molecular energy or forces as dynamic molecular configurations are simulated and analyzed. Electrostatic interactions of a molecule with an ionic solution are captured in the polarization term of the total potential energy. Since treating each solvent molecule discretely is extremely computationally expensive for a realistic number of molecules, a common and experimentally useful model for this polarization interaction is the Poisson-Boltzmann equation which treats the solvent as a continuous medium [29, 32].

Finite difference, finite element, and boundary element methods have all been used to solve the linearized Poisson-Boltzmann equation numerically [53]. Discretizing space with a regular lattice, the earliest solvers were based on finite difference methods [33, 56, 65]. Later, finite difference approaches incorporated multigrid techniques [39, 41] and an alternate formulation [62] to improve efficiency. However, discontinuous coefficients and Dirac point charges often limit the accuracy of these methods.

Finite element methods eliminate some of these challenges by allowing the domain to be discretized with a more geometrically accurate mesh. Finite element methods have been developed and analyzed for the linearized [10, 20, 24, 25] and nonlinear Poisson-Boltzmann equation [9, 10, 22, 40]. Both finite difference and finite element methods require a discretization of three-dimensional space. If a uniform mesh of size h is used, then the number of degrees of freedom is O(h⁻³). Boundary element methods provide an alternative in which all degrees of freedom lie on the molecular boundary and (for a uniform mesh) only O(h⁻²) degrees of freedom are needed.

Zauhar and Morgan [75, 76, 77] formulated the linearized Poisson-Boltzmann equation as a system of boundary integral equations (the nonderivative boundary integral equations, nBIE) and solved this system numerically. The original system has been observed to exhibit poor conditioning for iterative linear solvers [50], but an alternative formulation (the derivative boundary integral equations, dBIE) first stated by Juffer et al. [43] is well conditioned. Since the boundary element method leads to a dense linear system, and these and other [81] early methods suffer from need to compute this entire matrix.

Due to the special structure of the boundary element system, the fast multipole method [36] can be used to efficiently approximate the necessary matrix-vector products without creating the full matrix. This has been applied to several formulations of the molecular electrostatics problem: nBIE [1, 46, 51], dBIE [19, 52], models involving only Poisson’s equation [15, 69] and a formulation involving only single layer densities [17]. Nearly all of these codes utilize the solvent-exposed surface produced by MSMS [61], which is composed of spherical and toroidal patches but in some cases contains sharp corners, and some codes approximate this surface with a at triangulation [19]. This can give hypersingular integrals which are challenging to discretize and a resulting solution error which is dominated by the geometric approximation.

For the linearized Poisson-Boltzmann equation we have designed and implemented a boundary element method and additionally studied its accuracy and efficiency on real protein structures. Our solver combines several key features which produce meaningful electrostatics calculations with modest surface mesh sizes. First, the dBIE formulation of the problem is used providing a well conditioned system for iterative methods in linear algebra. Second, by defining the molecular domain using the C¹ algebraic spline molecular surface, solutions only reflect a second order geometric error from the domain approximation and numerically problematic hypersingular integrals are avoided. Third, a general purpose fast multipole package, KIFMM3d, is used to efficiently approximate dense matrix computations simplifying the algorithm by separating the details of the fast multipole method from the rest of the scheme. Our freely available solver (http://cvcweb.ices.utexas.edu/software) is tested on a suite of actual proteins important in molecular docking. We show that our software outperforms several alternative approaches (the nonderivative boundary integral formulation and linear or nondifferentiable surface geometry) and demonstrate benefits compared to a finite difference solver. For practical examples, key parameters including singular and non-singular quadrature orders, fast multipole approximation order, and GMRES termination tolerance are tuned to greatly improve the method efficiency with minimal impact on the solution error.

Motivation for computing the molecular polarization energy is contained in Section 2. In Section 3 the nonlinear and linearized Poisson-Boltzmann equations are stated and then the latter equation is formulated as a pair of boundary integral equations. Our numerical scheme for solving these equations is described in Section 4. Polarization energy is formulated as a post-processes to the Poisson-Boltzmann solution in Section 5. Sections 6 and 7 contain implementation details and computational experiments, respectively.

2. Motivation

We begin with a general outline of the molecular energetics problem including a description of the specific role of the polarization energy.

Molecular Potential Energy

The total free energy of the system G is given be G = U − TS where U is the potential energy, T is the temperature of the system, and S is the solute entropy. The potential energy of a molecule in solution is divided into two components: U = E_MM + G_sol, where E_MM is the molecular mechanical energy, and G_sol is the solvation energy. A common model for the molecular mechanical energy E_MM is given in [48]. For a molecule in solution, additional potential energy resulting from interaction of the solute and solvent is called the solvation energy G_sol. The solvation energy is often modeled by three terms:

$$G_{\text{sol}}=G_{\text{cav}}+G_{\text{vdw}}+G_{\text{pol}},$$ (2.1)

where G_cav is the energy to form a cavity in the solvent, G_vdw is the van der Waals interaction energy between solute and solvent atoms, and the polarization energy G_pol is the electrostatic energy due to solvation [28, 32, 38, 64, 66].

Polarization Energy

The polarization energy of a molecule occupying region Ω is the change in the electrostatic energy due to the induced polarization of the solvent,

$$G_{\text{pol}}=\frac{1}{2}{\displaystyle {\int }_{\mathrm{\Omega }}{\varphi }_{\text{rxn}}(\mathbf{z})}\rho (\mathbf{z})\mathrm{d}\mathbf{z},$$ (2.2)

where ρ(z) is the charge density at position z and the reaction electrostatic potential ϕ_rxn(z) indicates the change in electrostatic potential caused by solvation, i.e., ϕ_rxn = ϕ_sol − ϕ_gas where ϕ_sol and ϕ_gas are the potential of the molecular in solution and in a gas, respectively.

A number of applications involve the computation of polarization energy. For example, the binding effect of a drug (molecule 1) and its target (molecule 2) is the difference between the potential energy of the complex of the two molecules minus the sum of the potential energy of the individual molecules:

$$\mathrm{\Delta }{G}_{\text{bind}}=G_{\text{complex}}-(G_{{\text{molecule}}_1}+G_{{\text{molecule}}_2}).$$

Polarization energy is an important component of each of these energy calculations.

Different theoretical approaches for computing binding solvation energy can be divided into two broad categories: explicit[13, 34, 49, 54] and implicit [28, 32, 60, 68]. Explicit solvent models adopt an atomistic treatment of both solvent and solute. Explicit approaches sample the solute-solvent space by molecular dynamics or Monte Carlo techniques which involve a large number of ions, water molecules, and molecular atoms [68]. This requires considerable computational effort, and explicit solutions are often not practical especially for large domains [70].

Implicit solvent models treat the solvent as a featureless dielectric material and adopt a semi-microscopic representation of the solute. The effects of the solvent are modeled in terms of dielectric and ionic physical properties. The most widely used implicit model for molecular electrostatics is the Poisson-Boltzmann equation: it possesses a solid theoretical justification and has been used to explain a number of experimental observations [28, 29, 30, 60, 66, 70]. Since the solution to partial differential equations still requires substantial computational effort, several other implicit models have been developed to approximate results of the Poisson-Boltzmann model. The most common of these models is the Generalized Born formula [68, 5] which has also been used to successfully approximate polarization energy for some applications [2, 31].

3. The Poisson-Boltzmann Equation

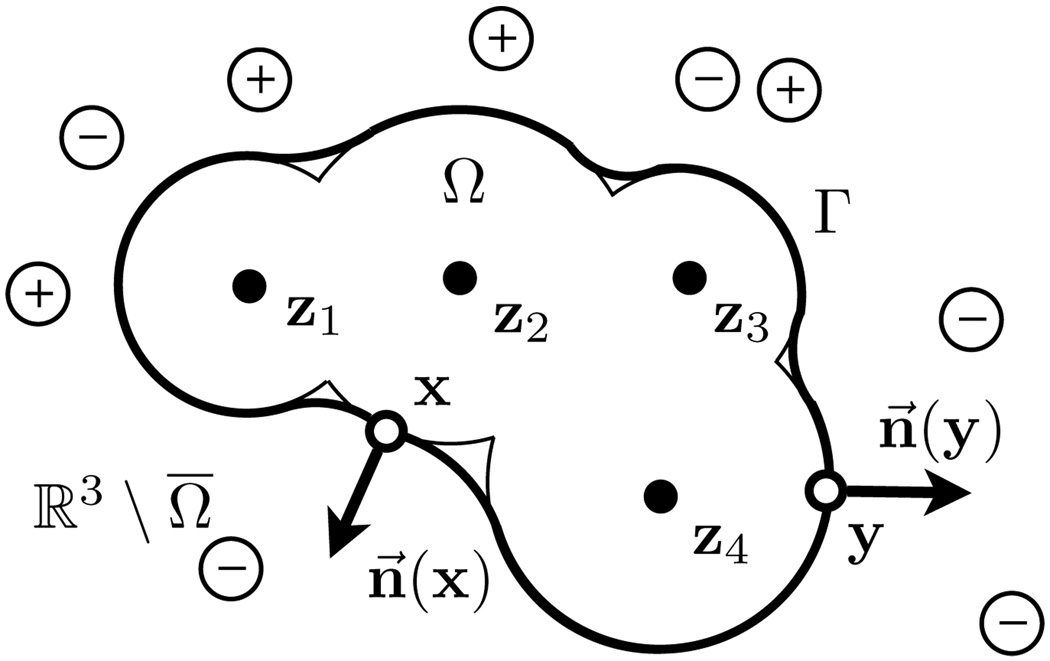
A molecule is defined as a stable group of at least two atoms in a definite arrangement held together by very strong chemical covalent bonds. For a molecule embedded in an ionic solution, the domain (ℝ³) is separated into open interior (Ω) and exterior regions (ℝ³ \ Ω) divided by the molecular surface $\mathrm{\Gamma }=\overline{\mathrm{\Omega }}\cap \overline{{ℝ}^3\backslash \mathrm{\Omega }}$ [47]; see Figure 3.1.

FIG. 3.1.

Molecular domain Ω for the boundary element formulation. Γ denotes the surface of molecular interior Ω. Atomic centers z_k are contained inside Ω while mobile ions in solution occur outside Ω. x and y are used to denote points on the molecular surface and the surface normal are denoted n⃗(x) and n⃗(y). In the discrete system, x is typically used to identify a collocation point while y usually represents a quadrature point.

Two important coefficients, the dielectric coefficient ε(z) and the ion strength 𝕀(z), are assumed to be constant over Ω and ℝ³ \ Ω:

$$\epsilon (\mathbf{z})=\{\begin{array}{cc}{\epsilon }_I,\hfill & \mathbf{x}\in \mathrm{\Omega },\hfill \\ {\epsilon }_E,\hfill & \mathbf{x}\in {ℝ}^3-\mathrm{\Omega },\hfill \end{array}\text{\hspace{1em}and\hspace{1em}}𝕀(\mathbf{z})=\{\begin{array}{cc}0,\hfill & \mathbf{z}\in \mathrm{\Omega },\hfill \\ 𝕀,\hfill & \mathbf{z}\in {ℝ}^3-\mathrm{\Omega }.\hfill \end{array}$$

The electrostatic potential in the interior and exterior of a molecule is governed by Poisson’s equation,

$$\nabla (\epsilon (\mathbf{z})\nabla \varphi (\mathbf{z}))=\rho (\mathbf{z}),$$ (3.1)

where ρ(z) is a variable charge density. This charge density contains two components: charged atoms belonging to the molecule itself and mobile ions as part of the solution. Atomic charges are assumed to be Dirac distributions while mobile ions in solution are modeled with the Boltzmann distribution,

$$\rho (\mathbf{z})≔{\rho }_c(\mathbf{z})+{\rho }_b(\mathbf{z})=-4\pi {\displaystyle \sum _{k=1}^{n_c}\frac{q_k}{{\epsilon }_I}\delta (\mathbf{z}-{\mathbf{z}}_k)+\mathrm{\lambda }(\mathbf{z}){\displaystyle \sum _i{e}_c{z}_i{c}_i{e}^{-e_c{z}_i\varphi (\mathbf{z})/k_{B}T}.}}$$ (3.2)

Since ρ(z) depends on ϕ, (3.1) is the nonlinear Poisson-Boltzmann equation rather than merely Poisson’s equation. Definitions of each of the parameters in (3.2) and a few other parameters needed for the linearized equation and its numerical discretization are in the table of variables below.

ε(z)	dielectric coefficient at z
qk	charge of the atom k
zk	location of charge qk
nc	number of point charges
λ(z)	characteristic function of the set ℝ3 \ Ω
ec	charge of an electron
kB	Boltzmann’s constant
T	absolute temperature
$𝕀=\frac{1}{2}{\displaystyle {\sum }_i{c}_i{z}_i^2}$	ionic strength
ci, zi	concentration and charge of ith ionic species
$\overline{\kappa }(\mathbf{z})=\sqrt{\frac{8\pi e_c^2𝕀(\mathbf{z})}{k_{B}T}}$	modified Debye-Huckel parameter
nd	number of basis functions
nq	number of quadrature points
nb	number of molecular surface mesh patches

Selecting a linear approximation to the nonlinear term ρ_b produces the linearized Poisson-Boltzmann equation,

$$\nabla (\epsilon (\mathbf{z})\nabla \varphi (\mathbf{z}))={\rho }_c(\mathbf{z})+{\rho }_b^L(\mathbf{z}),$$ (3.3)

where ${\rho }_b^L(\mathbf{z})={\overline{\kappa }}^2(\mathbf{z})\varphi (\mathbf{z})$ is the first term of the Taylor expansion of ρ_b(z). In many cases the linearized Poisson-Boltzmann equation provides a sufficiently accurate approximation of the nonlinear Poisson-Boltzmann equation; see [30] and references therein.

3.1. Boundary Integral Formulation

Potential theory [44, 67] provides the tools needed to derive a boundary integral formulation of the linearized Poisson-Boltzmann equation. We begin by separating (3.3) into the interior and exterior regions and explicitly stating interface conditions which must hold on molecular boundary Γ:

$$\nabla ({\epsilon }_I\nabla \varphi (\mathbf{z}))=-{\displaystyle \sum _{k=1}^{n_c}{q}_k\delta (\mathbf{z}-{\mathbf{z}}_k)}\mathbf{z}\in \mathrm{\Omega },$$ (3.4)

$$\nabla ({\epsilon }_E\nabla \varphi (\mathbf{w}))={\overline{\kappa }}^2\varphi (\mathbf{w})\mathbf{w}\in {ℝ}^3\backslash \overline{\mathrm{\Omega }},$$ (3.5)

$$\varphi (\mathbf{z}){|}_{\mathbf{z}=\mathbf{x}}=\varphi (\mathbf{w}){|}_{\mathbf{w}=\mathbf{x}}\mathbf{x}\in \mathrm{\Gamma },$$ (3.6)

$$\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}(\mathbf{z}){|}_{\mathbf{z}=\mathbf{x}}=\frac{{\epsilon }_E}{{\epsilon }_I}\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}(\mathbf{w}){|}_{\mathbf{w}=\mathbf{x}}\mathbf{x}\in \mathrm{\Gamma }.$$ (3.7)

Carefully applying Green’s second identity to the interior and exterior regions and taking limits approaching Γ yields the boundary integral equations,

$$\frac{1}{2}\varphi (\mathbf{x})+{\displaystyle {\int }_{\mathrm{\Gamma }}\left[\frac{\partial G_0(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}\varphi (\mathbf{y})-G_0(\mathbf{x},\mathbf{y})\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}(\mathbf{y})\right]\mathrm{d}\mathbf{y}={\displaystyle \sum _{k=1}^{n_c}\frac{q_k}{{\epsilon }_I}{G}_0(\mathbf{x},{\mathbf{z}}_k),}}$$ (3.8)

$$\frac{1}{2}\varphi (\mathbf{x})+{\displaystyle {\int }_{\mathrm{\Gamma }}\left[\frac{\partial G_{\kappa }(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}\varphi (\mathbf{y})-\frac{{\epsilon }_I}{{\epsilon }_E}{G}_{\kappa }(\mathbf{x},\mathbf{y})\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}(\mathbf{y})\right]\mathrm{d}\mathbf{y}=0,}$$ (3.9)

where G₀ and G_κ denote the fundamental solutions of the Poisson-Boltzmann equations,

$$G_0(\mathbf{x},\mathbf{y})=\frac{1}{4\pi \Vert \mathbf{x}-\mathbf{y}\Vert },\text{\hspace{1em}\hspace{1em}and\hspace{1em}\hspace{1em}}{G}_{\kappa }(\mathbf{x},\mathbf{y})=\frac{e^{-\kappa \Vert \mathbf{x}-\mathbf{y}\Vert }}{4\pi \Vert \mathbf{x}-\mathbf{y}\Vert }.$$

Recall Figure 3.1 for an example domain including normal vectors at labeled boundary points x and y.

An alternative boundary element formulation of the linearized Poisson-Boltzmann equation was proposed by Juffer et al. [43]. This system (dBIE) is produced by taking linear combinations of the original boundary integral equations and their derivatives.

$$\frac{1}{2}+(1+\frac{{\epsilon }_E}{{\epsilon }_I})\varphi (\mathbf{x})+{\displaystyle {\int }_{\mathrm{\Gamma }}\left(\frac{\partial G_0(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}-\frac{{\epsilon }_E}{{\epsilon }_I}\frac{\partial G_{\kappa }(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}\right)\varphi (\mathbf{y})\mathrm{d}\mathbf{y}-}{\displaystyle {\int }_{\mathrm{\Gamma }}(G_0(\mathbf{x},\mathbf{y})-G_{\kappa }(\mathbf{x},\mathbf{y}))\frac{\partial \varphi (\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}\mathrm{d}\mathbf{y}={\displaystyle \sum _{k=1}^{n_c}\frac{q_k}{{\epsilon }_I}{G}_0(\mathbf{x},{\mathbf{z}}_k),}}$$ (3.10)

$$\frac{1}{2}+(1+\frac{{\epsilon }_I}{{\epsilon }_E})\frac{\partial \varphi (\mathbf{x})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})}+{\displaystyle {\int }_{\mathrm{\Gamma }}\left(\frac{{\partial }^2{G}_0(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}-\frac{{\partial }^2{G}_{\kappa }(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}\right)\varphi (\mathbf{y})\mathrm{d}\mathbf{y}-}{\displaystyle {\int }_{\mathrm{\Gamma }}\left(\frac{\partial G_0(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})}-\frac{{\epsilon }_I}{{\epsilon }_E}\frac{\partial G_{\kappa }(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})}\right)\frac{\partial \varphi (\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}={\displaystyle \sum _{k=1}^{n_c}\frac{q_k}{{\epsilon }_I}\frac{\partial G_0(\mathbf{x},{\mathbf{z}}_k)}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})}\mathrm{d}\mathbf{y}.}}$$ (3.11)

This combination of the derivatives of (3.8) and (3.9) has been selected so the kernel $\frac{{\partial }^2{G}_0(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}-\frac{{\partial }^2{G}_{\kappa }(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{x})\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}$ in (3.11) is not hypersingular. For certain numerical schemes, this reformulation has been observed to produce a better well-conditioned linear system and fast convergence of iterative linear solvers when compared to the original boundary integral equations [50].

3.2. Discretization by the Collocation Method

The boundary integral equations (either dBIE or nBIE) are discretized by selecting a finite-dimensional function space and a set of collocation points. Each unknown function is required to belong to the selected function space and the integral equations are required to hold exactly at the collocation points. The most commonly selected pairs of function spaces and collocation points are piecewise constant functions with triangle centroid collocation points and piecewise linear functions with mesh vertex collocation points. Let ${\{{\psi }_i\}}_{i=1}^{n_d}$ be a basis for the finite-dimensional function space, i.e., $\varphi (\mathbf{x})={\displaystyle {\sum }_{i=1}^{n_d}{\varphi }_i{\psi }_i(\mathbf{x})\text{ and }\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}(\mathbf{x})=}{\displaystyle {\sum }_{i=1}^{n_d}\partial {\varphi }_i{\psi }_i(\mathbf{x})}$, and let x_i denote the collocation points. Then the nBIE formulation becomes a linear system of equations,

$$\frac{1}{2}{\displaystyle \sum _{j=1}^{n_d}{\varphi }_j{\psi }_j({\mathbf{x}}_i)+{\displaystyle {\int }_{\mathrm{\Gamma }}\frac{\partial G_0({\mathbf{x}}_i,\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}{\displaystyle \sum _{j=1}^{n_d}{\varphi }_j{\psi }_j(\mathbf{y})\mathrm{d}\mathbf{y}-{\displaystyle {\int }_{\mathrm{\Gamma }}{G}_0({\mathbf{x}}_i,\mathbf{y})}}{\displaystyle \sum _{j=1}^{n_d}\partial {\varphi }_j{\psi }_j(\mathbf{y})\mathrm{d}\mathbf{y}={\displaystyle \sum _{k=1}^{n_c}\frac{q_k}{{\epsilon }_I}{G}_0({\mathbf{x}}_i,{\mathbf{z}}_k),}}}}i=1‥n_d,$$ (3.12)

$$\frac{1}{2}{\displaystyle \sum _{j=1}^{n_d}{\varphi }_j{\psi }_j({\mathbf{x}}_i)+{\displaystyle {\int }_{\mathrm{\Gamma }}\frac{\partial G_{\kappa }(\mathbf{x},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}{\displaystyle \sum _{j=1}^{n_d}{\varphi }_j{\psi }_j(\mathbf{y})\mathrm{d}\mathbf{y}-{\displaystyle {\int }_{\mathrm{\Gamma }}\frac{{\epsilon }_I}{{\epsilon }_E}{G}_{\kappa }(\mathbf{x},\mathbf{y})}}{\displaystyle \sum _{j=1}^{n_d}\partial {\varphi }_j{\psi }_j(\mathbf{y})\mathrm{d}\mathbf{y}=0,}}}i=1‥n_d.$$ (3.13)

A similar system can be derived for the dBIE system. Solving this dense linear system (for unknowns ϕ_i and ∂ϕ_i) involves a number of complications and simplifications. We briefly outlines the general issues here and in the next section describe our specific approaches as applied to realistic proteins.

The integrals in (3.12) and (3.13) must be discretized by some quadrature rules, but the singular kernels prevent the use of a fixed quadrature rule over a triangulation (or similar discretization) of the boundary. For a boundary subdivided into patches ${\{{\mathrm{\Gamma }}_b\}}_{b=1}^{n_b}$, the integral is usually broken into three parts: nonsingular, nearly singular and singular components. A different quadrature rule is used for each type of boundary patch based on which component of the integral it belongs to. The singular and non-singular integrals are usually performed only in a small neighborhood of the singulatity x_i. The remaining integrals are evaluated using a fixed nonsingular quadrature rule and due to the rapid decay of the kernels, the simultaneous computation of these integrals for each collocation point can be accelerated with the fast multipole method [36]. For example, if the first integral in (3.12) is discretized using a quadrature rule ${\{({\mathbf{y}}_q,w_w)\}}_{q=1}^{n_q}$ then the resulting summations,

$${\displaystyle \sum _{q=1}^{n_q}\frac{\partial G_0({\mathbf{x}}_i,{\mathbf{y}}_q)}{\partial \overrightarrow{\mathbf{n}}({\mathbf{y}}_q)}{w}_q{\displaystyle \sum _{j=1}^{n_d}{\varphi }_j{\psi }_j({\mathbf{y}}_q),}}i=1‥n_d,$$ (3.14)

can be accurately approximated via the fast multipole in O(max(n_q, n_d)) operations assuming that the support of each basis function intersects a bounded number of boundary patches, i.e., the sum in j in (3.14) involves a bounded number of terms.

Following the fast multipole calculation, each of the values is corrected to include accurate singular and nearly singular quadrature rules for the appropriate boundary patches. Singular integration is usually performed with by quadrature rules tailored to the position of the singularity [27, 37, 42] while nearly singular integration usually involves (possibly adaptive) refinement of the boundary patches [18, 37, 42, 63]. In some cases singular and nearly singular integration has been studied with respect to certain specific surfaces associated with the linearized Poisson-Boltzmann equation [12, 71].

4. BEM for Molecular Surfaces

We describe the details of our boundary element method: how the molecular surface is defined and discretized, what basis functions are selected and how quadrature is performed.

4.1. Construction of the Molecular Surface

To define the molecular surface Γ, we begin with an experimentally derived protein structure from the RCSB Protein Data Bank (PDB) [14], a worldwide data repository containing thousands of large bio-molecules. Each PDB structure contains of list of spacial locations for each of the atoms in a molecule. The molecular model for electrostatic calculations is obtained from a PDB file by assigning charge and radius parameters derived from a variety of force fields, e.g., AMBER [58], CHARMM [21], etc. For example, the adaptive Poisson-Boltzmann solver, APBS, applies the all-atom AMBER 99 force field [26].

From a configuration of atomic positions and radii a molecular surface can be defined. The simplest surfaces, the van der Waals and solvent accessible surfaces, are merely the boundary of a union of balls [47]; see Figure 4.1(a). Alternatively, the solvent excluded surface [23, 59] is defined to be the boundary of the region outside this union of balls which is accessible by a probe sphere. The solvent excluded surface eliminates many, but not all, of the non-differentiable cusps which occur in the union-of-balls surfaces. For a smooth surface, the level-set of a sum of Gaussian functions associated with each atom is often considered; see [16, 35], for example.

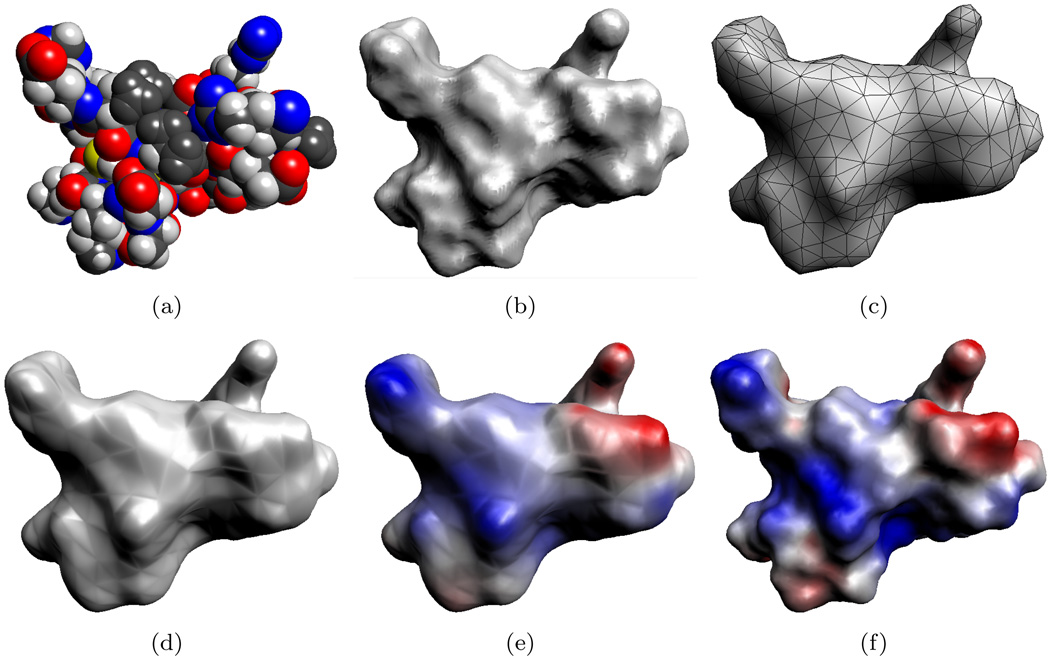
FIG. 4.1.

Molecular model of a protein (PDB id:1PPE, 436 atoms). (a) The van der Waals surface of the protein which models the molecule as a union of balls. (b) The variational molecular surface gives a smooth approximation of the van der Waals surface. (c) The variational surface is then triangulated and then decimated to produce a smaller mesh. This decimated mesh contains 1,000 triangles. (d) The algebraic spline molecular surface (ASMS) fits a smooth surface over the triangular mesh. (e) Electrostatic potential computed using the 1,000 patch ASMS. (f) Electrostatic potential using an ASMS with 74,812 patches. The surfaces in (e) and (f) are colored by the electrostatic potential, ranging from −3.8 k_bT/e_c (red) to +3.8 k_bT/e_c (blue).

We utilize the molecular surface constructed in [7, 8]; the surface is generated by constructing a Gaussian density function for the atom based on atomic positions and radii, evolving this function according to a variational formulation and then considering a level-set of this function; see Figure 4.1(b). For the resulting surface, a triangular mesh with surface normal vectors at the vertices is constructed using a dual contouring method [78]. If the surface mesh generated contains too many triangles, it is decimated following the approach in [4] and further mesh smoothing is performed as necessary; see Figure 4.1(c).

4.2. Surface Parametrization

To provide a smooth surface which interpolates mesh vertices and prescribed surface normals, we utilize the algebraic spline molecular surface (ASMS) [79]. This surface is constructed from algebraic patches or A-patches which are a kind of low degree algebraic surface with dual implicit and rational parametric representations [3]. The result is a molecular surface depicted in Figure 4.1(d) which can be parametrized in terms of the barycentric coordinates of the triangles allowing for easy construction of basis functions as described in the next section. We give a brief overview of this construction; complete details can be found in [79, 80].

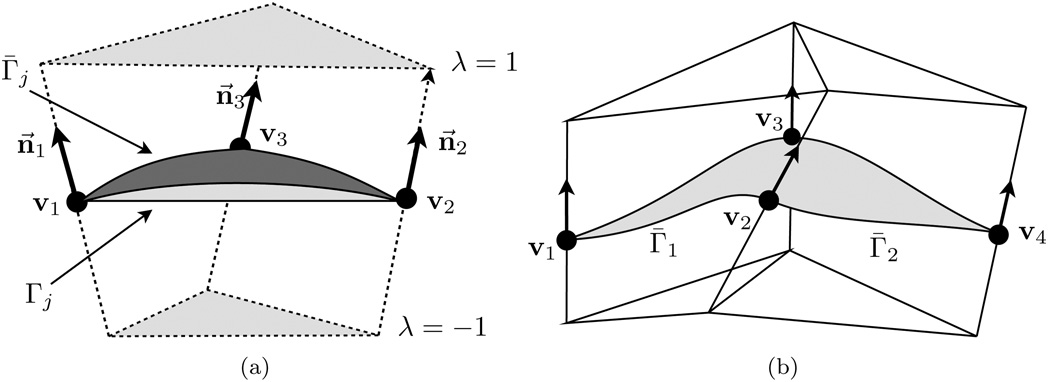
For some triangle element Γ_j with vertices v₁, v₂, and v₃ and normals n⃗₁, n⃗₂ and n⃗₃, the A-patch Γ̄_j is defined on this prism,

$$D({\mathrm{\Gamma }}_j)≔\{\mathbf{y}:\mathbf{y}=b_1{\mathbf{v}}_1(\mathrm{\lambda })+b_2{\mathbf{v}}_2(\mathrm{\lambda })+b_3{\mathbf{v}}_3(\mathrm{\lambda }),-1\le \mathrm{\lambda }\le 1\},$$

where v_i(λ) = v_i + λn⃗_i and (b₁, b₂, b₃) are the barycentric coordinates of the triangle; see Figure 4.2. We define a function over the prism D(Γ_j) in Benstein-Bezier spline form by

$$F_d(b_1,b_2,b_3,\mathrm{\lambda })={\displaystyle \sum _{i+j+k=d}{b}_{\mathit{\text{ijk}}}(\mathrm{\lambda })B_{\mathit{\text{ijk}}}^d}(b_1,b_2,b_3),$$

where $B_{\mathit{\text{ijk}}}^d(b_1,b_2,b_3)=\frac{d!}{i!j!k!}{b}_1^i{b}_2^j{b}_3^k$. For d ≥ 3 coefficients b_ijk(λ) can be selected so that F_d is continuous between adjacent patches and for each vertex F_d(v_i) = 0 and ∇F_d(v_i) = n⃗_i.

FIG. 4.2.

(a) A single prismatic scaffold region for the triangle with vertices v₁, v₂, and v₃ and associated surface normals n⃗₁, n⃗₂, and n⃗₃. The surface patch Γ̄_i interpolates these normals. (b) The ASMS is smooth between two scaffold patches Γ₁ and Γ₂.

The molecular surface Γ̄_j is the zero level-set of F_d,

$${\overline{\mathrm{\Gamma }}}_j=\{\mathbf{y}:\mathbf{y}=b_1{\mathbf{v}}_1(\mathrm{\lambda })+b_2{\mathbf{v}}_2(\mathrm{\lambda })+b_3{\mathbf{v}}_3(\mathrm{\lambda }),F_d(b_1,b_2,b_3,\mathrm{\lambda })=0\}.$$ (4.1)

This can be viewed as a parametric representation in two parameters b₁ and b₂. The third barycentric coordinate can be computed from the first two, b₃ = 1 − b₁ − b₂ and under some mild restrictions on the mesh shape and vertex normals, F_d(b₁, b₂, b₃, λ) = 0 can be solved for λ in terms of b₁ and b₂. In practice this nonlinear equation is solved numerically with Newton’s method.

4.3. Selection of Basis Functions

We consider two different types of basis functions for the solution space and associated collocation points: piecewise constant basis functions with triangle centroids as collocation points and piecewise linear basis functions with mesh vertices as collocation points. In both cases these functions are defined based on the barycentric coordinates of an underlying triangular mesh. Since the A-patches can be parametrized by the barycentric coordinates, this construction can be directly applied to the ASMS.

4.4. Quadrature

Let ${\{({\mathbf{b}}_q,w_q)\}}_{q=1}^{n_q}$ be a (generic) quadrature rule for a reference triangle T where b_q denote the barycentric coordinates. Using a change of variables, this rule can be transferred to an arbitrary A-patch using the parametrization (4.1). The resulting quadrature rule on Γ̄_j is ${\{(\mathbf{y}({\mathbf{b}}_q),J({\mathbf{b}}_q)w_q)\}}_{q=1}^{n_q}$ where J(b_q) denotes the Jacobian of the parametrization.

Next we outline the quadrature rules for nonsingular, singular, and nearly singular integrals to be computed. In each case, quadrature rules on a reference triangle can be transferred to the curved molecular surface using the aforementioned change of variables.

Nonsingular Quadrature and the Fast Multipole Method

Nonsingular quadrature is performed using a fixed Gaussian quadrature rule. This gives a single quadrature rule for the entire surface producing integrals of the form of (3.14). The source density $w_q{\displaystyle {\sum }_{j=1}^{n_d}{\varphi }_j{\psi }_j({\mathbf{y}}_q)}$ must be computed at each quadrature point y_q. Since the basis functions are locally supported, the summation over j only involves a bounded number of terms for any particular quadrature point. Then for all collocation points x_i the summation in q can be approximated by the fast multipole method in O(n_q · n_b) operations.

Singular Quadrature

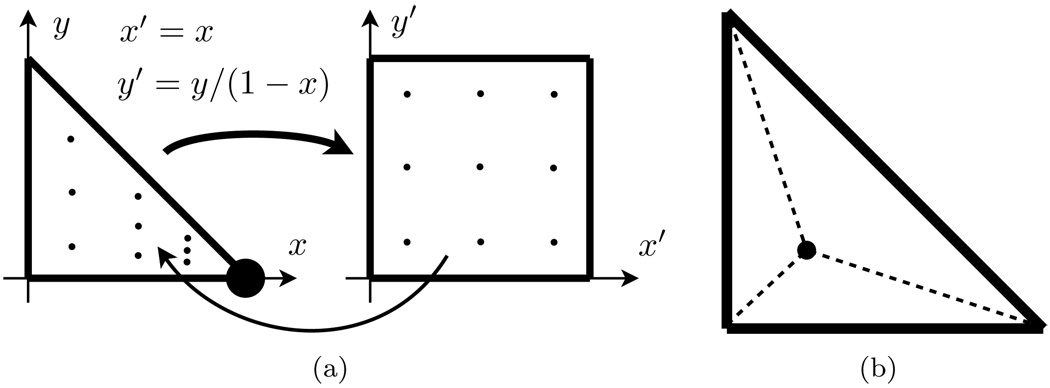
For smooth surfaces, the kernels in (3.8)–(3.11) are all integrable. By performing a change of variables to polar coordinates around the singularity, a smooth integrand is produced. For singularities occurring at a vertex of a triangle, a more computationally useful change of variables is described clearly in [27]. This coordinate change maps the a triangle into a square where a tensor-product Gaussian quadrature rule can be applied; see Figure 4.3(a).

FIG. 4.3.

Singular quadrature rules. (a) Quadrature rule for a triangle with a weak singularity at a triangle vertex. (b) When singularity occurs in the triangle interior, the triangle is divided into three subtriangles at the singularity and then the scheme depicted in (a) can be applied to each subtriangle.

When a triangle centroid is selected to be a collocation point, the integrand singularity occurs in the interior of the triangle. Suitable quadrature rules are formed by subdividing the triangle into three new triangles with the singularity as a new vertex; see Figure 4.3(b). Then the previous quadrature rule (which was designed for triangles with singularities at a vertex) can be applied to each of the three new triangles.

Nearly Singular Quadrature

Nearly singular quadrature is performed by subdivision. On each subdivided triangle a Gaussian quadrature rule is applied. Precise convergence analysis imposes many restrictions on how this refinement should be performed and which integrals must be considered nearly singular; for examples, see [42, 73]. In Section 7 we demonstrate that nearly singular quadrature has limited importance for molecular structures and thus have avoided implementing a more complex (and computationally demanding) quadrature procedure.

5. Polarization Energy Computation

After solving for the electrostatic potential ϕ and its normal derivative $\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}$, the total polarization energy can be computed. Combining the expressions for the polarization energy (2.2) and the charge density (3.2) gives

$$G_{\mathit{\text{pol}}}={\displaystyle {\int }_{\mathrm{\Omega }}}{\varphi }_{\text{rxn}}(\mathbf{z}){\displaystyle \sum _{k=1}^{n_c}}{q}_k\delta (\mathbf{z}-{\mathbf{z}}_k)d\mathbf{z}=\frac{1}{2}{\displaystyle \sum _{k=1}^{n_c}}{\varphi }_{\text{rxn}}({\mathbf{z}}_k)q_k$$ (5.1)

where ϕ_rxn(x) = ϕ(x) − ϕ_gas(x) is the difference between the potential induced by the molecule in solution and the molecule in a gas.

Using Green’s second identity as in the derivation of the boundary integral equations, formulas for the potential both inside and outside the molecule can be obtained; see [43] for complete details. For a point z ∈ ℝ³ \ Γ,

$$\frac{\epsilon (\mathbf{z})}{{\epsilon }_I}\varphi (\mathbf{z})={\displaystyle {\int }_{\mathrm{\Gamma }}}(\frac{{\epsilon }_E}{{\epsilon }_I}\frac{\partial G_{\kappa }(\mathbf{z},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}-\frac{\partial G_0(\mathbf{z},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})})\varphi (\mathbf{y})\mathrm{d}\mathbf{y}+{\displaystyle {\int }_{\mathrm{\Gamma }}}(G_0(\mathbf{z},\mathbf{y})-G_{\kappa }(\mathbf{z},\mathbf{y}))\frac{\partial \varphi (\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}d\mathbf{y}+{\displaystyle \sum _{k=1}^{n_c}}\frac{q_k}{{\epsilon }_I}{G}_0(\mathbf{z},{\mathbf{z}}_k).$$ (5.2)

The potential of the molecule in a gas is the solution to Poisson’s equation (3.1) with constant dielectric ε(z) ≔ ε_I, and no charge density due to mobile ions ρ(z) = ρ_c(z). As the right hand side contains only a sum of Dirac functions, ϕ_gas is the sum of fundamental solutions to Poisson’s equation,

$${\varphi }_{\text{gas}}(\mathbf{z})={\displaystyle \sum _{k=1}^{n_c}}\frac{q_k}{{\epsilon }_I}{G}_0(\mathbf{z},{\mathbf{z}}_k).$$ (5.3)

Subtracting (5.3) from (5.2) yields

$${\varphi }_{\text{rxn}}(\mathbf{z})={\displaystyle {\int }_{\mathrm{\Gamma }}}(\frac{{\epsilon }_E}{{\epsilon }_I}\frac{\partial G_{\kappa }(\mathbf{z},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}-\frac{\partial G_0(\mathbf{z},\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})})\varphi (\mathbf{y})+(G_0(\mathbf{z},\mathbf{y})-G_{\kappa }(\mathbf{z},\mathbf{y}))\frac{\partial \varphi (\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}(\mathbf{y})}d\mathbf{y},$$

for all z ∈ Ω The fast multipole method is then used to efficiently evaluate ϕ_rxn at each atomic position z_k for the energy computation (5.1).

6. Implementation Details

Here we outline the steps in our software pipeline followed by a description of the key parameters to the algorithm.

6.1. Data Pipeline and Software Architecture

Given a molecular structure, a force field, and the concentrations of ions in solution, our code computes polarization energy in the following steps.

1. Molecular Structure Preparation. Molecular structures contained in the Protein Data Bank [14] contain the types and positions of most of the atoms in a molecule. The software package PDB2PQR [26] places missing hydrogen atoms in the original structure and assigns partial charges and atomic radii based on the force field selected.

2. Molecular Surface and Triangular Surface Mesh Construction. Based on the positions and radii of the atoms, a molecular surface is constructed through a level-set formulation with software described in [7, 8]. The level-set surface is approximated as a quality triangular mesh with surface normal directions specified at the vertices using a dual contouring method [78]. If necessary, this triangular mesh is decimated, and a geometric flow algorithm is applied to improve mesh quality [4].

3. Surface Parametrization. The molecular surface is locally parametrized using the algebraic spline construction described in Section 4.2. Quadrature points are computed for each type of integral listed in Section 4.4.

4. Numerical Solution. The linear system (equations (3.12) and (3.13) or the equivalent system for the dBIE formulation) is solved using the GMRES routine provided by PETSc (Portable, Extensible Toolkit for Scientific Computation) [11]. Matrix-vector products are implemented manually using PETSc’s shell matrix construction. Inside each matrix-vector product, KIFMM3d (Kernel-Independent Fast Multipole 3d Method) [72] is used to efficiently perform summations for a fixed quadrature rule and then singular and near field quadrature rules are used to provide a local correction to the least accurate portions of the integrals.

5. Energy Computation. The polarization energy is computed using the formulation in Section 5. Numerical integration is again performed using KIFMM3d with local quadrature corrections to singular or nearly singular integrals.

6. User Interface and Visualization. The molecular visualization and computation package TexMol [6] provides a graphical interface for the algorithm parameters as well as immediate visualization of the results.

6.2. Algorithm Parameters

When running the algorithm, a particular formulation must be selected and a number of parameters must be set. One boundary integral formulation (nBIE or dBIE) must be selected and either piecewise constant or piecewise linear basis functions can be used. Additionally, the following parameters must be selected.

Ng	Number of points in triangular Gaussian quadrature rule
Ns	Number of points in triangular singular quadrature rule
Nns	Number of subdivisions for the nearly singular quadrature rule
Dns	Depth of triangles for the nearly singular quadrature rule
εtol	Tolerance for terminating PETSc GMRES routine
Nfmm	KIFMM3d accuracy parameter

The parameter N_fmm is the number of points used by KIFMM3d to represent equivalent densities and effects the accuracy of the fast multipole evaluations. KIFMM3d runs in $O(N_{\text{fmm}}^{\frac{3}{2}})$ time.

7. Experimental Results

Two types of experiments are considered: a simple example with a known solution and realistic protein complexes from the ZDOCK benchmark [55]. Results are compared to solutions of the linearized Poisson-Boltzmann equations produced by the multigrid finite difference method provided in APBS version 1.2.1 [10, 41].

7.1. Single Ion Model

We begin by studying the simplest molecule: a single atom with radius r and charge q. In this case an explicit solution to the linearized Poisson-Boltzmann equation is known [45]:

$${\varphi }^{*}(\mathbf{x})=\{\begin{array}{cc}\frac{q}{4\pi {\epsilon }_I|\mathbf{x}|}+\frac{q}{4\pi r}\left[\frac{1}{{\epsilon }_E(1+\kappa )}-\frac{1}{{\epsilon }_I}\right]\hfill & \mathbf{x}\in \mathrm{\Omega },\hfill \\ \frac{q{e}^{-\kappa (|\mathbf{x}|-r)}}{{\epsilon }_E(1+\kappa r)|\mathbf{x}|}\hfill & \mathbf{x}\notin \mathrm{\Omega }.\hfill \end{array}$$ (7.1)

The resulting polarization energy is

$$G_{\text{pol}}^{*}=\frac{q^2}{8\pi r}[\frac{1}{{\epsilon }_E(1+\kappa )}-\frac{1}{{\epsilon }_I}].$$ (7.2)

This example is used to test the various parameter settings for PB-CFMM. Relative error between the exact solution ϕ^* and the numerical solution ϕ is measured in the L²-norm,

$$\text{Error}=\sqrt{\frac{{\displaystyle {\int }_{\mathrm{\gamma }}}{({\varphi }^{*}(\mathbf{y})-\varphi (\mathbf{y}))}^2+{(\frac{\partial {\varphi }^{*}(\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}}-\frac{\partial \varphi (\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}})}^2\mathrm{d}\mathbf{y}}{{\displaystyle {\int }_{\mathrm{\gamma }}}{({\varphi }^{*}(\mathbf{y}))}^2+{\left(\frac{\partial {\varphi }^{*}(\mathbf{y})}{\partial \overrightarrow{\mathbf{n}}}\right)}^2\mathrm{d}\mathbf{y}}.}$$ (7.3)

While derivatives of ϕ suggest that this expression is more closely related to the H¹-norm, ϕ and $\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}$ are independent unknowns in the boundary integral formulation. So (7.3) is the L²-norm of the unknown vector $\left(\varphi ,\frac{\partial \varphi }{\partial \overrightarrow{\mathbf{n}}}\right)$.

We begin by selecting acceptable quadrature rules. Table 7.1 contains a comparison of the solution error under different quadrature configurations. The simplified nature of our nearly singular quadrature scheme means that eventually (i.e., when the size of the triangles in the surface mesh becomes small enough) the quadratic convergence rate of the method will be lost. The table demonstrates that if the nonsingular and singular quadrature rules are of high enough order, nearly singular quadrature can be avoided. In practice we see that the three-point Gaussian quadrature rule for nonsingular integrals and the nine-point (i.e., three by three) rule for singular integrals are sufficient to preserve the convergence rate in the typical ranges that we consider. Higher degree integration rules do not reduce the solution error for the mesh sizes listed.

TABLE 7.1.

Comparison of solution error under several quadrature procedures on the single ion example. Each quadrature scheme is listed as N_g/N_s/D_ns. In all cases N_ns = 6 and ε_tol = 10⁻⁷.

h	Mesh Vertices	Quadrature Scheme
		3/9/3	3/9/0	3/4/0	1/9/0	1/4/0
4.9e-1	42	5.88e-2	5.91e-2	6.05e-2	6.15e-2	6.29e-2
2.5e-1	82	1.93e-2	1.94e-2	1.98e-2	2.13e-2	2.18e-2
1.2e-1	162	5.36e-3	5.38e-3	5.55e-3	6.47e-3	6.64e-3
6.2e-2	322	1.41e-3	1.41e-3	1.49e-3	1.98e-3	2.06e-3
3.1e-2	642	3.62e-4	3.65e-4	4.06e-4	6.50e-4	6.90e-4
1.6e-2	1282	9.54e-5	9.70e-5	1.17e-4	2.38e-4	2.58e-4

Table 7.2 contains a comparison of nonderivative ((3.8) and (3.9)) and derivative ((3.10) and ((3.11)) boundary integral formulations. In [50] it is reported that matrices corresponding to the derivative boundary integral equations are better conditioned for iterative solvers. We observe this when performing the computation for small ε_tol. However for modest ε_tol values we find that both formulations terminate in many fewer iterations without an impact on the solution error. Since the dBIE formulation requires four times as many fast multipole calls as the nBIE formulation (and thus typically four times the runtime), it can be desirable to use the nBIE formulation in certain situations. This likely explains how the nBIE formulation has been used successfully by some research groups; e.g. [1].

TABLE 7.2.

Comparison of the nBIE and dBIE formulations for the single ion model.

εtol	10−5				10−8
	nBIE		dBIE		nBIE		dBIE
h	Error	It.	Error	It.	Error	It.	Error	It.
4.9e-1	1.63e-1	5	5.91e-2	6	1.63e-1	10	5.91e-2	8
2.5e-1	4.47e-2	11	1.93e-2	9	4.47e-2	26	1.93e-2	15
1.2e-1	1.15e-2	6	5.38e-3	6	1.15e-2	28	5.38e-3	13
6.2e-2	2.95e-3	4	1.41e-3	6	2.95e-3	34	1.41e-3	13
3.1e-2	7.49e-4	3	3.65e-4	6	7.58e-4	43	3.65e-4	12

Table 7.3 contains a comparison of a curved A-spline molecular surface and a linear approximation of the geometry. Polarization energy converges at the expected quadratic rate for the curved geometry and at a linear rate for the linear geometry. Even for very coarse meshes (i.e., before the faster convergence rate has taken effect) the curved geometry performs much better. This is likely due to the hypersingular integrals associated with corners of the polygonal domain. Since the A-spline molecular surface is differentiable, it produces no hypersingular integrals and thus no associated numerical problems.

TABLE 7.3.

Comparing the performance of the algebraic spline molecular surface (ASMS) to a linear approximation of the domain. The exact energy value is −81.450 kcal/mol.

	A-Spline			Linear
h	L2 Error	Energy	It.	L2 Error	Energy	It.
4.9e-1	5.90e-2	−75.56	6	5.81e-1	−137.67	4
2.5e-1	1.94-2	−80.08	9	3.60e-1	−100.73	9
1.2e-1	5.38e-3	−81.61	6	1.92e-1	−89.37	10
6.2e-2	1.41e-3	−81.43	6	9.80e-2	−85.01	9
3.1e-2	3.65-4	−81.44	4	1.65e-3	−83.14	9

Table 7.4 contains a comparison of our solver with APBS for the single ion example. While the computational time for each method is linear in the number of degrees of freedom, the number of degrees of freedom grows at O(h⁻³) for the finite difference solver compared to O(h⁻²) for the boundary element solver. The finite difference solver is much more efficient per degree of freedom: this is expected because the linearity of the fast multipole method involves a larger constant then the local finite difference computations. The boundary element method gives a more accurate result when compared to finite difference grids with the same length scale.

TABLE 7.4.

Comparison of APBS and PB-CFMM for the single ion example. The exact polarization energy is −81.450 kcal/mol with the interior and exterior dielectric constants 2 and 80.

solver name	h	# degrees of freedom	Gpol (kcal/mol)	memory (mb)	time (seconds)
	4.0e-1	173	−87.663	1.4	0.56
	2.0e-1	333	−84.476	8.2	1.18
APBS	1.0e-1	653	−82.178	59	8.83
	5.0e-2	1293	−81.831	448	57.73
	2.5e-2	2573	−81.594	3510	426.30
	2.5e-1	82	−80.077	38	5.90
	1.2e-1	162	−81.358	68	13.60
PB-CFMM	6.2e-2	322	−81.428	125	46.56
	3.1e-2	642	−81.444	275	203.60
	1.6e-2	1282	−81.449	995	830.09

7.2. Protein Binding Examples

We focus our experiments on a set of 212 ligand-receptor protein complexes from the ZDOCK benchmark [55]. Based on our experiments on the single ion model, we choose a conservative parameter set for PB-CFMM: N_g = 3, N_s = 9, D_ns = 0, ε_tol = 10⁻⁵, and N_fmm = 6. These parameter settings were seen to preserve the expected convergence rates for the single ion model at small length scales. Atomic charge and radius information is generated using the AMBER 99 force field.

Table 7.5 contains a summary of the results of running PB-CFMM and APBS on the set of test molecules. The runtime of both solvers is observed to be linear in the number of degrees of freedom as expected. Error in the energy values is computed with respect to the energy computed at the finest level. We see that PB-CFMM-computed energy values are more consistent than those computed with APBS.

TABLE 7.5.

Comparison of PB-CFMM and APBS on 212 molecules from the ZDOCK Benchmark. Error in the energy value is computed with respect to the finest mesh using the same solver and reported as a percentage.

solver # of DOF	PB-CFMM			APBS
	2000	8000	32000	653	1293	2573
median energy error %	2.72	0.44	-	5.36	3.94	-
max energy error %	32.68	3.58	-	44.06	7.4	-
median # of iterations	19	22	24	-	-	-
max # of iterations	78	53	46	-	-	-
median compute time	37.14	173.45	801.94	13.84	80.29	524.64
median time per iter	1.92	8.12	32.08	-	-	-
median memory usage	65	150	469	126	535	3577

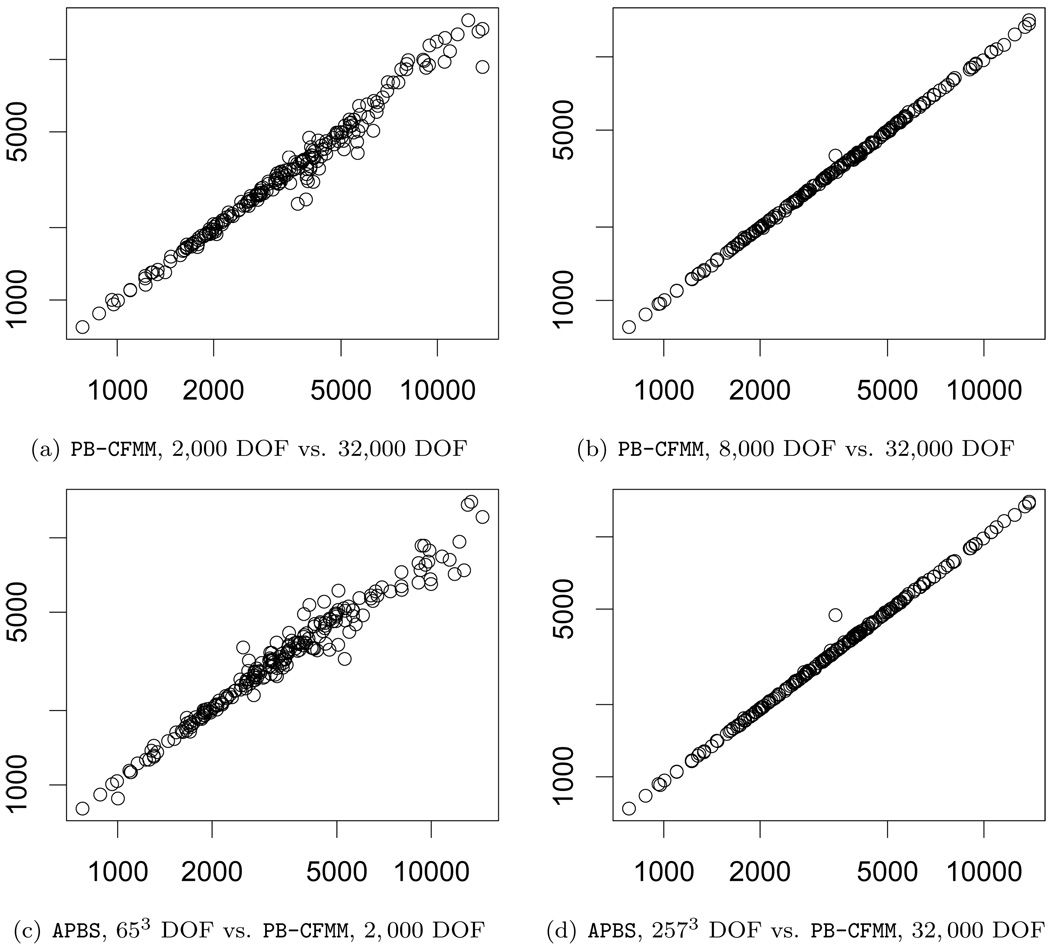
Note that the median difference between the finest scale PB-CFMM and APBS results is 3.15%. This appears to be much higher than the error in the PB-CFMM computations. Some of this discrepancy is due to the differences in the molecular surfaces used by the two solvers since the surfaces given to PB-CFMM involve some pre-processing; recall Section 4.1. Figure 7.1 contains plots of the energy values computed under the different solvers and mesh sizes.

FIG. 7.1.

Scatter plots of polarization energy values computed for 212 proteins using different solvers and mesh sizes.

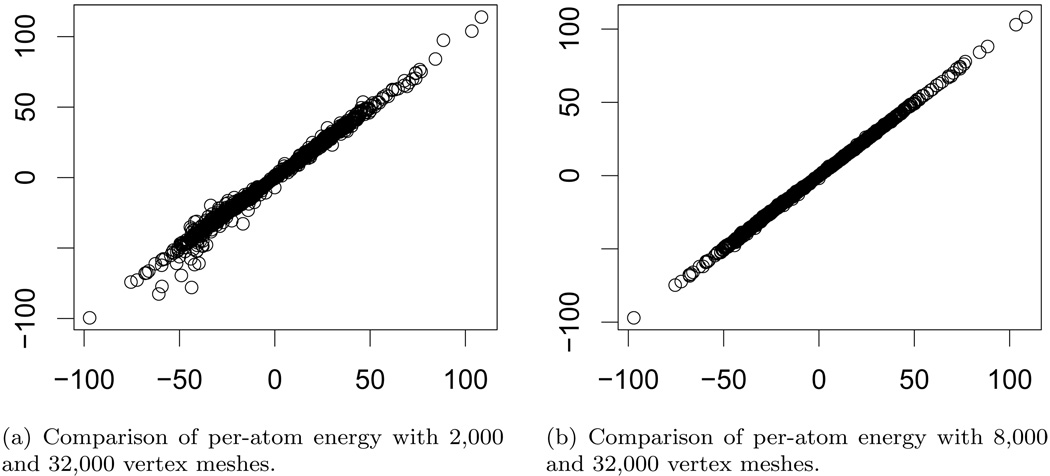
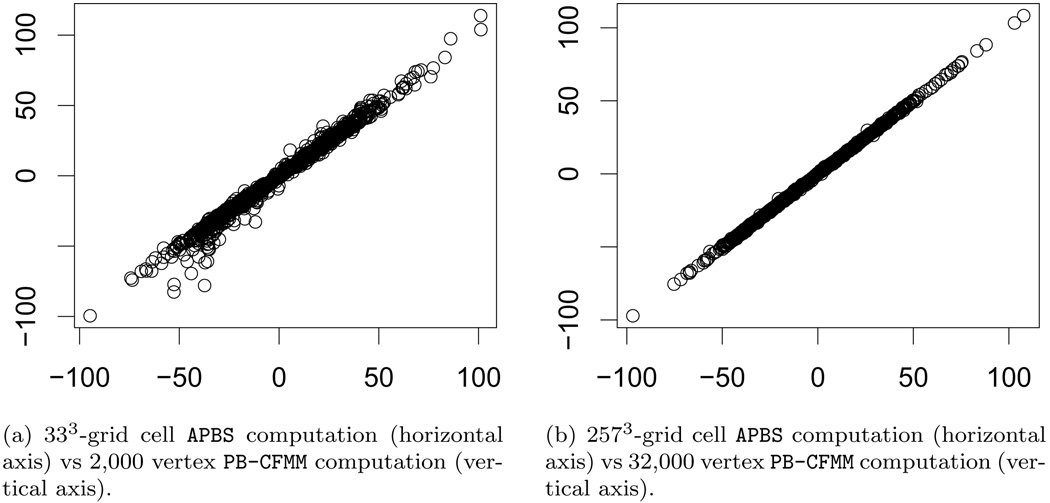
For a more detailed look at the results, we consider the per-atom energy values (i.e. individual terms in the summation (5.1)) for a particular molecule, nuclear transport factor 2 (PDB id: 1A2K). Figure 7.2 contains plots of the per-atom energy values for different mesh resolutions. The per-atom energies are consistent, especially between the highest resolution meshes. The median error over all atoms is 0.03 kcal/mol while the maximum error is 3.29 kcal/mol. Of the 3; 179 atoms, 46 have errors larger than 1 kcal/mol, and only two atoms have error larger than 2 kcal/mol. Figure 7.3 contains comparisons of per-atom energies resulting from the APBS solver.

FIG. 7.2.

Per-atom polarization energy values are compared for nuclear transport factor 2 (PDB id: 1A2K). Polarization energy is computed using surface meshes with 2,000, 8,000, and 32,000 mesh vertices. The energy values for the high-resolution (32,000 vertex) mesh are given on the horizontal axis.

FIG. 7.3.

Per-atom polarization energy values are compared for nuclear transport factor 2 (PDB id: 1A2K). Polarization energy is compared between PB-CFMM and APBS.

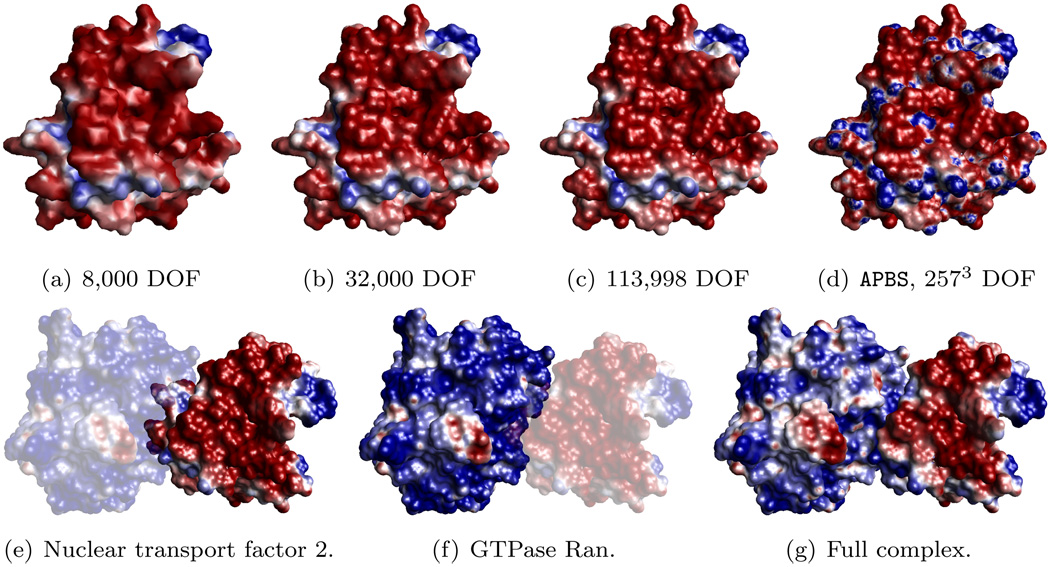
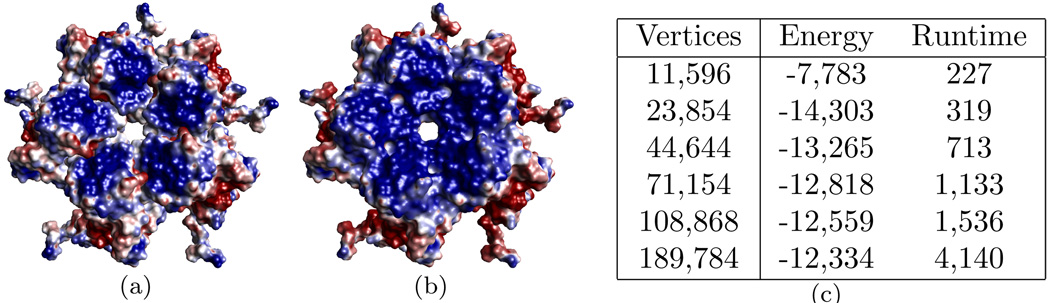
Figure 7.4 demonstrates an electric potential computation for a typical protein complex. Figures 7.4(a–c) depict electric potential a molecule using different resolution surfaces meshes. These results can be compared to those produces by APBS shown in Figure 7.4(d). Figures 7.4(e–f) depict the potential computed separately for the two components. Finally Figure 7.4(g) contains the surface potential for the entire complex. An example of a pentamer (a complex of five identical proteins) from the Cucumber Mosaic Virus is given in Figure 7.5. Each of the five monomers in the pentamer contain 2,486 atoms. The full viral capsid contains 180 monomers highlighting the need for scalable methods to process molecules with millions of atoms and surfaces discretized with a comparable number of triangles.

FIG. 7.4.

The electrostatic potential on molecular surface for the complex between nuclear transport factor 2 and GTPase Ran (PDB id: 1A2K). In all cases, the potential is between −3.8 k_bT/e_c (red) and +3.8 k_bT/e_c (blue). (a–c) Electric potential of the nuclear transport factor 2 molecule using surface meshes containing 8,000, 32,000, and 113,998 vertices. (d) The surface potential computed by APBS. (e–f) Electric potential of the two component molecules. (g) Electric potential of the molecular complex.

FIG. 7.5.

Pentamer of the Cucumber Mosaic Virus (PDB id: 1F15). Electrostatic potential for each of the monomers computed separately (a) and as a single subunit (b). Energy (in kcal/mol) and runtime (in seconds) for the combined subunit is given for several different resolution surface meshes.

We demonstrate the need for the derivative boundary formulation and a curved approximation of the geometry by comparison to simpler alternatives. For this task we considered a set of 20 proteins from the ZDOCK benchmark. The derivative boundary integral formulation requires fewer iterations to terminate and for a fixed tolerance ε_tol, gives a more accurate solution. Specifically we compared the dBIE and nBIE formulations for a very modest GMRES tolerance, ε_tol = 10⁻³. The results are tabulated in Table 7.6. The dBIE formulation requires noticeably fewer GMRES iterations, but the dBIE formulation requires more computation time because it requires 16 fast multipole calls per iterations compared to only four required in the nBIE formulation. However, the advantage is of the dBIE formulation is seen by looking at the error in the energy value computed after termination: the dBIE energy values are very near the final value for a large ε_tol while the nBIE energy values contain substantial error.

TABLE 7.6.

Comparison of nBIE and dBIE formulations on 20 example proteins. Error is computed with respect to the numerical solutions on the same mesh using a much lower GMRES tolerance (10⁻⁷).

geometry formulation	A-Spline nBIE	A-Spline dBIE	Linear dBIE
median # iterations	40	17	*
max # iterations	47	26	*
median energy error	11.28	0.12	50.65
max energy error	17.55	0.46	61.92

^*Computation was halted after 100 GMRES iterations: each computation involving linear geometry reached 100 iterations.

The curved representation of the geometry yields a similar, yet more dramatic, impact on the energy computation: the computation requires more GMRES iterations while yielding much poorer energy values.

Table 7.7 contains results of our algorithm on the 20 protein test set when varying the fast multipole accuracy parameter N_fmm. Meaningful differences in the final energy computation are only apparent for the lowest N_fmm value and even then these differences are small. In practice, we observe that polarization energy computations are not very sensitive to the fast multipole accuracy, especially when compared to the effects of the problem formulation and the molecular surface selection.

TABLE 7.7.

Results of polarization energy computation on 20 example proteins when varying N_fmm. Error in the energy computation is reported as a percentage.

Nfmm	2	4	6	8
median energy error	0.77	4.21 × 10−3	1.24 × 10−4	-
median compute time	316	493	737	1151

8. Final Remarks

We have described a complete software pipeline for computing the electrostatic potential and polarization energy of biomolecules based on atomic descriptions. Our software is based on general purpose scientific computing codes PETSc and KIFMM3d, and performs favorably against a specialized linearized Poisson-Boltzmann solver. Our experiments demonstrate the benefits of the dBIE formulation of the Poisson-Boltzmann equation and a smooth representation of the molecular surface when simulating actual proteins.

In a similar fashion to the polarization energy, interior and exterior electrostatic potential and per-atom forces can also be computed as a post-process to the Poisson-Boltzmann solver. Integral formulations of the interior and exterior electrostatic potential are given in [43] while a derivation of the atomic forces can be found in [32]. Also worth consideration are more detailed models of molecular electrostatics including an ion exclusion layer surrounding the molecule and regions of differing dielectric constant. Altman et al. [1] formulate a system including these features with respect to the nBIEs and a similar extension should apply to the dBIE system. Moreover, the construction of the ASMS [80] should be useful in generating parallel surfaces required by the ion exclusion layer by picking different level sets a single function over the prismatic scaffold region.

Both PETSc and KIFMM3d are designed for parallel computation [74] and can be applied to our solution approach. However, for a number of problems the Poisson-Boltzmann equation must be solved many times; for example, the molecular docking problem requires polarization energy to be computed over many potential docked configurations. In such cases it is often more natural to find separate Poisson-Boltzmann solutions in parallel rather than parallelize the individual computations.