Free energy reconstruction from nonequilibrium single-molecule pulling experiments

Abstract

Laser tweezers and atomic force microscopes are increasingly used to probe the interactions and mechanical properties of individual molecules. Unfortunately, using such time-dependent perturbations to force rare molecular events also drives the system away from equilibrium. Nevertheless, we show how equilibrium free energy profiles can be extracted rigorously from repeated nonequilibrium force measurements on the basis of an extension of Jarzynski's remarkable identity between free energies and the irreversible work.

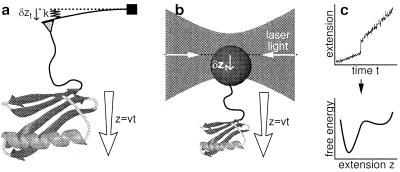
Recent advances in the micromanipulation of single molecules have led to new insights into the dynamics, interactions, structure, and mechanical properties of individual molecules (1–4). Single-molecule manipulation with an atomic force microscope (AFM) (5–9), laser tweezer stretching (10), and analogous computer experiments pioneered by Schulten and coworkers (11–13) have revealed details about unfolding and unbinding events of individual proteins and their complexes. In an AFM experiment, a molecule is subjected to a time-varying external force, for instance by pulling on the end of a linear polymer (Fig. 1). The applied force is determined from the time-dependent position of the cantilever tip with respect to the sample. Thus, one can drive rare molecular events (14), determine their force characteristics, and simultaneously monitor them with atomic resolution. However, both experiments and simulations actively perturb the system, leading to hysteresis and nonequilibrium effects.

Figure 1.

Single-molecule force measuring experiments by using AFM (a) and laser tweezers (b). In the AFM experiment (a), the sample is moved at a constant speed v relative to the cantilever with spring constant k. The position z_t = vt + δz_t of the cantilever tip with respect to the sample is recorded, where δz_t is the displacement of the cantilever tip. From repeated measurements of z_t, the free energy profile G₀(z) of the unperturbed system can be determined exactly (c).

How can one extract equilibrium properties from such measurements that drive the system away from equilibrium (15, 16)? From the second law of thermodynamics, we know that on average, the mechanical work of pulling will be larger than the free energy. Only if the experiment is performed reversibly, i.e., infinitely slowly, will the work equal the free energy. Thus, making rigorous thermodynamic measurements by pulling appears to require an extrapolation to zero pulling speed. However, Jarzynski (17, 18) recently discovered a remarkable identity between thermodynamic free energy differences and the irreversible work, thus extending the inequality of the second law of thermodynamics. This identity, although not directly applicable to atomic force measurements, suggests that in principle one should be able to extract free energy surfaces from repeated pulling experiments. In this paper, we show how this can be done in practice.

Theory.

We begin by showing that Jarzynski's identity follows almost immediately from the Feynman–Kac theorem for path integrals (19). This derivation leads directly to the appropriate extension, which forms the basis for the solution of the free energy reconstruction problem. This extension has been obtained by Crooks (20) as a special case of an even more general relation between forward and backward path averages. Consider a system whose phase–space density evolves according to a Liouville-type equation:

1

ℒ_t is an explicitly time-dependent evolution operator that has the Boltzmann distribution as a stationary solution, ℒ_te^{−βℋ(x,t)} = 0, where ℋ(x, t) is a time-dependent Hamiltonian, and β⁻¹ = k_BT, with T the temperature and k_B Boltzmann's constant. For example, for diffusive dynamics on a potential V(x, t), the time evolution is governed by ℒ_{t =} D∇e^−βV(x,t)∇e^βV(x,t), where D is the diffusion coefficient and ∇ = ∂/∂x. Other examples include systems that undergo Newtonian, Langevin, Nosé–Hoover thermostat, or Metropolis Monte Carlo dynamics. Now consider the unnormalized Boltzmann distribution at time t,

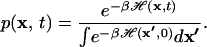2

Because this distribution is stationary (ℒ_tp = 0), and because ∂p/∂t = −β(∂ℋ/∂t)p, it follows that the above p(x, t) is a solution of the sink equation,

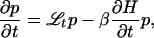3

as can be verified by direct substitution. However, the solution of this sink equation, starting from an equilibrium distribution at time t = 0, can also be expressed as a path integral by using the Feynman–Kac theorem (19). Equating these two different solutions immediately gives:

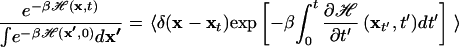4

where δ(x) is Dirac's δ distribution. This identity between a weighted average of nonequilibrium trajectories (right) and the equilibrium Boltzmann distribution (left) is implicit in the work of Jarzynski (18), and is given explicitly by Crooks (equation 24, ref. 20). The average 〈…〉 is over an ensemble of trajectories starting from the equilibrium distribution at t = 0 and evolving according to Eq. 1. Each trajectory is weighted with the Boltzmann factor of the external work w_t done on the system,

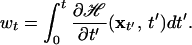5

Integrating both sides of Eq. 4 with respect to x, we obtain Jarzynski's identity (17, 18)

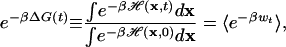6

between the Boltzmann-averaged work w_t and the equilibrium free energy difference ΔG(t) between times t and 0.

Free Energy Surfaces from Cantilever Positions.

Eq. 4 allows us to reconstruct the underlying free energy surface from repeated single-molecule AFM experiments. The setup in Fig. 1a can be described by a Hamiltonian ℋ(x, t) = ℋ₀(x) + k(z − vt)²/2, where ℋ₀(x) is the Hamiltonian of the resting, unperturbed system, and z = z(x). Here, we have assumed for simplicity that the cantilever is vibrating in a harmonic potential with spring constant k. Substituting this Hamiltonian into Eq. 4, multiplying both sides by δ[z − z(x)], integrating over all x, and finally taking the logarithm, we have:

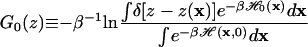7

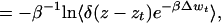where G₀(z) is (to within an additive constant) the unperturbed free energy profile along the pulling coordinate z; and Δw_t is the external work minus the instantaneous biasing potential, Δw_t = w_t − k(z_t − vt)²/2 = kv(vt²/2 − ∫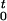z_t′ dt′) − k(z_t − vt)²/2. At time t = 0, the trajectories are started from points z₀ drawn from a Boltzmann distribution corresponding to Hamiltonian ℋ(x, 0) = ℋ₀(x) + kz²/2.

Given the positions z_t of the cantilever at time t obtained from repeated pulling experiments, we can reconstruct the unperturbed free energy profile G₀(z) along z by using Eq. 7. At each time slice t, one can in principle obtain an estimate of the whole free energy surface. In practice, at any given time t, only a small window around the equilibrium position z = vt will be sampled adequately. Thus, an average over several time slices and repeated trajectories is required to obtain an optimal estimate of the free energy surface. At every time slice t, one obtains an ensemble of positions z_t and corresponding w_ts. The positions z_t are binned, and the corresponding histogram values are incremented by e^−βw_t. The complete free energy surface G₀(z) can then be reconstructed by adapting the weighted histogram method (21):

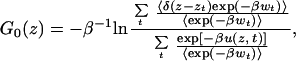8

where the sum is over time slices t and u(z, t) is the time-dependent biasing potential [here: u(z, t) = k(z − vt)²/2]. As in the weighted histogram method (21), this procedure can be refined by making Eq. 8 self-consistent through replacement of 〈exp(−βw_t)〉 with exp[−βΔG(t)] = ∫exp {−β[u(z, t) + G₀(z)]}dz/∫exp{−β[u(z, 0) + G₀(z)]}dz, thus requiring an iterative solution for ΔG(t).

To illustrate in detail how this formalism is implemented, we simulate a pulling experiment by conducting Brownian-dynamics simulations on a double-well free energy surface. Ten trajectories were generated on the time-dependent surface V(z) + k(z − vt)²/2 with a pulling velocity v = 1 μm s⁻¹, a diffusion coefficient D = 10⁻⁷ cm² s⁻¹, and a cantilever spring constant k = 20.6 pN nm⁻¹ (=0.0206 mN m⁻¹). The pulling velocities and cantilever spring constants are typical of AFM experiments (2, 6). For this diffusion coefficient, the escape rate from the stable minimum is about 10⁻⁶ s⁻¹ on the basis of Kramers' theory, in the range of unfolding rates for fairly large proteins under native conditions. The free energy difference between the two states separated by a barrier is ≈14 kcal/mol (at 298 K), again typical of protein unfolding. Nevertheless, this simple one-dimensional model is only a crude approximation to real experiments where several other factors intrude, such as viscous damping of the cantilever motion or slow conformational relaxation orthogonal to the pulling direction (14).

In the pulling simulations, the “cantilever” is moved relative to the “sample” by 20 nm within a time of 20 ms. The position z_t and accumulated work w_t = kv(vt²/2 − ∫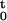z_t′ dt′) are recorded for 10 runs and analyzed by using Eq. 7. For every pulling trajectory k (k = 1,… ,K; here: K = 10), we determine at discrete times t_i (i = 0,… ,N; here: N = 100 time points separated by 0.2 ms) the position of the cantilever z_ik with respect to the sample, and the corresponding deflection δz_ik = z_ik − vt_i. From the deflection, we obtain the instantaneous deflection energy u_ik = kδz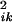/2. The external work is determined by numerical integration: w_ik = kv[vt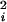/2 − Σ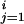(t_j − t_j−1)(z_jk + z_j−1,k)/2] with w_ik = 0 for i = 0. The results of repeated trajectories are then combined. At every time slice t_i, we average 〈exp(−βw_t)〉 ≈ η_i ≡ K⁻¹Σexp(−βw_ik). To approximate the average in the top numerator of Eq. 8, we also collect histograms h_i(l) at times t_i with z-position intervals of Δz:

9

where θ_l(z) is one if z is in the lth interval [(l − 1)Δz ≤ z < lΔz] and zero otherwise. We then estimate the free energy profile by averaging over all time slices t_i:

10

Fig. 2 compares the reconstructed and exact free energy surfaces. With the exception of the poorly sampled barrier region because of snapping motion (Fig. 2 Inset), the surface is accurately reproduced. We note that at high pulling speeds, the increasing variance of w_t will lead to a systematic bias of the estimator for −β⁻¹ln〈δ(z − z_t)exp(−βw_t)〉, which can be approximately corrected for by using a cumulant expansion.

Figure 2.

Simulated pulling experiment over a 30 k_BT barrier. The solid line and symbols show the reference free energy V(z) and the reconstruction from 10 pulling simulations, respectively. Inset shows the force-versus-extension curve for one of the pulling simulations.

Free Energy Surfaces from Pulling Forces.

So far, we made use of position-versus-time curves. However, it is force-versus-position curves that are commonly reported from pulling experiments. As above, we assume a Hamiltonian ℋ(x, t) = ℋ₀(x) + u[z(x), t]. The unperturbed system described by ℋ₀ is coupled to the measurement apparatus through u[z(x), t], which will typically be a harmonic potential, u[z(x), t] = k(z − vt)²/2. The work entering the free energy expression Eq. 9 can be rewritten as

11

where the restoring force is F(z, t) = −∂u(z, t)/∂z, and the integral is along the position-versus-time contour connecting z₀ and z_t. This identity follows from du = (∂u/∂z)dz + (∂u/∂t)dt. Combining Eqs. 7 and 11 leads to the surprising result that the work entering into the free energy profile G₀(z) is not given simply by the force-versus-distance integral, but by an additional factor reflecting the biased choice of the initial state,

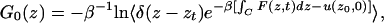12

where the initial points are drawn from a Boltzmann distribution according to ℋ(x, 0) (i.e., for the system interacting with the cantilever, as above). Therefore, if force integrals of two or more trajectories are combined, individual trajectories should be weighted by the reciprocal Boltzmann factor exp[βu(z₀, 0)]; i.e., one should subtract from the integrated work the energy stored in the deflected cantilever at time t = 0.

In an AFM experiment, it is thus important to record the zero-force position (δz = 0 in Fig. 1) with the cantilever sufficiently far from the sample. As the cantilever tip is brought into contact with the sample, a sufficiently long relaxation is important to draw initial states from an equilibrium Boltzmann distribution. We note that this new equilibrium will normally not be centered around δz = 0, but according to the combined Hamiltonian ℋ(x, 0) of the sample coupled to the cantilever spring. Nevertheless, the center of this initial distribution can be used to align the z positions of repeated pulling traces. As the cantilever is retracted, both z_t and δz_t are recorded. With known cantilever spring constant k and pulling speed v, the work can then be obtained from time or position integration.

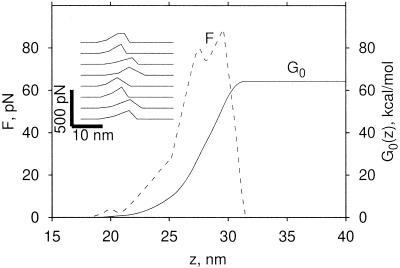
As a final illustration, we analyze force spectra for extracting individual bacteriorhodopsin molecules from purple membrane patches of Halobacterium salinarum as measured by Oesterhelt et al. (8). In these experiments, a cantilever tip was attached to bacteriorhodopsin, and the protein was slowly pulled out of the membrane. This led to sequential unraveling of the transmembrane helices, resulting in unfolding of the protein. Specifically, we analyze the force-versus-distance curves for one of the experiments (G241C mutant) and estimate a free energy profile for extraction and unfolding of helices D and E, corresponding to the second peak at pulling distances of 20–30 nm in figure 5 of ref. 8. Because the force is fluctuating around the baseline before and after this force peak, we assume (i) that the additional bias u(z₀, 0) in Eq. 12 is of the order of k_BT and thus negligible on the scale of the integrated work; and that (ii) a quasiequilibrium was established before the force peak. We also assume (iii) that the force curves are aligned. We can then integrate the forces and use Eq. 12 to estimate the underlying free energy profile G₀(z), as shown in Fig. 3. Also shown is the mean restoring force, F(z) = dG₀(z)/dz, corresponding to reversible pulling. The noise in the force F(z) reflects uncertainties in the z-position alignment and the finite number of measurements. For extraction and stretching of the 57-amino acid stretch with 56 amino acids contained in helices D and E, we estimate a free energy of about 64 kcal/mol, or about 1.1 kcal/mol per residue, and a mean-force peak of about 89 pN. Although these values seem overall reasonable, they should not be considered to be accurate before the above assumptions are removed by appropriate experimental design. In addition, one must account for instrument resolution, which leads to increased variation of the integrated work. Finally, the influence of the pulling speed needs to be investigated. In general, to extract accurate thermodynamic information from a small number of pulling experiments, it will be important to achieve small standard deviations of the work, possibly of a few k_BT, by pulling sufficiently slowly.

Figure 3.

Free energy G₀(z) (solid line, right-hand scale) and mean restoring force F(z) = dG₀(z)/dz (dashed line, left-hand scale) of extracting and unfolding the D and E helix of the G241C mutant of bacteriorhodopsin. Eq. 12 was used to estimate G₀(z) from linear approximations (Inset) to the second peak of eight force-versus-distance curves reported in figure 5, Oesterhelt et al. (8).

Conclusions

We have shown how free energy surfaces can be reconstructed rigorously from repeated molecular pulling experiments. With this formalism, thermodynamic properties such as binding equilibria can be extracted from repeated measurements by using AFM (2, 5–9, 12), laser tweezers (1, 4), or magnetic beads (3). In addition, this work has implications in the area of computer simulations. For example, when a time-dependent harmonic potential is added to the Hamiltonian as above, our procedure is a dynamic generalization of umbrella sampling (22). The weighted-histogram method permits the combination of dynamic umbrella sampling runs with different pulling speeds or directions. Moreover, this generalization has the immediate advantage that no equilibration is required in different windows, and thus the entire trajectory can be used to reconstruct the underlying free energy surface.

Abbreviation

AFM

atomic force microscopy