High-Throughput Variation Detection and Genotyping Using Microarrays

Abstract

The genetic dissection of complex traits may ultimately require a large number of SNPs to be genotyped in multiple individuals who exhibit phenotypic variation in a trait of interest. Microarray technology can enable rapid genotyping of variation specific to study samples. To facilitate their use, we have developed an automated statistical method (ABACUS) to analyze microarray hybridization data and applied this method to Affymetrix Variation Detection Arrays (VDAs). ABACUS provides a quality score to individual genotypes, allowing investigators to focus their attention on sites that give accurate information. We have applied ABACUS to an experiment encompassing 32 autosomal and eight X-linked genomic regions, each consisting of ∼50 kb of unique sequence spanning a 100-kb region, in 40 humans. At sufficiently high-quality scores, we are able to read ∼80% of all sites. To assess the accuracy of SNP detection, 108 of 108 SNPs have been experimentally confirmed; an additional 371 SNPs have been confirmed electronically. To access the accuracy of diploid genotypes at segregating autosomal sites, we confirmed 1515 of 1515 homozygous calls, and 420 of 423 (99.29%) heterozygotes. In replicate experiments, consisting of independent amplification of identical samples followed by hybridization to distinct microarrays of the same design, genotyping is highly repeatable. In an autosomal replicate experiment, 813,295 of 813,295 genotypes are called identically (including 351 heterozygotes); at an X-linked locus in males (haploid), 841,236 of 841,236 sites are called identically.

The central goal of human genetics is to identify, characterize and ultimately understand the specific DNA variants that contribute to human phenotypes in general, and human disease in particular (Lander and Schork 1994; Chakravarti 1999; Zwick et al. 2000, 2001; On-line Mendelian Inheritance in Man 2001). The genetic approach to this problem is, in principle, straightforward. First, we identify individuals showing phenotypic variation for the trait of interest. Second, we genotype genetic variants, such as microsatellites or SNPs, in all of the individuals in a study. Third, we perform appropriate statistical tests to identify any genetic variants correlated with variation in the phenotype. Finally, if such variants are found, we perform additional experiments to demonstrate a causal relationship.

Step two poses a question: What genetic variants should be examined? The answer to this question must balance technological and practical considerations. Nevertheless, in the best of all worlds, a researcher would be able to determine the genotype of every base in every sample, that is, a complete resequencing of the entire genome of all individuals under study. No technology currently exists to do this in an economical manner. Moreover, any technology used for this purpose must be capable of extraordinary resequencing accuracy.

Nucleotide diversity in the general human population is ∼8 × 10⁻⁴ per site (Cargill et al. 1999; Halushka et al. 1999; The International SNP Map Working [TISMW] Group 2001; Venter et al. 2001; this study). This implies that a randomly selected chromosome will differ from the human reference sequence at ∼8 of every 10,000 bases. Now, imagine a technology that allowed one to rapidly and inexpensively determine the genotype of an individual at every nucleotide site of interest with an accuracy of 99.9%. Such a technology would be remarkable, but insufficient. The problem with only 99.9% accuracy is that this implies 10 errors for every 10,000 bases. Because the true rate of variation is eight in 10,000, 55.5% of the identified variants will be errors. This is unacceptably high. The error rate needs to be much lower.

Microarrays are inherently parallel devices that offer the promise of determining the genotypes of individuals at every site of interest with a limited level of effort (Fodor et al. 1991; Southern et al. 1992; Pease et al. 1994; McGall et al. 1996; Lipshutz et al. 1999). Variation Detection Arrays (VDAs) manufactured by Affymetrix have been used to such an end with success (Chee et al. 1996; Hacia et al. 1996, 1998a,b, 1999, 2000; Hacia and Collins 1999; Halushka et al. 1999; Wang et al. 1998). Unfortunately, it has also been reported that between 12% and 45% of the detected variants are false (Cargill et al. 1999; Halushka et al. 1999; Wang et al. 1998). This indicates that VDAs are, on average, between 99.99% and 99.93% accurate.

Although microarrays may be, on average, insufficiently accurate, it is certainly possible that a large fraction of genotype calls are, in fact, much more accurate than 99.9% and a smaller fraction are much less than 99.9% accurate. The approach used here is to construct an objective statistical framework to distinguish genotype calls that can be made with extraordinary accuracy from those less reliable. The need to build such a framework for microarrays is not a new idea (Southern et al. 1992) and the objectives are to strive for some of the accomplishments that Green and colleagues (Nickerson et al. 1997; Ewing and Green 1998; Ewing et al. 1998; Gordon et al. 1998; Rieder et al. 1998) have made for automated sequencing, namely the assignment to individual genotype calls of a quality score that is larger for calls more likely to be accurate. Green and colleagues, in fact, have done even more; phred provides not only a quality score that increases with increasing accuracy, but also a direct estimate of the probability that a base call is correct.

Researchers performing automated sequencing routinely rely on these phred scores (Ewing and Green 1998; Ewing et al. 1998), and in conjunction with certain other neighborhood quality rules (Altshuler et al. 2000; Mullikin et al. 2000), can achieve an extremely high level of accuracy for SNP discovery (T.I.S.M.W. Group 2001). This work attempts the same task. An objective statistical framework is developed to assign to each VDA genotype call a quality score. Certain simple neighborhood rules are applied, and sites in which extraordinarily high confidence can be placed are distinguished from those less reliable sites. In contrast to automated sequencing experiments that employ only haploid targets (Altshuler et al. 2000; Mullikin et al. 2000), this statistical method can be applied to both haploid and diploid targets. We call the system ABACUS (from Adaptive Background genotype Calling Scheme, see below) and will show that, in general, greater than 99.9999% accuracy can be achieved on >80% of the genotype calls on a VDA.

RESULTS

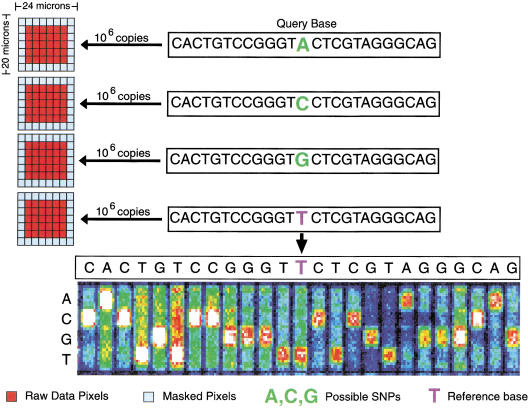
High-density VDAs were fabricated using standard photolithography and solid-phase DNA synthesis by Affymetrix, Inc., as described previously (Fodor et al. 1991; McGall et al. 1996; Lipshutz et al. 1999). Each of the 70 distinct VDA designs, designated CWRS-1 through CWRS-70, consisted of ∼300,000 features with a feature size of 24 × 20 μm (Fig. 1). A feature consists of ∼10⁶ copies of a 25-bp long oligonucleotide probe of defined sequence. To query a specific site determined from the human genome reference sequence, four features are tiled on the VDA. The four features differ only by the central or 13th base, which consists of each of the four possible nucleotides (Fig. 1). Each human genome site is queried for both the forward and reverse strands at different locations on the VDA.

Figure 1.

Eight features (four for the forward strand and four for the reverse complement strand) are associated with every queried site. Each feature consists of a 25-base oligonucleotide. The 13th base is the query base and all possible genotypes are tested. Each feature is divided into 56 equal pixels, and the pixels are scanned individually. The outermost 26 pixels are “masked,” so that only the 30 interior pixels are used for any calculation.

After amplification and hybridization of the target DNA to the oligonucleotide probe features (see Methods for detailed description of protocols employed), each VDA feature is scanned. The scanner measures the fluorescence intensity for each feature by dividing each feature into 56 equal-sized pixels. The 26 pixels located at the border of the features are masked and their fluorescence intensity values are not used in any subsequent calculations. The fluorescence intensity at the remaining 30 pixels constitute the raw data measured by the detector.

ABACUS: An Automated Statistical System for Calling VDA Genotypes

ABACUS is an automated statistical system for determining individual VDA genotypes whether the site is polymorphic or not. It can be applied in experiments in which the target DNA sequences are either haploid or diploid. In effect, the ABACUS system allows an investigator using VDAs to determine the DNA sequence in a sample of interest. ABACUS has been implemented in ANSI standard C code, and is available to academic colleagues on request. The fundamental assumption underlying the ABACUS algorithm is that the observed florescence intensities are normally distributed within features. We make this assumption relying on the central limit theorem. Each feature consists of ∼1 million distinct oligonucleotides of identical composition. If an appreciable fraction of these oligonucleotides are relatively independent in their chance of binding a labeled target, the overall florescence intensity of this feature ought to be normally distributed under some strong version of the central limit theorem. Of course, this assumption can and should be tested, and, if necessary, later relaxed. A series of statistical models are developed under the assumption of the presence or absence of various genotypes in the target sample. The likelihood of each statistical model for a given genotype is calculated independently for both the forward and reverse strands and is combined for the overall likelihood of the model. A “quality score,” which is the difference between the log (base 10) likelihood of the best fitting model and the second best fitting model, is assigned to each VDA genotype. A site genotype is “called” when one model fits the data sufficiently better than all other models. After all the individual VDA genotypes are called, additional heuristic, reliability rules are applied. On the completion of this procedure, all sites are assigned a genotype with a corresponding quality score. Individual VDA genotypes deemed unreliable are designated N. The system is divided into six stages.

Stage One: Data Integrity Check

No Signal

If in a given sample, any feature within any site (either forward or reverse strand) has a mean intensity within two standard deviations of zero, the site is said to have failed in that individual, and this site is ruled N in that individual.

Extremely Weak Signal

If, in a given sample, the highest mean intensity feature on the forward or reverse strand is 20-fold lower than the average highest mean intensity feature, averaged over all samples on that same strand, than this site is said to have failed in this individual, and this genotype is called N in the individual. In our experience, when this situation occurs at any site, it often occurs over a large number of adjacent sites in the same individual, indicating weak PCR products, improper digestion of sample DNA before hybridization.

Saturation

Among the four features on either the forward or reverse strands, if two (for haploid data) or three (for diploid data) of the features are within two standard deviations of 43,000, the detector is said to have saturated and this site is called N in the given individual. Decreasing the amount of labeled target DNA hybridized to the VDA easily solves saturation.

Aberrant Signal-to-Noise Ratio

The ratio of the mean intensity to the standard deviation of the intensity for a feature will be called the signal-to-noise ratio (SN) of that feature. Over the 57 autosomal VDA designs (∼513 million features), >90% of all features had an SN <20 with a median of ∼8. The tail of the distribution is extremely long, including >100,000 features with an SN above 1000. Sites with one or more features having aberrantly large SN generate aberrantly large likelihoods because as the signal approaches detector limits, it becomes truncated by the detector and appears to have an unusually small variance. As a consequence of these unusually low variances, genotype calls at these sites tend to be highly unreliable. Therefore, to avoid statistical aberrations associated with this, any site with an SN >20 is assigned a variance, so that SN = 20.

Stage Two: Building Models With an Even Background

Assumptions for All Modeling

Within any given feature, the florescence intensities of all pixels are assumed to be independent and identically distributed. The distribution is assumed to be Gaussian (normal); forward and reverse strands are treated as independent replicates (with different parameters). The final likelihood for a model is calculated by multiplying the likelihood on the forward strand by the likelihood on the reverse strand. Therefore, the log (base e) likelihood of a set of pixel florescence intensities is given by

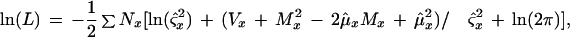where N_x is the number of pixels observed in feature x (N_x generally is equal to 30, but this number can vary slightly with imperfect grid alignment), V_x is the observed variance for feature x, M_x is the observed mean for feature x, μ_x is the estimated mean for feature x under the model in question, and ς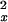 is the estimated variance for feature x. The sum is taken over all features x, where x is either A, C, G, or T, on the forward and reverse strands.

Null Model

All features on the forward strand are assumed to have identical means and variances. All features on the reverse strand are assumed to have identical means and variances, but these may differ between the two strands; these parameters are set equal to their maximum likelihood estimators. Maximum likelihood estimates can be found by differentiating Equation 1, with respect to all parameters and solving simultaneously. This results in the naive estimators, which are

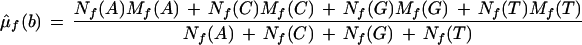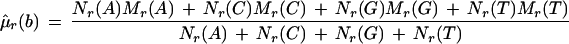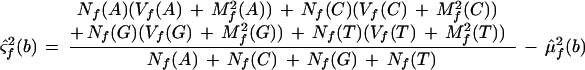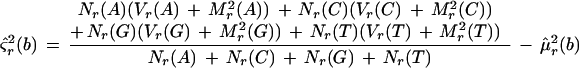where μ̂_f(b) and μ̂_r(b) are the estimated mean background intensities on the forward and reverse strands, respectively. The ς̂²s are the analogous variances. Let L_f(0) and L_r(0) be the likelihoods of the null model restricted to the forward or reverse strand, respectively. L(0) = L_f(0)L_r(0) is the overall likelihood of the null model.

Homozygote Models

Consider the hypothesis that the sample is an A homozygote. Under this model, features C, G, and T on the forward strand are assumed to be independent and identically distributed. The background mean and background variance is estimated by maximum likelihood to be

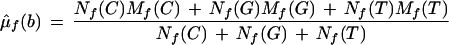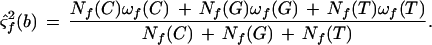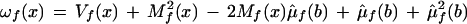Feature A on the forward strand is assumed to have a different mean and variance, and these are estimated by maximum likelihood to be the observed values. Therefore,

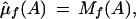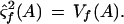The reverse strand is treated analogously.

Let L_f(A) and L_r(A) be the likelihoods of the A homozygote model restricted to the forward strand and reverse strand, respectively. If the estimated mean for A is less than the estimated mean for the background, the likelihood is set equal to the null model likelihood. Therefore, if μ̂_f(A) < μ̂_f(b) then L_f(A) = L_f(0). Similarly, if μ̂_r(T) <μ̂_r(b) then L_r(A) = L_r(0). L(A) is the overall likelihood of the A homozygote model, L(A) = L_f(A)L_r(A).

All other homozygote models are treated analogously.

Heterozygote Models

When examining diploid data, six (A-C, A-G, A-T, C-G, C-T, G-T) heterozygote models, beyond the four homozygote models, are also considered. Consider an A-C heterozygote. Background features G and T on the forward strand are assumed to be independent and identically distributed. The mean and variance is estimated by maximum likelihood and given in the supplemental text available on-line at http://www.genome.org. Features A and C on the forward strand are assumed to be independent and identically distributed, and parameter estimates are given in the supplemental text available on-line at http://www.genome.org.

Stage 3: Compare Models

For haploid data, a total of five models are examined (Null, A, C, G, T). For diploid data, a total of 11 models are examined (Null, A, C, G, T, AC, AG, AT, CG, CT, GT).

Quality Scores for Each Model

For each model, three quality scores are calculated. For Model A, Q_f(A) = Log₁₀(L_f(A)) − Log₁₀(L_f(max other)), where L_f(max other) is the maximum over all models other than A (also notice that these logs are taken base 10, not base e). Therefore, Q_f(A) is the difference between the log likelihood of model A on the forward strand and the best fitting model on the forward strand, excluding A. If Q_f(A) is positive, A is the best fitting model on the forward strand. We will call Q_f(A) the quality score for model A on the forward strand. Q_r(A) = Log₁₀(L_r(A)) − Log₁₀(L_r(max_other)) is the analogous quality score on the reverse strand. The overall quality score for model A is Q(A) = Log₁₀(L(A)) − Log₁₀(L(max_other)). Therefore, Q(A) is the difference between the likelihood of model A, overall, and the best fitting model, excluding A, overall. If Q(A) is positive, A is the best fitting model, overall. Similar statistics are calculated for all other models.

In addition, two further likelihoods are calculated: L_f(Perfect) and L_r(Perfect). These likelihoods correspond to the likelihood of the best possible fitting model on the forward and the best possible fitting model on the reverse strand. A “perfect” fitting model is defined by the predicted mean intensity for all features equaling the observed mean, and the predicted variance for all features equaling the observed variance. This “perfect fit” model is simply the unconstrained, fully parameterized model. All other models are nested within it. Therefore, L_f(Perfect) is the largest likelihood possible on the forward strand, and L_r(Perfect) is the largest likelihood possible on the reverse strand.

There are two set of criteria (quality thresholds) necessary to call a site. One set of quality thresholds corresponds to a single model fitting the data exceptionally well (nearly perfectly). A second, more stringent set of requirements, corresponds to no model fitting nearly perfectly, but one model fitting the data much better than any other model.

Calling a Near-Perfect Fit

The perfect fitting model has eight parameters per strand. Any particular genotype model has four parameters per strand, and each of these models is nested within the perfect fitting model. Therefore, standard likelihood ratio tests can be used to compare the fit of any particular model with the perfect fitting model. Therefore, D_f = 2[ln(L_f(perfect)) −ln(L_f(model))] ought to be χ² distributed with 4 degrees of freedom (D_r is defined similarly). We will consider a model to fit nearly perfectly if D_f and D_r are sufficiently small. For this work, sufficiently small is defined as <6.63 (∼85% confidence interval).

When one model fits nearly perfectly, and all other models fit much more poorly, we will call this model a near-perfect fit. Comparing the fit of one model to another is not straight forward, as these models are not nested and have the same number of parameters. If we naively assume that the difference in the fit between any two non-nested models is χ² distributed with 1 degree of freedom, then Q_f(near-perfect fit model) >5.2 would imply that there is less than a 10⁻⁶ chance that the difference in fit is attributable to chance. Therefore, if any model fits nearly perfectly, with Q_f(model) >5.2 and Q_r(model) >5.2, then the genotype associated with this model is called.

Calling an Imperfect Fit

It is rare for any model to fit nearly perfectly. When no model fits nearly perfectly, there is no obvious way to relate quality scores to statistical probabilities. With no a priori predictions for what a good quality score ought to be, quality scores necessary to call a model have been determined empirically by examining the data generated from this project. Two thresholds for quality scores have been established, a “total threshold,” T_total, and a “strand threshold,” T_strand. A model is said to fit significantly better than any other model when Q(model) >T_total, and Q_f(model) >T_strand and Q_r(model) >T_strand. When one model fits significantly better than all others, the genotype associated with this model is called. For the experiments described in this paper, T_total has been chosen to be 30, and T_strand has been chosen to be −2 (justification is described below).

If, for a given sample, no model can be called either a near-perfect fit, or an imperfect fit, N is assigned to this genotype.

Stage 4: Building Models With an Uneven Background (For Diploid Data Only)

All of the previous modeling (Stages 2 and 3) assumed that all background features had identical means and variances. This assumption is false. Moreover, background features with uneven means can appear very similar to heterozygotes. Table 1 gives the observed florescence intensities of two sites. One of the sites (CWRS-10) is taken from haploid data (X-linked locus in a male); the other (CWRS-50) is from a diploid locus (RET), and is a known (from previous genotyping) heterozygote. Our interpretation of these observations are: (1) There can be substantial cross-hybridization to background features and (2) cross-hybridization can create the appearance of heterozygotes. The interpretation that this phenomenon is attributable to cross-hybridization makes a strong prediction, namely that all samples should exhibit roughly the same unevenness of background features. This intuition motivates the design of the uneven background models. The uneven background models assume that the background features have means and variances that are constant ratios of each other. These ratio constants (αs and βs in the notation of the supplemental text available at http://www.genome.org) are obtained by averaging over all samples with the same genotype. We call this an adaptive background because the genotypes are, of course, not known a priori. We therefore infer the genotypes and the background in an iterative manner, changing the background constants as genotype calls change.

Table 1.

Uneven Background Features

CWRS-10 VDA design
Forward	Average intensity	Standard deviation	Reverse	Average intensity	Standard deviation
A	1510.5	164.6	T	2220.5	142.6
C	1209.0	99.1	G	1115.0	65.8
G	1263.0	94.9	C	1105.3	107.5
T	1724.8	96.4	A	2360.5	148

CWRS-50 VDA design
Forward	Average intensity	Standard deviation	Reverse	Average intensity	Standard deviation
A	2575.0	225.9	T	4889.5	345.3
C	1548.0	176.2	G	3412.0	509.5
G	2856.0	225.0	C	7411.5	370.6
T	4278.5	460.9	A	5680.0	389.2

Exemplar data from two different sites. CWRS-10 is from an X-linked region (FMR1) and the sample is male. Hence, the sample is haploid and cannot be a heterozygote. Nevertheless, it appears to be an A-T heterozygote. CWRS-50 is from an autosomal region (RET) and this particular sample is known to be a G-T heterozygote from previous genotyping (Carrasquillo, in prep.). By the criteria described in sections 1–3 (even background), the CWRS-10 site would be called a heterozygote, and the CWRS-50 site would be called N. 

Ten (four homozygote, six heterozygote) new models are derived, with unequal background intensities. Detailed description can be found in the supplemental text available at http://www.genome.org.

Calls

For each sample, a genotype will be called if any model satisfies the criteria specified in Stage 3.

Guesses

For samples that are unable to be called, if any model has Q(model) > 0, and Q_f(model) > 0 and Q_r(model) > 0, then this model is said to be “guessed.” Models are guessed when they fit better than any other model on both the forward and the reverse strands, but the fit does not reach the significance threshold necessary to be called.

No Guesses

Samples that are unable to be called or guessed are signified as “no guesses.”

A Posteriori Modification of Thresholds in the Presence of Two Different Homozygotes

Calling two different homozygote models (say, A and G) at the same site in two different samples indicates that there may be heterozygotes (A-G) among the samples. Any sample where the features associated with the heterozygote (A and G) are the two most intense features on the forward strand, and their complements (T and C) are the two most intense features on the reverse, is possibly a heterozygote. To call a non-heterozygote model at such a site requires additional confidence. In particular, to call a non-heterozygote model at such a site requires that Q(model) > 2T_total. Very loosely, calling a non-heterozygote model at this site requires the quality to be twice as good. If no model is called at such a site, the heterozygote model is guessed.

Stage 5: Iterate an Adaptive Background (For Diploid Data Only)

1. Apply the even background models. Make calls and guesses.

2. If >75% of the calls are heterozygotes, call all individuals N; make no guesses.

3. Make a posteriori modification to thresholds, if applicable.

4. Build adaptive background models. Make calls and guesses.

5. If any sample is called N for the 10th time, remove it from the analysis. If any sample has changed its call for the 20th time, remove it from the analysis.

6. If any call has changed since the last iteration, return to step 3.

 After stopping, if >90% of the samples are called heterozygotes, call all individuals N.

Stage 6: Apply Final Reliability Rules

Primer Failure

If, in a given sample, >50% of all sites between a given pair of PCR primers are designated N, then this PCR product is presumed to have failed. All sites covered by this primer pair are ruled N in this sample. Additionally, if the sites covered between a given pair of PCR primers are >5% different from the reference sequence, the experiment is said to have failed, and all sites covered by this primer pair are ruled N in this sample.

Neighborhood Rules

For a given site in a given sample, for a site to be considered reliable, at least 50% of the surrounding sites must be called. In particular, if in the surrounding 20 sites (10 on each side) there are >10 Ns, then this site is ruled unreliable, and it is designated N as well.

Elimination of SNP Doublets

Samples that harbor variants from the reference sequence (samples with SNPs) are often difficult to call reliably at the sites immediately surrounding the variant. In particular, samples homozygous for a site different from the reference often appear to be heterozygotes for the reference base and this SNP at sites near to the actual SNP position, but not at the SNP. The following procedure is used to eliminate these SNP doublets.

1.

Two SNPs within five bases of each other are considered a doublet. Designate these two SNPs as SNP 1 and SNP 2. Call an individual homozygous for the reference base, “wild-type.” Call all others “mutant.”

2.

If the mutant base at SNP 1 appears in an individual with the wild-type base at SNP 2, and another individual with the mutant base at SNP 2 has the wild-type base at SNP 1, both SNPs are believed and no further action is taken.

3.

If a mutant base at SNP 1 appears in an individual with wild-type at SNP 2, but mutants at SNP 2 only appear in individuals mutant at SNP 1 or called N at SNP 1, SNP 2 is not trusted. This site is called N in all individuals. Reverse SNP 1 and 2, and a similar logic applies.

4.

If mutants at SNP 1 always appear in individuals called mutant at SNP 2 (or N), and vice versa, the site with the fewer number of Ns is believed. The other site is called N in all individuals. If both sites have an equal number of Ns, both SNPs are considered unreliable and both SNPs are made N in all individuals.

Sample Reliability

A site must be called in at least 50% of the samples to be considered reliable. Any site designated N in >50% of the samples is ruled unreliable, and all samples are designated N at this site.

Application of the ABACUS Algorithm

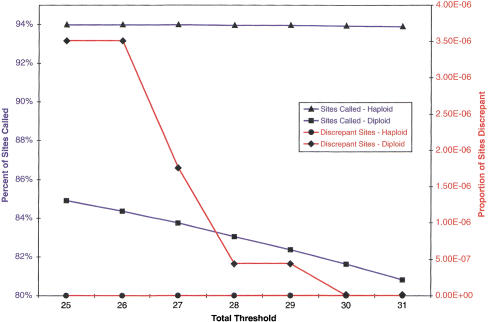
In general, the total threshold and strand threshold parameters will determine the number of sites called and the number of errors made in those calls. Choice of these values is inherently arbitrary and subject to trade-offs (Fig. 2). Increasing either threshold decreases the total number of sites called. It should also decrease the number of errors in those calls. Individual researchers can set these values as they desire depending on their individual assessment of the costs and benefits of this trade-off. We chose an ABACUS total threshold of 30 and a strand threshold of −2 for our data analysis in an attempt to maximize the number of site calls, while minimizing the number of discrepancies in two separate replicate experiments (see below). We then applied these ABACUS threshold values to analyze the data from 70 distinct VDA designs that screened the unique sequence from 32 autosomal and eight X-linked genomic regions (Supplemental Tables 1 and 2, available on-line at http://www.genome.org). The amount of unique sequence surveyed in each genomic region varied, but averaged 49,638 bp (range: 31,697 to 62,668) and was of variable GC content (range: 33.0% to 57.7%, Supplemental Tables 1 and 2, available at http://www.genome.org; see Methods). With our parameter selection, we are able to read ∼80% of all sites (402 kb of X-linked sequence in each of 40 individuals, calling 13,006,341 of 15,396,840 sites, 84.5%; 1.6 Mb of autosomal sequence in each of 40 individuals, calling 51,422,913 of 64,097,240 sites, 80.2%). We identified 5285 autosomal and 755 X-linked SNPs. The estimated nucleotide diversity (Watterson 1975) for autosomal regions is 7.8 × 10⁻⁴, whereas that for the X-linked regions is 5.3 × 10⁻⁴. These values are largely concordant with previous estimates (Cargill et al. 1999; Halushka et al. 1999) and remarkably similar to recent whole-genome estimates (T.I.S.M.W. Group 2001; Venter et al. 2001).

Figure 2.

In both haploid and diploid replicate experiments, the effect of varying the total threshold. Strand threshold = −2; total threshold is allowed to vary; for these thresholds; haploid data varies far less than diploids.

Repeatability and Accuracy of ABACUS Calls

We employed replicate experiments, consisting of independent amplifications of identical samples followed by hybridization to distinct microarrays of the same design, to determine the repeatability of ABACUS genotype calls. Using a total threshold of 30 and a strand threshold of −2, in the CWRS-10/10R X-linked replicate experiment in males (haploid), we call 91.7% and 96.1% in each replicate, and 90.4% of the total possible sites in both replicates. Among the sites we call in both experiments, 841,236 of 841,236 sites are called identically in the haploid replicate experiment (Tables 2 and 3, below). If repeatability could be equated to accuracy, then this level of repeatability in haploid genotype calls would correspond to a phred score of at least 54 (assume a binomial error probability of P. The 95% confidence interval for P is the solution to (1 − P)⁸⁴¹²³⁶ = 0.05; P = 3.56 &times 10⁻⁶. To relate P-values to phred scores, note that phred = −10 log₁₀P). In the CWRS-14R/R2 diploid autosomal replicate experiment, we call 83.0% and 80.2% of the site genotypes in each replicate, and 71.4% of the total possible genotypes are called in both replicates. Of the sites called in both diploid replicates, 813,295 of 813,295 genotypes are called identically, also indicating a phred score of at least 54, if repeatability equaled accuracy. Among these identically called genotypes were 351 heterozygotes (Table 2). This number of heterozygotes is somewhat lower than would be seen in an equilibrium, neutral population, but consistent with a growing and slightly subdivided human population. As is evident from both of these experiments, the large majority of individual VDA genotype calls are extraordinarily repeatable. ABACUS can successfully identify genotype calls that are extremely likely to be repeatable from those calls that are not as reliable.

Table 2.

Microarray Repeatability in Haploid and Diploid Replicate Experiments

A. Repeatability in a Haploid Replicate Experiment
Total number of haploid sites	930,176
Total number of haploid sites called in Replicate 1	853,285 (91.7%)
Total number of haploid sites called in Replicate 2	893,692 (96.1%)
Total haploid sites called in both replicate experiments	841,236 (90.4%)
Total number of haploid sites called differently	0
Percent of haploid sites called identically	100.0%
B. Repeatability in a Diploid Replicate Experiment
Total number of diploid genotypes	1,138,480
Total number of diploid genotypes called in Replicate 1	944854 (83.0%)
Total number of diploid genotypes called in Replicate 2	913231 (80.2%)
Number of homozygous genotypes called identically	812944 (71.4%)
Number of heterozygous genotypes called identically	351
Total number of diploid genotypes called identically	813,295
Total number of diploid genotypes called differently	0
Percent of diploid genotypes called identically	100.0%

Replicate experiments: A replicate consists of independent amplification and hybridization of identical samples to two VDAs (for Table 2A, CWRS-10 and CWRS-10R; for Table 2B, CWRS-14R and CWRS-14R2) of the same design. 

(A) Haploids. Thirty-two distinct samples were replicated. Each array probed the genotype at 29,068 sites in the FMR1 region. (B) Diploids. Forty distinct samples were replicated. Each array probed the genotype at 28,462 sites taken from the GABBR1 and ANK2 regions. 

Table 3.

ABACUS SNP Detection and Genotyping Accuracy

A. Accuracy of autosomal SNPs detection
	Verified	Total Possible
Singleton SNPs	17	17
Non-singleton SNPs	91	91
Total SNPs	108	108
B. Number of autosomal SNPs electronically verified
Number of SNPs electronically verified	371
C. Accuracy of autosomal genotype calls
Number of verified homozygous genotype calls	1515
Number of incorrect homozygous genotype calls	0
Percent correct homozygote calls	100.00%
Number of verified heterozygous genotype calls	423
Number of incorrect heterozygous genotype calls	3
Percent correct heterozygote calls	99.30%
D. Accuracy of haploid genotype calls
Number of bases sequenced (6X coverage)	17,423
Number of bases different from microarray chip calls	0
Percent of bases identical	100.00%

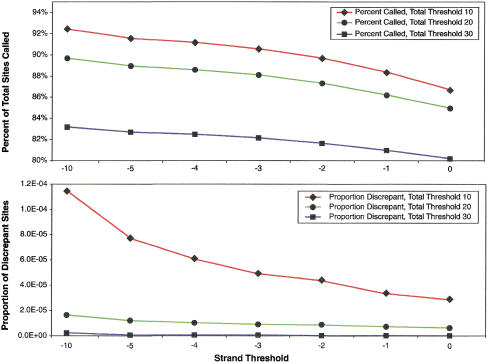
The effects of varying the total threshold and the strand threshold are as expected—decreasing either value increases both the percent of sites called, and the proportion of sites called discrepantly between replicate experiments (Fig. 2 and 3; Supplemental Fig. 1, available at http://www.genome.org). The percent of sites called in the haploid replicate experiment is higher than that in the diploid replicate experiment for all thresholds. Likewise, the proportion of discrepant genotype calls in the haploid replicate experiment is less than or equal to the proportion in the diploid replicate experiment for all total thresholds. In a similar fashion, increasing the strand threshold decreases the percent of sites called and the proportion of discrepant sites in both the haploid and diploid replicate experiments. In general, ABACUS analysis of VDAs in haploids will usually be able to call a higher percentage of sites, for the same number of errors, than a comparable diploid experiment. It appears possible, however, to pick parameters to make the expected error rates less than any desired threshold for both types of experiments (Fig. 2).

Figure 3.

Strand threshold varies in diploids. Total threshold fixed at 10, 20, or 30.

When a genotype is called discordantly in a replicate experiment, one knows that at least one of those two calls must have been in error. The converse is not necessarily true. A site called identically in both replicates is not necessarily correct. It may be that ABACUS makes repeatable systematic errors. To rule out systematic, repeatable errors, sequencing and genotyping must be done by some independent method.

The accuracy of haploid genotype calls was determined through library based 6× sequencing of 17,423 bp in a single individual from the CWRS-10/10R replicate experiment. All sites were called identically with ABACUS calls. This strongly indicates that ABACUS calls on haploids are both highly repeatable and highly accurate.

The accuracy of diploid genotype calls was assessed by independent ABI sequencing and RFLP analysis (see Methods). Because levels of variation are low (only eight of 10,000 bases likely to vary), any ABACUS error is nearly certain to be at a site where ABACUS calls a polymorphism, that is, all errors are likely to be at sites where SNPs are detected. Therefore, we performed independent genotyping at 108 SNPs that ABACUS detected from four VDA designs (CWRS-1, CWRS-14, CWRS-49, and CWRS-50). Homozygous genotype assays (1515 ) were conducted; all 1515 were identical with ABACUS genotype calls. At these same 108 sites, 423 heterozygote calls were examined; of these, 420 were confirmed (Table 3). All three of these apparent ABACUS errors exhibited the same pattern. They occurred at highly polymorphic sites (confirmed in other samples, and with minor allele frequency over 30%). In each case, ABACUS called a heterozygote, and independent genotyping showed a homozygote. Two out of the three errors occurred in a single amplified long PCR fragment in a single individual. None of the three errors occurred in the replicate experiment. This indicates to us that all three errors may have resulted from sample mislabeling, or cross-contamination between samples. In any case, genotyping accuracy at “segregating sites” appears to be well in excess of 99%.

As can be expected from such genotyping accuracy, SNP detection is also highly accurate. We assayed 108 (Table 3) of the 6040 SNPs using an independent methodology and all have been confirmed. Of these 108 SNPs, 17 were singleton heterozygotes, and all of these confirmed as well. An additional 371 SNPs from from 37 of the 40 genomic regions, have been confirmed electronically ( T. I. S. M. W. Group 2001). This indicates a false-positive rate for SNP detection of <2.7% (95% confidence interval for zero errors in 108 assays is 2.7%, with a maximum likelihood estimate of 0% errors).

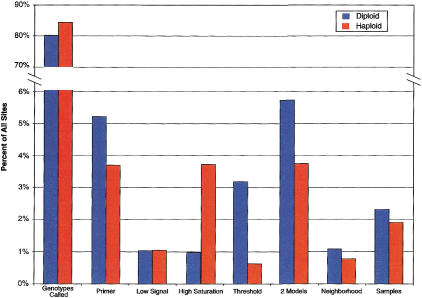
For the thresholds used in this study, ∼20% of all sites are called N (Fig. 4). Moreover, there is enormous correlation across samples in our ability to call genotypes. To a first approximation we either call all samples, or we call no samples (see below). As a result, one expects to miss ∼20% of all SNPs, that is, the SNP false-negative rate should be roughly 20%. To assess this prediction, CWRS-49 and CWRS-50 were designed to cover portions of the RET locus for which we had previously discovered 24 SNPs. As expected, ABACUS called N in all individuals at five of these sites, and therefore failed to detect 20.8% of the SNPs (at lower thresholds, 23 out of 24 SNPs were detected). All the remaining 19 SNPs were discovered, indicating that the SNP false-negative rate is roughly equal to the proportion of Ns in the sample. Finally, we examined whether the false-negative rate is different for heterozygote versus homozygote genotypes. At the 19 RET sites we could have made 328 homozygous genotype calls. We called N for 21 of these, calling the other 307 correctly. At these same 19 RET sites, we could have called 183 heterozygotes. Eight of these genotypes were called N, and the remaining 175 were correctly called heterozygotes. This indicates that at sites with known polymorphism, if we are able to make any call at the site, we call ∼5% of the genotypes N regardless of whether the genotype is a heterozygote or homozygote, and the remaining 95% of the sites are correctly called. Of course, it should be noted that 24 sites is probably too few to draw any strong inference about false-negative behavior.

Figure 4.

All sites were characterized as either called or N. All Sites designated N were partitioned into one of seven categories. (1) Primer: Primer failure indicating that <50% of the sites between a pair of PCR primers were called; (2) Low Signal: Mean florescence intensity extremely low; (3) High Saturation: Mean florescence intensity near detector limits; (4) Threshold: No model obtained quality score greater than the total threshold; (5) Two Models: Different models fit best on the forward and reverse strands so that no model obtained strand thresholds on both strands; (6) Neighborhood: <50% of the 20 surrounding sites could be called; and (7) Sample: <50% of the samples could be called at a particular site.

Characterizing Unreliable Genotype Calls

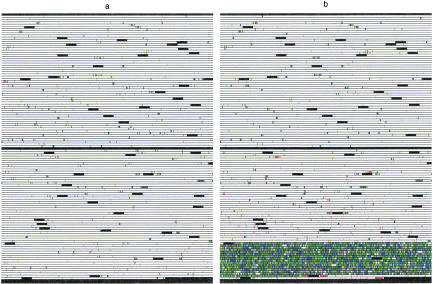
Approximately 80% of all genotypes can be called with extremely high confidence. Of course, one would like to understand why 20% of the genotype calls are of lower quality. To help visualize the pattern of failure on individual VDAs, we developed software that creates a graphical representation of each VDA (Fig. 5, below). Some types of failure, particularly PCR failure (Fig. 5b), are readily apparent from these schematics. Other causes of failure are less easily interpreted.

Figure 5.

VDA schematics. The schematic is colored as follows. (black) Control regions; (white) sites where high reliability ABACUS calls could be made; (red) sites with signal saturation; (violet) sites with low signal; (green) sites where different models fit best on the forward and reverse strand; (blue) sites where no model reached the total threshold; and (yellow) all other sources of failure. Both of these schematics come from VDA design CWRS-13. (a) An excellent VDA—very little failure of any kind distributed relatively evenly across the VDA. (b) PCR failure—the last PCR primer pair failed. Notice small spots of white mixed among the failure.

This project was designed to be high-throughput and limited experimental failure was deemed tolerable. Approximately 7% of the loss was caused by factors under the direct control of the experimentalist (Fig. 4). Of this 7%, 3%–5% were lost due because of “primer failure.” A primer pair was declared to have failed whenever <50% of the sites between the pair could be called (see ABACUS stage 6). There are many possible causes of primer failure, including PCR failure, pooling errors of PCR products, insufficient or excess digestion of amplified DNA, grid alignment errors on the VDA, or VDA manufacturing failure. In all of these cases, however, greater replication or lower thresholds for experimental failure could allow the recovery of genotype calls at these sites. Additionally, the 1% of sites lost because of insufficient signal may be recovered simply by increasing DNA concentrations. Similarly, the 1%–3% loss caused by saturation should be correctable by lowering DNA concentrations. During the course of the experiment, which consisted of 70 distinct VDA designs, at CWRS-47, VDA manufacturing dramatically improved. Mean florescence intensities increased by approximately a factor of two across the VDA. Unfortunately, the amount of DNA applied to the VDAs was not changed to compensate. As a result, the number of saturated features was far higher on later VDAs than on earlier ones. X-linked loci were assayed with CWRS-57 through CWRS-70, and all reflect the improved manufacturing.

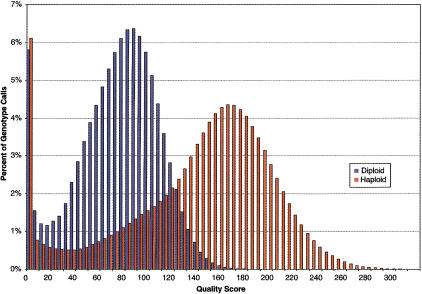
In any case, replication in instances of experimental failure in conjunction with accurate quantification of the amount of target DNA applied to the VDAs could increase the total percentage of genotype calls. Our results, however, indicate that, in general, it is more difficult to call diploid genotypes than it is to call haploid genotypes. First, as evident in Figure 7 (see below), mean quality scores for haploid VDA genotype calls are higher than diploid VDA genotype calls. Second, during the course of this experiment, we call ∼4% more haploid genotypes. This difference arises because diploid genotype calls are less likely to reach the total threshold and more often, two different models fit best on the forward and reverse strands (Fig. 4). Nevertheless, the vast majority of the genotypes for which we fail to make reliable calls, share one remarkable sequence specific characteristic in common.

Figure 7.

ABACUS quality scores for genotype calls. More than 64.5 million diploid genotype calls and >16.1 million haploid genotype calls were made.

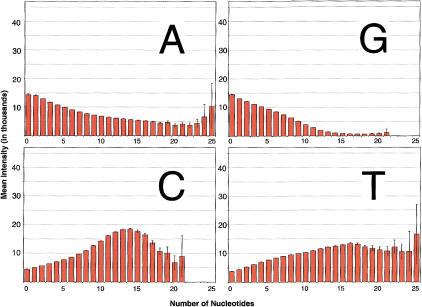
Effect of G-Rich Probes

Figure 6 plots the mean intensity of the reference feature as a function of the number of As, Cs, Gs, or Ts in that probe. One remarkable trend stands out. Florescence intensity declines as a function of the number of purines, in general, and with the number of Gs in particular. This is true for both autosomal (Fig. 6) and X-linked (Supplemental Fig. 2, available at http://www.genome.org) VDAs. Furthermore, the decreased mean intensity associated with the number of Gs is strongest when Gs occur at or near the center base and the effect declines uniformly in both directions (both 5′ and 3′) as the Gs move away from the center (data not shown). The cause of this observation is still unknown, but the effects are clear. Decreased mean intensity is directly associated with an inability to make high reliability calls in both haploid and diploid VDA experiments. Supplemental Figure 3 (available at http://www.genome.org) plots the proportion of haploid and diploid sites at which we can make high reliability calls as a function of the maximum number of Gs on either the forward or reverse strand. Because mean intensities are so low, we cannot make high reliability calls at sites with G rich probes.

Figure 6.

Florescence intensity for autosomal (diploid) loci. VDA features are tiled with 25mers. The number of As, Cs, Gs, and Ts were counted for the reference 25mer on both the forward and reverse strand. The florescence at each pixel within the feature was measured (>3.9 billion pixels in total). Error bars represent two standard errors, under the assumption that separate features are independent but pixels within a feature are not.

DISCUSSION

Previous work has indicated that, on average, microarray-based variation detection and genotyping achieves between a 99.93% and 99.99% accuracy (Wang et al. 1998; Cargill et al. 1999; Halushka et al. 1999). Unfortunately, because the total rate of variation in humans is quite low, this level of accuracy results in 12%–45% of all detected variation being error. Although 99.9% accuracy may not be sufficient, the goal of this work is to determine whether or not there was a subset of genotype calls that were far more reliable than 99.9%, and if so, to develop a set of tools to allow researchers to focus their attention only on those calls for which they have extraordinary confidence.

To this end, we developed ABACUS, an objective statistical framework for assigning to each genotype a quality score. We show that by focusing one's attention only on sites with high quality scores and in good neighborhoods, one can identify ∼80% of the haploid and diploid genotype calls that have an extraordinary likelihood of being correct. In replicate experiments, one can call >800,000 genotypes identically, with no discrepancies. This indicates that 80% of both haploid and diploid genotypes can be read with a repeatability consistent with a phred score >54.

Although repeatability certainly suggests accuracy (or at the very least, lack of repeatability proves inaccuracy), we also assessed accuracy in two independent manners. For haploid data, a 6× shotgun resequencing on a single individual was done, obtaining 17,423 base calls that were identical to ABACUS calls. To assess accuracy at segregating sites in diploids (nonsegregating sites identical to the reference are extraordinarily likely to be correct, as overall polymorphism rates are so low), 1938 genotypes were obtained at 108 segregating sites. Of these, 1935 were identical to ABACUS calls, but three were different. This indicates that genotyping accuracy at segregating sites >99.8% (and of course this ignores the nonsegregating sites also likely to be correctly called). To put this statistic in context, 99% accuracy at known segregating sites is claimed by several technologies (Hirschhorn et al. 2000). These results indicate that microarrays can be used for both detection and genotyping of variation simultaneously, and the accuracy of the genotyping approaches or exceeds most other widely available standalone genotyping technologies.

Of course, this level of accuracy comes at a cost. Twenty percent of surveyed diploid sites and 16% of surveyed haploid sites are not readable at this quality level. The failure comes from several sources. Roughly 7% (over both haploids and diploids) of the loss comes from sources a researcher can control, namely PCR failure and sub-optimal target DNA concentrations being applied to the VDAs. Replication in instances of experiment failure in conjunction with accurate quantification of the amount of target DNA applied to the VDAs could increase the total percentage of genotype calls.

The remaining 13% in diploids and 9% in haploids are lower quality genotype calls. In general, it is harder to call diploid genotypes. This difference is probably inherent to the biology. Loosely, heterozygotes have half as much DNA of each type, and there are more than twice as many possibilities (four haploid models vs. 10 diploid models). Simply put, there are more possibilities and less information. Doing somewhat worse in diploids may be unavoidable.

Two further caveats need to be mentioned. Large-scale VDA-based genotyping is still relatively new. Large replicated data sets with independent genotyping data are not readily available. ABACUS was developed (trained in some sense) using the data generated by this project. Further large-scale testing and independent evaluation should occur. Second, ABACUS uses information from multiple samples simultaneously. For this project, 40 samples were available. ABACUS's behavior with very small samples has not been characterized. Sub-sampling our data in groups of 10 yields quantitatively similar results (∼80% of all genotypes are called at our thresholds, and no discrepancies arise in the replicate experiment), but further testing should occur.

Of course, our purpose was principally to demonstrate that high reliability calls could be made and distinguished from lower quality calls. To do this, we developed quantitative measures, quality scores, to associate with each genotype call. The definition of high reliability that we used was quality scores above a certain threshold (total threshold of 30, strand threshold of −2), but these thresholds can be set by individual investigators to meet their individual needs. Irrespective of the total threshold an investigator may choose to employ, the critical feature of the ABACUS algorithm is that it assigns these quality scores to each VDA genotype call. Therefore, researchers might employ this critical piece of information in different experiments in a variety of fashions.

In particular, we can imagine the following use of ABACUS. Consider an extremely large (thousands of samples) case-control association study of a complex disease. Suppose previous studies have found linkage to a megabase region. The unique sequence portion of this genomic region will fit on 17 VDA designs. One can imagine first assaying, say, 50 individuals (perhaps 25 affected, 25 normal) with all 17 VDA designs. Analyze this initial data set with ABACUS set at a low quality threshold, say, T_total = 10, T_strand = −5, calling nearly all the sites, discovering virtually all polymorphic sites in this sample. Of course, there will also be ∼100 low-quality “false” polymorphisms on each VDA. One will have the genotype and an associated quality score at nearly all segregating sites in the 50-sample set. Test for association with each site in the reduced set. Now, genotype all (thousands) of the samples, but prioritize the genotyping by the strength of the association in pilot portion (50) as well as by the quality of the genotype call. First genotype high-quality, high-association sites, and work down from there. In any event, ABACUS combined with Affymetrix VDAs appears to be a technology that can facilitate high-throughput variation detection and genotyping of relatively large genomic regions.

METHODS

Selection of Genomic Regions

Our experiment consisted of surveying 32 autosomal and nine X-linked genomic regions (Supplemental Tables 1 and 2, available at http://www.genome.org). The genomic regions surveyed consist of contigs no smaller than 100 kb in size accessible in the nr, NT, or HTGS divisions of GenBank. Each genomic region contained a complete (or nearly complete) genomic structure of a gene, most of which have been implicated to have a role in the function or development of the human brain. Genomic regions were checked for paralogy by using BLAST against the nr, NT, and HTGS databases (Altschul et al. 1997). Target genomic regions that appeared to have paralogus copies (>95% identical) were excluded from analysis. Autosomal genomic regions were chosen from a wide variety of genomic locations—27 of the 32 autosomal genomic regions surveyed were chosen from distinct chromosome arms. The X-linked genomic regions surveyed were widely spaced, with three regions from the p arm and six from the q arm.

Identification of Unique Sequences within Genomic Regions

Microarrays are expected to perform optimally when the tiled probes consist of unique sequences. To identify the unique sequences within a selected genomic region, we first identified and masked common repetitive sequences with Repeatmasker (A. Smit and P. Green, unpubl.). Repetitive sequences within a contig were identified using Miropeats at its default threshold (Parsons 1995). The cDNA exon location in the genomic sequence was then determined with Sim4 (Florea et al. 1998). Genomic regions were visualized and the remaining unique sequences identified with viewGene 1.0b (C. Kashuk, unpubl.), a Java-based tool that allows a graphic visualization of a genomic region while incorporating the results from Repeatmasker, Miropeats and Sim4. Within each genomic region, we then selected among the remaining stretches of unique sequence to obtain ∼50 kb of unique sequence. We excluded unique sequences 100 bp or less and ultimately selected 29.5 kb of unique sequence for each VDA design. To avoid breaking up long stretches of genomic regions, in some cases, we added back short (<100 bp) stretches of previously masked sequence. The total number of unique VDA designs was 70 and they were numbered sequentially from CWRS-1 through CWRS-70. Some VDA designs contained tiled sequence from more than one genomic region. The replicate X-linked VDA design was identified as CWRS-10 and CWRS-10R. The replicate autosomal experiments were identified as CWRS-14, CWRS-14R, and CWRS-14R2.

Sample Identification

DNA sample employed for the survey of the autosomal genomic regions consisted of DNA samples 1–40 from the National Institutes of Health (NIH) Polymorphism Discovery Resource at the Coriell Institute for Medical Research (Collins et al. 1998). DNA samples employed for the survey of the X-linked genomic regions consisted of those donated by males. These samples were: 6–7, 12, 15–16, 18–19, 21–22, 24–25, 29, 31, 35, 37, 40–42, 44–46, 50, 51, 54–57, 59–63, 66, 68, 70, 73–75, 77, and 81. The 32 samples surveyed in the CWRS-10 and CWRS-10R VDA designs from FMR1, were male samples chosen from both the NIH Polymorphism Discovery Resource (3, 6–7, 12, 15–16, 18–19, 21–22, 24–25, 29) and 20 samples from an NIH Diversity Panel at Coriell (D.J. Mathews, C. Kashuk, G. Brightwell, E.E. Eichler, and A. Chakravarti, unpubl.).

PCR Amplification and Pooling Samples

To minimize the number of assays for each VDA design, long PCR was used to amplify genomic regions containing one or more unique sequence blocks tiled onto the variant detector array. Long PCR primers were 30 to 32 base pairs long and were selected by using Amplify 1.2 (Engels 1993) to ensure that they bound uniquely within a 29-kb region and had a primer stability value between 70 and 80. Primers were also chosen to ensure that their GC content was between 45%–60% with the last nucleotide being a C or a T.

Amplification of genomic DNA was accomplished in 30-μL PCRs carried out in thin-walled polypropylene tubes or plates using TaKaRa LA Taq (TaKaRa Biomedicals). The manufacturer's general reaction mixture was used, with the exception that the primers were kept separate from the Taq polymerase until the samples were spun down and place into the MJ Tetrad thermal cycler. In addition, reactions either were standard or contained 5% DMSO to aid in the amplification of GC-rich regions. The cycling conditions for all reactions were: (1) 94°C for 2 minutes; (2) 94°C for 10 seconds; (3) 68°C for 1 min/kb fragment size; (4) repeat step 2 29 times; (5) final extensions—time at step 3 plus 5 min. For amplifying autosomal regions, 100 ng of genomic DNA was used, whereas for X-linked regions, 150 ng was used. Most fragments were between 6–7 kb long and the yield of a PCR reaction was 10–50 ng/μL, as determined by visually comparing 4 μL sample of the reaction product on a 1% agarose gel with a low mass ladder concentration standard.

To obtain optimal performance across the microarray, we pooled samples to ensure that an equal number of targets existed for each probe. The quantity (ng) of DNA for each differently sized long PCR fragment was first calculated as 6 × (fragment size/100). The final volume to pool from the reaction mixture was them simply calculated as the quantity of DNA × the concentration of the PCR reaction × 1.25.

Determination of the Accuracy of ABACUS Genotype Calls in Replicate Experiments

To verify the haploid site calls from the CWRS-10/10R replicate experiment, the identical primers were used to amplify fragments from a single individual (#8). The resulting fragments were then individually physically sheared (hydrosheared) and subcloned with end repair into a PUC library. The resulting clones were single-pass sequenced using M13 primers until the entire genomic region had at least 6× coverage. Cross_match was used to assemble the generated sequences to the reference sequence and to each other (Green; Smith and Waterman 1981).

Verification of diploid genotype site calls from the CWRS-14R/R2 replicate experiment and from the CWRS-1 VDA design was carried out with either of two strategies. First, segregating sites recognized by a restriction enzyme were identified and short PCR primers were chosen to amplify a fragment 200–500 bp long fragments that included the putative segregating site. The amplified DNA was digested and run on a 1% agarose gel to score the genotype. The second strategy employed 4–8× sequencing of a diploid short PCR product, combined with polyphred (Nickerson et al. 1997; Rieder et al. 1998) to identify heterozygotes. The minimum phred score was set to 10 and the identified genotypes at segregating sites had to be polyphred rank three or higher to be considered confirmed.

Hybridization of Amplified Target DNA to VDAs

Hybridization of amplified target DNA to VDAs was performed by the HTS group at Affymetrix, Inc. During the course of this project, the concentration of genomic DNA hybridized to the VDAs was variable (Supplemental Table 3, available at http://www.genome.org). The amplified genomic samples were first subjected to DNaseI digestion using the established Affymetrix HTS Departmental Operating Procedure protocols. The fragmentation master mix consisted of One Phor All Buffer (Pharmacia Biotech Catalog #27–0901–02), 0.2U/μg DNA of DNaseI and Acetylated-BSA (Life Technologies Inc. Catalog #1556–020). Sufficient genomic DNA and digestion mixture were mixed to a total volume of 35 μL and digested for 15 min at 37°C. Samples were then incubated at 99°C for 15 min to inactivate the DNaseI. Samples were subsequently visualized on a polyacrylamide gel to verify fragmentation.

DNA samples were subsequently labeled by adding 2.5 μL from a master mix consisting of 1mM Biotin-N6-ddATP (NEN Life Sciences Catalog #NEL508) and 15U/μL rTdT enzyme (GIBCO BRL Catalog #10533–032). Samples were incubated at 37°C for 90 min followed by inactivation for 15 min at 99°C. Samples were then cooled on ice and stored at −20°C until hybridization.

Pre-hybridization, hybridization, washing, and scanning of polymorphism probe arrays were carried out in accordance with the Affymetrix HTS DOP. The pre-hybridization was carried out for at least 5 min and consisted of 3M TMACL, 1% Triton X-100, and 10 mM Tris pH 7.8. The hybridization solutions consisted of 3M TMACL, 100 μg/mL HS DNA, 500 μg/mL BSA, 10 mM Tris pH 7.8, 0.01% Tween 20, and 200 pM control oligo, and were hybridized for 16 h at 44°C, rotated at 60 rpm. On the completion of hybridization, the sample was removed from the VDA. The VDA then underwent two 10-min washes at 25°C in a buffer of 6× SSPE, 0.01% Tween 20. The VDAs were stained for 15 min in a solution consisting of 5 μg/mL SAPE, 6× SSPE, 0.01% Tween 20, and 2 mg/mL BSA. One additional wash cycle was followed by antibody staining for the all VDA designs up through CWRS-22. VDA designs starting with CWRS-23 were not antibody-stained and were only washed (Supplemental Table 3, available at http://www.genome.org). All VDAs were scanned at 570 nM, with a pixel size of 3 μ/pixel averaged over two scans.