Numerical assessment of time-domain methods for the estimation of local arterial pulse wave speed

Abstract

A local estimation of pulse wave speed c, an important predictor of cardiovascular events, can be obtained at arterial locations where simultaneous measurements of blood pressure (P) and velocity (U), arterial diameter (D) and U, flow rate (Q) and cross-sectional area (A), or P and D are available, using the PU-loop, sum-of-squares (${\sum }^2$), lnDU-loop, QA-loop or new D²P-loop methods. Here, these methods were applied to estimate c from numerically generated P, U, D, Q and A waveforms using a visco-elastic one-dimensional model of the 55 larger human systemic arteries in normal conditions. Theoretical c were calculated from the parameters of the model. Estimates of c given by the loop methods were closer to theoretical values and more uniform within each arterial segment than those obtained using the ${\sum }^2$. The smaller differences between estimates and theoretical values were obtained using the D²P-loop method, with root-mean-square errors (RMSE) smaller than $0.18\mathrm{m}{\mathrm{s}}^{-1}$, followed by averaging the two c given by the PU- and $\ln \mathit{DU}$-loops (RMSE $<2.99\mathrm{m}{\mathrm{s}}^{-1}$). In general, the errors of the PU-, $\ln \mathit{DU}$- and QA-loops decreased at locations where visco-elastic effects were small and nearby junctions were well-matched for forward-travelling waves. The ${\sum }^2$ performed better at proximal locations.

1. Introduction

The changes in blood pressure and flow at the ascending aorta generated by the contraction of the left ventricle propagate throughout the systemic arterial network in the form of waves, referred to as pulse waves (Caro et al., 1978; Pedley, 1980). The speed at which pulse waves travel in the absence of any convective velocity, known as pulse wave speed c, is a measure of arterial stiffness, which has been identified as an important predictor of cardiovascular events (Blacher et al., 1999; Laurent et al., 2001; Meaume et al., 2001). Knowledge of c is also of paramount importance for pulse wave analysis; in particular to separate the pressure and flow waveforms measured at a single location into forward- and backward-travelling components (Parker and Jones, 1990).

Several methods have been proposed to estimate c from in vivo arterial waveforms. In a clinical setting, the most widely used method calculates c non-invasively as the ratio of the distance between two measuring sites (usually the carotid and femoral arteries) and the transit time between these sites (Laurent et al., 2006; Mancia et al. 2007). The recent Arteriograph method estimates c from the pressure waveform measured at the brachial artery with an occluding cuff (Horváth et al., 2010). By their nature, both methods provide some average estimation of c over a length of the arterial tree. Local estimations of c at a single measurement site are possible if simultaneous measurements of blood pressure (P) and velocity (U) (Khir et al., 2001; Davies et al., 2006), arterial diameter (D) and U (Feng and Khir, 2010), or flow rate (Q) and luminal area (A) (Rabben et al., 2004) are available. These methods are referred to as the PU-loop, sum-of-squares (${\sum }^2$), $\ln \mathit{DU}$-loop and QA-loop, respectively, and will be described in Sections 2.3–2.6.

All these methods were developed in the time domain. Frequency-domain methods for the estimation of c have also been developed (O’Rourke and Taylor, 1967; Cox and Bagshaw, 1975; Milnor and Bertram, 1978; van Huis et al., 1987; Stergiopulos et al., 1999). However, they showed greater variation than the PU-loop and ${\sum }^2$ when applied to P and U measurements in the human carotids in normal conditions (Aguado-Sierra et al., 2006).

The accuracy of each method is difficult to assess in vivo, since the real value of c is usually unknown. Numerically simulated pulse waveforms allow us to compare estimates of c given by each method with theoretical values obtained from the parameters of the model. Pulse wave propagation in large systemic arteries can be accurately simulated at a reasonable computational cost using the one-dimensional (1-D) equations of blood flow in compliant vessels (Olufsen et al., 2000; Steele et al., 2003; Matthys et al., 2007; Bessems et al., 2008; Reymond et al., 2009). Trachet et al. (2010) applied these equations to compare theoretical values of c with estimates given by the carotid–femoral and Arteriograph methods, showing that both methods underestimate c.

The aim of this work is to test the performance of the PU-loop, ${\sum }^2$, $\ln \mathit{DU}$-loop and QA-loop methods using pulse waveforms generated in a 1-D model of the 55 larger human systemic arteries in normal conditions (Fig. 1). This model can capture the main features of in vivo pulse waveforms (Stergiopulos et al., 1992). In addition, a new method to estimate c from simultaneous P and D measurements (the D²P-loop) will be described (Section 2.7) and tested. The effect on the performance of each method of visco-elasticity and reflections at arterial junctions will be analysed, and the mechanisms underlying the discrepancies between theoretical and estimated c will be discussed.

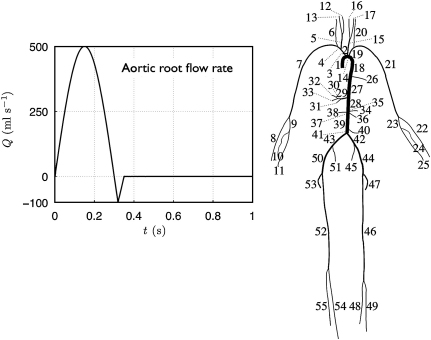
Fig. 1.

Connectivity of the 55 larger systemic arteries in the human. Their names and properties were taken from Alastruey (in press) and are shown in Tables 1 and 2 of the supplementary material. A periodic flow rate with a mean flow of 5.6 l min⁻¹ was prescribed at the aortic root for the first 10 s, followed by zero flow for $t>10\mathrm{s}$.

2. Materials and methods

2.1. Numerical pulse waveforms

Pulse waveforms were simulated in the 55-artery network in Fig. 1 using the nonlinear 1-D equations of incompressible and axisymmetric flow in Voigt-type visco-elastic vessels

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial A}{\partial t}}+{\displaystyle \frac{\partial \left(\mathit{AU}\right)}{\partial x}}=0\hfill \\ \hfill \\ {\displaystyle \frac{\partial U}{\partial t}}+U{\displaystyle \frac{\partial U}{\partial x}}+{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial x}}={\displaystyle \frac{f}{\rho A}}\hfill \\ \hfill \\ P={\displaystyle \frac{\beta }{A_0}}(\sqrt{A}-\sqrt{A_0})+\Gamma {\displaystyle \frac{\partial A}{\partial t}}\hfill \end{array},\right)$$ (1)

$$f=-22\mu \pi U,\beta =4/3\sqrt{\pi }\mathit{hE},\Gamma =\gamma /2\sqrt{\pi A_0}\text{,}$$

where x is the axial coordinate along the vessel, t the time, A(x,t) the cross-sectional area of the lumen, U(x,t) the average axial velocity, P(x,t) the average internal pressure over the cross section, $\rho =1050$ Kg m⁻³ the mass density of blood, f the friction force per unit length, and $\mathrm{\mu }=4.0\mathrm{mPa}\mathrm{s}$ the blood viscosity. The arterial wall is assumed to be thin, homogeneous, incompressible and visco-elastic, with each cross section deforming axisymmetrically and independent of the others. The parameters h(x), E(x) and $\gamma (x)$ are the thickness, Young's modulus and Voigt-type viscous modulus of the arterial wall, respectively, and A₀(x) is the luminal area at P=0. $\beta$ and $\Gamma$ are assumed to be constant and related to the elastic and visco-elastic properties of the arterial wall, respectively.

Eq. (1) were solved in the arterial network of Fig. 1 using a discontinuous Galerkin scheme with a spectralhp spatial discretisation and zero pressures and flows as initial conditions. The time step was $100\mathrm{\mu }\mathrm{s}$ for the elastic-wall models and $5\mathrm{\mu }\mathrm{s}$ for the visco-elastic-wall model. Arterial segments were divided into non-overlapping elements with a 2 cm length (when physically possible) and a polynomial and quadrature order of 3. Elements or segments shorter than 2 cm were given a polynomial and quadrature order of 2. Further details on the 1-D formulation are given in the supplementary material.

The physiological data of the models were taken from Alastruey (in press) and are shown in Tables 1–3 (supplementary material). A version of the 55-artery model with purely elastic vessels and modified radii so that junctions are well-matched for forward-travelling waves (i.e. waves are initially reflected at terminal branches) was also considered. This model will be referred to as the ‘well-matched model’.

The periodic flow rate shown in Fig. 1 was prescribed at the aortic root for the first 10 s, followed by zero flow to study the relaxation of the system. Terminal branches were coupled to matched three-element windkessel models, as described by Alastruey et al. (2008), with the parameters shown in Table 2 (supplementary material). Conservation of mass and continuity of the total pressure $P+1/2\rho U^2$ was enforced at the arterial junctions.

2.2. Theoretical pulse wave speed

System (1) is hyperbolic and admits wave-like solutions for P and U when $\Gamma =0$. In that case, Riemann's method of characteristics shows that disturbances to the flow create changes in pressure $\mathrm{d}P$ and velocity $\mathrm{d}U$ across the wave fronts, which propagate forward (in the positive x-direction) with speed U+c and backward (in the negative x-direction) with speed U−c, where $c^2=A/(\rho \mathrm{d}A/\mathrm{d}P)$ (Parker and Jones, 1990). For the tube law in (1), with $\beta$ and A₀ constant, we have

$$c=\sqrt{\frac{\beta }{2\rho A_0}}{A}^{1/4}\text{.}$$ (2)

Moreover, $\mathrm{d}P$ and $\mathrm{d}U$ consist of a forward- (indicated with the subscript +) and a backward- (indicated with the subscript −) travelling component, which are related through the ‘water hammer’ equation

$$\mathrm{d}{P}_{+}=\rho c\mathrm{d}{U}_{+},\mathrm{d}{P}_{-}=-\rho c\mathrm{d}{U}_{-}\text{.}$$ (3)

In this work the theoretical value of the local c was calculated using Eq. (2) with A the mean cross-sectional area over the cardiac cycle.

2.3. PU-loop

This method assumes that there is a period in early systole when there are no reflected waves, so that $\mathrm{d}{P}_{-}$ and $\mathrm{d}{U}_{-}$ are zero. This leads to $\mathrm{d}P=\mathrm{d}{P}_{+}$ and $\mathrm{d}U=\mathrm{d}{U}_{+}$, so that $\mathrm{d}P=\rho c\mathrm{d}U$ according to Eq. (3). Therefore c can be obtained as

$$c=\frac{\mathrm{d}P}{\rho \mathrm{d}U}\text{.}$$ (4)

In the arteries simulated, the part of the PU-loop corresponding to early systole is approximately linear (Fig. 2a). Its slope is $\rho c$ (Eq. (4)), which allows us to determine c using a reasonable approximation for $\rho$ (Khir et al., 2001). Later in the cardiac cycle, forward and backward waves are present and the PU-loop is no longer linear.

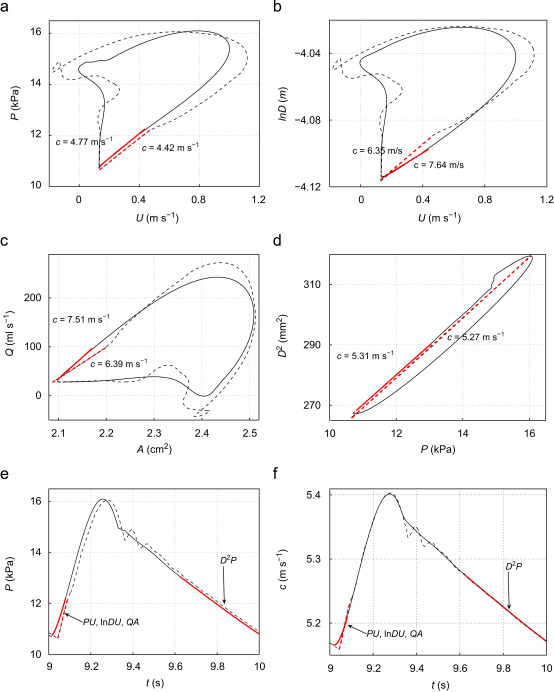
Fig. 2.

PU-loop (a), $\ln \mathit{DU}$-loop (b), QA-loop (c) and D²P-loop (d) in the midpoint of the thoracic aorta II (Segment 27) in the purely elastic (dashed lines) and visco-elastic (solid lines) 55-artery models. Wave speeds c calculated using the linear least-squares fit highlighted in red. The theoretical c is 5.28 m s⁻¹. Pressure (e) and c (f) with time at the same location for the elastic (dashed lines) and visco-elastic (solid lines) models. The linear regions used in the loops are highlighted in red. (The complete pressure waveform was used for the D²P-loop in the purely elastic model.) (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.4. Sum of squares (${\sum }^2$)

This method was derived to estimate c in the coronary arteries, where the PU-loop does not show a period of time when pulse waves are unidirectional. Given simultaneous P and U measurements at a single location, c is obtained as

$$c=\frac{1}{\rho }\sqrt{\frac{\sum {(\mathrm{d}P)}^2}{\sum {(\mathrm{d}U)}^2}}\text{,}$$ (5)

where the sums extend over a cardiac cycle. Eq. (5) follows from Eq. (3) assuming $\sum (\mathrm{d}{U}_{+}\mathrm{d}{U}_{-})$ to be small compared with $\sum [{(\mathrm{d}{U}_{+})}^2+{(\mathrm{d}{U}_{-})}^2]$. This is equivalent to finding the value of $\rho c$ that minimises net wave energies (Davies et al., 2006).

2.5. $\ln \mathit{DU}$-loop

Feng and Khir (2010) showed that c, $\mathrm{d}U$ and changes in the natural logarithm of the arterial diameter $\mathrm{d}(\ln D)$ are related through

$$c=\frac{1}{2}\frac{\mathrm{d}U}{\mathrm{d}(\ln D)}$$ (6)

during a reflection-free period of the cardiac cycle. In the arteries simulated, the part of the $\ln \mathit{DU}$-loop corresponding to early systole is approximately linear (Fig. 2b). Its slope is 1/(2c) according to Eq. (6).

2.6. QA-loop

If there is a reflection-free period in the cardiac cycle, c can be estimated as the ratio between the change in flow rate $\mathrm{d}Q$ and the change in cross-sectional area $\mathrm{d}A$ (Rabben et al., 2004); i.e.

$$c=\frac{\mathrm{d}Q}{\mathrm{d}A}\text{.}$$ (7)

In the arteries simulated, the part of the QA-loop corresponding to early systole is approximately linear (Fig. 2c). Its slope is c according to Eq. (7).

2.7. D²P-loop

Assuming the arterial wall to be a Voigt-type visco-elastic material, the numerical results show that the visco-elastic term in the tube law in (1) becomes increasingly constant with time in diastole and the elastic term leads to an approximately linear relationship between D² and P in late diastole (Fig. 2d). The slope can be calculated by differentiating the elastic term in the tube law, with $\beta$ and A₀ assumed to be constant. This leads to

$$\mathrm{d}A=\frac{2A_0^{3/2}}{\beta }\mathrm{d}P=\frac{A_0}{\rho c^2}\mathrm{d}P$$ (8)

at (P, A)=(0, A₀). Eq. (2) with A=A₀ was used for the second equality. Solving Eq. (8) for c with $D^2=4A/\pi$ and ${(D_0)}^2=4A_0/\pi$ yields

$$c=D_0\sqrt{\frac{\mathrm{d}P}{\rho \mathrm{d}(D^2)}}\text{.}$$ (9)

Eq. (9) allows us to calculate c from the slope of the D²P-loop in late diastole using a reasonable value for $\rho$ and approximating D₀ by the mean arterial diameter.

3. Results

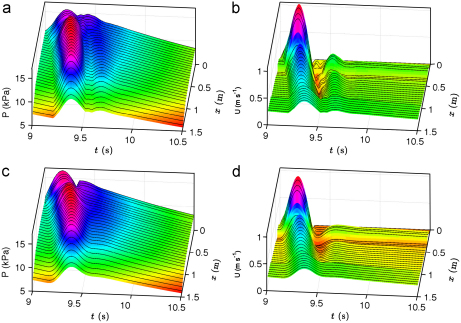
The simulated pressure and velocity waveforms along the aorta and left iliac, femoral and tibial arteries of the purely elastic and visco-elastic 55-artery models are shown in Fig. 3 for the tenth cardiac cycle, when the pulse waveform has become periodic. At the aortic root, the systolic pressure is 15.6 kPa and the diastolic pressure 10.9 kPa for the purely elastic model. The corresponding values for the visco-elastic model are 16.6 and 10.6 kPa. The difference between these pressures (the pulse pressure) increases in the aorta toward distal locations. In both models, fluid viscosity decreases the mean pressure from 13.3 kPa at the aortic root to 13.2 kPa at the end of the aorta and 7.7 kPa at the end of the tibial arteries (Segments 49 and 55). The feet of the pressure waveforms show that the speed of pulse wave propagation increases distally; this is observed more clearly in the purely elastic model. In early diastole, the flow reverses in most of the aortic and iliac segments. Later in diastole pulse waveforms decrease approximately exponentially with similar time constants, especially for the pressure wave. This decay continues after 10 s, when a zero flow rate at the aortic root was prescribed.

Fig. 3.

Pressure (a,c) and velocity (b,d) versus time and distance in 2 cm increments from the aortic root (x=0, Segment 1) to the end of the left anterior tibial artery (Segment 49), through Segments 2, 14, 18, 27, 28, 35, 37, 39, 41, 42, 44 and 46. The aortic bifurcation is at x=44.4 cm. Pulse waveforms generated using the purely elastic (a,b) and visco-elastic (c,d) formulations in the normal 55-artery model. Continuous pressure and velocity magnitudes are shown using coloured surfaces interpolated from the simulated pulse waveforms every 1 cm. After t=10 s, a zero flow rate was prescribed at the aortic root to show the relaxation of the models. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

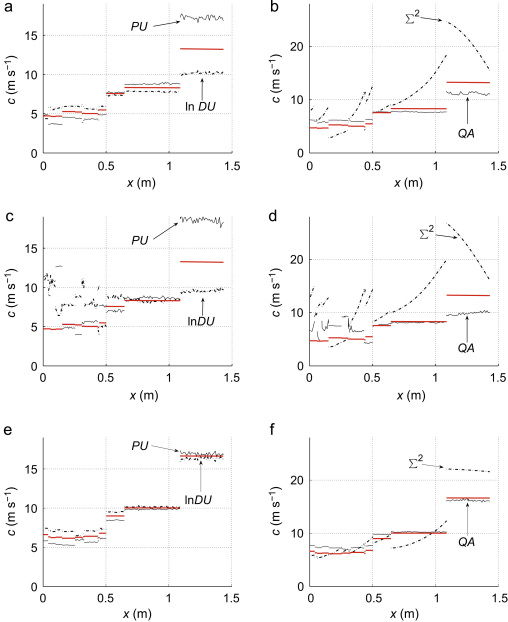
Fig. 4 shows the theoretical wave speed c calculated using Eq. (2) along the aortic–iliac–femoral–tibial path in 1 cm increments, for the (a, b) purely elastic, (c, d) visco-elastic and (e, f) well-matched models. They are compared against the speeds determined using the PU-loop, ${\sum }^2$, $\ln \mathit{DU}$-loop, and QA-loop. Overall, the estimations of c given by these loop methods are closer to the theoretical value and more uniform within each segment than those obtained using the ${\sum }^2$. The errors of these four methods increased in the visco-elastic model, especially at proximal locations, and decreased in the well-matched model. In those segments where the PU-loop overestimated c, the $\ln \mathit{DU}$-loop underestimated it, and vice versa. This result suggests that c could be estimated closer to the theoretical value using the average of the two values obtained from the PU- and $\ln \mathit{DU}$-loops. The c values estimated using the D²P-loop cannot be distinguished from the theoretical values in the scale of Fig. 4. Similar qualitative comparisons of c estimates and theoretical values were obtained in other arterial segments.

Fig. 4.

Theoretical (red lines) and estimated pulse wave speed with distance in 1 cm increments from the aortic root (x=0) to the end of the left anterior tibial artery, through the same segments as in Fig. 3. Estimated values calculated using the PU-loop, $\ln \mathit{DU}$-loop, QA-loop and sum-of-squares (${\sum }^2$) methods with the pulse waveforms from the (a,b) purely elastic and (c,d) visco-elastic normal models and the (e,f) well-matched model. Estimated values using the D²P-loop method are not shown, since they cannot be distinguished from the theoretical values in the scale of the figures. Note the different scales of c in the left and right figures, and the different theoretical values for the normal and well-matched models. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 1 shows the root-mean-square errors (RMSE) between theoretical and estimated c in the three arterial models. Absolute errors were calculated at 304 locations: the inlet, midpoint and outlet of each arterial segment, and at all the locations on the aortic–iliac–femoral–tibial path of Fig. 4. RMSE were then calculated for all the segments in the aorta and each generation of bifurcations from the aorta. The larger RMSE are mostly obtained in the 4th and 5th generation of bifurcations, which are terminal segments except for Segment 9 in the right arm.

Table 1.

Root-mean-square errors (RMSE) in m s⁻¹ between theoretical c and those estimated using the PU-loop, sum-of-squares (${\sum }^2$), $\ln \mathit{DU}$-loop, QA-loop, and D²P-loop methods in the 55-artery network. Absolute errors $\mathcal{E}$ were calculated at 304 locations. RMSE $=\sqrt{{\sum }_{i=1}^N{\mathcal{E}}_i^2/N}$ were then grouped according to the number of generations of bifurcations from the aorta, with N the total number of samples in each group. At least three locations were considered in each arterial segment (inlet, midpoint and outlet), including all the locations on the aortic–iliac–femoral–tibial path of Fig. 4. The last row shows the errors of estimating c as the average of the two c from the PU- and $\ln \mathit{DU}$-loop methods. All errors are given in a triad of numbers: the first corresponds to pulse waveforms simulated using the purely elastic formulation, the second using the visco-elastic formulation (in italics) and the third using the purely elastic formulation in the well-matched network (in bold).

	Aorta	1st gen.	2nd gen.	3rd gen.	4th gen.	5th gen.
Samples	70	39	50	80	59	6
PU-loop	0.78 2.900.69	0.82 1.990.49	0.93 1.100.54	0.54 0.420.33	3.09 3.980.47	0.63 2.141.08
${\sum }^2$	2.56 4.660.65	6.89 9.183.04	4.75 6.684.96	4.37 6.063.63	6.98 8.357.50	8.21 11.5123.45
$\ln \mathit{DU}$-loop	0.76 3.580.64	0.69 0.650.43	1.90 2.400.50	0.57 0.360.28	2.41 2.850.50	0.68 1.971.11
QA-loop	1.01 2.250.89	0.87 0.740.73	1.10 2.130.85	0.59 0.490.42	1.77 2.680.74	1.33 1.991.35
D2P-loop	0.02 0.180.00	0.02 0.020.01	0.02 0.010.01	0.02 0.020.02	0.01 0.010.02	0.01 0.010.02
Average loops	0.04 2.990.03	0.13 0.890.06	0.52 0.880.03	0.03 0.190.03	0.35 0.630.03	0.03 0.370.03

RMSE for the ‘loop’ methods decreased in most of the locations if bifurcations were well-matched for forward-travelling waves and the arterial wall was purely elastic. Estimation of c using the average of the two c from the PU- and $\ln \mathit{DU}$-loops considerably reduced the errors in any group and model (with the exception of the segments of the aorta and first generation in the visco-elastic model), leading to RMSE smaller than 0.52 m s⁻¹ in the purely elastic model, 2.99 m s⁻¹ in the visco-elastic model, and 0.06 m s⁻¹ in the well-matched model. RMSE for the ${\sum }^2$ decreased at all locations if visco-elastic effects were neglected, and mainly at proximal locations if bifurcations were well-matched. They increased considerably in the 5th generation of bifurcations of the well-matched model. Absolute errors smaller than 0.67 m s⁻¹ were obtained using the D²P-loop at any location for any model.

In the visco-elastic model, the diastolic region of the pulse waveform used for the linear fitting in the D²P-loop was longer than the systolic region in the PU-, $\ln \mathit{DU}$- and QA-loops. Fig. 2e compares these regions in an aortic pressure waveform.

The ${\sum }^2$ produced RMSE smaller than 1.4 m s⁻¹ in the well-matched model if terminal boundary conditions were completely absorbent. If, in addition, the flow was inviscid ($\mu =0$), then P, U, D, Q and A were approximately proportional at any location in the network and the absolute errors of any of the methods studied were less than 0.1 m s⁻¹.

4. Discussion

The ability of the PU-loop, ${\sum }^2$, $\ln \mathit{DU}$-loop, QA-loop, and D²P-loop methods to estimate theoretical values of c was tested using pulse waveforms generated in a nonlinear 1-D model of the 55 larger systemic arteries in the human in normal conditions. Although these data are an approximation to in vivo pulse waveforms, they have the advantage of being free of measurement and alignment errors, and of providing theoretical values of c from the parameters of the model to compare with the estimates. The use of the 1-D formulation is justified because all the methods studied are based on this formulation.

Overall, the loop methods produced estimations of c closer to the theoretical value than did the ${\sum }^2$. The D²P-loop led to the smallest RMSE, followed by averaging the estimations from the PU- and $\ln \mathit{DU}$-loops. The latter method, however, requires simultaneous measurements of three waveforms (P, U and D), instead of the two required by the other methods studied. This limits its in vivo applicability.

The absolute errors in the estimates of c using the PU-, $\ln \mathit{DU}\text{‐}$, and QA-loops increased in most of the arterial locations studied if visco-elasticity was modelled. They decreased if bifurcations were well-matched for forward-travelling waves. These observations are in agreement with the assumptions of purely elastic wall and absence of any reflected wave in early systole made in the derivation of these methods. Indeed, Alastruey et al. (2009) showed, for a 55-artery network with the same reflection coefficients as in the normal model used here, the arrival of waves reflected at nearby junctions in early systole, when the relationship between P and U, $\ln D$ and U, or Q and A is still approximately linear (e.g. within the red regions in Fig. 2). These waves change the slope of the linear part of the PU-, $\ln \mathit{DU}$- and QA-loops and, hence, are responsible for the errors observed in their estimates of c. Consequently, these loop methods are more useful for estimating the theoretical c at locations where the visco-elastic effects are small and nearby junctions are distant and close to well-matched for forward-travelling waves. Moreover, the difference between the estimates of c obtained from the PU- and $\ln \mathit{DU}$-loops seem to correlate well with the intensity of reflected waves in the system; the greater the intensity is, the greater the difference is. The demonstration of the utility of this difference to estimate the intensity of reflected waves remains to be explored fully.

The new D²P-loop method does not have the problems discussed above, but it has only been tested using a Voigt-type visco-elastic model of the arterial wall. Although several studies have shown that this model provides a good approximation to the relationship between P and D observed in vivo (Armentano et al., 1995; Craiem et al., 2005; Čanić et al., 2006), more complex wall models have been proposed (e.g. Bessems et al., 2008; Devault et al., 2008; Valdez-Jasso et al., 2009) for which the D²P-loop was not tested. Moreover, the D²P-loop might not be linear in late diastole for short cardiac cycles. According to the simulations, it is linear when the pressure waveform becomes uniform in space. The PU-, $\ln \mathit{DU}$- and QA-loops also have a linear part at the end of diastole, but their slopes seem not to be related to c.

The ${\sum }^2$ was originally derived for the coronary arteries, which were not considered in this study. Nevertheless, the errors obtained here should be similar or even greater in these arteries, since vessel movement due to myocardial contraction (which was not considered in the derivation of the ${\sum }^2$) is a potential additional source of error. Theoretically, the ${\sum }^2$ can provide flawed results when measurements are taken close to a reflection site with a large reflection coefficient, so that there is significant correlation between forward- and backward-travelling waves (Davies et al., 2006). According to Kolyva et al. (2008), however, the main source of error of the ${\sum }^2$ in the coronary arteries is their windkesselness nature rather than the existence of reflections. Indeed, they concluded that the ${\sum }^2$ is inappropriate for estimating c in coronary arteries. In the present study, the performance of the ${\sum }^2$ improved at proximal locations if bifurcations were well-matched for forward-travelling waves. This suggests that wave reflections should have some effect on the ${\sum }^2$. Aguado-Sierra et al. (2006) showed, using in vitro data measured in a thin-walled latex tube, that the ${\sum }^2$ overestimated the foot-to-foot calculation of c by 3.5 m s⁻¹ on average, with differences larger than 4.0 m s⁻¹ at locations more than 10 cm away from the reflection sites. These differences are smaller than most of the RMSE reported in Table 1, but significant taking into account the relatively larger distance from the reflection sites of the experiment. The errors of the ${\sum }^2$, however, do not seem to be critical when calculating the total wave energy carried during the heart cycle by forward- and backward-travelling waves in the coronary circulation (Siebes et al., 2009).

The PU-loop, ${\sum }^2$ and D²P-loop methods require knowledge of the blood density $\rho$. The latter method, however, is less sensitive to changes in $\rho$; e.g. a 5% change in $\rho$ yields changes in the estimation of c smaller than 3% for the D²P-loop and of about 5% for the PU-loop and ${\sum }^2$. Moreover, c varies nonlinearly with A (Eq. (2)) and, hence, P. The methods studied here, therefore, provide some average estimation of c over the cardiac cycle (Fig. 2f). Once the flow became periodic in the 55-artery models, changes in A within a cardiac cycle were smaller than 25% at aortic locations and 11% at the terminal branches of the head and limbs, leading to changes in the theoretical c smaller than 8% and 3%, respectively.

In vivo, the applicability and performance of the methods studied depends upon the feasibility of accurate measurements of the data they require. For the loop methods, a good accuracy is critical during the linear period, which is usually less than 50 m s (Khir et al., 2001; Rabben et al., 2004; Feng and Khir, 2010). Thus, a high sampling frequency is fundamental. According to this study, the D²P-loop is approximately linear for more than 50 ms (Fig. 2e), but this has not been tested in vivo. The existence of a time lag between P and U measurements is a potential additional source of error for the PU-loop, which can be corrected as described by Swalen and Khir (2009). The evolution of D can be measured non-invasively at some locations using ultrasound-based echo-tracking (Rabben et al., 2002). However, this technique, which is not applicable in the coronary arteries, may well introduce an additional error that limits the good performance of the D²P-loop method shown here.

5. Conclusions

According to the results presented here, the estimation of c closest to the theoretical value is obtained from simultaneous diameter and pressure measurements using the D²P-loop. If pressure and velocity measurements are available, the PU-loop produces estimates of c closer to the theoretical values than the ${\sum }^2$, which performs better at proximal locations. The average c obtained from the PU- and $\ln \mathit{DU}$-loops has a smaller error than the estimate provided by either method. Particular care should be taken when applying the PU-, $\ln \mathit{DU}$- and QA-loops at locations with significant visco-elastic effects and reflected waves. These conclusions, however, still need to be assessed using in vivo data.

Conflict of interest statement

There is no conflict of interest between the author of this paper and other external researchers or organisations that could have inappropriately influenced this work.