Trimming, Weighting, and Grouping SNPs in Human Case-Control Association Studies

Abstract

The search for genes underlying complex traits has been difficult and often disappointing. The main reason for these difficulties is that several genes, each with rather small effect, might be interacting to produce the trait. Therefore, we must search the whole genome for a good chance to find these genes. Doing this with tens of thousands of SNP markers, however, greatly increases the overall probability of false-positive results, and current methods limiting such error probabilities to acceptable levels tend to reduce the power of detecting weak genes. Investigating large numbers of SNPs inevitably introduces errors (e.g., in genotyping), which will distort analysis results. Here we propose a simple strategy that circumvents many of these problems. We develop a set-association method to blend relevant sources of information such as allelic association and Hardy-Weinberg disequilibrium. Information is combined over multiple markers and genes in the genome, quality control is improved by trimming, and an appropriate testing strategy limits the overall false-positive rate. In contrast to other available methods, our method to detect association to sets of SNP markers in different genes in a real data application has shown remarkable success.

The current emphasis on searching for disease susceptibility genes is carried out by association to tens of thousands of SNP markers (Collins et al. 1998). Such association analyses may be carried out in a variety of data designs, for example, by testing for differences in SNP allele frequencies between affected and unaffected individuals (case-control studies), or by comparing whether a SNP allele is transmitted to an affected offspring more or less often than expected by chance (the transmission disequilibrium test, TDT; Spielman and Ewens 1996). Because complex traits presumably arise from multiple interacting genes located throughout the genome, it would be appropriate to search for sets of marker loci in different genes and to analyze these markers jointly rather than testing each marker in isolation. Forming haplotypes over multiple neighboring markers in one gene can increase the power of gene mapping studies (Fallin et al. 2001), as can scan statistics (Hoh and Ott 2000); but these methods only work locally in a given genomic region.

Most current approaches essentially evaluate one SNP marker at a time, that is, by focusing on its marginal effect on disease. Those SNPs with a significant association to disease are taken to be close to or within susceptibility genes. Testing each SNP for association with disease leads to a locus-specific probability of a false-positive result (type I error). Such a type I error can easily be inflated when large numbers of SNPs are tested simultaneously and treated independently (Risch and Merikangas 1996); the problems involving such multiple testing and its effect on the genomewide type I error are the subject of a presently ongoing debate (Lin et al. 2001). For genomewide linkage analysis, appropriate measures have been developed to keep this problem under control (Lander and Kruglyak 1995). For genomewide association analysis, however, no general treatment exists because the interactions between markers do not follow a known pattern. But apart from these problems of multiple testing, this marker-by-marker approach completely ignores the multigenic nature of complex traits and does not take into account possible interactions between susceptibility genes.

Although various authors have postulated the need for investigating multiple disease genes jointly, few viable approaches in this direction exist. Looking at all possible pairs of marker loci in the genome and evaluating the significance level of each pair may not be the answer because of the high number of tests required (Dupuis et al. 1995), although, for a small number of candidate marker loci, this method does seem to have merit (Cordell et al. 1995). Conditional approaches, in which a new locus is searched for, given good evidence for an existing locus or set of loci, appear more promising (Dupuis et al. 1995; Cordell et al. 2000).

In addition to a small number of multilocus approaches (Stoesz et al. 1997; Blangero et al. 2000), an intriguing method has recently been proposed to allow for the joint analysis of multiple marker loci (Nelson et al. 2001). This combinatorial partitioning method (CPM) works by evaluating all possible partitions of marker loci and retaining only those partitions fulfilling certain optimality criteria. Of course, the possible number of partitions is astronomical. Focusing on partitions comprising two marker loci each, Nelson et al. (2001) showed that this approach identified biological interactions between loci. Unfortunately, the CPM may not easily reach genomewide statistical significance—in an application to candidate genes for coronary heart disease, the overall significance level was 0.14 (Nelson et al. 2001).

In this paper, we introduce an alternative approach, set-association, to evaluate sets of SNP markers at various positions in the genome (in particular, in different susceptibility genes). This method performs a simultaneous significance test on several sets of loci while keeping the overall type I error in control. To increase the power of the test, that is, to limit the false-negative error rate, we combine relevant sources of information for a given SNP: allelic association (AA), Hardy-Weinberg disequilibrium (HWD), and evidence for genotyping errors. Contributions from multiple SNPs in different genomic regions are combined by forming a sum of single-marker statistics, which results in a single genomewide test statistic with high power. The principle of summing over single-locus statistics is based on an extension of Tukey's compound covariates in a linear regression setting (Tukey 1993). In Tukey's case, covariates were summed to form a new compound covariate, and the association between such a compound covariate and the dependent variable was evaluated via regression analysis. In our case, a trait-association statistic for each marker is suitably chosen, sets of such statistics are summed, and the significance levels are evaluated via computer-based randomization (permutation) procedures. Our set-association method for detecting a set of possibly interacting trait-associated SNP markers has an accurate and small overall false-positive rate but does not incur the penalty of low power. And, most importantly, this method is easily implemented in a computer algorithm.

Set-Association Approach

Previous work has shown that deviations from Hardy-Weinberg equilibrium (Crow 2001) in affected individuals may be indicative of the presence of susceptibility loci (Feder et al. 1996; Nielsen et al. 1999). On the other hand, it is allelic association (due to proximity of an SNP to a susceptibility gene) that measures overrepresentation of genomic variants in cases versus controls. For this reason, we consider both of these effects, AA and HWD, where each may be expressed by a χ-square statistic. The extent of AA is measured, for example, by the χ-square in a 2 × 2 table with rows corresponding to cases and controls, and columns corresponding to SNP alleles 1 and 2; a simpler measure is the mean difference in the number of 1 alleles between cases and controls. HWD is defined as the χ-square for deviation from Hardy-Weinberg equilibrium, which may be obtained with one of our utility programs (http://linkage.rockefeller.edu/ott/linkutil.htm#HWE). As outlined in detail below, we combine these two sources of information for a given SNP by simply forming the product of the corresponding two statistics.

Trimming

There are two aspects to HWD. Although moderately high values (in affected individuals) are indicative of genetic association to a susceptibility locus, extremely high values indicate problems, for example, genotyping errors. Therefore, to ensure quality control, we trim unusually large HWD values. Trimming is based on HWD in control individuals, where each SNP furnishes one χ-square for HWD. A suitable procedure for determining “outlying” HWD values is then applied to determine the number, d, of largest HWD values that should be set equal to zero (i.e., trimmed). For example, the 99th percentile of χ-square for HWD is equal to 6.6, that is, only 1% of SNPs are expected to show HWD in excess of 6.6. If d SNPs show HWD > 6.6, then trimming will consist of setting the d largest values of HWD equal to zero.

HWD As an Association Measure

For a given SNP, the HWD in affected individuals is taken to be indicative of association of the SNP with disease. In regular case-control studies, case individuals are “affected,” and control individuals are “unaffected.” Depending on the study, however, both case and control individuals may be considered affected as shown in the application discussed below. In the first situation, HWD for association will be computed based on case individuals only. In the latter situation, the sum of χ-square for HWD in cases and HWD in controls serves as our HWD value for association. Whatever the situation, the d largest such HWD values will be set equal to zero.

Weighting

Effects of AA and HWD for association are merged by building the product, t_i × u_i, where t_i is the AA statistic and u_i is the HWD for association in the ith SNP, with the d largest u_i values set equal to zero. Thus, the t_i values are modified or “weighted” by the u_i values. To combine the resulting evidence for association over multiple SNPs and genes, we simply form the sum, S = ∑_i(t_i × u_i), over a suitable set of SNPs. We expect that marker loci close to or inside susceptibility genes will tend to show elevated test statistics, and that the sum, S, comprising these markers will be more powerful than any corresponding statistic for a single marker. Also, some forms of interactions between susceptibility genes may be captured in S, which, in turn, may enhance its power. Previously, we used a simple sum statistic based only on AA, which was designed to select influential SNPs in a bootstrap procedure. That procedure does not control the genomewide type I error and has insufficient power when the false-positive rate is being controlled (data not shown; Hoh et al. 2000).

Grouping

The crucial question is which SNPs to include in our sum statistic. Presently, we base this decision simply on the size of the value of t_i × u_i at each SNP. Because the number and locations of susceptibility genes are unknown, we test sums with varying numbers, n, of terms (i.e., marker loci) as follows: Order all markers, irrespective of their genomic locations, so that the one with the highest value, s_i = t_i × u_i, has rank 1 and so on (s₍₁₎ ≥ s₍₂₎ ≥ s₍₃₎ ≥ …). Then, sums with increasing numbers of terms are formed, starting with the markers ranked highest: S(n = 1) = s₍₁₎, S(n = 2) = s₍₁₎ + s₍₂₎, and so on up to a fixed N. The primary interest will be to find the number, n, of SNPs comprised in S that reflects association of the corresponding SNPs with disease.

Significance Tests

The significance level, p_n (p-value), associated with the nth sum is determined in a randomization test, where the labels “case” and “control” are permuted. Because the total number of possible permutations,

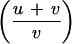for u cases and v controls, is very high, we perform a computer-based test, that is, take a random sample of all possible permutations. To obtain an adequate representation of these permutations, we use samples of 20,000 computer-generated permutation replicates for sample sizes of ∼800, with about half of them being cases. Note that trimming is applied in each permutation sample as it is in the observed data.

As the number n of terms in S increases, a pattern is expected, where initially the P-values decrease until a minimum, min_np_n, is reached when the sum includes k terms, for example. When more terms (SNPs) are added to S, p-values tend to increase again as seen, for example, in Figure 1. This presumably occurs because the markers ranked 1 through k are close to or inside a disease susceptibility gene, and adding additional markers simply introduces noise to S. Therefore, the number k estimates the number of SNPs in g susceptibility genes. Because several SNPs may be located in a given susceptibility gene, we expect g to be smaller than k. In genomewide association studies, at least initially, g will generally be unknown.

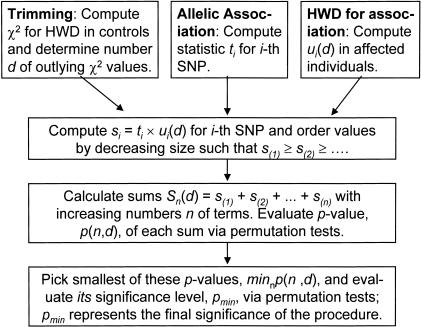
Figure 1.

Flow diagram illustrating the algorithm implemented in the set-association approach.

To test N sums with associated P-values, p_i, and declare the smallest of the p_is the significance level for our analysis would lead to yet another multiple-testing problem. Thus, we define the smallest empirical significance level, min_np_n, as our statistic of interest and assess its significance level, p_min. Determining this significance level is again achieved on the basis of permutation samples (Manly 1997), that is, p_min is estimated by the proportion of permutation samples with min_np_n smaller than that in the observed data. The min_np_n is a single statistic applied to the whole genome, and its significance level is global. This is how we overcome the multiple-testing problem encountered when testing each marker separately.

We may also evaluate S for different levels of trimming, that is, untrimmed, with only the highest HWD value trimmed, the two highest values trimmed, and so on. This represents another situation that needs to be controlled for multiple testing. We do this by the same principle as above, that is, we determine the smallest P-value, p_min-min, of the p_min-values obtained for each trimming level and evaluate its significance level in the randomization procedure. The end result of our approach, set-association analysis, is a small subset of SNP markers selected from a potentially huge initial number of markers. A low genomewide false-positive rate will ensure that the selected markers are in fact associated with disease genes. A summary of the various steps in our approach is shown in Figure 1.

The set-association approach has been implemented in a computer program, Sumstat, which is freely available (no cost to academic researchers). The program documentation is available at http://linkage.rockefeller.edu/ott/sumstat.html.

Application

The set-association approach worked successfully on the following case-control study (R. Zee, pers. comm.). In 779 heart disease patients, 6 mo after angioplasty, 342 showed restenosis (“cases”), the rest being “controls.” All individuals were genotyped for 89 SNP markers in 62 candidate genes. Clearly, this study is not a genomewide association study, but it serves the purpose of showing our method. The results of this study have not yet been published, which is why we report marker ID numbers rather than marker names below.

For trimming, we considered HWD values exceeding the 99th percentile of χ² (= 6.6, 1 df) in control individuals as unusually large. Among the 89 SNPs, under the hypothesis of Hardy-Weinberg equilibrium, <1 SNP is expected to be in this region. Here we have four HWD values larger than 6.6, corresponding to SNPs #13 (HWD = 29.4), #50 (HWD = 21.7), #22 (HWD = 12.6), and #23 (HWD = 6.9). Therefore, we decided to trim the d = 4 largest HWD χ-square values in observed and randomized data.

For the AA statistic, t_i, we simply chose the absolute difference in mean frequencies of the 1 allele between cases and controls for the ith SNP. Initially, we computed HWD values, u_i, for association in case individuals. With this, we used t_i × u_i as the single-marker statistic for the ith SNP, with the d = 4 largest values of u_i to be trimmed. Testing up to N = 20 sums furnished the smallest P-value, min_np_n = 0.061, for a sum comprising n = 12 SNPs. The corresponding associated global significance level was obtained as p_min = 0.101, that is, a nonsignificant result.

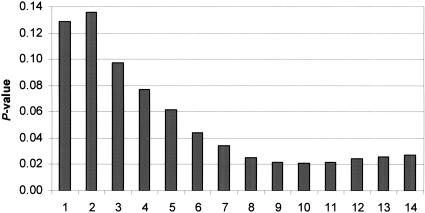
As all individuals are heart disease patients (“affected”), it makes sense to consider the combined χ-square for HWD in cases and controls as the measure indicative for association, the idea being that HWD may pick up SNPs correlated with restenosis and heart disease. Therefore, we computed u_i as the sum of HWD for cases and HWD for controls, again trimming the four largest of these summed values, and tested up to N = 20 sums, S_n, as above. This furnished min_np_n = 0.021 for a sum comprising n = 10 SNPs (a subset of the 12 SNPs identified above), with an associated global significance level of p_min = 0.040. Of the n = 10 SNPs, only 2 are in the same gene. Therefore, we conclude that the g = 9 genes identified through the SNPs are likely to confer susceptibility to restenosis. The significance level of S_n as a function of the number n of SNPs included in S_n is shown in Figure 2. Note that the (global) significance level associated with testing the single best marker (#23) is 0.129. This value is much higher than the significance level, p_min = 0.040, for our minimum-p-value statistic, which shows the power of our set-association approach. Because with four clearly inflated HWD χ² values the trimming was obvious, there was no need to evaluate p_min-min.

Figure 2.

Significance level of S_n statistic as a function of the number n of SNPs in different genes that are included at each step. The smallest significance level, min_np_n, occurs with 10 SNPs included in S_n. The 10 SNPs represent 9 different genes.

DISCUSSION

Our set-association approach furnishes a list of SNP markers that presumably are in the vicinity or within susceptibility genes. One of the main features of our method is that it furnishes a clearly defined genomewide significance level. Of course, SNPs identified this way must be scrutinized to see whether the genes implicated make biological sense for the trait under study, for example, whether genes identified by these SNPs are reasonable candidate genes. We present our approach as an alternative to other multilocus methods of gene mapping, in particular, the partitioning methods of Nelson et al. (2001). Each of these approaches presumably looks at the data from a different angle, and each has its advantages and disadvantages. We believe that we have a found a way to control the genomewide significance level with excellent power for detecting disease-causing genes.

Application of our method worked well for the restenosis data in the sense that it furnished significant results with a global significance below 5%. Of course, there is no absolute guarantee that this method correctly identified loci contributing to restenosis. Trimming and the use of HWD for association were essential elements in the significance of the result. Using only AA without trimming and no HWD for association resulted in a global significance level of 0.38. On the other hand, differences in HWD between case and control individuals are not significant (P-value = 0.69). Therefore, it really is the combined effect of AA and HWD, coupled with quality control through trimming, that gives our method its power.

Trimming could be applied in one of two ways: Either an SNP is eliminated from analysis altogether (removed from observed and permuted data), or the process of trimming is handled in a dynamic way, that is, applied in observed and permuted data. In our experience, the latter approach is more powerful than the former.

Several unresolved questions need to be addressed. For one thing, the method of incorporating SNPs in sums with increasing numbers n of terms rests solely on the test statistic, t × u, for each SNP. However, SNPs in close proximity to each other in the same gene may be correlated, and having one SNP in the sum may make it less desirable to have another that is strongly correlated with it. We are working on finding more sophisticated ways of building these sums. However, the fact that some SNPs may be correlated with each other does not have a negative impact on the significance level. Permutation tests elegantly allow for such substructure in the data. Another discussion point is that, as expected, results of our approach depend on the statistic, t_i, used for measuring association between SNPs and case and control individuals. It will be important to find the most powerful statistic for such studies.

Genotyping errors have deleterious effects on association and linkage disequilibrium analysis (Akey et al. 2001) and thus will also affect our set-association method. If, in addition, errors occur with different frequencies in cases and control individuals, this would lead to different estimates of SNP allele frequencies and HWD in the two groups, which would seriously affect our method. The easiest solution to the error problem is increased quality control in the laboratory. Another avenue to be explored is incorporating error frequencies in the analysis model as it has successfully been done for a specific disequilibrium test (Gordon et al. 2001).

Population admixture (substructure) is a problem in any association study. If cases and controls have different ethnic backgrounds with different SNP allele frequencies, this will adversely affect our set-association method. At this time, our recommendation is to proceed in analogy to previously proposed solutions, which require genotyping of SNPs known to be unrelated to the trait under study (Pritchard and Rosenberg 1999; Bacanu et al. 2000).