Genotyping errors in a calibrated DNA register: implications for identification of individuals

Abstract

Background

The use of DNA methods for the identification and management of natural resources is gaining importance. In the future, it is likely that DNA registers will play an increasing role in this development. Microsatellite markers have been the primary tool in ecological, medical and forensic genetics for the past two decades. However, these markers are characterized by genotyping errors, and display challenges with calibration between laboratories and genotyping platforms. The Norwegian minke whale DNA register (NMDR) contains individual genetic profiles at ten microsatellite loci for 6737 individuals captured in the period 1997-2008. These analyses have been conducted in four separate laboratories for nearly a decade, and offer a unique opportunity to examine genotyping errors and their consequences in an individual based DNA register. We re-genotyped 240 samples, and, for the first time, applied a mixed regression model to look at potentially confounding effects on genotyping errors.

Results

The average genotyping error rate for the whole dataset was 0.013 per locus and 0.008 per allele. Errors were, however, not evenly distributed. A decreasing trend across time was apparent, along with a strong within-sample correlation, suggesting that error rates heavily depend on sample quality. In addition, some loci were more error prone than others. False allele size constituted 18 of 31 observed errors, and the remaining errors were ten false homozygotes (i.e., the true genotype was a heterozygote) and three false heterozygotes (i.e., the true genotype was a homozygote).

Conclusions

To our knowledge, this study represents the first investigation of genotyping error rates in a wildlife DNA register, and the first application of mixed models to examine multiple effects of different factors influencing the genotyping quality. It was demonstrated that DNA registers accumulating data over time have the ability to maintain calibration and genotyping consistency, despite analyses being conducted on different genotyping platforms and in different laboratories. Although errors were detected, it is demonstrated that if the re-genotyping of individual samples is possible, these will have a minimal effect on the database's primary purpose, i.e., to perform individual identification.

Background

Microsatellites, also known as short tandem repeats (STRs), are repeating sequences of DNA where the repeat motif includes 1-6 bases [1,2]. Variation in the number of repetitions within the sequence forms the basis of the alleles. Since their discovery in the 1980's, microsatellite DNA markers have been a prominent tool in ecological, medical and forensic genetics, among other things because of their high levels of variability, co-dominant inheritance, and abundance in most organisms [3-5].

Microsatellites are almost exclusively genotyped by amplification of the DNA sequence via the polymerase chain reaction, which is subsequently subject to electrophoresis and sized (i.e., length of repeat) in relation to known DNA fragments (i.e., the size standard). The relative migratory properties of the microsatellite fragment to the DNA size standard is influenced by a range of factors and is dependent on the conditions under which the electrophoresis is performed [6]. In part due to the way in which microsatellites are genotyped, this class of markers is prone to genotyping errors [7], which occur when the observed genotype does not correspond to the real genotype [8]. Genotyping errors in microsatellites cannot be avoided completely, and have a range of origins including scoring mistakes, contaminated multiplex assays, biochemical anomalies, and degenerated DNA samples [9]. Error rates in the range 0.005-0.01 per locus have frequently been reported in the literature [9]. Furthermore, error rates as low as 0.002 per locus are non-negligible, and may lead to false conclusions about, for example, confidence in assigned paternities [10].

The implementation of DNA based methods for the identification and management of wildlife resources represents a broad and rapidly growing field. In the future, it is likely that DNA-registers are going to become an increasingly important component of this development. For example, DNA-registers may contain information about animal pedigrees in living gene banks for conservation of endangered species, and monitor trade in wildlife [11,12]. DNA registers may be built upon a multitude of approaches and genetic markers, for example, relying upon allele frequencies for population identification [13], exact genotype profiles for individual identification [12], as well as sequence recognition for species identification in DNA barcoding [14]. Irrespective of primary purpose, a common feature of all DNA-registers is the fact that they accumulate data over time. This generates special challenges to data acquisition and quality, not least because developments in genotyping platforms and technology over time may cause calibration and continuity issues. Despite having similar genotyping equipment, different laboratories may still produce deviating allelic values for microsatellites on the same locus [6,15-17].

DNA-registers should be annotated with estimates of genotyping error rates from blinded experiments. For the purpose of matching profiles against a DNA-register, it is the across-profile error rate that is of importance, not the per-locus rates. If loci can be assumed independent, the former is given as

(1)

when there are L loci, and p_l is the error rate at locus l. However, when loci are positively correlated, i.e., the fact that an error occurs at one locus increases the error rate on other loci, the profile-wise error will exceed the value given by (1). We propose to account for this using a mixed regression model.

The Norwegian minke whale (Balaenoptera acutorostrata) DNA-register (NMDR) consists of individual DNA profiles from all whales captured legally (according to international law) by Norway since its establishment in 1997, and includes 6736 individuals up to the 2008 catch. The Norwegian whaling operations are controlled by the Norwegian Directorate of Fisheries, which also owns and operates the NMDR. In the period 1997-2008, four independent laboratories have had responsibility for the genotyping: Lab 1 from Canada (1997-2002), Lab 2 (2003-2005) and Lab 3 (2006), both from Iceland, and Lab 4 from Norway (2007-2008). All laboratories performed electrophoresis of the DNA fragments using Applied Biosystems genetic analyzers (Lab 1 = gel-based 377 machine, while laboratories 2-4 used capillary based machines). The initial analysis protocol was designed by the Norwegian forensic science institute using an ABI 377 genetic analyzer, and was based upon creating an allele size ladder for each of the markers. Each of the laboratories that have conducted genotyping for the register were first given sets of samples (up to 80 individuals) to calibrate their analyses against, and were also subject to and passed a blind calibration test with at least 20 known individuals prior to conducting analyses. Lab 1 started their analyses in the year 2000, thus, all 1668 individuals caught in 1999 or earlier were genotyped then. The NMDR was primarily established for forensic purposes, and low error rates have therefore been a high priority for the Norwegian government. The register includes >99.9% genotyping coverage for all markers in all individuals, which presents extra challenges when dealing with individual samples of low quality. Consequently, the NMDR provides a unique opportunity to check how the error rates in a high-quality DNA register has developed in an eight year period, and allows us to evaluate the precautions taken to deal with calibration issues between laboratories during a time of technological progress.

Methods

Genotyping and comparison to the NMDR

In order to check genotyping quality in the NMDR, 20 individual tissue samples from each year (1997-2008) were randomly selected for re-analysis. In total, 240 samples were subject to DNA isolation and amplification of 10 microsatellites that the register is based on: GT509, GT310, GT211, GT575, GT023 [18], GATA098, GATA417, GATA028 [19], EV001PmG09074, EV037MnG09081 [20]. Genotyping was conducted at the Institute of Marine Research in Bergen, Norway. This is the laboratory currently with responsibility for the register. In short, DNA was isolated from alcohol preserved muscle tissue in 96 well format using a commercial kit (Qiagen DNeasy). For Lab 1, Lab 2 and Lab 4 microsatellite DNA markers were amplified in three multiplex reactions, which was consistent with the original protocol. Lab 3 amplified fragments in two multiplexes for a single year class only. Full genotyping protocol is available [21].

After the first round of genotyping, individuals not providing full amplification of all markers were subject to PCR and electrophoresis again. Once samples were 100% genotyped, these data were compared to the genotypes stored in the DNA-register. A set of mismatch individuals (i.e., individuals where the genotype for at least one marker deviated between register and re-analysis here) was then subject to PCR and electrophoresis for a further 3-5 times in order to fully elucidate the genotype. All genotyping was manually inspected by two experienced researchers. After repeated analyses, genotypes still deviating from the DNA-register were considered as the true genotype, when, and only when, the re-run sample gave 100% consistent genotypes for the deviating marker in the 3-5 runs it was subject to in the present study. All genotyping errors detected within fulfilled this criterion, and no diffuse or inconsistent genotypes were accepted as the true genotype.

Six individual samples failed to amplify fragments for most of the markers, and were therefore excluded from the statistical analyses (two samples from 1997, one from 2008). The low and only partially amplified genotype peaks were indicative of poor DNA quality, probably caused by sub-optimal storage of those individual samples. While it is acknowledged that exclusion of these six samples may potentially decrease the overall estimate of genotyping errors if they were also of sub-optimal quality when originally genotyped, it was not possible to examine this here. Nevertheless, the primary purpose of this study, to test genotyping quality in a DNA register over time, through the application of a mixed regression model, was not compromised by exclusion of these six samples.

Statistical methods

Logistic regression [22] was used to account for explanatory variables, such as locus effects, in the error rate estimation. It was not a priori assumed that errors occur independently, neither for the two alleles within a locus nor across loci. Errors are said to be independently distributed within a locus of an individual, if the event that the first allele (gene copy) is erroneously recorded does not affect the probability of an error occurring at the second allele of that same locus. Such independence yields the relationship

(2)

where p_l is the per-locus error rate, and p_a is the per-allele (gene copy) error rate. The per-locus error rate is the probability that at least one error occurs at a locus of an individual. The data was analyzed both with respect to p_l and p_a, but no differences of consequence were detected. We shall therefore focus on p_l, as it is the most commonly used metric among the two [23,24].

Mixed (regression) models are commonly used to relate correlated observations to explanatory variables [22]. We distinguished between fixed effects (LAB, LOCUS and YEAR), which affected all individuals in the population equally, and random effects which were individual specific effects. The fixed effects LAB and LOCUS were taken to be factors (ANOVA type) representing systematic differences between laboratories and loci caused by, e.g., diverging protocols and differing ranges of allele sizes. One parameter was estimated per level of the factors. The fixed effect YEAR was a continuous covariate (regression type), expressing the effect of a steady advance in technology. Two random effects, IND (individual sample) and MP:IND (intersection between individual and multiplex assay), were considered. IND affected the error rate at all loci equally, while MP:IND affected only those loci (within a particular individual) ran together on a multiplex. They expressed discrepancies due to varying sample quality and mishandling of equipment, respectively, and were taken to be normally distributed with mean zero and standard deviations σ_IND and σ_MP:IND, respectively. Low values of σ_IND and σ_MP:IND means little difference between individuals, and hence little impact on the error rates, because the random effects are centered at zero. Due to the facts that no laboratory has been responsible for the analyses more than three years (Table 1), and that not all labs were assessed each year in the study (Table 1), YEAR and LAB are confounded covariates, and consequently never appear in the same model (Table 2).

Table 1.

Empirical estimates of error rates by laboratory.

			LOCUS		ALLELE		PRED
Lab (country)	Period	Sample size	pl	SD(pl)	pa	SD(pa)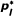
Lab 1 (Canada)	97-02	116 (120)	0.02373	0.00443	0.01422	0.00246	0.02825
Lab 2 (Iceland)	03-05	60	0.00500	0.00288	0.00333	0.00166	0.00666
Lab 3 (Iceland)	06	19 (20)	0	-	0	-	0
Lab 4 (Norway)	07-08	39 (40)	0.00256	0.00256	0.00128	0.00128	0.00256
Total	97-08	234 (240)	0.01325	0.00236	0.00812	0.00131	0.01617

The column "Period" shows the catch period for which each laboratory had responsibility for the NMDR. Except for the catches from 1997-98, which were genotyped in the year 2000, all individuals were genotyped the year following capture. The column "Sample size" contains the number of successfully regenotyped individuals from the laboratories, with the total number of regenotyping attempts in parenthesis. Initially 20 samples were selected from each year, but 6 samples had to be thrown out because of amplification failure. Locus EV001 was included for all probabilities of error in this table. In columns labeled LOCUS and ALLELE, p_l and p_a are the mean error rates (number of errors detected divided by number of loci/alleles), and SD(p) the corresponding empirical standard deviations. The column labeled PRED contains the predicted values, 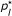, of p_l, calculated from p_a using (2).

Table 2.

Candidate model set for NMDR study.

Model	Fixed	Rand	σ	AIC	p	SD(p)	CV(p)	W
M1	LOCUS + YEAR	IND	1.35	295.7	0.0774	0.0214	0.28	5.76e-1
M2	YEAR	IND	1.24	297.5	0.0243	0.0045	0.19	2.34e-1
M3	LAB + LOCUS	IND	1.43	299.3	0.0514			9.52e-2
	Lab1				0.0823	0.0242	0.29
	Lab2				0.0185	0.0088	0.48
	Lab4				0.0102	0.0089	0.87
M4	LAB	IND	1.32	301.0	0.0162			4.07e-2
	Lab1				0.0261	0.0045	0.17
	Lab2				0.0054	0.0024	0.44
	Lab4				0.0029	0.0025	0.86
M5	LOCUS + YEAR	-	-	303.1	0.0768	0.0239	0.29	1.42e-2
M6	LOCUS + YEAR	MP:IND	1.22	303.5	0.0771	0.0237	0.33	1.17e-2
M7	YEAR	-	-	303.6	0.024	0.0046	0.2	1.11e-2
M8	YEAR	MP:IND	1.13	304.0	0.0242	0.0047	0.2	9.08e-3
M9	LAB + LOCUS	-	-	307.1	0.0511			1.92e-3
	Lab1				0.0822	0.0263	0.32
	Lab2				0.0182	0.0118	0.65
	Lab4				0.0094	0.0097	1.04
M10	LAB + LOCUS	MP:IND	1.31	307.2	0.0516			1.83e-3
	Lab1				0.0828	0.0405	0.49
	Lab2				0.0193	0.0172	0.89
	Lab4				0.0102	0.0131	1.28
M11	LAB	-	-	307.5	0.016			1.58e-3
	Lab1				0.0259	0.0048	0.19
	Lab2				0.0056	0.0032	0.58
	Lab4				0.0028	0.0031	1.08
M12	LAB	MP:IND	1.20	307.9	0.0162			1.29e-3
	Lab1				0.0261	0.038	0.15
	Lab2				0.0056	0.081	1.44
	Lab4				0.0028	0.062	2.15
M13	LOCUS	IND	1.52	308.3	0.0513	0.0129	0.25	1.06e-3
M14	-	IND	1.41	309.9	0.016	0.0026	0.17	4.75e-4
M15	LOCUS	MP:IND	1.50	318.3	0.0523	0.0057	0.11	7.12e-6
M16	-	MP:IND	1.36	319.1	0.0162	0.0055	0.36	4.78e-6
M17	LOCUS	-	-	319.5	0.0512	0.0156	0.3	3.91e-6
M18	-	-	-	319.8	0.016	0.0030	0.2	3.37e-6

Model fit and estimated error rates for different covariate models sorted according to the AIC score (column five). "σ" contains the standard deviations of the random effects. The values in "p" are the probabilities that an error occurs at locus GATA417 in year 2001. Whenever LAB is included in the model, weighted means and laboratory specific error rates are given (Lab 1, Lab 2, Lab 4). "SD(p)" and "CV(p)" are the bootstrap based standard deviations and coefficients of variance of p. The column "W" contains the Akaike weights of the models.

Because the response variable was dichotomous (i.e., error vs. not error), a logistic regression model was used ([22], p 274). Denote by p_il the probability that an error occurs at locus l of individual i. A logistic map was used to model the effect of the explanatory variables on p_il,

(3)

where η_il is a linear predictor, expressed in Witkinson-Rogers notation as

(4)

This is referred to as the full model. The notation in (4) is standard in, e.g., R, and is a simplification of 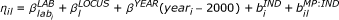, where the β's are regression parameters, the b's are normally distributed random variables and lab_i denotes the laboratory of the i'th individual. There were in total 215 random b^IND parameters, and 645 b^MP:IND parameters. Submodels, with individual terms in (4) removed, were also fitted to the data. For models without "LOCUS" the error rate does not depend on the index "l", and we hence write p_i. In the absence of both IND and MP:IND, the model reduced to an ordinary logistic regression with no individual specific effects. The AIC criterion [25] was used to balance goodness of fit and parsimony, and Akaike weights ([26], p 75) were calculated. The Akaike weight for the k'th model is

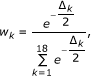where Δ_k = AIC_k - AIC_min, and AIC_min is the smallest AIC-value. For models where individual specific effects (IND or MP:IND) were included, the probability (3) was averaged over individual effects using Monte Carlo simulations (Appendix A).

All models were fit using the R package "glmmADMB" which builds on the software package AD Model Builder (AD Model Builder project, 2009). Because glmmADMB could not fit models with more than one random effect present simultaneously, we relied on SAS PROC GLIMMIX in such situations. A bootstrap approach was used to obtain the standard deviations of the error rate, p, given by (3). Individuals were randomly sampled from the data with replacement to create 500 bootstrap datasets. For each of these the model was refit, and finally, standard deviations were calculated empirically across the 500 bootstrap replica. Due to the use of sampling with replacement, the number of genotyping errors differed across the replica, and also from the original data set. When fitting a model using bootstrap replica which happened to have few genotyping errors, the software sometimes produced warnings indicating non-convergence of the numerical method. However, such warnings were rare (1.6% for M1, 0.6% for M10, 3.6% for M15 and zero for the others), and only modestly affected the estimated standard deviations. To obtain an upper bound for the effect of the non-convergence, we counted all error estimates from bootstrap replica producing warnings as zero. Results for M1 are showed in Table 3.

Table 3.

Estimates of (per locus) error rates for best fitting model (M1).

Locus	p	SD(p)	CV(p)
GATA417	0.0774	0.0214 (0.0241)	0.28
EV037	0.0283	0.0112 (0.0122)	0.41
GATA028	0.0283	0.0130 (0.0134)	0.46
GT575	0.0213	0.0110 (0.0112)	0.52
GT509	0.0141	0.0093 (0.0095)	0.66
GT310	0.0141	0.0101 (0.0102)	0.71
GT211	0.0141	0.0083 (0.0085)	0.59
GT023	0.0141	0.0091 (0.0092)	0.64
GATA098	0.0071	0.0084 (0.0084)	1.19
EV001	0	0	-

The values in "p" are the probabilities that an error occurs at a particular locus in year 2001. "SD(p)" and "CV(p)" are the bootstrap based standard deviations and coefficients of variance of p. In parenthesis are the "upper limit" standard deviations (i.e., we included bootstrap replica which produced warning messages as having zero errors).

Results

Descriptive statistics

The mean genotyping error rate varied both between laboratories and from year to year (Table 1). For the analyses of the catches from 2007-8, conducted by Lab 4, the mean error rate was approximately a ninth of what was found for the oldest analyses, conducted by Lab 1. Lab 3 and locus EV001 had error rates of zero, and were therefore left out of the subsequent statistical analyses, as these data did not provide information about other parameters than those associated with the respective factor levels (Lab 3 and locus EV001). Using the p_a estimated from the data, (2) predicted the corresponding value of p_l to three decimal points for Lab 4 (Table 1). On the other hand, for Lab 2 and Lab 1 the predicted values of p_l (still using the estimated p_a and (2)) were off by 33% and 19%, respectively (Table 1), indicating the presence of individual or multiplex assay effects, which is consistent with [8]. False allele size constituted 18 of the 31 errors (Table 4). A third of those were incorrectly called at both gene copies, again pointing in the direction of the presence of individual sample or multiplex effects. The remaining errors were ten false homozygotes (i.e., the true genpotype was a heterozygote) and three false heterozygotes (i.e., the true genotype was a homozygote).

Table 4.

Summary of genotyping errors observed in the NMDR according to laboratory.

	Lab 1			Lab 2			Lab 4
Type of error	Total	= 1 bp	>1 bp	Total	= 1 bp	>1 bp	Total	= 1 bp	>1 bp
Single false allele size	10	7	3	2	0	2	0	0	0
Double false allele size	6	1	5	0	0	0	0	0	0
False homozygote	9	5	4	1	1	0	0	0	0
False heterozygote	2	0	2	0	0	0	1	0	1

Columns labeled "Total" contain the total number of errors of a specific kind for each laboratory. False allele size is when an allele was erroneously sized compared to the true size for single and double alleles. " = 1 bp" denotes that the erroneously called allele is a distance one from the true allele, whereas ">1 bp" means that the distance was greater than one. False homozygote is where the true genotype was a heterozygote, and false heterozygote is where the true genotype was a homozygote.

Model selection

Models were arranged according to their AIC value, which balances goodness of fit against model complexity (Table 2). The covariate YEAR is confounded with LAB, but had a better fit than LAB according to the AIC criterion. Models including YEAR had a combined Akaike weight of 0.86, while the Akaike weights of models containing LAB only summed to 0.14 (Table 2). Part of the reason is that YEAR gave a more parsimonious representation (1 extra parameter) of the fact that technology has improved over time than did LAB (2 extra parameters). The addition of LOCUS to a model always improved the fit (e.g., M1 vs. M2, Table 2). The combined Akaike weight of models including IND was 0.95, whereas models featuring MP:IND had Akaike weights summing to 0.024 (Table 2). In all cases where IND and MP:IND were present in the same model, σ_MP:IND was estimated to be equal to zero, reducing the model to one including only IND. Therefore, models including both random effects were omitted from further consideration.

Error rates

The non-model based mean error rate across all labs and years, including locus EV001 and Lab 3, was 0.013 per locus and 0.008 per allele (Table 1). Excluding EV001 and Lab 3, the mean error rate was 0.016 per locus. Under the best fitting model (M1), the across-locus error rate was 0.022 in the middle of the period (year 2001). The locus with the highest error rate was GATA417, at which the rate (0.077) was almost three times as high as at any other locus (Table 3). In 2004 and 2008 the error rates for GATA417 had dropped to 0.032 and 0.008, still according to M1.

Models containing the same fixed effects yielded similar error rate estimates, regardless of the choice of random effects (e.g., M1, M5 and M6, Table 2), so to compare laboratories, we discuss models including LAB and LOCUS apart from models featuring only LAB. In both scenarios the error rate at Lab 1 was several times higher than at the other laboratories, and Lab 4 always had lower error rates than Lab 2 (e.g., M3, Table 2). This is consistent with the estimated regression coefficient for YEAR translating to a decreasing annual trend. Note that, in Table 2, p was calculated for GATA417, where errors were abundant, and in the year 2001, which is why p rose when LOCUS or YEAR was added to a model (e.g., M14 vs. M2, and M2 vs. M1, Table 2).

Our suspicion that errors tend to accumulate within individuals was strengthened by σ being greater than zero in all models featuring random effects (Table 2). The importance of this fact becomes obvious when considering how it affects the probability of more errors occurring at individuals with at least one error. Due to the dependence between loci, we expect more than one in five such individuals to have at least two errors, whereas independence would yield less than one in ten (Table 5).

Table 5.

Multilocus error rates.

	P(E > 0)	P(E = 1)	P(E > 1)	P(E > 1|E > 0)
Dep.	17.0	13.4	3.60	21.2
Ind.	20.1	18.3	1.77	8.84

Probability of having E errors in a 10 loci profile for model M1. The top row (Dep.) assumes dependence between the loci within an individual, and the bottom row (Ind.) assumes independence. P(E > 1|E > 0) is the conditional probability of having two or more errors given that an error occurs.

In the mixed model framework, the per locus error probability varies among individuals according to a distribution (Figure 1). For the estimated value of σ this distribution was unimodal, but skewed to the right. Because the random effect was shared among loci, individuals in the right hand tail of the distribution were error prone at all loci. In an artificial experiment, where σ was increased by a factor of three, the population distribution became bimodal, with the two groups of individuals being 1) those with almost zero error rate 2) those with p_il > 0.50 (Figure 1).

Figure 1.

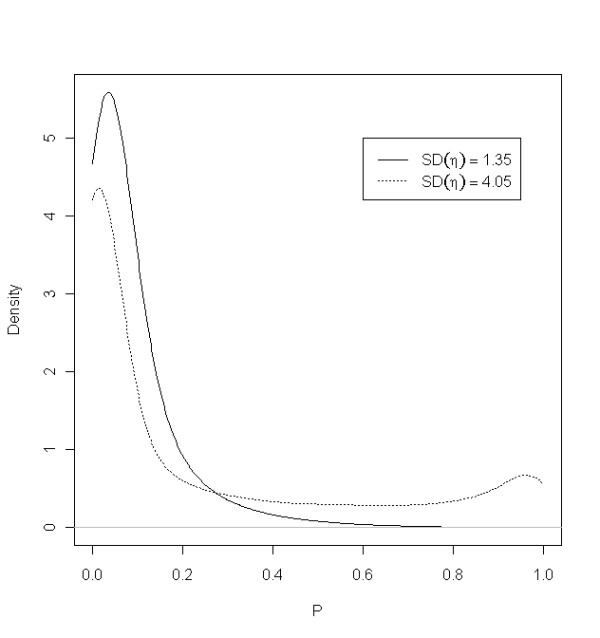
Probability densities for error rates, p, for model M1 (SD (η) = 1.35) and a model with a three times larger standard deviation (SD (η) = 4.05).

Table 6 shows the mean allele lengths for each marker, and the corresponding coefficients for model M1 (Table 2), sorted according to mean error rate. GATA417 was by far the most error prone locus. At the most ancient laboratory, Lab 1, there were nine occurrences of the true genotype, 221, being erroneously recorded as 220 (data not shown) for GATA417. Both 220 and 221 were present on the allelic ladder. Apart from those, GATA417 had two errors.

Table 6.

Error rates and allele lengths.

Parameter	Coef	SD(coef)	Amax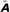
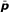GATA417	1.59	0.38	252	223	0.0512
EV037	0.40	0.52	211	203	0.0186
GATA028	0.40	0.52	223	202	0.0186
GT575	0.09	0.58	166	155	0.0140
GT509	-0.35	0.68	217	203	0.0093
GT310	-0.35	0.68	125	117	0.0093
GT211	-0.35	0.68	116	106	0.0093
GT023	-0.35	0.68	115	103	0.0093
GATA098	-1.08	0.93	107	93	0.0047
EV001	-	-	175	153	0
YEAR	-0.36	0.11	-	-	-
Intercept	-4.74	0.45	-	-	-
VAR(IND)	1.81	0.94	-	-	-

The second column is the values of the coefficients in M1 (Table 2), and the third is their standard deviations. A_max is the length of the largest allele, and 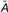is calculated using the population allele frequencies. 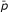is the mean error rate at the locus. EV001 was not in the analyses, and has therefore no coefficient in M1. Its correct value would have been -∞.

Discussion

To our knowledge, this study represents the first investigation of genotyping error rates in a wildlife DNA register, and the first application of mixed models to examine multiple effects of different factors influencing the genotyping quality, such as time, microsatellite marker and sample quality.

A major challenge with microsatellite data sets is sharing data between laboratories, and comparing data from different analytical platforms. Despite the importance of these challenges, systematic shifts of allelic scores have, with few exceptions, not been thoroughly examined (e.g., [6,15,16]). Furthermore, to our knowledge no studies have investigated how calibration between laboratories over time influences the ability to produce calibrated data. Although nine true values of 221 were recorded as 220 at GATA417 and Lab 1, we did not detect any systematic shift of allelic values for any of the markers implemented in the NMDR. This was despite the fact that the analyses were conducted in four separate laboratories in three countries, and over a period almost stretching a decade. We conclude that even though the genotyping for the NMDR has been conducted by several laboratories, and during a period in which genotyping platforms have displayed significant technological changes from gel to capillary based electrophoresis instruments, systematic genotyping errors due to allele size calibration were not present. This demonstrates the importance of calibrating genotyping scoring between laboratories, in addition to conducting blind proficiency tests prior to new laboratories overtaking an existing DNA register, as was performed for the NMDR.

Assuming genotyping errors disperse identically and independently (or almost independently) across the markers within an individual can be convenient when dealing with calculations regarding the genotyping error rate. Among studies utilizing simulations, it is therefore a common simplification [10,24,27,28]. However, such an assumption is often not realistic [7,27,29]. This is well illustrated by a study of genotyping errors in 510 loci [8]. In that study, ten errors were detected, and all occurred in the same individual. Within-individual dependencies like this can easily be modeled by increasing the standard deviation of the random effects MP:IND and IND in the mixed models (4).

Because all individual whales caught by Norway are required to be genotyped at all markers in the NMDR, samples of questionable quality cannot be disregarded or left as missing data, as is possible in many studies [8,30]. Despite this fact, the overall error rate of 0.013 per locus in the NMDR is in concordance with the published literature on microsatellites from tissue samples [7-9,31]. Still, the inclusion of bad samples in the analysis is an error source beyond the control of any laboratory, and contributes to the standard deviation of IND, σ_IND, representing the effect of variability in sample quality between individuals, being greater than zero in all models featuring IND (Table 2).

We initially investigated an interaction effect between individual and multiplex (MP:IND), but it turned out to be superfluous if a model also contained an individual random effect (IND). Further, the inclusion of MP:IND alone in a model not containing IND did not affect the model fit much (Table 2). This leads to the conclusion that sample quality was dominating over the mishandling of multiplex assays as a source of errors, but the same conclusion may not apply in other studies.

Among the fixed effects, YEAR was the most important. Because LAB and YEAR were confounded, we were unable to assess their individual impacts on the genotyping error rate. However, models including YEAR had the best AIC scores (Table 2). This can partly be explained by LAB being a less parsimonious representation of technological and procedural advances than YEAR, and partly by models including YEAR being closer to the data than models including LAB (Table 2). Examining the difference between technological and procedural advances, we conclude that the considerable impact of sample quality (IND) relative to that of the mishandling of multiplex assays (MP:IND) implies that the importance of YEAR is mostly due to progress regarding apparatus. Although the complete eradication of genotyping errors seems unlikely, we have documented a positive development taking place over the last decade in the NMDR.

In addition to the time aspect, a large variation between the genotyping error rate on different markers was detected (Table 6). Such variation was expected [29], and was the reason for the positive impact of LOCUS on the model fit. It is also known that larger alleles may be more prone to genotyping errors than shorter ones [32-34], which is consistent with the trend seen here (Table 6). The relationship between allelic size and error rate is not deterministic however, as illustrated by locus EV001 harboring zero errors (Table 6).

Initially the R function "lmer" was used to fit the mixed models. However, due to convergence problems on the bootstrap datasets, we switched to the R package "glmmADMB" which turned out to be more numerically robust, but had the limitation that only a single random effect can be included at a time. This is the reason why models including both the factors IND and MP:IND were run in SAS.

Since the beginning of the millennium, the number of peer reviewed articles mentioning genotyping errors has drastically increased [9]. It has been discussed how to best obtain estimates for genotyping error rates [23,31,35], reduce the number of errors [7,8] and statistically handle the uncertainty necessarily accompanying errors [10,27]. We have focused on how to accurately model the genotyping error rate. This is important both in order to understand the underlying mechanisms concerning errors, and to be able to use data for purposes of statistical inference.

The presence of genotyping errors weakens the ability to accurately match individual samples to a DNA register. On average there is a 17% chance of a mismatch between a true multilocus genotype and the corresponding genotype in the NMDR for data accumulated over a decade (Table 5). Tissue samples from all individuals are stored, so it is possible to analyze them again, and thereby correct prospective errors. This is handy, e.g., in a juridical setting [12], where a high confidence in the validity of the genotypes is imperative in order to take legal action, and only few samples are involved. The use of genetic tagging to obtain abundance estimates [36-39] and to monitor populations [19,40-42] is widespread. For such applications, reanalyzing all close mismatches (sample matching at all but a few markers) may not be feasible due to financial or other reasons. If a rule is applied to allow for close mismatches to count as a recapture, the within-individual dependence structure described by σ is of great importance. Assuming independence (σ = 0) when it is not the case, the probability of more errors occurring at individuals harboring at least one error will potentially be grossly underestimated (Table 5). Genotyping errors may also strongly influence the outcome of parentage analysis [10,43]. As with individual identification, one can compensate by assigning parentage even if a candidate parent-offspring pair does not have at least one allele in common at all markers [44,45]. A somewhat related matter is the degree of relatedness represented by LOD score [46,47] used in, e.g., [48-50] to do inference about population structure and size from identified close kin. In both cases it matters whether few individuals contain many genotyping errors or the errors are more evenly spread.

Conclusions

Microsatellite DNA markers with associated genotyping quality issues can be challenging to handle, especially in the context of a DNA register that requires accurate data over many years. Nevertheless, results of the present study have demonstrated that accurate, calibrated and reproducible genotypic data are possible to achieve despite conducting analyses over a number of years and a number of analytical platforms. In addition, the mixed models approach implemented in the present study has provided further clarification of how genotyping errors occur. Once an error is present at one marker of an individual sample, it is more likely that other markers of that same individual have also been erroneously recorded. This has important consequences when making inference on individual matches, parental assignment, or degree of relatedness.

Authors' contributions

All authors have read and approved the final manuscript, contributed to the design of the study, and contributed to interpretation of data. BBS and KAG conducted genetic analyses while ØAH and HJS conducted statistical modeling of error rates. ØAH coordinated writing of the manuscript to which all authors contributed.

Appendix A

In this appendix our first goal is to explain how the individual specific error probability (3) is averaged over the individual effects. Letting p_l = P (Error at locus 1), we get

(5)

where f_l(η) is the Gaussian probability distribution function at locus l with mean μ_l = LAB + LOCUS_l + YEAR, and variance 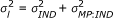. Drawing N different η_il (i = 1,...,N) from f_l (η), (5) may be approximated by the Monte Carlo estimate

(6)

A second goal of this appendix is to derive Table 5. Begin by letting E be the number of errors at an individual across all loci. For an individual i

(7)

and,

(8)

where p_il is as in (6). Assuming that errors are independently distributed across the loci of that same individual, we may simply substitute p_il in (7) and (8) with p_l from (6), to get the population means

as already seen in (1), and

Without the independence assumption, the calculations require the simultaneous consideration of all nine loci for each of the N simulated individuals. Hence, Monte Carlo estimation gives

with P_i (E > 0) given by (7), and

with P_i (E = 1) given by (8). In both the independence- and dependence scenario

and

Acknowledgements

This study was jointly funded by the Norwegian research council (Grant number 178712), the Institute of Marine Research, and the Norwegian Ministry of Fisheries. We would like to thank the referees for encouraging comments.