Label-free classification of cultured cells through diffraction imaging

Abstract

Automated classification of biological cells according to their 3D morphology is highly desired in a flow cytometer setting. We have investigated this possibility experimentally and numerically using a diffraction imaging approach. A fast image analysis software based on the gray level co-occurrence matrix (GLCM) algorithm has been developed to extract feature parameters from measured diffraction images. The results of GLCM analysis and subsequent classification demonstrate the potential for rapid classification among six types of cultured cells. Combined with numerical results we show that the method of diffraction imaging flow cytometry has the capacity as a platform for high-throughput and label-free classification of biological cells.

1. Introduction

Function correlates with structure for biological cells. Investigation of cellular shape and structure, defined here as 3D morphology, can yield insights on many biochemical processes underlying various cellular activities such as cell reproduction and differentiation [1,2]. Consequently, morphological features provide powerful and often critical markers for clinical diagnosis and cell study. In nearly all cases morphological study of cells relies on conventional microscopy methods and manual analysis of image data is often necessary due to the diverse and complex cell morphology. It is in this perspective that one would be interested in a flow cytometry method for automated and real-time analysis of large cell populations based on 3D morphology. Most of the existing flow cytometers, however, are designed on the concept to detect angularly integrated signals of scattered light and fluorescence for rapid and automated cell classification [3]. This approach yields very limited morphology information and relies mainly on fluorescent signals from stained cells as the molecular labels for analysis and classification. Even though non-diffraction imaging becomes available for probing cell morphology with a flow cytometer, automated analysis of the image data for rapid cell classification remains a challenge [4]. Different from the above methods, an approach of scanning flow cytometry has been developed to obtain polar-angle-resolved light scattering signals to derive the intracellular refractive index distribution with coated sphere models of cells [5,6].

Elastic light scattering (or light scattering as used here) is a result of heterogeneity in refractive index. When a highly coherent light beam excites a cell, the spatial distribution of elastically scattered light can be recorded as a diffraction image using an imaging detector. Through modeling study of light scattering by single cells, it has been shown that the spatial distribution of scattered light intensity correlates with the 3D morphology of biological cells in the forms of intracellular distribution of refractive index [7–12]. These results have motivated us to develop a flow cytometry method as a label-free platform for fast acquisition of high-contrast diffraction images from single cells carried by a hydrodynamically focused flow through a laser beam [13,14]. Despite validation with microspheres, it remains unknown if this new flow cytometry method has the capacity for rapid cell analysis and classification in real time. We report here the initial results of image analysis and classification of measured diffraction images to answer this critical question. These results are also compared to numerical simulations performed using cell models with nucleus only to investigate the dependence of the diffraction image textures on cell morphology, refractive index and orientation.

2. Methods

The measured diffraction images presented in this report were obtained by recording the far-field distributions of light scattered from a single cell illuminated by an incident light beam using a diffraction imaging flow cytometer [13,14]. Six types of cultured cells were used to acquire image data with the flow cytometer or to obtain confocal images for reconstruction of their 3D morphology for simulations. Among these cells three (Jurkat cells, NALM-6 cells and U937 cells) were derived from the malignant white blood cells (WBC) and three (MCF-7 cells, B16F10 cells and TRAMP-C1 cells) from the epithelial cancer cells. The cells were incubated at 37°C in 5% CO₂ atmosphere in standard culture media, removed during the exponential growth phase and transported from cell labs to the laser lab in centrifuge tubes on ice as cell suspensions with a concentration of about 10⁶ cells/mL. Using separate cell samples, we also performed confocal imaging on all six cell types to investigate their 3D morphology with single or double fluorescence staining. For simulation of diffraction images, three cell models were obtained from the confocal images of selected NALM-6 cells derived from leukemic pre-B cells. We stained the nuclei of these cells only for investigating numerically the effects of cell orientation, 3D morphology, nuclear index and volumes on diffraction image.

To measure the diffraction images of cells, we employs a “jet-in-fluid” design of the flow chamber in our diffraction imaging flow cytometer to immerse the laminar flow of the core and sheath fluids in a water-filled glass cuvette. This design feature is the key to obtain high-contrast diffraction images for analysis and feature extraction. The imaging configuration is similar to the one depicted in Fig. 1 except an imaging unit is placed between the flow chamber and a CCD camera. A cw solid-state laser provided an unpolarized incident beam of 15mm in diameter and 532nm in wavelength after beam expansion and a power of up to 48mW before focused into a spot of about 25μm in diameter at the core fluid in the flow chamber. The scattered light was collected in an angular region centered at 90° from the incident light direction of a half-cone angle of about 25° using an infinity-corrected long working distance objective followed with a beam splitter and tube lenses. A 16-bit CCD camera was employed for acquisition of one diffraction image per flowing cell with a 1ms exposure time and another camera for real-time monitoring. Because of the relatively long exposure time, the flow speed of the cells was intentionally set to very small values of about 2 to 5 mm/s to reduce blurring. Additional details of the flow chamber design, imaging unit and alignment procedures can be found in earlier publications [13,14].

Fig. 1.

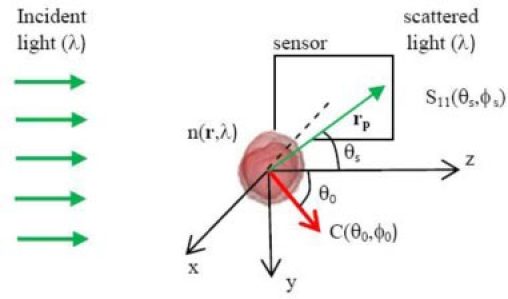
Configuration of FDTD simulation of light scattering at wavelength λ in terms of the Mueller matrix elements using imported 3D cell morphology at an orientation given by C(θ₀,ϕ₀) and diffraction images by projecting the element S₁₁(θ_s,ϕ_s) to the sensor plane centered at the negative x-axis.

We conducted numerical simulations of the diffraction images to gain insights on the correlation between 3D morphology and fringe patterns and texture parameters. A parallel finite-difference-time-domain (FDTD) code [9] was used for simulation of light scattering using cell models reconstructed from confocal images of NALM-6 cells. The NALM-6 cells were first stained with a fluorescence dye (Syto-61, Invitrogen) binding to DNA molecules and then imaged with a confocal microscope (LSM 510, Zeiss). The 3D structures of the selected cells were obtained with an in-house developed software from the confocal image stacks with nucleus only [11]. After assignment of refractive index to the host medium (n_h), cytoplasm (n_c) and nucleus (n_n), the cell model was imported into the FDTD code to calculate Mueller matrix S_ij((θ_s,ϕ_s) for i,j = 1, 2, 3, 4 with θ_s as the scattering polar angle and ϕ_s as the azimuthal angle [10]. The element S₁₁(θ_s,ϕ_s) was projected onto a plane intercepting with the x-axis as shown in Fig. 1 as a simulated diffraction image of the side scatters within a half-cone angle of about 30°. In projecting the S₁₁ element towards a pixel located at r_p = (–x₀, y, z) both effects of distance |r_p| to the projected plane and incident angle of r_p are considered. The pixel intensity I of unpolarized light scatters can thus be written as

$$I(y,z)=\frac{\left|\cos {\varphi }_s\sin {\theta }_s\right|}{x_0{}^2(1+{\tan }^2{\varphi }_s+\frac{1+{\tan }^2{\varphi }_s}{{\tan }^2{\theta }_s})}{S}_{11}({\theta }_s,{\varphi }_s)\cdot$$ (1)

where x₀ is the distance of the projection plane to the origin which was eliminated after image normalization.

After investigation of various methods for analyzing the textures of the measured diffraction images, we selected the gray level co-occurrence matrix (GLCM) algorithm for quantitative characterization of the fringe patterns presented in a diffraction image [15–17]. The GLCM algorithm analyzes the second-order correlations among pixels in an input image. The input image textures are quantified by a matrix with its elements determined by the occurrence probability of paired intensities or gray levels at two pixels separated by a pre-determined distance vector d. The row and column positions of a GLCM element are given by the gray levels of paired pixels and, therefore, GLCM can also be presented as a square image of a size equal to the number of gray levels. In our analysis the pixel pairs are neighbors and thus the pair distance d is considerably small in comparison to the sizes of speckles within the input images. This leads to GLCM with non-zero elements clustering on and near the main diagonal running from the upper-left to lower-right corner as shown by the intensified GLCM presented in Fig. 2 . Note here that the row-column designation of the GLCM images follows that of the matrices and thus the bright pixels close to the main diagonal represent the high probability of neighboring pixels having similar gray levels.

Fig. 2.

Typical pairs of measured diffraction images (1) and intensified GLCM images (2) of single flowing cells acquired at λ = 532nm: (a1/a2) Jurkat; (b1/b2) NALM-6; (c1/c2) U937; (d1/d2) MCF-7; (e1/e2) B16F10; (f1/f2) TRAMP-C1. The GLCM images are placed to the right of the diffraction images respectively. The scale bar on the left indicates the pixel values of the normalized diffraction images after conversion to 8-bit pixel values and the one on the right indicates the values of GLCM elements with p_max = (a2) 0.0172; (b2) 0.0204; (c2) 0.0160; (d2) 0.00302; (e2) 0.00175; (f2) 0.00297.

Up to 14 statistical feature parameters have been defined for extraction of textures or the spatial variation of gray levels of the input image via GLCM elements [15,16]. Based on analysis and classification test of these GLCM parameters for the measured diffraction images, we chose 5 parameters as listed in Table 1 to demonstrate their potential utility for cell classification. In this report we follow the terminology defined by Haralick for the chosen GLCM parameters. Two of these are the sum and difference entropy. Similar to the widely used entropy parameter, these parameters measure the randomness or the degree of organization of gray levels in the input image. The difference among the three entropy parameters lies in the summation over different combinations of the GLCM elements. The sum or difference entropy is obtained by summing combined GLCM elements along a line parallel to the diagonal or the main diagonal, respectively, while the entropy is obtained by summing over single GLCM elements. As a result, the sum and difference entropy are more sensitive than the entropy to the arrangement of the non-zero GLCM elements clustered around the main diagonal as the cases reported here. The other two parameters, inverse difference moment (IDM) and dissimilarity, are calculated by summing over single GLCM elements with a weight favoring the elements on or near the main diagonal and off-diagonal elements, respectively, to measure the contrast of the input image. The last of the 5 parameters is correlation which can be used to gauge the degree of inter-dependence of the two gray levels in the paired pixels for an input image.

Table 1. GLCM feature parameters for 6 types of cells (n)*.

Cell types (n)*	Sum Entropy	Difference  Entropy	IDM#	Dissimilarity^	Correlation
Jurkat (40)	4.51 ± 0.37	2.88 ± 0.30	0.218 ± 0.085	8.28 ± 1.8	0.940 ± 0.037
NALM-6 (40)	4.48 ± 0.45	2.67 ± 0.26	0.279 ± 0.092	6.71 ± 0.99	0.970 ± 0.0098
U937 (30)	4.47 ± 0.42	2.97 ± 0.38	0.204 ± 0.11	9.34 ± 2.2	0.914 ± 0.042
MCF-7 (40)	5.39 ± 0.14	3.37 ± 0.12	0.113 ± 0.015	11.0 ± 1.3	0.913 ± 0.022
B16F10 (40)	5.52 ± 0.16	2.97 ± 0.10	0.178 ± 0.026	7.05 ± 0.77	0.972 ± 0.0073
Tramp (30)	5.55 ± 0.15	2.91 ± 0.17	0.172 ± 0.032	6.69 ± 1.2	0.970 ± 0.015

*n = cell number in the training set.

#IDM = inverse difference moment.

^Dissimilarity corresponds to the k = 1 case of the contrast defined in [16].

Calculation of GLCM can be pursued with different distance vector d. Even with d = 1 for neighboring pixels as pairs and only 5 GLCM parameters as discussed above, performing GLCM calculations can be computational expensive for multiple directions of d. Consequently much effort has been devoted to develop an effective pre-processing algorithm so that the rapid GLCM calculations can be achieved for only one direction of d. For this purpose, an image processing software was developed to process the diffraction images before calculation of GLCM and extraction of feature parameters. Once a measured diffraction image was imported into the image analysis software, a histogram based algorithm was used to reduce the pixel depth from 16-bit to 8-bit for higher processing speed by removing background followed with pixel normalization. Then a coordinate transform was applied to the measured diffraction image so that the gray level variations mostly aligned along the radial directions become mainly horizontal in the transformed image. This allows the subsequent calculation of GLCM from the transformed image being executed only on horizontal pixel pairs, which significantly increases the speed of calculations to reach a rate of 70 images per second with a PC of 2.5GHz CPU even though our current image acquisition speed is much slower than the above rate.

3. Results

3.1. Measured diffraction and confocal images of 6 cell types

Using diffraction imaging flow cytometer system we have acquired unpolarized side scatters centered at 90° from the direction of incident light as the diffraction images from 6 types of cultured cells. At the time of measurement, the suspended cells received from one of the cell biology labs were injected into the core fluid reservoir and carried by the core flow through the incident laser beam for diffraction imaging. All measurements were carried out at a room temperature of about 22°C and completed within 6 hours from the time the cells were detached or taken out of the incubator. For each cell type, we acquired single-cell diffraction images from up to 70 flowing cells with an one-hour limit of measurement to maintain cell viability. The 50x microscope objective was placed at an off-focus position of 200μm towards the flow chamber along the x-axis (see Fig. 1). The measured diffraction images consist of 1600x1200 pixels with a 16-bit pixel intensity to accommodate the large dynamic range of the scattered light signals.

An image processing software was developed for GLCM analysis of each imported diffraction image and extracted feature parameters from the GLCM or image as the outputs. Examples of diffraction and intensified GLCM image pairs are shown in Fig. 2 for the 6 cell types. The intensified GLCM images were obtained from the GLCM for improved visibility using a 3x3 window average for each pixel with a weight of 1 for the center pixel and 0.5 for other pixels in the window followed by pixel normalization. It becomes immediately apparent by visual inspection that significant differences exist in fringe patterns or image textures between the cells derived from the malignant WBC (Jurkat T cells, NALM-6 pre-B cells and U937 monocytic cells) and those derived from epithelial cancer cells (MCF-7 breast cancer cells, B16F10 melanoma cells and TRAMP-C1 prostate cancer cells). This distinction is further observed to remain quite consistently in all of the measured diffraction images. To quantitatively investigate these differences for automated classification, we randomly selected 30 to 40 diffraction images from the measured data as a training set.

The rest of the measured diffraction images were used as a testing set for investigation of automated classification based on the GLCM parameters. The GLCM analysis was applied to the training set for obtaining 12 statistical parameters for each image as defined in [16] and 5 were selected as the classifiers for the automated classification. Another software developed with the support vector machine (SVM) algorithm [18] was used to classify cells with diffraction images in the testing set. Table 1 lists the mean values and standard deviations of the 5 GLCM parameters of the diffraction images from the training set and Table 2 presents the results of cell classification with the diffraction images from the testing set.

Table 2. Results of cell classification.

		WBC derived cells				Epithelial derived cells			Accuracy (%)
Cell types	n*	Jurkat	NALM-6	U937		MCF-7	B16	Tramp
Jurkat	20	15	4	1		0	0	0	75
NALM-6	20	6	13	0		0	1	0	65
U937	14	4	0	8		2	0	0	57
MCF	14	2	0	1		10	1	0	71
B16F10	30	0	0	0		1	28	1	93
Tramp	10	0	0	0		1	0	9	90

* n = cell number in the testing set.

To analyze the correlation between the diffraction images and cell morphology, we present in Fig. 3 the fluorescence images of double-stained cells taken from the same cell labs. For these images, we stained the cells with two fluorescent dyes of Syto-61 and Mito-Tracker Orange binding mainly to the nuclei and mitochondria, respectively, before the confocal imaging. The choice of nucleus and mitochondria as the targeted intracellular organelles is based on previous studies of their effects on light scattering [8,11,12]. The image slices shown in Fig. 3 are the ones near the center of cell imaging stack and thus represent the typical sizes of the cells in each type. Even though the 3D morphology varies among the imaged cells within each type, one can clearly identify certain features to distinguish cell types from the confocal image stacks. For example, the linear sizes of the epithelial cancer cells are typically 40% to 60% larger than those derived from malignant WBC with similarly larger nuclei and numbers of mitochondria.

Fig. 3.

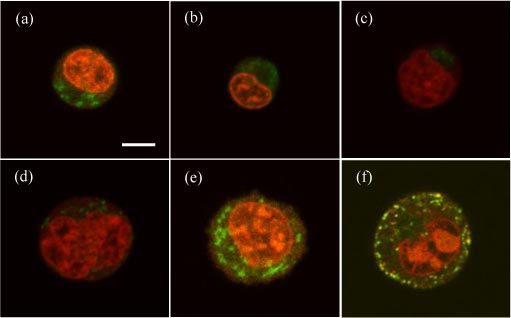
Typical confocal image slices acquired from cells with double fluorescent stains for nucleus and mitochondria: (a) Jurkat; (b) NALM-6; (c) U937; (d) MCF-7; (e) B16F10; (f) TRAMP-C1. Bar = 5μm.

3.2. Simulated diffraction of different cell morphology and nuclear refractive index

With the FDTD method, we simulated the unpolarized diffraction images I(y, z) by projecting the Mueller matrix element S₁₁(θ_s,ϕ_s) to the y-z plane as images of 800x600 pixels in a configuration shown in Fig. 1. For these results, we used a simplified cell model obtained from the confocal images of NALM-6 cells and constant indices of refraction for cytoplasm and nucleus. We should also point out that the simulated diffraction images do not account for the effect of imaging optics used in our flow cytometer setup between the cell and CCD imaging sensor. Despite these differences, numerical simulations with these cell models allow detailed analysis of different aspects of cell’s 3D morphology and intracellular distribution of refractive index on the GLCM parameters which is impossible to implement experimentally. For each of the 3 cell models, light scattering distributions with different cell orientations were simulated with 2 different values of nuclear index of n_n = 1.45 or 1.50 and a wavelength of λ = 850nm. Figure 4 shows examples of simulated diffraction images for the 3 cell models of varied orientation, nuclear index and volume. As shown in the left-most column of Fig. 4, both of the #1 and #8 cell models have single nuclei while the #9 is in the mitosis stage of cell cycle with a splitting nucleus. GLCM analysis was applied to the simulated diffraction images and values of the 5 parameters are listed in Table 3 .

Fig. 4.

Simulated diffraction images with 3 reconstructed NALM-6 cell models: top row from (a) to (d): Cell #1; middle row from (e) to (h): Cell #8; bottom row from (i) to (l): Cell #9. All cells have the same index of refraction as n_h = 1.33 for host medium and n_c = 1.368 for cytoplasm. The column of (a), (e) and (i) are for cells of orientation along the z-axis or C(θ₀ = 0, ϕ₀ = 0) and n_c = 1.45 for the nucleus; the column of (b), (f) and (j) are for cells of C(θ₀ = 109°, ϕ₀ = 118°) and n_c = 1.45; the column of (c), (g) and (k) are for cells of C(θ₀ = 0, ϕ₀ = 0) and n_c = 1.50; the column of (d), (h) and (l) are for cells of C(θ₀ = 0, ϕ₀ = 0) and n_c = 1.50 with cell and nuclear volumes proportionally reduced to half. The left most column shows the projection images of #1, #8 and #9 cell models from top to bottom with the two numbers denoting the total cell volume in μm³ and volume ratio of nucleus to cell respectively.

Table 3. GLCM parameters of simulated diffraction images.

Cell	Parameters* nc; C; vol	Sum Entropy	Difference Entropy	IDM	Dissimilarity	Correlation
#1	1.45; C1; full	5.75	2.78	0.301	5.60	0.988
	1.45; C2; full	5.72	2.78	0.263	5.49	0.986
	1.50; C1; full	5.83	2.80	0.273	5.64	0.989
	1.50; C1; half	5.62	2.62	0.335	4.72	0.988
#8	1.45; C1; full	5.46	2.40	0.402	3.73	0.995
	1.45; C2; full	5.79	2.99	0.247	6.99	0.979
	1.50; C1; full	5.28	2.37	0.415	3.78	0.995
	1.50; C1; half	5.70	2.69	0.318	5.08	0.989
#9	1.45; C1; full	5.38	2.78	0.287	5.80	0.984
	1.45; C2; full	5.67	2.92	0.240	6.45	0.969
	1.50; C1; full	5.36	2.75	0.307	5.83	0.989
	1.50; C1; half	5.25	2.64	0.353	5.30	0.993

*n_c = refractive index of nucleus; C₁ = C(θ₀ = 0, ϕ₀ = 0), C₂ = C(θ₀ = 109°, ϕ₀ = 118°); vol = cell and nuclear volumes (full referring to the volumes same as those determined from confocal images and half referring to both cell and nuclear volumes reduced by half proportionally).

4. Discussion

Diffraction imaging is nothing new. In fact, diffraction images through x-ray crystallography are widely used in biomedical research as a tool to reconstruct 3D morphology of macromolecules such as proteins in crystallized arrays. This technique has also been used for x-ray microscopy of biological cells through time-consuming image acquisition at multiple angles and reconstruction calculations [19]. The key questions we intend to answer here are whether an optical diffraction images of biological cells correlates highly with the cells’ 3D morphology in the presence of other factors such as cell orientation and, if yes, whether the correlation can be utilized to rapidly classify cells in a flow cytometer setting. In this report, we present the first set of experimental data that strongly suggest positive answers to both questions. However, much remain unknown on the details of correlation between the textures of diffraction images and cell morphology.

GLCM provides a statistical approach for analysis of image textures with feature parameters that can be implemented for rapid classification of cells as demonstrated in our case here with proper selection of the distance vector d between the paired pixels of the diffraction images. Because the selected d is smaller than the size of speckles in our analysis, most of the bright pixels in the GLCM images presented in Fig. 2 locate along the main diagonal. The value of sum entropy tends to be large among the epithelial derived cell group in comparison to the WBC derived cell group, while the difference entropy exhibits mixed variations among the 6 cell types. Despite these differences, the two entropy parameters have coefficients of variation ranging from 3% to 13% within each cell type and relatively large differences in mean values among the different types. They can thus serve as good classifiers along with the other three parameters. We should point out here that the cell size does not appear to influence these GLCM parameters. As can be seen from Fig. 3 that the 6 cell types separate clearly in two groups according to their sizes: the WBC derived ones are from about 8 to 10μm while the epithelial derived ones are in the range of 13 to 16 μm. This clear difference in cell size does not correlate with the values of the GLCM parameters presented in Table 1 and Table 3 in a consistent way. Therefore, the diffraction images measured with the side scatters provide very little size information as expected, which will be further illustrated in the discussion of the simulation results below.

To test the capacity of the GLCM features for cell classification, we have developed an SVM based software for automated classification of the diffraction images in the testing set. As shown in Table 2, the accuracy of classification reaches a maximum of 93% for the B16F10 mouse melanoma cells and a minimum of 57% for the U937 monocytes. Here the accuracy is defined as the number of correctly classified cells or images divided by the total number of tested cells. From this table it can be seen again that the cells are well distinguished among the two groups of different origins. If the classification is performed between these two groups the accuracy can increase to 94% for each group. So the misclassification occurs mainly among the cells within the same group. A further examination of the misclassified images demonstrates that the errors can be attributed to the variation of the angular field-of-view in acquiring the diffraction image, which is mostly likely due to the shift of cell location relative to the imaging unit as a result of instability of core flow. This problem could be solved effectively with improved design and fabrication of laminar flow nuzzles and flow speeds much higher than what we used. It should also be noted that the numbers of cells for each cell type in our training and test sets are between 50 and 70 which yield statistically significant results but not very large as indicated by the potentially high throughput of the flow cytometry method. This was due to the use of a slow CCD camera for acquiring the diffraction images, manual file saving and the limited time of cell measurement.

Besides the imaging errors as discussed above, fluctuations in cell morphology, refractive index and orientation are expected to cause variation of the GLCM parameters for cells within the same type in the training set as listed by the standard deviations in Table 1. Nevertheless, the fluctuations are relatively small and cell classification is reliable for most cells in the test set according to the selected GLCM feature parameters of the measured diffraction images. This fact seems to be in strong contrast with the results of the same GLCM analysis performed on the simulated diffraction images as shown in Table 3 which allows controlled variation of cell properties. Among the four factors of different nuclear index, cell orientation, cell/nuclear volumes and nuclear shape, the cell orientation in Cell #8 and #9 affects the GLCM parameters more significantly than the other factors. We expanded the simulations for each cell model to 8 orientations equally distributed in the 4π solid angle range and the results (not shown here) demonstrate again that the cell orientation play a significant role in affecting the GLCM parameters of simulated images. Despite the fact that our modeling does not include the imaging optics, we have shown that the imaging optics merely “bent” the fringe patterns of the diffraction images if the objective is placed on an off-focused position towards the flow chamber [14]. Consequently the simulation results presented here provide useful results to improve our understanding of diffraction imaging approach for single cell study. Comparison of the dependence of GLCM parameters on cell properties in the simulated results and in the measured results, one can conclude that even with the cell models reconstructed from confocal images as we presented here it is still not sufficiently accurate if we consider only a homogeneous nucleus. Indeed, by comparing Fig. 2 and Fig. 4 one can immediately see that the simulated images carry much higher degrees of symmetry in the diffraction patterns than the measured images. To improve the modeling accuracy one has to take into account of heterogeneity in intracellular distribution of refractive index such as the non-uniformity in nucleus and addition of mitochondria. On the other hand the simulation results with simple cell models show that the patterns or textures of a real diffraction images contributed by the side scatters are dominated by the cell’s fine details in its 3D morphology or intracellular heterogeneity in the index of refraction.

5. Summary

We have applied a GLCM algorithm to automate feature extraction from diffraction images of 6 cultured cell types acquired with a flow cytometer. The measured data clearly demonstrate that the method of diffraction imaging flow cytometry has the capacity for rapid and label-free cell classification. Further comparison of the experimental results with the confocal imaging and simulation results shows that the diffraction images acquired with side scatters centered at 90° from the incident light direction depends mainly on the 3D morphology of the cells with very little sensitivity to the cell size. The classification capability of this platform technology can be further improved with increased flow stability and enhanced by combining with wider range of angles or multiple angular ranges.