Metabolic labeling of RNA uncovers principles of RNA production and degradation dynamics in mammalian cells

Abstract

Regulation of RNA levels is determined through the interplay between RNA production, processing and degradation. However, since most global studies of RNA regulation do not distinguish the separate contributions of these processes, relatively little is known about how they are temporally integrated to determine changes in RNA levels. In particular, while some studies emphasize the role of changes in the rate of transcription, others suggest a prominent involvement of time-varying degradation rates. Here, we combine metabolic labeling of RNA at high temporal resolution with advanced RNA quantification assays and computational modeling to estimate RNA transcription and degradation rates during the model response of immune dendritic cells (DCs) to pathogens. We find that changes in transcription rates determine the majority of temporal changes in RNA levels, but that changes in degradation rate are important for shaping sharp ‘peaked’ responses. Furthermore, transcription rate changes precede corresponding changes in RNA level by a small lag (15-30 min), which is shorter for induced than for repressed genes. We used massively parallel sequencing of the newly-transcribed RNA population – including non-polyadenylated transcripts – to estimate constant RNA degradation and processing rates. We find that temporally constant degradation rates vary significantly between genes and contribute substantially to the observed differences in the dynamic response, and that specific groups of transcripts, mostly cytokines and transcription factors, are undergoing faster mRNA maturation. Our study provides a new quantitative approach to study key steps in the integrative process of RNA regulation.

Introduction

Cellular RNA levels are determined by the interplay of tightly regulated processes for RNA production (transcription), processing (e.g., polyadenylation, splicing, transport, localization), and depletion (degradation). In addition to transcriptional regulation^1,2, changes in RNA degradation can also significantly affect differential gene expression^3,4, particularly in mammalian cells where RNA half-lives are typically longer³.

The response of immune dendritic cells (DCs) to pathogens provides a compelling model of a temporal transcriptional sensory response in mammalian cells^5,6. DCs initiate and regulate immune responses. Upon stimulation with pathogen components, DCs activate a regulatory program, which unfolds over ~24h and involves the activation of ~1700 genes and repression of ~2000 genes⁷, some peaking as early as 30 minutes, whereas others peak after 6 hours or more. In a recent study, we identified over a hundred transcription factors, and at least a dozen RNA binding proteins controlling this response⁷.

There are two key questions on the roles of transcription and degradation in regulating RNA levels in this response. (1) Which of the two processes contributes most to shaping changes in RNA levels over time? (2) Do such changes primarily result from variation of constant rates between genes or from variability of the rates for each gene over time?

The extent to which RNA stability contributes to dynamic changes in RNA levels is still unclear and debated. Most works focus on transcriptional mechanisms^8-12, tacitly assuming that degradation rates (per gene) are constant over time¹³ (‘constant degradation hypothesis’). However, recent studies suggest that changes in a gene’s mRNA level following stimulation are strongly affected by corresponding changes in its RNA degradation rate^13,14, modeled either by a single change^3,4,15 or as a continuous shift^16,17 over time (‘varying degradation hypothesis’). Indeed, it was proposed that such changes in degradation rates may determine up to half of the temporal changes in RNA levels in mammalian cells¹⁶. Distinguishing between these two hypotheses is hampered by the shortcomings of the indirect methods used for determining transcription and degradation rates, which may limit their relevance in vivo. For example, nuclear run-on assays for measuring transcription rates are conducted ex-vivo in isolated nuclei^15,16,18, and methods for estimating degradation rates by transcriptional inhibition, either with antibiotics or temperature sensitive mutants^3,4,13,17,19, are not well adapted to dynamic settings and severely affect cell growth and survival²⁰.

Improved direct measurement of RNA production rates may allow us to address these questions. Recent studies used metabolic labeling of RNA with 4-thiouridine (4sU), a naturally occurring modified Uridine, to distinguish recently-transcribed RNA from the overall RNA population, with minimal interference to normal cell growth^21-26. The modified base is incorporated into the growing RNA chain in place of Uridine, marking it, and serving as an attachment point for a biotin tag for easy separation of newly transcribed RNA from the total RNA population (Supplementary Fig. 1). In previous work, labeled RNA was hybridized to standard microarrays, requiring relatively large quantities of RNA and hence lengthier 4sU labeling times (1-2h). Thus, most existing studies focused on variation between genes during steady state conditions^22,25,26, and a single 4 time points microarray study²³, though promising, lacks a systematic dynamic analysis.

Here, we use metabolic labeling coupled with advanced RNA quantification assays and computational modeling to study RNA regulation in the response of mouse DCs to Lipopolysaccharide (LPS). Leveraging the Nanostring nCounter technology for accurate multiplex measurement of RNA²⁷ and massively parallel sequencing²⁸, we significantly reduce metabolic labeling time to directly measure RNA transcription rates at high temporal resolution for a selected set of signature genes, and at a lower temporal resolution on a genome-scale. We develop new computational models to decompose RNA levels into the separate contributions of RNA production and degradation, and estimate changes in degradation rates between genes and over time. We leverage the reduced abundance of rRNA and other stable RNA populations in recently transcribed RNA, to sequence a broad representation of the labeled RNA transcriptome, and determine the processing rates of precursor mRNA (pre-mRNA).

We discover key principles of temporal RNA regulation in mammalian cells. We find that changes in transcription rate highly correlate with changes in RNA level, preceding them by ~15-30 min, with about twice as long a delay in down-regulated than up-regulated genes. In contrast to recent works^16,17, we find that dynamic changes in degradation rates have minimal effect on most RNA profiles, but that they do play a unique role in genes with sharp ‘peaked’ responses. Genome-wide analysis shows substantial variation in both degradation and processing rates between genes, rather than over time, consistent with their regulatory and functional differences. Our method is a new and effective tool for studying key processes controlling cellular RNA levels.

Results

Assessing RNA transcription rates by short metabolic labeling

We used short metabolic labeling with 4sU²³ (Methods) to directly estimate RNA transcription rates in DCs. Total cellular RNA levels (RNA-Total) globally integrate the effects of RNA transcription and degradation over the entire lifetime of the cell, whereas newly-transcribed RNA (RNA-4sU) contains only RNA that was actively transcribed during the labeling pulse, and hence represents a ‘local integration’ of average transcription and degradation. When labeling time is sufficiently short, the labeled RNA is still in the nucleus, and is subjected to little, if any, degradation (with the notable exception of aberrant transcripts), thus reflecting the average transcription rate. We chose a labeling time of 10 minutes as an appropriate ‘short’ duration, based on the time required for 4sU uptake by cells²³ and for RNA-4sU transcription and processing in the nucleus.

4sU ‘short’ metabolic labeling in mouse DCs (Fig. 1a) is specific, reproducible and has no significant effect on cellular function or transcriptional response of primary DCs (Supplementary Fig. 1-5; Supplementary Notes, section 1). Furthermore, we used Pol-II binding and sub-cellular fractionation to show that it directly measures transcription rates (Fig. 1b; Supplementary Fig. 6; Supplementary Notes, section 1).

Figure 1. Changes in transcription rates during the response of DCs to LPS.

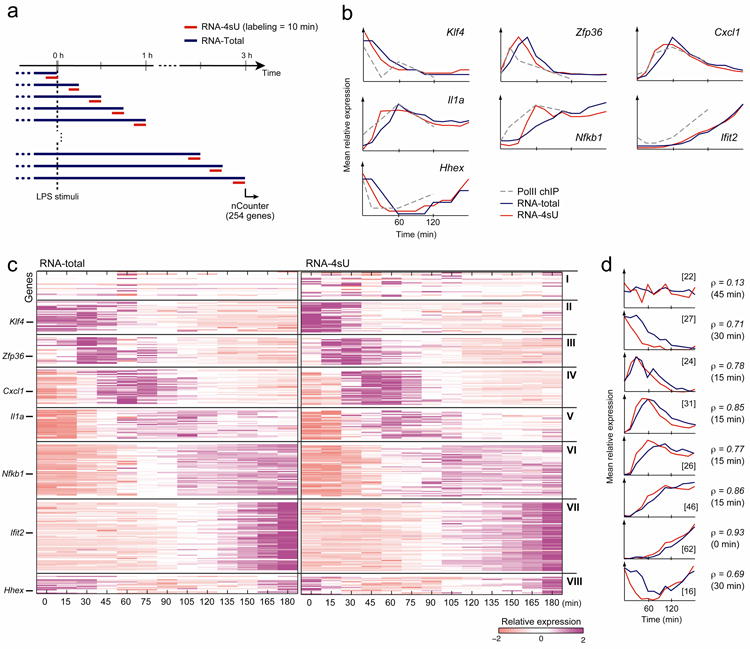
(a) Measuring transcription rates with short metabolic labeling. We used short metabolic labeling (10 min, red lines), and measured the expression of RNA-Total (blue) and RNA-4sU (red) for 254 ‘signature’ genes at 13 time points in 15 min intervals (rows) over the first 3 hours post-LPS stimulation. (b) Changes in RNA-4sU levels follow changes in pol-II binding and precede changes in total RNA levels. Shown are example time course profiles for selected genes for RNA-4sU expression (nCounter, red), RNA-Total expression (nCounter, blue) and pol-II binding at the promoter (ChIP, dashed gray). (c) Distinct temporal clusters of newly transcribed and total RNA. Shown are clusters of expression profiles (nCounter) for 254 ‘signature’ genes (rows) based on RNA-Total (left) and RNA-4sU (right) measurements across 13 time points (columns). Cluster I includes the control genes. Cluster numbers (I-VIII) are noted on right; representative member genes are noted on left. Purple: high relative expression; white: mean expression; pink: low relative expression. (d) Peak transcription precedes peak expression by 15-30 minutes. Shown are average profiles (Y axis) for RNA-4sU (red) and RNA-Total (blue) for each cluster at each time point (X axis), ordered by cluster numbers (cluster I topmost; cluster VIII bottommost). The size of each cluster is indicated in brackets. Pearson correlation coefficient (ρ) of the best time-lag correlation between transcription and expression is indicated on right, with the optimal time lag in square brackets.

Dynamic changes in RNA expression levels usually lag behind transcription rate changes by 15-30 min

We used short metabolic labeling (10 min) followed by nCounter measurements to assess transcription rates and RNA levels of 254 representative signature genes along a high-resolution time course, during the response of DCs to LPS (Fig. 1a). We selected the 254 transcripts (Supplementary Table 1; Methods) based on our previous study⁷, as representative of global mRNA profiles in this response, including key regulators, cytokines and other effectors, whose expression changes in this system. We measured RNA-Total and RNA-4sU at 15 min intervals over the first 3 hours post-LPS stimulation (spanning most changes in mRNA abundance in this response⁷; Supplementary Table 2).

We found eight coherent groups with distinct temporal patterns that cluster based on their transcription rates and expression profiles (Fig. 1c; Methods), distinguishing subtle temporal differences. For example, both group III (e.g., Egr1, Zfp36) and group IV (e.g., Cxcl1, Tnf) genes peak early in the response, but with a 30-minute difference in their peak times. Likewise, the expression of groups VI (e.g., Il12b, Il6, Nfkb1) and VII (e.g., Ifit2, Il12a) genes constantly increases, but with different onset and saturation times.

Changes in RNA-Total levels temporally correlate with corresponding changes in transcription rates (mean ρ = 0.73±0.3 SD), but on average lag behind them by ~15-30 min (Fig. 1d; Supplementary Fig. 7; Methods). There is about twice as long a delay for down-regulated than for up-regulated genes, possibly because degradation rates are generally slower than transcription rates, delaying their effect on RNA levels. Overall, using the optimal time shift, variation in transcription rates explains 64% of the variation in RNA levels.

A computational model for RNA transcription and degradation dynamics

We developed a computational approach to estimate the temporal profiles of transcription and degradation rates from measurements of RNA-Total and RNA-4sU (Fig. 2a; Methods). Our generative model assumes that total RNA levels are determined by a simple (first-order) integration of production and degradation rates over time, and that the temporal behaviors of transcription and degradation rates follow a parametric function (constant or ‘impulse’ model^29,30). While we directly measured transcription (as RNA-4sU) and RNA levels (RNA-Total), we cannot currently measure degradation in a comparably accurate way without impacting cell viability. We therefore used a maximum-likelihood estimation to find the parameters of the production and degradation profiles that best fits the observations (Methods; Supplementary Fig. 8).

Figure 2. Changes in transcription rate account for most expression changes; changes in degradation rate contribute to ‘peaked’ responses.

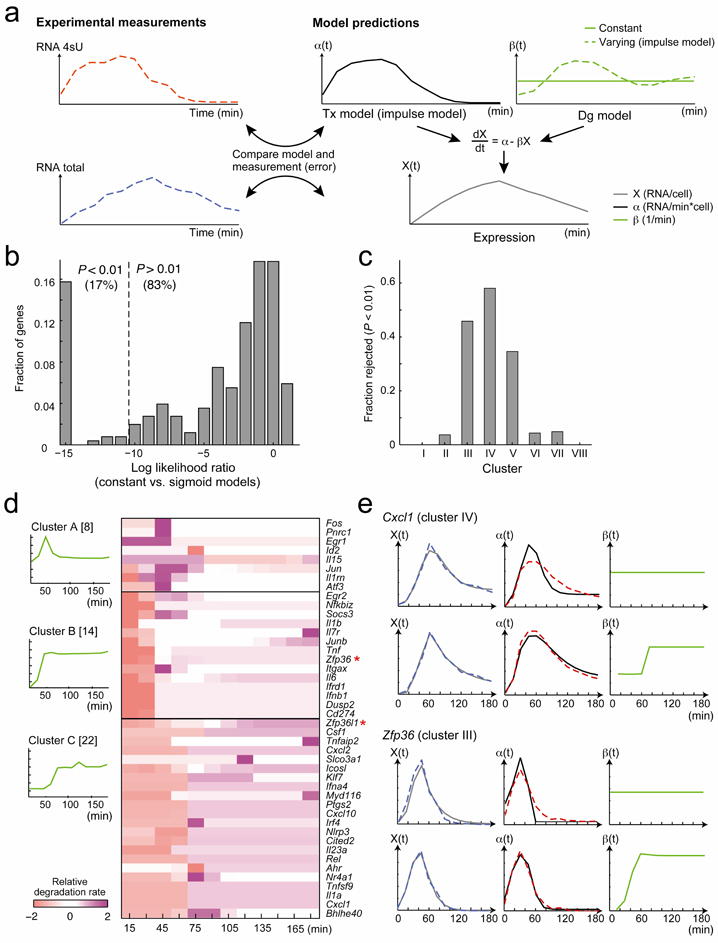
(a) The ‘constant degradation’ and ‘varying degradation’ models. A first-degree dynamical model (formula, right) models the expression level of a gene (grey curve) as a function of transcription (black) and degradation (green) rates. Parameters include an ‘impulse’ model^29,30 for transcription (black curve), and either a constant function for degradation (‘constant degradation’ model, solid green line), or an ‘impulse’ model (‘varying degradation’ model, dashed green line). We fit them to our data (left, RNA-Total, blue, and RNA-4sU, red) by optimizing the likelihood function (separately per gene). We compare the model’s fit (black and grey curves) to the data (red and blue curves, respectively) and calculate the error. (b) The ‘constant degradation’ model fits the majority of genes well. Shown is the distribution of the log likelihood ratios between the ‘constant degradation’ and ‘varying degradation’ models. Dashed line indicates the threshold for rejecting constant degradation (p<0.01). (c) The percent of genes per cluster (numbered as in Fig. 1c) that reject the constant degradation model. (d) Varying degradation profiles estimated for the 44 genes that reject the ‘constant degradation’ model. Right: estimated degradation rates (relative rate; purple: high; pink: low) for the 44 genes (rows), clustered into 3 groups (A-C), across 12 time points (columns; excluding t=0 which is highly sensitive to noise due to low RNA levels). Asterisk: known regulators of RNA degradation (see Discussion). Left: mean degradation rate profile per cluster (bracket: number of genes in cluster). (e) Genes with peaked responses reject the ‘constant degradation’ model. Shown are two example genes (top: Cxcl1, bottom: Zfp36). For each, upper row: ‘constant degradation’ model fit (solid line) to the data (dashed line); lower row: ‘varying degradation’ model fit (solid line) to the data (dashed line). Left: expression level; middle: transcription rate; right: degradation rate (estimate only).

We compared two alternative models for degradation. The simpler ‘constant degradation’ model assumes that each gene has a temporally constant degradation rate (Fig. 2a, solid line); the rate can vary between genes. This simple model is often implicitly assumed in computational models of gene expression^8-13. The more complex ‘varying degradation’ model assumes that the degradation rate of a gene changes over time (Fig. 2a, dashed line), and represents such changes with an ‘impulse’ model. We used a likelihood ratio test (Methods; Supplementary Notes, section 2) to compare the ‘constant’ to the ‘varying’ degradation models. Genes that confidently (p < 0.01) reject the ‘constant degradation’ model in favor of the alternative ‘varying degradation’ model represent cases in which changes in degradation rate significantly contribute to shaping temporal changes in RNA levels. In all other cases we retain the ‘constant degradation’ model and assume that changes in degradation rate contribute minimally.

Changes in transcription rates shape temporal RNA profiles of most genes

Most signature genes (83%, 210/254) retain the ‘constant degradation’ hypothesis (Fig. 2b), suggesting that changes in degradation rates contribute minimally to shaping their RNA levels dynamics during the first 3 hours of the response. On average, the ‘constant degradation’ model explains 78% (± 19% SD) of a gene’s RNA levels variation, while the ‘varying degradation’ model, despite its substantial complexity, extends this by less than 10% (86% ± 14% SD; Supplementary Fig. 9). While the predicted constant RNA half-lives range from 10 to 70 min (Supplementary Fig. 10a), the predicted varying half-lives span a much wider range (1-200 min; Supplementary Fig. 10b). Measuring degradation rates by standard Actinomycin D treatment (Methods), although severely impacting cell growth and survival²⁰, supports the predicted fit to these models (Supplementary Notes, section 3, Supplementary Fig. 11-12).

These results contradict recent works^16,17, which proposed that changes in RNA degradation rates significantly affect temporal expression patterns in mammalian sensory pathways. Instead, they support an earlier view^8-13 of the ‘constant degradation hypothesis’ that during such responses RNA levels are predominantly affected by changes in transcription rates.

Temporal changes in degradation are important for shaping ‘peaked’ responses

In a minority of genes (44 genes, 17%) changes in degradation rate significantly affect changes in RNA levels (Fig. 2b). The predicted degradation rate profiles are partitioned into 3 groups (A, B, C, Fig. 2d) and have only one or two prominent rate changes (Fig. 2d,e), suggesting a single underlying regulatory event (Discussion).

These changes in degradation may uniquely contribute to shaping sharp ‘peaks’. First, the genes that reject the ‘constant degradation’ model are concentrated in three clusters (III-V, Fig. 2c) containing many immediate-early genes (e.g., Fos, Jun, Egr1, Zfp36) with a sharper ‘peak’ in their expression profile. Second, the maximal peak height (Methods) and the error of the fit to the ‘constant degradation’ model are highly correlated (Pearson ρ=0.61, p<10^-26; Supplementary Fig. 13). Finally, the fit error concentrates at the peak, and changes in the ‘varying degradation’ rate overlap the peak (Fig. 2e, Supplementary Fig. 14).

Genome-wide measurements of a broad population of newly transcribed RNAs by 4sU-Seq

To generalize our findings to genome-scale, we adapted the 4sU metabolic labeling protocol for massively parallel sequencing (4sU-Seq, Fig. 3a). First, to extract labeled RNA in sufficient quantities for sequencing, we extended the labeling time to 45 minutes. As labeling time increases, RNA-4sU no longer directly approximates transcription rates, but a ‘local integration’ of the average transcription and degradation rates. Second, due to the lower proportion of rRNA and other stable RNAs in newly transcribed RNA (1.8-4 fold reduction, Supplementary Fig. 2d), we generated 4sU-Seq libraries without prior poly-A selection. Indeed, while RNA-A+-Seq libraries are mainly enriched for mRNA exons (80%), 4sU-Seq libraries represent a greater diversity of RNAs (pre-mRNA introns 47%, rRNA 14.2% and pre-miRNAs 0.1%; Fig. 3b, Supplementary Fig. 15-17, Supplementary Tables 3-4, Supplementary Notes, section 4). Finally, to account for the reduced temporal resolution and the longer labeling time in the genomic data, we adapted our modeling approach (Supplementary Methods) and used only the simpler ‘constant degradation’ model.

Figure 3. Genome-wide analysis of RNA transcription and degradation rates using RNA- and 4sU-Seq.

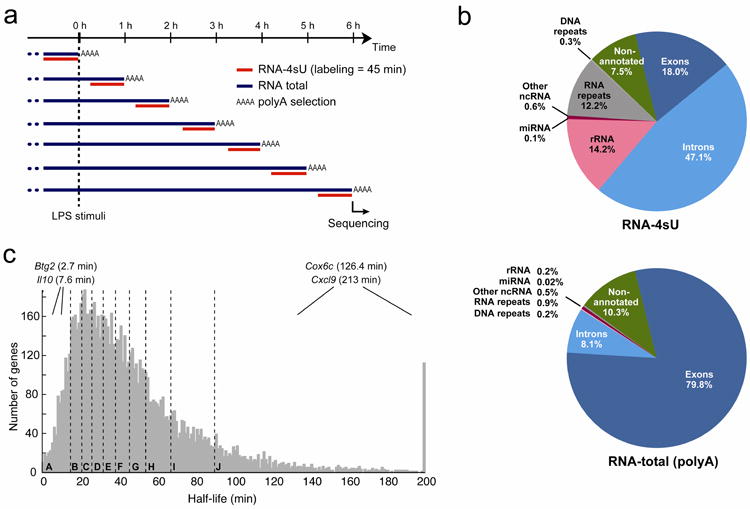
(a) Experiment overview. We isolated RNA-4sU (after 45 min of 4sU labeling, red) and polyA+ RNA-Total (blue) at 1h intervals (rows) over the first 6 hours of the response of DCs to LPS stimulation, and used massively parallel sequencing to measure RNA levels. (b) 4sU-Seq captures a broader representation of transcripts compared to polyA+ RNA-Seq. Shown is the fraction of reads in RNA-4sU-Seq libraries (left) and polyA+ RNA-Seq libraries (right), across several annotation categories. Only reads that are mapped to a unique location in the genome or to rRNA are considered. (c) Distribution of predicted constant mRNA half-lives for the 9,448 genes expressed during the first 6 hours of the response to LPS stimulation that do not reject the ‘constant degradation’ model. Dashed lines distinguish 10 deciles (A-J, 10% increments, 35 transcripts with >200min half-life are included in the last decile).

Consistent genome-wide and small-scale measurements of newly transcribed RNA

We applied 4sU-Seq to mouse DCs in response to LPS stimulation, with an expanded temporal scope and reduced temporal resolution (Fig. 3a). We estimated expression by Reads Per Kilobase exon model per Million mapped reads (RPKM) (Methods), and found that these match the nCounter data (Supplementary Fig. 18).

The genome-wide analysis shows similar patterns as our signature set. Of the 9,838 expressed Refseq³¹ genes, the majority (83%) fit the patterns of the signature-set clusters (clusters II-VIII) based on their 0-3h expression profiles (Methods; Supplementary Fig. 19), with subgroups of genes (in clusters II, III, VI) that differ in their behavior during later time points (4-6h). The minority of genes (17%, cluster I) that did not fit the signature patterns included genes repressed (Ia) or induced (Ib) after 3h.

Each of the eight clusters is enriched with distinct functional annotations, consistent with their temporal pattern (Supplementary Table 5). For example, Cluster I, showing minimal changes in transcription rate or expression (during 0-3h), is enriched for glycolysis and ribosomal proteins, whereas Clusters II and III, with transient or sustained down-regulation of transcription rates, are enriched for cell cycle, mitochondrial, or oxidative phosphorylation genes. The transiently early induced Cluster V (1h peak) is enriched for inflammatory regulators (e.g. Tnf, Nfkbiz, Il1a, Il1b) and differentiation factors. Conversely, in cluster VI, which is enriched for their targets (inflammatory and immune signaling genes and differentiation factors’ targets), the early induction is sustained.

Constant degradation rates are a genome-wide phenomenon and contribute to shaping temporal RNA levels

For the vast majority of genes, dynamic changes in degradation rates contribute little to changes in expression during the first 6 hours of the response. Most expressed genes (94%, 9,274/9,838) show only a minimal discrepancy between the measured data and the expected values under the ‘constant degradation’ model (‘goodness of fit’ test, Methods).

For the remaining 6% (564/9,838), the ‘constant degradation model’ is rejected, suggesting that at least one of the model’s assumptions is inaccurate (such as varying degradation or other post-transcriptional events, see Discussion). This group is enriched for inflammatory and immune signaling genes, and for targets of NF_KB signaling, suggesting that these processes are dynamically regulated both transcriptionally and post-transcriptionally. Notably, unlike the high-resolution signature data, we cannot fit the ‘variable degradation model’ to 4sU-Seq data, nor can we use a likelihood ratio test (Methods) to determine that the degradation model per se is at fault.

Large differences in constant degradation rates between genes are associated with distinct functional and temporal patterns, and suggest that variation in degradation rates between genes contributes to shaping temporal RNA levels. For the 93% ‘constant degradation’ genes, the estimated ‘constant’ mRNA half-lives range from 3 to 200 min (Fig. 3c), match the nCounter predictions, and are correlated – albeit shorter on average – to other available estimates in our system and others (Supplementary Fig. 20; Supplementary Notes, section 5; Discussion). The long half-life genes (groups I-J; Methods) are enriched for proteasome, ribosomal proteins, oxidative-phosphorylation and glycolysis genes (Supplementary Table 6): all are stable mRNAs that constitute a major fraction of total cellular mRNA. These genes are mostly members of cluster I (e.g. Rpl18a, Cox8a) with a stable, minimally changing expression pattern in the first 3h of the response. Short half-life genes (groups A-B) are enriched for transcription regulators (e.g., Klf7, Dmtf1), and for targets of many known miRNAs and TFs (e.g., Foxo1, Hif1a, p53). Furthermore, some sharp ‘peaked’ expression genes from clusters III-V (e.g., Il10, Btg2) have constant high degradation rates (rather than varying rates), an alternative means to the same end.

Genome-scale measurement of mRNA maturation by 4sU-Seq

We monitored mRNA maturation by distinguishing intronic and exonic reads in 4sU-Seq data (Fig. 4a; Methods). Reads covering introns and intron-exon junctions (Fig. 3b; Supplementary Fig. 21) likely arise from pre-mRNAs, while reads covering exons arise both from pre-mRNA and mRNA. Since 4sU-Seq libraries are not polyA-selected, intronic and exonic reads reliably represents the relative frequencies of pre- and total-RNA within the recently-transcribed RNA population. Thus, exon-RPKM estimates the overall (pre-mRNA and mature mRNA) newly-transcribed RNA, and intron-RPKM estimates the newly-transcribed pre-mRNA levels (Methods and Supplementary Notes, section 6, on controlling for overlapping transcripts). Indeed, expressed introns and exons profiles correlate well (Spearman ρ=0.81), and show similar patterns in all clusters (Supplementary Fig. 22). Intronic reads (not overlapping intron-exon junctions) can hypothetically arise from sequencing of the excised introns, leading to over-estimated pre-mRNA expression levels and under-estimated processing rates. However, this is unlikely given the reported fast degradation of excised introns^32-35, and the comparable coverage of introns and intron-exon junctions in 4sU-Seq (data not shown).

Figure 4. Genome-wide analysis of RNA processing rates.

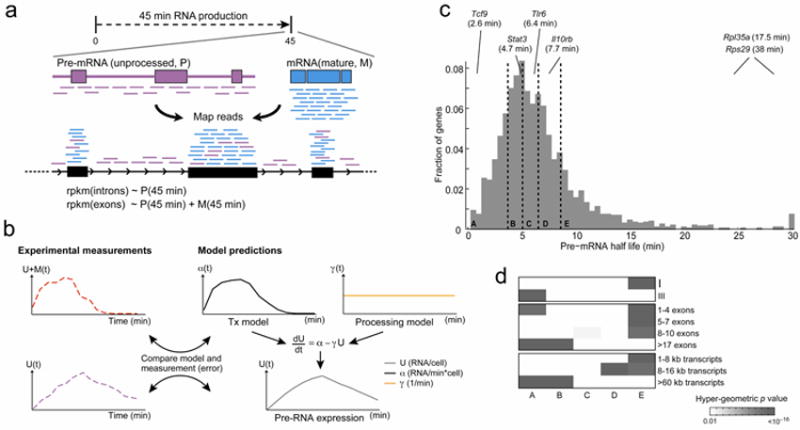
(a) Using 4sU-Seq data to study RNA processing. Sequencing reads in the 4sU-Seq libraries originate from either pre-mRNA (U; purple) or mature mRNA (M; light blue). While mRNA reads map only to exons, the pre-mRNA reads map to both exons and introns. We estimate newly transcribed pre-mRNA expression by the RPKM of a gene’s introns alone, and overall newly transcribed RNA expression (pre-mRNA + mRNA) by the RPKM of a gene’s exons. (b) An overview of the ‘constant degradation and processing’ model. The model expands on our ‘constant degradation’ model (Fig. 2a) by adding a constant processing rate (right; orange). We fit the model parameters to our data (left; mRNA-4sU, dashed red, and pre-mRNA-4sU, dashed purple) by optimizing the likelihood function (separately per gene) and using the degradation rates predicted by the ‘constant degradation’ model. (c) Distribution of predicted constant processing rates for 3,011 genes with exonic and intronic expression during the first 6 hours of the response to LPS stimulation. Dashed lines distinguish 5 quintiles (a-e, 20% increments), and transcripts with >30min half-life are added to the last bin. Pre-mRNA half-lives for illustrative genes are denoted in each bin. (d) Transcripts with low or high pre-mRNA half-lives are enriched in functional categories, clusters, exon structures or transcript lengths. Shown are the enrichments (P-value, hypergeometric test, grey), of the overlap between the genes in each of the half-life bins in (c) (A-E, columns) and each tested category (rows). Only categories with at least one significant enrichment are shown.

We fit the data with an extended model (‘constant processing and degradation’) that includes an additional RNA processing step (Fig 4b; Methods). This model assumes that mRNA is produced by pre-mRNA transcription followed by processing into mature mRNA, and that only mature mRNA is exported to the cytoplasm, where it is degraded. The pre-mRNA half-life reflects the processing rate, whereas mRNA half-life reflects its degradation rate. We use constant functions for both degradation and processing rates, and an ‘impulse’ model for transcription rates. We conservatively analyzed only the 2,122 genes for which both exons and introns are expressed above a minimal value, excluding genes with expressed anti-sense transcripts or significant alternative isoforms biases (Methods, Supplementary Notes, section 6).

Differences in pre-mRNA processing rates between genes contribute to regulation of mRNA levels

Most expressed genes (95%, 2,014/2,122; Methods) show only a minimal discrepancy between the measurements and the expected values under the ‘constant processing and degradation’ model (‘goodness of fit’ test). Of these, 8% (161/2,014) are genes that rejected the previous ‘constant degradation’ model (above), suggesting that for these genes, regulation of pre-mRNA maturation is important for shaping final mRNA levels. For the remaining 5% (108/2,122), one or more of the model’s assumptions is inaccurate (e.g., changes in pre-mRNA processing rate or in RNA stability), but we cannot determine which one. A few examples highlight that changes in processing rate over time may be a regulatory event for at least certain genes (Supplementary Fig. 23).

Predicted constant pre-mRNA half-lives (for 95% of genes) are shorter than the mRNA half-life (21±13% SD of mRNA half-life; Supplementary Fig. 24a), and range between 1-30 min (Fig. 4c). Pre-mRNA half-lives significantly correlate with mRNA half-lives (Spearman ρ=0.46, Supplementary Fig. 24b), possibly due to the relationship between the ‘constant degradation’ and ‘constant degradation and processing’ models (Methods), which makes our processing and degradation rates estimates somewhat dependent.

Differences in constant pre-mRNA half-lives among genes are consistent with exon structure and temporal expression pattern, and suggest that variation in RNA maturation rates between genes serves as a regulatory mechanism. The slow processed pre-mRNAs (group E; Methods) are enriched (Fig. 4d) for constantly expressed genes (clusters I), with 1-10 exons, and with short transcripts (1-16 kb unprocessed length). Conversely, fast processed pre-mRNAs (group A) are enriched for genes with sharp ‘peaked’ expression (cluster III), with few (1-4) exons, and surprisingly, with long transcripts (>60kb unprocessed length) and many exons (>17).

Discussion

In this work we combined metabolic labeling of RNA with advanced RNA quantification assays and computational modeling to quantitatively dissect the contribution of different steps to RNA levels during the model response of DCs to pathogens. We highlight three principles. (1) Changes in transcription rates dominate most temporal mRNA profiles, whereas changes in degradation rates are important for shaping ‘peaked’ responses. (2) Temporally constant degradation rates vary significantly between genes, and contribute to the differences in the dynamic response. (3) There are marked differences in pre-mRNA processing rates between genes, suggesting a regulatory role for RNA maturation.

Our work highlights the need for an unbiased method to directly measure degradation rates on a genome scale. While existing direct methods are significantly biased, and particularly in dynamic settings, our approach avoids such biases, but only indirectly infers degradation rates. In comparing different estimates we find our predictions to be highly correlated – albeit consistently shorter – than other estimates in our system and others (Supplementary Notes, section 5). While a proportional decrease in rates may result from difference in cell type or from the inherent limitations in all existing methods (ours as well as others), the RNA stability rankings, on which we base our analysis, seems more comparable between methods and reliable. One promising direction in settling these discrepancies is chasing 4sU with Uridine²², which allows to estimate RNA degradation directly and with minimal biases, but may be challenging for highly induced genes (MR, IA, NF and AR, unpublished results).

Our work opens many directions for future research. First, it will be important to generalize our findings to other systems and responses, and test whether the difference between our conclusions and those achieved in other immune cells^16,17 stem from technology or biological factors. Second, monitoring RNA production, processing and degradation at the single-cell level will allow us to distinguish between changes that arise from intrinsic properties of the molecular system and those that are affected by cell-to-cell variation. Third, correlating RNA production and degradation rates to proteomics and ribosome occupancy studies can connect the mRNA life cycle with protein production and protein regulators. Fourth, 4sU-Seq provides opportunities to study additional post-transcriptional regulatory processes (e.g., poly-adenylation, alternative splicing), to improve non-coding RNA annotations, and to identify new classes of short-lived functional transcripts. Fifth, monitoring distinct splice isoforms (through strand-specific sequencing and transcript assembly³⁶) can further enhance our models beyond the canonical splice variants and constitutive exons in this analysis. For example, we can distinguish splice variants with different production, processing or degradation rates, or estimate processing rates of individual introns.

Finally, the ability to measure transcription, processing and degradation during a complex temporal response provides an experimental framework to decipher the molecular mechanisms controlling variations in these rates between genes or time points (for one gene). For example, several lines of evidence suggest that the RNA binding protein Zfp36 may play an important role in regulating changes in degradation rates in our system. First, Zfp36 is a known regulator of RNA stability that de-stabilizes its mRNA targets by binding AU-rich elements in their 3’UTR³⁷. Zfp36 is known to auto-regulate its own stability, consistent with the increased degradation rate, which our model predicted for it (Fig. 2d). Second, the same signaling pathways that activate the transcriptional machinery are known to also induce Zfp36 and other proteins that regulate RNA degradation^5,37. Third, Zfp36’s most well-established target, Tnf³⁸, also shows a similar increase in degradation rate, and 20 of the 44 genes with variable degradation rates have the target AU-rich consensus sequence in their 3’UTR (p<1.5×10^-3) associated with RNA destabilization by Zfp36³⁷. Additional studies are required to test this hypothesis and explore other regulatory mechanisms⁷, including the role of miRNAs in regulating RNA decay rates, to which our enrichments analysis hints (Supplementary Table 6).

Overall, our method provides a new tool to simultaneously study several key cellular regulatory processes and model their interactions with each other, generating a complementary view to any RNA expression analysis, and deepening our understanding of the RNA life cycle.

Methods

Dendritic cell isolation, culture, LPS treatment and metabolic labeling

All animal protocols were reviewed and approved by the MIT / Whitehead Institute / Broad Institute Committee on Animal Care (CAC protocol 0609-058-12). Details on the DCs isolation and treatment are presented in full in⁷. Briefly, 6-8 week old female C57BL/6J mice were obtained from the Jackson Laboratories. Bone marrow-derived dendritic cells (BMDCs) were collected from femora and tibiae and plated on non-tissue culture treated plastic dishes in RPMI medium (GIBCO, Invitrogen), supplemented with 10% FBS, L-glutamine, penicillin/streptomycin, MEM non-essential amino acids, HEPES, sodium pyruvate, β-mercaptoethanol, and GM-CSF (15 ng/μL; Peprotech, Rocky Hill, NJ). At day 5, floating CD11c+ cells were sorted on the autoMACS separator with the CD11c (N418) MicroBeads kit (Myltenyi Biotec), re-plated at a concentration of 10⁶ cells/ml and stimulated 16 hours post sorting. LPS (rough, ultra-pure E. coli K12 strain LPS) was purchased from Invivogen and used at a concentration of 100 ng/ml. For metabolic labeling of RNA, 4-thiouridine (Sigma) was added to a 150 μM final concentration at the appropriate times prior to RNA extraction.

Biotinylation and purification of 4sU labeled RNA

Total RNA was extracted with the miRNeasy kit’s procedure (Qiagen), and sample quality was tested on a 2100 Bioanalyzer (Agilent). For the high-resolution (signature) analysis, we extracted RNA starting at 0h and until 3h after LPS stimulation in 15 minutes intervals. We generated replicated samples for the 0, 30, 45, 60 and 75 minutes samples. For the lower resolution analysis (4sU-Seq), we extracted RNA starting 0h and until 6h after LPS stimulation in 60 minutes intervals.

We used 20 μg total RNA for the biotinylation reaction. 4sU-labeled RNA was biotinylated using EZ-Link Biotin-HPDP (Pierce), dissolved in dimethylformamide (DMF) at a concentration of 1 mg/mL, and stored at -80°C. Biotinylation was done in labeling buffer (10 mM Tris pH 7.4, 1 mM EDTA) and 0.2 mg/mL Biotin-HPDP for 2h at room temperature. Unbound Biotin-HPDP was removed by chloroform/isoamylalcohol (24:1) extraction using MaXtract (high density) tubes (Qiagen). RNA was precipitated at 20,000g for 20 min with a 1:10 volume of 5M NaCl and an equal volume of isopropanol. The pellet was washed with an equal volume of 75% ethanol and precipitated again at 20,000g for 10 min. The pellet was re-suspended in 100 μL RNAse-free water. Biotinylated RNA was captured using Dynabeads MyOne™ Streptavidin T1 beads (Invitrogen). Biotinylated RNA was incubated with 100 μL Dynabeads with rotation for 15 min at room temperature. Beads were magnetically fixed and washed with 1x Dynabeads washing buffer. Flow-through was collected for unlabeled preexisting RNA recovery. RNA-4sU was eluted with 100 μL of freshly prepared 100 mM dithiothreitol (DTT). RNA was recovered from eluates and washing fractions with RNeasy MinElute Spin columns (Qiagen).

Cell fractionation

Nuclear and cytoplasmic fractions were separated using NE-PER nuclear and cytoplasmic extraction (Thermo Scientific). RNA from each compartment was extracted following the miRNeasy kit’s procedure (Qiagen), and sample quality was tested on a 2100 Bioanalyzer (Agilent). On average, we obtained 5 times more cytoplasmic than nuclear RNA. We used 20 μg total RNA from the cytoplasmic fraction, and 4 μg total RNA from the nuclear fraction for the biotinylation reaction to reflect the original ratio. Purification of labeled RNA was done as described above.

qPCR measurement

RNA was reverse transcribed with the Sensiscript RT kit (Qiagen). Real time quantitative PCR reactions were performed on the LightCycler 480 system (Roche) with FastStart Universal SYBR Green Master Mix (Roche), and every reaction was run in duplicate. The 28S-rRNA levels were used as an endogenous control for normalization.

Design and selection of ‘signature’ gene-set

Our ‘signature set’ consists of 254 transcripts (Supplementary Table 1) that we identified in our previous study⁷ as key representatives of the LPS response. These include 19 control genes, whose expression levels were unchanged under LPS stimulation, but whose (constant) basal levels varied from low to high. The other 235 genes were differentially expressed during the LPS response, and identified as dominant players in the biological pathways involved⁷. An information-theoretic approach we implemented (the GeneSelector algorithm⁷) incrementally chooses genes (from a full expression data set) whose expression profile improves our discrimination of several different stimuli, and we added to that candidate regulators with detectable expression during the response to LPS.

nCounter measurements and data processing

Details on the nCounter system are presented in full in²⁷. We hybridized 50-100 ng of RNA for 16 hours with the code set and loaded into the nCounter Prep Station followed by quantification using the nCounter Digital Analyzer. Code sets were designed and constructed to detect the 254 ‘signature’ genes, and to capture multiple splice isoforms. Each probe set matches ~100 bases long exonic sequence of the target genes, and therefore detects both pre-mRNA and mature mRNA (see Supplementary Methods for full details). We normalized the nCounter data (Supplementary Table 2) in two steps: (1) with internal positive spiked-in controls provided by the nCounter system, and (2) with a set of 8 control genes (see Supplementary Methods for details). We used the ratio of RNA quantity in each sample before and after RNA-4sU purification (0.022 ± 0.015 SD), to normalize RNA-total and RNA-4sU samples relative to each other.

RNA-polymerase II ChIP

Dendritic cells were fixed with 1% formaldehyde, quenched with glycine, and washed with ice-cold PBS. Pelleted cells were re-suspended in SDS lysis buffer. Samples were sonicated with a Branson 250 Sonifier, centrifuged at 13,000g for 10 min, and diluted 10-fold in ChIP dilution buffer. After removing a control aliquot (whole-cell extract), sample was incubated at 4°C overnight with antibodies against the CTD domain of Pol-II (Covance MMS-128P). Complexes were precipitated with protein G-Dynabeads. Beads were washed sequentially with low-salt immune complex wash buffer, high-salt immune complex wash buffer, LiCl immune complex wash buffer, and TE. Immunoprecipitated chromatin was eluted in elution buffer, incubated at 65°C for 8 hr, and treated with RNase A, proteinase K and purified with a MinElute Kit (Qiagen). Quantification of relative binding was done by hybridization to an nCounter codeset covering the promoter regions of the indicated genes.

Time-lagged correlation

We calculated the k-th time-shifted correlation between a gene’s expression {e₁…e_n} and transcription {t₁…t_n} profiles by corr_k(e,t) = corr({e_k+1…e_n},{t₁…t_n−k}) (shifted Pearson correlation). We calculated the time-shifted correlation per gene, than average over clusters, and looked for the shift k with the maximal average correlation.

Estimating the ‘fraction of explained variance’

The percent of variance in a set of measurements that is explained by the model’s predictions was estimated by the standard ‘coefficient of determination’ (r²) of the regression model, and was corrected to account for the non-linearity of our model (see Supplementary Methods for details).

Clustering nCounter expression data

We standardized (subtracted the mean and divided by standard deviation) the log₂(expression) of a gene, separately per time series, and applied k-means clustering with random initialization and multiple executions, finally selecting the best result. We iteratively increased the number of clusters as long as none of the clusters had less than 2% of the genes.

Dynamic model of RNA transcription and degradation in the signature set

Modeling

Let α be the transcription rate (RNA/min*cell), β the degradation rate (1/min) and X be the expression level of a gene x (RNA/cell), than the time evolution of X is described by a first-degree dynamic equation:

$$\frac{\mathit{dX}}{\mathit{dt}}=\alpha (t)-\beta (t)X$$

While RNA-total globally integrates this equation over the entire lifetime of the cell, RNA-4sU only locally integrates it over the (short) labeling time. We assumed that: (1) both α and β are approximately constant during the (short) labeling period, and (2) with short enough labeling time (<10 min) RNA-4sU is mostly nuclear and is therefore subjected to little if any degradation (β=0); and concluded that RNA-4sU directly estimates the average α during the labeling period (see Supplementary Methods for details). We built a generative modeling scheme that describes α(t) and β(t) by a parametric function, and uses an additive Gaussian noise model (estimated from experimental repeats). We used an ‘impulse’ model, a 6-parameter double-sigmoid function^29,30, which describes temporally varying rates, for α(t), and compared two alternative parametric descriptions of β(t): a simple one-parameter constant function (‘constant degradation’) and an impulse model that models temporally varying rates (‘varying degradation’).

Fitting the model to the data

We optimized the likelihood of the data given each model predictions using the Nelder-Mead simplex algorithm³⁹ (see Supplementary Methods for details).

Statistical tests

We used two complementary statistical tests. The first is a goodness of fit test that measures how well the data fits each model (separately). Rejecting the model in this case means that one of the modeling assumptions does not hold in the data, but without determining which assumption that is. We estimated the variance from data points measured in replicates, and used the standard least-square error and associated chi-square distribution with n degrees of freedom⁴⁰ to calculate a p-value. The second test is a likelihood ratio test, which compares the two alternative models, and identifies in which cases the simpler model (‘constant degradation’) should be rejected in favor of the more complex model (‘varying degradation’). We used a standard nested likelihood ratio test⁴¹.

Measuring the maximal peak height

We defined the ‘maximal peak height’ in the temporal profile of RNA levels (X(t)) by P_max = max_t {2X(t) − (X(t − 1) + X(t + 1))}, and ranked genes according to the ‘peakiness’ of their expression profiles (genes with highest ‘maximal peak height’ have the sharpest peaks).

Actinomycin D treated cells

We added actD (3 μg/ml) directly to untreated cells (‘0h experiment’) and collected cells at 0.5, 1, 2, 4 and 6 hours after actD addition. We added actD (3 μg/ml) directly to LPS-treated cell cultures for 2.5h (‘2.5h experiment’) without removal of LPS, and collected cells at 2, 3 and 4h after actD addition. RNA levels for the ‘signature set’ genes were quantified using nCounter, and normalized only with the internal nCounter provided controls.

Comparing model predictions and Actinomycin D data

We used our standard first-degree model: $\raisebox{1ex}{$\mathit{dX}$}\!\left/ \!\raisebox{-1ex}{$\mathit{dt}$}\right.=\alpha (t)-\beta (t)X$. We assumed that after actD treatment: (1) transcription is blocked, i.e. α (t) = 0 and (2) a constant decay rate; and therefore the model becomes: $\raisebox{1ex}{$\mathit{dX}$}\!\left/ \!\raisebox{-1ex}{$\mathit{dt}$}\right.=-\beta X$. We compared the actD data to our model predictions with two complementary methods. First, we compared RNA levels from actD experiment and model predictions: we used the ‘constant degradation’ model with α(t)=0 and with the β(t) predicted by the model at actD treatment time (0h or 2.5h), and the RNA-total levels measured at actD treatment time, to predict expected RNA levels following actD treatment. We compared these with actD data by least square error (normalized by each gene’s average expression level). Second, we compared the degradation rates (β) predicted by our models with those calculated directly from actD decay profiles. Based on the assumptions (above), the analytic solution is a first-order exponential decay: X(t) = X₀ · e^−βt ⇒ log X(t) = log X₀ − βt. We fit a first-order linear model to the log-decay profile to estimate the degradation rate (β). Only genes with a good fit (R² > 0.8) were used for further analysis (100/254 genes).

Estimating mRNA half-life

We estimated mRNA half-life directly from the degradation rate (β), per time point, by: $X(t_{1/2})=X_0\cdot e^{-\beta t_{1/2}}=\frac{X_0}{2}\Rightarrow t_{1/2}(T)=\frac{log(2)}{\beta (T)}$. Therefore, for varying degradation rates, the half-life at time T represents the expected half-life if the degradation rate was fixed to its value at that time point.

Preparation and sequencing of RNA-Seq and 4sU-Seq libraries

We prepared the 4sU-Seq libraries using the ‘control (non–strand-specific)’ protocol as described in²⁸, with the following modifications: after DNase treatment, we used the entire RNA sample (without polyA-RNA isolation) and fragmented RNA by incubation in 1X RNA fragmentation buffer (Affymetrix) at 80 degrees for 4 minutes. We prepared the RNA-A+-Seq libraries using the ‘dUTP second strand (strand specific)’ protocol as described in²⁸, except we fragmented RNA as for the 4sU samples. We used the Illumina Genome Analyzer (GAII). We sequenced two lanes for each RNA-A+-Seq sample, corresponding to 45 million paired-end reads/sample (90 million single reads, 76 bases long) on average (Supplementary Table 3); and a single lane for RNA-4sU sample, corresponding to 33 million paird-end reads/sample (68 million single reads, 76 bases long) on average (Supplementary Table 4).

Read mapping

We aligned all reads to the mouse reference genome (NCBI 37, MM9) using the TopHat aligner⁴² with default parameters (See Supplementary Methods for details). To estimate rRNA levels, we mapped all reads (with the same procedure) to mouse rRNA sequences from GenBank⁴⁴. About 80% of RNA-Seq (RNA-total) reads were uniquely mapped to the genome, and 85% of these mapped in pairs (average insert size of 644 bases ± 2886 SD), while only 0.2% of the reads mapped to rRNA (Supplementary Table 3). About 60% of 4sU-Seq (RNA-4sU) reads were uniquely mapped to the genome, and 65% of these mapped in pairs (average insert size of 699 bases ± 5746 SD), while 30% of the reads mapped to rRNA (Supplementary Table 4). Thus, in 4sU-Seq libraries, rRNA accounts for the high fraction of reads that were not aligned (or not uniquely aligned) to the genome.

Estimating percentage of reads mapped to specific genomic annotations

We extracted mouse Refseq genes (exons and introns), microRNA and tRNA annotations from the UCSC genome browser⁴⁵. We extracted rRNA sequences from GenBank⁴⁴ and other non-coding RNA sequences from Rfam⁴⁶. We generated non-coding RNA annotations by aligning their sequences to the mouse genome using BLAST⁴⁷.

Quantification of transcript abundance from RNA-Seq data

We estimated the expression of a transcript X in both RNA-A+-Seq and RNA-4sU-Seq by standard ‘Reads Per Kilobase exon model per Million mapped reads’ (RPKM), as previously described in⁴⁸, but defined it over exons alone (see Supplementary Methods for details). We normalized RPKM estimates using: (1) a selected set of control genes as previously described⁴⁹, and (2) adjusting the mean and standard deviation of each sample’s log(RPKM) values. We used the ratio between RNA quantity in each sample before and after RNA-4sU purification (0.046 ± 0.019 SD), to normalize RNA-total and RNA-4sU relative to each other. We took genes with log₂(RPKM) >= 2 for at least one time point (10,106 genes, which are ~40% of the Refseq³¹ genes), and excluded transcripts with significant antisense expression (to avoid biases arising from strand-specificity; see Supplementary Notes, section 6), leaving us with 9,838 genes.

Assigning RNA-Sequencing expression profiles to clusters

We assigned each RNA-Seq gene to the nCounter cluster (out of clusters II-VIII) with the maximal Pearson correlation between the gene’s RNA-Seq expression profile and the cluster’s centroid (as calculated by k-means at 0, 1, 2 and 3 hours). If the correlation p-values for all clusters was non significant (p > 0.01), we assigned the gene to cluster I (the control genes cluster). We divided each cluster into sub-groups by applying our k-means clustering procedure separately per cluster, and required a minimal cluster size of at least 3% of the genes (globally).

Grouping genes based on predicted constant degradation rates

We divided the 9,448 genes with non-significant discrepancy from the ‘constant degradation’ model into 10 deciles (~900 genes per group) based on their predicted mRNA half-life (A-J, Fig 3c).

Quantification of mRNA and pre-mRNA abundance from 4sU-Seq data

We estimated the pre-mRNA expression by intron-RPKM, and the overall (pre-mRNA+mRNA) expression by exon-RPKM (see Supplementary Methods for details). We focused on genes with significantly expressed introns and exons (RPKM >= 2) for at least one time point (3,011/10,106; ~30% of expressed genes), and excluded transcripts with antisense transcription or significant alternative isoforms biases (see Supplementary Notes, section 6), leaving us with 2,122 genes.

Dynamic modeling of processing rates

Modeling

Let α be the transcription, β the degradation and γ the processing rate, and let P be the pre-mRNA level, and M be its mature mRNA level of gene x, than we extended the dynamic model to include the processing rate as following:

$$\begin{array}{l}\frac{\mathit{dP}}{\mathit{dt}}=\alpha -\gamma P\\ \frac{\mathit{dM}}{\mathit{dt}}=\gamma P-\beta M\end{array}$$

This model assumes that mRNA is transcribed as pre-mRNA, processed into mature mRNA, and only the mature mRNA is degraded. Our 4sU-Seq data measures (separately) the local integration of P(t) and of M(t). We directly estimated α(t) from M(t) data by assuming that during the (short) labeling period: (1) pre-mRNA is at steady state, (2) all rates (α, β and γ) are approximately constant and (3) the temporally constant β that was estimated by the simpler model. We used an ‘impulse’ model^29,30 for transcription rate, and a constant degradation and processing rates.

Fitting the model to the data

We optimized the likelihood of the data (α(t) and P(t)) to the first equation of the model as before.

Testing the fit

We used a goodness-of-fit test (see Supplementary Methods for details).

Functional Enrichments

We calculated the enrichment of a query set of genes X for an annotation A using hypergeometric p-value between two groups⁴⁰, and a 1% False Discovery Rate (FDR) significance threshold, across all annotations we tested. Functional annotations of the mouse genome were taken from the Molecular Signature Database (MSigDB)⁵⁰, c2 (curated gene sets), c3 (motif gene sets) and c5 (GO gene sets).