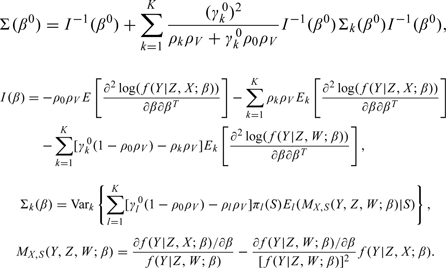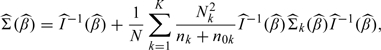Semiparametric inference for a 2-stage outcome-auxiliary-dependent sampling design with continuous outcome

Abstract

Two-stage design has long been recognized to be a cost-effective way for conducting biomedical studies. In many trials, auxiliary covariate information may also be available, and it is of interest to exploit these auxiliary data to improve the efficiency of inferences. In this paper, we propose a 2-stage design with continuous outcome where the second-stage data is sampled with an “outcome-auxiliary-dependent sampling” (OADS) scheme. We propose an estimator which is the maximizer for an estimated likelihood function. We show that the proposed estimator is consistent and asymptotically normally distributed. The simulation study indicates that greater study efficiency gains can be achieved under the proposed 2-stage OADS design by utilizing the auxiliary covariate information when compared with other alternative sampling schemes. We illustrate the proposed method by analyzing a data set from an environmental epidemiologic study.

1. INTRODUCTION

Biomedical studies are often designed to assess the relationship between some exposure X of interest and the corresponding outcome Y of individual adjusted by some confounding covariates Z. In many situations, due to limited budget, the assessment of X is not feasible to be conducted on all subjects under study. One useful approach to accommodating this issue is to use a 2-stage stratified sampling design, originally introduced by Neyman (1938), to enhance the study efficiency while minimizing the costs. At the first stage of a typical 2-stage design, a relatively large random sample is drawn and measurements are conducted on outcome Y and Z, which are easier to measure, while at the second stage, ascertainments on the X are made for a subsample drawn randomly, without replacement.

There is great literature on the variations of 2-stage sampling designs with binary outcomes. For example, White (1982) proposed a stratified case–control design of a rare disease (i.e. Y) and a rare exposure (i.e. X), where a large preliminary random sample is drawn at the first stage, from which strata are identified on the basis of both the disease and the exposure. At the second stage, a subsample is drawn from within the strata identified in the first stage and measurements of the potential confounding variables are made on the subsample. Compared with the simple random sampling at the second stage regardless of either the disease or the exposure status, great efficiency gains can be achieved by selecting the desirable number of cases and controls within each stratum identified in the first stage. Rathouz and others (2002) considered a matched case–control study with binary outcome using the conditional logistic regression method. Recently, Schildcrout and Rathouz (2010) extended this stratified case–control design to a more general case where the response is a longitudinal binary variable.

On the other hand, when there exists an additional auxiliary variable W for the expensive X, which is easily obtained for all subjects under study at the first stage, it is necessary to incorporate the information implied by W into the statistical analysis. For instance, in a lung cancer biomarker study, one of the aims is to assess the epidermal growth factor receptor (EGFR) mutations (X) as a predictive biomarker for whether a subject responds to a greater extent to EGFR inhibitor drugs (Y). Due to high cost of genotyping EGFR genes, it is prohibitive to ascertain the genotype of EGFR genes on all samples at the first stage. However, the likelihood score of EGFR mutations (W) obtained by a designed questionnaire has been shown to relate to the EGFR mutations and can be easily observed for all patients in Paez and others (2004). Wang and Zhou (2010) considered inference of the 2-stage outcome-auxiliary-dependent sampling (OADS) design to increase the study efficiency by utilizing the auxiliary covariate information when the outcome is categorical. Zhang and others (2008) and Lu and Tsiatis (2008) also showed that using the available baseline auxiliary covariate information can achieve more efficient estimators in the analysis of randomized clinical trials and survival data, respectively.

As the scope of biomedical studies inquiry grows, it is important to investigate the relationships between continuous biological outcomes and exposure of interest adjusted by other covariates. It is cost-effective to adopt a 2-stage design when the exposure is hard to obtain. However, most current 2-stage designs have been developed for categorical outcomes, the statistical method for the 2-stage design with continuous outcome is limited. When an auxiliary W does not exist, Chatterjee and others (2003) considered a pseudoscore estimator for regression parameter with a 2-stage sampling. Weaver and Zhou (2005) proposed a 2-stage outcome-dependent sampling (ODS) design for continuous outcome regression models, wherein the subsample was drawn at the second stage within the stratum that was achieved by subdividing the range of continuous outcome variable into class intervals.

In this paper, we proposed a 2-stage OADS design when outcome Y is continuous and there exists auxiliary variable W at the first stage. Specifically, outcome Y, auxiliary variable W for exposure X, and other covariates Z are all observed for all patients at the first stage. Then we selected the subsample within each stratum defined by the partition of the domain of Y×W to ascertain the value of X at the second stage. An estimated likelihood function by estimating its infinite-dimensional nuisance parameter through the kernel smoother is proposed and the estimator maximizing the estimated likelihood is used to estimate the regression parameter. The proposed 2-stage OADS design with continuous outcome is shown to be more efficient than other alternative competing sampling schemes.

The rest of this paper is structured as follows. We describe the 2-stage OADS design, data structure, and the model in Section 2. The estimated likelihood function method and the asymptotic properties of the resulting estimator are presented in Section 3. We conduct a simulation study to assess the small sample approximation under the 2-stage OADS design in Section 4. In Section 5, a real data example is analyzed to illustrate our proposed method. Some conclusions are provided in Section 6, and the proof of the asymptotic properties of proposed estimator is investigated in the supplementary material available at Biostatistics online.

2. DESIGN AND MODEL

2.1. Two-stage OADS design and data structure

To fix notation, let Y denote a continuous outcome variable, {Z,X} be a covariate vector, and W be a continuous auxiliary variable for X. We assume that the conditional distribution of Y given Z and X is known up to a finite vector of unknown parameters, that is,

(2.1)

where β⁰ is the true value of q-vector regression parameter β of interest. Assume that W offers no additional information regarding the outcome Y given covariate X.

Assume that the domain of (Y,W) is denoted by 𝒴×𝒲. Let 𝒴 be partitioned into J mutually exclusive and exhaustive strata by the known constants − ∞ = a₀ < a₁ < ⋯ < a_{J − 1} < a_J = ∞, and let the jth stratum be denoted by A_j = (a_{j − 1},a_j], for j = 1,…,J. Similarly, let 𝒲 be partitioned into T mutually exclusive and exhaustive strata by the known constants − ∞ = b₀ < b₁ < ⋯ < b_{T − 1} < b_T = ∞, and let the tth stratum be denoted by B_t = (b_{t − 1},b_t], for t = 1,…,T. For subsequential use, we define B₀ = ( − ∞,∞) when T = 0, which indicates that there is no partition on 𝒲. Therefore, we have 𝒴×𝒲 partitioned into J×T mutually exclusive and exhaustive rectangles A_j×B_t, for j = 1,…,J and t = 1,…,T. For simplicity, we rewrite these rectangles as Δ_k for k = 1,…,K. Hence, {A_j×B_t:j = 1,…,Jandt = 1,…,T} = {Δ_k:k = 1,⋯,K} and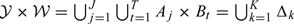

At the first stage, N subjects are sampled at random from a population with (Y_i,Z_i,W_i)_{i = 1}^N being observed. Suppose that there are N_k observations of (Y,W) falling into stratum Δ_k, then 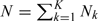. The second stage, where X is observed, are comprised of 2 components: (i) a simple random sample (SRS) of size n₀ and (ii) a supplemental OADS sample of size n_k from the kth stratum Δ_k for k = 1,…,K. Let R_i be an indicator for the ith subject whether X_i is observed (R_i = 1) or not (R_i = 0). Let n_0k denote the number of subjects in the SRS falling into the kth stratum Δ_k. Furthermore, let 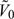denote all the subjects in the SRS and define V_k = {i:R_i = 1,(Y_i,W_i)∈Δ_k} and 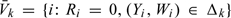, then n_k + n_0k = |V_k| and 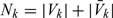, where and hereafter, we use notation |A| to denote the cardinality of a set A. Let 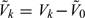representing the supplemental OADS samples in the stratum Δ_k, where A − B is defined as the set consisting of elements that are in set A but not in set B. Let V = cup_{k = 1}^KV_k and 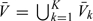, representing the validation set (set with X observed, i.e. the second-stage set) and nonvalidation set (i.e. the first stage set that are not sampled at the second stage), respectively. Hence, the observed data structure for the proposed 2-stage OADS design with continuous outcome can be summarized as follows: the first stage: {Y_i,Z_i,W_i} for i = 1,⋯,N; the second stage: (i) the SRS sample: {Y_i,X_i,Z_i,W_i} for i ∈ 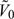; (ii) the OADS sample: {X_i|(Y_i,W_i)∈Δ_k,Z_i} for and k = 1,…,K; and (iii) the nonvalidation sample: {Y_i,Z_i,W_i} for .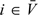

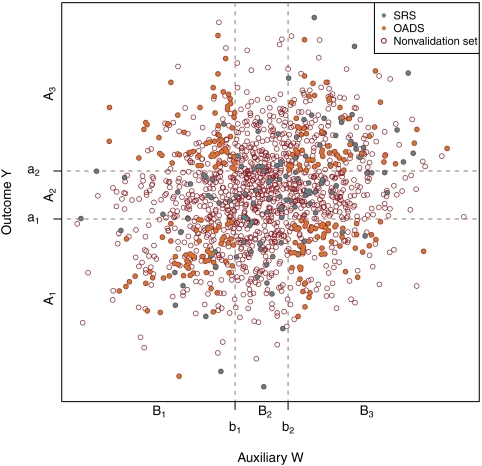
To better illustrate the proposed OADS design with continuous outcome, we present Figure 1 when J = T = 3. At the second stage, except for the SRS samples, the supplemental OADS samples are selected within strata at the 4 corners Δ₁ = A₁×B₁,Δ₂ = A₁×B₃,Δ₃ = A₃×B₁, and Δ₄ = A₃×B₃ based on the consideration that these combinations of the extreme values of both Y and W contain more information for the relationship of interest between outcome Y and exposure X. Hence, the advantage of such 2-stage OADS design is that, while providing overall information about the population from the SRS samples, it allows the investigator to oversample certain segments of the population that are believed to be more informative.

Fig. 1.

Illustration for the proposed 2-stage OADS design with continuous outcome. Y-axis denotes outcome variable Y. X-axis denotes auxiliary variable W.

The 2-stage ODS design proposed by Weaver and Zhou (2005) assumed that only the outcome variable is observed in the first stage and the covariates are ascertained for a subsample drawn at the second stage from strata defined by the outcome. Our proposed 2-stage OADS design includes this design when T = 0 and the information in Z and W is discarded. We call this design a 2-stage ODS design with only the outcome observed at the first stage. However, in many studies, some covariates such age, gender, and race so forth can be observed for all subjects in the cohort study. To this point, we extended the design by Weaver and Zhou (2005) to this more practical situation. When the auxiliary information is available for all subjects, our proposed 2-stage OADS design can accommodate the 2-stage ODS design with outcome, some covariates, and auxiliary observed at the first stage by letting T = 0. It is worth noting that the subsequential methodology development on the 2-stage OADS design is still valid for the 2-stage ODS design in several abovementioned scenarios.

2.2. Likelihood function

Let G(x|z,w) and g(x|z,w) be the conditional cumulative distribution function and the conditional probability function of X given (Z,W). We will construct the likelihood function based on all the observations under the 2-stage OADS design. First, the contribution from the SRS at the second stage to the full likelihood is proportional to

(2.2)

Second, the likelihood for the supplemental OADS sample at the second stage can be shown to be proportional to (Zhou and others, 2002)

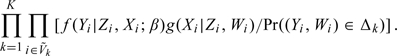(2.3)

Furthermore, the observations in the nonvalidation sample contribute the following term to the full-information likelihood function:

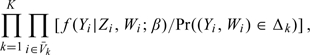(2.4)

where f(Y|Z,W;β) = ∫_𝒳f(Y|Z,x;β)dG(x|Z,W).

Finally, as shown by Weaver and Zhou (2005), conditional on the component size of the OADS being fixed, the kth stratum size for the nonvalidation sample 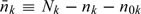follows a multinomial law such that

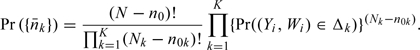(2.5)

Conditional on the observed size 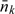, the observations in the nonvalidation sample are independent of those in the validation sample. After combining and simplifying terms (2.2–2.5), we have derived the full likelihood based on all the observations under the 2-stage OADS design, which is proportional to

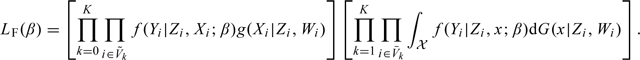(2.6)

The presence of the nuisance function G(x|z,w) makes the inference for β challenging. Obviously, direct maximization of L_F(β) is not feasible since the function G(x|z,w) cannot be factored out. A simple method is to assume a parametric distribution for G(x|z,w), but this could lead to a biased conclusion if the underlying model is misspecified in that, generally, the relationship between W and X may not be known to be specified through a parametric model. A more attractive approach is to model it nonparametrically.

3. AN ESTIMATED LIKELIHOOD METHOD

In the estimated likelihood method, an unspecified nuisance parameter, such as the conditional distribution function G(x|z,w) in (2.6), is replaced by a consistent estimator. When the validation sample is a simple random sample, one could estimate G(x|z,w) using data from validation sample by an empirical imputation method for discrete auxiliary (Pepe and Fleming, 1991) and by kernel smoothing (Carroll and Wand, 1991) for continuous auxiliary. Zhou and Pepe (1995), Zhou and Wang (2000), and Liu and others (2009) applied the estimated likelihood approach to time-to-event data subject to random censoring.

Due to the 2-stage OADS design, the validation sample is not a simple random sample so we cannot use a simple global empirical distribution function to estimate G(x|z,w). Hence, one should account for the sampling mechanism under the 2-stage OADS design to estimate G(x|z,w) nonparametrically. Let S denote the informative components of (Z,W) in the sense that G(X|Z,W) = G(X|S) almost surely. Without loss of generality, assume that S is a continuous variable with dimension d. Note that 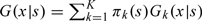where π_k(s) = Pr((Y,W)∈Δ_k|s) and G_k(x|s) = G(x|s,(Y,W)∈Δ_k). Then we estimate π_k(s) and G_k(x|s), respectively, by 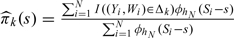and 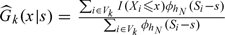where I(·) is an indicator function and 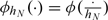is a d-dimensional kernel function with the bandwidth h_N. For simplicity, we suppress the subscript of h_N hereafter. Hence, G(x|s) can be subsequently estimated by 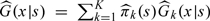which is a consistent estimator as shown in the supplementary material available at Biostatistics online.

The estimated likelihood function is obtained by substituting G(x|s) in (2.6) with 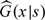and the corresponding estimated log-likelihood function is denoted by 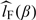, where

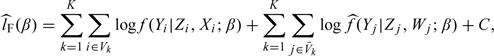with

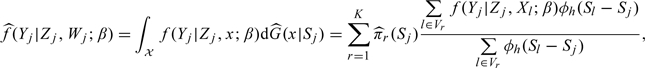and 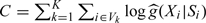, which is not dependent on β.

The solution to the estimated score equations 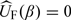, denoted by 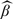, is used to estimate β⁰, where

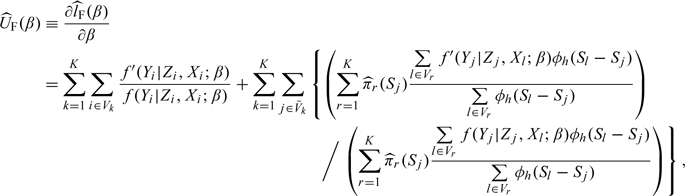with f^′(y|z,x;β) = ∂f(y|z,x;β)/∂β. One can adopt the Newton–Raphson iteration method to obtain the estimator 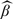. A simple ad hoc bandwidth selection 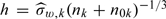can be used if S = W almost surely, where 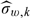is the sample standard error of {W_i,i∈V_k}.

The true value of parameters are indicated by superscript “0.” Let E_k denote a conditional expectation given (Y,W)∈Δ_k, under the true parameters. Assume that |V|/N→ρ_V > 0 and n_k/|V|→ρ_k ≥ 0 for k = 0,⋯,K, as N→∞. Let γ_k = Pr{(Y,W)∈Δ_k}. The regularity conditions needed to derive the asymptotic properties are given in the supplementary material available at Biostatistics online. Then the asymptotic properties of the proposed estimator are summarized in the following theorem.

THEOREM 1.

Under the regularity conditions, converges in probability to β⁰, while converges weakly to a normal distribution with mean zero and covariance Σ(β⁰), where

The proof of Theorem 1 is provided in the separate supplementary material available at Biostatistics online. The consistent variance estimator is stated in the following theorem.

THEOREM 2.

Under the regularity conditions, a consistent estimator for the asymptotic covariance matrix Σ(β⁰) is

where and with .

4. SIMULATION STUDY

We conducted a simulation study to assess the small sample performance of our proposed estimator. The data were generated from a linear regression model of the form:

where X, Z, and ς were generated independently from standard normal distribution. Thus, the conditional distribution of Y given X and Z is normal with mean β₀ + β₁X + β₂Z and variance 4. Let W = X + ϵ, where ϵ was generated from a zero-mean normal distribution with variance σ². Note that the value of σ² indicates the strength of information contained in W for X. We set σ = 1 in simulation, which represents a moderate association between the W and X. Here, we take S = W.

Suppose there are N subjects available at the first stage. Let a_i and b_i denote the i/3 percentile of Y and W, respectively, for i = 1,2. First, we use the method depicted in Figure 1 to obtain the second stage samples for the 2-stage OADS design. Then the size of the validation set is 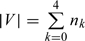Second, while selecting the same SRS sample of size n₀, we also select the 2 supplemental ODS samples in the stratum A₁ of size n₁ + n₂ and stratum A₃ of size n₃ + n₄, respectively, to mimic the design proposed by Weaver and Zhou (2005). Note that the sizes of validation set V obtained at the second stage through the above 2 sampling designs are the same.

Having obtained the data under the 2-stage OADS design, we denote the proposed estimator by 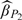. We also denote the reduced proposed estimator by 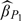for the 2-stage ODS design with (Y,Z,W) observed at the first stage. We compare estimators 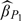and 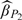with some competing estimators. The first estimator, denoted by 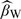, is the inverse probability weighted estimator (Horvitz and Thompson, 1952) based on the 2-stage OADS design. The second estimators to be compared, as discussed in the Section 2.1, are the estimator 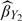for the 2-stage ODS design with (Y,Z) observed at the first stage and, similarly, the estimator 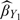for the 2-stage ODS design with only Y observed at the first stage and (X,Z) observed at the second stage. The bandwidth 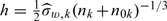is used for these estimators involving kernel smoothing, where 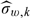is the sample standard error of {W_i,i∈V_k}. Finally, as a benchmark, we also consider the efficient linear regression estimator, denoted by 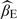, which is a hypothetical situation in which all subjects at the first stage have X observed, and the ordinary linear regression estimator, denoted by 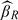, from a simple random sample of the same size as the validation set at the second stage. Note that the efficiency difference for methods β_Y1, β_Y2, β_P1, and β_P2 should be attributed to the study design instead of estimating procedure. However, β_P2 and β_W are different estimating procedures under the same 2-stage OADS design.

For narrative simplicity, we define an allocation function denoted by allocation(μ,ν) to allocate the validation set of size μ + 4ν at the second stage, which means that n₀ = μ and n₁ = n₂ = n₃ = n₄ = ν under the 2-stage OADS design as illustrated in Figure 1. Under the 2-stage ODS design, allocation(μ,ν) means SRS sample of size μ and 2 supplemental ODS samples in the stratum A₁ of size 2ν and in stratum A₃ of size 2ν are allocated. We also investigate the impact on the parameter estimation of different allocations of total validation sample size between the SRS sample and the supplemental OADS (ODS) samples at the second stage, with (N,β₀,β₁,β₂) = (1500,0.5,0.3,0.5) fixed.

For each simulation configuration, 1000 replicated samples were generated and the results were presented in Table 1. Under the model studied, we make the following observations on the estimator 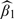, the parameter of interest. Note that the estimator 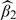works quite well in all scenarios. First, all the methods in all the scenarios yield consistent estimators, the variance estimators accurately reflect the true variations, and the confidence intervals have proper coverage probabilities. Second, the proposed estimators 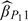and 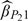are more efficient than the estimators 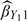and 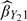, which indicates that taking auxiliary information into consideration indeed gains substantial estimation efficiency. Furthermore, 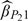is more efficient than 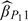. This fits our expectation since 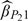not only utilizes the auxiliary in the stratification (i.e. study design) but also incorporates it into the estimation procedure, while 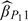uses it just in the estimation procedure. On the other hand, although the precision of estimator 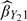and that of 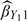are almost the same in the scenarios considered, the efficiency gains of 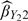over 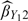are apparent due to the fact that the covariate Z is observed for all subjects in 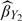. The estimator 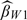is less efficient than 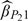since 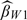just utilizes the second-stage sample and sampling probability under the 2-stage OADS design. Third, when we increase the size of the validation set from |V| = 240 to |V| = 360, more accurate estimators (including 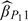, , 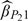, , 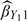, 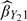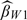and 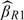) are obtained as expected. Here, we consider 3 different ways to add the additional 120 samples to the validation set |V| = 240. It can be seen that more efficiency gains are achievable through the way from allocation(120,30) to allocation(180,45), that is, putting half of the additional 120 samples to the SRS part and the other half to the OADS part averagely, than that from allocation(120,30) to allocation(240,30), that is, putting the additional 120 samples to the SRS part. Efficiency gains are also achieved through the way from allocation(120,30) to allocation(120,60), which puts the additional 120 samples to the OADS part evenly. These different allocation patterns indicate that adding the additional sample to both the SRS part and the supplemental OADS part or the supplemental OADS part is better than to the SRS part only. Finally, under the allocation(120,60), when the cutpoints vary from the 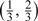to 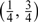, that is, when the product sample space 𝒴×𝒲 is stratified by more extreme cutpoints, more precise estimators (including 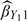, , 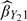, 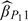and 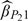) are obtained, and the efficiency advantage of 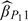over 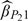becomes more obvious. We also investigate the effect of the strength of W for X, represented by σ, on the efficiency of estimator 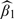, under the methods considered. Please see Figure A.1 in the supplementary material available at Biostatistics online.

Table 1.

Simulation study for the proposed estimators. Results are based on 1000 replicated data sets with 1500 subjects at the first stage for each data set^†

Cutpoints	|V|	Method
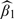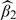			Mean	SE		CI		Mean	SE		CI
—	—	βE	0.299	0.050	0.052	0.966		0.497	0.052	0.052	0.946
—	240	βR	0.298	0.124	0.130	0.962		0.500	0.126	0.130	0.958
—	360	βR	0.297	0.107	0.106	0.943		0.496	0.105	0.106	0.943
				allocation(120, 30)
	240	βW	0.303	0.113	0.123	0.978		0.502	0.138	0.134	0.931
			0.304	0.113	0.112	0.955		0.505	0.121	0.102	0.906
			0.305	0.116	0.116	0.953		0.499	0.050	0.052	0.960
			0.305	0.072	0.068	0.941		0.500	0.050	0.052	0.957
			0.301	0.070	0.068	0.948		0.500	0.050	0.052	0.953
				allocation(180, 45)
	360	βW	0.302	0.095	0.100	0.967		0.494	0.110	0.109	0.951
			0.299	0.094	0.093	0.951		0.502	0.092	0.087	0.941
			0.300	0.096	0.096	0.952		0.500	0.053	0.052	0.943
			0.307	0.068	0.066	0.940		0.500	0.053	0.052	0.947
			0.303	0.064	0.065	0.954		0.500	0.053	0.052	0.945
				allocation(240, 30)
	360	βW	0.303	0.091	0.099	0.971		0.496	0.103	0.105	0.952
			0.301	0.099	0.095	0.936		0.498	0.096	0.089	0.936
			0.305	0.098	0.098	0.947		0.500	0.053	0.052	0.939
			0.308	0.070	0.066	0.933		0.500	0.053	0.052	0.948
			0.302	0.069	0.066	0.932		0.503	0.053	0.052	0.939
				allocation(120, 60)
	360	βW	0.302	0.100	0.107	0.967		0.504	0.118	0.120	0.952
			0.295	0.093	0.091	0.950		0.502	0.093	0.086	0.935
			0.304	0.097	0.093	0.931		0.500	0.053	0.052	0.943
			0.308	0.069	0.065	0.928		0.502	0.053	0.052	0.943
			0.299	0.067	0.065	0.938		0.502	0.053	0.052	0.944
	360	βW	0.303	0.114	0.114	0.942		0.510	0.135	0.131	0.940
			0.303	0.085	0.085	0.954		0.505	0.086	0.082	0.942
			0.300	0.084	0.086	0.949		0.500	0.053	0.052	0.942
			0.304	0.067	0.064	0.936		0.499	0.051	0.052	0.956
			0.293	0.061	0.063	0.963		0.499	0.051	0.052	0.958

^†Results are based on the model Y = β₀ + β₁X + β₂Z + 2ς with true values β₀ = 0.5, β₁ = 0.3, and β₂ = 0.5, where X, Z, and ς are mutually independently standard normal variables. The auxiliary variable W is defined to be equal to X plus a standard normal error term. 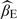: the regression estimator when X is observed for all subjects at the first stage; 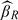: the regression estimator from a simple random sample of the same size as the validation set at the second stage; 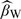: the inverse probability weighted estimator using the validation set under the 2-stage OADS design; 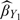: the estimator for the 2-stage ODS design with only Y observed at the first stage and (X, Z) observed for the second-stage sample; 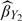: the estimator for the 2-stage ODS design with (Y, Z) observed at the first stage; 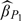: the estimator for the 2-stage ODS design with (Y, Z, W) observed at the first stage; 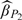: the estimator for the proposed 2-stage OADS design with (Y, Z, W) observed at the first stage.

It should be noted that in above simulation results, the covariate X was generated independently from Z. Therefore, we took S = W and then adopted a univariate kernel smoothing method to estimate the function g(X|Z,W) = g(X|W) nonparametrically. As suggested by one of the referees, here we intend to investigate our proposed estimators when g(X|W) is specified parametrically instead of being estimated by kernel smoothing. Note that in our above simulation setups g(X|W) is a normal density function with mean W and variance 2. The resultant estimate is denoted by 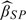. Furthermore, we also consider this estimate in the misspecified situation in which the X was generated from the model 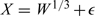but the working model remains to be X = W + ϵ. The related results are formulated in Table 2. Obviously, when g(X|W) is correctly specified, the estimate 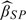outperforms the nonparametric methods. However, when g(X|W) is misspecified, the estimate 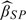is biased with low coverage probability while the nonparametric smoothing estimates, including our proposed estimates 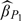and 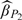, still work well.

Table 2.

Simulation study for the proposed estimators. Results are based on 1000 replicated data sets with 1500 subjects at the first stage and allocation pattern allocation(120, 60) at the second stage under the cutpoints 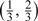for each data set^†

g(X|W)	Method
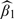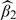		Mean	SE		CI		Mean	SE		CI
Specified	βW	0.302	0.100	0.107	0.967		0.504	0.118	0.120	0.952
		0.295	0.093	0.091	0.950		0.502	0.093	0.086	0.935
		0.304	0.097	0.093	0.931		0.500	0.053	0.052	0.943
		0.308	0.069	0.065	0.928		0.502	0.053	0.052	0.943
		0.299	0.067	0.065	0.938		0.502	0.053	0.052	0.944
	βSP	0.302	0.060	0.059	0.951		0.504	0.052	0.052	0.947
Misspecified	βW	0.307	0.104	0.108	0.969		0.505	0.121	0.121	0.955
		0.307	0.098	0.095	0.932		0.504	0.096	0.090	0.931
		0.310	0.099	0.096	0.925		0.508	0.059	0.057	0.941
		0.309	0.075	0.074	0.926		0.503	0.058	0.057	0.947
		0.306	0.071	0.068	0.934		0.505	0.057	0.056	0.941
	βSP	0.269	0.066	0.063	0.903		0.512	0.059	0.051	0.929

^†See note for Table 1.

On the other hand, as suggested by another referee, in some practice, d, the dimension of W, could be greater than one, and then multivariate kernel smoothing method would be involved. Hence, it is of practical importance to see how sensitive the resulting inference on the parameters of interest is with regard to the dimension d of kernel smoothing. We explore this issue with some modifications of the simulation models, where we generate Z from model Z = W² + ϵ₂, where W and ϵ₂ are both generated independently from a standard normal distribution. We keep the remaining parametric simulation settings unchanged. We use 2 dimensional product standard normal kernels to estimate g(X|Z,W) with bandwidth matrix diag(h₁,h₂), where 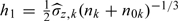, h₂ is defined in a similar pattern, and 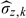is the sample standard error of {Z_i,i∈V_k}. The corresponding estimates are listed in Table 3. It can be seen that when the dimension of kernel smoothing d equals 2, the resultant estimates of β₁ of main interest are slightly biased with low coverage probability except for the inverse probability estimate 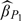. Even then, our proposed estimators 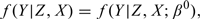and 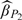outperform 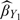and .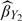

Table 3.

Simulation study for the proposed estimators. Results are based on 1000 replicated data sets with 1500 subjects at the first stage and allocation pattern allocation(120, 60) at the second stage under the cutpoints 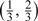for each data set with S = (Z, W)^†

Method
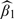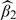	Mean	SE		CI		Mean	SE		CI
βE	0.302	0.053	0.054	0.957		0.506	0.057	0.056	0.949
βR	0.294	0.113	0.110	0.941		0.498	0.107	0.109	0.949
βW	0.297	0.109	0.109	0.953		0.506	0.115	0.117	0.956
	0.315	0.101	0.100	0.929		0.512	0.098	0.092	0.930
	0.317	0.099	0.096	0.926		0.503	0.059	0.058	0.949
	0.315	0.076	0.074	0.927		0.505	0.059	0.058	0.946
	0.287	0.072	0.071	0.929		0.506	0.059	0.057	0.941

^†See note for Table 1.

5. ANALYSIS OF THE COLLABORATIVE PERINATAL PROJECT DATA

As an illustration, we applied our proposed method to a data set from the Collaborative Perinatal Project (CPP) to evaluate the effect of maternal pregnancy serum level of polychlorinated biphenyls (PCB) of a mother on her children's intelligence quotient (IQ) test performance. Pregnant mothers were enrolled through university-affiliated medical clinics and data were collected on the mothers each prenatal visit. The children born during the study were also followed for various outcomes for up to 8 years. One hypothesis is that PCB levels are related to the performance on the Weschler Intelligence Scale for children at 7 years of age (Longnecker and others, 1997). To investigate the in utero exposure of PCB in relation to neurodevelopmental abnormality, the PCB levels were measured by analyzing the third trimester blood serum specimens that had been preserved from mothers in the CPP study. Due to the expense of conducting the blood serum assay to measure the PCB level, the study investigators decided to assess the PCB levels for an overall simple random sample of 849 subjects from the underlying population. In addition to the PCB level as the exposure variable of interest, other confounding variables available for all subjects under study include socioeconomic status of the child's family (SES), gender (SEX) and race (RACE) of the child indicating for female and black, respectively, the mother's education (EDU) and age (AGE).

To illustrate our methods, we use the simple random sample of 849 subjects as our underlying population. We then construct a 2-stage OADS design for this base population as an illustration. The first stage sample is the 849 subjects, that is, N = 849. We first explore the relationship between SES and PCB based on the first-stage sample data. A linear model fit for PCB given SES yields the estimate of slope 0.154(p < 0.0001), which indicates a linear association between SES and PCB. On the other hand, in terms of practical consideration in environmental epidemiology, higher SES usually leads to higher PCB level. Hence, we use SES as the auxiliary variable for PCB.

The 1/3 and 2/3 sample quantiles of IQ are 3.7 and 5.3, and the 1/3 and 2/3 sample quantiles of SES are 90 and 101, respectively. Hence, we can take a₁ = 3.7,a₂ = 5.3,b₁ = 90, and b₂ = 101. With respect to the second-stage samples, assume that 60 SRS samples and 30 supplemental OADS samples in each corner are selected under the allocation pattern allocation(60,30). We use the chi-square statistics to test the independence between IQ and SES, given PCB. In particular, we discretize PCB by dPCB = (PCB > median(PCB)). Under condition dPCB = 0, we can also define dIQ and dSES in a similar pattern, and then use the chi-square test yielding p-value 0.6038. Similarly, under condition dPCB = 1, the chi-square test yields p-value 0.4386. Hence, we think conditioning on PCB level, IQ does not further depend on SES. The fitted model is

where ε is a zero-mean normal variable with unknown variance.

The results for the CPP data analysis are summarized in Table 4. Note that since the other confounding covariates such EDU, SES, AGE, and so on are observed for all subjects, the method β_Y1 which assumes that only the outcome is observed at the the first stage is not considered in the data analysis. First, we are interested in the estimate for PCB under various methods. It is evident that all the analyses confirm that the PCB level of mother's third-trimester blood serum specimen is not significantly related to the IQ scores for children at 7 years of age. Second, a more precise 95% confidence interval ( − 0.432,1.002) is achieved for the estimate of PCB using method β_P2. For example, the 95% confidence intervals for the estimates of PCB are ( − 0.425,1.253), ( − 0.531,1.303), and ( − 0.791,1.149) using methods β_W, β_Y2, and β_P1, respectively. Meanwhile, the estimated standard error for the estimate of PCB in the hypothetical case β_E is the smallest one among all the methods considered. Also, the method β_E yields the most accurate 95% confidence interval ( − 0.190,0.702) for the estimate of PCB. Third, the estimators for the remaining covariates under various methods considered are all almost the same as confirmed in the simulation study. Finally, despite that slightly different conclusions are obtained under methods β_R and β_W, the methods β_E, β_Y2, β_P1, and β_P2 all confirm that SES, EDU, and RACE have a positive impact on the IQ scores of children while there is no evidence that both the AGE and SEX have any effect on the IQ scores.

Table 4.

Analysis results for the CPP study^†

Method		Intercept	PCB	EDU	SES	AGE	RACE	SEX
βE	Est.	80.025∗	0.256	1.258∗	1.078∗	0.018	– 7.942∗	– 0.590
		2.795	0.228	0.223	0.266	0.070	0.927	0.842
	LCI	74.546	– 0.190	0.822	0.558	– 0.118	– 9.759	– 2.240
	UCI	85.504	0.702	1.694	1.599	0.155	– 6.125	1.060
βR	Est.	77.897∗	0.711	1.122∗	0.847	0.131	– 7.355∗	– 0.423
		6.912	0.496	0.534	0.619	0.167	2.071	1.934
	LCI	64.349	– 0.262	0.076	– 0.367	– 0.195	– 11.414	– 4.214
	UCI	91.446	1.683	2.168	2.061	0.458	– 3.296	3.368
βW	Est.	78.391∗	0.414	1.322∗	0.592∗	0.199∗	– 7.752∗	– 1.085
		2.732	0.428	0.207	0.245	0.061	0.876	0.779
	LCI	73.036	– 0.425	0.916	0.112	0.079	– 9.469	– 2.612
	UCI	83.746	1.253	1.728	1.072	0.319	– 6.036	0.442
	Est.	79.154∗	0.386	1.264∗	1.102∗	0.028	– 7.841∗	– 0.611
		3.015	0.468	0.222	0.263	0.068	0.917	0.839
	LCI	73.245	– 0.531	0.830	0.586	– 0.106	– 9.638	– 2.255
	UCI	85.063	1.303	1.699	1.617	0.162	– 6.044	1.034
	Est.	79.759∗	0.179	1.268∗	1.088∗	0.031	– 7.825∗	– 0.597
		2.947	0.495	0.222	0.273	0.068	0.917	0.839
	LCI	73.982	– 0.791	0.833	0.553	– 0.103	– 9.623	– 2.242
	UCI	85.536	1.149	1.702	1.623	0.165	– 6.027	1.048
	Est.	80.722∗	0.285	1.269∗	1.174∗	0.034	– 7.732∗	– 0.588
		2.894	0.366	0.222	0.273	0.068	0.921	0.839
	LCI	75.049	– 0.432	0.834	0.639	– 0.100	– 9.538	– 2.232
	UCI	86.395	1.002	1.703	1.709	0.168	– 5.926	1.055

^†The outcome is the IQ scores for children at 7 years of age. PCB is the level measured from the third-trimester blood serum specimens, EDU is the mother's education level, SES is the socioeconomic status of the child's family, AGE is the mother's age, and RACE and SEX are the race and gender of the child, respectively. The fitted model is IQ = β_int + β₁PCB + β₂EDU + β₃SES + β₄AGE + β₅RACE + β₆SEX + ϵ, where ϵ is zero-mean normal variable with unknown variance. The auxiliary variable is SES, the cutpoints are 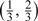, and the allocation pattern is allocation(60, 30). “Est.” is the estimation of the covariate's effect, “” is the estimated standard error, “LCI” is the lower bound of the 95% confidence interval, and “UCI” is the upper bound of the 95% confidence interval. The symbol “^∗” means the corresponding parameter estimate is significant at 5% level.

6. CONCLUDING REMARKS

We proposed a new 2-stage OADS design in which the selected supplemental samples at the second stage are allowed to depend on both a continuous outcome variable and a continuous auxiliary variable. This 2-stage OADS design can be easily reduced to the 2-stage ODS design with auxiliary covariate information. An estimated likelihood function based on nonparametric kernel smoothing method is developed to accommodate the 2-stage OADS design with continuous outcome variable. The proposed estimator is shown to be consistent and asymptotically normal. The simulation study suggests that greater efficiency can be gained in estimating the effect of the exposure variable on the outcome using the proposed 2-stage OADS design over the existing or other competing 2-stage ODS designs. Additionally, using the available auxiliary data information can also substantially improve the efficiency of the study. A real data analysis is provided to illustrate our proposed method.

When the dimension d of S is moderately large (e.g. d > = 3), the proposed method will not work well due to the curse of high dimensionality. One possible way is to specify g(X|S) parametrically. However, this parametric method could lead to some biased results when g(X|S) is misspecified. In practice, we suggested using our proposed method when d < = 2 and using the parametric method when d > = 2.

The proposed 2-stage OADS design allows the investigators to focus their attention on the subjects who are more informative for study aims. Generally, the issue of how to appropriately divide the domain of 𝒴×𝒲 to obtain the strata Δ_k^′s may affect the efficiency of estimators. Taking the CPP data as an example, we want to select those subjects with very high or low IQ scores and SES values as much as possible. On the other hand, the number of those subjects that we can sample is decreasing along with higher or lower values of both the IQ scores and SES. Hence, one needs to balance between the 2 above points when using a 2-stage OADS design. Our experience shows that the cutpoints consisting of 1/3 (or 1/4) and 2/3 (or 3/4) quantiles of both the outcome and auxiliary are usually feasible in practice.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://www.biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (R01 CA79949 to H.Z., Y.W.; R01 HL57444 to J.C.); China Postdoctoral Science Foundation (20100480877 to Y.W.); National Nature Science Fund of China (10771163 to Y.L.).