Abstract
Computational models of the neuromuscular system hold the potential to allow us to reach a deeper understanding of neuromuscular function and clinical rehabilitation by complementing experimentation. By serving as a means to distill and explore specific hypotheses, computational models emerge from prior experimental data and motivate future experimental work. Here we review computational tools used to understand neuromuscular function including musculoskeletal modeling, machine learning, control theory, and statistical model analysis. We conclude that these tools, when used in combination, have the potential to further our understanding of neuromuscular function by serving as a rigorous means to test scientific hypotheses in ways that complement and leverage experimental data.
Index Terms: Biomechanics, computational methods, modeling, neuromuscular control
I. Introduction: Why is Neuromuscular Modeling So Difficult?
For the purposes of this review, we define computational models of neuromuscular function to be algorithmic representations of the coupling among three elements: the physics of the world and skeletal anatomy, the physiological mechanisms that produce muscle force, and the neural processes that issue commands to muscles based on sensory information, intention, and a control law. Some of the difficulties and challenges of neuromuscular modeling arise from differences in the engineering approach to modeling versus the scientific approach to hypothesis testing. From the engineering perspective, computational modeling is a proven tool because we are able to use modeling to design and build very complex systems. For example, airliners, skyscrapers, and microprocessors are three examples of systems that are almost entirely developed using computational modeling. The obvious extension of these successes is to expect neuromuscular modeling to have already yielded deeper understanding of brain–body interactions in vertebrates, and revolutionized rehabilitation medicine.
To explain why this is not a reasonable extrapolation, we point out that engineers tend to apply an inductive approach and build models from the bottom-up, where the constitutive parts are computational implementations of laws of physics and mechanics known to be valid for a particular regime (e.g., turbulent versus laminar flow, continuum versus rigid body mechanics, etc.) that we understand well, or have at least been validated against experimental data in those regimes. The behavior of the model that emerges from the interactions among constitutive elements is carefully compared against the engineers' intuition and further experimental data before it is accepted as valid.
Neuromuscular modeling, on the other hand, tends to be used for scientific inquiry via a deductive approach to proceed from observed behavior in a particular regime that is measured accurately (e.g., gait, flight, manipulation), to building models that are computational implementations of hypotheses about the constitutive parts and the overall behavior. This deductive top-to-bottom approach makes the emergent behavior of the model difficult to compare against intuition, or even other models, because the differences that invariably emerge between model predictions and experimental data can be attributed to a variety of sources ranging from the validity of the scientific hypothesis being tested, to the choice of each constitutive element, or even their numerical implementation. Even when models are carefully built from the bottom-up, the modeler is confronted with choices that often affect the predictions of the model in counterintuitive ways. Some examples of choices are the types of models for joints (e.g., a hinge versus articulating surfaces), muscles (e.g., Hill-type versus populations of motor units), controllers (e.g., proportional-derivative versus linear quadratic regulator), and solution methods (e.g., forward versus inverse).
Therefore, we have structured this review in a way that first presents a critical overview of different modeling choices, and then describes methods by which the set of feasible predictions of a neuromuscular model can be used to test hypotheses.
II. Overview of Musculoskeletal Modeling
Computational models of the musculoskeletal system (i.e., the physics of the world and skeletal anatomy, and the physiological mechanisms that produce muscle force) are a necessary foundation when building models of neuromuscular function. Musculoskeletal models have been widely used to characterize human movement and understand how muscles can be coordinated to produce function. While experimental data are the most reliable source of information about a system, computer models can give access to parameters that cannot be measured experimentally and give insight on how these internal variables change during the performance of the task. Such models can be used to simulate neuromuscular abnormalities, identify injury mechanisms, and plan rehabilitation [1]–[3]. They can be used by surgeons to simulate tendon transfer [4]–[6] and joint replacement surgeries [7], to analyze the energetics of human movement [8], athletic performance [9], design prosthetics and biomedical implants [10], and functional electric stimulation controllers [11]–[13].
Naturally, the type, complexity, and physiological accuracy of the models vary depending on the purpose of the study. Extremely simple models that are not physiologically realistic can and do give insight into biological function (e.g., [14]). On the other hand, more complex models that describe the physiology closely might be necessary to explain some other phenomenon of interest [15]. Most models used in understanding neuromuscular function lie in-between, with a combination of physiological reality and modeling simplicity. While several papers [16]–[23] and books [24]–[26] discuss the importance of musculoskeletal models and how to build them, we will give a brief overview of the necessary steps and discuss some commonly performed analyses and limitations using these models. We will illustrate the procedure for building a musculoskeletal model by considering the example of the human arm consisting of the forearm and upper arm linked at the elbow joint as shown in Fig. 1.
Fig. 1.
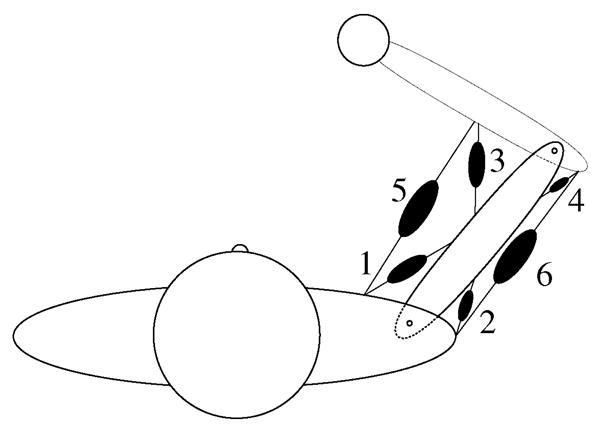
Simple model of the human arm consisting of two planar joints and six muscles.
A. Computational Environments
The motivation and advantage of graphical/computational packages like SIMM (Motion Analysis Corporation), Any-Body (AnyBody Technology), MSMS, etc. [27]–[29], is to build graphical representations of musculoskeletal systems, and translate them into code that is readable by multibody dynamics computational packages like SDFast (PTC), Autolev (Online Dynamics Inc.), ADAMS (MSC Software Corp.), MATLAB (Mathworks Inc.), etc., or use their own dynamics solvers. These packages allow users to define musculoskeletal models, calculate moment arms and musculotendon lengths, etc.
This engineering approach dates back to the use of computer-aided design tools and finite-element analysis packages to study bone structure and function in the 1960s, which grew to include rigid body dynamics simulators in the mid 1980s like ADAMS and Autolev. Before the advent of these programming environments (as in the case of computer-aided design), engineers had to generate their own equations of motion or Newtonian analysis by hand, and write their own code to solve the system for the purpose of interest. Available packages for musculoskeletal modeling have now empowered researchers without training in engineering mechanics to assemble and simulate complex nonlinear dynamical systems. The risk, however, is that the lack of engineering intuition about how complex dynamical systems behave can lead the user to accept results that one otherwise would not. In addition, to our knowledge, multibody dynamics computational packages have not been cross-validated against each other, or a common standard, to the extent that finite-elements analysis code has [30] and the simulation of nonlinear dynamical systems remains an area of study with improved integrators and collision algorithms developed every year. An exercise the user can do is to simulate the same planar double or triple pendulum (i.e., a limb) in different multibody dynamics computational packages and compare results after a few seconds of simulation. The differences are attributable to the nuances of the computational algorithms used, which are often beyond the view and control of the user. Whether these shortcomings in dynamical simulators affect the results of the investigation can only be answered by the user and reviewers on a case-by-case basis, and experts can also disagree on computational results in the mainstream of research like gait analysis [31]–[33].
B. Dimensionality and Redundancy
The first decision to be made when assembling a musculoskeletal model is to define dimensionality of the musculoskeletal model (i.e., number of kinematic degrees-of-freedom and the number of muscles acting on them). If the number of muscles exceeds the minimal number required to control a set of kinematic degrees-of-freedom, the musculoskeletal model will be redundant for some submaximal tasks. The validity and utility of the model to the research question will be affected by the approach taken to address muscle redundancy. Most musculoskeletal models have a lower dimensionality than the actual system they are simulating because it simplifies the mathematical implementation and analysis, or because a low-dimensional model is thought sufficient to simulate the task being analyzed. Kinematic dimensionality is often reduced to limit motion to a plane when simulating arm motion at the level of the shoulder [34]–[36], when simulating fingers flexing and extending [37], or when simulating leg movements during gait [38]. Similarly, the number of independently controlled muscles is often reduced [39] for simplicity, or even made equal to the number of kinematic degrees-of-freedom to avoid muscle redundancy [40]. While reducing the dimensionality of a model can be valid in many occasions, one needs to be careful to ensure it is capable of replicating the function being studied. For example, an inappropriate kinematic model can lead to erroneous predictions [41], [42], or reducing a set of muscles too severely may not be sufficiently realistic for clinical purposes.
A subtle but equally important risk is that of assembling a kinematic model with a given number of degrees-of-freedom, but then not considering the full kinematic output. For example, a three-joint planar linkage system to simulate a leg or a finger has three kinematic degrees-of-freedom at the input, and also three kinematic degrees-of-freedom at the output: the x and y location of the endpoint plus the orientation of the third link. As a rule, the number of rotational degrees-of-freedom (i.e., joint angles) maps into as many kinematic degrees-of-freedom at the endpoint [43]. Thus, for example, studying muscle coordination to study endpoint location without considering the orientation of the terminal link can lead to variable results. As we have described in the literature [44], [45], the geometric model and Jacobian of the linkage system need to account for all input and output kinematic degrees-of-freedom to properly represent the mapping from muscle actions to limb kinematics and kinetics.
C. Skeletal Mechanics
In neuromuscular function studies, skeletal segments are generally modeled as rigid links connected to one another by mechanical pin joints with orthogonal axes of rotation. These assumptions are tenable in most cases, but their validity may depend on the purpose of the model. Some joints like the thumb carpometacarpal joint, the ankle and shoulder joints are complex and their rotational axes are not necessarily perpendicular [46]–[48], or necessarily consistent across subjects [46], [49], [50]. Assuming simplified models may fail to capture the real kinematics of these systems [51]. While passive moments due to ligaments and other soft tissues of the joint are often neglected, at times they are modeled as exponential functions of joint angles [52], [53] at the extremes of range of motion to passively prevent hyper-rotation. In other cases, passive moments well within the range of motion could be particularly important in the case of systems like the fingers [54], [55] where skin, fat, and hydrostatic pressure tend to resist flexion.
Modeling of contact mechanics could be important for joints like the knee and the ankle where there is significant loading on the articulating surfaces of the bones, and where muscle force predictions could be affected by contact pressure. Joint mechanics are also of interest for the design of prostheses, where the knee or hip could be simulated as contact surfaces rolling and sliding with respect to each other [56]–[58]. Several studies estimate contact pressures using quasi-static models with deformable contact theory (e.g., [59]–[62]). But these models fail to predict muscle forces during dynamic loading. Multibody dynamic models with rigid contact fail to predict contact pressures [7].
For the illustrative example carried throughout this review, we will use the simple two-joint, six-muscle planar limb shown in Fig. 1. We model the upper arm and the forearm as two rigid cylindrical links connected to each other by a pin joint representing the elbow and shoulder joints as hinges. We will neglect the torque due to passive structures and assume frictionless joints. We will not consider any contact mechanics at the joints. This model will simulate the movement and force production of the hand (i.e., a fist with a frozen wrist) in a two-dimensional plane perpendicular to the torso as is commonly done in studies of upper extremity function [34]–[36].
Commentary 1
Modeling contact mechanics is the first of several elements we will point out throughout this review where the community of modelers diverge in approach and/or opinion. The computational approach to use when simulating contact mechanics among rigid and deformable bodies remains an area of active research and debate, and no definitive method exists to our knowledge. This affects neuromuscular modeling in two areas.
Joint mechanics. An anatomical joint is a mechanical system where two or more rigid bodies make contact at their articular surfaces (e.g., the femoral head and acetabulum for the hip, the distal femur, patella and tibial plateau for the knee, or the eight wrist bones and distal radius for the wrist). Their congruent anatomical shape, ligaments, synovial capsule, and muscle forces interact to induce kinematic constraints and produce the function of a kinematic joint. These mechanical systems are quite complex and their behavior can be load-dependent [63]. Most modelers correctly assume that the system can be approximated as a system of well-defined centers of rotation for the purposes of whole-limb kinematics and kinetics (e.g., [12], [29], [64]). However, including contact mechanics in joints like the knee and ankle could affect force predictions in muscles crossing these joints. For example, modeling a joint as deformable surfaces that remain in contact introduces additional constraints, thereby reducing the solution space when solving for muscle forces from joint torques [65]. If joint behavior or the specific loading of the articular surfaces is the purpose of the study as when studying cartilage loading, osteoarthritis or joint prostheses (e.g., [56], etc., among many), then it is critical to have detailed models of the multiple constitutive elements of the joint. Recent studies have combined dynamic multibody modeling in conjunction with deformable contact theory for articular contact which makes it possible to simultaneously determine contact pressures and muscle forces during dynamic loading [65]–[69].
Body-world interactions. Faithful and accurate simulations of the interactions among rigid and deformable bodies have been an active area of investigation, including foot–floor contact, accident simulation, surgical simulation, and hand–object interactions (e.g., [70]–[72]). Most recently, there have been advances that have crossed over from the computer animation and gaming world that provide so-called “dynamics engines” that can rapidly compute multibody contact problems [70], [73], [74]. Some recent examples of fast algorithms to simulate body–object interactions include [73] and [75]. While some of these dynamics engines emphasize speed and a realistic look over mechanical accuracy, some examples of new techniques can be both accurate and fast [75], [76].
D. Musculotendon Routing
Next, we need to select the routing of the musculotendon unit consisting of a muscle and its tendon in series [77], [78]. The reason we speak in general about musculotendons (and not simply tendons) is that in many cases it is the belly of the muscle that wraps around the joint (e.g., gluteus maximus over the hip, medial deltoid over the shoulder). In other cases, however, it is only the tendon that crosses any joints as in the case of the patellar tendon of the knee or the flexors of the wrist. In addition, the properties of long tendons affect the overall behavior of muscle like by stretching out the force-length curve of the muscle fibers [77]. Most studies assume correctly that musculotendons insert into bones at single points or multiple discrete points (if the actual muscle attaches over a long or broad area of bone). Musculotendon routing defines the direction of travel of the force exerted by a muscle when it contracts. This defines the moment arm r of a muscle about a particular joint, and determines both the excursion δs the musculotendon will undergo as the joint rotates an angle δθ defined by the equation, δs = r * δθ, as well as the joint torque τ at that joint due to the muscle force fm transmitted by the tendon τ = r * fm, where r is the minimal perpendicular distance of the musculotendon from the joint center for the planar (scalar) case [78]. For the three-dimensional (3-D) case, the torque is calculated by the cross product of the moment arm with the vector of muscle force τ = r × fm.
In today's models, musculotendon paths are modeled and visualized either by straight lines joining the points of attachment of the muscle; straight lines connecting “via points” attached to specific points on the bone which are added or removed depending on joint configuration [79] or as cubic splines with sliding and surface constraints [80]. Several advances also allow representing muscles as volumetric entities with data extracted from imaging studies [81], [82], and defining tendon paths as wrapping in a piecewise linear way around ellipses defining joint locations [12], [64]. The path of the musculotendon in these cases is defined based on knowledge of the anatomy. Sometimes, it may not be necessary to model the musculotendon paths but obtaining a mathematical expression for the moment arm (r) could suffice. The moment arm is often a function of joint angle and can be obtained by recording incremental tendon excursions (δs) and corresponding joint angle changes (δθ) in cadaveric specimens (e.g., [83], [84]).
For the arm model example (Fig. 1), we will model musculotendon paths as straight lines connecting their points of insertion. We will attach single-joint flexors and extensors at the shoulder (pectoralis and deltoid) and elbow (biceps long head and triceps lateral head) and double-joint muscles across both joints (biceps short head and triceps long head). Muscle origins and points of insertion are estimated from the anatomy. In our model of the arm in Fig. 1, we shall model musculotendons as simple linear springs. We then assign values to model parameters like segment inertia, elastic properties of the musculotendons, etc. At this point the model is complete and ready for dynamical analysis.
Commentary 2
Until recently, tendon routing was defined and computed using via points along the portions of its path where it crossed a joint. However, the more realistic extension of this process uses tendon paths that wrap around tessellated arbitrary bone surfaces, but defined to pass along specific via points, but the tendon path between via points need not be straight and can be affected by the shape of the bones and the tension in the tendon [76], [80]. Another approach is to eliminate via points altogether and calculate the behavior of the tendons as they drape over surfaces. This allows calculating the way tendon structures slide over complex bones, where tension transmission is affected by finger posture and tendon loading [80], [85]–[88]. These methods come at a computational cost but are arguably necessary in some cases, as when simulating the tendinous networks of the hand [80], [86], [88].
E. Musculotendon Models
The most commonly used computational model of musculotendon force is the one based on the Hill-type model of muscle[77], largely because of its computational efficiency, scalability, and because it is included in simulation packages like SIMM (Motion Analysis Corporation). In Hill-type models, the entire muscle is considered to behave like a large sarcomere with its length and strength scaled-up, respectively, to the fiber length and physiological cross-sectional area of the muscle of interest. This model consists of a parallel elastic element representing passive muscle stiffness, a parallel dashpot representing muscle viscosity, and a parallel contractile element representing activation-contraction dynamics, all in series with a series elastic element representing the tendon. The force generated by a muscle depends on muscle activation, physiological cross-sectional area of the muscle, pennation angle, and force-length and force-velocity curves for that muscle. These parameter values are generally based on animal or cadaveric work [89]. Five parameters define the properties of this musculotendon model. Four of these are specific to the muscle: the optimal muscle fiber length, the peak isometric force (found by multiplying maximal muscle stress by physiological cross-sectional area), the maximal muscle shortening velocity, and the pennation angle. The fifth is the slack length of the tendon (tendon cross-sectional area is assumed to scale with its muscle's physiological cross-sectional area [90]). Model activation-contraction dynamics is adjusted to match the properties of slow or fast muscle fiber types by changing the activation and deactivation time constants of a first order differential equation [77]. This Hill-type model has undergone several modifications but remains a first-order approximation to muscle as a large sarcomere with limited ability to simulate the full spectrum of muscles, or of fiber types found within a same muscle, or the properties of muscle that arise from it being composed of populations of motor units such as signal dependent noise, etc. Several researchers have developed alternative models for muscle contraction, which were used in specific studies [91]–[94].
The alternative approach has been to model muscles as populations of motor units. While this is much more computationally expensive, it is done with the purpose of being more physiologically realistic and enabling explorations of other features of muscle function. A well-known model is that proposed by Fuglevand and colleagues [95], which has been used extensively to investigate muscle physiology, electromyography, and force variability. However, the computational overhead of this model has largely limited it to studies of single muscles, and is not usually part of neuromuscular models of limbs. In order to develop a population-based model that could be used easily by researchers, Loeb and colleagues developed the Virtual Muscle software package [96]. It integrates motor recruitment models from the literature and extensive experimentation with musculotendon contractile properties into a software package that can be easily included in multibody dynamic models run in MATLAB (The Mathworks, Natick, MA).
Commentary 3
Most investigators will agree that defining and implementing more realistic muscle models is a critical challenge to be overcome in musculoskeletal modeling. The reasons include the following.
Muscles are the actuators in musculoskeletal systems, and the neural control and mechanical performance of the system depend heavily on their properties. There is abundant experimental evidence that the nonlinear, time-varying, highly individuated properties of muscles determine much about neuromuscular function and performance in health and disease. Therefore, before realistic muscle models are available, testing theories of motor control will remain a challenge.
Muscle models today fall short of replicating some fundamental physiological and mechanical features of muscles. In a recent study, for example, Keenan and Valero-Cuevas [97] showed that the most widely used model of populations of motor units does not robustly replicate two fundamental tenets of muscle function: the scaling of EMG and force variability with increasing muscle force. Therefore, there are some critical neural features of muscle function that are yet to be characterized experimentally and encoded computationally (for another example, see [98]).
Is it even desirable or possible to build a “complete” model of muscle function? A good model is best tailored to a specific question because it can make testable predictions and/or explain a specific experimental phenomenon. Thus, such models are more likely to be valid and useful. For example, some researchers focus on time- and context-sensitive properties like residual force enhancement [98] or force depression [99], others investigate the complex 3-D architecture of muscles and muscle fibers [100], and others mentioned above focus on total force production or populations of motor units. Therefore the challenge is to decide what is the best combination of mechanistic and phenomenological elements to make the model valid and useful for the study at hand.
Muscle energetics is another important aspect of modeling that deserves attention. An obvious disadvantage of Hill-type muscle models is that they do not capture the distribution of cross bridge conformations for a given muscle state (length, velocity, activation, etc.) because the details of energy storage and release in eccentric and concentric contractions associated with cross bridge state and parallel elastic elements are vaguely understood [101], [102]. Therefore, muscle energetics is a clear case where, in spite of what is said in the above paragraph, it may be necessary to create models that span multiple “scales” or “levels of complexity.” Several authors have repeatedly pointed out the need for accurate muscle energetics to understand real-world motor tasks such as [103] and [104].
Lastly, modeling and understanding muscle function will require embracing the fact that muscle contraction is an emergent dynamical phenomenon mediated (or even governed?) by spinal circuitry. So far most modelers have focused on driving muscle force with an unadulterated motor command. Motor unit recruitment, muscle tone, spasticity, clonus, signal dependent noise, to name a few, are features of muscle function affected to a certain extent by muscle spindles, Golgi tendon organs, and spinal circuitry. Thus advancing and using models of muscle proprioceptors and spinal circuitry will become critical to our understanding of physiological muscle function [105]–[107].
III. Forward and Inverse Simulations
In “forward” models, the behavior of the neuromuscular system is calculated in the natural order of events: from neural or muscle command to limb forces and movements. In “inverse” models, the behavior is assumed or measured and the model is used to infer and predict the time histories of neural, muscle, or torque commands that produced it. The same biomechanical model governed by Newtonian mechanics is used in either approach, but it is used differently in each analysis [24], [26].
A. Forward Models
The inputs to a forward musculoskeletal model are usually in the form of muscle activations (or torque commands if the model is torque driven) and the outputs are the forces and/or movements generated by the musculoskeletal system. The system dynamics is represented using the following equation:
| (1) |
where I is the system mass matrix, θ̈ the vector of joint accelerations, θ the vector of joint angles, C the vector of Coriolis and centrifugal forces, G the gravitational torque, M the instantaneous moment arm matrix, FM the vector of muscle forces, and Fext the vector of external torques due to ground reaction forces and other environmental forces. This system of ordinary differential equations is numerically integrated to obtain the time course of all the states (joint angles θ and joint angle velocities θ̇) of the system. The input muscle activations could be derived from measurements of muscle activity (electromyogram) or from an optimization algorithm that minimizes some cost function, for example, the error in joint angle trajectory for all joints and energy consumed [108]. Forward dynamics has also been used in determining internal forces that cannot be experimentally measured like in the ligaments during activity or contact loads in the joints. It gives insight on energy utilization, stability and muscle activity during function for example in walking simulations [109]. It gives the user access to all the parameters of the system and to simulate effects when these are changed. This makes it a useful tool to study pathological motion and for rehabilitation. [22] provides a review on many of the applications of forward dynamics modeling.
B. Inverse Models
Inverse dynamics consists of determining joint torque and muscle forces from experimentally measured movements and external forces. Since the number of muscles crossing a joint is higher than the degrees-of-freedom at the joint, multiple sets of muscle forces could give rise to the same joint torques. This is the load-sharing problem in biomechanics [110]. A single combination is chosen by introducing constraints such that the number of unknown variables is reduced and/or based on some optimization criterion, like minimizing the sum of muscle forces or muscle activations. Several optimization criteria have been used in the literature [111]–[113]. Muscle forces determined by this analysis are often corroborated by electromyogram recordings from specific muscles [114], [115]. Since inverse dynamics consists of using the outputs of the real system as inputs to a mathematical model whose dynamics do not exactly match with the real system, the predicted behavior of the model does not necessarily match with the measured behavior of the real system. This is an important problem in inverse dynamics and is discussed in more detail in [116].
Both forward and inverse models are useful and can be complementary and the choice is largely driven by the goals of the study. The main challenge with both these analyses is experimental validation because many of the variables determined using either approach cannot be measured directly. The reader is directed to articles and textbooks that describe these methods in detail [12], [24], [64], [117]–[119].
IV. Computational Methods for Model Learning, Analysis, and Control
We have discussed the computational methods used to define and assemble known musculoskeletal elements of models. However, there exist complementary computational methods to expand the utility of these models in several ways. For example:
use experimental data to “learn” the complex patterns or functional relationships, and thereby create model elements that are not otherwise available (e.g., the inverse dynamics of a complex limb, mass properties, complex joint kinematics, etc.);
find families of feasible solutions when problems are high dimensional, nonlinear, etc. (e.g., characterize kinematic and kinetic redundancy);
find specific optimized solutions for a specific task;
establish the consequences of parameter variability and uncertainty;
explore possible control strategies used by the nervous system;
predict the consequences of disease, treatment, and other changes in the neuromusculoskeletal system;
consider noise in sensors and actuators.
The computational methods that allow such explorations stem from the interface of three established fields combining engineering, statistics, computer science, and applied mathematics: machine learning, control theory, and estimation-detection theory. While these fields are vast, and the subject of active research in their own right, we portray a categorization of their techniques and interactions as they relate to our topic (Fig. 2). Experts in these fields will have valid and understandable objections to our specific simplifications and categorizations. However, we believe that nonspecialists will nevertheless benefit from it at the onset of their exploration of these areas; and nuance will emerge as they become proficient.
Fig. 2.
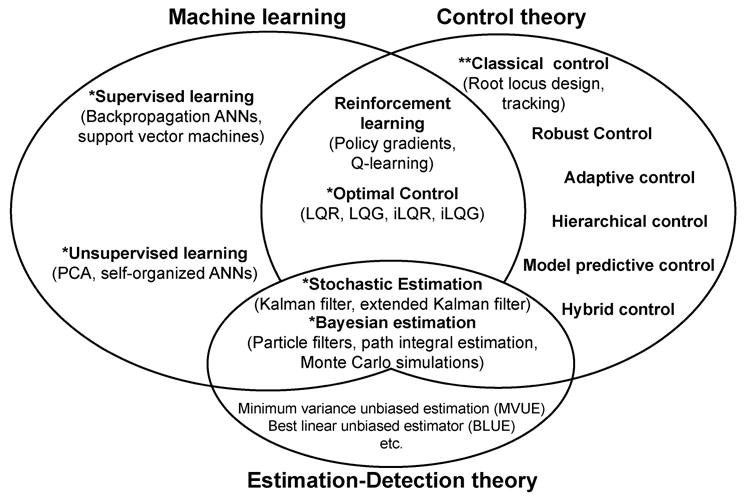
Schematic description of the interactions among machine learning, control theory, and estimation-detection theory.
What is most important to extract from this categorization is that, even though most of these areas matured decades ago, only a few techniques are commonly used in neuromuscular modeling (indicated with **) and a few others are beginning to be used (indicated with *). To be clear, several of these techniques are routinely used, and even overused, in the context of psychophysics, biomechanical analysis, gait, and EMG analysis, data processing, motor control, etc. Therefore, they will not be altogether new to someone familiar with those fields. However, neuromuscular modeling has not tapped into these available computational techniques. Our aim here is to succinctly describe them in the context of neuromuscular modeling and point to useful literature.
Another important idea we wish to convey is that the expertise you may have with one of these techniques in a different context enables their use for neuromuscular modeling. For example, you may be familiar with the use of principal components analysis for EMG analysis, and the same techniques can be used to approximate the main interactions among the parameters of a model.
Lastly, we wish to invite the community of practitioners and students in machine learning, control theory, and estimation-detection theory to join forces with our community of neuromuscular modelers. For example, we can find collaborators in those fields, train students with backgrounds in those fields, or expand our use of those techniques. This commitment is particularly necessary to move beyond traditional discipline-based training where, for example, control theory is taught in the electrical engineering curriculum, and machine learning in computer science—and each is taught as mutually independent, and separate from the problems of neuromuscular systems.
V. Machine-Learning Techniques for Neuromuscular Modeling
Machine learning is the general term used for a scientific discipline whose purpose is to design and develop computational algorithms that allow computers to learn based on available data (such as from experiments or databases) or on-line during iterative or exploratory behavior [120]–[122]. For the purposes of this review, we will use the two-link arm model introduced in Section II to illustrate two main classes of machine-learning approaches.
Learning functional relationships. It is often necessary to use experimental data to arrive at a computational representation of model elements lacking analytical description. Or even if such analytical representation exists, it may only be an approximation that needs to be refined due to structural or parameter uncertainty. Learning functional relationships has been called a “black box” approach.
Learning solutions to redundant problems (i.e., one-to-many mappings). Machine-learning techniques can be used to solve the redundancy problem common in neuromuscular systems when these solutions cannot be found analytically, particularly, if the problem is nonlinear, nonconvex or high-dimensional.
A. Learning Functional Relationships
In neuromuscular models, a functional relationship may describe, for example, the inertia tensor, moment arm matrix, Jacobian matrix, or inverse dynamics. Such relationships could be derived analytically, but often an analytical solution is not available or feasible, e.g., due to intersubject variability or structural uncertainties, like variability or uncertainty about link lengths, joint centers of rotation, centers of mass, and inertial properties. For minor uncertainties, where only a few parameters need to be determined, these parameters could be inferred by fitting the model to experimental data. For example, limb lengths could be extracted from motion tracking data using probabilistic-inference methods [123]. Such an approach, however, becomes increasingly difficult if too many parameters are unknown or uncertain. Apart from computational problems, the state that fully defines the dynamics of the neuromuscular system may be unobservable [124]. These shortcomings motivate methods to learn functional relationships, as described in this section. These methods focus on the so-called “model-free” approach that does not require an a priori analytical model.
This model-free approach avoids finding the underlying structure of a system. Examples of finding the structure, e.g., the number of model elements and their connectivity, can be found in [87] and [125]–[127]. Typically, the search space for these problems is large and the fitness landscape is often fragmented and discontinuous: that is, the fitness of a model can change dramatically when a model element is added or removed [87], [128]. In this section, however, we focus on the aim of replacing unknown elements of neuromuscular models by learned functional representations.
We illustrate learning functional relationships using our arm-model example (Section II). Our task is to track a given trajectory with the hand. Here, we omit finding and implementing a controller. Instead, we want to find a computational representation of the inverse dynamics—which in turn may be used by a controller for tracking. For this simple example, the inverse dynamics can be found analytically, but for illustration purposes, we assume it is unknown.
In our task, the goal of the machine-learning algorithm is to find a computational function that maps from desired accelerations of the endpoint onto joint torques. Before learning this mapping, we need to identify the dependencies across variables so that they can be measured. That is, the appropriate data need to be collected. Note that this implies that the modeler has (or will spend time acquiring) an intuitive sense of the underlying causal interactions at play to properly identify the data to collect. For example, the joint torques τ will depend on the limb's mass and inertial properties, the state variables of the system (joint angles, x, and angular velocities, ẋ), and, finally, on the desired hand acceleration, ẍ*; thus, the torques are τ = f(x, ẋ, ẍ*) if mass and inertia parameters are assumed constant. For ease of illustration, we assume that the limb is controlled by torque motors (finding muscle commands is illustrated later in this section) and that the Jacobian of the system is full rank (i.e., the dynamics is invertible). Problems with noninvertible mappings are illustrated in Section V-B. We now critically review several techniques to find the target mapping from measurements.
1) Computational Representation of Functional Relationships
A foundation of machine-learning methods is to find numerical functions that approximate relationships in data. These functions can take numerous forms that range from linear and polynomial to Gaussian and sinusoidal or sum of these. In the machine-learning framework, these functions are called basis functions [120], [122]. A typical scenario in a machine-learning problem is for the modeler to prespecify the basis functions to fit to the data. In this case, the modeler has an a priori opinion of what the underlying structure of the mapping should be. If the a priori opinion is valid, then these algorithms converge quickly to the desired mapping and have good performance. However, for many problems in neuromuscular biomechanics, such intuition or prior knowledge is not available. More advanced machine-learning algorithms can select from among families of basis functions, as well as estimate their parameter values [122], [129]. As the basis functions become more complex, however, the model becomes more opaque and provides less intuition. We now discuss the use of basis functions in the context of supervised learning.
2) Supervised Learning Methods
In supervised learning, for a given input pattern, we posit an a priori function to produce the corresponding output pattern. Thus, the problem is function approximation, which is also known as regression analysis. Generally, the input–output relationship will be nonlinear. A common approach to nonlinear regression is to approximate an input–output relationship with a linear combination of basis functions [121]. Popular examples of this approach are neural networks [130], support vector regression [131], and Gaussian process regression [132]; the latter has been introduced to the machine-learning community by Williams and Rasmussen [133], but the algorithm is the same as the 50-year-old “Kriging” interpolation [134], [135] developed by Daniel Krige and Georges Matheron.
Some supervised learning methods go beyond producing a functional mapping, and also predict confidence boundaries for each predicted output. Gaussian process regression is an example of these methods that has a solid probabilistic foundation and therefore enjoys high academic interest. Unfortunately, however, Gaussian process regression is computationally expensive: the training time (i.e., computational cost) scales with the cube of the number of training patterns. Faster variants have been developed, but they essentially rely on choosing a small enough set of representative data points to make the solution computationally feasible [132]. If the computation of confidence boundaries is not important, then support vector regression is a faster alternative because the training time scales with the square of the number of training patterns.
An alternative for fast computation and with the option to compute confidence boundaries is locally weighted linear regression [136]–[138]. A challenge with locally weighted regression is the placement of the basis functions, which are typically Gaussian. An optimal choice for centering Gaussian functions is often numerically infeasible. A further problem of locally confined models arises in high-dimensional spaces: the proportional volume of the neighborhood decreases exponentially with increasing dimensionality; thus, eventually this volume may not contain enough data points for a meaningful estimation of the regression coefficients—see the “curse of dimensionality” [139]. Counteracting this problem using local models with broad Gaussian basis functions is often infeasible, since these may lead to over-smoothing and loss of detail. Fortunately, many biological data distributions are confined to low-dimensional manifolds, which can be exploited for supervised learning [137], [138], [140].
Generally, finding the model parameters to fit a functional relationship is an optimization problem; therefore, we discuss briefly convergence and local minima. Some of the above-mentioned techniques, like linear regression and Kriging interpolation, provide analytic solutions to function approximation and, thus, avoid problems with lack of convergence and local minima. However, finding a proper family of basis functions and their parameters is typically a complex optimization problem requiring an iterative solution. Whereas most established methods have guaranteed convergence [122], they may result in local minima, which are not globally optimal. This problem has been addressed by using, for example, annealing schemes [141], [142] and genetic algorithms [143]. The latter are particularly useful if the parameter domain is discrete, like, e.g., for the topology of neural networks [144]. As a downside, these optimization methods tend to be computationally complex and provide no guarantee to find a globally optimal solution; the problem of local minima remains, therefore, an area of active research.
Commentary 4
Artificial neural networks (ANNs) are perhaps the best-known example of supervised learning. They are widespread, but their use has also been controversial.
There are largely two communities who use ANNs. From the perspective of one community, the network connectivity, parallel processing, and learning rules are biologically inspired. Therefore, the focus is on understanding computation in biological neurons, and the fact that certain networks can do function approximation efficiently is simply an additional benefit [145]. In contrast, the statistical-machine-learning community sees ANNs as a specific algorithmic implementation and focuses on the function-approximation problem per-se and, thus, sees no need to address this problem exclusively with neural networks [121], [122].
The selection of the topology of the network (number of neurons and their connectivity) is to a large extent heuristic, and unrelated to the a priori knowledge of the underlying structure of the mapping.
The more complex the network, the more it will tend to overfit the data and lack generalization. Heuristics have been developed to mitigate overfitting: for example, the number of parameters to learn should be less than 1/10 of the training data [130].
3) Data Collection and Learning Schemes
Having presented the nature of function approximation, we now describe different strategies for collecting training data necessary to compute the approximation (Fig. 3). Here, we focus on learning inverse mappings, like the inverse dynamics of a limb, which pose a challenge for data collection (Fig. 4).
Fig. 3.
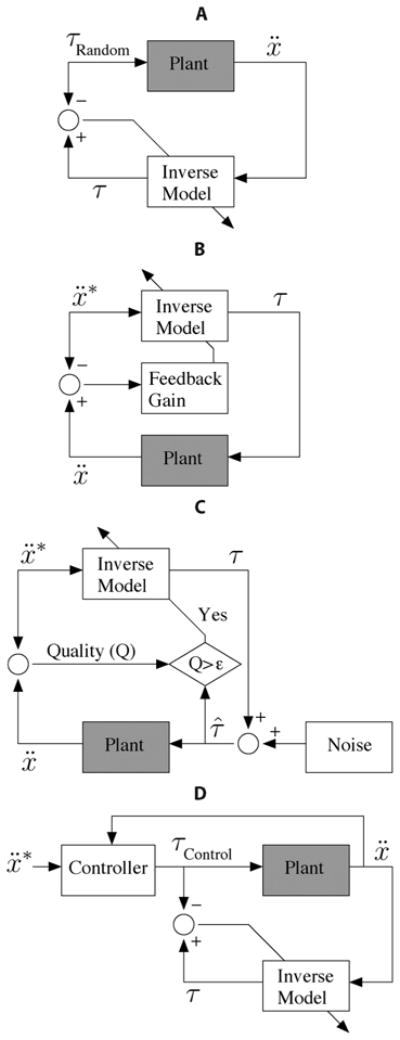
Block diagram representation of data collection and supervised learning schemes (see text for detailed description of each case). In every case, data is collected in the real world by feeding joint torques to the real-world Plant (gray block). These torques can be: (A) selected at random, (B) based on a preliminary inverse model that may (C) include noise and selective use of training data, or (D) selected with the benefit of a demonstrator. For simplicity of illustration, the dependence of the inverse model and controller on state, x, ẋ, is omitted. (A) Direct inverse modeling. (B) Feedback-error learning. (C) Staged learning. (D) Learning from demonstration.
Fig. 4.
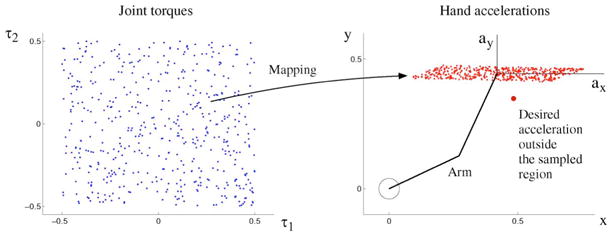
Illustration that an exploration in input space (here, torque) may not sample a desired output (acceleration). Sampling in input space is limited to the range ±0.5—any practical setting requires limits of exploration.
In direct inverse modeling [146], a sequence of random torques is delivered to the system to produce and record hand accelerations [Fig. 3(a)]. To assemble input–output training patterns, we take as input the observed time series of the arm state (posture, velocity) and acceleration, and as output the corresponding torque time series. The inverse mapping is then obtained using a supervised learning method (e.g., locally weighted linear regression with Gaussian basis functions [136]). Whereas feeding random sequences of torques is the most straightforward way to collect training patterns, its disadvantage is that it may not produce the desired accelerations, and therefore, the mapping found may not generalize well to the desired accelerations—see Fig. 4 and [147].
To better explore the desired set of accelerations, feedback-error learning [148] and distal supervised learning [147] directly feed the inverse model with desired accelerations [Fig. 3(b)]. This method requires a preliminary inverse model, found perhaps using direct inverse modeling. Since the errors in torque space are not directly accessible, the resulting errors in acceleration space are mapped back onto torque space. Feedback-error learning uses a linear mapping, and distal supervised learning requires the ability to do error-backpropagation (as in ANNs [130]) through an a priori learned forward model (which learns the opposite direction). If the errors are small and the underlying mapping is locally linear, feedback-error learning is the method of choice. However, small errors require a well initialized inverse mapping. Distal supervised learning, to our knowledge, is not often used in practice today.
Staged learning [149], [150] also feeds the inverse model with desired accelerations, but does not require a well initialized model [Fig. 3(c)]. The output of the inverse model is augmented with noise before applying it as torques to the arm. If the resulting accelerations show a better performance—based on some quality criterion—the applied torque is used as training pattern for a new generation (new stage) of inverse models. Compared to feedback-error learning, this method can be applied to a broader set of problems (see feedback-error learning above), but comes at the expense of a longer training time.
Alternatively, we may learn from demonstration. For example, a proportional-integral-derivative (PID) controller could be used to demonstrate (i.e., bias and/or guide) the production of training data to learn the inverse-dynamics mapping close to the region of interest [Fig. 3(d)] [151]–[153]. If a suitable demonstrator is available, this last option is the method of choice.
B. Learning Solutions to Redundant Problems
There is a long history of ways to solve the “muscle redundancy” problem with linear and nonlinear optimization methods based on specific cost functions [110], [154]. However, these methods provide single solutions that minimize that specific cost function, which is often open to debate. An alternative method is to solve for the entire solution space so as to explore the features of alternative solutions. If the system is linear for a given posture of the limb [44], [45], [155], the complete solution space can be found, which explicitly identifies the following:
the set of feasible control commands, e.g., the feasible activation set for muscles;
the set of feasible outputs, e.g., the feasible set of accelerations or forces a limb can produce;
the set of unique control commands that achieve the limits of performance;
the nullspace associated with a given submaximal output, e.g., the set of muscle activations that produce a given submaximal acceleration or force.
By knowing the structure of these bounded regions (i.e., feasible sets of muscle activations, limb outputs, and nullspaces), the modeler can explore the consequences of different families of inputs and outputs such as the level of cocontraction, joint loading, metabolic cost, etc. Methods to find these bounded regions are well known in computational geometry [44], [45], [156]. However, these methods risk failure if the problem is high dimensional or nonlinear. In these cases, it is best to first use machine algorithms to “learn” the topology of the bounded regions, and then use that knowledge to explore specific solutions.
1) Redundancy Poses a Challenge to Learning
We use again our two-link arm model to illustrate a challenge in redundancy for learning. Note, the redundancy could be eliminated by providing sufficiently many constraints. Here, however, we focus on problems where such constraints are missing. In our model, we want to learn the set of muscle activations that bring the hand to a given equilibrium position. For simplicity, we model muscles as springs (see Section II); thus, we control spring rest lengths. The mapping from spring rest lengths onto hand position is unique. However, the inverse mapping is one-to-many (Fig. 5). Moreover, we map a single hand position onto a nonconvex region.1 For such a mapping, function approximation fails because it will average over the many possible solutions, i.e., over the nonconvex region, to obtain a single output [157]. Applying this output to our arm model, however, does not bring the hand to the desired position (Fig. 5). Thus, a different approach is needed to learn this mapping. This mapping problem could be addressed in the following ways.
Fig. 5.
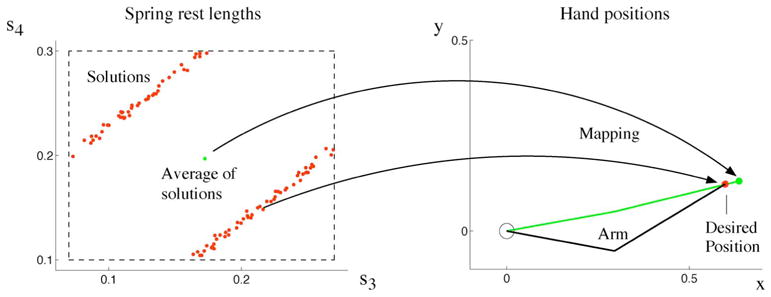
Mapping from spring resting lengths (si) to hand positions (x, y). Several redundant resting lengths are solutions for one desired hand position (red). The graph on the left shows a two-dimensional projection of a cross section of the six-dimensional nullspace of spring resting lengths: s1 and s2 were set to constant values; s3 and s4 were randomly drawn (within dashed box), and all values of s5 and s6 were projected onto the displayed plane. The original six-dimensional nullspace in rest-length space is, therefore, nonconvex. Thus, the average of all rest-lengths solutions does not map onto the desired hand position.
Instead of learning a mapping onto a point, we could learn a mapping onto a probability distribution, and thus, accommodate the above-mentioned nonconvex nature of the solution space. Diffusion networks address this task [157].
Recurrent neural networks store training patterns as stable states [158]. In our case, such a pattern could be a combination of muscle activation and hand position. If only part of a pattern is specified (e.g, the hand position), the network dynamics completes this pattern to obtain the complement (here, the muscle activation). For fully connected symmetric networks, the dynamics converge to a stable pattern [158]. As an example for such an application, Cruse and Steinkühler showed that the relaxation in a recurrent neural network can be used to solve the inverse kinematics of a redundant robot arm [159], [160].
Finally, analogue to the use of recurrent neural networks, we could—in a first step—learn a representation of the manifold or distribution of the data points that contain input and output, and—in a second step—use this learned representation to compute a suitable mapping. Here, we want to focus on this latter solution.
2) Learning the Structure of Data Sets: Unsupervised Learning Methods
Unsupervised learning methods are designed to find the structure in data sets and do not need pairs of input and target patterns. Several methods exist for extracting linear and nonlinear approximations to the distribution of data points that will represent such a data structure. In this context, the data set represents a manifold in a multidimensional space, and learning the structure of this manifold is the goal.
Here, we will only briefly mention various linear and nonlinear methods—see references for more details. Methods for finding linear subspaces that represent data distributions are principal components analysis (PCA) [161], probabilistic PCA [162], independent component analysis [163], and nonnegative matrix factorization [164]. When applied to nonlinear distributions, these linear methods may give misleading solutions [165], [166].
Several methods exist to find the structure of nonlinear manifolds in data: auto-associative neural networks [145], [167], point-wise dimension estimation [166], self-organizing maps (SOMs) [168]–[170], probabilistic SOM [171], [172], semidefinite embedding [173], locally linear embedding [174], Isomap [175], Laplacian eigenmaps [176], stochastic neighbor embedding [177], kernel PCA [178], [179], and mixtures of spatially confined linear models (PCA or probabilistic PCA are commonly used as their linear models) [130], [150], [165], [180].
3) Going From the Structure of an Input–Output Data Set to Creating a Functional Mapping
Once a representation has been found, we need to construct a mapping from a specified input to the corresponding output. This mapping could be obtained as follows.
An input pattern specifies a constrained space in the joint space of input and output. To find output samples, this constrained space can be intersected with the learned representation of the data distribution/manifold. One possibility is to find the point on the constrained space that has the smallest Euclidean distance to our manifold representation [150], [165], [172]. For mixtures of locally linear models, efficient algorithms exist to find such a solution [150], [165]. If the manifold representation intersects the constrained space at several or infinitely many points, a solution has to be chosen out of this set of intersections.
Alternative to the minimum distance, we could define arbitrary cost functions on the set of intersections and find a solution accordingly. This path has not been fully exploited and explored.
VI. Applications of Control Theory for Neuromuscular Modeling
Control theory is a vast field of engineering where information about a dynamical system (from internal sensors, outputs, or predictions) is used to issue commands (corrective, anticipatory, or steering) with the goal of achieving a particular performance. We begin by giving a short overview of the uses of classical and optimal control theories as they are now used in the context of neuromuscular modeling. We then provide an overview of alternative approaches such as hierarchical optimal control, model predictive control, and hybrid optimal control. Our presentation of each of these types of optimal control are motivated by the characteristics of the dynamical systems found in neuromuscular systems. Hierarchical optimal control is motivated by the high dimensionality of neuromuscular dynamics; model predictive control is motivated by the need to impose state and control constrains such as uni-directional muscle activation (e.g., muscles can actively pull and resist tension, but cannot push). Finally, hybrid optimal control is motivated by the need to incorporate discontinuities and/or changes in the dynamics arising from making and breaking contact with objects and the environment (e.g., as in locomotion, grasping and object manipulation).
In the context of neuromuscular modeling, a dynamical system is one where differential equations can describe the evolution of the dynamical variables (called the state vector denoted by x) and their response to the vector of control signals (denoted by u). The reader is referred to any introductory text in control theory such as [181] for details. The dynamics of neuromuscular systems is generally nonlinear and they are formulated by the following equations:
| (2) |
For the dynamics of a limb model (Fig. 1), x is the state vector of two angles and two angular velocity while u are the controls that correspond to the two applied joint torques. The control of nonlinear systems is a problem with no general solution, and the traditional approach is to linearize the nonlinear dynamics around an operating point, or a sequence of operating points in state and control space. In the linearized version of the problem, the linear dynamics (3) are valid for small deviations from the operating point. For the example of the limb model, the operating point can be a prespecified arm posture, or a sequence of prespecified arm postures. The linearized dynamics have the form
| (3) |
The matrix A is the state transition matrix that defines how the current state x affects the derivative of the state ẋ (i.e., like when the change in position of a pendulum along its arc defines its velocity). B is the control transition matrix that defines how the control signals u affect the state derivatives. The matrix H is the measurement matrix that defines how the state of the system produces the output y. In some cases, the control signals u can also act directly on the outputs y via the matrix D, which is called the control output matrix. Control theory comes into the picture when we apply a control signal u to correct or guide the evolution of the state variables.
With very few exceptions, the vast majority of neuromuscular modeling attempts to find the sequence of control gains ut1, ut2, …, uT that will force the neuromuscular system to execute a task—which in most cases is to track a prespecified kinematic or kinetic trajectory in the time horizon t1, …, tT. Importantly, a valid sequence of control gains u = u(t) is defined as meeting the constraints imposed by the prespecified trajectories. The underlying control strategy is open loop. Obviously, any small disturbance or change in dynamics will cause the controller to fail drive the system to the desired state since control is open loop and therefore the controller is “blind” in any state changes. We draw the analogy to inverse modeling (see Section III) where an inverse Newtonian analysis is used to find the muscle forces or joint torques that are compatible with the measured kinematics and kinetics. Inaccuracies, simplifications, and assumptions in the analysis invariably produces solutions that, when “played forward,” do not produce stable behavior when the solutions are used to drive forward simulations. Thus, most of the work in control of neuromuscular systems to date has two dominant shortcomings:
Control problems are formulated as tracking problems and need a prespecified trajectory in state space. This approach can be very problematic for high-dimensional systems where part of the state is hidden or only obtained by approximation. For example, if the model includes muscle activation-contract dynamics, then muscle activation becomes part of the state vector. Usually, EMG is used to estimate muscle activation, but it is a poor predictor of the actual activation state of the muscle (for a brief discussion of limitations of EMG and references to follow, see [182]). Therefore, even though the part of the state vector obtained from measured limb kinematics and kinetics is well defined, the part of the state vector related to muscle activation is effectively hidden and must be approximated.
Control policies are open loop u = u(t) and apply only to the time histories used to calculate them. Therefore, if used to drive a forward simulation, they are independent of the new time history of the state. In these conditions, the stability of the neuromuscular system is not guaranteed, even for small disturbances, inaccuracies or noise in the dynamics.
The remainder of this section is motivated by the need to overcome these two shortcomings. We attempt to provide an overview of techniques that have the potential to lead to controls frameworks for high-dimensional nonlinear dynamical systems with hidden states that produces stable closed-loop feedback control laws.
A. Optimal Control
In the optimal control framework as described by [124], [183], and [184], the goal is to control a dynamical system while optimizing an objective function. In optimal control theory, the controller has direct or indirect access to the state variables x (often estimated from sensors and/or predictions) and output variables y to be able to both implement a control law and quantify the performance of the system (3). The objective function is an equation that quantifies how well a specified task is achieved. In mathematical terms, a general optimal control problem can be formulated as
| (4) |
subject to
| (5) |
| (6) |
where x ∈ ℜn×1 is the state of system (e.g., joint angles, velocities, muscle activations), and u ∈ ℜm×1 are the control signals (e.g., torques, muscle forces, neural commands). The quantity y ∈ ℜp×1 corresponds to observations or outputs that are functions of the state. The stochastic variables w ∈ ℜn×1 and ω ∈ ℜp×1 correspond to process and observation noise. For neuromuscular systems, the process noise can be signal-dependent while the proprioceptive sensory noise plays the role of observation noise. The cost to minimize J(x, u) consists of three terms. The quantity ϕ(xtN) is the terminal cost that is state-dependent (e.g., how well a target was reached); the term q(x) is the state-dependent cost accumulated over the time horizon tN – t0 (e.g., were large velocities needed to perform the task?), and uT Ru is the control-dependent cost accumulated over the time horizon (e.g., how much control effort was used to achieve the task). The control cost does not have to be quadratic, however, quadratic is used mosly for computational convenience. The term J(x, u) is the standard variable used for the cost function and V(x) is the scalar value representing the minimal value of the cost function, indicating that the task was performed (locally or globally) optimally as per this formulation of the problem and choice of cost function.
For the case of deterministic linear systems F(x, u, w) = Ax + Bu, with quadratic state cost functions and q(x) = xTQx, and full state observation y = H(x, u, v), the solution to the optimal control problem can be found analytically and is one of the more significant achievements of engineering theory in the 20th century. The solution provides controls of the form u = −Kx with feedback gains K ∈ ℜm×n which guarantee stability of the system while minimizing the objective function J(x, u). This is called the Linear Quadratic Regulator (LQR) method and it is one of the most well-known and explored control frameworks in control theory. Some examples of using this approach in neuromuscular modeling are [185]–[187].
Under certain conditions, optimal control can be applied to stochastic linear and nonlinear dynamical systems with noise that can be either state- or control-dependent. For linear stochastic systems F(x, u, w) = Ax + Bu + Γw, under the presence of observation noise y = Hx + v, optimal stochastic filtering is required (Fig. 2). Kalman filtering (KF) is a stochastic algorithm to estimate states of dynamical systems under the presence of process and observation noise. For linear systems with Gaussian process and observation noise, KF is the optimal estimator since it the minimum variance unbiased estimator (MVUE) [188]. The intuition behind KF is that, if x̂tk is the current estimate of the state, KF provides the Kalman gains L that under the update law guarantee to reduce the variance E{(x(t) − x̂(t)) (x(t) − x̂(t))T} = E{e(t)e(t)T}, where the term e(t) is the estimation error defined as e(t) = x(t) − x̂(t).
The full treatment of optimal control and estimation is the so-called Linear Quadratic Guassian Regulator (LQG) control scheme. The equations for the LQG are summarized below
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
Since the very first applications of optimal control, it has been known that the stability of the estimation and control problem affect the stability of the LQG controller. To see the connection between stability of estimation and control, and the overall stability we need to combine both problems under one mathematical formulation. It can been shown that [124], [184]
| (12) |
or
| (13) |
where the matrices F and G are appropriately defined.
The stability of the LQG controller depends on the eigenvalues of the state transition matrix F. Since F is lower triangular, its eigenvalues are given by the eigenvalues of A − BK and A − LH. In addition, the control gain K stabilizes the matrix A − BK while the Kalman gain L stabilizes the matrix A − LH. Therefore, the overall LQG controller is stable if and only if the state and estimation dynamics are stable.
Another important characteristic of LQG for linear systems is the separation principle. The separation principle states that the optimal control and estimation problems are separated and, therefore, the control gains are independent of the Kalman gains. Finding the control gains requires using the backward control Riccati equation, which does not depend on Kalman gain L, nor on the mean and covariance of the process and observation noise. Similarly, computation of the Kaman gain requires the use of the forward estimation Riccati equation, which is not a function of the control gain K nor of the weight matrices Q, R in the objective function J(x, u).
Importantly, when multiplicative noise with respect to the control signals is considered, the separation principle breaks down and the control gains are a function of the estimation gains (Kalman gains). The stochastic optimal controller for a dynamical system with control-dependent noise will only be active in those dimensions of the state relevant to the task. If the controller were active in all dimensions, it would necessarily be suboptimal because control actions add more noise in the dynamics.
The use of stochastic optimal control theory as a conceptual tool towards understanding neuromuscular behavior was proposed in, for example, [189]–[191]. In that work, a stochastic optimal control framework for systems with linear dynamics and control-dependent noise was used to understand the variability profiles of reaching movements. The influential work by [191] established the minimal intervention principle in the context of optimal control. The minimal intervention principle was developed based on the characteristics of stochastic optimal controllers for systems with multiplicative noise in the control signals.
The LQR and LQG optimal control methods have been mostly tested on linear dynamical systems for modeling sensorimotor behavior; e.g, in reaching tasks, linear models were used to describe the kinematics of the hand trajectory [190], [192]. In neuromuscular modeling, however, linear models cannot capture the nonlinear behavior of muscles and multibody limbs. In [187], an Iterative Linear Quadratic Regulator (ILQR) was first introduced for the optimal control of nonlinear neuromuscular models. The proposed method is based on linearization of the dynamics. An interesting component of this work that played an influential role in the studies on optimal control methods for neuromuscular models was the fact that there was no need for a prespecified desired trajectory in state space. By contrast, most approaches for neuromuscular optimization that use classical control theory (see Section VI) require target time histories of limb kinematics, kinetics, and/or muscle activity. In [193], the ILQR method was extended for the case of nonlinear stochastic systems with state- and control-dependent noise. The proposed algorithm is the Iterative Linear Quadratic Gaussian Regulator (iLQG). This extension allows the use of stochastic nonlinear models for muscle force as a function of fiber length and fiber velocity. Fig. 6 illustrates the application of LQG to our arm model (Section II). Further theoretical developments in [194] and [195] allowed the use of an Extended Kalman Filter (EKF) for the case of sensory feedback noise. The EKF is an extension of the Kalman filter for nonlinear systems.
Fig. 6.
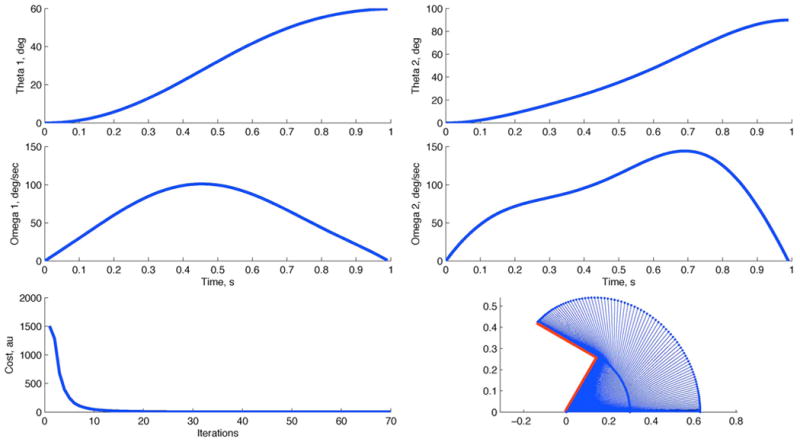
Simulation results for our two-link arm model using an optimal feedback controller. The task is to move the two-link arm from the initial configuration of (θ1, θ2) = (0, 0) to (θ1, θ2) = (60°, 90°) in the time horizon of 1 s and with 0 terminal velocity (ω1(T), ω2(T)) = (0, 0)). The lower left panel illustrates the reduction of the cost function for every iteration of the ILQG algorithm. The algorithm convergences quickly (after about 15 iterations), and yields smooth joint-space trajectories with close to bell-shaped velocity profiles.
1) Hierarchical Control
The hierarchical optimal control approach is motivated by the redundancy and the hierarchical structure of neuromuscular systems. The hierarchical optimal control framework is mentioned in, for example [196] and [197] for the case of a two link muscle driven arm with six muscles. In [198], the complete treatment of the control of a 7DOF arm with 14 muscles—two for each join—is presented.
In the hierarchical control framework, the dynamics of neuromuscular systems are distinguished into different levels. For the case of arm [197], the dynamics can be distinguished in two levels. The higher level dynamics includes the kinematics of end effector such as position p, velocity v, and force f. The low level dynamics consists of the join angles θ and θ̇ velocities and as well as the muscle activation α. The state space model of the high level dynamics can be represented as
| (14) |
| (15) |
| (16) |
where m is average hand mass, uH is the control in the higher level, and f is the force at the end effector. The parameters Hf (p, v, m) and Hv(p, v, m) are a function of position velocity and mass that correspond to some approximation error of the high level dynamics. A cost function relative to a task is imposed and the optimal control problem in the higher level can be defined as
| (17) |
subject to the equations of the kinematics of the end effector. The optimal control in higher dynamics will provide the required input force—control uH. The low level dynamics are defined by the forward dynamics of the arm and the muscle dynamics
| (18) |
| (19) |
| (20) |
The matrix I(θ) ∈ ℜn×n is the inertia, C(θ, θ̇) ∈ ℜn×1 is the vector centipentral and coriolis force, and G(θ) is the gravitational force. The term T(α, l(θ), l̇(θ, θ̇)) is the tension of the muscle that depends on the levels of activation a, the length l and the velocity l̇ of the corresponding muscle. The low level control is u. The low level dynamics are related to high level dynamics through the equations p = Φ(θ) and v = J(θ), where J(θ) is the Jacobian. The end effector forces are related to torques produces by the muscles and the gravity according to the equation J(θ)T f = τmuscles − G(θ). The analysis is simplified with zero gravity and therefore the end effector forces are specified by
| (21) |
Under the assumption that ȧ ≫ θ̇ differentiation of the end effector force leads to ḟ = J(θ)+ · M(θ) · Fvl(l(θ), l̇(θ, θ̇)) · ȧ. Since ḟ = −c(f − mg) + uH, it can be shown that uH = β2QuL, where Q is defined as Q = J(θ)+ · M(θ) · Fvl(l(θ), l̇(θ, θ̇)). The low level optimization is formulated as
| (22) |
Subject to 0 < uL < 1 and with H = β2QTQ + rI and b = −βQuH. The choice of cost function above is such that the control energy of the controller in lower dynamics is minimized.
The main idea in the hierarchical optimal control problem is to split the higher dimensional optimal control problem into smaller optimization problems. For the case of the arm movements, the higher optimization problem provides the control forces in end effector space. These end-effector forces play the role of the desired output for the low-level dynamics. The goal of the optimization for low level dynamics is to find the optimal muscle activation profiles that can deliver the desired end-effector. The optimal muscle activation is with respect to a minimum energy cost. Thus by starting from the higher level and solving smaller optimization problems that specify the desired output for the next lower level in the hierarchy, the hierarchical optimal control approach addresses the high dimensionality in neuromuscular structures. The dimensionality reduction and the computational efficiency that are achieved with hierarchical optimal control come with the cost of suboptimality.
A recent development in stochastic optimal control introduces a hierarchical control scheme applicable to a large family of problems [199], [200]. The low level is a collection of feedback controllers which are optimal for different instances of the task. The high-level controller then computes state-dependent activations of these primitive controllers, and in this way achieves optimal performance for new instances of the task. When the new tasks belong to a nonlinear manifold spanned by the primitive tasks, the hierarchical controller is exactly optimal; otherwise, it is an approximation. An appealing feature of this framework is that, once a controller is optimized for a specific instance of the task, it can be added to the collection of primitives and thereby extend the manifold of exactly solvable tasks.
2) Hybrid Control
In tasks that involve contact with surfaces such as locomotion, grasping, and object manipulation, the control problem becomes more difficult. From a control theoretic standpoint, the challenges are due to changes in the dynamics of the system when mechanical constraints are added or removed, for example, when transitioning between the swing and stance phases of gait, or during grasp acquisition. This change in plant dynamics requires switching control laws (hence the term “hybrid”). From the neuromuscular control point view, recent experimental findings about muscle coordination during finger tapping [201], [202] demonstrated a switch between mutually incompatible control strategies: from the control of finger motion before contact, to the control of well-directed isometric force after contact. These experimental findings motivated the work by [203] to extend the ILQR framework for modeling contact transition with the finger tip. For the motion phase of the tapping task, the objective of the optimal controller is to find the control law that minimizes the function
| (23) |
where ϕ(xtN) = (xtN − x*)T QN(xtN − x*) and subject to dynamics
| (24) |
The state x contains the angles and velocities of the neuromuscular system. For the case of the index finger, the state x includes the kinematics of the metacarpoplalangeal (MCP), proximal interphalangeal (PIP), and distal interphalangeal (DIP) joins. Upon contact with the rigid surface, the optimal control problem is formulated as
| (25) |
where ϕ(xtN) = (xtN − x*)T QN(xtN − x*) and subject to the constrained dynamics
| (26) |
where f is the contact force between the finger tip and the constrain surface. The relation between the contact forces f and the Lagrange multipliers λ in the cost function is given by f = ∇Φ(p)λ, where p position vector of the finger tip that satisfies the constraint Φ(p) during contact. The formulation for hybrid iLQR is rather general and it can be applied to a variety of tasks that involve contact with surfaces and switching dynamics. It is also an elegant methodology since it provides the optimal control gains during motion as well as during contact. The main limitation of the method is that it requires an a priori known switching time between the two control laws—instead of making the switching time itself a parameter to optimize. It is an open question whether or not optimal control for nonlinear stochastic systems can incorporate the time of the switch as a variable to optimize. In addition, further theoretical developments are required for the hybrid optimal control of stochastic systems with state and control multiplicative noise.
3) Model Predictive Control
The common characteristic in all types of optimal control mentioned so far, is that the control and estimation gains are computed off-line. In the model predictive control framework, or Receding Horizon Control [204], the control gains are calculated in real time. The objective of the model predictive control framework is to find the control law that minimizes the cost function
| (27) |
subject to dynamics: ẋ = F(x, u) and to control and state constrains g(x, u) < 0. In a predictive control model, the control gains u1, u2, …, uT are computed for the time window T. The first control u1 is applied to the system and the optimization is executed again to compute the new control gains u2, u3, …, uT+1 starting now from time t2. At time t = t2, only the control ut2 is applied and the optimization procedure is executed again to find the gains u3, u4, …,uT+2.
The online computation of control laws in model predictive control is a very attractive feature especially for tasks where online decisions regarding the applied control law have to be made. For the tasks of object manipulation, for example, it is possible that online neural processing takes place to regulate and adapt the applied forces. Another attractive feature of model predictive control is that it incorporates state and control constrains. The main assumption is that the process under control is slow enough such that the optimization scheme can compute the control laws on-line.
It remains an open question whether model predictive control is applicable to neuromuscular systems. Recent developments in [205] and [206] allow the application of model predictive control to linear stochastic systems with state and control multiplicative noise. Further theoretical developments for nonlinear stochastic systems with control- and state-dependent noise are required so that the nonlinear stochastic muscle dynamics can be considered.
B. Limitations of Optimal Control: A Step Towards Robust Control
In spite of the recent and upcoming advances in the application of optimal control theory to neuromuscular systems, additional tools are required. The main limitation of the optimal control framework is that it assumes almost perfect knowledge of the dynamics of the system (the state transition matrix). We use the qualifier “almost perfect” because the addition of stochastic terms in the state space dynamics can serve as a way to model unknown dynamics. However, the addition of randomness is an ad hoc and heuristic simple approach to modeling unknown dynamics, especially in cases where these unknown dynamics have a deterministic and highly nonlinear nature as is the case in neuromuscular systems. This limitation of optimal control motivated the birth and fast development of the general framework of robust control theory in the 1970s (see commentary below).
The influential work by Safonov and Athans [207] was the first to investigate the robustness of LQG controllers. In addition, a compact and solid proof on the limitations of optimal control and the lack of stability margins of LQG controllers is the 1978 paper by Doyle [208]. To understand the reasoning for the the lack of stability margins of LQG controllers for even single input single output systems (SISO) it helps to rewrite the formulation of the dynamical system as in (12). Namely, instead of defining the state vector as (x(t)T e(t)T)T, as in (12), we consider the state vector (x(t)T x̂(t)T)T, where x̂(t) is the estimated state. The overall dynamics can be written as follows:
| (28) |
or in more compact form
| (29) |
where the matrices Φ and Ψ are defined as
| (30) |
We can now follow the example in John Doyle 1978 for SISO system with state space dynamics
| (31) |
and observations
| (32) |
where w and v are the process and observation noise with zero mean and variance σw > 0 and σv = 1, respectively. The performance integral weights are R = 1 and
| (33) |
It can be shown that the control and the Kalman gains are given by the expressions
| (34) |
with and . The control gain K is scaled by a factor m and, therefore, the actual control gain is K̃ = mK. This scaling factor is motivated by the lack of perfect knowledge of the dynamics. For the case of perfect knowledge of the dynamics, the actual control gain K̃ equals the nominal control gain K (m = 1, nominal case). When unknown dynamics are present, the actual gain K̃ differs from the nominal gain K(m ≠ 1). Only the nominal control gain is known to the filter. The matrix Φ for the SISO system (31) is expressed as follows:
| (35) |
Given the closed-loop state transition matrix Φ, the necessary condition for stability is that d − f − 4 + 2(m − 1)df > 0 and 1 − (1 − m)df > 0. When these conditions hold, the eigenvalues of Φ have negative real parts and, therefore, the overall system (29) is stable. It is easy to see that for sufficient large d and f or (q and σ) small perturbations in m cause violation of the second stability condition.
Commentary 5
The limitations of optimal control vis-à-vis unknown dynamics are quite relevant to the study of sensorimotor systems. For example, in psychophysical studies testing whether optimal control (of the LQR variety) is used by subjects during motor learning of arm movements [209], the inaccuracies in the dynamics of the arm-world system are reasonably posited to be “learned” by the nervous system via repeated trials. While such learning can certainly take place in the neural system, the iterative learning of the unknown dynamics is done heuristically in the model and does not necessarily have a theoretical foundation within the mathematics of optimal control (see supplemental material of that work). Thus a current challenge is to model such neural learning within a controls framework that seamlessly and rigorously accommodate the “learning” of the unknown dynamics.
These shortcomings of optimal control are well known, and have been addressed to a certain extent. Robust control addresses the goal of stability and performance under the presence of disturbances and unknown dynamics. An introduction to robust control would require an extensive discussion on control concepts for frequency-based controller design and analysis of dynamical systems; as well as an introduction to theorems and lemmas critical to the development of robust control theory. Space limitations do not allow such an introduction here, but the reader is referred to [210] for a full treatment of robust control theory.
C. Adaptive Control
Adaptive control is a perspective different from optimal control and robust control used in cases where the unknown dynamics are due to the existence of unknown parameters of the plant. In an adaptive control scheme, a parameter estimator (or an adaptive law) is responsible for identifying the unknown parameters while the control law is derived as if the parameters were known.
The are two ways to combine the adaptive law and the control law. In the first approach, the unknown parameters of the plant are estimated online, and the control law is a function of these estimated parameter values. Thus the control law is modified whenever the estimates change. This is called indirect adaptive control.
In direct adaptive control, the plant model is parametrized according to the controller parameters. Therefore, even though the source of uncertainty comes from the plant, the question remains: what is the structure of the adaptive controller that can control the uncertain plant under consideration? The structure of the controller is parametrized and the learning/estimation process of that parametrization does not require any intermediate step of identifying the parameters of the plant. There have been a variety of applications of adaptive control in industry. The reader can refer to [211] for an introduction and full treatment of Adaptive Control schemes.
VII. Monte Carlo Approaches to Feasible Model Predictions and Hypothesis Testing
A. Background
As mentioned in Section I, neuromuscular models are computational implementations of hypotheses about the constitutive parts and the overall behavior of neuromuscular systems. Models for neuromuscular function typically contain multiple elements and their respective parameter values. As discussed in Section V, some of these model elements and their parameter values may be difficult to estimate or measure, describe from first principles, and may vary naturally in the population. Before accepting the result from a simulation, and therefore, the test of a hypothesis, one must explain to the satisfaction of the research community the differences that invariably emerge between model predictions and experimental data and intuition. These differences can be attributed to a variety of sources ranging from the validity of the scientific hypothesis being tested, to the choice of representation selected for each constitutive element, parameter variability/uncertainty, or even numerical implementation. The use of sensitivity analysis (quantifying the effect of parameter variability on prediction variability) and cross-validation (testing how well a model replicates data not used during its development) are well-established techniques in machine learning and in engineering that that should be the standard of practice in neuromuscular modeling.
More specifically, the conceptual framework of this section revolves around defining the feasible predictions of a computational model to compare and contrast across models and against experimental data. The motivation, formulation, use, and validation of a model invariably hinges on experimental data—and only when experimental data are robustly replicated by the model should the model be considered valid and reliable. However, neuromuscular models are often designed and used to produce individual predictions; and the sensitivity of their predictions to variability and uncertainty in model structure and parameters is not usually explored systematically. We consider exploring the range of feasible predictions by a model to be important for several reasons including:
The range of feasible predictions of a model should ideally mirror the distribution of experimental data. That is, predictions should be centered on the distribution of experimental data (when the data are normally distributed), or exhibit multimodal predictions (when the data are similarly multimodal).
Many of the debates in modeling arise from our inability to compare across models and modeling approaches. That is, “simple” versus “complex”; “forward” versus “inverse”; “generic” versus “patient specific” models could perhaps be reconciled if we found that their range of feasible predictions overlap.
Our community is one that is united by our methods but fragmented by our results. We all agree on the physics of the world and musculoskeletal system, and the computational principles to simulate them, but the consequences of our choices about modeling physiological and neural processes are hard to reconcile if we cannot compare their resulting ranges of feasible predictions.
There exist numerous tools and approaches enabling the computation and comparison of ranges of feasible predictions that, in our opinion, remain unnecessarily underutilized.
Monte Carlo approaches are a means to quantify the sensitivity of numerical simulations to parameter variability [212] that have been used in numerous fields. Some of the earlier uses included Monte Carlo evaluations of orthopedic parameters [56], [213]. More recently, these methods have also been used in neuromuscular and musculoskeletal modeling for evaluating models of the shoulder [214], thumb [51], [215], knee [216], [217], and populations of motor units [97]. A practical impediment to the utility of Monte Carlo methods is computational power, which until recently proved critical but is increasingly less so. Achieving convergence of Monte Carlo simulations of complex, high-dimensional models often requires a large number of model iterations—often in the tens of thousands at times. Being able to perform a large number of iterations in a reasonable time requires that individual model iterations be fast and/or exploit the fact that Monte Carlo methods are “memory-less” and lend themselves to parallel computing. In neuromuscular systems, each iteration may actually involve a full dynamical simulation of behavior as in [97], or the solution of an optimization problem as in [51]. Such problems are usually best done with well-optmized and efficiently compiled computer languages like C. Performing these simuations in interpreted computer languages or packages such as MATLAB (Mathworks, Natick, MA), MSMS, or SIMM may be difficult. This problem is partially addressed in MATLAB with the profile and MEX (MATLAB Executable) functions. The profile function makes it possible to identify computational bottlenecks in interpreted code that can compromise performance. The MEX functionality of MATLAB allows bottleneck operations to be coded in C and compiled for the processor in use, and then be run as ordinary MATLAB functions. This procedure can maintain most of the researcher's coding in an interpreted language or package, while not sacrificing the computational performance required for Monte Carlo simulations. The Monte Carlo method iteratively simulates the model with stochastic variations in the model parameters within physiologically or anatomically tenable ranges (Fig. 7).2 This approached is aimed at answering the question: Is it possible that, given the chosen structure of my model, it can replicate the observed data using parameter values within reasonable ranges? For example, the ratio of upper to lower arm lengths or relative strength across muscles in Fig. 1 can and does vary across individuals. We and others have done such studies in the context of biomechanical structure and function [49], [51], [214], [218]. These approaches require experimental work with enough subjects, or strong intuition about the problem, to set the range of values of those parameters and the statistical distribution within that range. That is, build a parametric (e.g., Gaussian, Gamma distributions) or nonparametric descriptions (e.g., histogram) representation of the data. Thankfully, Monte Carlo methods work even if the details of those distributions are non known and must be assumed. In those cases, it is much preferable to assume a uniform distribution than to assume a Gaussian distribution [212]. Assuming Gaussian distributions is an overused and often incorrect practice because they have tails to infinity, which musculoskeletal parameters clearly do not, and truncating a Gaussian distribution to make it physiologically realistic is not valid because proper statistical sampling has to be done from a distribution with unit area. If the distribution of the parameter values is known to be close to Gaussian, then a symmetric Beta distribution can be used because it has fixed boundaries. Also, there are instances where parameters distributions are multimodal [51]. After identifying a model output of interest (e.g., force magnitude, limb kinematics, tendon excursion, etc.), the computer model is coded to iterate over numerous runs to simulate that output.
Fig. 7.
Monte Carlo approach to model evaluation and hypothesis testing. An experiment is performed that produces some data, from which a test statistic is calculated. A computer model is coded that generates an output comparable to the statistics of the experimental data (or target test statistic). All parameters are varied stochastically within their feasible range, and a distribution of possible test statistics are generated for that model. One can then determine whether there exist sets of parameter values for the model that can replicate the distribution of the experimental data. If possible predictions of the model cannot replicate the experimental data, the hypothesis encoded in the model is likely untrue and a new hypothesis needs to be developed and encoded. In addition, by investigating the sensitivity of model predictions to specific subsets of parameters, the components of the model of particular importance can be identified.
How many iterations are enough? Monte Carlo models need to be run to “convergence,” which is usually defined as the number of iterations after which the mean and standard deviation of the emerging distribution of the output ceases to change by a given small percentage. See [49], [51] for examples.
Upon convergence, the details of the distribution of the test statistic (i.e., mean, mode, dispersion, ranges, etc.) define the set of feasible output predictions as per the specific design and implementation of the model. This is also the set of feasible outcomes of the hypothesis implemented by the model. If the experimental data fall within this feasible range of predictions by the model, then it is possible that the underlying hypothesis is correct. If the measured values of the test statistic do not overlap with the feasible set of model predictions, then it is not possible to accept the hypothesis as posed and implemented in the model [51], [97], [218]. We say that is only “possible” because one must scrutinize the set of parameter values that produce realistic outputs before reaching any conclusions because of Monte Carlo methods assemble parameters values at random. This can be unrealistic at least in some cases where, for example, the upper arm is selected to be longer than the lower arm. One can, and should, introduce any known covariance among parameters to both reduce the number of truly independent parameters and enforce realistic relationships among parameters.
To be fair, most modelers certainly perform “sanity checks” and parameter sensitivity analyses on their models, which may or may not be reported in the final manuscript. The concept of safety margins and sanity checks is ingrained in engineering practice. However, the full description of the feasible set of model predictions is not often reported, which leaves the reader wondering about the robustness of the hypothesis being tested.
The greatest risk when using the Monte Carlo approach is that the parameter space is incompletely sampled, causing the distribution of model-generated test statistics to not represent the complete set of possible model outputs. For large numbers of parameters (i.e., >15) Monte Carlo methods, like supervised learning methods, fall prey to the curse of dimensionality (Section V-A2). There are multiple approaches to mitigate this obstacle. When the experiment can be modeled as a set of linear inequalities of the form Ax ≤ b, where A is a given matrix, b is a given vector, and x is the vector to be solved for, the complete set of possible solutions can be calculated by tools in computational geometry (cdd software package [156]). This “vertex enumeration” approach is the dual of the simplex method [219] and was used to calculate the complete set of muscle activation patterns for a given fingertip force [44]. If the model cannot be described as linear inequalities, then the number of samples in parameter space is increased gradually, and a criteria for the convergence of the model-generated test statistic distribution is applied [97]. In addition, if the model has a rigorous analytical representation, it may be possible to “map” statistical distributions through those equations—but if that is possible one would likely not be recurring to numerical methods in the first place. Alternatively, the state-of-the-art computational approach is to use the Monte Carlo Markov Chains [218], [220], [221], which starts random walks (each of which is called a “chain”) from different locations in the search space. If multiple chains converge to a location in the search space, one has at least some evidence to assume that the searching the entire parameter space will produce the same results and the statistics of the converged region are a reasonable representation of the dispersion of the performance of the system. To see two examples of the use of the Monte Carlo Markov Chain method, and the reader is referred to [218] and the supplemental material of [222] for details and uses of the Markov Chain approach applied to neuromuscular models.
B. Example 1: Biomechanical Model Analysis
Hughes and An performed a Monte Carlo analysis on a planar shoulder model to examine the effects of varying muscle moment arms on predictions of the muscle forces required to maintain posture [214]. The authors calculated both the average moment arms, as well as the moment arm covariance matrix, across a sample of 22 cadaver specimens. The second-order statistics (mean and standard deviation) of the moment arm data were used to generate distributions of moment arms for all six muscles examined: subscapularis, infraspinatus, supraspinatus, anterior deltoid, middle deltoid, and posterior deltoid. Sampling randomly from these distributions of moment arms, the authors predicted the necessary vector of muscle forces required to resist gravity and maintain a particular posture by minimizing the total squared muscle stress. This study found that muscle forces could vary considerably given the observed moment arm variability. This study highlights the utility of Monte Carlo methods for rigorously analyzing variability in experimentally driven biomechanical models. In Fig. 8, we perform a similar Monte Carlo analysis on the planar two-link arm shown in Fig. 1.
Fig. 8.
Example of Monte Carlo analysis of possible muscle activation patterns for the Planar Arm Example. 100 000 muscle force vectors that produced 50% maximal force in the forward direction were calculated, and then histograms were made of the valid solutions in each muscle for each of two postures. Notice that in both postures, some muscles are necessary (zero force is not a valid solution). Notice also that some muscles switch from being necessary in one posture to redundant (zero force is an allowed solution) in other postures (e.g., muscle 5). A similar example of this approach is presented in [182].
C. Example 2: Neuromuscular Model Analysis
A population-based approach to the study of muscle function was developed by Fuglevand and colleagues and is based on representing motor unit recruitment and rate coding [95]. The Fuglevand Model predicts isometric force and corresponding surface EMG given assumed excitatory drive and properties of the motor unit pool. These properties are encoded as coupled equations with multiple parameters, and include: the contractile properties of the motor units; threshold, gain, and saturation levels for motor unit firing; motor unit conduction velocity; muscle geometry including cross-sectional area, number of fibers, innervation number, and fiber length; electrical conductivities of bone, muscle, subcutaneous tissue, and skin; etc. This model of muscle has been used to both evaluate experimental methods [223]–[225] and to corroborate scientific hypotheses of muscle function [226]–[229]. Other models of muscle have also been used in these kind of studies [230]. However, sensitivity analyses in these studies are typically limited to variations in single parameters, with the other parameters held constant. Keenan and Valero-Cuevas used a Monte Carlo approach to test whether sets of parameter values exist such that the Fuglevand Model can replicate the fundamental and well-established experimental relationships between force and force variability, and between force and electromyograms [97]. The numerical values for each of nine muscle and neural parameters were drawn at random from uniform distributions covering physiological ranges. Each forward dynamical simulation generated two relations: one between average force and force variability, and the other between force and EMG (Fig. 9). The outputs of the model were the slopes of those two relationships. The authors found that very few parameter sets could produce test statistics approaching the experimental values; typically, parameter sets that produced EMG-force relations similar to those observed experimentally would also produce unrealistic relations between average force and force variability (Fig. 9). Using the Monte Carlo approach allowed a thorough exploration of this parameter space, and the identification of the key combination of parameters to which the model is most sensitive. More importantly, that study suggests the Fuglevand Model is able to approximate realistic muscle function (as per the two slopes) only when parameters are chosen with extreme caution, especially neural properties. Therefore, the most productive research direction to refine our working hypotheses about populations of motor units is to improve our understanding of the neural properties for the recruitment and activation of populations of motor units.
Fig. 9.
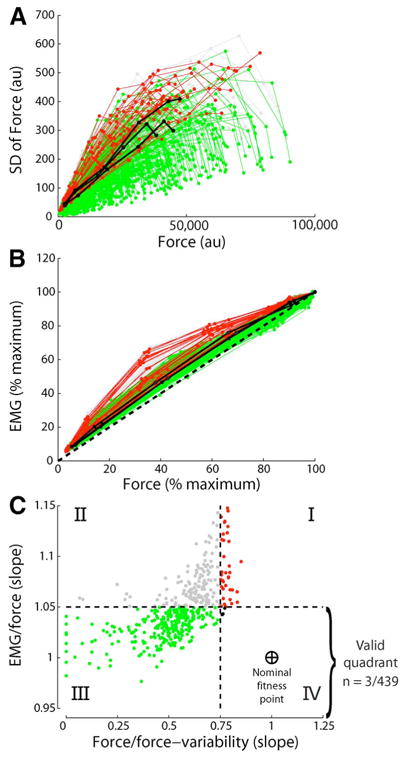
Monte Carlo analysis of the Fuglevand Model. (A) Each line shows the force/force-variability relation generated by different parameter sets. (B) Each line shows the EMG/force relation generated by the same parameter sets shown in (A). (C) Relations found in (A) and (B) are evaluated by test statistics that are regression slopes [log-log in the case of (A)]. Good fits to experimental data are force/force-variability slopes of greater than 0.75 and EMG/force slopes of less than 1.05; thus, very few parameter sets are able to reproduce experimental data. Adapted from [97].
D. Example 3: Hypothesis Testing in Neural Control of Motor Systems
In other cases, a researcher may want to use one model representing a null hypothesis and another for an alternative hypothesis, to determine if available data provide sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis. The Monte Carlo framework described above is also well-suited to this application. The approach is simple: generate test statistic distributions for the desired output using both models, and determine if one is implausible while the other is compatible with experimental data. An example of this approach is provided by Kutch et al., who used Monte Carlo simulation to determine if multidirectional force variability measurements from the human index finger provided enough evidence to reject a hypothesis of flexible muscle activation in favor of a hypothesis of synergistic activation [231]. Models were coded for both hypotheses, which included a number of unknown parameters including how muscles were grouped into synergies, how average muscle force translated into muscle force variability, and how muscle-level signal-dependent noise was correlated. A test statistic was chosen, and called “target-directedness,” that represented the shape of the endpoint force covariance ellipse in specific directions of force exerted by the index finger. Target-directedness was simulated to convergence for both models for randomly chosen parameters. It was found that parameter sets could be found for the flexible activation hypothesis that could replicate the data, but in general, no parameter sets could be found for the synergistic activation hypothesis that replicate the data (Fig. 10). The synergistic hypothesis could only replicate the data if synergy-level noise was made unrealistically strong, which would in turn induce unrealistic levels of correlation between muscle forces. This analysis provided rigorous evidence that the flexible activation hypothesis should not be rejected in favor of the synergistic activation hypothesis. Recent work at the level of electromyograms during fingertip force production also fails to support the synergistic activation hypothesis for finger musculature [222].
Fig. 10.
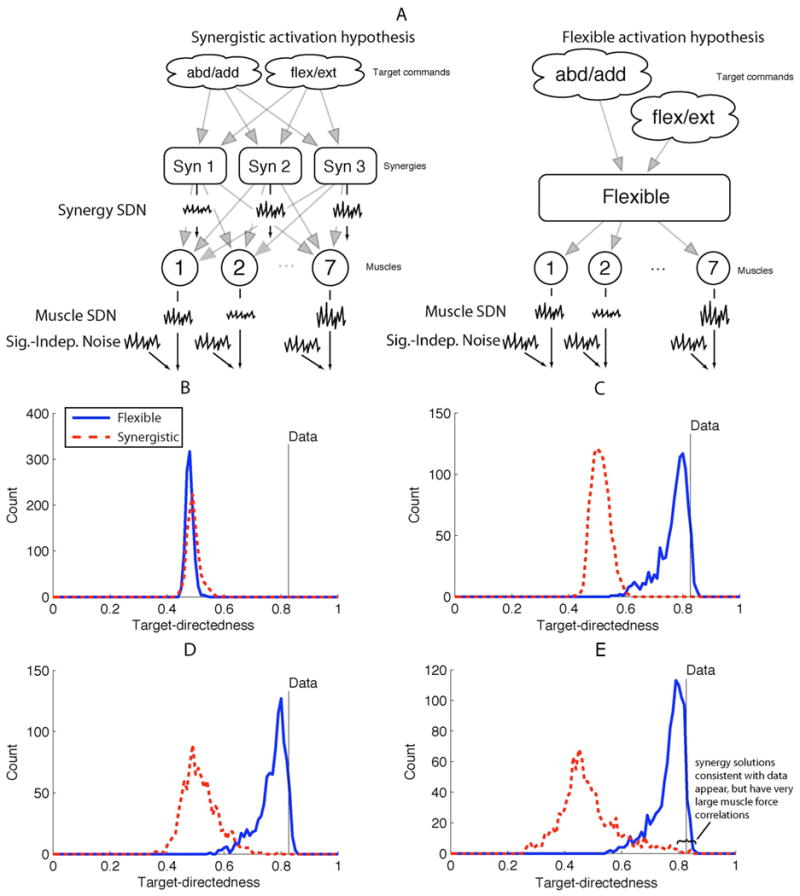
Example of Monte Carlo hypothesis testing. (A) Illustration of two hypotheses and sources of noise. (B)–(D) Monte Carlo distributions of test statistics (target-directedness) generated by the two models, as compared with the experimentally observed value. The synergistic hypothesis can only replicate the data under specific conditions, and induces muscle force correlations that are unrealistic. Adapted from [231]. (A) Hypotheses and noise sources. (B) Both hypotheses have Sig-Indep. Noise only. (C) Both hypotheses have Muscle SDN only. (D) Flexible hypothesis has only Muscle SD, synergistic hypothesis has Muscle SDN and Synergy SDN equally. (E) Flexible hypothesis has only Muscle SDN, synergistic hypothesis has Synergy SDN ten times Muscle SDN.
Acknowledgments
The authors gratefully acknowledge the useful comments by Dr. S. Salinas-Blemker, Dr. R. Neptune, Dr. G. Loeb, Dr. R. Lieber, Dr. B. J. Fregly, Dr. D. Thelen, Dr. W. Herzog, Dr. E. Todorov, G. Tsianos, and C. Rustin.
This material is based upon work supported by NSF Grant 0836042, NIDRR Grant 84-133E2008-8, and NIH Grant AR050520 and Grant AR052345 to F. J. Valero-Cuevas. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS), NIH, NSF, or NIDRR.
Biographies

Francisco J. Valero-Cuevas (M'01) received the B.S. degree in engineering from Swarthmore College (1988), and the M.S. and Ph.D. degrees in mechanical engineering from Queen's University, Kingston, Ontario, Canada (1991) and Stanford University (1997), respectively.
He is currently Associate Professor at the Department of Biomedical Engineering, and Division of Biokinesiology and Physical Therapy, University of Southern California, Los Angeles. His research interests focus on combining engineering, computational methods, robotics, applied mathematics and neuroscience to understand organismal and robotic systems for basic science, engineering, and clinical applications.
Prof. Valero-Cuevas is member of the ASME, IEEE Engineering in Medicine and Biology Society, the American and International Societies of Biomechanics, the American Society of Mechanical Engineers, the Society for Neuroscience, and the Society for the Neural Control of Movement. He has received a Research Fellowships from the Alexander von Humboldt Foundation (2005), the Post-Doctoral Young Scientist Award from the American Society of Biomechanics (2003), the Faculty Early Career Development Program CAREER Award from the National Science Foundation (2003), the Innovation Prize from the State of Tyrol in Austria (1999), a Fellowship from the Thomas J. Watson Foundation (1988), and was elected Associate Member of the Scientific Research Society Sigma-Xi (1988). He served as Associate Editor for the IEEE Transactions on Biomedical Engineering from 2003 to 2008, and as a regular member of the Motor Function, Speech and Rehabilitation Study Section of the National Institutes of Health from 2004 to 2009.

Heiko Hoffmann received the M.Sc. (Diploma) degree in physics from the University of Heidelberg, Germany, in 2000, and the Ph.D. degree in computer science from the University of Bielefeld, Germany, in 2004 for his work at the Max Planck Institute for Human Cognitive and Brain Sciences in Munich.
He worked as Postdoctoral Research Associate in the School of Informatics at the University of Edinburgh, U.K., and in Computer Science and Neuroscience at the University of Southern California (USC), Los Angeles. Currently, he is a Postdoctoral Research Associate in Biomedical Engineering at USC. His research interests focus on understanding the neural control of human movement and applying the resulting insights for robotic control.
Dr. Hoffmann is a member of the Society for Neuroscience and the Society for the Neural Control of Movement.

Manish U. Kurse received the B.Tech. degree in mechanical engineering from the Indian Institute of Technology Madras, India, in 2006, and the M.S. degree in biomedical engineering from the University of Southern California, Los Angeles, in 2008. Currently, he is working toward the Ph.D. degree in biomedical engineering at the University of Southern California.
He is a graduate research assistant in the Brain-Body Dynamics Laboratory, University of Southern California, headed by Dr. F. J. Valero-Cuevas. His research interests include using principles of mechanics and computational modeling in understanding complex biological systems. He is a member of the American Society of Mechanical Engineers and the American Society of Biomechanics.

Jason J. Kutch received the B.S.E. degree in mechanical engineering from Princeton University in 2001, and the Ph.D. degree in applied and interdisciplinary mathematics from the University of Michigan, Ann Arbor, in 2008.
He is currently a Postdoctoral Research Associate in Biomedical Engineering at the University of Southern California, Los Angeles. His research interests include applied mathematics and neurophysiology, with an aim of understanding motor unit and multimuscle coordination.
Dr. Kutch is a member of the Society for Neuroscience and the Society for the Neural Control of Movement.

Evangelos A. Theodorou received the Diploma (M.Sc. equivalent) in electrical and computer engineering form the Technical University of Crete, Greece, in 2001. In 2003, he received the M.Sc. degree in production engineering and management from the Technical University of Crete, and in 2007 he received the M.Sc. degree in computer science and engineering from the University of Minnesota. Currently he is working toward the Ph.D. degree in the Computer Science Department at the Viterbi School of Engineering, University of Southern California (USC), Los Angeles.
He holds research assistant positions in the Brain-Body Dynamics Laboratory, Department of Biomedical Engineering and in the Computational Learning and Motor Control Laboratory, Department of Computer Science, at USC. His current research interests span over the areas of control theory, estimation, and machine learning with a focus on stochastic optimal control, robust control, stochastic estimation and reinforcement learning, and applications to robotics, biomechanics, and systems neuroscience.
Mr. Theodorou is a recipient of a Myronis Fellowship for engineering graduate students at USC.
Footnotes
A convex set contains all line segments between each pair of points in the set. For example, a union of disjoint regions is nonconvex.
The name Monte Carlo is no accident: it was inspired by the analogy where a gambler repeatedly plays a game of chance to evaluate their own “fitness” to win money.
Contributor Information
Francisco J. Valero-Cuevas, Email: valero@usc.edu.
Heiko Hoffmann, Email: heiko@clmc.usc.edu.
Manish U. Kurse, Email: kurse@usc.edu.
Jason J. Kutch, Email: kutch@usc.edu.
Evangelos A. Theodorou, Email: etheodor@usc.edu.
References
- 1.Neptune RR. Computer modeling and simulation of human movement. Applications in sport and rehabilitation. Phys Med Rehabil Clinics North America. 2000;11(no. 2):417. [PubMed] [Google Scholar]
- 2.McLean SG, Su A, Van Den Bogert AJ. Development and validation of a 3-D model to predict knee joint loading during dynamic movement. J Biomech Eng. 2003;125:864. doi: 10.1115/1.1634282. [DOI] [PubMed] [Google Scholar]
- 3.Fregly BJ. Computational assessment of combinations of gait modifications for knee osteoarthritis rehabilitation. IEEE Trans Biomed Eng. 2008 Aug;55(no. 8):2104–2106. doi: 10.1109/TBME.2008.921171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Herrmann AM, Delp SL. Moment arm and force-generating capacity of the extensor carpi ulnaris after transfer to the extensor carpi radialis brevis. J Hand Surgery. 1999;24(no. 5):1083–1090. doi: 10.1053/jhsu.1999.1083. [DOI] [PubMed] [Google Scholar]
- 5.Magermans DJ, Chadwick EKJ, Veeger HEJ, Rozing PM, van der Helm FCT. Effectiveness of tendon transfers for massive rotator cuff tears: A simulation study. Clin Biomech. 2004;19(no. 2):116–122. doi: 10.1016/j.clinbiomech.2003.09.008. [DOI] [PubMed] [Google Scholar]
- 6.Valero-Cuevas FJ, Hentz VR. Releasing the A3 pulley and leaving flexor superficialis intact increases pinch force following the Zancolli lasso procedures to prevent claw deformity in the intrinsic palsied finger. J Orthop Res. 2002 Sep;20:902–909. doi: 10.1016/S0736-0266(02)00040-2. [DOI] [PubMed] [Google Scholar]
- 7.Piazza SJ, Delp SL. Three-dimensional dynamic simulation of total knee replacement motion during a step-up task. J Biomech Eng. 2001;123:599. doi: 10.1115/1.1406950. [DOI] [PubMed] [Google Scholar]
- 8.Kuo AD. Energetics of actively powered locomotion using the simplest walking model. J Biomech Eng. 2002;124:113. doi: 10.1115/1.1427703. [DOI] [PubMed] [Google Scholar]
- 9.Hull ML, Jorge M. A method for biomechanical analysis of bicycle pedaling. J Biomech. 1985;18(no. 9):631–644. doi: 10.1016/0021-9290(85)90019-3. [DOI] [PubMed] [Google Scholar]
- 10.Huiskes R, Chao EY. A survey of finite element analysis in orthopedic biomechanics: The first decade. J Biomech. 1983;16(no. 6):385. doi: 10.1016/0021-9290(83)90072-6. [DOI] [PubMed] [Google Scholar]
- 11.Schutte LM, Rodgers MM, Zajac FE, Glaser RM, Center VAM, Alto P. Improving the efficacy of electrical stimulation-induced leg cycle ergometry: An analysis based on a dynamic musculoskeletal model. IEEE Trans Rehabil Eng. 1993 Jun;1(no. 2):109–125. [Google Scholar]
- 12.Davoodi R, Brown IE, Loeb GE. Advanced modeling environment for developing and testing fes control systems. Med Eng Phys. 2003;25(no. 1):3–9. doi: 10.1016/s1350-4533(02)00039-5. [DOI] [PubMed] [Google Scholar]
- 13.Davoodi R, Loeb GE. A biomimetic strategy for control of fes reaching. Proc. 25th Annu. Int. Conf. IEEE Engineering in Medicine and Biology Society, 2003; 2003. [Google Scholar]
- 14.Garcia M, Chatterjee A, Ruina A, Coleman M. The simplest walking model: Stability, complexity, and scaling. ASME J Biomech Eng. 1998;120:281–288. doi: 10.1115/1.2798313. [DOI] [PubMed] [Google Scholar]
- 15.Van der Helm FCT. A finite element musculoskeletal model of the shoulder mechanism. J Biomech. 1994;27(no. 5):551–559. doi: 10.1016/0021-9290(94)90065-5. [DOI] [PubMed] [Google Scholar]
- 16.Pandy MG. Computer modeling and simulation of human movement. Annu Rev Biomed Eng. 2001;3(no. 1):245–273. doi: 10.1146/annurev.bioeng.3.1.245. [DOI] [PubMed] [Google Scholar]
- 17.Zajac FE. Understanding muscle coordination of the human leg with dynamical simulations. J Biomech. 2002;35(no. 8):1011–1018. doi: 10.1016/s0021-9290(02)00046-5. [DOI] [PubMed] [Google Scholar]
- 18.Zajac FE, Neptune RR, Kautz SA. Biomechanics and muscle coordination of human walking part i: Introduction to concepts, power transfer, dynamics and simulations. Gait and Posture. 2002;16(no. 3):215–232. doi: 10.1016/s0966-6362(02)00068-1. [DOI] [PubMed] [Google Scholar]
- 19.Buchanan TS, Lloyd DG, Manal K, Besier TF. Neuromusculoskeletal modeling: Estimation of muscle forces and joint moments and movements from measurements of neural command. J Appl Biomech. 2004;20(no. 4):367–395. doi: 10.1123/jab.20.4.367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hatze H. Towards a comprehensive large-scale computer model of the human neuromusculoskeletal system. Theoretical Issues in Ergonomics Sci. 2005;6(no. 3):239–250. [Google Scholar]
- 21.Thelen DG, Anderson FC, Delp SL. Generating dynamic simulations of movement using computed muscle control. J Biomech. 2003;36(no. 3):321–328. doi: 10.1016/s0021-9290(02)00432-3. [DOI] [PubMed] [Google Scholar]
- 22.Piazza SJ. Muscle-driven forward dynamic simulations for the study of normal and pathological gait. J NeuroEng Rehabil. 2006;3(no. 1):5. doi: 10.1186/1743-0003-3-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fernandez JW, Pandy MG. Integrating modelling and experiments to assess dynamic musculoskeletal function in humans. Experimental Physiol. 2006;91(no. 2):371–382. doi: 10.1113/expphysiol.2005.031047. [DOI] [PubMed] [Google Scholar]
- 24.Winter DA. Biomechanics and Motor Control of Human Movement. Hoboken, NJ: Wiley-Interscience; 1990. [Google Scholar]
- 25.Winters JM. Biomech Neural Control Posture and Movement. 2000. Terminology and foundations of movement science; p. 3. [Google Scholar]
- 26.Yamaguchi GT. Dynamic Modeling of Musculoskeletal Motion: A Vectorized Approach for Biomechanical Analysis in Three Dimensions. New York: Springer Verlag; 2005. [Google Scholar]
- 27.Delp SL, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Comput Bio Med. 1995 Jan;25(no. 1):21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
- 28.Davoodi R, Urata C, Hauschild M, Khachani M, Loeb GE. Model-based development of neural prostheses for movement. IEEE Trans Biomed Eng. 2007 Nov;54(no. 11):1909–1918. doi: 10.1109/TBME.2007.902252. [DOI] [PubMed] [Google Scholar]
- 29.Damsgaard M, Rasmussen J, Christensen S, Surma E, de Zee M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simulation Modelling Practice and Theory. 2006;14(no. 8):1100–1111. [Google Scholar]
- 30.Anderson AE, Ellis BJ, Weiss JA. Verification, validation and sensitivity studies in computational biomechanics. Comput Methods Biomech Biomed Eng. 2007;10(no. 3):171–184. doi: 10.1080/10255840601160484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Neptune RR, Kautz SA, Zajac FE. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. J Biomech. 2001;34(no. 11):1387–1398. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
- 32.Neptune RR, Zajac FE, Kautz SA. Muscle mechanical work requirements during normal walking: The energetic cost of raising the body's center-of-mass is significant. J Biomech. 2004;37(no. 6):817–825. doi: 10.1016/j.jbiomech.2003.11.001. [DOI] [PubMed] [Google Scholar]
- 33.Kuo AD, Maxwell Donelan J. Comment on contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking (neptune, 2001) and muscle mechanical work requirements during normal walking: The energetic cost of raising the body's center-of-mass is significant (neptune, 2004) J Biomech. 2009 Aug;42(no. 11):1783–5. doi: 10.1016/j.jbiomech.2009.03.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Abend W, Bizzi E, Morasso P. Human arm trajectory formation. Brain. 1982;105(pt. 2):331–348. doi: 10.1093/brain/105.2.331. [DOI] [PubMed] [Google Scholar]
- 35.Mussa-Ivaldi FA, Hogan N, Bizzi E. Neural, mechanical, and geometric factors subserving arm posture in humans. J Neurosci. 1985;5(no. 10):2732–2743. doi: 10.1523/JNEUROSCI.05-10-02732.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci. 1994;14(no. 5):3208–3224. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dennerlein JT, Diao E, Mote CD, Rempel DM. Tensions of the flexor digitorum superficialis are higher than a current model predicts. J Biomech. 1998;31(no. 4):295–301. doi: 10.1016/s0021-9290(98)00006-2. [DOI] [PubMed] [Google Scholar]
- 38.Olney SJ, Griffin MP, Monga TN, McBride ID. Work and powe in gait of stroke patients. Archives Phys Med Rehabil. 1991;72(no. 5):309–314. [PubMed] [Google Scholar]
- 39.An KN, Chao EY, Cooney WP, Linscheid RL. Forces in the normal and abnormal hand. J Orthop Res. 1985;3(no. 2):202–211. doi: 10.1002/jor.1100030210. [DOI] [PubMed] [Google Scholar]
- 40.Harding DC, Brandt KD, Hillberry BM. Finger joint force minimization in pianists using optimization techniques. J Biomech. 1993 Dec;26(no. 12):1403–1412. doi: 10.1016/0021-9290(93)90091-r. [DOI] [PubMed] [Google Scholar]
- 41.Valero-Cuevas FJ, Towles JD, Hentz VR. Quantification of fingertip force reduction in the forefinger following simulated paralysis of extensor and intrinsic muscles. J Biomech. 2000 Dec;33:1601–1609. doi: 10.1016/s0021-9290(00)00131-7. [DOI] [PubMed] [Google Scholar]
- 42.Jinha A, Ait-Haddou R, Binding P, Herzog W. Antagonistic activity of one-joint muscles in three-dimensions using non-linear optimisation. Math Biosci. 2006;202(no. 1):57–70. doi: 10.1016/j.mbs.2006.03.018. [DOI] [PubMed] [Google Scholar]
- 43.Murray R, Li Z, Sastry S. A Mathematical Introduction to Robotic Manipulation. Boca Raton, FL: CRC Press; 1994. [Google Scholar]
- 44.Valero-Cuevas FJ, Zajac FE, Burgar CG. Large index-fingertip forces are produced by subject-independent patterns of muscle excitation. J Biomech. 1998 Aug;31:693–703. doi: 10.1016/s0021-9290(98)00082-7. [DOI] [PubMed] [Google Scholar]
- 45.Valero-Cuevas FJ. A mathematical approach to the mechanical capabilities of limbs and fingers. Adv Exp Med Biol. 2009;629:619–633. doi: 10.1007/978-0-387-77064-2_33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hollister A, Buford WL, Myers LM, Giurintano DJ, Novick A. The axes of rotation of the thumb carpometacarpal joint. J Orthopaedic Res. 1992;10(no. 3):454–460. doi: 10.1002/jor.1100100319. [DOI] [PubMed] [Google Scholar]
- 47.Inman VT. Observations on the function of the shoulder joint. J Bone Joint Surgery. 1944;26(no. 1):1. [Google Scholar]
- 48.Van Langelaan EJ. A kinematical analysis of the tarsal joints. An X-ray photogrammetric study. Acta orthopaedica Scandinavica Supplementum. 1983;204:1. [PubMed] [Google Scholar]
- 49.Santos VJ, Valero-Cuevas FJ. Reported anatomical variability naturally leads to multimodal distributions of Denavit–Hartenberg parameters for the human thumb. IEEE Trans Biomed Eng. 2006 Feb;53(no. 2):155–163. doi: 10.1109/TBME.2005.862537. [DOI] [PubMed] [Google Scholar]
- 50.Cerveri P, De Momi E, Marchente M, Lopomo N, Baud-Bovy G, Barros RML, Ferrigno G. In vivo validation of a realistic kinematic model for the trapezio-metacarpal joint using an optoelectronic system. Annals Biomed Eng. 2008;36(no. 7):1268–1280. doi: 10.1007/s10439-008-9499-7. [DOI] [PubMed] [Google Scholar]
- 51.Valero-Cuevas FJ, Johanson ME, Towles JD. Towards a realistic biomechanical model of the thumb: The choice of kinematic description may be more critical than the solution method or the variability/uncertainty of musculoskeletal parameters. J Biomech. 2003 Jul;36:1019–1030. doi: 10.1016/s0021-9290(03)00061-7. [DOI] [PubMed] [Google Scholar]
- 52.Yoon YS, Mansour JM. The passive elastic moment at the hip. J Biomech. 1982;15(no. 12):905. doi: 10.1016/0021-9290(82)90008-2. [DOI] [PubMed] [Google Scholar]
- 53.Hatze H. A three-dimensional multivariate model of passive human joint torques and articular boundaries. Clin Biomech. 1997;12(no. 2):128–135. doi: 10.1016/s0268-0033(96)00058-7. [DOI] [PubMed] [Google Scholar]
- 54.Esteki A, Mansour JM. An experimentally based nonlinear vis-coelastic model of joint passive moment. J Biomech. 1996;29(no. 4):443–450. doi: 10.1016/0021-9290(95)00081-x. [DOI] [PubMed] [Google Scholar]
- 55.Sancho-Bru JL, Perez-Gonzalez A, Vergara-Monedero M, Giurintano D. A 3-D dynamic model of human finger for studying free movements. J Biomech. 2001;34(no. 11):1491–1500. doi: 10.1016/s0021-9290(01)00106-3. [DOI] [PubMed] [Google Scholar]
- 56.Bartel DL, Bicknell VL, Wright TM. The effect of conformity, thickness, and material on stresses in ultra-high molecular weight components for total joint replacement. J Bone Joint Surg Amer. 1986;68(no. 7):1041–1051. [PubMed] [Google Scholar]
- 57.Rawlinson JJ, Bartel DL. Flat medial-lateral conformity in total knee replacements does not minimize contact stresses. J Biomech. 2002 Jan;35(no. 1):27–34. doi: 10.1016/s0021-9290(01)00172-5. [DOI] [PubMed] [Google Scholar]
- 58.Rawlinson JJ, Furman BD, Li S, Wright TM, Bartel DL. Retrieval, experimental, and computational assessment of the performance of total knee replacements. J Orthop Res. 2006 Jul;24(no. 7):1384–1394. doi: 10.1002/jor.20181. [Online]. Available: http://dx.doi.org/10.1002/jor.20181. [DOI] [PubMed]
- 59.Wismans J, Veldpaus F, Janssen J, Huson A, Struben P. A three-dimensional mathematical model of the knee-joint. J Biomech. 1980;13(no. 8):677. doi: 10.1016/0021-9290(80)90354-1. [DOI] [PubMed] [Google Scholar]
- 60.Blankevoort L, Kuiper JH, Huiskes R, Grootenboer HJ. Articular contact in a three-dimensional model of the knee. J Biomech. 1991;24(no. 11):1019. doi: 10.1016/0021-9290(91)90019-j. [DOI] [PubMed] [Google Scholar]
- 61.Pandy MG, Sasaki K, Kim S. A three-dimensional musculoskeletal model of the human knee joint. Part 1: Theoretical construction. Comput Methods Biomech Biomed Eng. 1997;1(no. 2):87–108. doi: 10.1080/01495739708936697. [DOI] [PubMed] [Google Scholar]
- 62.Pandy MG, Sasaki K. A three-dimensional musculoskeletal model of the human knee joint. Part 2: Analysis of ligament function. Comput Methods Biomech Biomed Eng. 1998;1(no. 4):265–283. doi: 10.1080/01495739808936707. [DOI] [PubMed] [Google Scholar]
- 63.Valero-Cuevas FJ, Small CF. Load dependence in carpal kinematics during wrist flexion in vivo. Clin Biomech (Bristol, Avon) 1997 Apr;12:154–159. doi: 10.1016/s0268-0033(96)00071-x. [DOI] [PubMed] [Google Scholar]
- 64.Delp SL, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Comput Biology and Medicine. 1995;25(no. 1):21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
- 65.Lin Y, Walter J, Banks S, Pandy M, Fregly B. Simultaneous prediction of muscle and contact forces in the knee during gait. J Biomech. doi: 10.1016/j.jbiomech.2009.10.048. submitted for publication. [DOI] [PubMed] [Google Scholar]
- 66.Bei Y, Fregly BJ. Multibody dynamic simulation of knee contact mechanics. Med Eng Physics. 2004;26(no. 9):777–789. doi: 10.1016/j.medengphy.2004.07.004. [Online]. Available: http://dx.doi.org/10.1002/jor.20548. [DOI] [PMC free article] [PubMed]
- 67.Fregly BJ, Banks SA, D'Lima DD, Colwell CW. Sensitivity of knee replacement contact calculations to kinematic measurement errors. J Orthop Res. 2008 Sep;26(no. 9):1173–1179. doi: 10.1002/jor.20548. [Online]. Available: http://dx.doi.org/10.1002/jor.20548. [DOI] [PubMed]
- 68.Lin YC, Haftka RT, Queipo NV, Fregly BJ. Two-dimensional surrogate contact modeling for computationally efficient dynamic simulation of total knee replacements. J Biomech Eng. 2009 Apr;131(no. 4):041010. doi: 10.1115/1.3005152. [Online]. Available: http://dx.doi.org/10.1115/1.3005152. [DOI] [PubMed]
- 69.Halloran JP, Erdemir A, van den Bogert AJ. Adaptive surrogate modeling for efficient coupling of musculoskeletal control and tissue deformation models. J Biomech Eng. 2009;131:011014. doi: 10.1115/1.3005333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Hodgins JK, Wooten WL, Brogan DC, O'Brien JF. Animating human athletics. Proc. 22nd Annu. Conf. Computer Graphics and Interactive Techniques; New York. 1995. pp. 71–78. [Google Scholar]
- 71.Miller AT, Allen PK. Graspit! a versatile simulator for robotic grasping. IEEE Robot Autom Mag. 2004;11(no. 4):110–122. [Google Scholar]
- 72.Miller A, Allen P, Santos V, Valero-Cuevas F. From robotic hands to human hands: A visualization and simulation engine for grasping research. Industrial Robot: Int J. 2005;32(no. 1):55–63. [Google Scholar]
- 73.Kaufman DM, Edmunds T, Pai DK. Fast frictional dynamics for rigid bodies. Int. Conf. Computer Graphics and Interactive Techniques; New York. 2005. pp. 946–956. [Google Scholar]
- 74.Lee SH, Sifakis E, Terzopoulos D. Comprehensive biomechanical modeling and simulation of the upper body. ACM Trans Graphics. 2009;28(no. 4):1–17. [Google Scholar]
- 75.Johnson E, Murphey TD. Scalable variational integrators for constrained mechanical systems in generalized coordinates. IEEE Trans Robotics. 2009 Dec;25(no. 6):1249–1261. [Google Scholar]
- 76.Johnson ER, Morris K, Murphey TD. A variational approach to strand-based modeling of the human hand. Algorithmic Foundations of Robotics VII. 2010 to be published. [Google Scholar]
- 77.Zajac FE. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng. 1989;17(no. 4):359–411. [PubMed] [Google Scholar]
- 78.Zajac FE. How musculotendon architecture and joint geometry affect the capacity of muscles to move and exert force on objects: A review with application to arm and forearm tendon transfer design. J Hand Surg Amer. 1992 Sep;17(no. 5):799–804. doi: 10.1016/0363-5023(92)90445-u. [DOI] [PubMed] [Google Scholar]
- 79.Garner BA, Pandy MG. The obstacle-set method for representing muscle paths in musculoskeletal models. Comput Methods Biomech Biomed Eng. 2000;3(no. 1):1–30. doi: 10.1080/10255840008915251. [DOI] [PubMed] [Google Scholar]
- 80.Shinjiro S, Andrew K, Dinesh KP. Musculotendon simulation for hand animation. ACM Trans Graph. 2008;27(no. 3):1–8. [Google Scholar]
- 81.Blemker SS, Delp SL. Three-dimensional representation of complex muscle architectures and geometries. Annals Biomed Eng. 2005;33(no. 5):661–673. doi: 10.1007/s10439-005-1433-7. [DOI] [PubMed] [Google Scholar]
- 82.Blemker SS, Asakawa DS, Gold GE, Delp SL. Image-based musculoskeletal modeling: Applications, advances, and future opportunities. J Magn Reson Imaging. 2007;25(no. 2):441–451. doi: 10.1002/jmri.20805. [DOI] [PubMed] [Google Scholar]
- 83.Otis J, Jiang C, Wickiewicz T, Peterson M, Warren R, Santner T. Changes in the moment arms of the rotator cuff and deltoid muscles with abduction and rotation. J Bone Joint Surgery. 1994;76(no. 5):667–676. doi: 10.2106/00004623-199405000-00007. [DOI] [PubMed] [Google Scholar]
- 84.An KN, Ueba Y, Chao EY, Cooney WP, Linscheid RL. Tendon excursion and moment arm of index finger muscles. J Biomech. 1983;16(no. 6):419–425. doi: 10.1016/0021-9290(83)90074-x. [DOI] [PubMed] [Google Scholar]
- 85.Valero-Cuevas FJ, Yi JW, Brown D, McNamara RV, Paul C, Lipson H. The tendon network of the fingers performs anatomical computation at a macroscopic scale. IEEE Trans Biomed Eng. 2007 Jun;54(no. 6, pt. 2):1161–1166. doi: 10.1109/TBME.2006.889200. [DOI] [PubMed] [Google Scholar]
- 86.Valero-Cuevas FJ, Lipson H. A computational environment to simulate complex tendinous topologies. Conf Proc IEEE Eng Med Biol Soc. 2004;6:4653–4656. doi: 10.1109/IEMBS.2004.1404289. [DOI] [PubMed] [Google Scholar]
- 87.Valero-Cuevas FJ, Anand VV, Saxena A, Lipson H. Beyond parameter estimation: Extending biomechanical modeling by the explicit exploration of model topology. IEEE Trans Biomed Eng. 2007 Nov;54(no. 11):1951–1964. doi: 10.1109/TBME.2007.906494. [DOI] [PubMed] [Google Scholar]
- 88.Kurse M, Lipson H, Valero-Cuevas F. A fast simulator to model complex tendon-bone interactions: Application to the tendinous networks controlling the fingers. presented at the 2009 Summer Bioengineering Conf.; Lake Tahoe, CA. [Google Scholar]
- 89.Lieber RL, Jacobson MD, Fazeli BM, Abrams RA, Botte MJ. Architecture of selected muscles of the arm and forearm: Anatomy and implications for tendon transfer. J Hand Surgery. 1992;17(no. 5):787. doi: 10.1016/0363-5023(92)90444-t. [DOI] [PubMed] [Google Scholar]
- 90.An K, Linscheid R, Brand P. Correlation of physiological cross-sectional areas of muscle and tendon. J Hand Surgery (Edinburgh, Scotland) 1991;16(no. 1):66. doi: 10.1016/0266-7681(91)90130-g. [DOI] [PubMed] [Google Scholar]
- 91.Zahalak GI, Ma SP. Muscle activation and contraction: Constitutive relations based directly on cross-bridge kinetics. J Biomech Eng. 1990;112:52. doi: 10.1115/1.2891126. [DOI] [PubMed] [Google Scholar]
- 92.Karniel A, Inbar GF. A model for learning human reaching movements. Biol Cybern. 1997;77(no. 3):173–183. doi: 10.1007/s004220050378. [DOI] [PubMed] [Google Scholar]
- 93.Gonzalez RV, Hutchins EL, Barr RE, Abraham LD. Development and evaluation of a musculoskeletal model of the elbow joint complex. J Biomech Eng. 1996;118:32. doi: 10.1115/1.2795943. [DOI] [PubMed] [Google Scholar]
- 94.Soechting JF, Flanders M. Evaluating an integrated musculoskeletal model of the human arm. J Biomech Eng. 1997;119:93. doi: 10.1115/1.2796071. [DOI] [PubMed] [Google Scholar]
- 95.Fuglevand AJ, Winter DA, Patla AE. Models of recruitment and rate coding organization in motor-unit pools. J Neurophysiol. 1993;70(no. 6):2470–2488. doi: 10.1152/jn.1993.70.6.2470. [DOI] [PubMed] [Google Scholar]
- 96.Cheng EJ, Brown IE, Loeb GE. Virtual muscle: A computational approach to understanding the effects of muscle properties on motor control. J Neurosci Methods. 2000;101(no. 2):117–130. doi: 10.1016/s0165-0270(00)00258-2. [DOI] [PubMed] [Google Scholar]
- 97.Keenan KG, Valero-Cuevas FJ. Experimentally valid predictions of muscle force and EMG in models of motor-unit function are most sensitive to neural properties. J Neurophysiol. 2007 Sep;98:1581–1590. doi: 10.1152/jn.00577.2007. [DOI] [PubMed] [Google Scholar]
- 98.Walcott S, Herzog W. Modeling residual force enhancement with generic cross-bridge models. Math Biosci. 2008 Dec;216(no. 2):172–186. doi: 10.1016/j.mbs.2008.10.005. [DOI] [PubMed] [Google Scholar]
- 99.McGowan CP, Neptune RR, Herzog W. A phenomenological model and validation of shortening induced force depression during muscle contractions. J Biomech. 2009 doi: 10.1016/j.jbiomech.2009.09.047. to be published. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Blemker SS, Delp SL. Rectus femoris and vastus intermedius fiber excursions predicted by three-dimensional muscle models. J Biomech. 2006;39(no. 8):1383–1391. doi: 10.1016/j.jbiomech.2005.04.012. [DOI] [PubMed] [Google Scholar]
- 101.Woledge RC, Barclay CJ, Curtin NA. Temperature change as a probe of muscle crossbridge kinetics: A review and discussion. Proc Biol Sci. 2009 Aug;276(no. 1668):2685–2695. doi: 10.1098/rspb.2009.0177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Linari M, Woledge R, Curtin N. Energy storage during stretch of active single fibres from frog skeletal muscle. J Physiology. 2003;548(no. 2):461–474. doi: 10.1113/jphysiol.2002.032185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Ruina A, Bertram JEA, Srinivasan M. A collisional model of the energetic cost of support work qualitatively explains leg sequencing in walking and galloping, pseudo-elastic leg behavior in running and the walk-to-run transition. J Theor Biol. 2005 Nov;237(no. 2):170–192. doi: 10.1016/j.jtbi.2005.04.004. [DOI] [PubMed] [Google Scholar]
- 104.Biewener AA. Patterns of mechanical energy change in tetrapod gait: Pendula, springs and work. J Exp Zoolog A Comp Exp Biol. 2006 Nov;305(no. 11):899–911. doi: 10.1002/jez.a.334. [DOI] [PubMed] [Google Scholar]
- 105.Mileusnic MP, Brown IE, Lan N, Loeb GE. Mathematical models of proprioceptors. I. Control and transduction in the muscle spindle. J Neurophysiol. 2006 Oct;96(no. 4):1772–1788. doi: 10.1152/jn.00868.2005. [DOI] [PubMed] [Google Scholar]
- 106.Sachs NA, Loeb GE. Development of a bionic muscle spindle for prosthetic proprioception. IEEE Trans Biomed Eng. 2007 Jun;54(pt. 1):1031–1041. doi: 10.1109/TBME.2007.892924. [DOI] [PubMed] [Google Scholar]
- 107.Song D, Lan N, Loeb GE, Gordon J. Model-based sensorimotor integration for multi-joint control: Development of a virtual arm model. Ann Biomed Eng. 2008 Jun;36(no. 6):1033–1048. doi: 10.1007/s10439-008-9461-8. [Online]. Available: http://dx.doi.org/9-008-9461-8. [DOI] [PubMed]
- 108.Hatze H. A myocybernetic control model of skeletal muscle. Biol Cybern. 1977;25(no. 2):103–119. doi: 10.1007/BF00337268. [DOI] [PubMed] [Google Scholar]
- 109.Neptune RR, McGowan CP, Kautz SA. Forward dynamics simulations provide insight into muscle mechanical work during human locomotion. Exercise and Sport Sci Rev. 2009;37(no. 4):203. doi: 10.1097/JES.0b013e3181b7ea29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Chao EY, An KN. Graphical interpretation of the solution to the redundant problem in biomechanics. J Biomech Eng. 1978;100:159–167. [Google Scholar]
- 111.Patriarco AG, Mann RW, Simon SR, Mansour JM. An evaluation of the approaches of optimization models in the prediction of muscle forces during human gait. J Biomech. 1981;14(no. 8):513. doi: 10.1016/0021-9290(81)90001-4. [DOI] [PubMed] [Google Scholar]
- 112.Anderson FC, Pandy MG. Dynamic optimization of human walking. J Biomech Eng. 2001;123:381. doi: 10.1115/1.1392310. [DOI] [PubMed] [Google Scholar]
- 113.Prilutsky BI, Zatsiorsky VM. Optimization-based models of muscle coordination. Exercise and Sport Sci Rev. 2002;30(no. 1):32. doi: 10.1097/00003677-200201000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Kaufman KR, An KA, Litchy WJ, Chao EYS. Physiological prediction of muscle forces. II, Application to isokinetic exercise. Neuroscience. 1991;40(no. 3):793–804. doi: 10.1016/0306-4522(91)90013-e. [DOI] [PubMed] [Google Scholar]
- 115.Happee R, Van der Helm FCT. The control of shoulder muscles during goal directed movements, an inverse dynamic analysis. J Biomech. 1995;28(no. 10):1179–1191. doi: 10.1016/0021-9290(94)00181-3. [DOI] [PubMed] [Google Scholar]
- 116.Hatze H. The fundamental problem of myoskeletal inverse dynamics and its implications. J Biomech. 2002;35(no. 1):109–115. doi: 10.1016/s0021-9290(01)00158-0. [DOI] [PubMed] [Google Scholar]
- 117.Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. Opensim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007 Nov;54(no. 11):1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- 118.An KN, Chao EYS, Kaufman KR. Basic Orthopaedic Biomechanics. New York: Raven; 1991. Analysis of muscle and joint loads; pp. 1–50. [Google Scholar]
- 119.Andriacchi TP, Natarajan RN, Hurwitz DE. Basic Orthopaedic Biomechanics. New York: Raven; 1991. Musculoskeletal dynamics, locomotion, and clinical applications; p. 51. [Google Scholar]
- 120.Duda R, Hart P, Stork D. Pattern Classification. Hoboken, NJ: Wiley-Interscience; 2000. [Google Scholar]
- 121.Bishop CM. Pattern Recognition and Machine Learning. New York: Springer; 2007. [Google Scholar]
- 122.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference and Prediction. New York: Springer; 2009. [Google Scholar]
- 123.Todorov E. Probabilistic inference of multijoint movements, skeletal parameters and marker attachments from diverse motion capture data. IEEE Trans Biomed Eng. 2007 Nov;54(no. 11):1927–1939. doi: 10.1109/TBME.2007.903521. [DOI] [PubMed] [Google Scholar]
- 124.Stengel R. Optimal Control and Estimation. 3rd. New York: Dover; 1994. [Google Scholar]
- 125.Paul C, Lipson H, Valero-Cuevas FJ. Design and control of tensegrity robots for locomotion. IEEE Trans Robotics. 2006 Oct;22(no. 5):944–957. [Google Scholar]
- 126.Rieffel J, Valero-Cuevas F, Lipson H. Morphological communication: Exploiting coupled dynamics in a complex mechanical structure to achieve locomotion. J Royal Society Interface. doi: 10.1098/rsif.2009.0240. to be published. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Bongard J, Zykov V, Lipson H. Resilient machines through continuous self-modeling. Science. 2006;314(no. 5802):1118–1121. doi: 10.1126/science.1133687. [DOI] [PubMed] [Google Scholar]
- 128.Bongard J, Lipson H. Nonlinear system identification using co-evolution of models and tests. IEEE Trans E Comput. 2005 Aug;9(no. 4):361–384. [Google Scholar]
- 129.Bongard J, Lipson H. Automated reverse engineering of nonlinear dynamical systems. Proc. National Academy of Sciences; 2007. p. 9943. Paper 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Bishop CM. Neural Networks for Pattern Recognition. London, U.K.: Oxford Univ. Press; 1995. [Google Scholar]
- 131.Vapnik VN. The Nature of Statistical Learning Theory. New York: Springer-Verlag; 1995. [Google Scholar]
- 132.Rasmussen CE, Williams CKI. Gaussian Processes for Machine Learning. Cambridge, MA: MIT Press; 2006. [Google Scholar]
- 133.Williams C, Rasmussen C. Advances in Neural Processing Systems. Vol. 8. Boston, MA: MIT Press; 1996. Gaussian processes for regression; pp. 598–604. [Google Scholar]
- 134.Matheron G. Principles of geostatistics. Economic Geology. 1963;58(no. 8):1246–1266. [Google Scholar]
- 135.Cressie N. Statistics for Spatial Data. Hoboken, NJ: Wiley; 1993. [Google Scholar]
- 136.Atkeson CG, Moore AW, Schaal S. Locally weighted learning. Artif Intell Rev. 1997;11:11–73. [Google Scholar]
- 137.Vijayakumar S, D'Souza A, Schaal S. Incremental online learning in high dimensions. Neural Comput. 2005;17:2602–2634. doi: 10.1162/089976605774320557. [DOI] [PubMed] [Google Scholar]
- 138.Hoffmann H, Schaal S, Vijayakumar S. Local dimensionality reduction for non-parametric regression. Neural Process Lett. 2009;29:109–131. [Google Scholar]
- 139.Bellman RE. Adaptive Control Processes: A Gwuided Tour. Princeton, NJ: Princeton Univ. Press; 1961. [Google Scholar]
- 140.Vlassis N, Motomura Y, Kröse B. Supervised dimension reduction of intrinsically low-dimensional data. Neural Comput. 2002;14:191–215. doi: 10.1162/089976602753284491. [DOI] [PubMed] [Google Scholar]
- 141.Rose K. Deterministic annealing for clustering, compression, classification, regression, and related optimization problems. Proc IEEE. 1998 Nov;86(no. 11):2210–2239. [Google Scholar]
- 142.Kloppenburg M, Tavan P. Deterministic annealing for density estimation by multivariate normal mixtures. Phys Rev E. 1997;55:R2089–R2092. [Google Scholar]
- 143.Goldberg DE. Genetic Algorithms in Search, Optimization, and Machine Learning. Reading, MA: Addison-Wesley Professional; 1989. [Google Scholar]
- 144.Whitley D. Genetic Algorithms in Engineering and Computer Science. Hoboken, NJ: Wiley; 1995. Genetic algorithms and neural networks; pp. 191–201. [Google Scholar]
- 145.Hertz J, Krogh A, Palmer RG. Introduction to the Theory of Neural Computation. Redwood City, CA: Addison-Wesley; 1991. [Google Scholar]
- 146.Kuperstein M. Neural model of adaptive hand-eye coordination for single postures. Science. 1988;239:1308–1311. doi: 10.1126/science.3344437. [DOI] [PubMed] [Google Scholar]
- 147.Jordan MI, Rumelhart DE. Forward models: Supervised learning with a distal teacher. Cognitive Science. 1992;16:307–354. [Google Scholar]
- 148.Kawato M. Feedback-error-learning neural network for supervised motor learning. In: Eckmiller R, editor. Advanced Neural Computers. Amsterdam, The Netherlands: Elsevier, North-Holland; 1990. pp. 365–372. [Google Scholar]
- 149.Schenck W, Möller R. Staged learning of saccadic eye movements with a robot camera head. In: Bowman H, Labiouse C, editors. Connectionist Models of Cognition and Perception II. London: World Scientific; 2004. pp. 82–91. [Google Scholar]
- 150.Hoffmann H, Schenck W, Möller R. Learning visuomotor transformations for gaze-control and grasping. Biol Cybern. 2005;93(no. 2):119–130. doi: 10.1007/s00422-005-0575-x. [DOI] [PubMed] [Google Scholar]
- 151.Demiris J, Hayes G. Imitative learning mechanisms in robots and humans. Proc. Eur. Workshop on Learning Robotics; Dortmund, Germany. 1996. [Google Scholar]
- 152.Schaal S. Is imitation learning the route to humanoid robots. Trends Cognitive Sci. 1999;3:233–242. doi: 10.1016/s1364-6613(99)01327-3. [DOI] [PubMed] [Google Scholar]
- 153.Nehaniv C, Dautenhahn K. Imitation in Animals and Artifacts. Cambridge, MA: MIT Press; 2002. [Google Scholar]
- 154.Prilutsky BI. Muscle coordination: The discussion continues. Motor Control. 2000;4(no. 1):97–116. doi: 10.1123/mcj.4.1.97. [DOI] [PubMed] [Google Scholar]
- 155.Kuo AD, Zajac FE. Human standing posture: Multi-joint movement strategies based on biomechanical constraints. Prog Brain Res. 1993;97:349–358. doi: 10.1016/s0079-6123(08)62294-3. [DOI] [PubMed] [Google Scholar]
- 156.Avis D, Fukuda K. A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra. Discrete Comput Geometry. 1992;8(no. 3):295–313. [Google Scholar]
- 157.Movellan JR, McClelland JL. Learning continuous probability distributions with symmetric diffusion networks. Cogn Sci. 1993;17:463–496. [Google Scholar]
- 158.Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc Nat Acad Sci USA. 1982;79:2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Cruse H, Steinkühler U. Solution of the direct and inverse kinematic problems by a common algorithm based on the mean of multiple computations. Biol Cybern. 1993;69:345–351. [Google Scholar]
- 160.Steinkühler U, Cruse H. A holistic model for an internal representation to control the movement of a manipulator with redundant degrees of freedom. Biol Cybern. 1998;79:457–466. [Google Scholar]
- 161.Diamantaras KI, Kung SY. Principal Component Neural Networks. Hoboken, NJ: Wiley; 1996. [Google Scholar]
- 162.Tipping ME, Bishop CM. Probabilistic principal component analysis. J Royal Statist Soc, ser B. 1999;61:611–622. [Google Scholar]
- 163.Hyvärinen, Karhunen, Oja E. Independent Component Analysis. 1, Introduction. Hoboken, NJ: Wiley; 2001. pp. 1–12. [Google Scholar]
- 164.Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401(no. 6755):788791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- 165.Hoffmann H. PhD thesis. Bielefeld University; 2004. Unsupervised Learning of Visuomotor Associations. Berlin, Germany: Logos Verlag, 2005, vol. 11, MPI Series in Biological Cybernetics. [Google Scholar]
- 166.Clewley RH, Guckenheimer JM, Valero-Cuevas F. Estimating effective degrees of freedom in motor systems. IEEE Trans Biomed Eng. 2008 Feb;55(no. 2, pt. 1):430–442. doi: 10.1109/TBME.2007.903712. [DOI] [PubMed] [Google Scholar]
- 167.Kambhatla N, Leen TK. Dimension reduction by local principal component analysis. Neural Comput. 1997;9:1493–1516. [Google Scholar]
- 168.Kohonen T. Self-organized formation of topologically correct feature maps. Biol Cybern. 1982;43:59–69. [Google Scholar]
- 169.Kohonen T. Self-Organizing Maps. Berlin: Springer; 1995. [Google Scholar]
- 170.Ritter H, Martinetz T, Schulten K. Neuronale Netze. Bonn, Germany: Addison-Wesley; 1990. [Google Scholar]
- 171.Ritter HJ, Gielen S, Kappen B, editors. Parametrized self-organizing maps. Proc. Int. Conf. Artificial Neural Networks; Berlin. Springer; 1993. pp. 568–575. [Google Scholar]
- 172.Walter JA, Nölker C, Ritter H. The PSOM algorithm and applications. Proc. Symp. Neural Computation; 2000. pp. 758–764. [Google Scholar]
- 173.Weinberger KQ, Sha F, Saul LK. Learning a kernel matrix for nonlinear dimensionality reduction. Proc. 21st Int. Conf. Machine Learning; 2004. pp. 106–115. [Google Scholar]
- 174.Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 175.Tenenbaum JB, de Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. 2000 Dec;290:2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 176.Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003;15(no. 6):1373–1396. [Google Scholar]
- 177.Hinton G, Roweis ST. Advances in Neural Information Processing Systems. Boston, MA: MIT Press; 2003. Stochastic neighbor embedding; pp. 857–864. [Google Scholar]
- 178.Schölkopf B, Smola AJ, Müller KR. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998;10:1299–1319. [Google Scholar]
- 179.Hoffmann H. Kernel PCA for novelty detection. Pattern Recognit. 2007;40:863–874. [Google Scholar]
- 180.Tipping ME, Bishop CM. Mixtures of probabilistic principal component analyzers. Neural Comput. 1999;11:443–482. doi: 10.1162/089976699300016728. [DOI] [PubMed] [Google Scholar]
- 181.Ogata K. Modern Control Engineering. 3rd. Upper Saddle River, NJ: Prentice-Hall; 1997. [Google Scholar]
- 182.Valero-Cuevas FJ. Predictive modulation of muscle coordination pattern magnitude scales fingertip force magnitude over the voluntary range. J Neurophysiol. 2000 Mar;83:1469–1479. doi: 10.1152/jn.2000.83.3.1469. [DOI] [PubMed] [Google Scholar]
- 183.Bertsekas D. Dynamics Programming and Optimal Control. 2nd. Belmont, MA: Athena Scientific; 2007. [Google Scholar]
- 184.Maybeck P. Stochastic Models Estimation and Controls. Englewood Cliffs, NJ: Prentice-Hall; 1979. [Google Scholar]
- 185.Kuo AD. An optimal control model for analyzing human postural balance. IEEE Trans Biomed Eng. 1995 Jan;42(no. 1):87–101. doi: 10.1109/10.362914. [DOI] [PubMed] [Google Scholar]
- 186.Runge C, Zajac F, III, Allum J, Risher D, Bryson A, Jr, Honegger F. Estimating net joint torques from kinesiological data using optimal linear system theory. IEEE Trans Biomed Eng. 1995 Dec;42(no. 12):1158–1164. doi: 10.1109/10.476122. [DOI] [PubMed] [Google Scholar]
- 187.Li W, Todorov E. Iterative nonlinear quadratic regulator design for nonlinear biological movement systems. Proc. Int. Conf. Informatics in Control, Automation, and Robotics; 2004. pp. 222–229. [Google Scholar]
- 188.Kay M. Fundamentals of Statistical Signal Processing: Estimation Theory. Vol. 1 Englewood Cliffs, NJ: Prentice-Hall; 1993. [Google Scholar]
- 189.He J, Levine W, Loeb GE. Feedback gains for correcting small perturbations to standing posture. IEEE Trans Autom Control. 1991 Mar;36(no. 3):322–332. [Google Scholar]
- 190.Harris C, Wolpert D. Signal dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- 191.Todorov E. Optimality principles in sensorimotor control. Nature Neurosci. 2004;7:907–915. doi: 10.1038/nn1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Todorov E, Jordan M. Optimal feedback control as a theory of motor coordination. Nature Neurosci. 2002;5(no. 11):1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- 193.Todorov E, Li W. A generalized LQG method for locally optimal feedback control of constrained nonlinear stochastic systems. Proc. American Control Conf.; 2005. p. 300.p. 307. [Google Scholar]
- 194.Li W, Todorov E. Iterative optimal control and estimation design for nonlinear stochastic systems. Proc. 45th IEEE Conf. Decision and Control; San Diego, CA. 2006. pp. 3242–3247. [Google Scholar]
- 195.Li W, Todorov E. Iterative linearization methods for approximately optimal control and estimation of non-linear stochastic systems. Int J Control. 2007;80(no. 12):1439–1453. [Google Scholar]
- 196.Loeb G, Brown I, Cheng E. A hierarchical foundation for models of sensorimotor control. Experimental Brain Res. 1999;126(no. 1):1–18. doi: 10.1007/s002210050712. [DOI] [PubMed] [Google Scholar]
- 197.Li W, Todorov E, Pan X. Hierarchical control of redundant biomechanical systems. Proc. 26th Annu. Int. Conf. IEEE Engineering in Medicine and Biology Society; San Francisco, CA. 2004. pp. 4618–4621. [DOI] [PubMed] [Google Scholar]
- 198.Liu D, Todorov E. Hierarchical optimal control of a 7-DOF arm model. Proc. 2nd IEEE Symp. Adaptive Dynamic Programming and Reinforcement Learning; 2009. pp. 50–57. [Google Scholar]
- 199.Todorov E. Compositionality of optimal control laws. presented at the Neural Information Processing Systems Conf.; Vancouver, BC, Canada. 2009. [Google Scholar]
- 200.Todorov E. Efficient computation of optimal actions. Proc Nat Acad Sci USA. 2009 Jul;106(no. 28):11478–11483. doi: 10.1073/pnas.0710743106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Venkadesan M, Valero-Cuevas FJ. Neural control of motion-to-force transitions with the fingertip. J Neurosci. 2008 Feb;28:1366–1373. doi: 10.1523/JNEUROSCI.4993-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Venkadesan M, Valero-Cuevas FJ. Effects of neuromuscular lags on controlling contact transitions. Philos Trans A Math Phys Eng Sci. 2009 Mar;367:1163–1179. doi: 10.1098/rsta.2008.0261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Li W, Valero-Cuevas F. Linear quadratic optimal control of contact transition with the fingertip. Proc. Amer. Control Conf.; St. Louis, MO. 2009. [Google Scholar]
- 204.Coodwin G, Seron M, De done A. Constrained Control and Estimation. An Optimization Approach. London, U.K.: Springer-Verlang; 2005. [Google Scholar]
- 205.Primbs J, Chang HS. Stochastic receding horizon control for constrained linear systems with state and control multiplicative noise. IEEE Trans Autom Control. 2009 Feb;54(no. 2):221–230. [Google Scholar]
- 206.Primbs J, Sung C. Stochastic receding horizon control of constrained linear systems with state and control multiplicative noise. IEEE Trans Autom Control. 2009 Feb;54(no. 2):221–230. [Google Scholar]
- 207.Safonov MG, Athans M. Gain and phase margins for multiloop LQG regulator. IEEE Trans Autom Control. 1977 Apr;22(no. 2):173–179. [Google Scholar]
- 208.Doyle JC. Guaranteed margins for LQG regulators. IEEE Trans Autom Control. 1978 Aug;AC-23(no. 4):756–757. [Google Scholar]
- 209.Izawa J, Rane T, Donchin O, Shadmehr R. Motor adaptation as a process of reoptimization. J Neurosci. 2008;28(no. 11):2883–91. doi: 10.1523/JNEUROSCI.5359-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 210.Skogestad S, Postlethwaite I. Multivariable Feedback Control. Analysis and Design. Hoboken, NJ: Wiley; 2004. [Google Scholar]
- 211.Ioannou P, Sun J. Robust Adaptive Control. Englewood Cliffs, NJ: Prentice-Hall; 1996. [Google Scholar]
- 212.Fishman GS. Monte Carlo: Concepts, Algorithms, and Applications. New York: Springer-Verlag; 1996. (Springer Series in Operations Research). [Google Scholar]
- 213.Bartel DL, Johnston RC. Mechanical analysis and optimization of a cup arthroplasty. J Biomech. 1969 Mar;2(no. 1):97–103. doi: 10.1016/0021-9290(69)90045-1. [DOI] [PubMed] [Google Scholar]
- 214.Hughes RE, An KN. Monte carlo simulation of a planar shoulder model. Med Biol Eng Comput. 1997;35(no. 5):544–548. doi: 10.1007/BF02525538. [DOI] [PubMed] [Google Scholar]
- 215.Santos V, Valero-Cuevas FJ. A bayesian approach to biomechanical modeling to optimize over large parameter spaces while considering anatomical variability. 26th Annu. Int. Conf. IEEE Eng. Medicine and Biology Society, 2004 (IEMBS '04); 2004. pp. 4626–4629. [DOI] [PubMed] [Google Scholar]
- 216.McLean SG, Su A, Van Den Bogert AJ. Development and validation of a 3-D model to predict knee joint loading during dynamic movement. J Biomech Eng. 2003;125:864. doi: 10.1115/1.1634282. [DOI] [PubMed] [Google Scholar]
- 217.Lin C, Gross M, Ji C, Padua D, Weinhold P, Garrett W, Yu B. A stochastic biomechanical model for risk and risk factors of non-contact anterior cruciate ligament injuries. J Biomech. 2009;42(no. 4):418–423. doi: 10.1016/j.jbiomech.2008.12.005. [DOI] [PubMed] [Google Scholar]
- 218.Santos V, Bustamante C, Valero-Cuevas F. Improving the fitness of high-dimensional biomechanical models via data-driven stochastic exploration. IEEE Trans Biomed Eng. 2009 Mar;56(no. 3):552–562. doi: 10.1109/TBME.2008.2006033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219.Chvátal . Linear Programming. New York: Freeman; 1983. (A Series of Books in the Mathematical Sciences). [Google Scholar]
- 220.Roberts G. Markov Chain Monte Carlo in Practice. Vol. 57. 1996. Markov chain concepts related to sampling algorithms. [Google Scholar]
- 221.Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970 Apr;57:97–109. [Google Scholar]
- 222.Valero-Cuevas FJ, Venkadesan M, Todorov E. Structured variability of muscle activations supports the minimal intervention principle of motor control. J Neurophysiol. 2009 Jul;102:59–68. doi: 10.1152/jn.90324.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223.Kutch JJ, Suresh NL, Bloch AM, Rymer WZ. Analysis of the effects of firing rate and synchronization on spike-triggered averaging of multidirectional motor unit torque. J Comput Neurosci. 2007;22(no. 3):347–361. doi: 10.1007/s10827-007-0023-0. [DOI] [PubMed] [Google Scholar]
- 224.Taylor AM, Steege JW, Enoka RM. Motor-unit synchronization alters spike-triggered average force in simulated contractions. J Neurophysiol. 2002;88(no. 1):265–276. doi: 10.1152/jn.2002.88.1.265. [DOI] [PubMed] [Google Scholar]
- 225.Wakeling JM. Patterns of motor recruitment can be determined using surface emg. J Electromyography Kinesiology. 2009;19(no. 2):199–207. doi: 10.1016/j.jelekin.2007.09.006. [DOI] [PubMed] [Google Scholar]
- 226.Barry BK, Pascoe MA, Jesunathadas M, Enoka RM. Rate coding is compressed but variability is unaltered for motor units in a hand muscle of old adults. J Neurophysiol. 2007;97(no. 5):3206–3218. doi: 10.1152/jn.01280.2006. [DOI] [PubMed] [Google Scholar]
- 227.Jones KE, Hamilton AF, Wolpert DM. Sources of signal-dependent noise during isometric force production. J Neurophysiol. 2002;88(no. 3):1533–1544. doi: 10.1152/jn.2002.88.3.1533. [DOI] [PubMed] [Google Scholar]
- 228.Moritz CT, Barry BK, Pascoe MA, Enoka RM. Discharge rate variability influences the variation in force fluctuations across the working range of a hand muscle. J Neurophysiol. 2005;93(no. 5):2449–59. doi: 10.1152/jn.01122.2004. [DOI] [PubMed] [Google Scholar]
- 229.Zhou P, Suresh NL, Rymer WZ. Model based sensitivity analysis of emg-force relation with respect to motor unit properties: Applications to muscle paresis in stroke. Annals Biomed Eng. 2007;35(no. 9):1521–1531. doi: 10.1007/s10439-007-9329-3. [DOI] [PubMed] [Google Scholar]
- 230.Chang EJ, Loeb GE. On the use of musculoskeletal models to interpret motor control strategies from performance data. J Neural Eng. 2008;5:232–253. doi: 10.1088/1741-2560/5/2/014. [DOI] [PubMed] [Google Scholar]
- 231.Kutch JJ, Kuo AD, Bloch AM, Rymer WZ. Endpoint force fluctuations reveal flexible rather than synergistic patterns of muscle cooperation. J Neurophysiol. 2008;100(no. 5):2455–2471. doi: 10.1152/jn.90274.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]


