Spot Variation Fluorescence Correlation Spectroscopy Allows for Superresolution Chronoscopy of Confinement Times in Membranes

Abstract

Resolving the dynamical interplay of proteins and lipids in the live-cell plasma membrane represents a central goal in current cell biology. Superresolution concepts have introduced a means of capturing spatial heterogeneity at a nanoscopic length scale. Similar concepts for detecting dynamical transitions (superresolution chronoscopy) are still lacking. Here, we show that recently introduced spot-variation fluorescence correlation spectroscopy allows for sensing transient confinement times of membrane constituents at dramatically improved resolution. Using standard diffraction-limited optics, spot-variation fluorescence correlation spectroscopy captures signatures of single retardation events far below the transit time of the tracer through the focal spot. We provide an analytical description of special cases of transient binding of a tracer to pointlike traps, or association of a tracer with nanodomains. The influence of trap mobility and the underlying binding kinetics are quantified. Experimental approaches are suggested that allow for gaining quantitative mechanistic insights into the interaction processes of membrane constituents.

Introduction

Most cellular signaling processes have their origin in the plasma membrane. In particular, proximity or separation of enzymes and substrates on the nanometer scale are believed to regulate a variety of processes such as signal initiation (1,2), cellular adhesion (3–6), or endocytic uptake (7). Understanding the dynamic organization of the plasma membrane requires methods of gaining information both at the spatial and temporal levels (2,8–10). The lateral diffusion of molecules within the membrane can report on transient confinements due to molecular interactions, local heterogeneities, or corrals. Currently, two complementary approaches are applied for the analysis of molecular mobility: single particle tracking (SPT) determines the time evolution of the spatial coordinates $\overrightarrow{x}\left(t\right)$ (11,12), whereas fluorescence correlation spectroscopy (FCS) measures the spatial dependence of the transit time, τ, of a molecule through the focus of a laser beam (13). In recent years, an enormous advancement in spatial resolution was achieved with the emergence of a variety of superresolution microscopy concepts (11,14), which yielded spatial heterogeneities in biological samples below the classical diffraction limit. Similar concepts for temporal superresolution are still lacking.

In a conventional FCS experiment, the two-dimensional diffusion time of a tracer through the focal spot is obtained by fitting the autocorrelation curve (ACF) using

$$G\left(t\right)\sim {\left(1+\frac{t}{{\tau }_{D^{\prime }}}\right)}^{-1}.$$ (1)

The diffusion time, ${\tau }_{D^{\prime }}={\omega }^2/4D$, limits the time resolution for recovering changes in diffusion behavior (15). We base our argument on the example of a tracer that alternates between immobile trapped states (trapping times τ_trap) and periods of free diffusion τ_free (see Table 1 for list of parameters). In the case of negligible diffusion times, ${\tau }_{D^{\prime }}\ll {\tau }_{\text{trap}}$, and rare trapping events $n={\tau }_{D^{\prime }}/{\tau }_{\text{free}}\ll 1$, the ACF shows well separated shoulders that allow for direct extraction of τ_trap (see Fig. 1 a and Note 1 in the Supporting Material). In this case, the two characteristic timescales ${\tau }_{D^{\prime }}$ and τ_trap and the proportion β = τ_trap/(τ_trap + τ_free) can be easily extracted from the ACF for two-dimensional diffusion (15,16)

$$G\left(t\right)=\frac{1}{N}\left[\left(1-\beta \right)\frac{1}{1+\frac{t}{{\tau }_{D^{\prime }}}}+\beta \text{exp}\left(-\frac{t}{{\tau }_{trap}}\right)\right].$$ (2)

Table 1.

List of parameters

ω	FCS beam waist
${\tau }_{D^{\prime }}$	Free diffusion time through the FCS spot
τfree	Average free diffusion time between trapping events
τtrap	Mean time in the trapped state
β	Fraction of trapped particles	β = τtrap/(τtrap + τfree)
n	Mean number of trapping events during the focal transit
D = Dfree	Free diffusion constant
Dtrap	Trap mobility
Deff	Effective mobility	Deff = Dfree(1−β)
τ	Overall diffusion time through the focal spot	τ = τ0 + ω2/(4Deff)
r	Domain radius
Din	Mobility inside domains
τresidence	Residence time in domains
Dresidence	Effective mobility inside domains	Dresidence = 2r2/4τresidence
fdistr	Offset multiplication factor for different distributions
fdistr, free	Distribution factor for free diffusion times
fdistr, trap	Distribution factor for trapping times
fmobility	Mobility reduction factor
τ0	Offset in the FCS diffusion law	τ0 = β × τtrap × fmobility × (fdistr,trap + fdistr,free)

Figure 1.

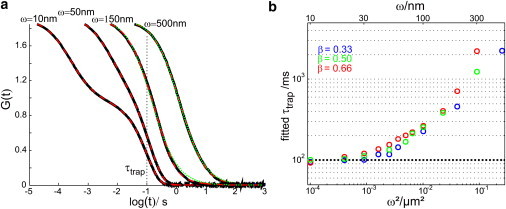
Trapping-time resolution of conventional FCS. (a) shows the results of Monte Carlo simulations for stop-and-go diffusion, assuming exponentially distributed transition times with mean values of τ_free = τ_trap = 100 ms; simulations were performed for the indicated beam waists, ω. We assumed immobile traps, and a free diffusion constant D_free= 0.1 μm²/s. Black lines indicate the simulated autocorrelation functions. Red dashed lines show fits using a two-component model (Eq. 2), green dotted lines show fits using the model for one-component two-dimensional free diffusion (Eq. 1). For ω < 150 nm, the one-component free-diffusion model failed to describe the data and was therefore not plotted. (b) Fit results for the trapping time τ_trap obtained with Eq. 2. For beam waists of ω > 30 nm, the determined τ_trap gets biased toward larger values, although the fit appears to describe the data well. To test for dependencies on the proportion β we made simulations for τ_free = 50 ms, 100 ms, and 200 ms.

As an example, we determined the ACFs by Monte Carlo simulations using the parameters τ_trap = τ_free = 100 ms and a diffusion constant, D = 0.1 μm²/s, which are realistic values for plasma membrane proteins (12,17,18) (Fig. 1 a). For spot sizes well below the diffraction limit, ω < 200 nm, we indeed see the separation in the ACF, allowing for the direct extraction of τ_trap.

However, closer inspection of the fit results revealed a substantial bias in the obtained trapping times that increases with increasing ω (Fig. 1 b). Only for ω ≤ 40 nm is unbiased fitting possible for these parameter settings (relative errors in τ_trap ≤ 20%). Shorter trapping times further reduce the required spot size accordingly. Yet, subdiffraction spot sizes are difficult to achieve: Stimulated emission depletion- (STED-) FCS requires the usage of special dyes and high-power lasers (17), near-field methods require the manufacturing and implementation of sub-wavelength apertures (19, 20). The according time regime would therefore be essentially inaccessible for conventional FCS analysis. We can invert the calculation for estimating the time resolution to recover trapping times by conventional diffraction-limited FCS. Assuming a spot size of ω = 200 nm, a limit of τ_trap ≥ ω²/(4D_free × 0.04) = 2.5 s can be specified. Note that substantial bias for τ_trap already appears in regions with high goodness of fit. For example, the curve for ω = 50 nm (Fig. 1 a) shows no apparent deviation from the data, but yields a bias of 36%. In contrast, for high n, tracers show frequent transitions between confined and free diffusion during the transit through the focal area, and the ACF approximates effective long-range diffusion described by Eq. 1 (Fig. 1 a, green curves). Conventional FCS does not provide access to kinetic parameters in this regime.

We show below that the recently introduced method of spot-variation FCS (sv-FCS) allows access to this regime by sensing trapping times at dramatically improved time resolution. sv-FCS can be viewed as the perfect analogon to SPT in the time domain: transit times are measured for various focal areas, τ_D(ω²), where ω denotes the radius of the laser spot (Fig. 2 a) (21–23). With increasing ω, the transit times of many investigated membrane molecules were found to follow the empirical function τ_D = τ₀ + ω²/4D_eff, which shows a nonzero offset τ₀ in the limit of small focal areas, and effective long-range diffusion with diffusion constant D_eff (24). The time-versus-area relation was termed the diffusion law. Experiments revealed that the offset τ₀ depends on membrane properties like lipid composition or actin cytoskeleton organization, thereby providing biological insights into the origin of the observed phenomenon (17,24–28). Although the method is rather simple to apply, its full strength can hardly be exploited, since the interrelation between the recorded diffusion law and the diffusion processes are not well understood. A full analytical treatment is only available for particles diffusing in a periodic meshwork of barriers (29). In addition, Monte Carlo simulations of a few special cases have been published (17,21), but a general description of diffusion laws is still lacking (30). In the following we show that the diffusion-law offset τ₀ measured with sv-FCS senses confinement times, trap mobility, and the stochastic distributions of on- and off-times.

Figure 2.

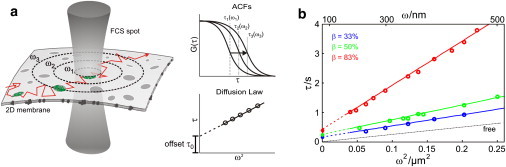
Diffusion law recorded with sv-FCS. (a) By increasing the area of the excitation spot, the transit times in the autocorrelation curves increase accordingly. Fitting each ACF with an effective two-dimensional diffusion yields τ_D(ω²). From the y-intercept, the diffusion law offset, τ₀, is obtained. (b) Full ACF Monte Carlo simulations were performed for tracers that were stochastically immobilized with exponentially distributed transition kinetics. Simulation data (symbols) follow the theoretical curves (lines). A trapping time of τ_trap = 500 ms was adjusted.

Methods

Monte Carlo simulations

Simulations were performed in MATLAB (R2009a, The MathWorks, Natick, MA) and run on an eight-core standard PC with 8 GB RAM under Windows XP-X64. We implemented simulations close to real FCS experiments on fluid membranes. Off-lattice random walks were generated for the special cases of free diffusion, stop-and-go diffusion, and confined diffusion in fixed permeable domains. The total number of simulated steps/trajectory was typically set to 1e6–1e7 for all simulations. Reflective boundary conditions were applied at the border of the square simulation area, which was adapted to the different spot sizes. We scaled all data to biologically relevant values: laser spot sizes were varied between 150 nm and 1.2 μm (21,22,24), diffusion constants between 0 and 1 μm²/s (31), and immobilization times between 20 and 500 ms (21,24,25). The xy positions of the generated random walks were used to calculate intensity values. For this purpose, a virtual Gaussian-shaped excitation beam with I(x,y) = I₀exp(−(x² + y²)/ω²) was positioned in the center of a square simulation area. The side length, L, of the square simulation box was set to at least L = 14ω, so that the effect of limiting the excitation profile becomes negligible. Simulations were performed with a mean number of 0.5 particles in the excitation spot. Autocorrelation functions were determined via the MATLAB procedure xcorr and fitted with the free two-dimensional diffusion model (Eq. 1) (13). Simulations were performed at different beam waists, and the diffusion law τ_D versus ω² was determined. Offset values were obtained from a linear regression using four different beam waists; typically 10–30 offset values were averaged.

Free diffusion and stop-and-go diffusion

For the trapping model, we consider a freely diffusing particle in a two-dimensional plane with diffusion constant D_free that immobilizes after an average time τ_free at arbitrary locations for a time τ_trap. Initial conditions in the simulation were chosen so that the random walker starts at a random point of the simulation area in either a trapped or a free state according to the time fraction β = τ_trap/(τ_trap + τ_free). Trap mobility was varied in the range 0 ≤ D_trap ≤ D_free for different simulations. The delay time t_del between consecutive steps was kept at least 10 times smaller than the maximum value of τ_trap andτ_free. At each time step, the particle performs a jump, which is determined by a normally distributed length (μ = 0, $\sigma =\sqrt{2D{t}_{\text{del}}}$) for each dimension, where D denotes either D_trap or D_free.

Domain model

We used 30% surface coverage of fixed circular domains with radius r = 20 nm. Domains were placed at random positions in a nonoverlapping way. Permeability of domains was adjusted by the probabilities of entering or exiting, P_in or P_out, respectively. Whenever the molecule hits a domain a number rand is generated at random between 0 and 1, and compared to P_in or P_out. If the molecule is not allowed to pass the barrier, it remains in the same position. Note that the confinement strength is a function of P_out and the average diffusion step length. The delay time was set small enough to assure that the mean diffusion step size is five times smaller than the domain radius. Diffusion constants inside the domain, D_in = 0.1 μm²/s, and outside the domain, D_out = 0.2 μm²/s, were chosen.

First passage time model

For free lateral diffusion, the transit time calculated from the ACF is given by τ_D′ = ω²/4D. τ_D′ is identical to the first passage time a freely diffusing random walker needs to reach the boundary of a circle with radius ω when starting in the center. In the asymptotic case characterized by a transit time of τ_D >> τ_trap, stop-and-go diffusion approximates the free-diffusion case, yet with altered time, τ_D ≠ τ_D′. This regime can therefore be adequately described by the first-passage-time model. See Fig. 3 b, which compares results from a first-passage-time model (circles) with those from a full-ACF simulation (squares). All data are in perfect agreement. We therefore derived all formulas assuming a first-passage-time model, and checked the equations with Monte Carlo simulations using the full-ACF model.

Figure 3.

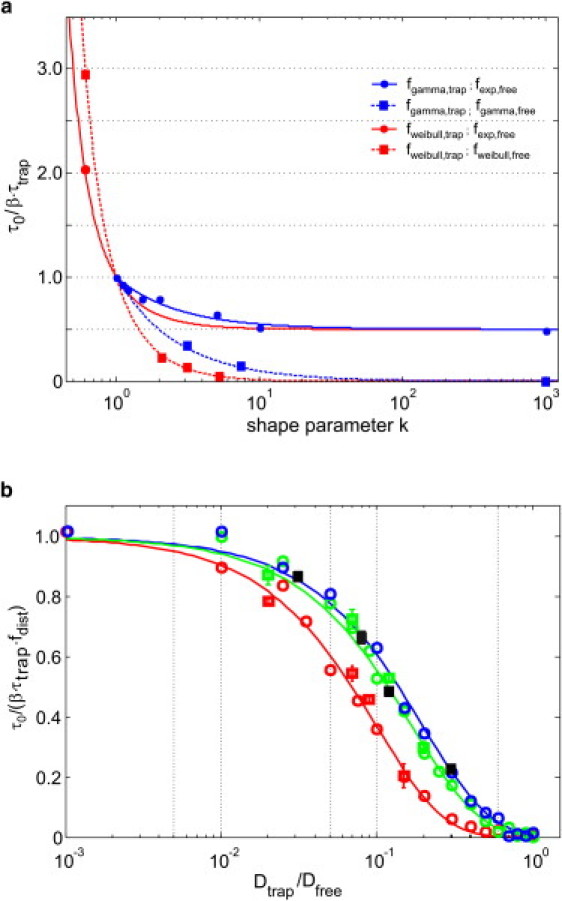
(a) Dependence of the FCS diffusion law offset on the distribution of the kinetic rate constants. We assumed here immobile traps (D_trap = 0) and plotted ${\tau }_0/\beta {\tau }_{\text{trap}}=\left[f_{{\text{distr}}_1,\text{trap}}+f_{{\text{distr}}_2,\text{free}}\right]$ for various combinations of distribution functions. Gamma and Weibull distributions were parameterized by the shape factor, k. Lines show the results of the analytical models (Table 2); symbols indicate results of Monte Carlo simulations of the full ACFs. (b) The effect of trap mobility on the offset was calculated by full-ACF Monte Carlo simulations (squares) or using the first-passage-time model (circles). The color code is identical to Fig. 2. Full lines indicate the empirical function of Eq. 4. We further tested gamma-distributed trapping times for β = 0.5 (black squares).

We calculated mean first passage times of random walkers that were placed in the center of a circular region of radius ω and derived diffusion laws for various circle radii. Particles started in a trapped or free state according to the time fraction β. Step lengths were adjusted to ω/5000. Diffusion constants were set to D_free = 1 μm²/s and 0 ≤ D_trap ≤ D_free for the estimation of an offset reduction by trap mobility. Free diffusion times, τ_free, and trapping times, τ_trap, were exponentially distributed, rendering start conditions for particles unproblematic.

Results

We first consider a model in which a tracer becomes stochastically immobilized. The transition times τ_free and τ_trap specify the average duration of free diffusion and immobilization, respectively, and are assumed to follow an exponential distribution, as frequently observed in biological systems. Between two stops, the tracer moves freely with diffusion constant D_free. On average, the particles are thus immobilized for a time fraction β = τ_trap/(τ_trap + τ_free). In the subsection First-passage-time model of Methods, we show that the diffusion time obtained via Eq. 1 is identical to the first passage time a random walker needs to reach the boundary of a circle with radius ω when starting from the center; we will use this equivalence for further derivations. The first passage time is given by τ_D = τ_D′ + nτ_trap, with n specifying the average number of stops the tracer experiences before it reaches the boundary and τ_D′ the free diffusion time through the spot. The problem can therefore be reduced to a determination of the number of stops within an interval τ_D′; stops are generated by an underlying stochastic process based on the distribution function of τ_free. We discriminate tracers starting with free diffusion (proportion 1 − β) from tracers starting in the trapped state (proportion β). For tracers starting with free diffusion, a randomly chosen interval τ_D′ contains on average n = τ_D′/τ_free stops. Tracers starting in a trapped state first experience a time penalty τ_trap, whereas the rest of the process is identical to that for the free tracer, yielding a total number n = 1 + τ_D′/τ_free. Together, the average first passage time over both fractions is given by ${\tau }_D=\beta {\tau }_{\text{trap}}+\frac{{\omega }^2}{4D_{\text{free}}\left(1-\beta \right)}$. We thus obtain a diffusion law with an effective mobility D_eff = D_free(1 − β) and an offset

$${\tau }_0=\beta {\tau }_{\text{trap}}.$$ (3)

In Fig. 2 b, we show Monte Carlo simulations (symbols) of the diffusion law for τ_trap = 500 ms and various values of β that perfectly agree with our theoretical model (see the Supporting Material for details on the simulations and the models). Increasing β results in a reduced effective mobility and thus an increased slope; it is important to note that the offset τ₀ captures trapping times far below the transit times, τ_D.

As a generalization, we next considered alternative distribution functions for the trapping times: gamma functions to account for sequential unbinding processes (discussed in relation to molecular interactions in the immune synapse, for example (32)), and Weibull functions to account for heavy-tail kinetics (frequently observed in mobility studies on membrane constituents (33)). Indeed, we found that the shape of the distributions affected the offset according to τ₀ = βτ_trapf_distr,trap, where f_distr,trap describes a distribution-dependent constant (Note 2 in the Supporting Material, and Fig. 3 a) given by

$$f_{\text{distr},\text{trap}}=\frac{1}{2}\left[{\left(CV\left(t_{\text{trap}}\right)\right)}^2+1\right],$$

where $CV\left(t_{\text{trap}}\right)=\frac{\mathrm{std}\left(t_{\mathrm{trap}}\right)}{\mathrm{mean}\left(t_{\mathrm{trap}}\right)}$ denotes the coefficient of variation. An exponential distribution yields f_distr,trap = 1. For $\text{std}\left(t_{\text{trap}}\right)\frac{>}{<}\text{mean}\left(t_{\text{trap}}\right)$, we obtain $f_{\text{distr},\text{trap}}\frac{>}{<}1$. In other words, a distribution yields an offset larger (smaller) than an exponential distribution if its standard deviation is larger (smaller) than its mean, i.e., the distribution is of high variance (low variance). A lower limit of f_distr,trap = 0.5 is given at zero variance.

We also considered nonexponential distributions of τ_free, which altered the offset to τ₀ = $\beta {\tau }_{\text{trap}}\left[f_{{\text{distr}}_1,\text{trap}}+f_{{\text{distr}}_2,\text{free}}\right]$, with $f_{{\text{distr}}_1,\text{free}}=f_{{\text{distr}}_1,\text{trap}}-1$ (Note 3 in the Supporting Material and Fig. 3 a). The two indices shall indicate that the two distributions may be chosen independently, since the kinetics of binding and unbinding processes generally originate from different mechanisms.

Plasma membrane proteins or lipids may well interact with traps that experience residual mobility D_trap themselves; in this case, the effective diffusion constant is given by D_eff = (1 − β)D_free + βD_trap. To estimate the effect on the offset, we performed Monte Carlo simulations using the first-passage-time model and full ACFs. Fig. 3 b shows a decrease in the normalized diffusion-law offset, τ₀/(βτ_trapf_distr), that can be well approximated by an exponential decay according to

$${\tau }_0=\beta {\tau }_{\text{trap}}{\mathit{f}}_{\text{distr}}{\mathit{f}}_{\text{mobility}}\text{with}{\mathit{f}}_{\text{mobility}}\approx \text{exp}\left(-\frac{4}{\sqrt{1-\beta }}\frac{D_{\text{trap}}}{D_{\text{free}}}\right).$$ (4)

For immobile traps with exponential binding kinetics, τ₀ = βτ_trap (Eq. 3) is recovered. For vanishing mobility difference (i.e., D_trap/D_free = 1), the offset should approach zero, which is well approximated by the above equation. We further varied β, yielding a more pronounced effect of trap mobility: the higher the bound fraction, the lower the offset. It is interesting that since the system is sensitive to retardations, the offset is not symmetric with respect to D_free and D_trap. In other words, the consequence of a short period of rapid diffusion differs from that of a short period of slow diffusion. Still, for the extreme limits β → 1and β → 0, the offset vanishes as the system converges against single-component diffusion. Table 2 gives an overview of the derived equations.

Table 2.

Factors influencing sv-FCS diffusion law offsets

Offset	${\tau }_0=\beta \times {\tau }_{\text{trap}}\times f_{\text{mobility}}\times \left(f_{{\text{distr}}_1,\text{trap}}+f_{{\text{distr}}_2,\text{free}}\right)$
β	β = τtrap/(τtrap + τfree)
$f_{{\text{distr}}_1,\text{free}}$	fdistr1,trap − 1
fexp,trap	1
fconstant,trap	1/2
fgamma,trap	1/2 + 1/(2k)
fweibull,trap	1/2(Γ(1 + 2/k)/Γ(1 + 1/k)2)
fmobility	≈ $\text{exp}\left(-4/\sqrt{1-\beta }\times D_{\text{trap}}/D_{\text{free}}\right)$

In a cell membrane, a tracer may experience encounters with different traps of slow mobility D_i = D_free (i.e., f_mobility ≈ 1), which bind the tracer with different affinities, τ_trap,i; on average, the tracer will be bound to the ith trap for a time fraction β_i. For simplicity, we assume here exponential transition kinetics (i.e., f_distr = 1). Then, the diffusion-law offset is given by the weighted mean

$${\tau }_0=\sum _i{\beta }_i{\tau }_{\text{trap},i}.$$

Essentially, slow traps with long interaction times dominate the diffusion-law offset.

In the current literature, diffusion-law offsets are discussed in the context of plasma membrane domains (17,21,24–27,34). From the theoretical solution described in this work, we can interpret domains as special cases of traps with radius r at a fixed location on the timescale of the measurement (see the Supporting Material for details on the domain model). For strong confinement, the time a tracer spends outside or inside a single domain is exponentially distributed (Fig. 4), and the offset is set by the mean residence time τ_residence according to τ₀ = βτ_residence. However, the domain size may further reduce the offset if the particle's effective mobility for crossing the domain, D_residence = 2r²/4τ_residence, gets close to D_free; the factor f_mobility can be extracted from Fig. 3 b by replacing D_trap with D_residence. If the domain permeability is increased, the distribution functions for both τ_free and τ_residence become short-tailed; in this case, f_distr also needs to be considered, which further reduces the diffusion-law offset. Note that even barrier-free domains may yield a measurable offset, if the mobility inside the domain, D_in, is substantially smaller than D_free. Also in that case, the mobile trap approximation can be used now by replacing D_trap with D_in.

Figure 4.

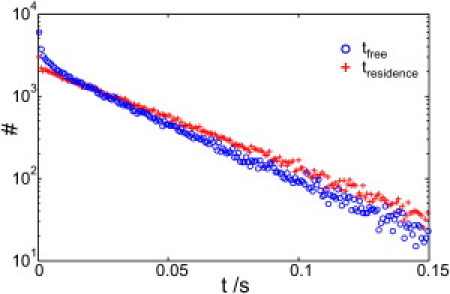
Histogram of domain entry and exit times. We estimated the entry time (t_free) and exit time (t_residence) distribution for circular nonoverlapping domains distributed randomly in the simulation area. Domains covered an area fraction of 30%. By setting the permeability of the domain boundary very low (P_out = 0.01; P_in = 0.02), we found that both transition times follow exponential decays (blue, t_free; red, t_residence). For the simulations, average time decays of τ_free = 30.1 ms and τ_residence = 36.4 ms were adjusted.

Discussion

We have shown here that sv-FCS allows for sensing retardations or immobilizations of two-dimensional tracers at a time resolution way below the transit time through the focal volume. Previously, corresponding offsets in the range of a few milliseconds have been measured in various biological contexts (17,21,22,24,25,34); such time resolution is out of reach using standard FCS (15), and extremely difficult to reach using SPT (18,35,36). Until now, however, data interpretation was hampered by the lack of precise mathematical models describing the determinants of τ₀. We found here that the trapping time influences not only the obtained offset, but also the trap mobility, the time fraction the tracer spends in the slowly diffusing state, and the statistical distribution describing the transition kinetics. Let us briefly discuss some implications of this study for real-life experiments:

• 1.Positive diffusion-law offsets arise from any retardations of the tracer during transit through the spot. Origins may include transient immobilizations, transitions between different diffusion regimes due to changes in the membrane viscosity, or confinement to regions of different lipid composition.
• 2.The diffusion-law offset can be used to determine trapping times. Note that τ₀ is proportional—but not equal—to the trapping time. Let us assume here for simplicity that the tracer binds to immobile traps (i.e., f_mobility = 1) and transition kinetics are exponential (i.e., f_distr = 1). Then, a blocking experiment could be used to reveal directly the trapping times. Without loss of generality, we consider one trapped state only. By varying the degree of blockage, one can vary β without affecting τ_trap. A diffusion law is recorded for each drug concentration, c, yielding τ₀(c) = β(c)τ_trap and D_eff(c) = D_free(1 − β(c)). Already two drug concentrations allow for solving the equation system. If β can be reduced to zero—i.e., the trap can be completely blocked—this approach becomes very simple: the block experiment directly reveals the unknown D_free from the diffusion law slope, which can be used to determine β and τ_trap directly.Alternatively, one may use an analogous approach by influencing τ_trap without affecting τ_free.
• 3.The diffusion law offset reveals insights into the interaction mechanism. In cell biological studies it is common practice to perform additional experiments on mutated proteins for drawing conclusions on the interaction mechanism. By using the strategy delineated in step 2, one can determine β and τ_trap for each mutant.
• 4.The broad sensitivity range makes attractive a screening assay with low false negatives. We envision a screening assay where the diffusion-law offset is used as a sensitive and general readout parameter that senses the influence of drugs on the local environment and interaction properties of the diffusing probe.

Note that in this study, all data were assumed to be recorded under optimal conditions, whereas in a real-life experiment, there are multiple potential causes for noise, as follows:

• 1.Only a limited number of traces can be recorded. Small statistical samples only reduce the precision of the τ_D, and thus τ₀ values obtained, without altering their absolute values (37).
• 2.Photon emission is not continuous but shows antibunching or blinking due to transitions to a triplet state. These processes are typically much faster than the observed diffusion kinetics and can be accounted for by appropriate fit functions (38).
• 3.In cells, additional species may be present that are not membrane-anchored, and different kinetics are observable that can be accounted for (24).
• 4.The fluorophores may bleach during transit through the excitation spot. This can be tested by determining the offset as a function of the laser power.
• 5.Only a limited measurement window is available. In any FCS experiment, the ACF has to be determined beyond the value of τ_D to obtain stable, nonbiased results.
• 6.The spot profile may not be exactly Gaussian, and the deviation may depend on the spot size. This can be approached by z-scan FCS, where the same excitation profile is scanned through the membrane (22).
• 7.The exact spot size has to be determined. A calibration via diffusion-law offsets using a freely diffusing probe can be used to calculate the spot size.

Conclusions

In conclusion, sv-FCS is a fascinating new tool for studying protein and lipid dynamics in the live-cell plasma membrane. Above all, compared to alternative methods, it demonstrates an enormous gain in resolution for measuring the transient confinement times of mobile tracers. The basic idea is very similar to superresolution concepts applied currently in microscopy, where single-molecule localization errors represent the ultimate limit to spatial resolution (11,14). In sv-FCS, time resolution is limited only by measurement errors for the diffusion time τ_D and the confocal spot size ω, not by the tracer's diffusion time through the confocal spot as in conventional FCS. Utilizing the full strength of the method, however, relies on understanding the relation between observables and the underlying physical processes. For SPT, many interdependencies between the recorded single-molecule mobility and system parameters like the diffusion constant, confinement size and strength, local topology, and nature of the binding processes have already been characterized (11). This article describes a step toward putting sv-FCS on a similar analytical basis, so that quantitative analysis of the biological results and the full utilization of the time resolution become possible.