Abstract
Integrins are transmembrane receptors involved in crucial cellular biological functions such as migration, adhesion, and spreading. Upon the modulation of integrin affinity toward their extracellular ligands by cytoplasmic proteins (inside-out signaling) these receptors bind to their ligands and cluster into nascent adhesions. This clustering results in the increase in the mechanical linkage among the cell and substratum, cytoskeleton rearrangements, and further outside-in signaling. Based on experimental observations of the distribution of focal adhesions in cells attached to micropatterned surfaces, we introduce a physical model relying on experimental numerical constants determined in the literature. In this model, allosteric integrin activation works in synergy with the stress build by adhesion and the membrane rigidity to allow the clustering to nascent adhesions independently of actin but dependent on the integrin diffusion onto adhesive surfaces. The initial clustering could provide a template to the mature adhesive structures. Predictions of our model for the organization of focal adhesions are discussed in comparison with experiments using adhesive protein microarrays.
Introduction
Integrins (1) are allosteric transmembrane adhesive proteins with a key role in cell-substrate adhesion and in mechanotransduction, a process by which mechanical forces are transduced into biochemical signals (2). This inside-outside signaling relies on intracellular soluble factors such as talin being able to bind to the integrin cytoplasmic tail (3–5). They induce a conformational change from an inactivated to an activated state with an increase in affinity for the extracellular matrix (6). A general property of all adhesive structures—in their nascent, focal, or fibrillar states—is the recruitment and the clustering of integrins together with compositional changes depending on their maturation stage. Understanding the coupling between integrin activation and integrin clustering is of crucial importance, because integrin activation and clustering regulate cell adhesion and migration through mechanotransduction.
In this article, we focus on the physical mechanisms that regulate lateral assembly of integrins, i.e., initial clustering, in the absence of F-actin (7) but that are talin-dependent. Talin-binding-mediated activation of integrins is β-subunit-specific and occurs with a weak affinity (8–10). In this limit, we show that integrin activation and integrin clustering can be described within the same inside-outside signaling framework. The essential ingredient of our model is the switch between the two integrin affinity states when this switch is induced by a diffusible factor. Previous work (11) has shown that talin binding in the absence of force or other proteins is sufficient to induce the activated form of integrin. To this end, we develop an elementary mechanotransduction model based on an activator field to mimic the role of talin regulating integrin binding to the extracellular matrix.
Due to the competition between the stress and the allosteric activation, talin concentration is increased by diffusion on stressed integrins. This, in turn, provides a robust mechanism for integrin clustering into stationary structures. The existence of such clusters can be experimentally tested by modifying the elementary molecular modules for integrins activation and adhesion (12). As a result, we show that affinity regulation can induce by itself the clustering in nascent adhesion complexes that provide the template of mature focal adhesion patterns (7,13). The principal result reported in this article is that neither direct nor indirect interaction with actin cytoskeleton is necessary to trigger the initial clustering which results only from the activation field sensed by the stressed integrins.
By comparison, former theoretical works have already emphasized the role of acto-myosin mechanical forces for the maturation focal adhesions (14). Stress-sensing models such as the clutch model studied in Bruinsma (15), anisotropic growth of focal adhesions in the direction of the applied force by Nicolas et al. (16,17), force-induced recruitment of integrin partners by Besser et al. (18), or integrin redistribution caused by substrate rigidity by Novak et al. (19) have already been modeled. This article, however, introduces what we believe to be a new mechanotransduction model—one that should be valid for nascent focal adhesions and which does not require the acto-myosin activity but only talin binding to integrins.
To make connections with experimental studies, we include in this article experimental results for cells adhering on adhesive protein microarrays. In the last section, our model will be discussed in the light of these experimental findings by predicting different geometries integrin clusters depending on the size of the adhesive spots.
Methods
Materials
Alexa 488-, 546-, and 633-conjugated secondary antibodies were from Invitrogen (Carlsbad, CA). TRITC-conjugated phalloidin and Pluronic F127 is from Sigma Aldrich (l'isle d'Abeau, France).
Cell culture
NIH 3T3 fibroblasts were cultured in α-MEM (GIBCO-Invitrogen, Oxon, UK) supplemented with 10% inactivated fetal calf serum, penicillin, and streptomycin and were harvested with trypsin/EDTA. Cells were plated with 60,000 cells in 2 mL on microstructured arrays (area of 440 mm2) in 30-mm Petri dishes and were left to spread for 4 h.
Micropatterning and functionalization
Patterned protein glass coverslips were performed according to Guillou et al. (20) with slight modifications. Glass coverslips (22 × 22 mm) were washed in a solution of sulfuric acid and hydrogen peroxide (7:3, vol/vol) for 30 min, dried, and then dipped for 1 h in a solution of octadecyltrimethoxysilane and aminopropyltrimethoxy silane (3:1, mol/mol; Sigma-Aldrich) in toluene. Positive photoresist resin (Shipley, S1805; Rohm & Haas Electronic Materials, Villeurbane, France) was spin-coated and cured according to the manufacturer's protocol to form a uniform, UV-sensitive film 0.5-μm thick. The coated coverslips were then insolated with UV light using a Karl Süss aligner (MJB3; SUSS MicroTec, Saint-Jeoire, France) at 436 nm and 15 mJ/cm2 through a chromium mask.
The irradiated pattern was revealed with microposit developer concentrate in deionized water (1:1, vol/vol, Shipley, MF CD-26; Rohm & Haas Electronic Materials, Marlborough, MA). The patterned coverslips were incubated for 1 h at 37°C in a solution of gelatin-RITC and 10 μg/mL vitronectin in phosphate-buffered saline (PBS). Substrates were rinsed in PBS and then in absolute ethanol in an ultrasonic water bath to dissolve the photoresist resin. Finally, either antiadhesive triblock copolymer Pluronic F127 (Sigma Aldrich) at a concentration of 4% in water for 1 h 30 min at 37°C, or a solution of FN7–10-FITC (Fibronectin type II domains 7–10 conjugated to FITC) at 5–15 μm mL in PBS, was adsorbed to the complementary pattern revealed after resin dissolution by ethanol for 1 h at 37°C. After a last rinse in PBS, 155 cells/mm2 were seeded and incubated overnight, before fixation and staining.
Results
Cell were spread on protein microarrays with adhesive spots of either 4 × 4 μm or 2 × 2 μm made of the fibronectin cellular attachment domain (FN 7–10) and separated by antiadhesive surfaces of polyethylene oxide. On these surfaces, the final shape of spread cells is not predetermined because the cells can use one adhesive spot or another. Indeed, when the lateral distance between two consecutive islands was no more than 8 μm, NIH 3T3 cells attached and spread on the array in a manner similar to that usually observed on uniformly coated surfaces (not shown), whereas when the distance between adhesive islands increased up to 16 μm, most of the cells adopted simplified shapes corresponding to thermodynamic metastable states (21).
Vinculin staining of focal adhesions that are sustained by integrin clusters revealed that only external adhesive islands were used as attachment sites. This is due to pattern symmetries which imply that the resulting force applied by the stress fibers on an internal adhesive island is zero. Therefore, the lack of mechanical cues did not allow focal adhesion assembly on these spots. On 4 × 4 μm adhesive islands with 16-μm spacing (Fig. 1, left panels), however, one could always detect two focal adhesions by adhesive island even when the cells were only using two fibronectin spots. This latter result clearly demonstrates that tensions along actin stress fibers connected to focal adhesions are not the driving forces for integrin clustering. Surprisingly, when the dimensions of the adhesive plots were reduced to 2 × 2 μm, a single integrin clustering connected to fuzzier actin stress fibers was observed on external adhesive islands (Fig. 1, right panels). Even in the angles where orthogonal forces occurred, a single focal adhesion was detected. These experimental data indicated that, in addition to the tensions that promote focal adhesion growth, an additional mechanism is required to explain the splitting of adhesive clusters at constant tension.
Figure 1.
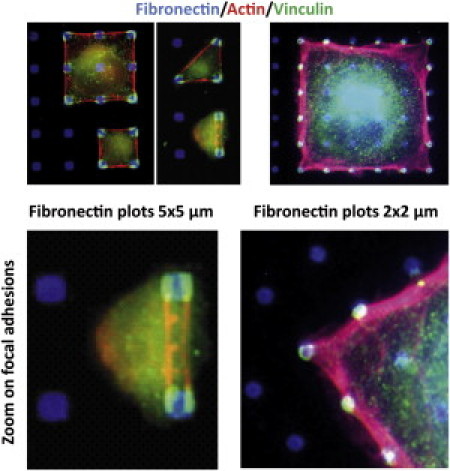
Fibroblasts adhering on fibronectin-patterned substrates. (Left panel) Cells adhering to 4 × 4 μm fibronectin plots. (Right panel) Cells adhering to 2 × 2 μm plots. Adhesive plots are visualized by Alexa350-labeled fibronectin. Actin filaments are labeled with TRITC phalloidin and focal adhesion by a monoclonal anti vinculin antibody and a Alexa488-labeled secondary antibody. For the largest plots, the focal adhesion complexes split into two parts with two stress fibers connecting opposite plots. For the smallest plots, however, the focal adhesive clusters appear homogeneous with only one stress fiber emerging from the adhesion complexes. The transition from one to two adhesive spots on the same plot is geometry-independent, as all cells adhering to square or triangular lattices exhibit the same behavior.
Discussion and Theory
Preliminaries
For what follows, it will be useful to consider the cycle of elementary reactions for talin as shown in Fig. 2. In the cytosol, talin is in the inactivated state with concentration ϕc. When adsorbed on the membrane, talin changes conformation and is activated by binding to PiP2 (22). Once activated, talin diffuses on the membrane and interacts with integrin receptors under the control of other proteins such as RIAM (5) and kindlins (23). Finally, downstream of integrin activation, talin ubiquitination, and degradation leads to disassembly of adhesive clusters (24).
Figure 2.
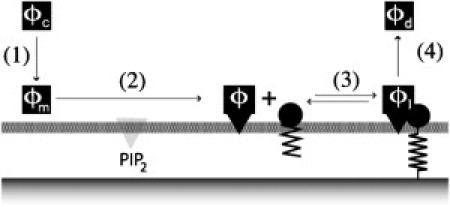
Schematic view of the talin activation cycle (after (44)). (Step 1) Talin in its inactivated state (ϕc) in the cytosol. (Step 2) Talin is recruited at the membrane (ϕm) and is activated by binding to PIP2. In this activated state, ϕ, talin interacts with the integrins (Step 3). The equilibrium between activated talin ϕ and the integrin (the bound complex is denoted ϕI) is crucial. (Step 4) Talin unbinds from the integrin and goes back to its cytosolic state (ϕc).
In particular, as shown in Huang et al. (24), increasing the rate of talin degradation by increasing the affinity of talin to ubiquitin ligase Smurf1 not only increases the turnover of focal adhesions but also, additionally, increases noticeably their number and their size (see Fig. 3 in Huang et al. (24)). This indicates that talin degradation may also be involved at the early stages of nascent adhesions and focal adhesion maturation processes.
Figure 3.
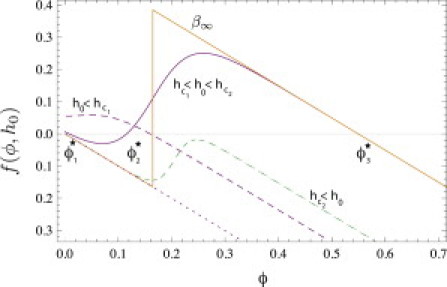
Plot of the effective source function f(ϕ, h0) as a function of ϕ for different values of h0. The figure shows f(ϕ, h0) for four different values of the strain index h0. For , f(ϕ, h0) has three roots instead of one. (Tooth-shaped curve) The β∞ approximation, as taken in the text when passing from Eq. 15 to Eq. 17. (Final curve for ) Nearly-saturated regime where ϕI = ϕ/(Km + ϕ) instead of ϕI = ϕ/Km as in the three previous plots. In this case, the source function f(ϕ, h0) has only one zero for some value of h(x0).
Overall, the cycle can be represented as
| (1) |
where talin is activated at a rate ν1 with concentration ϕ and can reversibly bind to an integrin I with rate constants k±1. Membrane-bound talin is also irreversibly inactivated at a rate γ1. Finally, γ2 is an irreversible dissociation rate and simulates adhesion complex disassembly by degradation.
Table 1 gives the order of magnitude of key physical constants used in our model. Among them, the lifetime 1/b ≃ 100 s of talin in its activated state gives a characteristic diffusion length
This characteristic length is comparable to critical size wc of the adhesive spots above which the focal adhesion clusters split into two clusters. Henceforth, the ratio of the diffusion length, λ, to the spot size, w0, will play a key role in determining different families of solutions for integrin clustering.
Table 1.
List of symbols with typical values used in this work
| Symbol | Meaning | Typical value | |
|---|---|---|---|
| kb | Effective spring constant for integrin-substrate rigidity | 0.3 mN.m–1 (36) | |
| 1/b | Effective residence time of talin | 80–100 s (37,38) | |
| h0 | Range for the elastic strain | 1–15 nm | |
| Dn | Integrin diffusion constant | 10−3–10−2μm2.s–1 (39) | |
| Dϕ | Effective diffusion constant of PIP2 bound talin | 0.2 μm2.s–1 (40) | |
| n∞ | Averaged integrin density at zero stress | 100–500 μm–2 (13) | |
| l0 | Length of the extracellular domain of an integrin | 10 nm (5,41) | |
| k–1 | Rate dissociation constant for the talin-integrin complex | 10−4–10−3 s–1 (25) | |
| AI | Interaction energy between talin and integrin | ≃10–20 kBT (43) | |
| AIϕI,0 | Talin-integrin interaction energy at zero stress | ≃1–5 kBT | |
| at zero stress | 10−3 | ||
| Km | Equivalent Michaelis-Menten constant for talin degradation | ≃103–104μm−2 | |
| 1/β | kBT ≃ 4.1 pN.nm |
In general, the concentrations depend both on space coordinates x and on time t. If x is taken along the cell adhesive substrate, ϕ(x, t) is the surface concentration of talin in the activated state and ϕI(x, t) is the average number of talin per integrin. If n0(x, t) is the total concentration of integrins, n0ϕI is the concentration per unit of surface of talin-integrin complexes. We will refer to this state as the “adsorbed phase”.
In what follows, we will work in the quasi-steady-state approximation where ϕI is in equilibrium with the local concentration of talin ϕ(x, t). When talin is bound to an engaged integrin, it cannot diffuse and local equilibrium fixes an algebraic condition between ϕ(x) and ϕI. This relationship is found from the last step of Eq. 1 and reads as
| (2) |
where Km is a Michaelis-Menten constant with the dimension of a concentration. The last approximation points out the importance of two pathways for talin unbinding, one of which is stress-sensitive. Typically, the dissociation rate k–1 is ∼7.4 10−4 s–1 (25) and if γ2 is of the same order of b ≃ 10−2 s−1, the variations of Km with k–1 can be neglected. Thus, Km is independent of the strain which influences the off-rate of talin unbinding. Using k+1 ≃ 103 l · Mol−1 (25), we find Km = 103–4 molecules per μm2.
Two limit cases will be of interest. For small concentrations ϕ, ϕI is simply proportional to ϕ. In the saturated limit, however, ϕI is independent of ϕ and approaches unity. To summarize for later use, we have
| (3) |
| (4) |
Other nonlinearities with ϕI = aϕγ/(1 + ϕm) where a, γ, m positive numbers can be included in the model without qualitative changes.
Model for integrin activation and engagement
Step 3 of Fig. 2 corresponds to the reversible binding of talin to integrin. In our model, these kinetic rate constants are determined by talin allosteric activation of integrins and by elasticity.
We recall that talin binding to an integrin induces a conformational change for the integrin receptor proteins. According to Anthis et al. (10), the integrin extracellular domain is in its extended conformation in the activated state with talin bound to the intracellular tail. In this state, an integrin is bound to its ligand. By contrast, in the other state, the head is in the bend conformation. In this nonactivated state, the integrin has a smaller probability to bind to its ligand. Henceforth, we will consider the very large affinity limit for extracellular ligand binding where an activated integrin is engaged, whereas a nonactivated one is free to diffuse. To summarize, binding talin to an integrin introduces a conformational change between two states with respective density nu, b, where the density of integrin is conserved nu + nb = n0.
Local equilibrium between these two states is always achieved at a timescale much smaller than the typical timescale for concentration changes due to diffusion. Let Ke(ϕI, h) be the effective equilibrium constant for integrin engagement. Ke(ϕI, h) depends both on the adsorbed talin field ϕI(x, t) and on a strain field h(x) and local equilibrium implies that the density of bound integrins obeys
| (5) |
Taken together, ϕI(x, t) and h(x) play antagonistic roles for adhesion when the concentration of talin ϕ(x) is homogeneous. On the one side, binding talin favors adhesion and thus increases the affinity constant for the extracellular matrix. On the other side, stretching the integrin extracellular head with a length l(x) that differs from a reference length l0 ≃ 10 nm induces a stretching energy ½kbh(x)2 with h(x) = l(x) – l0. By definition, kb is an effective rigidity constant which includes substrate deformability. Following Bell et al. (26), Ward et al. (27), and Munevar et al. (28), this energy is of the order of a few kBT ≃ 4 pN.nM and adds up to the bare energy difference Δfu, b between the two integrin states. This regime is only valid for l smaller than a maximum extension (≃25 nm), and we will henceforth restrict ourselves to this range.
Because binding talin decreases the free energy of the activated state, we have Δfu, b = – AIϕI where –AI is the interaction energy between talin and the cytoplasmic β-subunit. In the zero stress limit where ϕI = ϕI0, we have AIϕ0I ≃ 2.5 kBT (9,29). Summing the allosteric and the elastic contributions gives the enthalpy difference between the two states
| (6) |
Using the Van 't Hoff law, the equilibrium constant follows
| (7) |
where = Ke, 0 exp(AIϕI0) is the equilibrium constant in the absence of stress. This state is a reference state and the principle of the model is to perturb this reference state by strain elasticity with h(x) > 0. Ke0 fixes the number of bound integrins by Eq. 5 and is thus a small number (Ke0 = 10−3 in this work).
To comment Eq. 7 further, we note that NMR studies as in Anthis et al. (10) indicate that the interaction between the two different talin isoforms and the membrane-proximal domain of an integrin is specific of the integrin species. In parallel, small variations of the talin-integrin interaction AI lead to very different values of the equilibrium constant from Eq. 7 when the talin concentration varies. This, in turn, will demonstrate that integrin clustering behavior is specific of the integrin family.
Integrin engagement is stress-dependent
In our model, allosteric activation and tail elasticity contribute to the chemical potential μ(ϕI, h) per integrin. This chemical potential will influence the desorption rate k–1 in Eq. 1 and, thus, will modify the equation of motion for talin diffusing on the membrane. To compute the chemical potential, we neglect all entropic contributions and retain the most singular part as
| (8) |
which follows from Eq. 6 times the probability density to find an integrin in its activated-engaged state. From Eq. 5, nb(ϕI, h) is steplike when ϕ varies at constant strain h(x) = h0. Taking the derivative as done in Eq. 8 introduces a δ-like singularity in the chemical potential when talin allosteric activation compensates strain elasticity
| (9) |
which is approximately equal to 10 kBT for h0 = 5–10 nm.
Because the chemical potential depends on the strain h(x) by Eq. 8, varying h(x) influences integrin engagement and talin concentration. Experimentally, h(x) can be varied in numerous ways. For example, the use of micropatterned substrates concentrates the stress at the margin of the adhesive spots. Another way is to probe h(x) directly, using single molecule assays to stretch the integrin head in the nanometer range.
Henceforth, we will work in the thermodynamic ensemble where the strain is fixed at a given function h(x). For numerical and analytical convenience, h(x) will be taken as a Gaussian h0 exp(–x2/2w02) of width w0 and height h0. As shown below, the state of the system is globally independent of exact analytical form of h(x) as long as h(x) can be greater than some threshold value on a region of size w0 larger than the diffusion length .
Talin equation of motion
Step 3 of Fig. 2 is the adsorption-desorption process for the dynamic of the activated talin ϕ(x), which is otherwise allowed to diffuse on the membrane with diffusion constant Dϕ. The chemical potential of Eq. 6 influences the desorption rate of talin-integrin bound state to the free state. At the end, the theory is self-consistent, because this desorption rate for talin-integrin unbinding depends on the local concentration ϕ.
To derive this self-consistent equation, we define a reference state concentration ϕ0 of talin at zero stress (i.e., h(x) = 0; see Appendix A). When measured with respect to this reference state, ϕ → ϕ0, the equation of evolution for the relative excess of concentration ϕ is written as
| (10) |
where the last term is proportional to the excess of chemical potential in the bound phase due to strain elasticity. Physically, this term describes how an excess of talin compensates for the increase of the desorption rate due to integrin engagement. Using the model of Eq. 1, this equation is derived in Appendix A under the assumption that the kinetic rate constant for talin desorption is influenced by the chemical potential of Eq. 8, which contains stress elasticity. The diffusion-reaction equation, Eq. 10, is thus equivalent to the one used to study the growth of focal adhesions (see Besser et al. (18), but with a talin-dependent strain elasticity.
In Eq. 10, ΓI is a kinetic coefficient between the talin bound and free states and is proportional to the off-rate of the talin-integrin unbinding. Because ΓI is proportional to AI, i.e., ΓI reflects the talin affinity for an integrin, ΓI is also β-subunit specific. The last term is proportional to the density n0 of integrins. As the bare affinity is small, nb(ϕI, h) is a step function when ϕI varies. Thus, ∂nb/∂ϕI has a singularity to mimic the switch in integrin affinity toward its ligand (30). This term depends on ϕ by the quasi-steady-state condition gI(ϕ, ϕI) = 0. Thus the dynamic of the field ϕ(x) depends on diffusion by Dϕ, on the residence time of talin in its activated state by b, and, finally, on the strain h(x). This equation describes how elasticity provides a positive feedback loop for integrin activation when the source term in Eq. 10 is maximum.
Integrin equation of motion
Equation 10 gives the correct evolution of ϕ(x) as long as the integrin density n0(x) does not respond to the variations of ϕ(x). Because the integrin diffusion constant is smaller than the one for talin, this approximation holds at very short times. At longer times, however, there is a change in integrin concentration n0 = nu + nb, because unbound integrins nu diffuse (diffusion constant Dn). Because of local equilibrium, the equilibrium constant gives the fraction of bound to unbound integrins as
| (11) |
As a result, the effective diffusion equation for the integrin concentration field n0(x, t) reads as
| (12) |
Equation 12, together with Eq. 10, gives a complete system for a given strain profile h(x).
Effective diffusion-reaction equation
The essential property of our model is that it describes integrin activation in cooperation with changes in talin concentration. From now on, we will concentrate in the small talin concentration limit with ϕI = ϕ (see Eq. 3). The large ϕ limit of Eq. 4, where ϕI saturates, is studied in the last section. Mathematical analysis will focus on the one-dimensional case when the typical radius of curvature of the adhesive spot is larger than the diffusion length .
Using the two equations of motion, we solve the problem as follows. In the symmetric case h(x) = h(–x), Eq. 12 has the unique solution
| (13) |
Because Eq. 10 is valid for an arbitrary integrin density n0, we use Eq. 13 in Eq. 10. As a result, we solve the effective reaction-diffusion equation
| (14) |
with the source function f(ϕ, h)
| (15) |
To mimic adhesive spots surrounded by nonadhesive islands, boundary conditions are chosen so that both the strain h(x) and the concentration ϕ(x) vanish at infinity.
The characteristic shapes of f(ϕ, h) are given in Fig. 3 in the small and large h(x) = h0 limits. For , f(ϕ, h(x)) has only one zero whereas, for , it has three zeros ϕ1, 2, 3. In that case, the system is again bistable. Thus, for an homogeneous strain profile , the effective diffusion equation can be used to describe lateral excitation of a signal which propagates with a threshold response. The existence of three zeros for the source functions f(ϕ, h) at fixed h = h0 is a characteristic property of reaction-diffusion systems with propagating wave solutions. Henceforth, we will study stationary solutions of Eq. 14 with ∂ϕ/∂t = 0. These solutions may be seen as waves pinned by strain elasticity, because they are concentrated where the stress is maximum.
Integrin clustering is stress-dependent and is characterized by two families of solutions
In the allosteric model for integrin activation of Eq. 6, the elastic stress competes with the talin field to regulate integrin activation and engagement. When activated talin diffuses on the membrane, however, this competition leads on an amplification loop. To bias this competition, we vary the strain profile by changing h0 and compute the stationary solutions for ϕ(x) and nb(x). Stability of these solutions with respect to variations in integrin concentration is checked using the equivalent equations (Eqs. 10 and 12) for different initial conditions in the regime where ϕ3 in Fig. 3 tends smoothly to zero when x goes to infinity. Other strain functions h(x) with characteristic variations on a width w0 have been tested without qualitative changes. Solving the model amounts to comparing numerical solutions with asymptotic results, as done in the next section.
Small stress regime ϕI = ϕ/Km: numerical results
Fig. 4, a–c, for the talin and integrin concentration fields demonstrates that stress leads to integrin clustering. Depending on the strain, this clustering is described by two families of solutions.
Figure 4.
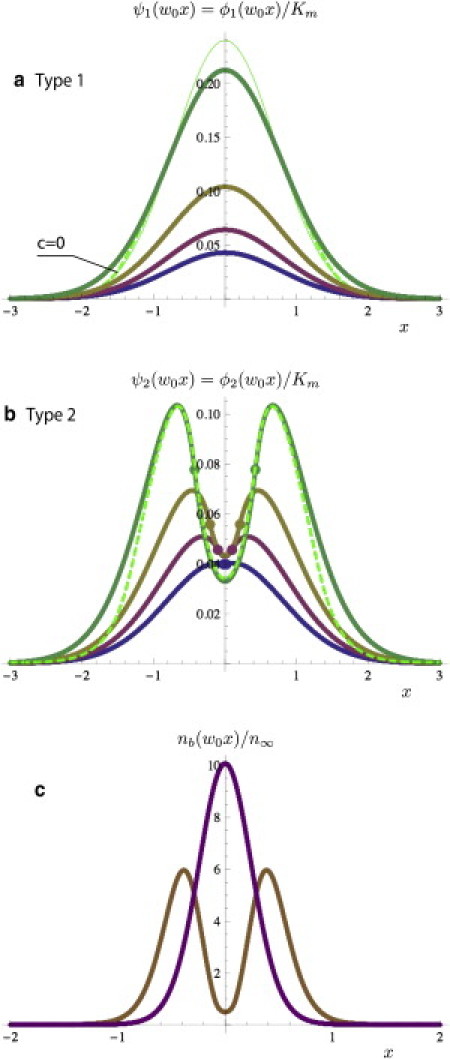
(a) Plot of the type 1 family talin concentration AIϕ1(w0x)/Km for parameter values taken from Table 1. (Dashed curve) Approximate analytical solution with c = 0 (see the Supporting Material). Otherwise, numerical solutions and thick curves corresponding to type 1 solutions of the β∞ model coincide on the scale of the figure. (Thin curve) Asymptotic expansion of the analytical solution given by Eq. S10 in the Supporting Material. It shows that asymptotic results are already reliable even if as in the case of this figure. Color-code (from the top to the bottom curve) indicates that 1/2βkbh02 decreases stepwise (15, 7.5, 4.5 to 3), with the largest value in green. (b) Plot of the type 2 family solutions AIϕ2(w0x)/Km. (Dashed curves) Numerical solutions. Thick and dashed curves coincide when ϕ3∗ goes to zero smoothly as |x| goes to infinity. (Circles) Boundary points x0 for type 2 solutions where the solution passes through the singularity of the β∞ model. Decreasing h0 changes the solution until it matches a type 1 solution at the bifurcation point. The color code (from the top to the bottom curve) for panel b is the same as for panel a. (c) Plot of the density of engaged integrin nb(w0x) for centered type 1 and type 2 solutions for the same parameters (½βkbh02 = 4.5). For convenience, type 1 solutions have been scaled down by a factor 10 (w0 = 10 μm).
Solution family type 1
For small stress values, , clustering corresponds to a unique centered distribution of ϕ which increases rapidly with h0. These solutions correspond to the long dashed curves shown in the figure and they will be compared to the analytical solution in the next section. Type 1 solutions are always characterized by a centered maximum of talin concentration at the origin The distribution of bound integrins follows from the solution of ϕ(x) because
| (16) |
where n∞ is fixed by the condition at infinity. Type 1 solutions for nb are characterized by a maximum at the origin. Only near bifurcation points, type 1 solutions for nb may exhibit a local minimum.
Solution family type 2
At larger strain, where the source function from Eq. 15 possesses three zeros, there is a new family of solutions. Type 2 solutions are characterized by a distribution of talin with a double symmetric maximum. These maxima merge with the centered maximum of type 1 solution when . Using Eq. 16, the distribution of bound integrins is always symmetric with respect to the origin and concentrates rapidly at the margin of the zone where the stress is applied when h0 is increased above . Type 1 and 2 solutions exist for if the diffusion length is small enough with respect to the characteristic width w0 of the strain h(x), D bw20 << 1. They are both stable for a large class of initial conditions (using Eqs. 10 and 12).
Small stress regime ϕI ≃ ϕ/Km: analytical results
To get insights into the two families of stationary solutions, we approximate the source function f(ϕ, h) by its β → ∞ limit. In this case, the Boltzmann function converges to the Heaviside θ[x] function with two inclines (see red curve of Fig. 3). The source function in Eq. 15 becomes
| (17) |
We call this the “β∞ model” and solve exactly for ϕ(x) as done in the Supporting Material. From this solution, we find n0(x) and nb(x) using Eqs. 11 and 13. Plots of solutions of this asymptotic model are also given in Fig. 4, a and b, for comparison with numerical data.
Type 1 solutions
Fig. 4 a corresponds to this case. This solution has a maximum (see Eq. S10 of the Supporting Material). In the small diffusion length limit D/bw02, we find (see thin curve in Fig. 4 a)
| (18) |
As expected, the concentration of talin increases with rigidity. Decreasing b, or equivalently increasing the lifetime of activated talin, has the same effect. From this, we find that the density of bound integrins for type 1 solution is asymptotically given by
| (19) |
What the model predicts is thus a local increase of ϕ, and therefore of ϕI, to counterbalance the negative effect of the strain h0 on integrin engagement. Because of the exponential dependence, Eq. 19 is very sensitive to variations in strain h0 and to changes in parameters. If the talin-integrin interaction energy AI is multiplied by a factor 2, ΓI changes by a factor of 4 and the exponential in Eq. 19 is raised to the same power. Such a sudden increase in integrin density upon small changes in AI is the distinctive mark of a positive feedback loop contained in the model.
Type 2 solutions
In contrast to type 1 solutions, solutions of type 2 are characterized by a minimum of talin concentration at the origin. The width of this depletion zone is set by the diffusion length λ with ϕ(x) ∝ cosh(x/λ). Thus, for type 2 solutions, the effect of the strain is to exclude talin proteins from the center with a maximum of concentration at a characteristic distance ± w0. The calculation reported in the Supporting Material demonstrates that type 2 solutions cannot be constructed if the ratio λ/w0 is too small. In this regime, diffusion smoothes out any irregularity in the strain profile h(x) and, by symmetry, the concentration field of talin can only have a centered maximum.
Fig. 5 a shows how the distribution of talin evolves when w0 decreases at fixed strain h0. Starting at large width w0, the distribution shrinks and the minimum is less pronounced as diffusion is more and more effective. At a critical width wc, the two maxima merge at the origin. Below wc, the unique solution is of type 1 with a centered maximum. Fig. 5 b is the accompanying figure for the distribution of bound integrins. Although the distribution of talin is centered below the bifurcation point, the distribution nb(x) may have a minima in its immediate vicinity.
Figure 5.
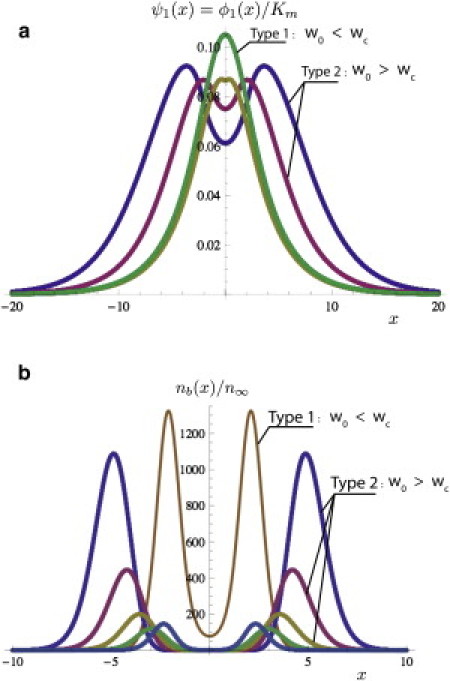
(a) Plot of the talin density AIϕ(w0x)/Km as a function of x. Decreasing the ratio w0/λ at fixed strain h0 decreases the characteristic distance between the two maxima. Decreasing this ratio further leads to a critical width where type 2 solutions stop existing. For w0 < wc, the only solution is of type 1 and corresponds to the centered distribution shown in this figure. (b) Plot of nb(w0x)/n∞. Although AIϕ1(w0x)/Km is always maximum at the origin, nb(x) for type 1 solution can be minimum in the near vicinity of the bifurcation point. In both figures, wc ≃ 25 μm (for both figures, λ = 2.8 μm and the color-code (from the top to the bottom curve) indicates that w0 decreases in steps of 1 μm from 6 to 2 μm).
The condition for existence of a type 2 solution in the Supporting Material is given by the matching conditions of the two branches below and above the singularity given by the θ function in Eq. 17 when ϕ2(x) satisfies the condition in Eq. 9. These conditions result from conservation laws which imply that concentration and current are conserved quantities when ϕ(x) passes through the singularity at x = x0. For all curves of Fig. 4 b, this point is indicated by a dot. At bifurcation, this point coincides with the origin. From this, we compute the critical width wc at given h0 (see Eq. S16 in the Supporting Material with x0 = 0)
| (20) |
As a result, the critical width decreases with AI and with the strain h0. Using Table 1, Fig. 5 a gives a value for wc of ∼2–3 μm.
Equation 20 is derived for a Gaussian profile h(x) = h0 exp [–x2/(2w20)]. Numerical experiments with other strain profiles show small changes in the critical width wc for different strain functions h(x). A reason for this is that the source function from Eq. 17 is independent of the strain profile near the origin, so that the cosh(x/λ) solution is universal and independent of the profile h(x).
Large stress regime: extension of the linear model to include the saturation limit of the bound talin field ϕI
Clearly, the linear regime ϕI = ϕ/Km is only valid at small strain h0, and ϕI must saturate above a critical value fixed by the equivalent Michaelis-Menten constant as in Eq. 4. As ϕ increases with h0 (see Eq. 18 for type-1 solutions), the boundary value ϕ above which the linear regime breaks-down sets an equivalent condition for h0.
In this saturated limit where ϕI tends to 1, the equilibrium concentration of talin bound to integrin is independent of ϕ, because all integrins are already activated. In that case, the equivalent source function for reaction-diffusion has only one fixed point instead of being tooth-shaped as in Fig. 3. Let us call , the value of h0 above which the equivalent source function f(ϕ, h0) has only one zero. For , type 1 solutions cease to exist. Numerically, adding Langevin noise to the equation of motion or steric repulsion between integrins leads to the same effect when n0(x) is large because the saturated limit for type 1 solutions is very sensitive to fluctuations in integrin density.
Discussion and Conclusion
To conclude, our approach leads to integrin clustering and embodies collective effects between different families of integrins. Thermodynamics provides an effective activation potential so that there is no need for direct or indirect interactions between the integrin receptors for clustering. The model can be represented as an effective reaction-diffusion system with the conclusion that integrin clustering is driven by integrin activation imposed by mechanical constraints. Mixing elasticity and chemical reactions reproduces the characteristic properties of excitable media, which has already been evoked in Wang et al. (31) for the mechanical activation of Src.
Activation mediated by talin binding depends on the β integrin cytoplasmic subunits and this dependence is explicit in the model through the interaction energy parameter AI. Small variations of this parameter lead to exponential variations of talin concentration, and influences markedly the locus of bifurcation lines. Testing the role of α5β1 and αvβ3 integrins for mechanotransduction has already been proposed in Roca-Cusachs et al. (32). Because our model links integrin activation to mechanical stress, we propose to test further these differences by varying other parameters such as the width of the zone where the stress is applied.
These results are with respect to the experimental findings of the first section. In our work, advanced lithography techniques allow us to control the size of the adhesive spots at the cell-substrate contact interface. For this, we take the width w0 as the typical size of the adhesive spots, which corresponds in the model to the parts of the contact zone where the integrins are submitted to a stress. Although our model applies only at short timescales after the first contacts and integrin ligation, we propose that it serves as a template to discuss more mature focal adhesion complexes which develop from these nascent adhesion clusters.
In short, by imposing a mechanical constraint, the model predicts different spatial organization for cell receptors which, thereby, may alter the specificity of their signaling functions. This hypothesis is explicit in Paszek and Weaver (33) and Salaita et al. (34), and a mark of our model is to define a framework from only three experimentally accessible quantities.
Acknowledgments
We thank V. Lorman and C. Picart for careful reading of the manuscript and useful comments.
This research was supported from the CellTissue grant No. GDR 3070. This work is supported in part by the NanoFab micro fabrication facility of Louis Neel Institute (Centre National de la Recherche Scientifique UPR 5051). This work is also supported by the “Ligue Nationale contre le Cancer” as an “Équipe Labellisée”.
Footnotes
H. Gullou's present address is Institut Néel, CNRS et Université Joseph Fourier, BP166, 38042 Grenoble cédex 9, France.
Appendix A
To find the local free energy per unit surface area, we work in the framework of a lattice gas model where each site can be occupied by an integrin of density n0. Activated talin is free to diffuse on the membrane seen an adlayer and it can get reversibly adsorbed on the sites occupied by the integrins:
| (21) |
To evaluate μ([ϕI], h) as in Eq. 8, we consider only the most singular term
| (22) |
Note that the derivative disappears if talin had a very high affinity for integrin, because nb would not vary.
Introducing the rate of production ν1 for activated talin, the equation of motion is
| (23) |
which, together with Eq. 2, can be used to find the stationary solutions.
A convenient way to solve Eq. 23 is to introduce a reference state at zero stress h(x) = 0. This reference state ϕ0 is homogeneous and solves the equation of motion,
| (24) |
with the steady-state condition equation, Eq. 2, at zero stress. Thus, ϕ0 is an increasing function of the rate of ν1 with which talin is activated by binding talin to the membrane with PIP2. If this rate is large enough, as is generally the case because PIP2 is produced at a very large rate, this state can used as a reference state.
Making the change of variable ϕ → ϕ0 + ϕ, we look for a solution ϕ(x, t) proportional to the rigidity kb. To linear order, eβΔμ ≃ 1 + βΔμ, because Δμ is linear in kb. We find that the relative excess of concentration ϕ(x, t) is solution of the equation used in text
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
with K0e evaluated in the reference state at zero stress:
| (30) |
To make this evolution equation as simple as possible, we have neglected terms ϕ∂nb/∂ϕ which are next order in kb and saturate in the large ϕ-limit by the condition Eq. 2. Finally, fewer singular contributions to the chemical potential such as nb(ϕ, h), which appear when taking the derivative Eq. 8, will change the low ϕ limit of f(ϕ, h0) in Fig. 3 without affecting the bistable characteristic property.
Supporting Material
References
- 1.Hynes R.O. Integrins: bidirectional, allosteric signaling machines. Cell. 2002;110:673–687. doi: 10.1016/s0092-8674(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 2.Vogel V., Sheetz M. Local force and geometry sensing regulate cell functions. Nat. Rev. Mol. Cell Biol. 2006;7:265–275. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
- 3.Calderwood D.A. Talin controls integrin activation. Biochem. Soc. Trans. 2004;32:434–437. doi: 10.1042/BST0320434. [DOI] [PubMed] [Google Scholar]
- 4.Moser M., Legate K.R., Fässler R. The tail of integrins, talin, and kindlins. Science. 2009;324:895–899. doi: 10.1126/science.1163865. [DOI] [PubMed] [Google Scholar]
- 5.Shattil S.J., Kim C., Ginsberg M.H. The final steps of integrin activation: the end game. Nat. Rev. Mol. Cell Biol. 2010;11:288–300. doi: 10.1038/nrm2871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Anthis N.J., Campbell I.D. The tail of integrin activation. Trends Biochem Sci. 2011 doi: 10.1016/j.tibs.2010.11.002. 2011 Jan 6. [Epub ahead of print] PubMed PMID: 21216149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cluzel C., Saltel F., Wehrle-Haller B. The mechanisms and dynamics of αvβ3 integrin clustering in living cells. J. Cell Biol. 2005;171:383–392. doi: 10.1083/jcb.200503017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bouaouina M., Lad Y., Calderwood D.A. The N-terminal domains of talin cooperate with the phosphotyrosine binding-like domain to activate β1 and β3 integrins. J. Biol. Chem. 2008;283:6118–6125. doi: 10.1074/jbc.M709527200. [DOI] [PubMed] [Google Scholar]
- 9.Calderwood D.A., Yan B., Ginsberg M.H. The phosphotyrosine binding-like domain of talin activates integrins. J. Biol. Chem. 2002;277:21749–21758. doi: 10.1074/jbc.M111996200. [DOI] [PubMed] [Google Scholar]
- 10.Anthis N.J., Wegener K.L., Campbell I.D. The structure of an integrin/talin complex reveals the basis of inside-out signal transduction. EMBO J. 2009;28:3623–3632. doi: 10.1038/emboj.2009.287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ye F., Hu G., Ginsberg M.H. Recreation of the terminal events in physiological integrin activation. J. Cell Biol. 2010;188:157–173. doi: 10.1083/jcb.200908045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Streicher P., Nassoy P., Bassereau P. Integrin reconstituted in GUVs: a biomimetic system to study initial steps of cell spreading. Biochim. Biophys. Acta. 2009;1788:2291–2300. doi: 10.1016/j.bbamem.2009.07.025. [DOI] [PubMed] [Google Scholar]
- 13.Wiseman P.W., Brown C.M., Horwitz A.F. Spatial mapping of integrin interactions and dynamics during cell migration by image correlation microscopy. J. Cell Sci. 2004;117:5521–5534. doi: 10.1242/jcs.01416. [DOI] [PubMed] [Google Scholar]
- 14.Bershadsky A., Kozlov M., Geiger B. Adhesion-mediated mechanosensitivity: a time to experiment, and a time to theorize. Curr. Opin. Cell Biol. 2006;18:472–481. doi: 10.1016/j.ceb.2006.08.012. [DOI] [PubMed] [Google Scholar]
- 15.Bruinsma R. Theory of force regulation by nascent adhesion sites. Biophys. J. 2005;89:87–94. doi: 10.1529/biophysj.104.048280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nicolas A., Geiger B., Safran S.A. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc. Natl. Acad. Sci. USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nicolas A., Besser A., Safran S.A. Dynamics of cellular focal adhesions on deformable substrates: consequences for cell force microscopy. Biophys. J. 2008;95:527–539. doi: 10.1529/biophysj.107.127399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Besser A., Safran S.A. Force-induced adsorption and anisotropic growth of focal adhesions. Biophys. J. 2006;90:3469–3484. doi: 10.1529/biophysj.105.074377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Novak I.L., Slepchenko B.M., Loew L.M. Cooperativity between cell contractility and adhesion. Phys. Rev. Lett. 2004;93:268109. doi: 10.1103/PhysRevLett.93.268109. [DOI] [PubMed] [Google Scholar]
- 20.Guillou H., Depraz-Depland A., Block M.R. Lamellipodia nucleation by filopodia depends on integrin occupancy and downstream Rac1 signaling. Exp. Cell Res. 2008;314:478–488. doi: 10.1016/j.yexcr.2007.10.026. [DOI] [PubMed] [Google Scholar]
- 21.Vianay B., Käfer J., Guillou H. Single cells spreading on a protein lattice adopt an energy minimizing shape. Phys. Rev. Lett. 2010;105:128101. doi: 10.1103/PhysRevLett.105.128101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Martel V., Racaud-Sultan C., Albiges-Rizo C. Conformation, localization, and integrin binding of talin depend on its interaction with phosphoinositides. J. Biol. Chem. 2001;276:21217–21227. doi: 10.1074/jbc.M102373200. [DOI] [PubMed] [Google Scholar]
- 23.Harburger D.S., Bouaouina M., Calderwood D.A. Kindlin-1 and -2 directly bind the C-terminal region of β integrin cytoplasmic tails and exert integrin-specific activation effects. J. Biol. Chem. 2009;284:11485–11497. doi: 10.1074/jbc.M809233200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huang C., Rajfur Z., Ginsberg M.H. Talin phosphorylation by Cdk5 regulates Smurf1-mediated talin head ubiquitylation and cell migration. Nat. Cell Biol. 2009;11:624–630. doi: 10.1038/ncb1868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yan B., Calderwood D.A., Ginsberg M.H. Calpain cleavage promotes talin binding to the β3 integrin cytoplasmic domain. J. Biol. Chem. 2001;276:28164–28170. doi: 10.1074/jbc.M104161200. [DOI] [PubMed] [Google Scholar]
- 26.Bell G.I., Dembo M., Bongrand P. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 1984;45:1051–1064. doi: 10.1016/S0006-3495(84)84252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ward M.D., Dembo M., Hammer D.A. Kinetics of cell detachment: peeling of discrete receptor clusters. Biophys. J. 1994;67:2522–2534. doi: 10.1016/S0006-3495(94)80742-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Munevar S., Wang Y.L., Dembo M. Regulation of mechanical interactions between fibroblasts and the substratum by stretch-activated Ca2+ entry. J. Cell Sci. 2004;117:85–92. doi: 10.1242/jcs.00795. [DOI] [PubMed] [Google Scholar]
- 29.Li F., Redick S.D., Moy V.T. Force measurements of the α5β1 integrin-fibronectin interaction. Biophys. J. 2003;84:1252–1262. doi: 10.1016/S0006-3495(03)74940-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ali O., Albigès-Rizo C., Fourcade B. Excitable waves at the margin of the contact area between a cell and a substrate. Phys. Biol. 2009;6:025010. doi: 10.1088/1478-3975/6/2/025010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang Y., Botvinick E.L., Chien S. Visualizing the mechanical activation of Src. Nature. 2005;434:1040–1045. doi: 10.1038/nature03469. [DOI] [PubMed] [Google Scholar]
- 32.Roca-Cusachs P., Gauthier N.C., Sheetz M.P. Clustering of α5β1 integrins determines adhesion strength whereas αvβ3 and talin enable mechanotransduction. Proc. Natl. Acad. Sci. USA. 2009;106:16245–16250. doi: 10.1073/pnas.0902818106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Paszek M., Weaver V. Biophysics. Enforcing order on signaling. Science. 2010;327:1335–1336. doi: 10.1126/science.1187865. [DOI] [PubMed] [Google Scholar]
- 34.Salaita K., Nair P.M., Groves J.T. Restriction of receptor movement alters cellular response: physical force sensing by EphA2. Science. 2010;327:1380–1385. doi: 10.1126/science.1181729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Reference deleted in proof.
- 36.Taubenberger A., Cisneros D.A., Franz C.M. Revealing early steps of α2β1 integrin-mediated adhesion to collagen type I by using single-cell force spectroscopy. Mol. Biol. Cell. 2007;18:1634–1644. doi: 10.1091/mbc.E06-09-0777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Himmel M., Ritter A., Ziegler W.H. Control of high affinity interactions in the talin C terminus: how talin domains coordinate protein dynamics in cell adhesions. J. Biol. Chem. 2009;284:13832–13842. doi: 10.1074/jbc.M900266200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lele T.P., Thodeti C.K., Ingber D.E. Investigating complexity of protein-protein interactions in focal adhesions. Biochem. Biophys. Res. Commun. 2008;369:929–934. doi: 10.1016/j.bbrc.2008.02.137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Duband J.L., Nuckolls G.H., Jacobson K. Fibronectin receptor exhibits high lateral mobility in embryonic locomoting cells but is immobile in focal contacts and fibrillar streaks in stationary cells. J. Cell Biol. 1988;107:1385–1396. doi: 10.1083/jcb.107.4.1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Golebiewska U., Nyako M., McLaughlin S. Diffusion coefficient of fluorescent phosphatidylinositol 4,5-bisphosphate in the plasma membrane of cells. Mol. Biol. Cell. 2008;19:1663–1669. doi: 10.1091/mbc.E07-12-1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Takagi J., Erickson H.P., Springer T.A. C-terminal opening mimics ‘inside-out’ activation of integrin α5β1. Nat. Struct. Biol. 2001;8:412–416. doi: 10.1038/87569. [DOI] [PubMed] [Google Scholar]
- 42.Reference deleted in proof.
- 43.Anthis N.J., Wegener K.L., Campbell I.D. Structural diversity in integrin/talin interactions. Structure. 2010;18:1654–1666. doi: 10.1016/j.str.2010.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Critchley D.R. Cytoskeletal proteins talin and vinculin in integrin-mediated adhesion. Biochem. Soc. Trans. 2004;32:831–836. doi: 10.1042/BST0320831. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


