Striated Acto-Myosin Fibers Can Reorganize and Register in Response to Elastic Interactions with the Matrix

Abstract

The remarkable striation of muscle has fascinated many for centuries. In developing muscle cells, as well as in many adherent, nonmuscle cell types, striated, stress fiberlike structures with sarcomere-periodicity tend to register: Based on several studies, neighboring, parallel fibers at the basal membrane of cultured cells establish registry of their respective periodic sarcomeric architecture, but, to our knowledge, the mechanism has not yet been identified. Here, we propose for cells plated on an elastic substrate or adhered to a neighboring cell, that acto-myosin contractility in striated fibers close to the basal membrane induces substrate strain that gives rise to an elastic interaction between neighboring striated fibers, which in turn favors interfiber registry. Our physical theory predicts a dependence of interfiber registry on externally controllable elastic properties of the substrate. In developing muscle cells, registry of striated fibers (premyofibrils and nascent myofibrils) has been suggested as one major pathway of myofibrillogenesis, where it precedes the fusion of neighboring fibers. This suggests a mechanical basis for the optimal myofibrillogenesis on muscle-mimetic elastic substrates that was recently observed by several groups in cultures of mouse-, human-, and chick-derived muscle cells.

Introduction

The cytoskeleton of adherent cells can organize into highly regular structures: Actin and myosin filaments can bundle into long fibers, and fibers can align parallel to each other (1), in a type of nematic ordering of the cytoskeleton (2,3). In a variety of cell types, different kinds of acto-myosin bundles additionally possess periodic internal structure with alternating localization of myosin filaments and the actin cross-linker α-actinin. Examples include striated stress fibers in fibroblasts (Fig. 1 A) and striated stress-fiber-like acto-myosin bundles in some developing muscle cells (Fig. 1 B) (4–7). The striated architecture of these fibers has similarity to the sarcomeric architecture of myofibrils in striated muscle, but is much less regular. In both adherent, nonmuscle cells and developing striated muscle cells, the striations of neighboring, but distinct fibers are often in registry, i.e., the positions of the respective α-actinin and myosin bands match (see Fig. 1, panel D versus panel C). This interfiber registry of striated fibers represents a further state of cytoskeletal order, which we term “smectic order” in analogy to liquid crystal terminology.

Figure 1.

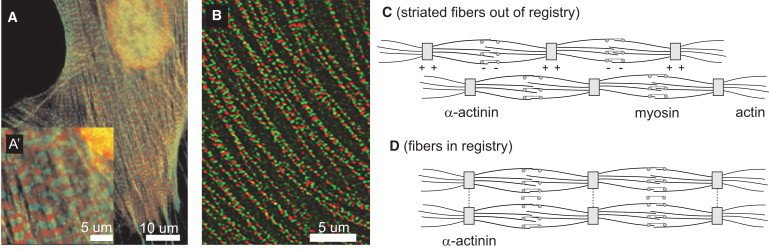
(A) Adherent, nonmuscle cells can exhibit striated stress fibers characterized by an alternating localization of the actin cross-linker α-actin (green; light gray in print) and nonmuscle myosin II (red; dark gray in print); calyculin stimulated gerbil fibroma cell, taken from Peterson et al. (44) with permission. Scale bar, 10 μm (A), 5 μm (A′). (B) Developing striated muscle cells can exhibit acto-myosin fibers close to the cell membrane, which are, like striated stress fibers, characterized by an alternating localization of the α-actin (red; dark gray in print) and nonmuscle myosin II (green; light gray in print). Cultured avian cardiomyocytes, taken from Du et al. (12) with permission. Scale bar, 5 μm. (C) Schematic view of two striated fibers. Striated stress fiberlike acto-myosin fibers form close to the cell-substrate interface of adherent, nonmuscle cells, but also in developing striated muscle cells, where they are proposed to represent precursor structures of the mature myofibrils (10). Each fiber is a bundle of aligned actin filaments that has a sarcomeric subarchitecture: Z-bodies that cross-link actin filament barbed ends alternate with regions rich in myosin II in a periodic fashion. Striated stress-fibers in nonmuscle cells share a similar architecture. (D) Striated fibers can slide past each other until their periodic structures are in phase (8). This interfiber registry has been suggested as a prerequisite for the lateral fusion of Z-bodies into nascent Z-disks.

Striated fibers in various types of muscle cells or those in nonmuscle cells can differ in their actin and myosin isoforms, and some scaffolding proteins like titin, nebulin, and N-RAP appear specific to muscle cells. Nevertheless, these striated fibers share important physical features that include a periodic architecture, stress generation via acto-myosin contractility, and some level of mechanical coupling to a substrate. Thus, despite their different protein compositions, a common physical mechanism may guide interfiber registry in these different cases.

Striated stress-fiber-like acto-myosin bundles, close to the plasma membrane of developing muscle cells, have been proposed to be important intermediate structures in at least one pathway of myofibrillogenesis, i.e., the formation of the mature contractile myofibrils in skeletal and cardiac muscle cells (7–10). These striated fibers in muscle cells are therefore referred to as either striated premyofibrils or nascent myofibrils, the distinction depending on the myosin II-isoform they contain: Premyofibrils are defined as to comprise only nonmuscle myosin filaments, which are then replaced by muscle-specific isoforms upon maturation into nascent myofibrils (10). These striated fibers can slide relative to each other on a timescale of hours to establish interfiber registry of their respective sarcomeric periodicity (8).

Interfiber registry is a prerequisite for the subsequent fusion of neighboring thin fibers into nascent myofibrils of increased width in this particular myofibrillogenesis pathway. Finally, myofibrils at the plasma membrane may template further myofibrillar growth into the bulk of the cell by an epitaxy-like mechanism, in which the basal myofibrillar layer serves as a seed-crystal. This so-called premyofibril hypothesis gives a unified account of myofibrillogenesis in several experimental systems (10). We would like to stress, however, that alternate pathways of myofibrillogenesis have been proposed and may indeed exist. In particular, there could be important differences between myofibrillogenesis in muscle tissues and myocytes in culture (11). Some authors did not observe premyofibrils containing nonmuscle myosin II in situ (11) (but see (12)). The generic theory of interfiber registry to be developed here is independent of molecular details and should apply to striated premyofibrils and nascent myofibrils, and even to striated stress fibers in nonmuscle cells.

Experiments with cultured cells plated on flexible substrates have shown that substrate stiffness is a regulating factor for cytoskeletal order in general, and myofibril assembly in particular (13–16). In the myogenic C2C12 mouse cell line and in primary human muscle cells, as well as in chick embryo and rat neonatal cardiomyocytes, the amount of striated myosin (which serves as a measure of myofibril condensation) depended on the stiffness of the matrix that the various cells were cultured upon, with a pronounced maximum at an optimal stiffness of E_m ≈ 10 kPa. Interestingly, this value is close to the lateral stiffness of relaxed muscle. Indeed, cells growing on top of a lower layer of muscle cells also resulted in similar optimal myofibrillogenesis (13). In these studies, cells that adhered directly to rigid plastic or glass (or probably a thin layer of compliant matrix on top of the rigid substrate) tended to exhibit less striation, either initially or over time. Such findings have implications for muscle structure and function in various disease states of fibrotic rigidification, helping to motivate the physical theory here.

It is not known which assembly stage of myofibrillogenesis is most susceptible to changes in substrate stiffness, but the observed proximity of striated stress-fiber-like precursor structures to the cell-substrate interface (17) suggests an effect of substrate stiffness on the early stages of myofibrillogenesis, including the establishment of interfiber registry of neighboring striated fibers. Such mechanosensitivity requires the transmission of active forces onto the substrate (18). In mature myofibrils, Z-bands are mechanically coupled to the substrate by means of specialized focal adhesions (19), so-called costameres, which have been identified as sites of force transduction (20). Costamerogenesis and myofibrillogenesis have been shown to be closely related. In particular, interference with costamere assembly impairs myofibril formation, and there is evidence that even at the stage of early myofibrillogenesis the Z-bodies of nascent myofibrils are mechanically coupled to the substrate by precursor structures termed precostameres (17). For striated stress fibers, sarcomeric localization of zyxin, an adhesion-related protein, was observed (21). Additionally, nanosurgery experiments give further evidence for adhesive coupling between striated stress fibers and the substrate along the fiber length (in addition to pronounced focal adhesions at the terminal points) (5,21).

Other experiments have highlighted the necessity of tension generated by nascent myofibrils (19) and the sensitivity to externally applied strains (22). Together, these experiments suggest the interesting possibility that elastic interactions with the substrate guide interfiber registry of striated fibers (and thus possibly myofibril assembly) in developing muscle cells, as well as of striated stress fibers in nonmuscle cell types. The elastic substrate effects considered here might also be generalizable to the effects of cytoskeletal compliance.

Here, we present a generic theory of substrate deformations induced by active stresses from striated acto-myosin bundles that applies to both striated fibers in adherent, nonmuscle cells and to developing striated muscle cells. As substrate deformations propagate laterally toward neighboring fibers, they induce an effective elastic interaction between fibers. These interactions bias the spatial reorganization of fibers and favor their smectic ordering. Other mechanisms that are not necessarily related to the elasticity of the underlying substrate, such as Z-body interactions, might also contribute to the establishment of interfiber registry. Nonetheless, the proposed elastic guidance mechanism for interfiber registry predicts a dependence on more readily controllable elastic properties of the substrate, including both the Poisson ratio and the Young's modulus.

Physical model of interfiber registry by elastic interactions

Contractile striated fibers as strings of active force dipoles

The striated stress-fiber-like structures in developing striated muscle cells (termed premyofibrils and nascent myofibrils) and the striated stress fibers in nonmuscle cells share important functional features and we will commonly refer to them as striated fibers. These striated fibers are under constant tension due to the activity of myosin filaments that link actin filaments of opposite polarity (see Fig. 2 A). These acto-myosin contractile forces strain the α-actinin-rich cross-linking regions, which are termed Z-bodies for the premyofibrils and nascent myofibrils in developing muscle cells. As the cross-linking regions are mechanically connected to the substrate by means of adhesive contacts, the tension generated in them is transmitted to the substrate. Thus, the substrate underneath a striated fiber is strained with regions of expansion below the cross-linking bands and regions of compression in between.

Figure 2.

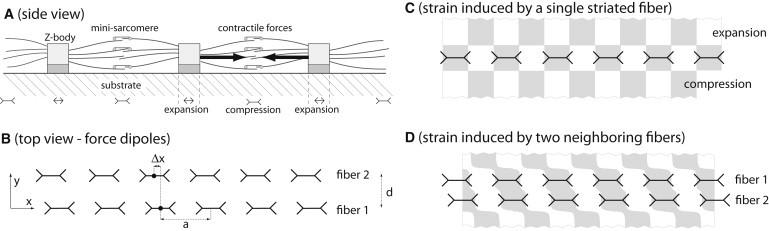
(A) Striated acto-myosin fibers such as premyofibrils and striated stress-fibers form at the cell-substrate interface and are mechanically coupled to the substrate by means of their cross-linking bands (Z-bodies) and adhesive contacts. Myosin activity within the minisarcomeres strains the Z-bodies and results in elastic deformations of the underlying substrate. These deformations are characterized by regions of expansion below the Z-bodies and regions of compression between them. (B) In our physical description, we model the forces exerted by a striated fiber onto the substrate as a line distribution of active force dipoles that is periodic with periodicity a equal to the spacing of Z-bodies. If two parallel fibers are separated by a lateral distance d, the respective strain fields in the substrate overlap. This results in substrate-mediated elastic interactions, which induce a registry force between the two fibers. This force depends on the relative phase shift Δx of the two fibers and tends to align them in registry. (C) Resultant principal strain u_xx induced by a single striated fiber in parallel direction for an incompressible substrate with Poisson ratio ν = 1/2. (D) Same as in panel C for a pair of neighboring fibers.

In the following, we present a minimal model for the deformations induced by a contractile striated fiber in its underlying substrate: We define the cell-substrate interface as the xy plane and consider a single contractile fiber parallel to the x axis (see Fig. 2 B). The forces transmitted by the fiber onto the substrate can be effectively described by a distribution Π_ij(x,y) of force dipoles (23). Force dipoles represent primary sources of applied stress and are related to the associated applied force field f_j(x,y) by f_j = −∇_iΠ_ij. In the case of striated fibers pulling on a substrate, force transmission is localized to the adhesive contacts in which lateral extension is ∼100 nm, and thus is much smaller than the spacing a ≈ 1 μm of Z-bodies. We can therefore approximate Π_ij(x,y) by a line distribution

$${\Pi }_{ij}\left(x,y\right)=\rho \left(x\right)\delta \left(y\right){\delta }_{ix}{\delta }_{jx}.$$ (1)

Here, the force dipole density ρ(x) is a periodic function of x due to the sarcomeric (i.e., periodic) architecture of a single striated fiber. For simplicity, we restrict our analysis to the principal Fourier mode and consider ρ(x) = ρ₀ + ρ₁ cos (2πx/a), where a corresponds to the sarcomeric periodicity of the striated fiber. A more general case is discussed in the Supporting Material.

Although we represent the force dipole field of a fiber by just a line, it should be kept in mind that the actin spindle has a finite extension in the lateral direction. Steric interactions can impede parallel fibers from getting closer than a distance d, where we estimate d = 200–500 nm (9).

Contractile fibers deform the underlying substrate

We model the substrate as an elastic half-space bounded by the xy plane, which extends infinitely in the z > 0 direction. The assumption of infinite substrate thickness is justified because the length-scale for induced strains is set by the size a ≈ 1 μm of a minisarcomere, which is much less than the thickness of the elastic substrate used in typical experiments. In experiments with cells plated on a rigid substrate like glass or plastic, a thin layer of very compliant matrix on top of the rigid substrate could behave as a composite system that is approximately characterized by a single effective stiffness of intermediate value (24). The elastic properties of the substrate are thus characterized by a Young's modulus E_m, which measures effective substrate rigidity, and its Poisson ratio ν, which quantifies the Poisson effect. The Poisson effect states that upon imposing an uniaxial stress σ_zz on a rod of this material along its long axis (say the z axis), the rod will not only expand in the z direction with strain u_zz = σ_zz/E_m, but will additionally contract in the normal directions with principal strain u_xx = u_yy = −νu_zz. In most experiments, incompressible substrates with a Poisson ratio close to 0.5 are used with a stiffness in the kiloPascal (kPa) range.

We now ask for the strain field u_ij(x,y) right at the surface of the substrate that is induced by the force dipole density Π_ij of a striated fiber (see Eq. 1). Using the superposition principle for force dipoles valid for linear elastic materials and a Green's function of elasticity, we find that the parallel strain component u₁₁(x,y) can be written as a product of a lateral propagation factor, Φ, that characterizes the propagation of strain in lateral (y) direction and a harmonic modulation in the (x) direction along the striated fiber (see the Supporting Material for the detailed derivation)

$$u_{11}\left(x,y\right)=\Phi \left(\left|y\right|/a,\nu \right)\frac{2{\rho }_1}{E_m{a}^2}\text{cos}\left(2\pi x/a\right).$$ (2)

The strain field u₁₁ is periodic in x direction with period a reflecting the periodicity of the striated fiber. The factor Φ characterizes the propagation of strain in lateral direction away from the centerline of the fiber. The Poisson-effect significantly affects strain propagation and Φ depends also on the Poisson ratio ν of the substrate. Fig. 3 displays the lateral propagation factor Φ for different values of the Poisson ratio ν. For an incompressible substrate with ν = 0, Φ is positive for all lateral distances |y| > 0 and the parallel strain field consists of alternating stripes of compression and expansion that run parallel to the y axis (not shown). For a compressible substrate with ν > 0, however, Φ becomes negative for lateral distances beyond a certain distance d^∗ and the parallel strain field is characterized by a checkerboard pattern as shown in Fig. 2 C. Note that in the limit |y| >> a, the factor Φ describes an exponential decay Φ ∼ exp(−2π|y|/a). In this limit, the strain field u₁₁ agrees with the strain field generated by a string of point force dipoles, which has been studied in Bischofs and Schwarz (25).

Figure 3.

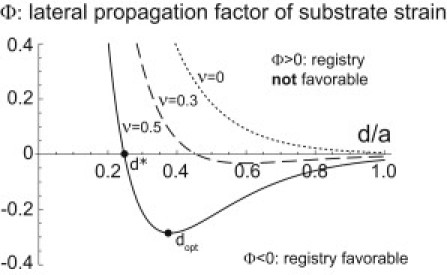
Lateral propagation of substrate strain induced by a single striated fiber is characterized by a factor Φ(d/a, ν) (see Eq. 2). This factor also characterizes the dependence of the elastic interaction energy between two parallel striated fibers in registry on their mutual lateral distance d (see Eq. 6). Negative values of Φ indicate that a configuration where the two striated fibers are in registry with zero phase shift Δx = 0 is energetically favorable. Different values for the substrate Poisson ratio were used, ν = 0 (highly compressible, dotted line), ν = 0.3 (dashed line), and ν = 0.5 (incompressible, solid line).

Active force dipoles minimize substrate deformation energy

The active contractility of cytoskeletal structures can elastically deform the substrates that support them and cause substrate strain u_ij and substrate stress σ_ij (20,26). As a consequence, the deformed substrate stores an elastic energy

$$W_{substrate}=\frac{1}{2}\int d^3\mathbf{x}{\sigma }_{ij}\left(\mathbf{x}\right)u_{ij}\left(\mathbf{x}\right),$$ (3)

where the integration extends over the whole substrate domain. This elastic energy is a measure of the work which the cell has to invest in order to deform the substrate. The substrate stress σ_ij is closely related to the force dipole field Π_ij associated with active cytoskeletal forces via the force balance condition, ∇_iσ_ij = ∇_iΠ_ij (23,27). We use this relation (and partial integration) to rewrite the expression for the elastic energy in terms of the dipole density Π_ij and, for the general case, some fictitious surface forces f_j as $W_{substrate}=\frac{1}{2}\int d^3\mathbf{x}{\Pi }_{ij}\left(\mathbf{x}\right)u_{ij}\left(\mathbf{x}\right)+{\int }_s{d}^2\mathbf{x}{f}_j\left(\mathbf{x}\right)u_j\left(\mathbf{x}\right)$. Here, f_j = (σ_ij – Π_ij)n_i represents normal surface forces, which act only at the surface S of the substrate domain. In our particular case, the cytoskeleton is assumed to exert only tangential forces at the z = 0 surface of the substrate; furthermore, the normal forces σ_ijn_i vanish at this free surface. Hence, the fictitious surface forces f_j vanish in our case and the elastic energy of the substrate can be written as a local interaction between the dipole density Π_ij and the strain field u_ij (28)

$$W_{substrate}=\frac{1}{2}{\int }_{z=0}{d}^2\mathbf{x}{\Pi }_{ij}\left(\mathbf{x}\right)u_{ij}\left(\mathbf{x}\right).$$ (4)

It has been proposed that actively powered force generators tend to minimize this deformation energy W while maintaining a constant pulling force (27). (This minimization principle can be refined by allowing a feedback of W on the pulling force (29); see also Force Transmission Reinforces with Substrate Stiffness, below.) The minimization principle successfully explains the migration of cells toward regions of higher substrate stiffness (durotaxis) or the alignment of cell in the direction of an external strain (27). We argue that this minimization principle also applies locally for subcellular cytoskeletal structures such as striated fibers and that it can account for the elastic interactions between them. To understand the origin of substrate-mediated elastic interactions, consider two force generators with respective dipole fields ${\Pi }_{ij}^{\left(1\right)}$ and ${\Pi }_{ij}^{\left(2\right)}$ on the surface of an elastic half-space. Each force generator alone would induce a substrate strain field $u_{ij}^{\left(k\right)}$, k = 1, 2; the total strain field $u_{ij}^{tot}$ in the presence of the two force generators is simply the superposition $u_{ij}^{tot}=u_{ij}^{\left(1\right)}+u_{ij}^{\left(2\right)}$ (see Fig. 2 D). Now, the energy W_substrate, which the first force generator, say, has to invest in order to deform the substrate, is

$$\begin{array}{l}{W}_{substrate}=\frac{1}{2}\int d^2\mathbf{x}{\Pi }_{ij}^{\left(1\right)}{u}_{ij}^{tot}=\frac{1}{2}\int d^2\mathbf{x}{\Pi }_{ij}^{\left(1\right)}{u}_{ij}^{\left(1\right)}+\frac{1}{2}\int d^2\mathbf{x}{\Pi }_{ij}^{\left(1\right)}{u}_{ij}^{\left(2\right)}\hfill \\ =W_{\text{self}}+\frac{1}{2}{W}_{\text{interaction}}.\hfill \end{array}$$ (5)

This energy is the sum of a self-energy of the first force generator, $W_{\text{self}}=1/2\int d^2\mathbf{x}{\Pi }_{ij}^{\left(1\right)}{u}_{ij}^{\left(1\right)}$, which accounts for the substrate deformation energy in the absence of the second force generator, and an interaction term $W_{\mathrm{int}}=\int d^2\mathbf{x}{\Pi }_{ij}^{\left(1\right)}{u}_{ij}^{\left(2\right)}$. The term W_int characterizes an effective, substrate-mediated interaction between the two force generators and can guide their spatial reorganization. (Note that, more generally, one could deduce the functional form $W_{\mathrm{int}}=\alpha \int {\Pi }_{ij}^{\left(1\right)}{u}_{ij}^{\left(2\right)}+\beta \int {\Pi }_{ii}^{\left(1\right)}{u}_{jj}^{\left(2\right)}$ for the effective elastic interaction from symmetry considerations. Using this form instead of Eq. 5 would give qualitatively similar results.) Communication via elastic interactions has been experimentally observed between spatially separated, contractile cells (30,31). Below, we discuss how such elastic interactions naturally arise also between contractile striated fibers and guide their relative sliding.

Elastic interactions between neighboring fibers can favor smectic ordering

We now apply the arguments of the preceding section to the particular case of neighboring striated fibers and their elastic interactions. In a simple, idealized geometry, we consider two infinite fibers, which are parallel and separated by a lateral distance d (see Fig. 2 B). As outlined above (see Eq. 1), we can model the force dipole densities associated with the two fibers as Π⁽¹⁾_ij = ρ⁽¹⁾(x) δ(y) δ_ixδ_jx and Π⁽²⁾_ij = ρ⁽²⁾(x) δ(y − d) δ_ixδ_jx, where ρ⁽¹⁾(x) = ρ₀ + ρ₁ cos(2πx/a) and ρ⁽²⁾ (x) = ρ₀ + ρ₁ cos(2π(x + Δx))/a, respectively. Note that there is a phase shift Δx between the periodic structures of the two fibers.

We insert the specific strain field induced by a single striated fiber, Eq. 2, into the general formula for elastic interactions, Eq. 5, and thus find the elastic interaction energy between the two fibers (per minisarcomere) as a function of the phase shift Δx,

$$W_{\text{interaction}}=\Phi \left(d/a,\nu \right)\frac{{\rho }_1^2}{a{E}_m}\text{cos}\left(2\pi \Delta x/a\right).$$ (6)

Here W^∗ = ρ₁²/(aE_m) sets a typical energy of the elastic interactions. In the Appendix, we estimate the order of magnitude of the interaction energy as W^∗ ∼ 1aJ ≈ 250 k_BT. The factor Φ(d/a, ν) was introduced below Eq. 2 and characterizes the lateral propagation of strain away from the centerline of a fiber. The sign of the propagation factor Φ determines whether a configuration with zero phase shift between the two striated fibers is favorable or not: registry of fibers with Δx = 0 is favored for Φ < 0. Fig. 3 shows this prefactor as a function of lateral distance d for different values of the Poisson ratio ν.

For highly compressible substrates with Poisson ratio ν = 0, we find that the elastic interaction energy is always positive if the two neighboring fibers are in-registry, W(Δx = 0) > 0, and negative if they are out-of-registry, W(Δx = a/2) < 0. This implies that elastic interactions would actually disfavor a configuration where striated fibers are in registry if cells were plated on a highly compressible substrate.

However, for incompressible substrates with Poisson ratio close to ν = 1/2, such as those used in experiments (13,32), we find that the sign of the prefactor Φ of the elastic interaction energy is negative provided the lateral fiber spacing is larger than some threshold d/a > d^∗/a ≈ 0.247. Hence, elastic interactions favor a configuration where neighboring fibers are in registry with Δx = 0. The strong impact of the substrate Poisson ratio ν on the elastic interaction is typical for elasticity problems (25).

In the case of an incompressible substrate with ν = 1/2, the elastic interaction energy W_int = W_int(Δx, d) attains a local minimum as a function of both phase shift Δx and lateral spacing d if the two fibers are in registry with Δx = 0 and are separated by a finite distance d_opt ≈ 0.380a > d^∗. It is therefore possible that elastic interactions also set a preferred lateral spacing of striated fibers. Additionally, steric interactions may prevent neighboring fibers from getting too close and could enforce the condition d > d^∗.

The lateral repulsion for small lateral distances d < d_opt of registered fibers with zero phase-shift can be understood analogously to the lateral repulsion of two parallel strings of finite size force dipoles. In our description of a striated fiber, we retain only the principal Fourier mode of the force dipole density ρ(x), which corresponds to an effective dipole size in the x direction of half a wave-length a/2. This is larger than the actual size of ∼100 nm of the Z-bodies, and thus our simple theory overestimates both d^∗ and d_opt. An extension of our theory to variable Z-body size is discussed in the Supporting Material.

Dynamic theory of interfiber registry

We consider an array of n parallel striated fibers with respective phase shifts Δx_i and lateral positions y_i = id, where i = 1, … n. The elastic interaction energy W_int between a pair of these fibers (see Eq. 6) induces longitudinal forces; the force acting on fiber number i induced by elastic interaction with fiber number j reads

$$f_{i,j}=-\partial W_{\text{interaction},i,j}/\partial \Delta x_i.$$ (7)

These registry forces will induce frictional drag of the adhesive contacts of the striated fibers as well as bias their assembly and disassembly dynamics. We describe the overdamped sliding dynamics of the fibers using a single, effective friction coefficient γ,

$$\gamma \Delta {\dot{x}}_i=\sum _{i\ne j}{f}_{i,j}+{\xi }_i.$$ (8)

Here, the f_i,j denote the registry forces from Eq. 7, and the ξ_i are uncorrelated noise terms that account for unbiased random motion of the fibers due to stochastic microscopic processes. For simplicity, we model the ξ_i as white Gaussian noise with 〈ξ_i(t₁)ξ_j(t₂)〉 = 2Dδ_ijδ(t₁ − t₂), where D denotes a noise strength. In the limit of long times t >> γa²/W^∗, the probability distribution of fiber positions is given by a Boltzmann factor, $\sim \text{exp}\left[-\gamma \sum _{i\ne j}{W}_{i,j}/D\right]$.

To characterize order in the array of striated fibers, we define a smectic order parameter as $(\text{with}{q}_0=2\pi /a)$

$$S=\sum _{i=1}^{n-1}\text{cos}\left[q_0\left(\Delta x_{i+1}-\Delta x_i\right)\right]/\left(n-1\right).$$ (9)

This order parameter is zero for random phase shifts Δx_i and takes the maximal value S = 1 for perfect smectic order. Fig. 4 shows an ensemble average S of this order parameter for an array of n = 10 fibers at different times t. For the given parameters, smectic ordering of fibers occurs on a timescale of t ∼ 1 h.

Figure 4.

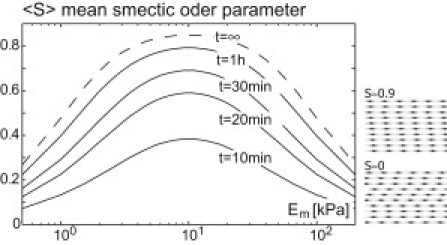
Elastic interactions can drive registry of striated fibers in a substrate-stiffness-dependent manner. Shown are simulation results for the smectic ordering of n = 10 fibers, for different values of substrate stiffness E_m after simulation times of t = 10 min, 20 min, 30 min, 1 h. The stochastic sliding dynamics of the fibers is governed by registry forces stemming from elastic interactions as well as effective random forces that relate to dynamic remodeling and resultant random translocation (see Eq. 8). The mean smectic order parameter 〈S〉 (ensemble average) as defined in Eq. 9 quantifies interfiber registry of the n striated fibers. (Right) Two example fiber configurations. For the simulation, realistic parameter values were used, ρ₁ = 40 pN, γ = 10 pN min/μm, a = 1 μm; the values for ρ₁ and γ are order-of-magnitude estimates that are derived in the Appendix. We used the Einstein relation D = k_BTγ with T = 300 K to obtain a lower bound for the noise strength D. Fibers are equidistantly spaced in y direction with lateral spacing d = 0.38a ≈ d_opt.

Force transmission reinforces with substrate stiffness

Cell-substrate junctions such as adhesive contacts or the more mature focal adhesions are mechanosensitive structures (composed of a layered protein plaque) that connect the cytoskeleton to the substrate (18). Focal adhesions were shown to reinforce with increased substrate stiffness: on a stiffer substrate, they grow to larger areas and transmit more force onto the substrate (33). We expect similar behavior for the much smaller adhesive contacts. Recent experiments indicate a fast traction force response of single cells to changes in effective substrate stiffness (34). Below, we use a phenomenological description, to predict the local force transmitted by a striated fiber onto the substrate and show that it is a saturating function of substrate stiffness: The amplitude ρ₁ of the periodic variations of the force dipole density ρ(x) is a measure of the contractile activity within each minisarcomere of the fiber. Regulatory processes are assumed to tune ρ₁ to a set-point ρ₁^∗; for mathematical convenience, we derive the forces involved in these regulatory processes from an effective pseudo-energy, which each fiber tries to minimize (29):

$$W_{\text{fiber}}=\chi {\left({\rho }_1-{\rho }_1^{\ast }\right)}^2.$$ (10)

Additionally, a nonzero value of ρ₁ will cause substrate deformations with a stored elastic energy that represents a self-energy of the contractile fiber,

$$W_{\text{self}}=A\left(\nu \right)q_c^2{\rho }_1^2/E_m.$$ (11)

Here, A(ν) is a function of the substrate Poisson ratio ν and q_c is a cut-off wave-length which is associated with the finite extension of the dipole density induced by the fiber in the lateral direction. (Note that the idealized dipole density Π_ij has zero extent in y and z directions. To account for the finite extent of the real dipole density and to prevent the self-energy from diverging, we employ a regularization procedure as in De and Safran (35).) Minimizing the total energy functional W_total = W_fiber + W_self with respect to ρ₁ yields the steady-state amplitude of the dipole density as a function of substrate stiffness,

$${\rho }_1={\rho }_1^{\ast }{E}_m/\left(E_m+E_m^{\ast }\right),$$ (12)

where E_m^∗ = Aq_c²/χ. Here, we have focused on a single striated fiber and neglected interaction energies W_int with neighboring fibers, because we expect W_self >> W_int. The set-point value ρ₁^∗ corresponds to the amplitude ρ₁ of the dipole density on very stiff substrates with E_m >> E_m^∗. On soft substrates with E_m < E_m^∗, however, ρ₁ is considerably smaller than ρ₁^∗.

Using the saturating dependence of ρ₁ on substrate stiffness, Eq. 12, we find that the registry force between two parallel striated fibers becomes a nonmonotonic function of E_m of Lorentzian type and has maximal magnitude for E_m = E_m^∗,

$$f_{\text{reg}}\sim -\frac{1}{E_m}{\rho }_1^2\sim -\frac{E_m}{{\left(E_m^{\ast }+E_m\right)}^2}.$$ (13)

Here we assume the lateral spacing d of the fibers is larger than the critical distance d^∗ and independent of substrate stiffness. Using this functional dependence, we find that also the smectic ordering of a simulated array of parallel, striated fibers depends nonmonotonically on substrate stiffness (see Fig. 4).

Experiments on interfiber registry

Relative sliding of striated acto-myosin bundles into registry has already been reported in McKenna et al. (8). Yet, the mechanism by which striated fibers align in registry to form a smectic-like structure remains unknown. Engler et al. (13) have observed that the formation of striated and fully mature myofibrils in cultured C2C12 cell line depends strongly on substrate stiffness and was most prominent at an intermediate stiffness of 10 kPa, which is characteristic of muscle tissue stiffness, and there has since been several other reports for a variety of primary muscle cells derived from both skeletal and cardiac muscle and from at least four different species, namely chicken, mouse, rat, and man.

To test our theoretical prediction that already the initial registry of striated fibers depends nonmonotonically on substrate stiffness, we examined the interfiber registry in human mesenchymal stem cells that were plated on PA-gels of different stiffness (ranging from 0.3 kPa to 40 kPa). Mesenchymal stem cells have been reported to be capable of committing to a myogenic lineage based on either serum-induced signals (36) or matrix elasticity signals (37). Mesenchymal stem cells express stress-fiber-like acto-myosin bundles with a striated localization of nonmuscle myosin. These fibers resemble the striated fibers found in both nonmuscle cells and developing muscle cells. Thus mesenchymal stem cells represent a model system to study interfiber registry of striated fibers.

Fig. 5 shows the organization of nonmuscle myosin-IIA within three cells that were plated on gels of different stiffness and cultured for 24 h. All three cells display nematically aligned acto-myosin bundles with striated myosin localization that follows ∼1 μm intrafiber periodicity. However, interfiber registry of adjacent striated fibers is observed only for the cell that was cultured on a 10 kPa gel (Fig. 5 B). Myosin bands perpendicular to the axis of nematic fiber organization are clearly visible and most likely connect neighboring acto-myosin bundles in registry. Out of ∼20 cells examined per gel, roughly 30–50% exhibited aligned, striated fibers. The cells shown in Fig. 5 are representative for these cells with striated fibers. This preliminary experimental evidence is consistent with our prediction of a nonmonotonic relationship between interfiber registry of striated fibers and substrate stiffness, also at very early stages within muscle-related precursors.

Figure 5.

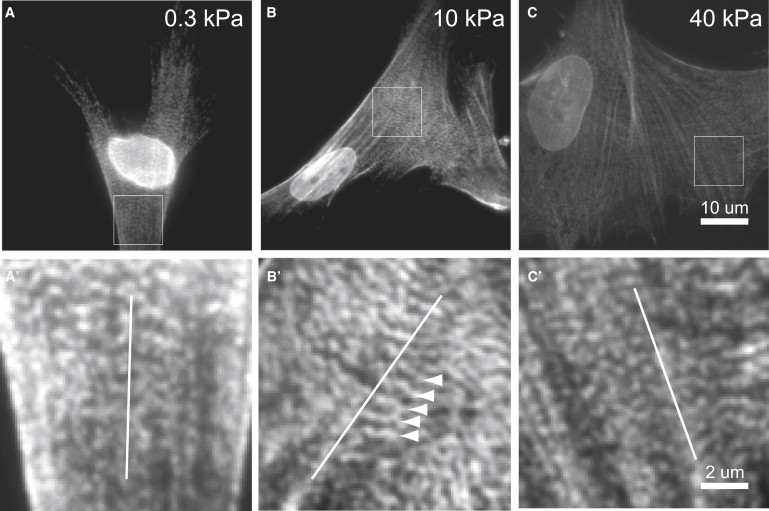
Mesenchymal stem cells plated on PA-gels of different stiffness stained for nonmuscle myosin-IIA. The substrate stiffness is 0.3 kPa, 10 kPa, and 40 kPa in panels A, B, and C, respectively. Actomyosin fibers with striated myosin localization are visible in all three cells. Regions indicated by a square are shown enlarged in panels A′–C′ (with contrast enhancement by linear remapping of intensity values). (Open lines) Average fiber orientation. (B′, arrowheads) Indication of myosin ribbons that connect neighboring acto-myosin fibers in registry.

Whereas the focus of this article is to describe our theoretical model in detail, additional experiments and analysis will follow and will be published elsewhere.

Materials and Methods

Gel substrates preparation

Collagen-coated polyacrylamide (PA) gels of different stiffness were prepared as described previously (32). In short, glass coverslips (22-mm square Premium Cover Glass No. 1; Fisher Scientific, Waltham, MA) were silanized in 0.1% allyltrichlorosilane (ATCS; Sigma-Aldrich, St. Louis, MO) and vacuum-desiccated. Gel precursor mixtures were polymerized directly on ATCS-silanized substrates (35 μl per substrate) with 25-mm square RCA-cleaned glass coverslips (Premium Cover Glass No. 1; Fisher Scientific). Elasticity of PA-gels was controlled by varying N,N-methylenebisacrylamide (Sigma-Aldrich) cross-linker concentration with 3–6% w/v acrylamide (40%; Sigma-Aldrich). Direct polymerization resulted in covalent binding to ATCS-silanized glasses whereas top coverslips were detached after 1 h immersion in water. Gels were coated with 0.2 mg/ml type-I rat tail collagen (BD Biosciences, Franklin Lakes, NJ) and ultraviolet-sterilized for 2 h before plating cells.

Cell cultures

Passage-5 human mesenchymal stem cells (Lonza, Basel, Switzerland) were expanded in plastic flasks in normal growth media (10% fetal bovine serum (FBS; Sigma-Aldrich) and 1% penicillin/streptomycin supplemented low glucose media Dulbecco's modified Eagle's medium (DMEM; Gibco, Billings, MT). Cells were harvested using 10 mM EDTA (ethylenediaminetetraacetic acid), 10% FBS in phosphate-buffered saline under gentle agitation and plated at 5000 cells per six-well plate well on collagen-coated gels. After 24 h in culture, cells were fixed in 3.7% formaldehyde (Fisher Scientific), permeabilized in 0.5% Triton X-100 (MP Biomedicals, Santa Ana, CA), immuno-labeled against nonmuscle Myosin-IIA (Sigma-Aldrich), and mounted. Fluorescently labeled cells were imaged using a 150×, NA 1.45 objective (UApo; Olympus, Melville, NY).

Discussion

In this article, we proposed that elastic interaction forces (mediated by cell-induced substrate deformations) serve as guidance cues in a particular cytoskeletal assembly process, the registry of striated acto-myosin fibers at the basal membrane of adherent cells. In our theory, acto-myosin contractility in a striated fiber induces a periodic strain field in the underlying substrate that propagates laterally to neighboring fibers and results in an effective elastic interaction between neighboring fibers that tends to register them in phase. It should be noted that in some cases, interfiber registry of striated fibers was observed for cells cultured on rigid substrates (8), which may seem to contradict our proposed mechanism. However, as we have already alluded, a layer of fibronectin coating the substrate will reduce the effective substrate stiffness sensed by a cell (32). Similarly, the disordered cytoskeleton that surrounds the striated fibers can equally well confer elastic interactions. In addition to elastic interactions, alternative mechanisms, such as direct Z-body interactions, might contribute to interfiber registry, and thus explain the results for cells cultured on rigid substrates. For example, the long and large molecular weight protein obscurin has been proposed to link Z-bodies and M-bands of neighboring premyofibrils and may thus stabilize registry of striated premyofibrils (38). Although the elasticity of such proteins might be similar to that of titin, if these linker proteins also contribute an active driving force already for the establishment of premyofibrillar registry, an initial tension in these linker proteins would be required. Nevertheless, the stabilization of interfiber registry by linker proteins together with stochastic fiber translocation might well allow for an alternative mechanism of fiber registry establishment. Future experiments that precisely measure fiber translocation dynamics could test this different mechanism.

The guidance mechanism for the registry of striated fibers by elastic interactions proposed here represents a plausible mechanism for the establishment of interfiber registry observed in experiments with both adherent nonmuscle and developing striated muscle cell types. Our theory predicts that this mechanism is most effective on incompressible substrates with Poisson ratios close to ν = 1/2. Using a substrate with a smaller Poisson ratio should reduce the registry force (and possibly even change its sign) and thereby negatively affect interfiber registry. We propose that experiments which measure the amount of interfiber registry plated on substrates of different Poisson ratios can test this theoretical prediction.

It has been suggested that striated acto-myosin bundles in developing skeletal and cardiac muscle cells represent intermediary structures that can fuse laterally in at least one pathway of myofibrillogenesis (8,10). Accordingly, the smectic ordering of premyofibrils and nascent myofibrils is a prerequisite for their lateral fusion and is expected to represent a crucial step in this myofibrillogenesis pathway. Experiments in which careful attention is paid to matrix thickness and elasticity show that myofibrillogenesis in various cultured cells strongly depends on the elastic properties of the underlying substrate and is maximal on a substrate stiffness of E_m = 10 kPa (13–16). Our theory qualitatively accounts for this dependence and predicts a registry force that depends nonmonotonically on substrate stiffness. Within our simple theory, the peak of the registry force as a function of substrate stiffness is not as sharp as the corresponding peak in some of the experimental data that measures the relative number of striated myosin patterns (which indicates successful myofibrillogenesis). Such differences might be due to a nonlinear relationship between the degree of fiber registry and the resulting amount of mature myofibrils.

Although our theory of elastic interactions between neighboring striated fibers can account for the dependence of myofibrillogenesis on substrate stiffness, other mechanisms can shape this dependence as well: It has been proposed that on a very stiff substrate, high stresses evolve inside the minisarcomeres, which could damage these possibly fragile structures (13), and so analyses of defects in these smectic structures could be useful. Furthermore, it is conceivable that on stiff substrates reinforcement of adhesive contacts reduces their mobility and slows down longitudinal sliding and hence registry of premyofibrils. On very soft substrates, reduced myofibrillogenesis can be alternatively explained by adhesive contacts that are weak and not stable enough to support premyofibril assembly. Several of these mechanisms could operate simultaneously and jointly shape the sensitivity of myofibrillogenesis to substrate stiffness.

Appendix

We provide order-of-magnitude estimates of model parameters. Due to lack of quantitative data, estimates are rough and mainly serve illustrative purposes. The registry force f_reg = ∂W_int/∂Δx between neighboring fibers scales quadratically with the amplitude ρ₁ of the force dipole density induced by a single fiber (see Eq. 5). This amplitude ρ₁ is related to the contractile force generated in each minisarcomere due to acto-myosin contractility. For mature stress fibers, contractile forces up to the nanoNewton range have been reported (39,40). As a conservative, lower estimate, we will use, however, a value ρ₁ ∼10–100 pN. Contractile force is generated by bipolar nonmuscle myosin minifilaments that constitute 10–30 double-headed myosins, i.e., there are 10–30 myosin heads per half-filament. If we assume a force of 1 pN generated by each attached myosin head at zero sliding velocity, and a duty ratio for attachment of 10% (41), we find that each minifilament contributes a contractile force a few pN; hence our value for ρ₁ should correspond to a number of ∼10–100 nonmuscle myosin filaments per minisarcomere.

We now estimate the registry force as f_reg ∼ ρ₁²/(E_ma²) and find f_reg ∼ 1 pN. Here, we used a = 1 μm for the minisarcomere spacing and E_m = 10 kPa for the substrate stiffness; for this value, experiments show that myofibrillogenesis is optimal (13). Similarly, we find for the typical energy scale of elastic interactions between neighboring fibers, W^∗ = ρ₁²/(E_ma) ∼ 1aJ ≈ 250 k_BT.

Next, we ask: Are the registry forces f_reg in the picoNewton range sufficient to cause a striated fiber to slide and align in registry with its neighboring fiber? This is indeed possible, as these forces are sustained for several hours (the typical timescale of myofibrillogenesis) (8,13). Premyofibrils are highly dynamic structures that constantly interchange proteins with the cytoplasm. Elastic interaction forces may bias the assembly/disassembly dynamics of the adhesive contacts that link Z-bodies to the substrate and cause them to translocate in the direction of the force (39,42,43).

Assuming a size of 10⁻² μm² for adhesive contacts, we estimate the stress due to elastic interaction forces to be in the range of 0.1 kPa. It is known that the much larger focal adhesions (area ∼ 10 μm²) relocalize at speeds of μm/min in the direction of an externally applied stress in the kiloPascal range (39,42). From these values, we obtain a rough estimate for the effective friction coefficient of the adhesive contacts used in Eq. 8 as γ = 1 kPa 10⁻² μm² (μm/min)⁻¹ = 10 pN min/μm. As the adhesive contacts are likely to be less stable than the more mature focal adhesions, this estimate represents an upper bound only. In any case, we conclude that stresses due to elastic interaction forces between neighboring premyofibrils could be large enough to translocate their adhesive contacts and move the premyofibrils into registry.