A novel computational framework for simultaneous integration of multiple types of genomic data to identify microRNA-gene regulatory modules

Abstract

Motivation: It is well known that microRNAs (miRNAs) and genes work cooperatively to form the key part of gene regulatory networks. However, the specific functional roles of most miRNAs and their combinatorial effects in cellular processes are still unclear. The availability of multiple types of functional genomic data provides unprecedented opportunities to study the miRNA–gene regulation. A major challenge is how to integrate the diverse genomic data to identify the regulatory modules of miRNAs and genes.

Results: Here we propose an effective data integration framework to identify the miRNA–gene regulatory comodules. The miRNA and gene expression profiles are jointly analyzed in a multiple non-negative matrix factorization framework, and additional network data are simultaneously integrated in a regularized manner. Meanwhile, we employ the sparsity penalties to the variables to achieve modular solutions. The mathematical formulation can be effectively solved by an iterative multiplicative updating algorithm. We apply the proposed method to integrate a set of heterogeneous data sources including the expression profiles of miRNAs and genes on 385 human ovarian cancer samples, computationally predicted miRNA–gene interactions, and gene–gene interactions. We demonstrate that the miRNAs and genes in 69% of the regulatory comodules are significantly associated. Moreover, the comodules are significantly enriched in known functional sets such as miRNA clusters, GO biological processes and KEGG pathways, respectively. Furthermore, many miRNAs and genes in the comodules are related with various cancers including ovarian cancer. Finally, we show that comodules can stratify patients (samples) into groups with significant clinical characteristics.

Availability: The program and supplementary materials are available at http://zhoulab.usc.edu/SNMNMF/.

Contact: xjzhou@usc.edu; zsh@amss.ac.cn

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

MicroRNAs (miRNAs) play crucial regulatory roles in repressing mRNA translation or mediating mRNA degradation by targeting mRNAs in a sequence-specific manner (Bartel, 2004). MiRNAs, transcriptional factors, and mRNAs combine to form complex regulatory systems, cooperatively determining the progression of many cellular behaviors and diseases (Garzon et al., 2006; Shalgi et al., 2007; Zhou et al., 2007). Great experimental and computational progress has been made on the problems of identifying which genes encode miRNAs (Bentwich et al., 2005; Lagos-Quintana et al., 2003; Lai et al., 2003; Rodriguez et al., 2004), predicting the target genes of miRNAs within multiple genomes (Enright et al., 2003; Lewis et al., 2003; Stark et al., 2003; Xie et al., 2005), and characterizing miRNA expression patterns based on microarray data (Lu et al., 2005). In addition, more and more labs are simultaneously producing expression profiles of miRNA and mRNA on the same set of samples, providing a global view on the dynamics of miRNA–mRNA regulatory relationships (Huang et al., 2007; Nunez-Iglesias et al., 2010). However, the vast majority of miRNAs still have unknown functions, and the mechanisms driving cooperative regulation between miRNA and genes are not yet well understood.

Several exploratory studies have attempted to decipher how miRNAs, genes and proteins interact on a systems level, e.g. global miRNA regulation in cellular networks (Cui et al., 2006; Hsu et al., 2008; Liang and Li, 2007; Yuan et al., 2009) or combinatorial miRNA regulation in cellular pathways (Gusev et al., 2007; Xu and Wong, 2008). Other researchers have studied coordination between the transcriptional and miRNA layers based on their combined regulatory networks (Shalgi et al., 2007; Zhou et al., 2007). All these studies have provided insights into miRNA-gene regulation, for example by showing that miRNAs tend to target highly connected genes or proteins in cellular networks (Yuan et al., 2009). However, we are still far from understanding the underlying mechanisms of miRNA regulation, and full-scale studies of the regulatory networks spanned by miRNAs are only now getting under way.

Recognizing the modular organization of biological networks has greatly advanced our understanding of complex cellular systems (Hartwell et al., 1999; Ihmels et al., 2002; Qi and Ge, 2006). However, little is known about the modules that exist in miRNA-gene regulation systems, and even less is known about these modules' role in specific biological processes and key regulation assemblies. Identifying functional miRNA-gene regulatory modules is a challenging task for several reasons. (i) One gene can be regulated by multiple miRNAs (Krek et al., 2005), and one miRNA can regulate a large number of genes (Lim et al., 2005). Given this multiplicity, the target of our search has to be a miRNA-gene comodule: a set of miRNAs and their co-regulated genes. (ii) The miRNA–mRNA target relationships differ among tissues and conditions. (iii) Although miRNAs physically interact with mRNAs, ultimately miRNA regulation affects the quantities of proteins in cells rather than the quantities of mRNAs. Thus, the expression levels of miRNAs are not always anti-correlated with those of their target genes. (iv) The genomic data are generally noisy and incomplete.

The complex and subtle nature of miRNA regulation poses unique challenges to the integration of heterogeneous data sources. Yoon and De Micheli (2005) developed an algorithm to reconstruct miRNA-gene regulatory modules based only on predicted miRNA-gene target information. Improved versions of this method have been proposed which also take into account coherent expression patterns between miRNAs and genes, or the (anti)-correlations measured between each pair of miRNAs and genes (Joung et al., 2007; Peng et al., 2009; Tran et al., 2008). However, these existing methods for discovering miRNA-gene regulatory modules focus only on one or two resources, and suffer from several limitations. For example, Peng et al. (2009) proposed a sequential integrative method based on enumerating maximal bi-cliques in a combined miRNA-gene network. Their method is sensitive to noise in the data, and produces too many star structures (one miRNA, many genes) which cannot be used to explore miRNA combinatorial regulation. Furthermore, none of these methods considers the coordination of miRNA and gene regulation, or the topological organization of transcriptional regulation and protein–protein interaction networks.

In this article, we propose a computational framework for reconstructing miRNA regulatory modules based on the integration of multiple genomic data sources. We use three types of data: predicted miRNA–gene interactions, the expression profiles of miRNAs and genes, and the gene–gene interaction network constructed based on protein–protein interaction and DNA–protein interaction networks. The predicted miRNA-gene targets serve as a static superset, while the dynamic expression profiles of miRNAs and genes are used to identify target relationships that are concurrently active. This signal is enhanced by the coordination of gene/protein interactions, since the ultimate effect of miRNA regulation is to regulate gene/protein activities. In order to integrate the three information sources, we propose a novel and efficient machine learning technique. The method integrates miRNA and gene expression profiles in a framework of multiple non-negative matrix factorization, and simultaneously integrates networked data in a regularized manner. To enhance the signal-noise separation and improve the interpretability of the modules, we look for sparse solutions of the membership functions by applying sparsity penalties. We prove with a theoretical derivation that the learning and optimization model can be effectively solved by an iterative algorithm.

We test the proposed method on a dataset of human miRNA and gene expression profiles [from the Cancer Genome Atlas (TCGA) ovarian cancer samples], a miRNA–gene interaction network, and a gene interaction network. We identified 49 human miRNA-gene regulatory comodules, each one composed of multiple miRNAs (the miRNA module) and multiple genes (the gene module). We show that the miRNA modules are significantly enriched with miRNAs clustered in their chromosomal locations, and that the gene modules are enriched with known functional gene sets (GO biological process terms and KEGG pathways). These properties confirm the biological relevance of the comodules. The overrepresented functional terms of gene modules can potentially be transferred to their corresponding miRNA modules, resulting in a functional prediction for miRNAs. Moreover, through a literature survey we find that the identified comodules include a significant number of cancer-related genes and miRNAs. Among these, many are involved with ovarian cancer as expected. The regulatory modules detected by our method can be used to reconstruct gene regulatory networks, and can provide candidates for the experimental validation of miRNA targets. Finally, we show that the common basis vectors of miRNA-gene comodules provide clues about the clinical characteristics of ovarian cancer.

2 MATERIALS AND METHODS

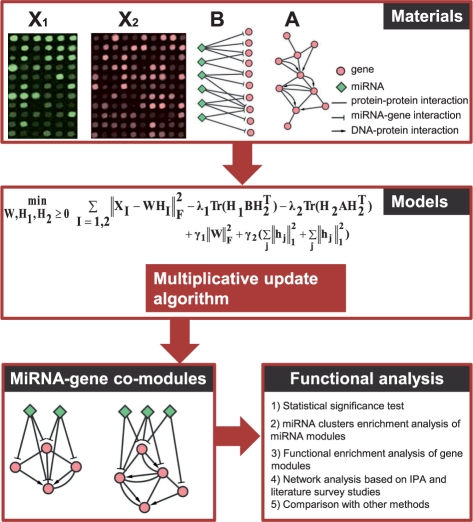
In this section, we describe our framework for the simultaneous integration of multiple data types to identify miRNA-gene comodules (Figure 1). We will begin by introducing the data, and then present our mathematical formulation of the problem. Next we describe our iterative multiplicative updating algorithm. Finally, we describe various validation experiments.

Fig. 1.

Overview of the proposed method for identifying miRNA-gene regulatory comodules. A miRNA-gene comodule is defined as the union of a set of miRNAs (a miRNA module) and a set of genes (a gene module). The inputs are (i) two sets of expression profiles (represented by the matrices X₁ and X₂) for miRNAs and genes, measured on the same set of samples; (ii) a gene–gene interaction network (represented by the matrix A), including protein–protein interactions and DNA–protein interactions; and (iii) a list of predicted miRNA–gene regulatory interactions (represented by the matrix B) based on sequence data. We simultaneously factor the miRNA and gene expression matrices into a common basis W and two coefficient matrices H₁ and H₂. At the same time, additional knowledge is incorporated into this framework with network-regularized constraints. Sparsity constraints are also imposed on this framework so as to obtain easily interpretable solutions. The decomposed matrix components provide information about miRNA-gene regulatory comodules. Then the comodules are identified based on shared components (a column in W) with significant association values in the corresponding rows of H₁ and H₂.

2.1 Data sources and preprocessing

Due to its large number of samples and rich clinical information, we tested our method on the ovarian cancer expression data from TCGA Project (McLendon et al., 2008). We downloaded miRNA and gene expression data for 385 ovarian cancer samples from the TCGA data portal (http://cancergenome.nih.gov/). We then filtered out miRNAs and genes with small absolute values and little variation across samples (see Supplementary Material), obtaining a dataset with the expression profiles of 559 miRNAs and 12 456 genes.

We constructed a gene–gene interaction network by combining the protein–protein interaction data obtained from Bossi and Lehner (2009) and the DNA–protein interaction data downloaded from TRANSFAC (Matys et al., 2006). We filtered these data for self-interactions and genes (proteins) that were not represented in our TCGA expression data. This process resulted in a network with 31 949 gene–gene interactions.

We obtained predicted miRNA–gene interactions from the MicroCosm website (http://www.ebi.ac.uk/enright-srv/microcosm/htdocs/targets/v5/). We removed interactions involving miRNAs or genes that were not present in the expression data. The resulting miRNA-gene bipartite network has a total of 243 331 interactions.

We transform the two expression matrices into non-negative matrices following the approach proposed by Kim and Tidor (2003). Specifically, for an input matrix M of size s by l, we create a matrix M′ of size s by 2l. For each element of the original matrix M(i,j)>=0, we set M′(i,j)=M(i,j) and M′(i,l+j)=0. For each element M(i,j)<0, we set M′(i,j)=0 and M′(i,l+j)=−M(i,j). In other words, each variable (miRNA or gene) is represented by two columns in the new matrix. One column contains the positive values of that variable, and the other contains the absolute values of its negative values. In this new representation, each network adjacency matrix is four times the original. The transformed non-negative expression matrices are our input matrices X₁ and X₂.

2.2 Problem formulation

To identify miRNA-gene comodules, we designed an objective function with three components. The first is based on the non-negative miRNA and gene expression matrices X₁ and X₂. The second considers the effects of gene–gene interactions. The last considers the effects of predicted miRNA–gene interactions. By optimizing this objective function, we obtain a joint decomposition of X₁ and X₂ that together reveals miRNA–gene regulatory modules inherent in the expression data and satisfies constraints based on prior information.

2.2.1 Objective function for modeling miRNA and gene expression profiles

The non-negative matrix factorization (NMF) technique divides a matrix into two non-negative matrices: a basis matrix of lower rank and a coefficient matrix (Lee and Seung, 1999; Paatero and Tapper, 1994). The squared error version of this factorization model can be defined as

where W and H are the basis matrix and coefficient matrix with dimensions s×k and k×n, respectively. The notation ‖•‖_F means the Frobenius norm of a matrix. The fact that W and H are non-negative guarantees that parts of the matrix can be combined additively to form a whole; hence, NMF is a useful technique for obtaining a part-based representation of the data. In other words, the factorization allows us to easily identify sub-structures in the data. Several approaches to solving NMF by iteratively updating W and H have been discussed in Berry et al. (2007), and additional bioinformatics applications of NMF are described in a recent review paper (Devarajan, 2008). Several variants of NMF have been proposed by incorporating various kinds of constraints: discriminative constraints (Zafeiriou et al., 2006), locality-preserving or network-regularized constraints (Cai et al., 2008; Gu and Zhou, 2009), sparsity constraints (Hoyer, 2004; Kim and Park, 2007), and others (Zhi et al., 2010).

However, the NMF method in its present form can only be applied to a matrix containing just one type of variable. It cannot be used to integrate multiple matrices for multiple types of variables together with prior knowledge such as networks that represent relationships among variables of the same type and/or between different types.

As our goal is to identify coordinated miRNA–gene comodules, we assume that there is a common basis matrix W for the miRNA and gene expression matrices X₁ and X₂. The two expression matrices have dimensions s×m and s×n, respectively, and will be factored into W and two coefficient matrices H₁ and H₂. This representation of the expression data can be derived by optimizing the following objective function:

(1)

where H₁ and H₂ have dimensions k×m and k×n, respectively. The parameter k is chosen prior to optimization.

The solution to Equation (1) is often not unique, and may be sensitive to noise in the expression data. Both of these limitations may confound the module discovery process. For these reasons, we will guide the optimization process toward reasonable biological solutions by incorporating prior knowledge into the objective function.

2.2.2 Network-regularized constraints

In this demonstration of our method, the prior knowledge consists of predicted miRNA–gene interactions and gene–gene interactions. The essence of our semi-supervised learning method is to define constraints for the comodule identification framework such that any variables linked in these two datasets are more likely to be placed into the same comodule. In addition to improving the biological relevance of the results, such constraints can greatly facilitate the discovery of comodules by narrowing down the large search space.

Let A denote the adjacency matrix of a gene interaction network, and B denote the adjacency matrix of a bipartite miRNA–gene network. We enforce ‘must-link’ constraints by maximizing the following objective function:

This term ensures that genes with known interactions have similar coefficient profiles.

Similarly, the interactions between genes and miRNAs can be encoded by the following objective function:

2.2.3 Network-regularized multiple NMF

Our inputs are the miRNA and gene expression matrices X₁ and X₂ with dimensions s×m and s×n, respectively, an m×n matrix B of predicted miRNA-target interactions, and an n×n gene–gene interaction network A. To discover miRNA-gene regulatory comodules, we combine the three objectives defined in the previous sections into a single optimization function:

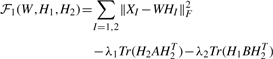(2)

The parameters λ₁ and λ₂ are weights for the must-link constraints defined in A and B. The first term favors modules with miRNA and gene expression profiles that are correlated in the common basis matrix W. The second term, Tr(H₂AH₂^T), summarizes all the must-link constraints in the gene-gene network. The third term, Tr(H₁B₁₂H₂^T), summarizes all the must-link constraints in the miRNA–gene network.

2.3 Sparse NMNMF

An important characteristic of the NMF method is that it often generates sparse representations of the data, allowing us to discover part-based patterns (Lee and Seung, 1999). However, studies have shown that the NMF representation is sensitive to the quality of the data and the researcher's choice of algorithm (Hoyer, 2004). Several approaches have been proposed to control the degree of sparseness in the W and/or H factors (Gao and Church, 2005; Hoyer, 2004; Kim and Park, 2007). For example, the idea of imposing L₁-norm constraints has been successfully applied to various problems (Tibshirani, 1996).

In our Network-Regularized Multiple NMF (NMNMF) framework, we adopt a strategy suggested by Kim and Park (2007) to make the coefficient matrices H₁ and H₂ sparse. This method, denoted Sparse NMNMF(SNMNMF), is formulated as follows:

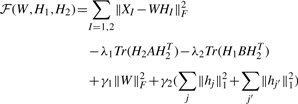(3)

where h_j and h_j′ are the j-th and j′-th columns of H₁ and H₂, respectively. The term γ₁‖W‖_F² limits the growth of W, while γ₂(∑_j|h_j‖₁²+∑_j′‖h_j′‖₁²) encourages sparsity.

2.4 The SNMNMF algorithm

In the basic NMF problem, the objective function (Equation 3) is not convex in W, H₁ and H₂. Therefore, it is unrealistic to expect a standard optimization algorithm to find the global minimum. We have developed an algorithm that efficiently converges to a local minimum by iteratively updating the matrix decomposition. Under the rules laid out below, the objective function ℱ is guaranteed not to increase when the decomposition is updated. Furthermore, the objective function remains invariant if and only if W, H₁ and H₂ are at a stationary point. This behavior can be proved in the same way as for the classical NMF algorithm (Lee and Seung, 2001). Derivations of the multiplicative updating rules and proof are provided in the Supplementary Material. We note that H₁ and H₂ are updated at the same time based on their current values at each iteration. The time complexity of the proposed algorithm is O(tk(s+m+n)²), where t is the number of iterations. We implemented our method in the Matlab language.

2.5 MicroRNA-gene comodule assignment

The coefficient matrices H₁ and H₂ produced by the above algorithm will be used to identify comodules. In other NMF applications (Brunet et al., 2004; Kim and Tidor, 2003), people have used the maximum coefficient in each column of H (or row of W) to discover patterns and determine memberships. However, this method presumes that each gene or sample can belong to one and only one pattern. In our application, some genes may be active in multiple modules and others might not participate in any module. In the former case, the gene could exert multiple functions under different conditions.

In this work we calculate a z-score for each element of the factorization based on the rows of H₁ and H₂:

where μ_i is the average value of miRNA j (or gene j′) in H₁ (or H₂), and σ_i is the standard deviation. We assign miRNA j (gene j′) to comodule i if z_ij (z_ij′) is greater than a given threshold T. Note that in our approach, each miRNA/gene may be assigned to multiple comodules, permitting the identification of multiple functionalities.

2.6 Assessing the statistical significance of (anti)-correlations between miRNAs and genes within a comodule

A miRNA–gene comodule is a pair of submatrices (sX₁ and sX₂) extracted from the matrices X₁ and X₂. The dimensions of the submatrices are s×m₁^s and s×n₁^s, respectively. We expect that within a comodule, miRNAs and genes are highly (anti-)correlated. In order to determine whether such relations are statistically significant, we performed the following assessment. First, we define the correlation S between two matrices with the same row dimensions as the sum of the correlations between any two columns, one from each matrix, i.e. S=∑s_i,j, where s_i,j=|corr(x_i¹,x_j²)|, ‘corr’ represents the Pearson's correlation coefficients. We derive the statistical significance (P-value) of the correlation between sX₁ and sX₂ by comparing it to the distribution of correlations between 1000 random matrix pairs. Each pair is composed of two matrices with dimensions identical to sX₁ and sX₂, whose elements are extracted from randomly permuted gene and miRNA expression matrices based on X₁ and X₂. Regulatory comodules with P-values smaller than 0.05/k were considered significant, where k is the number of columns in the basis matrix W.

2.7 Biological significance of the comodules

Studies have shown that miRNAs clustered on the genome are likely to be functionally related. Accordingly, we tested each comodule for miRNA cluster enrichment. We downloaded miRNA cluster data from the miRBase website (http://www.mirbase.org/), with a genomic cutoff distance of 50kb. This criterion resulted in a sample of 57 clusters containing from 2 to 49 miRNAs. The average number of members per cluster is 4.5. Most of the miRNA clusters (37 out of 57) contain only two miRNAs.

We also performed a functional enrichment analysis for genes in the identified comodules. Specifically, we looked for enrichment in Gene Ontology (GO) biological process (BP) terms and KEGG pathways. The annotations of GO (BP) terms were downloaded from http://www.geneontology.org/, and the KEGG pathways were downloaded from http://www.genome.jp/kegg/. We mapped the GO terms to NCBI gene IDs using the index file from ftp://ftp.ncbi.nlm.nih.gov/gene/. We filtered out functional sets with more than 300 genes or fewer than 5 genes, as the former are too general to be informative and the latter are too specific to be relevant. The statistical significance (P-value) of a module's enrichment in a functional set was calculated using Fisher's exact test. This statistic was transformed into a q-value using a false discovery rate correction (Storey and Tibshirani, 2003) with respect to the number of annotation groups.

2.8 Ingenuity Pathway Analysis

We also analyzed the genes in each comodule using Ingenuity Pathway Analysis (IPA, version 8.5, Ingenuity^® Systems, http://www.ingenuity.com Core 8.5, Ingenuity Analysis), a commercial application that calculates the association between a particular gene set and known functions and pathways. We used the default settings, where ‘Ingenuity Knowledge Base (Genes Only)’ is the reference set, and both direct and indirect relationships were considered in the network analysis.

2.9 Clinical characterization based on the basis matrix

We downloaded clinical data for the samples from the TCGA portal website. Based on the signals for all samples in each column of the common basis matrix W, we can characterize their level of associations with the discovered comodules. For each comodule, we divide the set of samples into three degrees of association (high, median or low). We then employed Kaplan–Meier method to compare the survival characteristics of the three groups, with significance determined using the log-rank test.

3 RESULTS

We applied the SNMNMF method to identify miRNA-gene comodules by integrating multiple independent data sources (the four matrices described in the Section 2). We set the reduced dimension of the matrix factorization k to 50, approximately equal to the number of miRNA clusters represented in our data (see Section 2.7). We set the weight parameters λ₁, λ₂, γ₁, and γ₂ to 0.0001, 0.01, 20 and 10, respectively (see Supplementary Material). The threshold T was set to 7 after conducting a series of tests, which are also described in the Supplementary Material. Among the 50 modules identified by the algorithm, one was empty and therefore deleted, and two contained only genes.

The 49 miRNA-gene comodules identified in this study have an average of 3.8 miRNAs and 78 genes per module. The size distributions are shown in the Supplementary Material, and each module is described in detail on our website. Based on a distribution of correlations derived from randomized miRNA-gene comodules (see Section 2), the (anti-)correlations between miRNAs and genes are statistically significant in 69.4% of the modules (permutation test with P-value <0.05/50) (see Table 2 and Supplementary Figure S3 for examples), indicating that the probability of finding similarly (anti-)correlated comodules by chance is close to zero.

Table 2.

Functional analysis of selected miRNA-gene comodules

No.	GO biological process terms	CG	PT	Cancer miRNAs	Num	OC miRNAs
7	Immune system process;	Yes	4.4e-165	mir-142-5p, mir-142-3p, mir-21*	3/3	mir-21*
	regulation of cell activation;
	regulation of cell proliferation
15	Immune response; immune system process;	Yes	8.6e-254	mir-142-5p, mir-142-3p, mir-150,	4/4
	defense response; inflammatory response;			mir-146a
	response to external stimulus; cell activation
23	Negative regulation of immune system;	Yes	1.9e-151	mir-22, mir-199a-5p, mir-145,	4/5	mir-22, mir-199a-5p,
	response to external stimulus;			mir-10b		mir-145, mir-10b
	regulation of cell division; cell adhesion;
	regulation of cell migration; cell communication;
25	Calcium-dependent cell–cell adhesion;		4.2e-4	mir-10b*, mir-135b, mir-10b	3/4	mir-10b*, mir-10b
	synaptic transmission; cell adhesion;
	extracellular structure organization
32	Cell cycle process; organelle organization;	Yes	2.0-44	mir-133b, mir-145	2/2	mir-145
	nuclear division; cell cycle; cell division;
37	Inflammatory response; defense response;	Yes	3.1e-47	mir-223, mir-146a	2/2	mir-223
	immune response; regulation of apoptosis;
	cell chemotaxis; regulation of DNA binding;
	cellular response to stimulus;
	regulation of cell death; anti-apoptosis;
40	Cell cycle; cell division;	Yes	2.7e-12	mir-99a, mir-135b, mir-222,	4/4	mir-99a
	nuclear division; mitosis;			mir-205
	organelle fission; microtubule-based process;
42	Reproductive developmental process;	Yes	7.5e-136	mir-214,mir-376a, mir-199b-3p,	5/7	mir-214, mir-199b-3p,
	BMP signaling pathway; cell differentiation;			mir-127-3p, mir-199a-5p		mir-199a-5p, mir-127-3p
	regulation of cell development

No.: the index of the comodule. CG: cancer genes. PT: permutation test with P-value×50<0.05. Num: the number of cancer-related miRNAs within this module, as well as the total number of miRNAs. OC miRNAs: those miRNAs in the module that are specifically related to ovarian cancer.

3.1 The comodules are enriched in genomic miRNA clusters

Previous studies have provided significant evidence that miRNAs often participate in combinatorial regulation (Krek et al., 2005; Zhang et al., 2010). The miRNA-gene comodules discovered in this article may shed light on these cooperative roles. Eleven of the identified modules are significantly enriched in at least one miRNA cluster, defined as a set of miRNAs that are located within 50kb of each other in the genome (q-value <0.05 after multiple testing correction; see Table 1). For example, comodule 48 contains nine miRNAs (mir-506, mir-507, mir-508-3p, mir-509-3p, mir-509-3-5p, mir-509-5p, mir-513b, mir-513c, mir-514), all of which belong to a miRNA cluster on chromosome Xq27.3.

Table 1.

Summary of miRNA modules that are enriched in miRNA clusters

No.	q-value	Overlap miRNAs	Loci	FS
10	0.002	mir-449b, mir-449a	5q11.2	Yes
	0.001	mir-34b*, mir-34c-5p	11q23.1	Yes
14	0.002	mir-143, mir-145	5q32	Yes
16	3.94e-05	mir-182*, mir-96, mir-183	7q32.2	Yes
17	0.001	mir-144, mir-451	17q11.2	Yes
18	0.001	mir-452, mir-224	Xq28	No
19	0.005	mir-30b*, mir-30d*, mir-30d,	8q24.22	Yes
		mir-30b
20	1.97e-5	mir-96, mir-183, mir-182	7q32.2	Yes
42	0.005	mir-199a-5p, mir-214	1q24.3	Yes
46	0.001	mir-144, mir-451, mir-144*	17q11.2	Yes
48	6.78e-12	mir-513b, mir-513c, mir-508-3p,	Xq27.3	No
		mir-506, mir-507, mir-509-3-5p,
		mir-514, mir-509-3p, mir-509-5p
50	0.008	mir-502-3p, mir-500*	Xp11.23	No

No.: the index of the comodule. q-value: the corrected P-value of enrichment. Loci: the chromosome locations of the enriched miRNA clusters. FS: indicates whether the enriched miRNA cluster has literature support on its functional roles.

Based on a literature survey, we found that spatially clustered miRNAs often have similar functions or play a cooperative role. An abundant literature supports the biological significance of the comodules identified in this study (the functional roles of miRNA clusters in our modules are described in Supplementary Table S1 of the Supplementary Material). For example, in comodule 10, two of the four member miRNAs (mir-449a and 449b) belong to a miRNA cluster on chromosome 5q11.2, while the other two (miR-34b* and 34c-5p) belong to a cluster on chromosome 11q23.11. In a recent study, miR-449a and 449b have been reported to have a tumor suppressing function by regulating Rb/E2F1 activity (Yang et al., 2009). In addition, miR-34b* and 34c-5p were reported to be targeted by p53 and they cooperatively control cell proliferation in ovarian cancer (Corney et al., 2007).

To take another example, three of the seven miRNAs in module 16 (miR-96, miR-182*, miR-183) are clustered on chromosome 7q32.2 and are reported to be dysregulated in various cancers. These miRNAs (along with others) cooperatively repress FOXO1, affecting cell cycle controls and apoptotic responses in endometrial cancer (Myatt et al., 2010). The differential expressions of these miRNAs appear to depend on the mismatch repair status, a behavior characteristic of undifferentiated proliferative states in colon cancer (Sarver et al., 2009). In addition, these miRNAs were identified as important biomarkers in the detection and prognosis of prostate cancer (Schaefer et al., 2010). All this evidence shows that our comodules can indeed group miRNAs with cooperative roles and provide insights into their functional mechanisms.

3.2 The comodules are enriched in known functional sets

To evaluate the biological relevance of the 49 comodules, we calculated their enrichment in GO biological process terms and KEGG pathways using the hypergeometric test. (This test applies only to the genes in the comodules.) Twenty-six (53.1%) of the gene modules have at least one overrepresented GO biological process term with an FDR-corrected q-value <0.05. Taken together, the modules are enriched in 367 different GO biological processes and 57 KEGG pathways. The most frequently enriched biological processes are nuclear division, immune system process, microtubule-based processes, inflammatory response, response to external stimulus, cell cycle and cell adhesion.

Table 2 provides a list of enriched GO biological processes for selected comodules. When we performed the same test on a set of random modules, only 3.0%(2.4%) were enriched in any GO biological process. These observations demonstrate the power of our method in grouping genes that participate in the same processes or pathways.

3.3 The miRNA-gene comodules are strongly implicated in cancer

Since our input data included the miRNA and gene expression profiles of ovarian cancer samples, we expect the identified comodules to be related to cancer. To verify this, we used a cancer miRNA benchmark dataset of 147 miRNAs from a review article (Koturbash et al., 2010). Each of these miRNAs was reported in the literature to be dysregulated in one or more cancers. Among these, 41 are relevant to ovarian cancer. Note that this dataset does not include any information from the TCGA ovarian cancer data. Our comodules involve 117 different miRNAs, 52 of which belong to the benchmark set of cancer miRNAs. This ratio is highly significant (P=1.1×10⁻⁶) (Figure 2). Even more importantly, 21 of the 52 miRNAs shared by our results and the benchmark are related to ovarian cancer, with an enrichment significance of P=7.2×10⁻⁶.

Fig. 2.

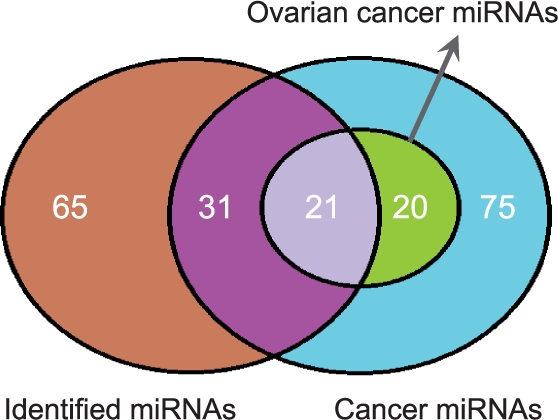
About 44.4% of the miRNAs in identified comodules have previously been reported to be cancer related (hypergeometric test, P=1.1×10⁻⁶). Of these, 21 miRNAs were specifically related to ovarian cancers (hypergeometric test, P=7.2×10⁻⁶).

Furthermore, 69.4% of the modules contain at least two miRNAs that are known to be cancer related (see Table 2). For example, module 42 has seven miRNAs, five of which belong to the benchmark. Four of them (mir-199a-5p, mir-199b-3p, mir-127-3p, mir-214) are also reported to play roles in ovarian cancer (Koturbash et al., 2010). Further supporting this interpretation, the genes of this comodule are enriched in numerous cancer-related pathways such as hedgehog signaling pathway, cell differentiation, TGFβ signaling pathway and Wnt signaling pathway.

We explored cancer gene enrichment in the gene modules using the large-scale, human-curated knowledge database of the IPA system. Most of the modules (63.3%) are highly enriched in cancer genes (multiple test corrected P-value <0.05, as reported by the IPA system). Moreover, 10 of the modules are significantly enriched in ovarian cancer genes (see Supplementary Table S2 in the Supplementary Material). For example, the 129 genes in module 23 include 64 cancer genes and 13 ovarian cancer genes. This module is overrepresented in several cancer-related pathways, including cell communication, TGFβ signaling pathway and PPAR signaling pathway. These observations confirm that the miRNA-gene comodules discovered in this study play important roles in various cancers, especially ovarian cancers.

3.4 Network analysis of the comodules shed light on regulatory circuits

Based on the principle of our method, the genes in a comodule are likely to function together as a network, and miRNAs in a comodule are likely to cooperatively target groups of networked genes. We found that in many of the comodules identified by our method, the genes can be organized into highly connected networks using the IPA system and its database of molecular interactions (Calvano et al., 2005). Specifically, based on the IPA system, we found 67.4% of the comodules are significantly connected to form at least one highly significant scored network with cutoff larger than 30.

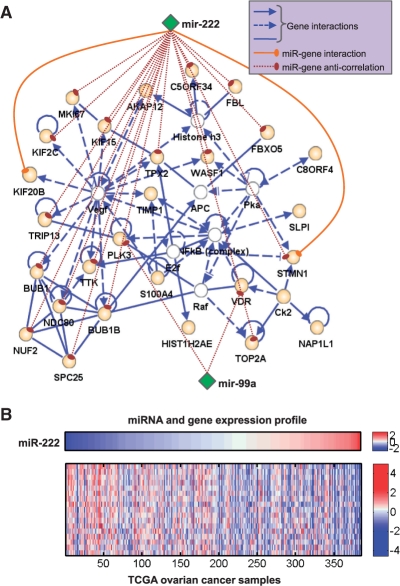
For example, from comodule 40 we constructed a dense network of 35 genes (based on the default settings of the software) (Figure 3). According to the IPA system, this network is significantly enriched with genes participating in cell death, the cell cycle, tumor morphology, cellular growth and proliferation and tissue development. Strikingly, miR-222 and miRNA-99a are anti-correlated with 19 genes in this network (Pearson's correlation coefficients <−0.21, P-values <5.0×10⁻⁵). This widespread anti-correlation strongly implies that the two miRNAs participate in regulating the overrepresented biological processes in the comodule. In other words, we can transfer those functions to these two miRNAs, especially to miR-222 which is anti-correlated with 17 genes. Moreover, the literature reports that both miR-222 and miR-99a are dysregulated in various cancers (Koturbash et al., 2010). In a recent study, miR-222 has been implicated in the survival rate of patients with sporadic ovarian cancer (Wurz et al., 2010).

Fig. 3.

Network analysis of comodule 40. (A) The highly connected network consists mainly of genes in comodule 40 (orange nodes), but also includes 6 genes identified using the IPA system (white nodes). Two miRNAs (miR-222, miR-99a, green nodes) are also shown. Based on the MicroCosm Targets V5.0 dataset, miR-222 targets two genes (solid line). Significant anti-correlations between miRNAs and genes are shown with dashed lines. (B) Anti-correlations between miR-222 and gene expression profiles (Pearson's correlation coefficients <−0.21, P-value <5.0×10⁻⁵).

Finally, we note that based on our input knowledge (the miRNA-gene interaction data), miR-222 is linked to this network through just two genes: KIF20B and STMN1. However, the complementary information on gene–gene connections and miRNA–gene expression (anti-)correlations permits us to place miR-222 in a comodule with many other genes that could be direct or indirect targets. These results, including the comodule's high level of enrichment in known cancer miRNAs, cancer genes, and cancer-related processes and interactions, shed light on a miRNA-gene regulatory circuit that plays an important functional role in ovarian cancer and possibly other cancers.

3.5 The comodules can stratify patients into groups with distinct clinical characteristics

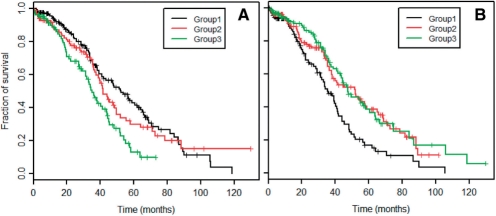
As described in the Section 2, for each miRNA-gene comodule we divided the patients into three groups by looking at their basis vectors in the matrix W. Specifically, patients with signals close to zero (less than 0.01) in the basis vector corresponding to the comodule are placed in the ‘low-association group’ (Group 1). The remaining patients are divided into two equal groups on the basis of this signal: the high-association group (Group 3) and the medium-association group (Group 2). We expected that for at least some of the comodules, the three groups would exhibit significant differences in their clinical parameters.

We tested this hypothesis by calculating Kaplan–Meier curves for the three groups. These curves plot the fraction of surviving patients against the time elapsed since their initial diagnoses. We found that the three groups often have significantly different survival characteristics (log-rank test P<0.05/50). For comodule 39, the log-rank test gives P=0.00016 and the median survival durations of the low-association (Group 1) and high-association (Group 3) groups are 52.3 months and 35.0 months, respectively (Fig. 4A). The patients in the high-association group faced greater risks.

Fig. 4.

Kaplan–Meier survival analysis for three patient groups defined using their signals in a column vector of W. The curves are plotted for comodules 39 (A) and 40 (B).

For comodule 40, on the other hand, the median survival durations of the low- and high-association groups are 35.5 and 47.6 months (Fig. 4B). In this case the low-association group was at greater risk (log-rank test P=6.4×10⁻⁵). Further studies of the mechanisms underlying such clinical segregation could point the way to patient-oriented therapeutic designs.

3.6 Comparison with other methods

The SNMNMF method discovers miRNA-gene comodules by integrating diverse data sources. To achieve this goal, we iteratively define a common basis matrix for the matrices representing datasets of miRNA and gene expression profiles, while incorporating terms representing the solution's sparsity and conformity with independent network data into the objective function. The sparsity penalties to the objective function help us to obtain easily interpretable solutions.

Compared with other recent methods for miRNA-gene regulatory comodule identification (Joung et al., 2007; Peng et al., 2009; Yoon and De Micheli, 2005), SNMNMF has several advantages: (i) it can incorporate prior knowledge such as a gene interaction network as a constraint on the solution space. To the best of our knowledge, this form of data has not been considered by any other algorithm for this task; (ii) it simultaneously integrates several different types of data; (iii) it provides sparse solutions that are more easily be interpreted in biological contexts; and (iv) it can be solved in a reasonable amount of computing time. Our general framework is applicable to many other problems involving heterogeneous data sources. In addition, our general framework is applicable to many other problems involving heterogeneous data sources.

Due to the diversity of our data sources, it is difficult to make a fair comparison between our results and those of other methods. Nevertheless, we implemented the EBC method developed by Peng et al. (2009) for comparative analysis. EBC is a sequential, integrative method with several preprocessing and post-processing steps. It constructs a miRNA-gene regulatory network by combining the miRNA-gene correlation network (based on our X₁ and X₂) with the miRNA-target interaction network (B). It enumerates all maximal bi-cliques in the data, then selects the most significant ones (see Supplementary Figure S6 for details). We applied EBC to our dataset, leaving out the protein interaction network (A). EBC identifies 126 miRNA-gene comodules, with on average 1.2 miRNAs and 24.4 genes per comodule. Most of the comodules (108/126) have one miRNA, and the others have only two (15/126) or three (3/126) miRNAs. One should note that star-shaped ‘one miRNA regulates multiple genes’ networks are the most basic structure in the bipartite network that can be extracted directly. The EBC method is not powerful when it comes to recognizing ‘combinatorial’ regulations among miRNAs, although such mechanisms are abundant.

Our method identified many miRNA modules that were enriched with miRNA clusters. Only 19.1% of the EBC gene modules are enriched in GO biological process terms (versus 1.2% for the random test), compared to more than 50% of our modules. Moreover, the EBC method's criterion for maximal bi-cliques to be comodules is very stringent and vulnerable to noisy data (e.g. predicted miRNA–gene interactions). Finally, the maximal bi-cliques contain a high level of redundancy (an example is shown in Supplementary Figure S7). All of these comparisons demonstrate that our procedure is more effective at identifying miRNA-gene comodules.

4 CONCLUSION

MiRNAs play crucial roles in gene regulation. However, little is known about the combinatorial regulations and cooperative mechanisms that occur between miRNAs and genes. The availability of miRNA and gene expression profiles from the same patients, miRNA-gene networks, and gene interaction networks provides an unprecedented opportunity to discover and accurately characterize miRNA-gene regulatory comodules. In this study, we developed a flexible and effective framework that integrates these three data sources to identify miRNA-gene regulatory comodules.

We tested the method on human data, specifically ovarian cancer samples from the TCGA database. The comodules reveal cooperation between miRNAs and genes in several functions and phenotypes of cellular systems, and provide new insights into the transcript and post-transcript regulatory organization of ovarian cancer. As genomic data sources increase in volume and diversity, our framework could provide new avenues for the systematic interpretation of combinatorial regulatory mechanisms.

In this article, we applied our SNMNMF method to the specific problem of miRNA-gene comodule identification. However, the method is equally useful for many biological problems requiring the integration of several types of inputs. In particular, it is suitable for problems involving multi-dimensional genomic data (profiling multiple variables on the same set of samples) and independent priors identifying known relationships between the variables (e.g. miRNA-gene and gene–gene relationships).

For example, Kutalik et al. (2008) explored gene-drug comodules based on gene expression and drug response data from 60 cancer samples. However, the quality of the modules obtained in that study suffered from the small number of samples and noisy input data. Using our framework, one could incorporate known gene–gene interactions, known gene–drug relationships and even drug–drug similarities to improve the module discovery.

Currently, we observe an increasing trend toward generating multi-dimensional genomic data including copy number variation, DNA methylation, histone modification, miRNA expression and gene expression data, all profiled on the same set of samples. At the same time, we are gaining more and more knowledge regarding the associations between different genomic variables. The new method described in this article can serve as a powerful framework for the simultaneous integration of diverse data to discover complex regulatory patterns.

Funding: National Institutes of Health (Grants R01GM074163 to X.J.Z.); National Science Foundation (Grants 0515936 and 0747475 to X.J.Z.); National Natural Science Foundation of China (No. 11001256 to S.Z.); Innovation Project of Chinese Academy of Sciences (CAS) (kjcx-yw-s7 to S.Z.); the Special Presidential Prize - Scientific Research Foundation of the CAS, and the Special Foundation of President of AMSS at CAS for ‘Chen Jing-Run’ Future Star Program (to S.Z.).

Conflict of Interest: none declared.