Exploring the Landscape of Protein-Ligand Interaction Energy Using Probabilistic Approach

Abstract

Analysis of protein/small molecule interactions is crucial in the discovery of new drug candidates and lead structure optimization. Small biomolecules (ligands) are highly flexible and may adopt numerous conformations upon binding to the protein. Using computer simulations instead of sophisticated laboratory procedures may significantly reduce cost of some stages of drug development. Inspired by probabilistic path planning in robotics, stochastic roadmap methodology can be regarded as a very interesting approach to effective sampling of ligand conformational space around a protein molecule. Protein-ligand interactions are divided into two parts: electrostatics, modeled by the Poisson-Boltzmann equation, and van der Waals interactions, represented by the Lennard-Jones potential. The results are promising; it can be shown that locations of binding sites predicted by the simulation are in agreement with those revealed by experimental x-ray crystallography of protein-ligand complexes. We wanted to extend our knowledge beyond the current molecular modeling tools to arrive at a better understanding of the ligand-binding process. To this end, we investigated a two-level model of protein-ligand interaction and sampling of ligand conformational space covering the entire surface of protein target. Supplementary Material is available at www.liebertonline.com/cmb.

1. Introduction

The identification of protein functional regions is an important first step in determination of its molecular function. For small molecule drug design, the most crucial are the locations of prospective binding sites, because a potential solution to the computer-aided rational drug design problem requires the ligand to match (both geometrically and energetically) the protein-binding site. Many computational approaches based on the analysis of protein structure (Laskowski, 1995; Weisel et al., 2007), sequence (Capra and Singh, 2007), or both (Capra et al., 2009) have been developed to predict ligand-binding sites (Laurie and Jackson, 2006). In this article, we focus on using structural information accompanied by an energy model to predict ligand-binding sites. Recent algorithms have focused on van der Waals interaction energy of a small, general probe used to build an interaction grid near the protein surface: PocketFinder uses an aliphatic carbon as the probe (An et al., 2005), and Q-SiteFinder uses a methyl group (Laurie and Jackson, 2005). In contrast, our approach uses directly the ligand of interest. However, the protein conformation may significantly change upon ligand binding; in the most current methods, the protein is usually assumed to be rigid. The analysis of changes in the protein conformation, especially these induced by interaction with a ligand, is still a challenging task. The latest review of methods used to account for protein flexibility can be found in the work by B-Rao et al. (2009). A similar form of exploration of protein-ligand interaction, also known as blind docking, was introduced for prediction of peptide-protein complexes by scanning the entire surface of protein (Hetenyi and van der Spoel, 2002) and, more recently, for docking of drug-sized compounds to relatively small proteins (Hetenyi and van der Spoel, 2006). This approach was further improved by focusing on predicted binding sites (Ghersi and Sanchez, 2009). These solutions are based on the most often used docking software AutoDock (Morris et al., 1998). We propose a different framework, based on the Stochastic Roadmap Simulation (SRS) (Apaydin et al., 2002, 2003), a Monte Carlo (MC) type method derived from planning methodology of robotic motion. The method consists of effective sampling of the combined transformational and conformational space of the ligand. Unlike a classical MC approach, SRS enables one to sample from all possible paths the ligand may choose moving around its protein target. The basic idea is to effectively scan the entire surface of the protein, using the ligand as a probe, to obtain a distribution of energetically favorable regions, which may be the potential binding sites. The original SRS approach is capable of detecting putative binding sites or even distinguishing the catalytic binding site. Apaydin et al. (2002, 2003) propose the time to escape from the so-called funnel of attraction as a measure of binding affinity. However, SRS does not provide information about the nature of interactions between the ligand and the binding site (e.g., hydrogen bonds), and it should be combined with a more direct model in order to analyze the bound state. We propose using the LUDI model as a tool for visual inspection of qualitative and quantitative properties of the interaction between the binding site of a protein and the bound ligand (Bohm, 1992).

2. Methods

2.1. Test set

The test set was selected according to Paul and Rognan (2002). The set consists of 60 protein-ligand complexes. Although enzyme-inhibitor complexes predominate, there are also examples of immunoglobulins with haptens and some proteins involved in active transport of amino acids or fatty acids. Protein structures deposited in the PDB database (Berman et al., 2000) often become a basis for structure-based rational drug design. An example of a designed drug can be thrombin (protein responsible for blood coagulation) inhibitor MQPA which, under the name argatroban, was accepted in 2002 by the Food and Drug Administration as a commercial anticlotting agent.

2.2. Modeling the ligand

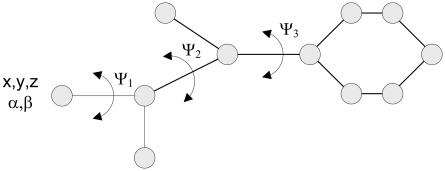
By a ligand, we understand a small molecule with a limited number of conformational degrees of freedom (up to 50). First, we assign to one terminal atom (called the base) three cartesian coordinates (x, y, z), which describe the location of the ligand in space, and two angles (α, β) describing the orientation of the base bond. Second, we assign one dihedral angle for each non-terminal atom (conformational degrees of freedom; Fig. 1). The structures of rings are assumed constant. Internal interactions between atoms are divided into Coulombic and van der Waals interactions (Apaydin et al., 2002).

FIG. 1.

Degrees of freedom of a hypothetical ligand.

2.3. Force field around protein

The environment around a protein molecule is modeled by electrostatic and van der Waals interactions. These interactions generate attractive and repulsive forces, which cause motion of molecules (Apaydin et al., 2002). The electrostatic part is modeled by the Poisson-Boltzmann Equation (PBE) (Sharp and Honig, 1990).

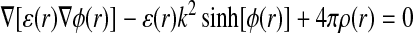(1)

where ɛ is dielectric constant, ϕ is electrostatic potential, ρ is charge density, κ is ionic strenght, and r is location vector in three-dimensional (3D) space.

The model associated with PBE (1) is far more accurate in this case than simple Coulombic models and incorporates features such as location-dependent dielectric constant (DC). DC varies in space: experimentally determined DC of proteins equals approximately 2, whereas for water DC equals 80 (Sharp and Honig, 1990). PBE also considers the contribution of mobile ions to the electrostatic potential (the natural environment for proteins is usually a salty aquatic solution). Protein is considered a rigid body limited by solvent accessible surface (Connolly, 1983). Analytical solution to the PBE is possible only for systems with very simple geometries. Since the protein surface contains many clefts and cavities, we use a numerical solution obtained using the finite difference methods. In order to solve PBE on a 3D grid, we use two computer programs: DelPhi (Rocchia et al., 2001) and APBS (Holst and Saied, 1995). The software is highly configurable with respect to simulation parameters as well as PBE solver parameters. Van der Walls interactions are modeled using Lennard-Jones potential (2) calculated for the same 3D grid as for PBE:

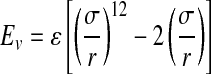(2)

where σ, collision diameter, is the distance r between atoms for which E_vdW equals 0, and ɛ is the depth of the potential well.

2.4. Modeling the binding site

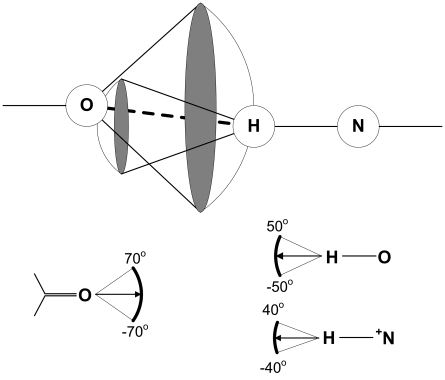
As a model for ligand-binding site interaction, we use the LUDI model first introduced by Böhm (1992) and adopted to the form of interaction surfaces by Rarey et al. (1996). The model considers several possible types of intramolecular interactions, mainly hydrogen bonds or specific hydrophobic contacts. The interaction itself is modeled by an interaction center and interaction surface located on a sphere with center in interaction center. The interaction to take place requires interaction center of the ligand to lie on interaction surface of the protein and vice versa. An interaction surface is modeled as a discrete set of points in 3D space. Such representation has an advantage of encoding a set of biochemical rules governing intramolecular interactions in a compact geometric form easy to store and process (for a few examples of molecular interaction surfaces, see Fig. 2). The data concerning other types of interaction surfaces can be found in Rarey et al. (1996). We use our own implementation of LUDI and interaction surfaces in Matlab 7.

FIG. 2.

Illustration of the idea of modeling molecular interactions by interaction surfaces. Examples of interaction surfaces. An interaction takes place if an interaction center of a ligand lies on the interaction surface of a receptor and vice–versa (upper part). Oxygen atom (lower left) plays the role of an acceptor, and oxygen and nitrogen (lower right) of donors of hydrogen bond. Interaction surfaces are spherical sections with a 1.9 Å radius.

2.5. Stochastic Roadmap Simulation

2.5.1. Roadmap construction

Apaydin et al. (2002, 2003) define a roadmap as a discrete representation of molecular motion. In this case, each node of a roadmap represents one conformation of a ligand. Formally, each conformation of n parameters is represented by a vector q. The set of all possible conformations forms the conformational space C. SRS assumes that the interactions are described by an energy function E(q), which depends only on the conformation q of the ligand. A pathway in C represents motion of the ligand around protein. A roadmap may be considered a directed graph G encoding many pathways in C. Each node of a roadmap is a randomly selected conformation q from C with associated energy E(q). Each directed edge between two nodes v_i and v_j has associated weight P_ij, which is equal to the probability of transition between the two nodes. In order to construct a roadmap, the algorithm samples n conformations, randomly and independently from C. Then for each node v_i one finds k nearest neighbors of that node according to selected metric (i.e., root mean squared deviation [RMSD] or Euclidean). After that, a transition probability P_ij is computed for every pair of neighboring nodes. P_ij calculation is based on difference of energy 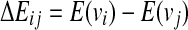between nodes v_i and v_j according to the formula:

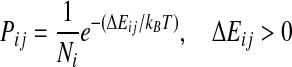(3)

or

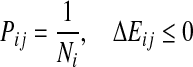(4)

where k_B is Boltzmann constant, T is system temperature, and N_i is number of neighbors of node. The self-transition probability is defined as:

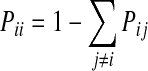(5)

which ensures that the transition probabilities from any node sum up to 1 (Apaydin et al., 2002, 2003).

2.5.2. Simulation

Although it is possible to perform a simulation on a roadmap, which corresponds to a discrete version of the standard Monte Carlo method (discretization is defined by a roadmap), Apaydin et al. (2002) suggest that usually it is not needed to generate individual trajectories on a roadmap but rather to evaluate a parameter of interest. Time to escape (expressed as a number of simulation steps) from the funnel of attraction around the protein binding site is given as an example. Apaydin et al. (2002, 2003) propose the escape time as a measure of affinity of a ligand to a putative binding site. The funnel of attraction F_i is defined as the set of conformations within 10 Å RMSD of the bound conformation. Expected value of the time to escape can be easily calculated using the first step analysis technique (Apaydin et al., 2002, 2003), from Markov chain theory (Taylor and Karlin, 1998) by solving the following system of equations (Apaydin et al., 2002):

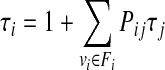(6)

where τ_I is time to escape starting from i–th node, F_i is funnel of attraction around i–th binding site, and v_i is i–th node.

2.5.3. Predicting the putative binding sites

The SRS method is used for prediction of putative binding sites of a protein. The process consists of several consecutive steps. First, a large number (i.e., 10⁵) of nodes is sampled at random. Next, the resulting nodes are ordered by increasing energy; then a small part of lowest energy nodes (in our case, 10 nodes) is selected for the next step, which consists of sampling of additional nodes in the direct neighborhood of previously selected nodes. Finally, the resulting lowest energy nodes are filtered by pairwise distance of 10 Å from each other, in order to avoid multiple representations of the same putative binding site region, and by 5 Å distance from the protein surface (assuming a binding site should be located close to the protein surface).

3. Results and Discussion

3.1. Analysis of the results

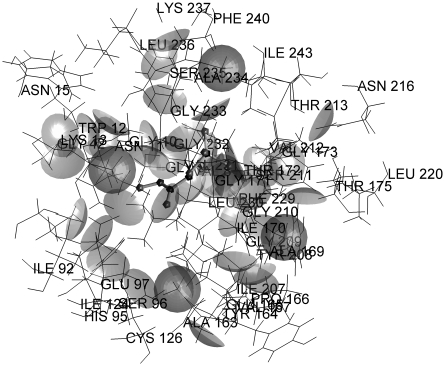
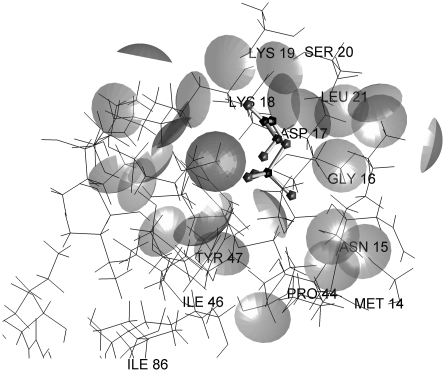
As a measure of accuracy of a given methodology used for prediction of protein-ligand interactions, RMSD from the ligand pose determined by x–ray crystallography is often used. By ligand pose, we understand its conformation (internal degrees of freedom), location, and orientation in 3D space. A method that is able to yield a solution which is closer than 2 Å RMSD from an experimentally determined pose is considered accurate. The solutions obtained using the predictive capabilities of the SRS method in most cases are concentrated in the parts of protein structure described by x–ray crystallography as the ligand-binding sites. In 51 out of 60 complexes, it was possible to obtain a solution closer than 2 Å RMSD to the experimental result. Moreover, it was possible without any prior information about location of the binding site, whereas in most of the current methods, some information about binding site location is always present and the search algorithm is limited to this location only. The most promising is the fact that the proposed method was able to predict dual binding sites shown by crystallography for the complexes 1fki, 1glq, 1hsl, 1imb, 1ldm, 1srj, and 1tph (Fig. 3). Concerning the data presented in Table 1, it was possible to obtain solutions close enough to the experimental ones, however these are not always the lowest energy solutions. The lowest energy solutions close to the experimental results were obtained for complexes 1cbx, 1coy, 1fkg, 1ghb, 1mup, 2ctc, and 2sim, but except for 1ghb they were located much farther than 2 Å RMSD from experimental ligand pose. The analysis of energy profiles of solutions showed that solutions with very low energy make no more than 10% of all the solutions, and the solution close to the experimental one must be looked for among solutions of typical energy. Another observation was that, as expected, for the ligands with negative total charges, solutions are concentrated in the regions of protein having positive electrostatic potential and vice–versa. An example of an analysis of a ligand-binding site interaction is shown in Figures 4 and 5 (for a complete set of figures, please see Supplementary Material, which is available at www.liebertonline.com/cmb). Figure 4 shows the model of the catalytic site of triosephosphate isomerase with a bound inhibitor, in this case phosphoglycolohydroxamic acid (PGH). It can be seen that PGH forms at least two hydrogen bonds with the protein (Gly233 and Ser211). However, for the lowest energy pose (Fig. 5), in spite of existing possibilities, no significant interactions have been detected according to the model.

FIG. 3.

Centers of gravity of solutions obtained by the simulation for 1tph. Both experimental binding sites (ball and stick ligands) were predicted by the simulation.

Table 1.

Results for the Test Set

PDB ID	RMSD 1	Rank	RMSD 2	min E	PDB ID	RMSD 1	Rank	RMSD 2	min E
1aaq	1.01	12	14.78	−44.03	1lst	0.88	137	10.86	−65.26
1acj	4.99	3	11.54	−18.11	1mdr	1.19	261	11.39	−17.59
1ack	4.67	60	7.10	−24.35	1mrg	0.70	400	13.02	−37.46
1aha	1.49	96	12.75	−21.77	1mrk	0.77	118	14.30	−39.64
1azm	1.32	91	17.31	−189.31	1mup	2.08	467	6.48	−11.13
1baf	5.41	99	16.72	−41.26	1pbd	2.11	751	11.45	−131.71
1cbs	1.18	55	11.20	−78.26	1poc	2.12	8	16.92	−46.69
1cbx	1.64	56	4.44	−84.30	1snc	1.60	103	15.93	−112.94
1cil	1.12	29	10.43	−214.63	1srj	0.47	226	14.73	−95.99
1coy	1.44	4	2.15	−27.46	1stp	1.55	95	17.37	−22.76
1cps	1.08	46	8.79	−39.46	1tdb	1.68	291	18.40	−164.09
1dbb	1.06	206	19.67	−40.33	1tng	1.25	69	17.23	−13.71
1dbj	1.05	54	16.14	−28.72	1tnl	0.75	157	17.37	−36.95
1dr1	1.03	122	12.26	−51.56	1tph	1.20	267	11.23	−150.81
1dwd	0.83	2	18.35	−24.83	1tpp	1.00	189	10.63	−98.97
1eap	1.81	46	14.86	−106.86	1ulb	0.87	662	11.33	−15.29
1eed	1.37	4	16.97	−27.07	1ukz	0.58	79	13.48	−161.94
1etr	0.66	71	14.95	−109.27	1xid	1.05	729	9.86	−32.43
1fkg	1.94	5	3.63	−30.39	1xie	1.32	205	12.62	−35.76
1fki	0.58	157	9.55	−71.19	2ak3	6.85	73	20.32	−163.77
1ghb	0.64	6	1.39	−20.98	2cgr	1.52	20	21.06	−46.91
1glq	4.19	22	18.92	−18.89	2cmd	0.99	192	18.30	−119.64
1hfc	2.63	730	13.68	−43.62	2ctc	1.32	309	6.98	−92.86
1hsl	1.22	324	11.80	−101.49	2gbp	0.81	146	9.64	−75.78
1hyt	0.98	171	13.49	−87.90	2phh	2.00	486	10.97	−96.61
1icn	1.61	116	15.20	−103.64	2sim	1.83	4	3.43	−48.85
1imb	0.87	629	12.31	−84.96	3cpa	1.49	70	10.86	−101.70
1lah	1.00	171	12.92	−115.91	3ptb	0.98	229	15.13	−20.34
1ldm	0.00	66	17.34	−16.23	3tpi	0.71	98	14.31	−101.80
1lmo	1.14	147	17.33	−27.12	4dfr	1.17	126	16.72	−86.10

RMSD¹, a best (closest to experimental) pose RMSD; RMSD², a lowest energy pose RMSD from the experimental pose; Rank, the rank of best pose concerning its E (kcal/mol).

FIG. 4.

Catalytic binding site of 1tph with the best pose ligand.

FIG. 5.

Putative binding site of 1tph with the lowest energy ligand.

4. Conclusion

The SRS methodology can be regarded as a promising new technique for exploration of protein–ligand interactions, especially the interaction energy landscape. It was shown that a reasonable solution can be obtained in most cases, but the underlying energy model must be further improved to serve the purpose of discrimination among the best results (Table 1). The electrostatic part of the total potential comes from the linearized PBE solved on a 3D grid using finite-difference method. The model treats solvent molecules implicitly. The accuracy of such a solution is naturally limited by the resolution of the grid. In addition, the most significant errors in solution to the PBE may occur at the boundary of regions of high and low dielectric constant, close to the protein surface. The continuous approximation of the solution to the linearized PBE, which does not suffer from resolution or boundary problems, can be the Generalized Born (GB) model (Leach, 2001). Models like PBE or GB do not include the effects of solute-imposed constraints on solvent molecules organization, better known as the hydrophobic interactions, which usually significantly contribute to the binding process. The classical way to account for hydrophobic effect is to add to the total potential a component dependent on solvent accessible surface area. Another candidate measure of ligand-binding affinity can be the time to escape from the funnel of attraction. The presented approach uses a grid representation of protein structure. We also discuss how the problem of flexibility of the protein can be potentially addressed. By adjusting the maximum energy threshold, we allow for a slight overlap of the protein and the ligand, which accounts for minor changes in protein conformation upon binding. Such a procedure is often called the soft docking. Another straightforward solution may assume scanning multiple grids representing multiple protein structures.

Acknowledgments

We would like to acknowledge Mehmet Serkan Apaydin and Zbigniew Starosolski for making their software available. Molecular graphics images were produced using the UCSF Chimera package from the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIH P41 RR-01081) (Pettersen et al., 2004). The research presented here was partially supported by Polish Ministry of Science and Higher Education funds for the year 2009.

Disclosure Statement

No competing financial interests exist.