Inference from Samples of DNA Sequences Using a Two-Locus Model

Abstract

Performing inference on contemporary samples of DNA sequence data is an important and challenging task. Computationally intensive methods such as importance sampling (IS) are attractive because they make full use of the available data, but in the presence of recombination the large state space of genealogies can be prohibitive. In this article, we make progress by developing an efficient IS proposal distribution for a two-locus model of sequence data. We show that the proposal developed here leads to much greater efficiency, outperforming existing IS methods that could be adapted to this model. Among several possible applications, the algorithm can be used to find maximum likelihood estimates for mutation and crossover rates, and to perform ancestral inference. We illustrate the method on previously reported sequence data covering two loci either side of the well-studied TAP2 recombination hotspot. The two loci are themselves largely non-recombining, so we obtain a gene tree at each locus and are able to infer in detail the effect of the hotspot on their joint ancestry. We summarize this joint ancestry by introducing the gene graph, a summary of the well-known ancestral recombination graph.

1. Introduction

Patterns of variation in contemporary samples of within-species DNA sequence data contain information both on the biological processes that gave rise to the data (such as rates of mutation, recombination, and selection) and on demographic forces (such as rates of population expansion and migration). However, extracting this information is a challenging task, made even more complicated when several of these processes are modelled simultaneously. One approach is to use summary statistics and then infer parameters from moment-based estimators, but these have the undesirable effect of discarding some information. It is preferable to make full use of the data by calculating its likelihood under an assumed model, but no closed-form expression for the likelihood is known except in the simplest special cases. This is true even for the very popular model of ancestry known as the coalescent (Kingman, 1982). In recent years, computationally intensive full-likelihood methods such as Markov chain Monte Carlo (MCMC) and importance sampling (IS) have been developed as a way to compute the likelihood by integrating over possible genealogies compatible with the observed data. A genealogy, that is, a tree or graph relating the lineages of the sequences back in time to a most recent common ancestor, is thus best viewed as a hidden random variable in this context. Examples of MCMC methods in the framework of the neutral coalescent with recombination (Hudson, 1983; Griffiths and Marjoram, 1997) include Kuhner et al. (2000), Nielsen (2000), and Wang and Rannala (2008); examples of IS include Griffiths and Marjoram (1996), Fearnhead and Donnelly (2001), and Griffiths et al. (2008).

These methods are sophisticated. The state space of genealogies is typically extremely large, limiting the number of samples and/or polymorphic sites to which the methods can be applied. This is particularly true of models of recombination, a process that acts to break up lineages as we trace them back in time; each site in the sequence may then have a different genealogical history. To make headway, researchers have turned more recently to approximate methods. For example, suppose we have a sample of sequences from several individuals, with a number of polymorphic sites in the sequences among these individuals. To calculate the likelihood, we should consider the joint ancestry of these sites together, but a simple alternative is to consider each pair of sites individually, and simply multiply together the likelihood of each observed pair as if they were independent observations. This is known as the (pairwise) composite likelihood (Hudson, 2001; McVean et al., 2002). Of course, in reality the pairs are highly dependent due to their shared ancestry, but the method has nevertheless found several successful applications, including estimates of gene conversion rates (Frisse et al., 2001; Ptak et al., 2004) and estimates of genome-wide fine-scale crossover rate variation in humans (McVean et al., 2004; Myers et al., 2005). Another example is the product of approximate conditionals (PAC) (Li and Stephens, 2003), which constructs a pseudo-likelihood by another approach. It also has a wide variety of applications, including estimation of crossover rates (Li and Stephens, 2003; Crawford et al., 2004), phasing of genotype data into haplotype data (Stephens and Scheet, 2005; Scheet and Stephens, 2006), and inferring the history of human colonization (Hellenthal et al., 2008). A third example is that of approximate Bayesian computation (ABC) (Beaumont et al., 2002; Marjoram et al., 2003), a rejection method that also has several interesting applications, such as evaluating competing models of demography (Sousa et al., 2009).

Due to their efficient nature, these approximate methods are clearly very popular. However, they do have their own drawbacks. For example, as estimators of the population-scaled recombination rate, the composite likelihood employed by McVean et al. (2002) is not consistent as the number of loci tends to infinity (Fearnhead, 2003), and the PAC-likelihood is biased (Li and Stephens, 2003). Standard assumptions regarding estimates of uncertainty also no longer apply. There is therefore a great need for full-likelihood methods to become more practicable. Importantly, only full-likelihood methods give an explicit genealogical construction for the data, and these may be of direct interest. Furthermore, since the building blocks of composite likelihood methods can themselves be evaluated by full-likelihood methods, an improvement in the latter can also improve the former. For example, the pairwise composite likelihood of McVean et al. (2002) applies the full-likelihood IS method of Fearnhead and Donnelly (2001) to each pair of sites.

In this article, we develop a full-likelihood IS method for a particular model of sequence ancestry introduced below. An IS method is defined by its proposal distribution for sampling from a distribution of genealogies given the data, and ours is inspired in part by that of Griffiths and Marjoram (1996). Their method was limited for two main reasons: First, a simple choice of proposal distribution is relatively inefficient at exploring the space of genealogies of high posterior probability. Second, a general model of recombination along the sequence induces a very large state space of genealogies for exploration. We deal with the first of these limitations by exploiting recent advances in the design of efficient IS proposal distributions (Stephens and Donnelly, 2000; De Iorio and Griffiths, 2004a,b; Griffiths et al., 2008). We deal with the second by focusing on a simpler model of recombination rate variation, based on recent evidence for the clustering of recombination events into ‘hotspots' and the block-like nature of the genome.

In recent years, several large-scale studies have obtained a wealth of human sequence data. One of the motivations for this research has been to elucidate the nature and distribution of linkage disequilibrium (LD) across the genome, that is, the correlation between alleles at different sites (Reich et al., 2001, 2002; Daly et al., 2001; Gabriel et al., 2002; Hinds et al., 2005; The International HapMap Consortium, 2007). We are now beginning to gain a clearer picture of patterns of LD across the genome (Wall and Pritchard, 2003; McVean et al., 2005). In particular, many regions conform to a pattern in which there exist extended stretches of appreciable LD, with little or no evidence for historical recombination, delimited by shorter regions in which there is much less LD and much more inferred recombination. Consequently, the genome is organized into haplotype “blocks”: regions in which almost all variation amongst individuals can be explained by very few haplotypes (Daly et al., 2001; Gabriel et al., 2002).

An important contributory explanation for these observations is the non-uniformity of recombination rates, which vary both on a coarse (megabase) and a fine (kilobase) scale (McVean et al., 2004; Myers et al., 2005). Explanations of decay in LD often reject a model of a uniform rate of recombination (Reich et al., 2002; Wall and Pritchard, 2003). Instead, fitting a genetic map to the data suggests that much recombination is concentrated in short stretches of 1–2 kb, known as recombination hotspots. Recent estimates suggest that as much as 60% of all recombination events occur inside hotspots, which compose 6% of the genome (The International HapMap Consortium, 2007).

It should be noted that the above description is an oversimplification. Patterns of LD are noisy, and there is much variation across the genome. While recombination hotspots typically denote the boundary of a haplotype block, the converse does not hold since regions of low LD are expected in models without recombination (Wall and Pritchard, 2003). Nor is it the case that hotspots are able to break down haplotype blocks fully; high-frequency haplotypes sometimes extend across hotspots (McVean et al., 2005). Although this block-like view of the genome fails to capture its true complexity, it is a very useful starting point for making inference on sequence data. In this article, we therefore consider a two-locus model in which recombination occurs at a single position along the sequence. That is, sites within each locus are assumed to be completely linked, with a region in which recombination can occur separating the two loci. The IS method is tailored to this model, which we describe in detail in Section 2.

The remainder of this article is structured as follows: In Section 2, we introduce the model for recombination in further detail, and the type of genealogies that this entails. In Section 3, we briefly describe how importance sampling may be used to approximate the posterior distribution of genealogies given the observed data, and in Section 4, we develop a proposal distribution for this model using the general approach of De Iorio and Griffiths (2004a,b). Sections 5 and 6 describe some properties of the proposal and compare its performance against another method that could be applied to the model. In Section 7, the method is then illustrated on some real sequence data from Jeffreys et al. (2000). We conclude with some brief discussion.

2. A Model for Recombination

Consider a large, randomly mating population of N diploid individuals (so that there is a population of 2N sequences) reproducing in discrete generations. A diploid population of size N essentially behaves in the same way as a haploid population of size 2N. The population is assumed to be at stationarity, i.e. it has been evolving in this manner for a long time. The sequence of interest is assumed to be neutral so that each member of the offspring generation samples its parent uniformly at random. We model each sequence as a continuous interval, mapped to [0, 1] for convenience. In our model, recombination only occurs at the position 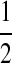, so that the two loci correspond to 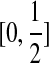and 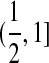. Call the loci A and B. Note that this notation is only for convenience; there is no requirement that the two loci be proximate on a chromosome. At each reproduction event, there is a probability μ_A of a mutation event at locus A and a probability μ_B of a mutation event at locus B. Also, with probability r there is a recombination event. From a genealogical perspective, this means that the offspring samples its parent for locus A and its parent for locus B independently; otherwise, with probability 1 − r both locus A and B are sampled from the same parent (also chosen uniformly at random).

N is large, and we pass to the usual diffusion limit, letting N → ∞ in such a way that the limits 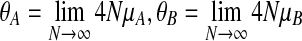, and 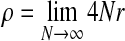all exist. The resulting genealogical process is a two-locus version of the well-known coalescent (Kingman, 1982; Hudson, 1983), in which time is continuous and measured in units of 2N generations. For a sample taken from the present, we trace time backwards, and coalescence, mutation, and recombination events occur to the lineages of the sample at times given by exponential random variables. A coalescence event corresponds to two individuals finding a most recent common ancestor (MRCA) in the parent generation, decreasing the current number of lineages by one. Since recombination events increase the number of ancestors back in time, the resulting genealogy is not a tree but a graph, known as the ancestral recombination graph (ARG) (Griffiths and Marjoram, 1997).

We make the infinite sites assumption: mutations occur to sites never previously mutant. This is biologically reasonable provided the mutation rate per site is small, and the assumption is often applied to analyses of single nucleotide polymorphism (SNP) data (Harding et al., 1997). The benefit of such an assumption is that an infinite sites dataset at a locus is equivalent to a gene tree relating the sequences (Griffiths, 1989). A gene tree is a perfect phylogeny relating each member of the sample, with mutation events as vertices and the sample at the leaves. In our two-locus model, the data is therefore equivalent to a pair of gene trees, which partitions the space of two-locus ARGs. If the rate of recombination is very small, then the two gene trees are highly correlated, whereas if it is large then they are almost independent. In this article, we further assume that the ancestral allele at each site is known—for example, by comparison with an outgroup.

A convenient way to encapsulate the infinite sites assumption is to label each mutation event by drawing a uniform random position from within the locus. For example, a mutation at locus A is labelled by a Uniform 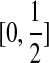random variable. The type of a sequence can be obtained by recording the mutation events as we trace back along its lineage in the gene tree. The type space is therefore 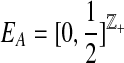, with the ith observed type denoted by a sequence 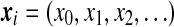. This is the sequence of time-ordered mutation events in the line of descent of the ith type in the sample, with x₀ the most recent. A sample of d_A types is then denoted by 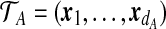. If type i is seen n_i times in the sample, and we define the multiplicity vector 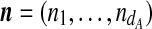, then the data at locus A is equivalent to the pair 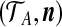. 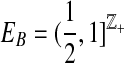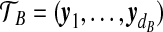Defining and similarly, the type space for our two-locus model is E_A × E_B. 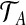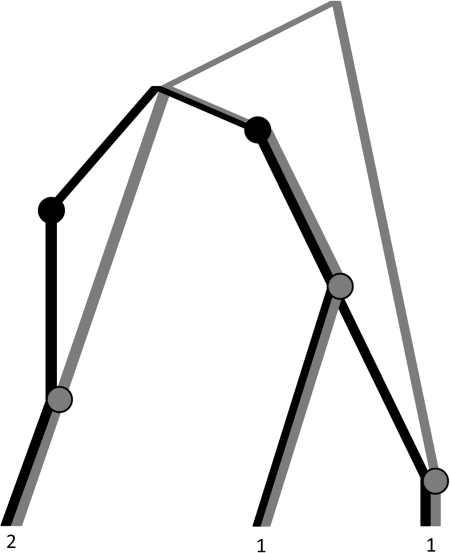The data can then be represented by (, , 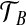n), where n = (n_ij) is a d_A × d_B matrix whose (i, j)th entry denotes the multiplicity of DNA sequences with the paths (x_i,y_j) at the two loci. This extends the one-locus representation described by Griffiths (1989). An example of a sample of four sequences conforming to the model, together with the equivalent pair of gene trees, is given in Figure 1. The sequences are labelled by their type (i, j). Mutations are colored balls (black at locus A and gray at locus B), and the recombination breakpoint is designated by a vertical line. Leaves of the gene trees are labelled by the multiplicity of each type. This model was also studied by Griffiths (1981).

FIG. 1.

(a) Sample of sequences under the two-locus model. (b) The equivalent pair of gene trees.

The algorithm we derive below will simulate a weighted collection of two-locus ARGs approximating their posterior distribution given the observed data. We have noted that recombination in the ARG can increase the number of lineages. This is inefficient, and also unnecessary, since the parental loci which did not contribute genetic material to the offspring (i.e., the non-ancestral loci) are of no concern and therefore do not have to be simulated. This problem can be solved by extending the state space to allow sequences to be left unspecified at one locus (Ethier and Griffiths, 1990). Backwards in time, a recombination event then creates two parents, one ancestral to the offspring at locus A but unspecified at locus B, and the other ancestral to the same offspring at locus B but unspecified at locus A. Recombination events are then only allowed to occur in lineages ancestral at both loci to some member of the present-day sample. The total number of contemporaneous lineages at any time point is therefore bounded above by 2n, for a sample of size n taken from the present. In addition, the alleles at non-ancestral loci do not have to be specified. Both Griffiths and Marjoram (1996) and Fearnhead and Donnelly (2001) implement a similar procedure, but because of their more general model of recombination, the bound is much larger. It is useful to think of the state space as comprising “fragments” of sequences, defined over 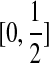, , 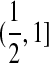or [0, 1]. However, a trade-off is that we now have to consider a more complicated process for coalescences, mutations, and recombinations of these fragments. Different types interact with each other at different rates going back in time. To deal with this, we must introduce some further notation.

Denote a sequence of type i at locus A that is ancestral only at locus A by (i,*); a sequence of type j at locus B that is ancestral only at locus B by (*,j); and a sequence of types i, j at each locus, respectively, ancestral at both loci, by (i, j). Denote their corresponding multiplicities a_i, b_j, c_ij. Define 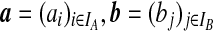, and 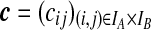. The sets I_A and I_B index the finite list of observed and inferred types associated with this dataset. Inferred types are states associated with nodes in the gene tree at one of the loci, but which are not observed in the sample directly. Throughout, we also use the following notation:

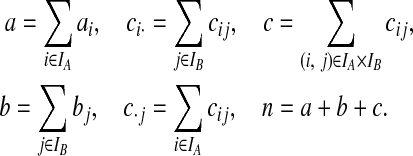The multiplicity of every type is contained in n = (a,b,c), so that the data is equivalent to the pair of marginal gene trees with multiplicity n. We denote this complete data by (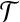, n). In this construction, we will usually observe an initial dataset with no unspecified alleles, i.e., n = (0,0,c), but sequences with missing data at a locus can be accommodated easily using a or b. In any case, these vectors are required because sequences with unspecified alleles appear when we think about the sample's ancestry.

Since the alleles at some loci are left unspecified, a sequence can coalesce with more than one other type. For example, the type (i,*) could coalesce with another (i,*), or with (i, j) for some j, or with (i,k) for some k ≠ j, or with (*,j), and so on. Below we will derive a recursion for the sampling distribution of (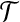, n) by conditioning on all possible most recent events back in time. It is therefore necessary to catalogue these different types completely, based on the coalescence or mutation events in which they can be involved. We call a type that could undergo mutation as the most recent event back in time a singleton. Possible types are:

• (i) A singleton type (i,*) (a_i = 1, c_i· = 0) with b = 0, so no coalescence is possible involving this type and it can only mutate.

• (ii) A singleton type (i,*) (a_i = 1, c_i· = 0) with b > 0, so it may undergo coalescence or mutation.

• (iii) A non-singleton type (i,*) that can coalesce with any of the type (i,*), (i, j), or (*, j), for some .

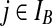• (iv–vi) Cases i–iii above can be treated similarly for a type (*, j) specified only at locus B.

• (vii) A type (i, j) which is non-singleton at both loci and can coalesce with any of (i,*), (*, j), or (i, j); or it can undergo recombination.

• (viii) A singleton type (i, j) with a removable mutation only at locus A which can mutate at locus A, or coalesce with the type (*,j), or recombine.

• (ix) A singleton type (i, j) with a removable mutation only at locus B which can mutate at locus B, or coalesce with the type (i,*), or recombine.

• (x) A singleton type (i, j) with a removable mutation at both loci which can undergo mutation at either locus, or it can undergo recombination.

The reason for this method of categorization should become clear from the description of the IS proposal distribution below. Two-locus ARGs can be simulated from the present sample by choosing a gene and one of its associated events with some probability (determined by the proposal distribution), modifying the sample to its previous state according to this event, and repeating the process until all sequences have found a most recent common ancestor at both loci. An example of a two-locus ARG compatible with the data in Figure 1 is shown in Figure 2. Lineages ancestral to a member of the sample at locus A are shown in black and those ancestral at locus B in gray. To illustrate, the events occurring to the ancestors of the two left-most sequences are, going backwards in time: coalescence of two types (vii), mutation of a type (x), recombination of a type (viii), mutation of a type (ii), coalescence of types (iii) and (vi), and so on.

FIG. 2.

A two-locus ARG.

3. Importance Sampling

Importance sampling (for an overview in the context of the coalescent, see Stephens [2001]) provides a way to weight simulated ARGs so that the collection approximates the true posterior distribution given the data. They can then be used to infer the parameters of the model, and to infer details of the ancestry such as the ages of mutations. Define a genealogical history by the sequence 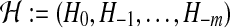of ancestral configurations at the embedded events in the Markov process where coalescence, mutation, or recombination events take place, to determine a genealogy for a sample of size n (Fig. 2). H_−m is a single type which is the most recent common ancestor (MRCA) of the sample. H₀ is the configuration of the present time (here, 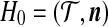) and is assumed to be observed with sampling probability p(H₀). By conditioning on each possible previous event back in time, the sampling distribution can be shown to satisfy the recursion relation

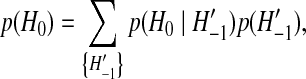(1)

where 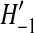is a dummy variable summing over all configurations one event ago that could have given rise to the current configuration, and 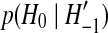are known transition probabilities from the coalescent process. Specific examples of (1) for a variety of models are studied by Griffiths (1989), Ethier and Griffiths (1990), Griffiths and Tavaré (1994), and Griffiths and Marjoram (1996).

A natural class of proposal distributions on histories arises by randomly constructing histories backwards in time. A sequential construction enables histories to be simulated from a proposal distribution 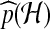by prescribing backwards transition probabilities 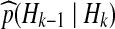depending only on the current configuration. The probabilities of interest can then be dealt with sequentially, by rewriting (1) and iterating:

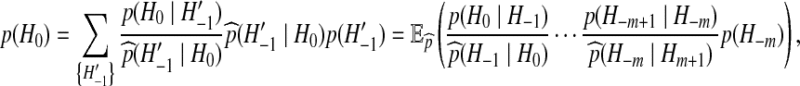(2)

where 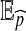denotes expectation with respect to 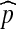. A Monte Carlo estimate of (2) provides an estimate of the likelihood; that is, one simulates a large number of genealogical histories from 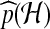. Associated with each is an IS weight, the quantity inside the expectation in (2). The sample mean of the IS weights is an estimate of the likelihood.

De Iorio and Griffiths (2004a) suggested a very general mechanism for constructing IS proposal distributions. They provided several justifications for their technique, and we refer the reader to their paper for details. From a practical point of view, their construction of a proposal distribution for infinite sites data at a single locus is achieved as follows. First, rewrite (1) as

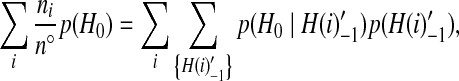(3)

where n° is the number of genes that can be involved in a coalescence or mutation event, 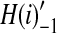is a configuration obtained from H₀ by applying a coalescence or mutation event to a type i, and the summation is over genes that can be involved in one of these events. Second, assume that we can equate terms inside the outer summation on each side of this equation. This leaves a soluble system of equations which determine the proposal distribution. How to modify this construction for two loci is considered below.

4. A Proposal Distribution for the Two-Locus Model

To apply the technique of De Iorio and Griffiths (2004a) described in the previous section, we must specify equation (1) for our two-locus model. For an ordered, random sample of size n corresponding to the unordered configuration 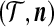, denote its sampling probability by 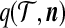. The recursion we derive below is for the quantity 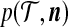defined by

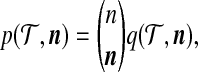(4)

where 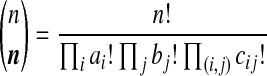is the multinomial coefficient. We choose to work with (4) so that it is analogous to the quantity Q(A, M, n) considered by Griffiths and Marjoram (1996). Working with 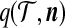instead of 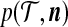would recover exactly the same proposal distribution.

Recall the notation introduced in Section 2. Also let 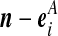denote (a − e_i, b, c), where e_i is a unit vector of length |I_A| whose ith entry is 1 and all others are zero, and define 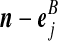similarly. Let 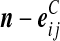denote 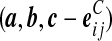, where e_ij is a unit I_A × I_B matrix whose (i, j)th entry is 1 and all others are zero, and so on.

Proposition 1. The quantity 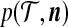satisfies the following recursion:

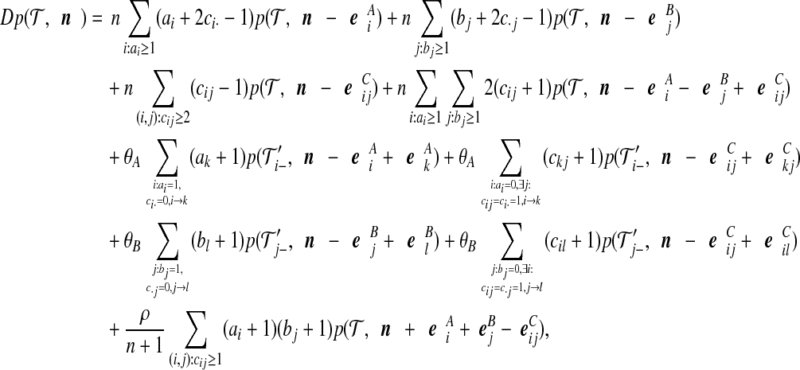(5)

where D: =n(n − 1) + (a + c)θ_A + (b + c)θ_B + ρc is the total rate of events. The notation i → k denotes that when the most recent mutation is removed from type i, the resulting type is k. Then 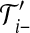denotes the corresponding pair of gene trees with this mutation removed. Note that after removing the mutation, the resulting type may or may not be present in the sample already. In the former case, we are implicitly assuming that the appropriate index in I_A is deleted to maintain consistent notation.

Proof. Equation (5) is a modification of the recursion considered by Griffiths and Marjoram (1996) in their equation (1). They were interested in a continuous model of recombination which resulted in an integro-recursion. By replacing this distribution with a point mass at 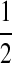, much of their terminology simplifies immediately. This enables the list of possible modifications to (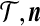) by coalescence, mutation, and recombination to be written out explicitly, each corresponding to a different term on the right-hand side of (5).     ■

Boundary conditions can be defined on (5) at the first time both locus A and locus B find an MRCA. However, we gain in efficiency by noting that when a locus reaches its MRCA, no further information is obtained by tracing the history of this locus any farther back in time. The appropriate condition is finally 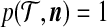when n = 1.

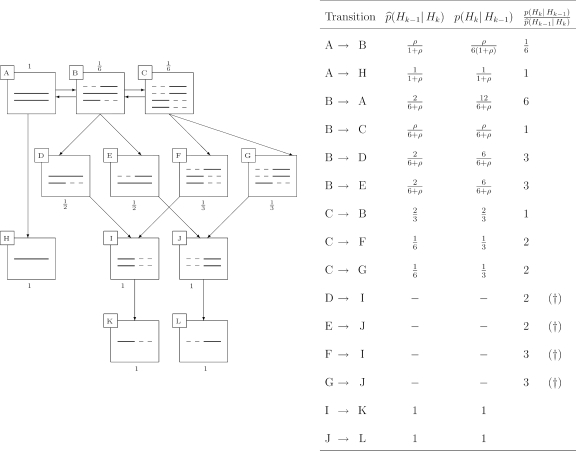
With appropriate modifications, it is possible to apply the technique of De Iorio and Griffiths (2004a) to equation (5), to obtain a proposal distribution which provides the probability of choosing a sequence of type 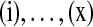, defined in Section 2. The proposal distribution is given in Table 1. Details are deferred to Appendix A. The choice of parameter values used in the IS proposal distribution are referred to as the driving values. A single set of driving values can be used to construct a complete likelihood surface accurate in a neighborhood of the driving values (Griffiths and Tavaré, 1994).

Table 1.

Proposal Distribution for the Two-Locus Infinite Sites Model with Recombination^a

Case	Hk−1	p(Hk−1|Hk)	IS weight
(R)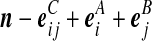
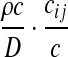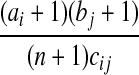(i)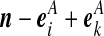
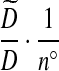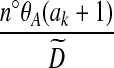(ii)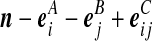
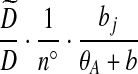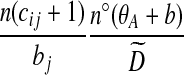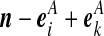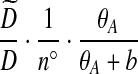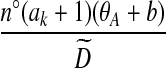(iii)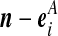
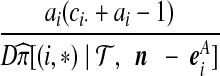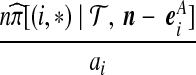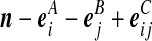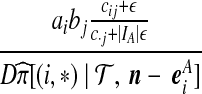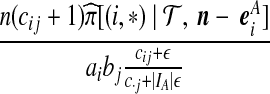(iv)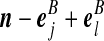
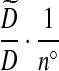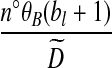(v)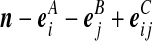
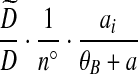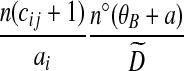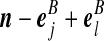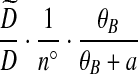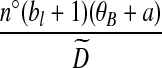(vi)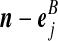
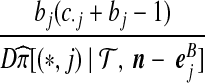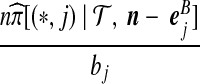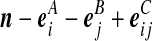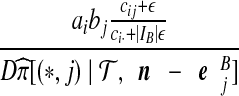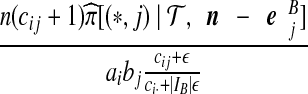(vii)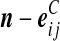
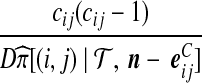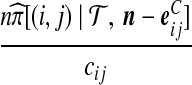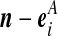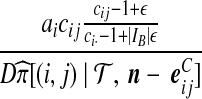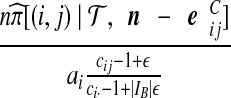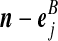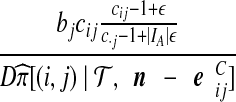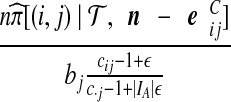(viii)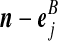
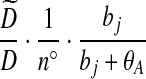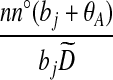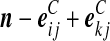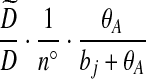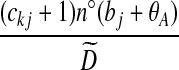(ix)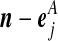
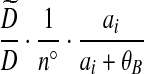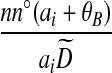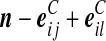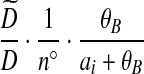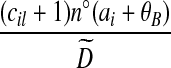(x)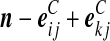

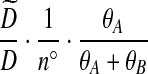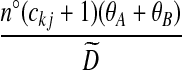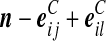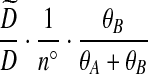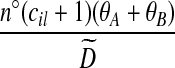^aNotation is defined in Appendix A. The expression for 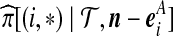is given by (9), 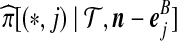is given by (10), and 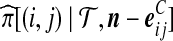is given by (11).

5. Properties and Implementation of the Proposal Distribution

Since the proposal distribution is based on the principles of De Iorio and Griffiths (2004a), it inherits a number of appealing properties, which are easily verified by direct inspection of Table 1:

Proposition 2. For the proposal distribution defined in Table 1, the following statements hold:

1. If a sample has all its sequences with information at only one locus, say n = (a, 0, 0), then the IS proposal distribution automatically generates a genealogy only at this locus, and it is simulated from exactly the same distribution as suggested by Stephens and Donnelly (2000) and De Iorio and Griffiths (2004a), the “Stephens-Donnelly” distribution for infinite sites data.

2. Suppose θ_A = θ_B and data is in the form n = (0, 0, c). In the limit ρ → 0, the proposal converges in distribution to the same Stephens-Donnelly proposal distribution (up to a labelling of mutations by their locus).

3. If ρ → ∞ then the proposal probability that the next event back in time is a recombination event tends to 1 when c > 0, and is 0 otherwise. Thus, the proposal has sensible limiting behaviour for both extremes of ρ.

4. In the absence of a mutation process, the proposal distribution is optimal for all configurations n = (a, b, c), and all values of ρ.

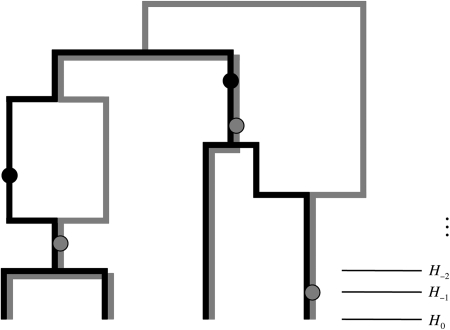
An illustration of statement 4 is given in Figure 3, which gives an exhaustive account of the Markov chain associated with IS in the case n = (0, 0, 2). The initial state is denoted A. Possible transitions are shown by arrows. Each sequence is represented by a line, with non-ancestral loci dashed. Also annotated is the current IS weight with each state, which must be a single-valued function for an optimal proposal distribution. Note that the exit states H, K, and L each have final weight 1, indicating that the distribution of weights from this IS scheme is a point mass on the true likelihood. Corresponding forward and backward probabilities, together with the IS weight accrued at each step, are shown in the accompanying table. (The entries marked with † are not IS weights, but are accrued as a result of discarding a lineage upon reaching the MRCA.) This Markov chain was also analyzed in detail by Simonsen and Churchill (1997).

FIG. 3.

Optimal importance sampling on the sample n = (0, 0, 2).

We implemented our proposal distribution in a C + + program rita (recombining, infinite-sites, two-locus ancestries) which we intend to make available. We thoroughly checked its output against exact solutions of (5) for some simple datasets. That it should have the same output as the Stephens-Donnelly distribution for data at a single locus also proved very useful. For a panmictic population, our program extends genetree (Bahlo and Griffiths, 2000) to two loci. The software can also estimate a likelihood hypersurface for (θ_A, θ_B, ρ), as well as collect information for ancestral inference, for example, times between events and the number of recombination events, as discussed later. To further improve the algorithm's efficiency, we implemented the stopping-time resampling procedure of Chen et al. (2005) with modifications detailed in Jenkins (2008) to account for infinite sites data and recombination.

6. Comparison with Existing Proposal Distributions

It would be interesting to compare our proposal distribution with existing IS schemes for infinite sites models with recombination, such as those implemented in the programs recom (Griffiths and Marjoram, 1996) and infs (Fearnhead and Donnelly, 2001). Each of these is based on a uniform recombination breakpoint distribution, but they can be modified without too much difficulty. However, a technical problem arises with the latter scheme, rendering it inapplicable to our model: an explanation is given in Appendix B. We must therefore content ourselves with a comparison of the performance against recom.

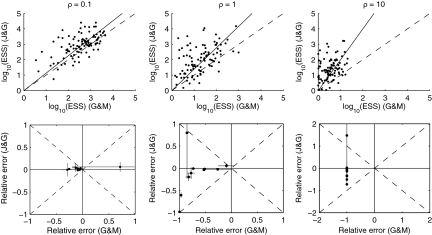
To compare the two proposal distributions, we performed the following simulation experiment: Simulate 100 datasets of n = 20 sequences using the program ms (Hudson, 2002) with θ_A = θ_B = 2.5 for each 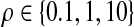. (We also investigated several other parameter values with similar results, not shown.) Reconstruct 100,000 ARGs with driving values equal to the true parameter values, using our proposal and that of recom. Results are shown in Figure 4. The upper plots measure relative performance by the effective sample size (ESS) (Liu, 2001) of the proposal distributions of Griffiths and Marjoram (1996) (G&M) and ours (J&G). Also plotted are lines of linear regression, assuming zero intercept, and dashed lines indicate the diagonals. The lower plots assess relative performance on 10 randomly selected datasets from the plot above, as measured by relative error. Relative error was measured with respect to an estimate of the true value derived from an independent run of 10,000,000 ARGs. Crosses show ± 1 standard error. It is clear that our proposal outperforms that of Griffiths and Marjoram across a range of recombination parameter values. For large ρ, the relative error of the latter scheme for most datasets was very close to −1, indicating that—compared to the true likelihood—all of the IS weights were effectively zero. Under our proposal distribution, each point in Figure 4 required a running time of the order of 1 minute on a standard desktop machine.

FIG. 4.

The relative performance of the proposal distributions of Griffiths and Marjoram (1996) and ours.

7. Application to SNP Data

The applicability of our inference algorithm depends on how well the two-locus model fits the data. For some regions of the genome, such as those for which the rate of recombination is consistently high, the model will clearly be inapplicable; for others, it will be more reasonable. For each of the two loci to be compatible with a gene tree, they must exhibit few or no failures of the four-gamete test (Hudson and Kaplan, 1985). If we label the two alleles at each site by 0 and 1, then the four-gamete test fails if for any four sequences and two sites, all four haplotypes (0, 0), (0, 1), (1, 0), (1, 1) are observed. This is referred to as an incompatibility. A failure of the infinite sites assumption, with more than one mutation event at the same site, can also result in incompatibilities. Inspection of the data to find incompatibilities can be used to infer regions in which historical recombination events or recurrent mutations have occurred. In practice, these recombinant haplotypes or incompatible sites are excluded from the analysis (Harding et al., 1997).

To illustrate our method, we applied it to the data of Jeffreys et al. (2000), a set of n = 60 haplotypes taken from 30 unrelated individuals from the United Kingdom. It contains 45 SNPs and two insertion/deletions (hereafter treated together with the SNPs). The ancestral alleles were determined by comparison with corresponding sequences from the chimpanzee and gorilla. Two pairs of SNPs were separated by a single base and in complete LD, so Jeffreys et al. (2000) gave each of these pairs a single label: the 47 polymorphic sites were therefore labelled T1–T45. There are 28 distinct haplotypes, labelled 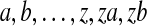. The data covers a 9.7 kb region containing the well-studied TAP2 hotspot: several lines of evidence confirm the existence of this hotspot, including for example the Phase II HapMap data (The International HapMap Consortium, 2007). LD plots of this data confirm extensive LD between pairs of sites both upstream or both downstream of the hotspot, with much lower levels of LD for pairs extending across the hotspot. Similar observations from their own data led Jeffreys et al. (2000) to divide the region into three domains, one on each side of the hotspot (domains 1 and 3) and one containing the hotspot (domain 2).

Applying the four-gamete test to the three domains, domains 1 and 3 show little evidence for recombination while the evidence for recombination within domain 2 is extensive. We therefore take domains 1 (T1–T16) and 3 (T32–T45) to be our locus A and B, respectively, and exclude domain 2 from the analysis. Allowing recombination between the domains resolves most but not all incompatibilities in the data. Removal of six sequences (haplotypes w, za, and zb) ensured domain 1 was compatible with a gene tree, and removal of one sequence (haplotype j) resolved the single incompatibility in domain 3. This left a “pruned” dataset of 53 sequences and 31 polymorphic sites—16 at locus A and 15 at locus B. To check that the data is in reasonable agreement with the assumptions of the model (neutrality, constant population size, stationarity, no intra-locus recombination, and so on), we calculated Tajima's D statistic (Tajima, 1989) and also performed the haplotype number test (HNT) (Innan et al., 2005). Denoting the number of haplotypes in a random sample configuration by K, the observed number by k, and the observed number of segregating sites by s, the HNT detects departures from the assumed model by simulating a large number of genealogies and estimating 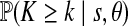and 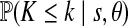. This assumes knowledge of θ; here we used Watterson's estimate as suggested by Innan et al. (2005). Watterson's estimate for the complete data was 6.83, with proportionally very similar estimates taking the loci individually; for simplicity, we therefore assume the same mutation parameter θ for both loci. Results are reported in Table 2 for both the full and pruned datasets. Significance for Tajima's D was determined by assuming a beta-distribution (Tajima, 1989); the 95th percentile for D under the null distribution for each of the tests in Table 2 is (−1.80, 2.05). Significance for k was determined by the p-values given in Table 2. None of the statistics were significant at the 5% level, indicating that there no important departures from our model, and that the removal of the seven sequences above does not affect this conclusion.

Table 2.

Test Statistics for Departures from the Assumed Model: Tajima's D Statistic and the Observed Number of Haplotypes k

	Locus A		Locus B
	Full	Pruned	Full	Pruned
D	0.11	0.11	−0.81	−0.84
k	9	7	12	10
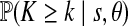	0.88	0.98	0.36	0.68
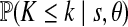	0.24	0.06	0.81	0.51

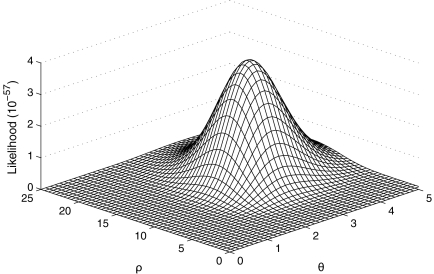
We applied our IS algorithm with driving values θ₀ = 3.42 and ρ₀ = 10.0 to construct a likelihood surface for (θ, ρ) (Fig. 5). To ensure the likelihood surface was accurate, we used the resampling scheme mentioned above (which uses a resampling threshold parameter B; we chose B = 100), a large number of genealogies (100, 000), and repeated the procedure independently 100 times. Individual replicates often gave maximum likelihood estimates (MLEs) in the vicinity of the driving values, which is a well-known phenomenon when the sample space is insufficiently explored, but taking the mean of the IS weights across all replicates provided more reliable MLEs. The likelihood surface in Figure 5 is also based on this overall estimate, and the overall joint MLE was 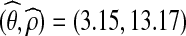; from here onwards, we assume these to be the true values. To confirm that they were reliable, we tried repeating the entire procedure using different driving values. For example, using ρ₀ = 15.0 resulted in a joint MLE of 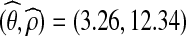. There is greater variation in the estimation of ρ since genetic data contains much less information about this parameter.

FIG. 5.

Likelihood surface for (θ, ρ) for the Jeffreys et al. (2000) data.

The MLEs can be related back to the biological parameters via θ = 4N_eu and ρ = 4N_er, where N_e is the diploid effective population size. Myers et al. (2005) estimated N_e = 9, 600 for the CEPH panel (a widely studied data source based on a sample of Utah residents with ancestry from northern and western Europe); using this estimate, we recover 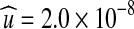and 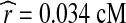. It is encouraging that these values are very close to estimates from other sources: for example, Nachman and Crowell (2000) suggest an average of 2.5 × 10⁻⁸ mutations per nucleotide per generation, and the (sex-averaged) genetic distance across the same region as estimated from the Phase II HapMap data is 0.038 cM (The International HapMap Consortium, 2007).

A Monte Carlo estimate of the posterior distribution of genealogies allows one to perform ancestral inference. Consider the following example. For the ith simulated genealogy, denote the number of recombination events by 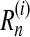and its IS weight by w⁽ⁱ⁾. Then an estimate of the expected number of recombination events is

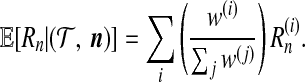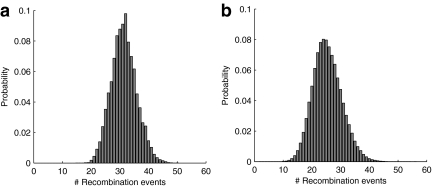
Moreover, the complete distribution for 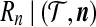can be estimated in this way. We estimated this using rita with the same settings as used in Figure 5 above. The result is shown in Figure 6, with the unconditional distribution also shown for comparison.

FIG. 6.

(a) Estimated distribution of the number of recombination events in the genealogy giving rise to the Jeffreys et al. (2000) data. (b) The same distribution over all datasets of n = 53 sequences.

An intriguing question is to ask how the gene trees at the two loci overlap (i.e., to infer those branches in the ARG that are ancestral to the sample at both loci). For example, denoting the time to the most recent common ancestor at locus l by T_MRCA(l) and repeating the procedure above, we obtained the point estimate 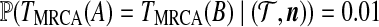. This addresses the simple question of the whether ancestry is shared at the time of the MRCA, but it is possible to generalize this concept much further. The idea of shared sequence ancestry is rather poorly explored, but some theoretical results were obtained by Wiuf and Hein (1999). Their definition was based on the fraction of time in which there exist no recombinant haplotypes in an ARG for two sequences. We are able to obtain even more: complete empirical estimates of the sharing of ancestral lineages in the genealogies of the two loci.

Recall the definition of a gene tree (Fig. 1). It is a perfect phylogeny summarizing the ancestry of sequence data at a locus, with the contemporary sample of sequences at the leaves, mutation events at the nodes, and with a final node representing the root. The gene tree can be constructed from any coalescent tree giving rise to the data. Now consider an ARG giving rise to data at two loci. The marginal gene trees can be inferred as before, but the regions in which they share ancestry can also be inferred by using mutations from both loci as vertices in each gene tree. An example of such a gene graph is given in Figure 7, which is derived from the ARG in Figure 2.

FIG. 7.

A gene graph.

We now formalize this idea. For a given two-locus ARG of n sequences, define its corresponding gene graph as follows. For sequence type i, let 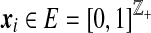be the age ordered sequence of mutation events occurring in any ancestor in the line of descent of locus A. Similarly, let 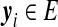be the age ordered sequence of mutation events occurring in the line of descent of locus B. For d distinct such pairs of paths, the gene graph is defined to be the set 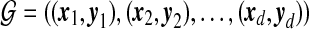of pairs of paths, together with their multiplicities n. We emphasize that for a single locus we record mutations occurring at either locus in its ancestry (e.g., look at the ancestry of locus A for the right-most sequence in Fig. 7). Thus, the two gene trees now share the same set of nodes. (We also explicitly record the root nodes in the sequences in 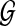, so that the appearance of a root in the gene tree for the other locus can also be identified.) Whereas there are an infinite number of ARGs compatible with the data, there are only a finite—albeit large—number of gene graphs. So by looking at gene graphs of high probability given the data, we hope to capture the important aspects of the joint ancestry of the two loci. Further properties of gene graphs are discussed in Jenkins (2008).

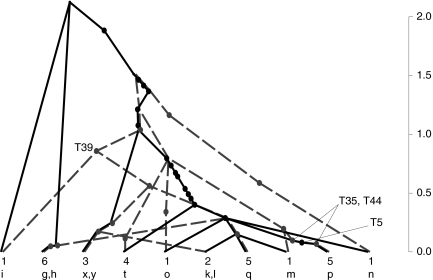
Using the same parameters as in the IS procedure discussed above, we recorded the first 100,000 gene graphs simulated from the Jeffreys et al. (2000) data. To summarize the joint ancestry of the two loci in this data, we took the mode of this empirical distribution. Because of the recombination hotspot, many sequences were inferred to have undergone recombination, and the resulting graph was rather complicated. We therefore illustrate it for a subset of 29 sequences (Fig. 8). Ancestry of locus A is shown as black solid lines and that of locus B as gray dashed lines. The haplotype label and the multiplicity of each leaf is annotated. The height of mutation events are drawn according to their expected age conditional on this gene graph, in coalescent units (right-hand axis).

FIG. 8.

An estimate of the most probable gene graph for the Jeffreys et al. (2000) data.

Assuming Figure 8 to be representative of the ancestry of the sequences, it provides visual confirmation of a number of features of the data. There is a large amount of recombination in the graph, with at least one recombination event in the lineage of every sequence as we follow its ancestry back in time. After the sequences have all undergone recombination, there is very little shared sequence ancestry between the two loci farther back in time. Most sequences recombine very quickly, but shared ancestry persists for longer in some sequences than in others. For example, Jeffreys et al. (2000) noted that sites T5, T35, and T44 were in complete LD despite straddling the hotspot. For each site, the mutant allele only appears on haplotype p. Jeffreys et al. (2000) suggested that this variant therefore arose by recent mutation on a haplotype which then attained significant population frequency without being disrupted by recombination. Figure 8 supports this explanation and provides an estimate of the age of this haplotype. It also suggests that a similar story seems to hold for haplotypes q, x, and y. For these haplotypes, identifying their ancestry from a direct inspection of the data is less clear; this time there do not exist polymorphic sites straddling the hotspot and in complete LD.

Jeffreys et al. (2000) also observed that domain 3 (i.e., locus B) was defined by minor variations on just two major haplotypes, which were identified by sites T33, T37, and T39. From a genealogical point of view, we should therefore expect these three sites to be in strong LD and to be relatively ancient, such that there are considerable numbers of sequences in the genealogy both beneath these mutations and not beneath these mutations. T39 is annotated in Figure 8; the other two sites are its immediate neighbors in the graph. Their positions and relative age are indeed as expected. Here, one coalescent unit corresponds to 40N_e years, assuming a generation time of 20 years for humans. Using the estimate for the diploid effective population size given above, this is 384,000 years. We estimated 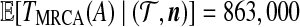years (standard error 113,000 years), and 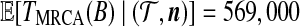years (standard error 143,000 years). These estimates should be taken as illustrative, since assumptions like a constant population size and panmixia are likely to be oversimplifications.

8. Discussion

We have developed an efficient IS proposal distribution for performing full-likelihood based analyses on DNA sequence data under a two-locus, infinite sites model. This is the first IS proposal distribution developed with this model in mind, and benefits from the general principles for designing IS schemes of De Iorio and Griffiths (2004a). We have verified by simulation that it significantly outperforms the only alternative approach which is obtained by adapting the existing IS proposal distribution of Griffiths and Marjoram (1996). Finally, we illustrated the method on a real sample of haplotype data (Jeffreys et al., 2000).

There are several possible further applications for our proposal distribution. By focusing on only two gene trees, it is particularly suited to a thorough analysis of the correlation between the ancestries of neighbouring loci, as well as more obvious questions of ancestral inference. We have only briefly illustrated these ideas, by directly inferring the joint ancestry of the two largely non-recombining domains identified by Jeffreys et al. (2000). It would also be desirable to extend our model to more than two loci. A way to achieve this is in a composite likelihood setting, offering a natural extension to Hudson's pairwise likelihood (Hudson, 2001). Rather than considering the genealogies of all pairs of segregating sites, one could consider pairs of clusters of completely linked sites, substantially reducing the number of pairwise comparisons, and possibly being robust to unusual or mis-typed allelic configurations at a single site.

9. Appendix

A. Details of the calculation of the proposal distribution

Direct application of the technique of De Iorio and Griffiths (2004a) to equation (5) does not work well. The reason essentially relies on the fact that the proposal is uniform on the choice of sequences which could be involved in the previous event back in time, which is not always appropriate. To illustrate, consider the sample shown in Figure 9. Sequence I is chosen with probability 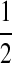, and after it is chosen it can only undergo recombination. This occurs independently of the value of ρ, so for small ρ the algorithm will generate too many recombination events, each contributing a very small IS weight.

FIG. 9.

A sample of two sequences, labelled I and II.

Instead, we propose to decouple recombination events in the proposal: First choose with some probability whether a recombination event occurs and then apply the technique of De Iorio and Griffiths (2004a) conditional on this choice. A natural value for this probability is the prior rate 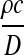of recombination events. Given that a recombination occurs, we select uniformly at random from among those sequences that can recombine. Thus, the proposal probability that type (i, j) recombines is

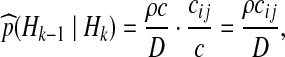where 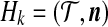and .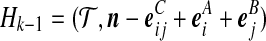

To apply the technique of De Iorio and Griffiths (2004a) conditional on the the next event not being a recombination, we set ρ = 0 in equation (5) and then apply the procedure described around equation (3). This is equivalent to writing the left-hand side of (5) as

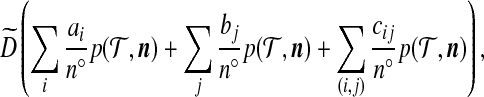(6)

where 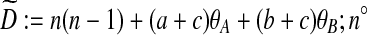denotes the number of sequences that can be involved in a coalescence or mutation in the next event back in time; and the summations are respectively over types (, *), (*, j), and (i, j), restricted to those that can be involved in a coalescence or mutation event. Next, equate terms inside the summations on either side of the recursion. There is some ambiguity here, since some terms on the right-hand side of (5) involve more than one type of gene. For example, 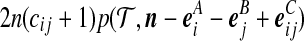represents the coalescence of types (i, *) and (*, j). To deal with terms of this type, we treat it as two separate events, one involving (i, *) and one involving (*, j), each assigned half of this coefficient. Both events result in a change of state 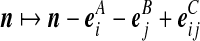. To avoid increasing the variance of the IS weights by this separate treatment, the IS algorithm accounts for both transitions when calculating the IS weight.

By equating terms inside the summations in (6) with their counterparts on the right-hand side of (5), we obtain an equation for each of the cases (i)–(x) described in the main text (excluding recombination events). In some cases ((i), (iv)), the sequence chosen determines the event, and the proposal probability follows immediately. In others ((iii), (vi), (vii)), this is not so, but we can find a simple approximate solution as follows. Consider for example case (iii), in which a type (i, *) can coalesce with another 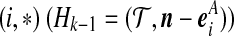, or with 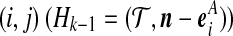, or with 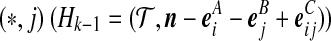, for some 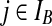. Equating terms in (6) and (5) yields

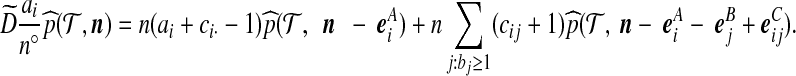(7)

We can make progress by expressing this in terms of 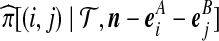, an approximation to the probability that the next gene we sample from the population is of type (i, j), given that we have already observed (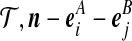). The sampling probabilities 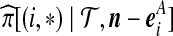and 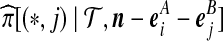are defined similarly. They may be substituted into (7) using the exchangeability condition

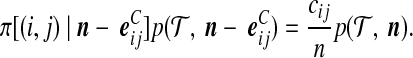(Stephens and Donnelly, 2000; De Iorio and Griffiths, 2004a). Other exchangeability conditions are defined in a similar manner. After some rearrangement, we obtain

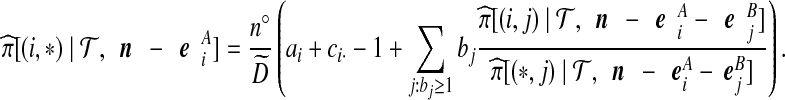(8)

To deal with terms in (8) multiplying the b_j, simulations suggest that the following approach is efficient. Interpret the ratio as an estimate of the probability of selecting type i at locus A, given type j at locus B, and given the sample (a − e_i, b − e_j, c). By using the sample estimate 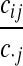, one can obtain a solution for 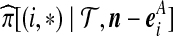. To avoid zero frequencies, we pre-suppose uniform prior counts across observed and inferred types 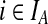for a fixed j. The posterior estimate becomes

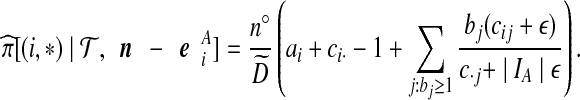(9)

The proposal appears to be robust to the choice of 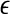; by default we let  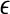= 1. Cases (vi) and (vii) yield similar approximations:

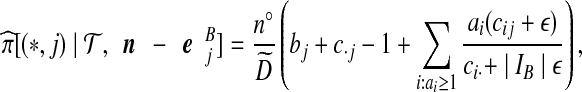(10)

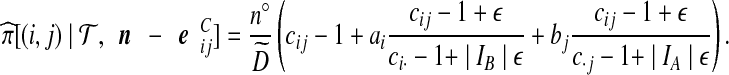(11)

For the remaining cases ((ii), (v), (viii), (ix), (x)), the expressions are recursive with respect to a subtree of , and so might recursively lead to a consideration of all subtrees of . An analogous situation arises in a model of subdivided population structure considered by De Iorio and Griffiths (2004b), and they suggest an easily computable approximate solution, which we also adopt here: backwards transition probabilities are taken to be proportional to the coefficients multiplying each unknown 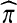term (Table 1).

The complete proposal distribution is given in Table 1, in which a recombination event is denoted (R). In Table 1, we have assumed n° > 0, which need not always hold. If n° = 0 then we set the probability of a recombination event to 1 and adjust the weights accordingly.

B. The proposal distribution of Fearnhead and Donnelly (2001)

To model the sampling distribution for new sequences, Fearnhead and Donnelly (2001) extend the sampling model of Stephens and Donnelly (2000), whereby new sequences are “copied” from existing ones, and this copying is imperfect to model the mutation process. To account for recombination, the source sequence at each site in the copying process is governed by a hidden Markov model, so that jump probabilities model recombination events between sites. In the infinite sites model, each mutation may occur only once, and in infs this includes the copying process. That is, for any mutation already observed somewhere in the rest of the sample, the emission probability for its appearance when copying from another sequence must be zero. This imposes a strong restriction on the hidden process: for a newly sampled sequence, any mutation on it (which is not on this sequence uniquely) can have been copied only from other sequences also exhibiting that mutation. A consequence is that in order to “copy” a given sequence, one might rely on jumps in the hidden process regardless of whether we have recombination in the model. An example is shown in Figure 10. Consider the probability of a recombination event occurring to sequence α between the second and third segregating sites, which is proportional to

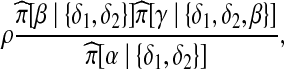FIG. 10.

(a) An example dataset n = {α, δ₁, δ₂}. (b) When α undergoes recombination at the right-hand breakpoint, the resulting types are β and γ.

where β and γ are the new types after the recombination event (Fearnhead and Donnelly, 2001, their Appendix B). Non-ancestral loci are marked in gray. Here, we need to write down 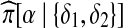. From left to right, the sequence of hidden states for this copying procedure can only be (δ₁, δ₂, δ₁) or (δ₂, δ₂, δ₁), and since in both cases there is at least one jump, it is straightforward to show that 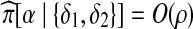as 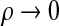. This is not true of terms in the numerator, 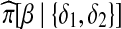and 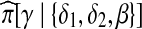. Since each of these new sequences have stretches which are non-ancestral, the crucial observation is that the hidden states associated with each of these sampling events do not require any jumps. At its ancestral locus, β can be copied from (δ₁), and similarly γ can be copied from (δ₂, δ₂). Hence, the probability of this recombination event is 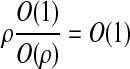; it does not vanish as we let ρ → 0. For example, if we suppose that the segregating sites are equally spaced along [0, 1] as shown, then the probability 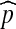of a recombination event occurring to α satisfies 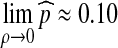when θ = 1.

Acknowledgments

We thank Chris Holmes and Carsten Wiuf for commenting on this work, and Yun Song for many useful discussions. This work was carried out while P.J. was a member of the University of Oxford Life Sciences Interface Doctoral Training Centre, funded by the EPSRC, and completed at the University of California, Berkeley, supported in part by an NIH grant R00-GM080099.

Disclosure Statement

No competing financial interests exist.