Effects of freezing-induced cell-fluid-matrix interactions on the cells and extracellular matrix of engineered tissues

Abstract

The two most significant challenges for successful cryopreservation of engineered tissues (ETs) are preserving tissue functionality and controlling highly tissue-type dependent preservation outcomes. In order to address these challenges, freezing-induced cell-fluid-matrix interactions should be understood, which determine the post-thaw cell viability and extracellular matrix (ECM) microstructure. However, the current understanding of this tissue-level biophysical interaction is still limited. In this study, freezing-induced cell-fluid-matrix interactions and their impact on the cells and ECM microstructure of ETs were investigated using dermal equivalents as a model ET. The dermal equivalents were constructed by seeding human dermal fibroblasts in type I collagen matrices with varying cell seeding density and collagen concentration. While these dermal equivalents underwent an identical freeze/thaw condition, their spatiotemporal deformation during freezing, post-thaw ECM microstructure, and cellular level cryoresponse were characterized. The results showed that the extent and characteristics of freezing-induced deformation were significantly different among the experimental groups, and the ETs with denser ECM microstructure experienced a larger deformation. The magnitude of the deformation was well correlated to the post-thaw ECM structure, suggesting that the freezing-induced deformation is a good indicator of post-thaw ECM structure. A significant difference in the extent of cellular injury was also noted among the experimental groups, and it depended on the extent of freezing-induced deformation of the ETs and the initial cytoskeleton organization. These results suggest that the cells have been subjected to mechanical insult due to the freezing-induced deformation as well as thermal insult. These findings provide insight on tissue-type dependent cryopreservation outcomes, and can help to design and modify cryopreservation protocols for new types of tissues from a pre-developed cryopreservation protocol.

INTRODUCTION

Successful cryopreservation of a wide variety of biomaterials is critically important to cell/tissue engineering and regenerative medicine because it can provide long-term storage and “off-the-shelf” availability of various cell/tissue engineering products [1-3]. Although successful preservation of cellular and/or simple tissue systems in the frozen state have been reported [4-6], it is still challenging to design and develop cryopreservation protocols for a wide variety of engineered tissues (ETs). The two most significant challenges are – 1) preserving tissue functionality, and 2) controlling highly tissue-type dependent preservation outcomes. Tissue functionality includes mechanical, optical and transport properties of ETs, which are critical to the physiological functions of ETs. Due to the wide spectrum and range of the functional properties of ETs, it is extremely difficult to develop a cryopreservation protocol targeting any given properties. Tissue-type dependent cryopreservation outcomes indicate that a successful cryopreservation protocol for any given type of tissue is difficult to adapt to others types of tissues [7, 8]. These two challenges are caused by lack of mechanistic understanding of tissue-level response to freezing and its effects on tissue functionality, and they become more significant as more diverse cell/tissue engineering products are developed.

Since many of the tissue functional properties are associated with the microstructure of the extracellular matrix (ECM), preserving the microstructure and integrity of the ECM may be the key for successful cryopreservation of functional ETs. Besides providing a structural scaffold and determining the functional properties, the ECM plays significant roles in tissue physiology through interaction with cells and interstitial fluid transport. These roles include regulating cell morphology and growth [9, 10], and intercellular signaling [11]. The ECM can also be reconfigured by cells during tissue remodeling and wound healing [12-14]. Thus, in order to cryopreserve functional tissue, its ECM microstructure should be maintained during cryopreservation as well as the cellular viability [15-17].

In spite of its significance, the effects of freeze/thaw (F/T) on the post-thaw ECM microstructure are not well understood. During cryopreservation, ice is formed in both the intra- and extra-cellular spaces, and extracellular ice formation (EIF) is thought to induce damage to the ECM microstructure. However, the extent of EIF and subsequent damage to the ECM microstructure are not well understood. Several studies have been performed to investigate the morphology of EIF, but its impact on the post-thaw ECM structure was not fully studied [18-21]. Later, the matrix of post-thaw cartilage was characterized using MRI, and significant MRI signal changes were observed [22]. A multiphoton-induced autofluorescence and second harmonic generation microscopy were performed on cryopreserved and vitrified cartilage, and these also reported changes to the post-thaw collagenous matrix structure [23]. Both studies recognized the F/T-induced changes to the ECM microstructure, but their measurements did not provide quantitative information on the underlying biophysical mechanisms during F/T. On the contrary, retained structural integrity of collagen and elastin within cryopreserved human heart valve tissue was reported using two-photon laser scanning confocal microscopy [15]. More recently, the collagen structure of fresh and cropreserved arteries was compared using second harmonic generation microscopy [24]. However, due to limited understanding of tissue-level biophysical phenomena during F/T, no mechanistic strategy has been established yet as to how to preserve the ECM microstructure as well as the cellular viability.

A few recent studies proposed that freezing-induced spatiotemporal deformation of the tissue determines the post-thaw ECM microstructure and ultimately the functionality of ETs [25, 26]. Han et al. [25] performed a theoretical study based on a poroelastic model and suggested that freezing of tissue may induce the spatial and temporal redistribution of interstitial fluid and subsequent spatiotemporal ECM swelling. In addition, the post-thaw microstructure of the collagen matrices was visualized to support the theoretical results. In a later study by Teo et al. [26], the spatiotemporal deformation of ETs during freezing was measured using a quantum dot mediated cell image deformetry technique. The results confirm that freezing induced complex deformation patterns of the ET as the freezing interface propagates, which might result from the interactions among the cells, ECM and interstitial fluid. Thus, understanding of the freezing-induced cell-fluid-matrix interactions could enable the mechanistic prediction of the post-thaw ECM microstructure and cell viability of various ETs. Moreover, this could also lay the groundwork for the knowledge-base to design and modify cryopreservation protocols for various types of ETs.

The objectives of this study, thus, are to delineate the role of each component of the cell-fluid-matrix interactions during freezing, and to characterize the effects of these interactions on the cells and ECM of ETs. To achieve these objectives, we designed experiments with dermal equivalents, which are constructed by seeding human dermal fibroblasts in type I collagen matrices, with different microstructures by varying cell seeding density and collagen concentration. Three different experimental groups were prepared and used: the nominal group (NORM), the high cell density (HCEL) group, and the high collagen concentration (HCOL) group. While these dermal equivalents underwent an identical F/T protocol, their spatiotemporal deformation during freezing was measured using the cell image deformetry technique. After F/T, the ECM microstructure was characterized using the scanning electron microscopy technique. The freezing-induced deformation and post-thaw ECM structural changes of all experimental groups were cross-compared and analyzed to delineate the role of each component in the cell-fluid-matrix interactions during freezing. The cryoresponse of fibroblasts was characterized by assessing the post-thaw cell viability, cell-matrix binding and cytoskeleton organization. These results were also correlated to the freezing-induced deformation of ETs and further discussed considering the implications for cryopreservation of functional ETs. The implications for cryopreservation of various types of tissues are also discussed in the context of addressing tissue-type dependent cryopreservation outcomes.

MATERIALS AND METHODS

Cells and Reagents

Early-passage hTERT-immortalized human dermal fibroblasts [27] were maintained in culture medium (DMEM/F12, Invitrogen, Grand Island, NY) supplemented with 10% fetal bovine serum, 2 mM L-glutamine, and 100 μg/mL penicillin/streptomycin. The fibroblasts were cultured up to the 15th passage in 75 cm² T-flasks at 37 °C and 5% CO₂. The cells were consistently harvested at 80% confluency by using 0.05% trypsin and 0.53 mM EDTA.

Engineered Tissues with Quantum Dot-Labeled Fibroblasts

ETs (i.e., dermal equivalents) for use in freezing-induced tissue deformation measurements were prepared by seeding quantum dot (QD)-labeled fibroblasts in collagen matrices. The detailed preparation procedure has been described elsewhere [26]. Briefly, the collected cells were first labeled with QDs (Qtracker 655, Invitrogen, Carlsbad, CA) according to the protocol suggested by the manufacturer (the cellular uptake of QDs was characterized and is shown in Figure S1). After labeling, the cells were suspended in 2 mL of collagen solution, which was prepared from high concentration type I rat tail collagen (BD Biosciences, Bedford, MA). The collagen solution with the cells was placed in a 48 × 18 mm chamber slide (Lab-Tek II, Nunc, Naperville, IL) and allowed to polymerize at 37 °C for 60 minutes. After polymerization, 2 mL of complete medium was added, and the ET was incubated for 24 hours before the freezing experiments. Three different experimental groups were prepared by varying cell seeding density and collagen concentration: the nominal (NORM) group (cell seeding density = 2 × 10⁵ cells/mL and collagen concentration = 3 mg/mL), the high cell density (HCEL) group (cell seeding density = 4 × 10⁵ cells/mL and collagen concentration = 3 mg/mL), and the high collagen concentration (HCOL) group (cell seeding density = 2 × 10⁵ cells/mL and collagen concentration = 6 mg/mL). The cell seeding density and collagen concentration of the NORM group were determined based on the values typically used for constructing dermal equivalents [28-31], and two-fold increased cell density and collagen concentration were used for the HCEL and the HCOL groups, respectively.

Cell Image Deformetry

Cell image deformetry (CID) was used to measure the spatiotemporal deformation of ETs during freezing. A detailed description of the CID technique can be found elsewhere [26]. Briefly, the ET was frozen on a directional solidification stage (Figure S2A). The local temperature history of the ET was characterized and is presented in Figure S2B. A fluorescence macro/microscope (MVX10, Olympus, Center Valley, PA) equipped with a long working distance objective lens and a TRITC filter was used to visualize the QD-labeled cells of the ET during freezing. The ET was continuously imaged with a 1 second interval using a high sensitivity CCD camera (PIXIS 512, Princeton Instruments, Trenton, NJ). The acquired sequential images were cross-correlated at a 10 second interval using commercial software (DaVis 7.1, LaVision, Ypsilanti, MI) to determine the local deformation rates (μm/s). These deformation rates were further analyzed to estimate dilatation. Dilatation (s^-1) was defined as the rate of area increase per unit area, i.e., expansion, as follows:

$$e=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}$$ (1)

where u and v are the deformation rates (μm/s) in the x and y directions, respectively. The central difference scheme was used to approximate the spatial derivatives needed to compute the strain rates. The experiments were repeated three times to determine the average deformation rates, u and v, along the x and y directions, respectively (n = 3).

Characterization of Post-thaw ECM Microstructure

The post-thaw ECM microstructure was assessed using quantitative scanning electron microscopy (SEM). After F/T, the ET was fixed with 2% tannic acid for 1 minute at room temperature. After the fixation, the ET was cut into 3 mm diameter disks from both the frozen/thawed region and the unfrozen region. The tissue disks were stained with 2% uranyl acetate, and were then encapsulated in wet-SEM sample holders (QX-302 capsule, Quantomix, Hartfield, PA) with 10 μL buffering solution (QX-302 imaging buffer, Quantomix). The tissue samples were then imaged in the hydrated state using a scanning electron microscope (JSM-35C, JEOL, Tokyo, Japan). At least five disks were imaged from any given ET. The SEM micrographs were quantitatively analyzed using NIH ImageJ for mean void area ratio [25, 32]. Briefly, at least 5 interrogation windows of 150 × 150 pixels were randomly cropped and despeckled. The interrogation windows were then binarized and skeletonized. The number of pixels occupied with voids was obtained and normalized to the total number of pixels.

Post-Thaw Cell Viability Assessment

Post-thaw cellular viability was assessed by a membrane integrity assay. Following the F/T experiments, the ETs were incubated in culture media with 9 μM Hoechst (H-33342, Molecular Probes) and 16 μM propidium iodide solution (P-1304, Molecular Probes) for 30 minutes at 37 °C. After the incubation, the cells, stained with each dye, were counted under a fluorescence microscope. The viability was assessed at several axial locations, and at least three different fields at each axial location were examined. This assay was performed at 3 hours after F/T. Besides typical percent viability (i.e., the percentage of live cells with respect to all the cells), the corrected viability was also evaluated with respect to the number of live cells in the unfrozen region (x = 12 mm) of a given sample as below:

$$\text{Corrected Viability}=\frac{\text{Number of Live Cells}}{\text{Number of Live Cells at}x=12\mathrm{mm}}\times 100\%$$ (2)

This concept of viability has been previously used to assess the viability of ETs [33], and is a relevant measure of cell survival and re-growth in ETs given that the cell number can be changing due to cell detachment, proliferation and/or migration. It assumes that cells detached from the matrix are dead or injured. The corrected viability can also be higher than 100% if the number of live cells is greater than the control due to cell proliferation and/or migration.

Immunofluorescence Microscopy for Cytoskeleton

Post-thaw ET samples were fixed with 3% paraformaldehyde (Ted Pella, Redding, CA) in DBPS at room temperature for 10 minutes. This was followed by a 30-minute treatment with 2% BSA (Fraction V, Equitech-Bio, Kerrville, TX) and 1% glycine (Sigma Aldrich, St. Louis, MO) in DPBS to block any non-specific staining. Samples were then permeabilized with 0.5% Triton X-100 (Sigma Aldrich, St. Louis, MO) in DPBS for 15 minutes. For actin staining, samples were incubated with Alexa-Fluor 488 conjugated phalloidin (1:150 dilution in 1% BSA/DPBS) at 37 °C for 30 minutes. Samples were mounted on glass slides with Fluoromount-G (Southern Biotech, Birmingham, AL). Confocal images of the samples were acquired using an OptiGrid structured illumination microscopic system.

Statistical Analysis

Each experimental group was repeated at least three times (n ≥ 3). Results are presented as mean ± standard error of the mean. Statistical analysis was performed using one-way ANOVA. The student t-test for comparing two groups and F-test for the equality of slopes of the regression lines in Figure 2(a) were performed at 95% confidence level [34].

RESULTS

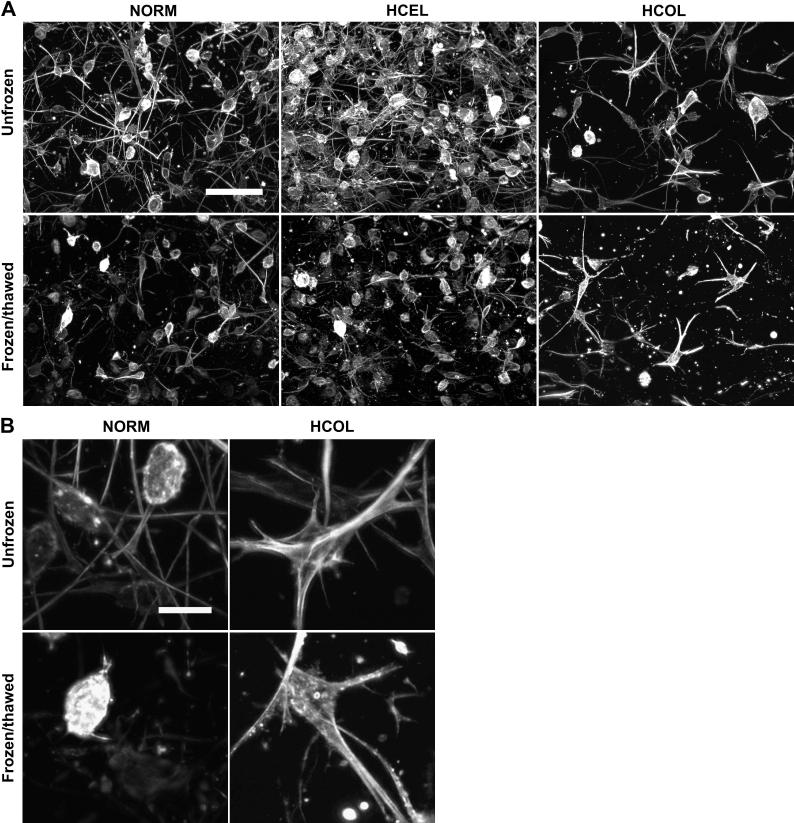
The macroscopic and microscopic appearances of three different groups of ETs are shown in Figure 1. The most notable macroscopic difference is the extent of cell-driven compaction. The NORM group compacts to 39.1 ± 1.2 mm (L) × 14.8 ± 0.7 mm (W) (n = 3) after 24 hours of incubation. The extent of its compaction lies between those of the HCEL group and the HCOL group. The HCEL group compacts most significantly and results in the size of 33.8 ± 0.7 mm (L) × 12.7 ± 0.4 mm (W) (n = 3). In contrast, the HCOL group barely shrinks and remains at 48.0 ± 0.1 mm (L) × 18.0 ± 0.1 mm (W) (n = 3), which is essentially its initial dimensions (48.0 mm (L) × 18.0 mm (W)). The microscopic images show that fibroblasts in the NORM and HCEL groups tend to have a rounded cell body and long cellular extensions, which are typically observed in three-dimensional tissue cultures, whereas the cells in the HCOL group have a slightly elongated cell body and short and branched cellular extensions, implying a higher mechanical loading on the cells [35, 36]. This may be caused by a stiffer matrix due to the higher collagen concentration in the HCOL group. Moreover, ETs in the HCOL group have a significantly lower cell density than ETs in the other groups after 24 hours of incubation. In addition to the difference in initial cell seeding density, this could also result from the lack of cell-driven compaction, which amplifies the differences in final cell density between the HCOL group and the other groups.

Figure 1.

Macro- and micrographs of three experimental groups of engineered tissues. Significant cell-driven compaction is observed in the HCEL group, resulting in an even higher cell density within the ET. In contrast, ETs in the HCOL group are not compacted, and have a very sparse cell distribution.

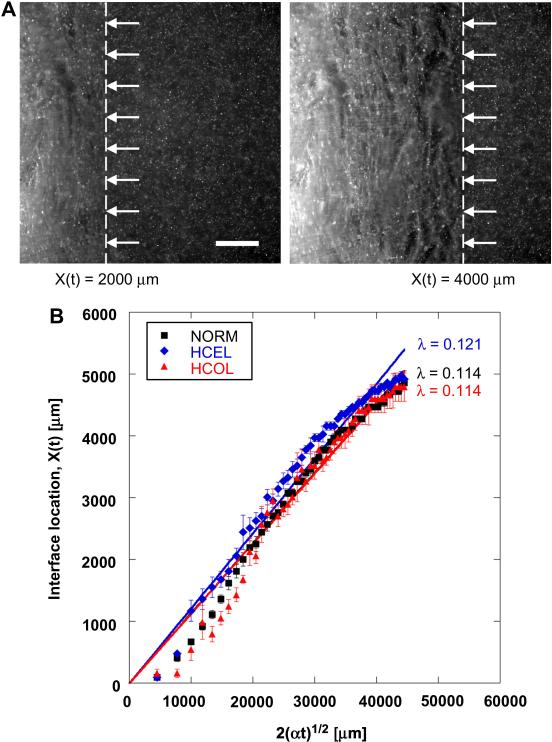
The fluorescence micrographs in Figure 2A show the propagation of the freezing interface across a given ET. Since the left side of the ET is exposed to the freezing temperature (i.e., -20°C), the freezing interface (noted with arrows and a dashed line) propagates from left to right. The propagation of the freezing interface in all three experimental groups is summarized in Figure 2B, in which the measured interface locations are correlated to time by the following:

$$X\left(t\right)=2\lambda \sqrt{\alpha t}$$ (3)

where λ is a parameter of the freezing conditions, and α is the thermal diffusivity of ice (1 × 10⁶ μm²/s). Other than at early times, the measured interface locations are well fitted using Equation (3). The physical meaning of λ is a measure of the freezing conditions including the magnitude of the difference between the initial and the freezing temperatures [37]. Since an identical temperature gradient is imposed on all three groups of ETs, they are expected to have the same λ values. The results show that λ for the NORM, HCEL, HCOL and control groups 0.114, 0.121, and 0.113, respectively. Although λ for the HCEL group is slightly higher than that for the other groups (p < 0.05), these values are very close, which implies that identical freezing conditions are indeed imposed on these ETs.

Figure 2.

Freezing interface propagation. (A) Fluorescence micrographs of an ET in the HCEL group during freezing (scale bar = 1000 μm). The freezing interface is noted with arrows and dotted lines. The freezing interface moves from left to right and the QD-labeled cells of the ET are observable during freezing. (B) The loci of the phase change interface during freezing. The freezing interfaces of all experimental groups generally move at a similar speed, but the HCEL group has a slightly higher speed than the other groups. The R²-values of the curve fits are 0.979 for NORM, 0.961 for HCEL, and 0.935 for HCOL.

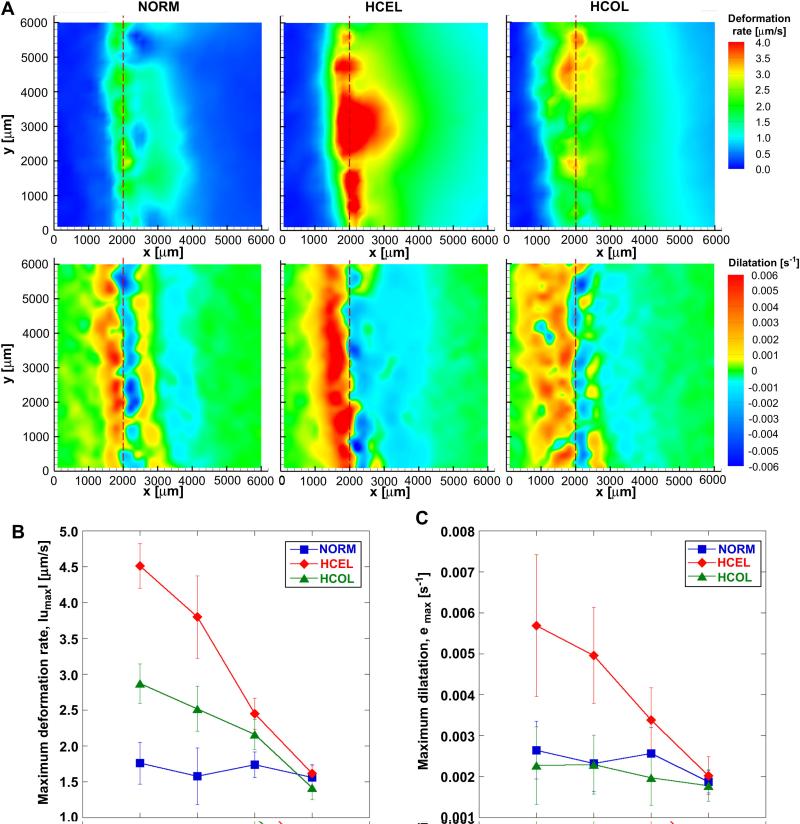
Figure 3A shows color contours of the two-dimensional freezing-induced deformation rate (μm/s) and corresponding dilatation (s^-1) when X(t) = 2000 μm for all three experimental groups. A significant local deformation is observed around the phase change interface. The unfrozen region also experiences local deformation with its magnitude decreasing as the distance from the interface increases. As the interface propagates, the deformation pattern moves along with the interface, and the magnitude of the deformation rates decreases. As shown in Figure 3B, when the interface is located at x = 2000 μm (i.e., X(t) = 2000 μm), the HCEL group undergoes a maximum average deformation rate of 3.8 ± 0.5 μm/s. Compared to the NORM group, this is a 153% increase in magnitude (i.e., from 1.5 ± 0.3 μm/s to 3.8 ± 0.5 μm/s), and a much wider region is affected by the freezing-induced deformation (as indicated in the deformation rate contours). Correspondingly, the dilatation contours for the HCEL group show a larger expansion (which occurs right after the phase change interface) than that for the NORM group (Figure 3C). In fact, the maximum average dilatation for the HCEL group (0.0050 ± 0.0012 s^-1) is significantly greater than that for the NORM group (0.0023 ± 0.0007 s^-1). On the other hand, the area of the compressed unfrozen region is much wider than for the NORM group. An interesting feature for the HCEL group, in contrast to the NORM group, is the absence of a secondary expansion peak in front of the compression zone.

Figure 3.

Freezing-induced local deformation of ETs (n = 3 for each group). (A) Deformation rate and dilatation contours of NORM, HCEL, and HCOL groups, respectively, at X(t) = 2000 μm. All the experimental groups were exposed to an identical F/T condition, but the HCEL and HCOL groups experienced larger deformation than the NORM group. In all groups, a significant local deformation occurs around the phase change interface and propagates along the x-direction. Compared to the NORM group, the magnitudes of the deformation rates of the HCEL and HCOL groups are larger (HCEL > HCOL > NORM), and the area affected by the deformation is much wider than for the NORM group. The magnitude of dilatation for the HCEL group is larger than for the NORM group. As for the HCOL group, the dilatation is similar to that for the NORM group, but the area of dilated frozen region is much wider. The deformation rate and dilatation of the NORM group were re-plotted from [26]. (B) The magnitude of the maximum deformation rate, |u_max|, for each experiment group. (C) The magnitude of the maximum and minimum dilatation, e_max and e_min, for each experimental group. Note that the freezing interface location, X(t), is proportional to $\sqrt{t}$.

As seen in Figure 3A, the HCOL group also experiences deformation near the freezing interface, and the magnitude of the maximum average deformation rate is 2.5 ± 0.3 μm/s when X(t) = 2000 μm. This is larger than that for the NORM group, but smaller than that for the HCEL group (Figure 3B). The corresponding maximum average expansion is 0.0023 ± 0.0007 s^-1 (Figure 3C). Although similar in magnitude to the NORM group, the region experiencing this expansion (and compression) pattern across the freezing interface is wider than that for the NORM group throughout the freezing process. Similar to the HCEL group, the secondary expansion peak is very weak and hardly noticed. This is thought to be due to the difference in the interstitial fluid transport within the ETs among the experimental groups, but further research is warranted to confirm this speculation. Overall, Figure 3 confirms that ETs with different cell-fluid-matrix parameters respond in substantially different manners to an identical freezing protocol.

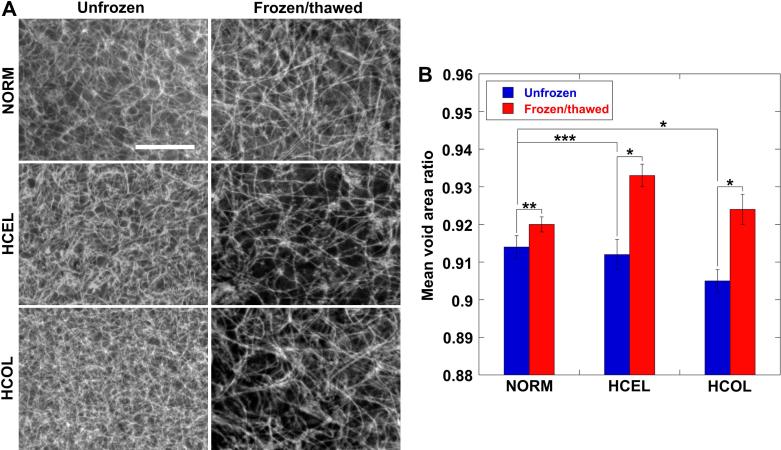
The ECM microstructures for all three different experimental groups before and after F/T are shown in Figure 4A. Before F/T, the HCEL group has a denser collagen fibril network than for the NORM group because of greater cell-driven compaction [36]. The HCOL group has the densest collagen network. This dense network is caused by the high collagen content and the smallest extent of ECM remodeling by the fibroblasts. After F/T, all three groups have enlarged pore structures and a coarser collagen network. These changes in the ECM microstructure can be quantified by assessing a parameter called “mean void area ratio” [25, 32] as shown in Figure 4B. The mean void area ratio can be interpreted as the two-dimensional projection of ECM porosity. Before F/T, the mean void area ratio is 0.914 ± 0.003 for the NORM group, 0.912 ± 0.004 for the HCEL group, and 0.905 ± 0.003 for the HCOL group, respectively (n = 3 for each group). As observed in the SEM micrographs, the HCOL group has a smaller mean void area ratio than for the NORM group (p < 0.01). The HCEL group also has a smaller mean void area ratio than for the NORM group, but the difference is not statistically significant (p = 0.25). These differences in the ECM microstructure might contribute to the groups’ different responses to the identical freezing protocol. The extent of enlargement of the ECM pore structures was also quantified. The HCEL group shows the largest increase of mean void area ratio (0.933 ± 0.003) (p < 0.01), followed by the HCOL group (0.924 ± 0.004) (p < 0.01), whereas the NORM group shows the smallest increase (0.920 ± 0.002) (p = 0.07). These results are consistent with the CID measurements; the largest dilatation is observed in the HCEL group, the second largest in the HCOL group, and finally the NORM group. This implies that the spatiotemporal deformation of the ET during freezing can be an indicator of post-thaw ECM microstructures.

Figure 4.

Microstructural changes of ECM after F/T. (A) Scanning electron micrographs of unfrozen and frozen/thawed ECM microstructures for the NORM, HCEL, and HCOL groups, respectively (scale bar = 10 μm), and (B) mean void area ratio. The HCOL group has the densest collagen network before freezing. The HCEL group has the largest increase in the mean void area ratio after F/T, which concurs with the freezing-induced deformation measurements (* p < 0.01, ** p = 0.07, and *** p = 0.25).

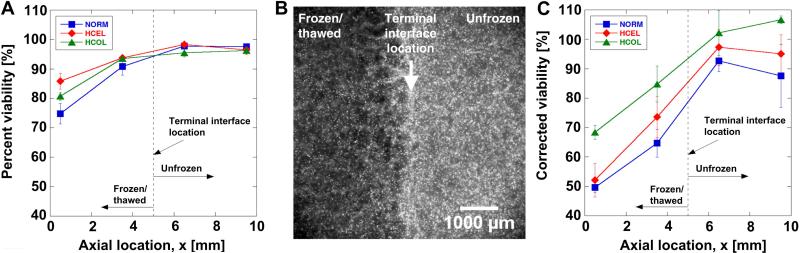
The corresponding acute cellular injury characteristics are summarized in Figure 5. The percent viability profiles of all experimental groups are shown in Figure 5A. In the frozen/thawed region (i.e., x < terminal interface location), the cell viability of all groups decreases with increasing distance from the interface. However, differences in the extent of acute injury are noted among the experimental groups. The lowest viability is observed in the NORM group, and the highest is observed in the HCEL group. Since the ETs of all three experimental groups were exposed to an identical F/T condition, the thermal insults experienced by the cells in the ETs are thought to be identical. Thus, the differences in viability imply that the cells were exposed to other insults besides thermal. However, contrary to anticipation, the HCEL group, experiencing the highest dilatation, shows the highest percent viability. A fluorescence micrograph of a typical ET is presented in Figure 5B, which shows all the cells stained with Hoechst near the terminal interface location. It is noted that the cell population density in the frozen/thawed region (i.e., left half) significantly decreases compared to the unfrozen region (i.e., right half). This cell density decrease indicates that cells may be detached from the ECM during F/T. Similar freezing-induced cell detachment has been reported in ETs with different cell types [33], and Woods et al. [38] have pointed out that detached cells may undergo apoptosis due to a signal induced by the MEEK group caspases.. The corrected viability profiles, which assume that cells detached from the matrix are dead or injured, are shown in Figure 5C. The corrected viability of the HCOL group in the frozen/thawed region is the highest among the experimental groups. The HCEL group, whose percent uncorrected viability was the highest, undergoes the most significant viability drop and becomes similar to the NORM group. This suggests that the number of detached cells in the HCEL ETs is the highest among all groups, which concurs with the observation that the HCEL group undergoes the largest deformation during freezing. However, this does not explain why the HCOL group has the highest corrected viability.

Figure 5.

Immediate response of fibroblast in ETs – (A) Percent viability, (B) a typical fluorescence micrograph of NORM group showing all Hoechst stained cells, and (C) corrected viability. Terminal interface location, where the freezing interface stopped at the end of the freezing protocol, is noted with a dashed line. In the frozen/thawed region (i.e., x < terminal interface location), the viability of all groups decreases with increasing distance from the interface. Without considering the decrease in the cell number, the highest viability is noted in the HCEL group. However, the fluorescence micrograph shows significant decreased cell number in the frozen/thawed region. If the decrease in the cell number is considered in calculating the cell viability, the highest (corrected) viability is observed in the HCOL group.

The effects of the freezing-induced deformation on cell-matrix binding and cytoskeleton organization were further investigated. The micrographs of the actin cytoskeleton of each experimental group are shown in Figure 6. For the NORM group, the cells in the unfrozen region have long and thin actin fibers developed along their cellular extensions. After F/T, the cellular extensions disappear or are shortened, which indicates that the cell-matrix adhesions have been damaged. For the HCEL group, the cells in the unfrozen region also have thin actin filaments formed in their cellular extensions similar to those in the NORM group. After F/T, similar damage to the cell-matrix binding and cell number decrease are noted. Contrary to the NORM and HCEL groups, the cells in the HCOL group have thicker and more condensed actin bundles, and their actin morphology does not show long and fine extensions. This indicates stronger cell-ECM binding than the other groups. After F/T, the cells appear to have experienced less severe damage of their cell-ECM adhesions and their morphology is better preserved, and consequently the smallest decrease in cell density among all experimental groups.

Figure 6.

Fluorescence micrographs of cytoskeleton of fibroblasts in the frozen/thawed and unfrozen regions – (A) Overall appearance of actin cytoskeleton of fibroblasts (scale bar = 100 μm), and (B) close-up images of actin cytoskeleton (scale bar = 20 μm). In both the NORM and HCEL groups, the cytoskeleton in the frozen/thawed regions is damaged, with shortened extensions and fewer number of cells. In the HCOL group, the cells have condensed and thick actin bundles, and less damage is observed after F/T than the NORM and HCEL groups.

DISCUSSION

Although all ETs have been subjected to an identical freezing condition, the extent and characteristics of freezing-induced tissue deformation are significantly different among the three experimental groups. The largest deformation rate and dilatation have been observed in the HCEL group. This large deformation is thought to be caused by the dense collagen fibril network and high cell density. The deformation and interstitial fluid transport of a poroelastic material can be described by the biphasic model, and these are directly affected by the hydraulic permeability and elastic modulus [39]. In particular, the hydraulic permeability can be significantly affected by the microstructure of the ECM. As discussed elsewhere [40, 41], the permeability, κ, can be correlated to the structural parameters of the ECM as follows:

$$\kappa =\frac{r_f^2{\varphi }^3}{4k{(1-\varphi )}^2}$$ (4)

where r_f is the radius of the fiber, ϕ is the porosity, and k is the Kozeny constant which depends on the architecture of the ECM. In addition, the porosity can be related to the fiber radius by

$$\varphi =1-\pi r_f^{2}l$$ (5)

where l is the length per unit volume of the fibers. Since the ETs in the HCEL group have a lower porosity and a shorter length l than for the NORM group due to the fibroblast-driven compaction, as observed both macroscopically (Figure 1) and microscopically (Figure 4), κ of the HCEL group should be lower than for the NORM group but higher than for the HCOL group. Moreover, the presence of the cells also contributes to the lower κ of the HCEL group given that the cells may act as a granular matrix which has not been accounted for in Equations (4) and (5).

Thus, when freezing induces interstitial fluid transport due to the volumetric expansion associated with the water-ice phase change, the fluid transport through the ECM might be hindered. This results in local swelling rather than interstitial fluid transport toward the unfrozen region of the ETs. Besides lowering the hydraulic permeability, the increased cell density in the HCEL group is thought to provide an additional source of interstitial fluid during freezing. This excess water from the dehydrated cells during freezing would increase the amount of interstitial fluid. Due to a higher cell density, the amount of excess water in the HCEL group would be greater than for any of the other groups, and this would help to augment tissue deformation during freezing. Due to the cell-fluid interactions as well as the given matrix microstructure, the ETs of the HCEL group would experience the largest deformation during freezing.

The present results also illustrate that the deformation rates and dilatation experienced by the ETs during freezing correlate well to the post-thaw ECM structural changes as shown in Figure 4. Based on both tissue deformation measurements and SEM analysis, ETs in the HCEL group have experienced the largest deformation and subsequently the largest increase in mean void area ratio, followed by the HCOL group. The NORM group shows the smallest tissue deformation and change in mean void area ratio. This supports our hypothesis that freezing-induced deformation can be a measure of post-thaw ECM microstructure. Many functional properties of tissues are associated with the ECM microstructure. For example, diffusion coefficients [42-44], hydraulic permeability [40, 41, 45] and elastic modulus [46, 47] have been correlated to the porosity and other structural parameters of the ECM. Thus, maintaining the ECM microstructure is important in preserving the functionality of tissues.

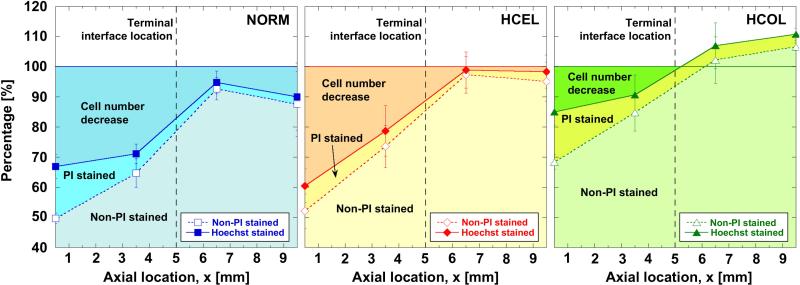
The post-thaw cell viability profiles and cell population densities are further analyzed to quantify the cellular injury by different mechanisms, and are shown in Figure 7. The analysis assumes that the initial cell population density is spatially uniform and the same as the control (i.e., the cell number at x = 12 mm). Hoechst staining indicates all adherent cells, non-PI staining indicates live cells (i.e., intact membrane), PI staining signifies cells with membrane damage, and the decrease in cell number is due to cellular detachment. As shown in Figure 7, the cellular injury experienced by the NORM and HCEL groups is mainly attributed to cell detachment. As anticipated in the corrected viability, the number of detached cells in the HCEL group is the highest. In contrast to the NORM and HCEL groups, the contribution of cell detachment is significantly less for the HCOL group. As mentioned previously, since these experimental groups were exposed to an identical F/T protocol, the extent of cellular injury induced by the freezing temperature is thought to be identical. Thus, the difference in the extent of cell detachment can be explained by the freezing-induced deformation of the ETs, which results from the cell-fluid-matrix interactions. As reported earlier, the HCEL group experiences the largest deformation, implying that the cells in the HCEL ETs experience the largest tensional strain, which causes more cells to detach from the ECM. However, the HCOL group undergoes a similar magnitude of local deformation as the NORM group, and yet its extent of cell detachment is the smallest. This may be caused by stronger cell-ECM binding in the HCOL group as compared to the other groups. Thus, when a cryopreservation protocol is developed, the freezing-induced cell-fluid-matrix interactions should be considered to minimize cellular detachment and ECM structural changes. Cryoprotective agents and other thermal variables should be selected to minimize the freezing-induced deformation as well as to protect cells from cryoinjury.

Figure 7.

Analysis of cellular injury in ETs. Cellular injury was evidenced through two observations - i) decreased cell number (i.e., cell detachment), and ii) PI staining of cell nuclei (i.e., damaged cell membranes). Although the number of PI stained cells in the frozen region is fairly similar among the three experimental groups, the decrease in the cell number is significantly different among the experimental groups. The HCEL group shows the greatest decrease in the cell number, while the HCOL group has the smallest decrease.

The present results have implications for addressing the issue of tissue-type dependent cryopreservation outcomes, which is one of the critical challenges of employing cryopreservation for various types of tissues. Due to the tissue-type dependent outcome and limited mechanistic understanding of tissue-level response to freezing, a successful cryopreservation protocol developed for a given type of tissue can not be adapted easily for other types of tissues. The current results can provide mechanistic strategies for designing and modifying cryopreservation protocols for tissues with different microstructures. For example, tissues with stiff and dense ECM structures would experience larger deformation and structural changes than soft tissues when being preserved using the same freezing protocol. Engineered tissues should be preserved with the consideration of the larger ECM structural changes and the greater loss of interstitial fluid as the cell density increases. Although these findings may also be applicable to native tissues, further research is still warranted, given that native tissues typically have a significantly stiffer ECM structure and higher cell density than the ETs studied herein.

The present results are well explained with averaged macroscopic continuum properties including hydraulic permeability and porosity, but further research is still necessary to elucidate the detailed effects of the ECM microstructure such as fiber diameter, pore structure, and cell-matrix adhesion, the latter of which is critical to understanding the mechanical stress imposed on the cells and ECM. A few recent studies imply the significance of these parameters. Pedersen et al. [45] suggested that the same hydraulic permeability could be obtained from tissues with different ECM architecture. In addition, Evans and Barocas [48] proposed that cell-driven compaction results in a highly dense ECM microstructure very near the cells causing a higher elastic modulus only near the cells. This may result in a highly inhomogeneous elastic modulus throughout the tissue, and the averaged macroscopic modulus may not be a good indicator for the mechanical cell-ECM interaction. Thus, cell-fluid-matrix interactions during freezing could be different even if the macroscopic properties of the tissues are the same. Mechanistic understanding of these interactions should therefore be developed considering these microstructural parameters.

CONCLUSIONS

In summary, the present results imply that freezing-induced tissue deformation is attributed to cell-fluid-matrix interactions during freezing. Moreover, these interactions can result in significantly different tissue-level responses including post-thaw ECM microstructure and hydration level even after undergoing identical freezing protocols. This also suggests that fibroblasts in each experimental group would experience different mechanical strain during the same freezing protocol. Thus, freezing-induced tissue deformation needs to be minimized or at least considered while designing cryopreservation protocols for different tissues. These findings can provide insights on tissue-type dependent cryopreservation outcomes, and help to design and modify cryopreservation protocols for different types of tissues.