Storage and binding of object features in visual working memory

Abstract

An influential conception of visual working memory is of a small number of discrete memory “slots”, each storing an integrated representation of a single visual object, including all its component features. When a scene contains more objects than there are slots, visual attention controls which objects gain access to memory.

A key prediction of such a model is that the absolute error in recalling multiple features of the same object will be correlated, because features belonging to an attended object are all stored, bound together. Here, we tested participants’ ability to reproduce from memory both the color and orientation of an object indicated by a location cue. We observed strong independence of errors between feature dimensions even for large (6 item) memory arrays, inconsistent with an upper limit on the number of objects held in memory.

Examining the pattern of responses in each dimension revealed a gaussian distribution of error centered on the target value that increased in width under higher memory loads. For large arrays, a subset of responses were not centered on the target but instead predominantly corresponded to mistakenly reproducing one of the other features held in memory. These misreporting responses again occurred independently in each feature dimension, consistent with ‘misbinding’ due to errors in maintaining the binding information that assigns features to objects.

The results support a shared-resource model of working memory, in which increasing memory load incrementally degrades storage of visual information, reducing the fidelity with which both object features and feature bindings are maintained.

1. Introduction

What limits the visual information that can be maintained in short-term memory? Historically, this question has been addressed by examining the frequency of recall errors as memory load is manipulated, either in studies of ‘partial report’ (Sperling, 1960; Irwin, 1991, 1992; Irwin and Andrews, 1996) or change detection (Phillips, 1974; Pashler, 1988; Luck and Vogel, 1997; Vogel et al., 2001, 2005; Todd and Marois, 2004; Rouder et al., 2008). The results of these studies have commonly been interpreted as supporting a limit on the number of objects that can be simultaneously represented in working memory. In one influential version of this model, the objects present in a visual scene compete for storage in a small number of independent memory ‘slots’. Each slot maintains a representation of a single integrated object (incorporating all its features, bound together) with high fidelity, and the allocation of visual attention determines which objects gain access to a slot (Irwin and Andrews, 1996; Luck and Vogel, 1997; Cowan, 2001; Hollingworth and Henderson, 2002).

Recently, this conception of working memory has been challenged by studies examining how recall errors are distributed in the space of possible responses, based on discrimination (Palmer, 1990; Bays and Husain, 2008, 2009) or reproduction tasks (Wilken and Ma, 2004; Zhang and Luck, 2008, 2009; Bays et al., 2009). These studies have revealed strict limits on the fidelity with which multiple visual objects can be maintained: the precision with which each visual feature is stored declines rapidly as the total number of items in memory increases. This finding is difficult to reconcile with the concept of storage in independent slots, and has led to the development of an alternative, shared-resource account of working memory (Wilken and Ma, 2004; Bays and Husain, 2008). According to this proposal, a single memory resource is flexibly distributed between the elements of a visual scene. As more items are stored, less resource is available per item, with the result that the features of each item are stored with increasing variability (‘noise’). Visual attention provides flexible control over distribution of this resource, such that salient or goal-relevant items are stored with enhanced resolution (Bays and Husain, 2008).

Importantly, in contrast to the slot model, this resource-based account does not predict a fixed upper limit on the number of objects that can be maintained. Indeed a mathematical model based on shared resources (Bays and Husain, 2008) predicts the appearance of such a capacity limit in change detection tasks, previously considered evidence in favor of a fixed slot model. Nonetheless, a number of attempts have been made to find a compromise position between the two models, in which varying resolution of storage co-exists with a fixed limit on the number of objects that can be stored (Alvarez and Cavanagh, 2004; Awh et al., 2007; Zhang and Luck, 2008). In particular, recent studies by Luck and colleagues (Zhang and Luck, 2008, 2009) have presented results from a color reproduction task which appear to provide support for such a ‘hybrid’ model.

In these studies, participants were presented with a memory array of colored squares. After a brief retention interval, one array location was indicated and participants were required to report the color they recalled at that location by clicking on a color wheel. The authors analyzed the distribution of responses on the color wheel as a mixture of two components: a gaussian distribution centered on the correct color of the probed item, and a uniform distribution spread equally over all possible responses. The gaussian component indicates variability in the stored representations of the colors in the memory array. Consistent with a resource-model account, the variability with which each item was stored depended on the total number of items in memory, as indicated by an increase in the gaussian width with increasing memory load. In addition, however, Zhang & Luck proposed that the uniform component corresponds to a proportion of trials on which subjects choose a response at random. As in a slot model, this might occur if no information was stored about the probed object as the result of exceeding an upper limit on the number of objects that can simultaneously be maintained in working memory.

Here we put this interpretation to the test, by examining the joint distribution of errors when subjects are required to reproduce from memory two different features (color and orientation) belonging to the same probed object. If only a subset of objects in an array can be stored, the absolute error in reporting color and orientation should be correlated, and the joint distribution of errors in the dual-feature task should consist of two components: one in which the object is stored and both features are recalled (with gaussian variability), and one in which the object is not stored and both responses are random. Neither result was observed: instead our results revealed that both the absolute error and the occurrence of uniform responses were strongly independent across feature dimensions.

This finding is inconsistent with the hypothesis of a fixed upper limit on the number of objects stored in memory. Instead these results support the proposal of Wheeler and Treisman (2002) that visual features in different dimensions are maintained in independent memory stores. These authors’ conclusions were based in part on the observation of ‘binding errors’ in a change detection task: errors caused by incorrectly combining in memory features that belong to different objects (Treisman and Schmidt, 1982; Treisman, 1998; Wolfe and Cave, 1999; Wheeler and Treisman, 2002; Robertson, 2003; Allen et al., 2006).

We have previously proposed (Bays et al., 2009) that the uniformly-distributed responses interpreted by Zhang & Luck (2008) as random guesses may instead correspond to mistakenly reporting the features of one of the other items held in memory. Here, by analysing the frequency of these ‘misreporting’ errors within and across feature dimensions, we confirm that they are the result of misbinding features held in independent memory stores, consistent with the storage of visual features in separate sensory representations (Pasternak and Greenlee, 2005). These results have important implications for the nature of visual working memory representations and the locus of binding of separate features belonging to an object.

2. Materials and methods

2.1. Experimental Protocol

Ten subjects (seven male, three female; age 22–26) participated in the study after giving informed consent. All had normal or corrected-to-normal visual acuity; none reported any difficulty in making color discriminations. Stimuli were displayed on a 21-in. CRT monitor at a viewing distance of 60 cm. Eye position was monitored online at 1000 Hz using a frame-mounted infra-red eye tracker (Eyelink 1000, SR Research Ltd., Canada).

Each trial began with the presentation of a central fixation cross (white, diameter 0.75° of visual angle) against a black background. Once a stable fixation was recorded on the cross, a memory array was presented, consisting of a number of colored oriented bars (0.75° × 4°) randomly distributed around fixation at eccentricities in the range 6°−10°, with a minimum centre-to-centre separation of 6° between items (example in Fig 1a). The color and orientation of each item were independently chosen at random from two circular parameter spaces. The orientation parameter space corresponded to the range of angles 0°−180° (i.e. the full range of possible bar orientations). For color, the parameter space was defined by a circle in CIE L*a*b* coordinates with constant luminance (L* = 50), center at a* = b* = 20, and radius 60.

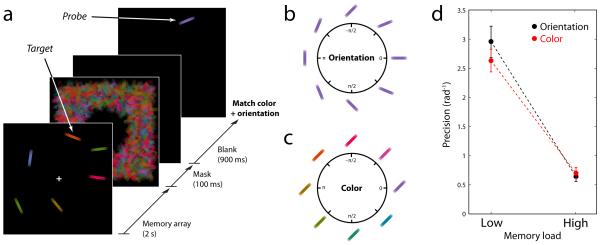
Figure 1. Precision of working memory in a dual-feature reproduction task.

(a) Subjects were presented with an array of colored, oriented bars, followed by a pattern mask. After a blank retention interval, a probe appeared and subjects used two response dials to adjust its color and orientation to match the item at the corresponding location in the memory array (the target).

(b & c) Turning each dial cycled the probe through a circular parameter space of possible colors or orientations. Some examples of orientations (b) and colors (c) are shown corresponding to different points in each response space.

(d) Recall precision as a function of memory load: 1 object (low) v 6 objects (high). Precision is defined as the reciprocal of the standard deviation of error in subjects’ responses: zero indicates chance performance.

The memory array was presented for 2 s, followed by a pattern mask for 100 ms and then a blank retention interval (900 ms). The pattern mask was included to ensure iconic memory did not contribute to performance. A single (probe) item was then presented at one randomly-chosen location from the preceding memory array. Subjects were instructed to adjust the orientation and color of the probe item to match the features of the item that had been presented at the same location in the memory array (the target). The probe’s features were adjusted using two input dials (PowerMate USB Multimedia controller, Griffin Technology, USA) one operated with each hand (randomly assigned). Turning one dial caused the probe to rotate through the range of possible orientations (Fig 1b, top); turning the other dial caused the probe’s color to cycle through the space of possible colors (Fig 1b, bottom). The probe’s initial features were randomly assigned. Subjects could adjust the two dials in any order or simultaneously, and indicated adjustment was complete by depressing the centre of either dial. Accuracy was stressed, and responses were not timed.

Each subject completed 300 trials in total: a block of 250 trials with six-item memory arrays (high-load), and a block of 50 trials with just one item in each array (low-load). Fewer trials were required in the low-load condition because there was no possibility of misreporting a non-target item, greatly simplifying the data-intensive modeling component of the analysis (§ 2.2.3). High- and low-load blocks were completed in a counter-balanced order.

Any trial on which gaze deviated more than 2° from the central cross during presentation of the memory array was aborted and restarted with new feature values. This constraint prevented subjects fixating individual memory array items, which otherwise might bias storage towards particular objects in the array (Bays and Husain, 2008).

2.2. Analysis

2.2.1. Within-dimension errors

Our initial analysis examined errors in recall of color and orientation separately. Responses in each dimension were analysed in terms of the circular parameter space of possible feature values (range −π to π radians; Fig 1b). For each trial, a measure of recall error in each dimension was obtained by calculating the angular deviation between the feature value reported by the subject and the feature value of the target item in the memory array. To obtain measures of performance comparable across feature dimensions, we calculated the recall bias, defined as the mean of the recall error, and precision, defined as the reciprocal of the standard deviation of error. As in a previous study (Bays et al., 2009), we used the definition of mean and standard deviation for circular data given by Fisher (1993), and subtracted from the precision estimate the value expected by chance (i.e. if the subject had responded at random on each trial).

To investigate the source of recall errors, we first examined the distribution of error in each feature dimension with respect to a probabilistic model of memory performance described by Zhang & Luck (2008). This model proposes that errors in a reproduction task arise from two sources: gaussian variability in memory for the target feature, and a fixed probability on each trial of guessing at random. The distribution of responses is therefore described by a mixture model (McLachlan and Peel, 2000) of general form:

$$p\left(\widehat{\theta }\right)=\sum _k{\alpha }_k{p}_k$$

where $\widehat{\theta }$ is the reported feature value, α_k is the probability that a response comes from the kth component $(\sum _k{\alpha }_k=1)$, and p_k is the probability density function describing the distribution of responses under that component. Zhang & Luck’s model has two components (k = 2) whose probability density functions are given in the first two rows of Table 1. The target component (T) corresponds to noisy recall of the target feature, resulting in a distribution of responses drawn from a circular gaussian (von Mises) distribution centered on the true feature value of the target; the uniform component (U) corresponds to random guessing, producing a uniform distribution of responses across all possible feature values.

Table 1. Mixture model components describing the distribution of responses within a single feature dimension.

θ is the true feature value of the target item, and $\widehat{\theta }$ the feature value reported by the subject (range −π < θ ≤ π). φ_i is the true feature value of the ith non-target item (m in total). ϕ_σ is the von Mises distribution with mean zero and standard deviation σ. Diagrams indicate how the response probabilities contributed by each component are distributed around target (T) and non-target (N) feature values (for illustration, only two non-targets are shown). The model proposed by Zhang & Luck (2008) is described by rows 1–2 (target and uniform components). Bays et al. (2009) added a third component (row 3) to distinguish non-target from uniform responses.

k		Mixture component	Response type	Probability density (pk)
1	T		target	${\varphi }_{\sigma }\left(\widehat{\theta }-\theta \right)$
2	U		uniform	$\frac{1}{2\pi }$
3	N		non-target	$\frac{1}{m}\sum _i^m{\varphi }_{\sigma }\left(\widehat{\theta }-{\phi }_i\right)$

Maximum likelihood estimates of the mixture parameters {α_T,α_U} and σ, the standard deviation of the von Mises distribution (Jammalamadaka and Sengupta, 2001), were obtained separately for each feature dimension, subject, and array size in MATLAB using a custom-written expectation-maximization algorithm (Bilmes, 1998; Dhillon and Sra, 2003; see also Lawrence, in press). The optimization procedure was repeated from a range of different initial parameter values to ensure that global maxima were obtained.

2.2.2. Joint distribution of color and orientation errors

In order to model the joint distribution describing responses in both feature dimensions, we extended the mixture model to include both color and orientation responses:

$$p({\widehat{\theta }}^O,{\widehat{\theta }}^C)=\sum _k{\alpha }_k{p}_k$$

where ${\widehat{\theta }}^O$ is the reported orientation value and ${\widehat{\theta }}^C$ is the reported color value. On each trial, the response for each feature dimension could come from target or uniform distributions, resulting in four possible combinations of color and orientation response distributions (Table 2, rows 1–4). Maximum likelihood estimates were obtained as above for mixture parameters {α_TT,α_UT,α_TU,α_UU} and σ_O and σ_C, the standard deviations of the Von Mises distributions describing variability in orientation and color recall, respectively.

Table 2. Mixture model components describing the joint distribution of responses in two feature dimensions.

θ^O and θ^C are the true orientation and color values, respectively, of the target item (range −π < θ ≤ π). ${\widehat{\theta }}^O$ and ${\widehat{\theta }}^C$ are the corresponding feature values reported by the subject. ${\phi }_i^O$ and ${\phi }_i^C$ are true feature values of the ith non-target item (m in total). ϕ_σO and ϕ_σC are von Mises distributions with mean zero and standard deviations σ_O and σ_C, corresponding to variability in recall of orientation and color, respectively. Rows 1–4 describe the extension to two feature dimensions of Zhang & Luck’s (2008) model, including only target and uniform components; rows 1–10 describe the corresponding expansion of the Bays et al. (2009) model, distinguishing non-target from uniform responses.

k	Mixture component	Response type		Probability density (pk)
		Orientation	Color
1	TT	target	target	${\varphi }_{{\sigma }_O}\left({\widehat{\theta }}^O-{\theta }^O\right){\varphi }_{{\sigma }_C}\left({\widehat{\theta }}^C-{\theta }^C\right)$
2	UU	uniform	uniform	${\left(\frac{1}{2\pi }\right)}^2$
3	TU	target	uniform	${\varphi }_{{\sigma }_O}\left({\widehat{\theta }}^O-{\theta }^O\right)\frac{1}{2\pi }$
4	UT	uniform	target	$\frac{1}{2\pi }{\varphi }_{{\sigma }_C}\left({\widehat{\theta }}^C-{\theta }^C\right)$
5	N=N	same non-target		$\frac{1}{m}\sum _i^m{\varphi }_{{\sigma }_O}\left({\widehat{\theta }}^O-{\phi }_i^O\right){\varphi }_{{\sigma }_C}\left({\widehat{\theta }}^C-{\phi }_i^C\right)$
6	N≠N	different non-targets		$\frac{1}{m(m-1)}\sum _i^m\sum _{j\ne i}^m{\varphi }_{{\sigma }_O}\left({\widehat{\theta }}^O-{\phi }_i^O\right){\varphi }_{{\sigma }_C}\left({\widehat{\theta }}^C-{\phi }_j^O\right)$
7	NT	non-target	target	$\frac{1}{m}\sum _i^m{\varphi }_{{\sigma }_O}\left({\widehat{\theta }}^O-{\phi }_i^O\right){\varphi }_{{\sigma }_C}\left({\widehat{\theta }}^C-{\theta }^C\right)$
8	TN	target	non-target	${\varphi }_{{\sigma }_O}\left({\widehat{\theta }}^O-{\theta }^O\right)\frac{1}{m}\sum _i^m{\varphi }_{{\sigma }_C}\left({\widehat{\theta }}^C-{\phi }_i^C\right)$
9	NU	non-target	uniform	$\frac{1}{m}\sum _i^m{\varphi }_{{\sigma }_O}\left({\widehat{\theta }}^O-{\phi }_i^O\right)\frac{1}{2\pi }$
10	UN	uniform	non-target	$\frac{1}{2\pi }\frac{1}{m}\sum _i^m{\varphi }_{{\sigma }_C}\left({\widehat{\theta }}^C-{\phi }_i^C\right)$

We examined two opposing hypotheses regarding the relationship between errors in the two feature dimensions. Under the hypothesis that color and orientation errors are fully independent, the joint response distribution should comprise a mixture of all four response combinations, occurring at the frequencies predicted by the product of the marginal probabilities obtained separately for each dimension (§ 2.2.1). That is, the parameters α_•• describing the frequencies of each combination of response types can be predicted directly from the parameters α_•^O and α_•^C obtained by fitting orientation and color responses separately: ${\alpha }_{TT}={\alpha }_T^C{\alpha }_T^O$, ${\alpha }_{TU}={\alpha }_T^O{\alpha }_U^C$, ${\alpha }_{UT}={\alpha }_U^O{\alpha }_T^C$, and ${\alpha }_{UU}={\alpha }_U^O{\alpha }_U^C$.

Under the opposing hypothesis that color and orientation errors are fully correlated, the joint response distribution should comprise a mixture of only two components: trials on which both the color and orientation of the target are reported, and trials on which both responses are random. Hence mixture parameters α_UT and α_TU (corresponding to trials in which one response is from the target distribution and one from the uniform) have predicted values of zero. This hypothesis predicts mixture parameters for target-target and uniform-uniform responses should equal the corresponding parameters obtained for orientation and color separately, i.e. ${\alpha }_{TT}={\alpha }_T^O={\alpha }_T^C$ and ${\alpha }_{UU}={\alpha }_U^O={\alpha }_U^C$. Because the marginal values of these parameters obtained in § 2.2.1 were not exactly identical, for modeling purposes we averaged across feature dimensions: ${\alpha }_{TT}=({\alpha }_T^O+{\alpha }_T^C)∕2$, ${\alpha }_{UU}({\alpha }_U^O+{\alpha }_U^C)∕2$.

As neither hypothesis was fully consistent with our results, we quantified the strength of correlation between feature dimensions by calculating Φ², the equivalent for binary variables of the coefficient of determination r²:

$${\Phi }^2=\frac{{({\alpha }_{TT}{\alpha }_{UU}-{\alpha }_{UT}{\alpha }_{TU})}^2}{{\alpha }_{T•}{\alpha }_{U•}{\alpha }_{•U}{\alpha }_{•T}}$$

where α_T• = α_TT + α_TU, etc. Like r², this measure falls in the range 0 ≤ Φ² ≤ 1, where Φ² = 0 indicates complete independence between feature dimensions, and Φ² =1 indicates full correlation.

2.2.3. Misreporting errors

Bays et al. (2009) proposed that the majority of responses captured by the uniform component of the Zhang & Luck (2008) model are not a result of random guessing. Instead they are instances of subjects mistakenly reporting the feature value of one of the non-target items in the memory array (misreporting errors). As in our previous study, we assessed the frequency of these errors by adding a third component to the mixture model describing responses in each feature dimension (Table 1, row 3). Responses due to this non-target component (N) are drawn with equal probability from von Mises distributions centered on the feature values of each of the non-target items in the memory array. Because the target item is unknown at the time of storage, the standard deviations of target and non-target von Mises distributions are equal in this model. Maximum likelihood estimates for this three-component model were obtained separately for color and orientation responses, as above.

To capture the joint distribution of color and orientation responses under this expanded model requires ten components (Table 2, rows 1–10). On each trial, the response for each feature dimension can come from target, non-target, or uniform distributions, resulting in nine possible combinations of color and orientation response types. In addition, on trials where both responses reflect non-target features, they can be due to reporting the orientation and color of the same non-target (N=N), or the orientation of one non-target and the color of a different non-target (N≠N).

We again compared the predictions of two opposing hypotheses regarding the relationship between misreporting errors in the two feature dimensions. Under the hypothesis of full correlation, non-target responses occur when the subject misidentifies which item from the memory array has been probed, resulting in color and orientation responses centered on the feature values of one of the non-targets. The frequency of these same non-target responses should therefore be equal to their marginal frequencies obtained separately for orientation and color responses: for modeling purposes we averaged across feature dimensions as above, ${\alpha }_{N=N}=({\alpha }_N^O+{\alpha }_N^C)∕2$. Other combinations involving non-target responses have zero probability under this hypothesis: α_NT = 0, α_TN = 0 and α_{N ≠ N} = 0.

Under the alternative independence hypothesis, non-target responses occur fully independently in each feature dimension: hence, ${\alpha }_{NT}={\alpha }_N^O{\alpha }_T^C$, ${\alpha }_{TN}={\alpha }_T^O{\alpha }_N^C$, ${\alpha }_{N\ne N}=\frac{m-1}{m}{\alpha }_N^O{\alpha }_N^C$ and ${\alpha }_{N\ne N}=\frac{1}{m}{\alpha }_N^O{\alpha }_N^C$ (where m is the number of non-targets).

2.2.4. Hypothesis testing

Data from each individual subject was analysed separately, and then paired sample t-tests used to make statistical comparisons at the group level. An arcsine transformation was used for tests on proportional data, including mixture parameters.

3. Results

3.1. Bias and precision

The recall task is illustrated in Fig 1a. On each trial, a subject was presented with an array of colored oriented bars surrounding a central fixation point. After a blank retention interval, one array location was indicated and the subject had to reproduce from memory both the color and the orientation of the item previously displayed at that location (the target item). For each feature dimension, the recall error was defined as the deviation within the space of possible responses (Fig 1b) between the reported and actual feature value of the target.

The fidelity of reproduction in each feature dimension can be characterized by two parameters, bias and precision. Bias indicates a systematic tendency to deviate from the correct target value in the same direction from trial to trial. No significant bias was observed in color or orientation responses (t < 1.7, p > 0.10). Precision measures the degree to which responses cluster around the correct feature value: a precision of zero indicates that responses are randomly distributed relative to the target. Consistent with previous studies, the recall precision varied substantially with changes in memory load (Fig 1c).

When only one item was present in the memory array (low-load), subjects recalled both color and orientation with considerable precision (orientation, 2.9 ± 0.3 rad⁻¹; color, 2.6 ± 0.2 rad⁻¹; mean ± S.E.; Fig 1c), comparable with performance in a previous study in which recall of just one feature (color) was required (3.4 rad⁻¹; Bays et al., 2009). The precision of recall did not significantly differ between feature dimensions (t = 1.4, p = 0.20).

When the number of items in the memory array was increased (high-load, 6 items), recall precision decreased significantly in both feature dimensions (orientation, 0.64 ± 0.08 rad⁻¹; color, 0.70 ± 0.09 rad⁻¹; t > 8.2, p < 0.001). Precision again did not differ significantly between dimensions (t = 0.81, p = 0.44) and was similar to that previously observed for color recall with six item arrays (0.51 rad⁻¹ in Bays et al., 2009; but see also Fougnie et al., 2010).

Subjects could choose to reproduce the orientation and color of the target in any order, or adjust both simultaneously. Whether a feature was adjusted first or second had no significant effect on recall precision under either load condition (t < 0.32, p > 0.75).

3.2. Distribution of errors

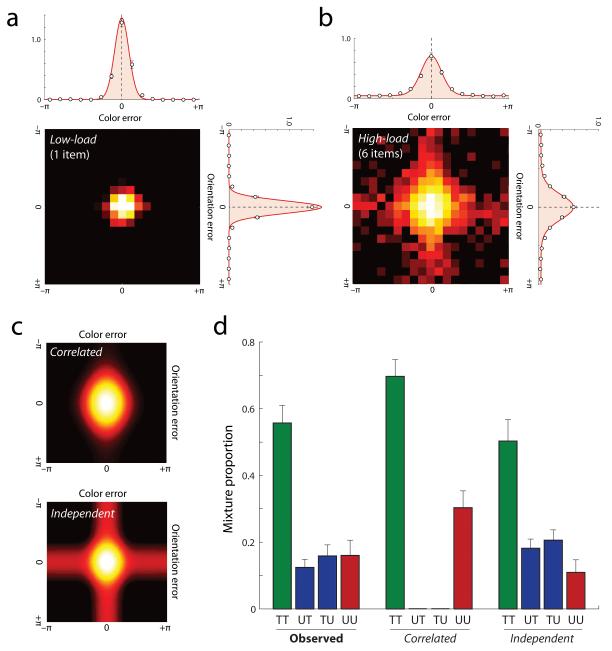
Fig 2a plots the distribution of responses relative to the target feature value for color (top) and orientation (right) on trials with just one item in the memory array (low-load). In both feature dimensions, the distribution of errors was accurately described by a (circular) gaussian centered on the target feature value (red curves; σ_C = 0.30 ± 0.01; σ_O = 0.29 ± 0.03). The joint histogram of errors in both dimensions is shown by the heat map in Fig 2a. The magnitudes of error in color and orientation on each trial were uncorrelated (r² < 0.01).

Figure 2. Distribution of errors relative to target feature values.

(a) Frequency of response as a function of the deviation between reported and target feature values in the low-load (1 object) condition: for color (top), orientation (right), and conjunction of both features (heat map). Colored lines indicate the response probabilities predicted by a mixture model combining a gaussian distribution centered on the target value and a uniform distribution spread equally across the response space.

(b) Error distributions plotted as in (a) for the high-load (6 object) condition.

(c) Predicted distributions of color and orientation responses under conditions of full correlation (top) and full independence (bottom) between feature dimensions. Compare with the observed distribution of errors shown in (b).

(d) Proportion of trials on which both responses are centered on target values (TT); both are uniformly distributed (UU); the orientation response is centered on the target and the color response is uniform (TU); and vice versa (UT). Estimates obtained by fitting a mixture model to observed responses are shown along with predictions under full correlation and full independence models.

The distribution of errors in each feature dimension in the high-load condition (6 items) is shown in Fig 2b (top & right). As observed in previous studies (Zhang and Luck, 2008; Bays et al., 2009), the pattern of responses was not consistent with a solely gaussian distribution of error in either feature dimension. Instead, the overall decline in precision (Fig 1c) appeared to result from increases in two sources of error.

First, unlike in the low-load condition, a significant proportion of responses in the high-load condition (orientation, 29% ± 6%; color, 32% ± 5%) were statistically unrelated to the true feature value of the target item (i.e. uniformly distributed). Second, the variability of those responses that were centered on the target feature value increased compared to the low-load condition (σ_C = 0.46 ± 0.03; σ_O = 0.60 ± 0.04, t > 6.9, p < 0.001), indicating that each feature was stored with increased noise. The mixture of gaussian and uniform components that best fit the observed distribution of errors for each feature dimension are shown by the red curves in Fig 2b.

3.3. Uniformly-distributed errors

The uniform response component has been interpreted as indicating a proportion of trials on which the probed object is not stored in memory. This hypothesis predicts that uniformly-distributed responses will be fully correlated across feature dimensions: a uniform color response will always coincide with a uniform orientation response, and vice versa. Based on the model parameters obtained from fitting orientation and color responses separately, we can predict the joint distribution of errors we would expect under this hypothesis: the prediction is shown by the heat map in Fig 2c (top). The magnitudes of color and orientation errors are correlated in this distribution, with r² = 0.20.

We also considered an alternative hypothesis in which uniform responses occur fully independently in the two feature dimensions: the prediction of this model is shown in Fig 2c (bottom). The independence hypothesis predicts a concentration of responses along horizontal and vertical axes of the joint distribution, corresponding to trials on which the color response comes from the gaussian distribution and the orientation response comes from the uniform distribution, and vice versa. The magnitudes of color and orientation errors are uncorrelated under this hypothesis.

The joint histogram of observed errors in the high-load condition is shown in Fig 2b (heat map). A concentration of responses along the axes is clearly visible along vertical and horizontal axes, as predicted under independence. Negligible correlation was observed between error magnitudes in color and orientation (r² = 0.02), also consistent with the independence hypothesis.

To examine in more detail the frequencies of uniform and target-centered responses, we fit a probabilistic model to subject’s responses in which trials could fall into four categories: those on which both color and orientation responses were centered on target values (TT), those on which both responses were unrelated to the target and drawn from a uniform distribution (UU), those on which the orientation response was centered on the target orientation and the color response was from the uniform distribution (TU), and vice versa (UT). The fitted parameter values are shown in Fig 2d, along with the predictions under correlated and independent uniform responses.

Inconsistent with the correlation hypothesis, which predicts that every trial will fall either into category TT or category UU, a highly significant proportion of trials were described by categories UT or TU (28% ± 3%; t = 14, p < 0.001). Overall, the observed parameter values indicated strong independence of uniformly-distributed responses in color and orientation dimensions (Φ² = 0.11).

3.4. Misreporting errors

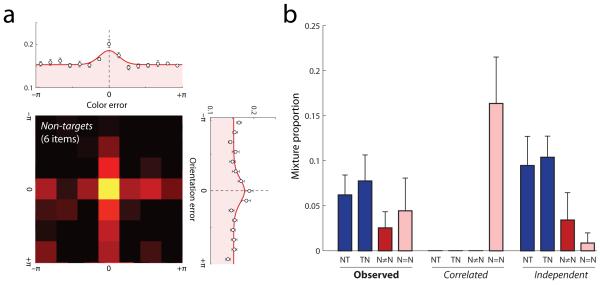
In a previous study (Bays et al., 2009) we proposed that a mixture model comprising only target and uniform components may be insufficient to fully describe the pattern of responses on reproduction tasks. We suggested that a third source of errors needed to be considered: instances of mistakenly reporting a feature value belonging to one of the other (non-target) items held in memory. Such ‘misreporting’ errors appear uniformly distributed when responses are plotted relative to the target feature value (as in Fig 2 and Zhang & Luck, 2008), and hence may be incorrectly attributed to random guessing. However, these errors appear as a significant concentration of the response distribution around zero when responses are plotted relative to each of the feature values of the non-target items in the memory array.

These non-target distributions are plotted in Fig 3a, for color (top) and orientation responses (right) in the high-load condition. Whereas the ‘guessing’ interpretation predicts that these distributions should be uniform, responses in each dimension centered on the feature values of the non-targets were significantly more frequent than expected by chance (color: t = 7.7, p < 0.001; orientation: t = 4.7, p = 0.001).

Figure 3. Distribution of errors relative to non-target feature values.

(a) Frequency of response as a function of the deviation between reported feature values and those of each non-target (unprobed) item, in the high-load (6 object) condition, for color (top), orientation (right), and conjunction of both features (heat map). Note the strong central tendency in each distribution, indicating that subjects frequently mistakenly report the features of non-target items.

(b) Proportion of trials on which color and orientation responses are both centered on the same non-target (N=N); each is centered on a different non-target (N≠N); the orientation response is centered on the target and the color response on a non-target (TN); and vice versa (NT). Estimates obtained by fitting a mixture model to observed responses are shown along with predictions of correlated-misreporting and independent-misreporting models.

Following Bays et al. (2009), we fit a three-component model to the data from each dimension, in which responses could come from a distribution centered on the target, a uniform distribution, or a distribution shared equally between each of the non-targets. The resulting parameter estimates indicated that misreporting errors formed a significant proportion of responses in each dimension (color: 17% ± 4%; orientation: 16% ± 6%; t > 4.7, p = 0.001). As a result, the proportion of responses attributed to the uniform component was significantly reduced in comparison to the two-component model (color: 15% v 32%; orientation: 14% v 29%; t > 2.3, p < 0.05).

We considered two possible sources of misreporting errors. One hypothesis was that they were caused by errors in storing the locations of items in the memory array; the alternative was that they were caused by misbinding of features during storage or maintenance in memory. Again the critical test is the degree of independence between responses on each trial.

The location-error hypothesis predicts that misreporting errors will be correlated across feature dimensions: mistakenly reporting the color of a non-target will always coincide with mistakenly reporting the orientation of the same non-target. In contrast, the misbinding hypothesis predicts that misreporting errors will occur independently in each feature dimension.

The joint distribution of responses relative to each non-target’s feature values are shown by the heatmap in Fig 3a. The magnitude of deviation of responses from non-target feature values was uncorrelated across feature dimensions (r² < 0.01) consistent with independence of non-target errors.

As before, we fit a probabilistic model to the joint response data allowing for all possible combinations of target, non-target and uniform responses. The critical parameters that distinguish the two hypotheses are those involving combinations of target and non-target responses, shown in Fig 3b. These parameters indicate the frequency of four categories of trial: those on which the subject responds with the orientation of the target but the color of a non-target (TN), or vice versa (NT); trials where the subject responds with both the color and the orientation of a single non-target (N=N); and those where they respond with the color of one non-target and the orientation of another (N≠N).

Fig 3b shows the observed frequencies of responses in each category. In addition, it displays the predicted frequencies under correlated- and independent-misreporting hypotheses, based on the model parameters obtained by fitting color and orientation responses separately.

The correlated-misreporting hypothesis predicts that non-target responses will occur only when the subject mistakenly responds with both the color and orientation of a single non-target (N=N). Inconsistent with this hypothesis, significant proportions of trials corresponded to one target feature and one non-target feature (NT or TN; 14% ± 3%; t = 10, p < 0.001), or responses to the color and orientation of two different non-targets (N≠N; 3% ± 1%; t = 2.8, p = 0.02). The independent-misreporting hypothesis, in contrast, predicts that non-target responses will occur independently for color and orientation dimensions. All non-target components estimated from the data were consistent with this full-independence model (t < 1.8, p > 0.11).

4. Discussion

The resolution with which visual features are stored in working memory is highly dependent on total memory load, and begins to decline as soon as the number of items in memory exceeds one (Palmer, 1990; Wilken and Ma, 2004; Bays and Husain, 2008; Zhang and Luck, 2008). However, it remains controversial whether this loss of fidelity alone accounts for all errors in recall, or whether it co-exists with a fixed upper limit on the number of objects that can be simultaneously maintained (Alvarez and Cavanagh, 2004; Awh et al., 2007; Zhang and Luck, 2008, 2009; Bays et al., 2009; Cowan and Rouder, 2009; Bays and Husain, 2009). Recent attempts to address this question have examined recall of items varying in a single feature dimension (typically color). Here, we presented arrays of objects that varied in two dimensions, color and orientation: participants were required to reproduce from memory both features of a single object, indicated by location.

As in previous studies, the precision with which subjects were able to reproduce each feature differed substantially between conditions of low (1 item) and high (6 item) memory load. Despite the substantial qualitative differences between feature dimensions, precision (calculated with respect to the range of possible feature values) was comparable for color and orientation responses. Precision values were also similar to those obtained in a previous study employing a very different response methodology (a mouse click on a wheel of color values in Bays et al., 2009, versus adjusting a dial to cycle through possible feature values in the present study). This provides an important validation of the precision measure as a reproducible and general measurement of recall performance. Significantly, the similarity of precision measures across dimensions did not reflect a simple trade-off in performance between color and orientation dimensions, as this would predict a negative correlation in the magnitudes of error in each dimension which was not observed.

While it is clear that increasing the number of items held in memory makes recall of each one less precise, the mechanisms underlying this increase in uncertainty are contentious. A critical focus of debate is the manner in which errors are distributed within the space of possible responses. In the current study, when only one object was stored in memory, the distribution of responses relative to the target feature value indicated that the stored representations of color and orientation were each independently corrupted by gaussian noise. When the task required that a larger number of objects be stored, the distribution of recall errors again indicated the presence of gaussian noise, but with a substantial increase in variability compared to the one-item condition. These results are consistent with a shared-resource model of working memory in which the variability of storage is determined by the fraction of total memory resources available per item (Wilken and Ma, 2004; Bays and Husain, 2008).

However, whereas performance in the low-load condition was accurately captured by gaussian variability alone, this provided only a partial description of the distribution of errors when memory load was increased. In this case, as in a previous analysis (Zhang & Luck, 2008), a better fit was obtained by a mixture model that also included a second, uniform distribution (spread equally across all possible responses). The correct interpretation of this additional, non-gaussian component is one of the key issues the present study sought to address.

4.1. Independence of memory stores for different visual features

The presence of the uniform error component under conditions of high memory load has been interpreted as supporting a “hybrid” model of working memory, in which recall performance is limited both by a decline in resolution with increasing memory load, and also by an upper limit on the number of objects that can be stored (Zhang and Luck, 2008, 2009). According to this account, when the number of items in the memory array exceeds the maximum capacity, only a subset of objects is selected for storage. Hence, if the probe corresponds to an object that was not selected, the subject will guess randomly in both feature dimensions. This model predicts that the occurrence of uniform responses will be fully correlated across feature dimensions: a uniform color response will always coincide with a uniform orientation response, and vice versa.

While estimates of the proposed (object) capacity limit vary, they have typically fallen in the range two to four: a large-scale study of 170 undergraduates using a change-detection task obtained a mean capacity of 2.9 items (reported in Vogel and Awh, 2008), while the estimate obtained from Zhang & Luck’s (2008) data was 2.3 items. In the present study we tested recall of 6 item arrays, comfortably exceeding these proposed limits, and implying that at least some objects should not have gained access to memory under the predictions of a hybrid model. Nonetheless, absolute errors in color and orientation were strongly independent (r² = 0.02), and a detailed analysis of the joint response distribution revealed negligible correlation (Φ² = 0.11) between uniform response components in recall of the color and orientation of the probed object.

These results are inconsistent with an upper limit on the number of integrated objects stored in working memory. The observed independence in errors across feature dimensions instead implies that the multiple visual features from different dimensions that make up an object may be maintained separately, in independent memory stores.

A similar conclusion was reached previously by Wheeler and Treisman (2002), based on analysis of a variant of the change detection task. These authors demonstrated that error rates were determined by the total number of features that needed to be remembered within each dimension (e.g. how many colors were in a memory array) rather than the number of separate objects those features were distributed between. While this outcome was contrary to a previous result obtained by Luck and Vogel (1997), it has been replicated in several subsequent studies (Xu, 2002; Olson and Jiang, 2002).

Instead of a single capacity-limited memory store maintaining integrated object representations, Wheeler and Treisman proposed parallel memory stores for each feature dimension, with independent capacities. In this account, the information required to combine the features into integrated objects (the ‘binding’ information) is maintained separately and independently from the features themselves. Such an account would also be consistent with a large range of findings that demonstrate that sensory representations, for example for different visual features, are associated with independent working memory representations (Pasternak and Greenlee, 2005).

While the integrated-object hypothesis predicts that an object’s features will always be remembered together, the independent-stores account allows for the possibility that one feature of an object could gain access to memory while another feature does not. However, the strong independence of storage between feature dimensions observed here is still unexpected. This is because the independent-stores hypothesis also assumes a fixed upper limit on memory capacity, although now reflecting a maximum number of features that can be stored per feature dimension rather than a maximum number of bound object representations (Wheeler and Treisman, 2002).

Assuming that selection of features for storage is governed by the allocation of visual attention to an object or location (Treisman and Gelade, 1980; Posner and Cohen, 1984; Duncan, 1984; Desimone and Duncan, 1995), this model still makes the prediction that storage of features belonging to the same object will be strongly correlated. The absence of such a correlation in the present analysis leads to one of two conclusions: either selection of a limited number of features for storage occurred independently in each feature dimension (inconsistent with most current models of attentional selection), or all the features in each array were stored in memory.

4.2. Misbinding of object features

In a previous study (Bays et al., 2009), we proposed an alternative explanation for the uniform component observed by Zhang & Luck (2008) that does not require a limit on the number of items stored. In these studies, subjects reported the color of one item from an array, indicated by a location cue. While superficially a simple test of memory for color, this task also requires memory for location: to respond accurately, subjects must not only remember the colors in the array, but also which color appeared where. Errors in recalling which color corresponds to the probed location will result in subjects mistakenly reporting the color of one of the other objects held in memory.

Consistent with this hypothesis, when we examined the distribution of responses relative to these non-target colors, we found that the responses captured by the uniform component in Zhang and Luck’s (2008) analysis were not in fact distributed equally across the response space, but instead predominantly clustered around colors belonging to other objects in the memory array. This was not apparent in previous analyses (Zhang and Luck, 2008, 2009) because errors were only considered in relation to the color of the probed item, and the other, non-target colors in the array were randomly distributed relative to this target color (see also Bays, 2010).

The frequency of these ‘misreporting’ errors in the present study was assessed by adding a third component to the mixture model, a gaussian component distributed equally between non-target color values. We confirmed that, as in the previous study (Bays et al., 2009), a substantial proportion of responses that Zhang and Luck’s model interpreted as random guesses were in fact instances of mistakenly reporting a feature value belonging to one of the other, non-probed objects held in memory.

Previously, we proposed that misreporting responses might be a consequence of variability either in memory for location or misbinding of object features during maintenance or recall from memory (Bays et al., 2009). Subjects were required to report the color of an object matching a particular probed location in the display: error in memory for locations could therefore result in a subject mistakenly reporting the color of one of the other, non-probed objects. Alternatively, both colors and locations in the array may have been stored accurately, but the information indicating which color belonged with which location may have become disrupted (Treisman and Schmidt, 1982; Treisman, 1998; Wolfe and Cave, 1999; Wheeler and Treisman, 2002; Robertson, 2003; Allen et al., 2006).

Because two feature dimensions other than location were tested, these hypotheses can be discriminated in the present study. The location-error hypothesis predicts that non-target responses will occur simultaneously in both dimensions: the subject will mistake which object’s location corresponds to the probe, and report both the color and orientation of an item at a different location in the memory array.

In contrast, we predicted that misbinding would occur independently for each feature, so one response might accurately reflect the target feature value whereas the other corresponds to a non-target; or color and orientation responses could correspond to the features of two different non-targets. The present results indicate that non-target responses occur independently in each feature dimension (r² < 0.01), consistent with the misbinding hypothesis.

While location errors are a predictable consequence of variability in storage of spatial information, it appears they did not contribute significantly to responses in the current study. This could be a consequence of the minimum separation maintained between objects in each memory array (6° of visual angle), which may have preserved accurate identification of the probed object even under considerable variability in recall of its location.

The observation of misbinding errors in the present study is consistent with previous results showing an increase in errors when recall is tested for feature conjunctions (e.g. color-shape pairs) as opposed to individual features (Wheeler and Treisman, 2002; Fougnie and Marois, 2009; Brown and Brockmole, 2010). A corollary of independent storage across feature dimensions is that a further mechanism is required to maintain the binding information that groups features into objects. A shared-resource account of working memory implies that the fidelity with which this binding information is maintained will decline monotonically with increasing memory load, as occurs for individual feature values. Bays et al. (2009) examined how the distribution of recall errors varied with both the number of items held in memory and the presentation duration of the memory array. The frequency of misreporting responses was not significantly affected by duration of presentation, but increased rapidly with memory load. Interpreted in light of the present results, this confirms that misbinding occurs with increasing frequency as total memory load increases.

A number of authors (Wolfe, 1999; Rensink, 2001; Wheeler and Treisman, 2002) have proposed that encoding and maintenance of binding information may be particularly dependent on the allocation of visual attention. In the present study, the demands of the task would have encouraged an equal distribution of attention between all items in the memory array; however, we have previously shown that drawing visual attention to one array item with an exogenous cue (a brief flash) results in an advantage for that item in terms of recall precision (Bays and Husain, 2008). This implies a role for attention in determining how limited memory resources are distributed within a visual scene. If, as the present results suggest, maintenance of binding information is similarly resource-limited, we would expect attentional manipulations to have similar effects on the frequency of misbinding.

4.3. Encoding limitations

While misreporting errors were not influenced by exposure duration in Bays et al. (2009), the proportion of trials attributed to the uniform response component dramatically declined as presentation duration increased, suggesting that these responses may reflect limitations on the speed with which visual information can be encoded rather than memory capacity. A previous estimate based on performance in a change detection task estimated the rate of encoding into memory at 50 ms per item (Vogel et al., 2006), or 300 ms for a 6 item array. However, detecting changes in color of the magnitude used in this task would have required only a coarse representation in memory. Our analysis of error distributions in the color report task demonstrated that encoding of a six item array was still in progress after 500 ms, and a small uniform component was still present even after 2 seconds (Bays et al., 2009).

Consistent with this latter result, in the present study a small proportion of responses (< 15%) were explained neither by gaussian recall variability nor by misreporting of non-target features. Critically, analysis of the joint distribution revealed that these responses occurred separately in each feature dimension, with less than 4% of trials corresponding to uniform responses for both color and orientation (i.e. UU in the full model described in Table 2). If the uniform response component is interpreted as reflecting instances where no information is stored about the target feature (as in Zhang & Luck, 2008), these results imply that at least one feature was stored for 5.8 of the 6 memory array items, and 5.1 out of 6 features were stored in each dimension. Accommodating these results within a ‘slot’ or ‘hybrid’ model of working memory would therefore require a substantial upward revision of the capacity limit compared to typical estimates (< 3 items, see § 4.1), in addition to whatever modification would allow independent allocation of this capacity in different feature dimensions.

Alternatively, the small proportion of responses attributed to the uniform component of the mixture model may reflect relatively minor sources of error not captured by the other (gaussian and misreporting) components of the model, e.g. incomplete encoding, lapses of attention, biases towards average or canonical feature values, or deviations from a strict gaussian distribution in recall variability.

Incomplete encoding may be one reason why a previous study investigating object integration came to different conclusions about independence of feature dimensions (Gajewski and Brockmole, 2006). These authors instructed subjects to explicitly report which conjunction of color and shape they had observed at a probed location, out of a canonical set of features. Trials on which both responses were correct or both incorrect were more frequent than expected under a simple assumption of uncorrelated error across feature dimensions. However, unlike in the present study, it is not possible using this partial-report methodology to distinguish errors caused by noisy recall of a stored feature from those caused by guessing or misbinding. Furthermore, the memory array was presented very briefly (< 200 ms) so these results may simply have reflected a failure to encode all the objects in the time available.

An important question for shared-resource models of working memory, not directly addressed by the present study, is to what extent visual features from different dimensions tap into the same memory resource. Previous studies based on change detection have typically observed little or no performance cost when additional features are added to a memory array if they belong to a different feature dimension (Luck and Vogel, 1997; Vogel et al., 2001; Wheeler and Treisman, 2002; Olson and Jiang, 2002), e.g. three colors and three shapes can be remembered as accurately as three colors alone (although there may be substantial errors in remembering which color belongs with which shape). These results have led to the conclusion that different feature dimensions recruit different storage capacities.

However, change detection performance may be relatively insensitive to changes in recall precision (Wilken and Ma, 2004; Bays and Husain, 2008). A recent study (Fougnie et al., 2010) has re-examined this question using a mixture model approach, as in the present study. These authors observed a significant, though modest (mean ~2°), increase in the standard deviation of the gaussian component of the model when a second set of features from a different dimension was added to the memory load. Additionally, a small (mean ~9%, equivalent to recall of 5.5 out of 6 items) uniform component was observed when features were distributed between different objects. These results suggest there may be some cost associated with maintaining multiple feature dimensions, overlooked by previous studies due to the use of change detection methodology. However, the very small size of these effects, despite doubling the total number of features in memory, does not appear consistent with a model in which features from different dimensions share a single resource.

4.4. Conclusions

The present results are difficult to reconcile with models of working memory in which only a subset of information in each array is selected for storage (Luck and Vogel, 1997; Cowan, 2001; Alvarez and Cavanagh, 2004; Awh et al., 2007; Zhang and Luck, 2008). However, our findings can be straightforwardly accommodated within resource-based accounts of visual working memory (Wilken and Ma, 2004; Bays and Husain, 2008).

Because a shared memory resource can be distributed equally between all the items in an array, this model does not predict that errors in different feature dimensions must be correlated. Instead, as the total memory load increases, the fidelity of storage declines. One consequence is that, as previously demonstrated, individual visual features (e.g. color, orientation, location) are recalled with increasing variability (Palmer, 1990; Wilken and Ma, 2004; Bays and Husain, 2008; Zhang and Luck, 2008).

The present results suggest that the binding information that groups features into objects also becomes degraded with increasing memory load, resulting in a systematic increase in the frequency with which independently-stored features are incorrectly combined.