Meta Analysis of Functional Neuroimaging Data via Bayesian Spatial Point Processes

Abstract

As the discipline of functional neuroimaging grows there is an increasing interest in meta analysis of brain imaging studies. A typical neuroimaging meta analysis collects peak activation coordinates (foci) from several studies and identifies areas of consistent activation. Most imaging meta analysis methods only produce null hypothesis inferences and do not provide an interpretable fitted model. To overcome these limitations, we propose a Bayesian spatial hierarchical model using a marked independent cluster process. We model the foci as offspring of a latent study center process, and the study centers are in turn offspring of a latent population center process. The posterior intensity function of the population center process provides inference on the location of population centers, as well as the inter-study variability of foci about the population centers. We illustrate our model with a meta analysis consisting of 437 studies from 164 publications, show how two subpopulations of studies can be compared and assess our model via sensitivity analyses and simulation studies. Supplemental materials are available online.

1 INTRODUCTION

Functional neuroimaging is a relatively young discipline within the neurosciences that has led to significant advances in our understanding of the human brain (Raichle 2003). The most widely used method, functional magnetic resonance imaging (fMRI), has grown from just 2 publications in 1993 to over 2100 in 2009 (based on a PubMed search for “fMRI” in the title or abstract). However, due to the relatively high cost of MRI scanner time a typical fMRI study consists of fewer than 20 subjects. Thus most studies suffer from inflated type II errors (i.e. low power) and poor reproducibility (Thirion et al. 2007). See, e.g., Jezzard et al. (2001) for an overview of fMRI analysis methods.

To overcome these limitations there has been a growing interest in meta analyses of functional neuroimaging studies. The goal of a functional neuroimaging meta analysis is similar to that of a single study: to identify regions of the brain that are activated by some thought, emotion or action. Given the statistic images from the studies, or the original data, an intensity based meta analysis (IBMA) can be conducted via either a fixed effects model or an hierarchical mixed effects model (Salimi-Khorshidi et al. 2009). However, published studies rarely provide the statistic images or original data (though we note that there is a growing interest among researchers in sharing full image data and statistic maps). Rather, they only provide the locations of local maxima in the statistic image in significant regions of activation; that is, (x, y, z) coordinates in a template space, typically the Montreal Neurological Institute (MNI) template (Mazziotta et al. 2001). We shall refer to these locations as foci, or a single focus. Thus, the data in most functional neuroimaging meta analyses consist of only the foci, allowing only a coordinate based meta analysis (CBMA). While a range of CBMA methods have been proposed, Fox et al. (1997), Nielsen and Hansen (2002), Turkeltaub et al. (2002), Wager et al. (2004), Kober et al. (2008), Eickhoff et al. (2009), Radua and Mataix-Cols (2009), we consider only the current versions of two commonly used methods, modified activation likelihood estimation (Eickhoff et al. 2009, modALE), and multilevel kernel density analysis (Kober et al. 2008, MKDA). See Salimi-Khorshidi et al. (2009) for a recent review of CBMA methods.

Both modALE and MKDA create a meta analysis statistic map based on the foci of each study, where the statistic value at each voxel (or volume element) summarizes the evidence for clustering at that location. Briefly, they start by creating an image for each focus, where the intensity in the image is based on the proximity of each voxel to the focus. These per-focus maps are then combined into a study map, and the study maps are in turn combined into a meta analysis map. The intensities in the meta analysis map are compared to maps generated by null hypothesis Monte Carlo simulation, creating P-values. The two methods differ in how they create the foci maps, and how they combine these into study and meta analysis maps. The modALE creates a focus map by placing a Gaussian density of size σ_modALE centered at the focus (normalized to integrate to unity over the map), where the intensity is interpreted as the probability that the focus arose from a given voxel. Assuming independence between foci, modALE combines focus maps with the probability addition rule, effectively computing the probability that one or more foci arose at a given voxel; this procedure is used both to combine focus maps into study maps, and to combine study maps into meta analysis maps. MKDA creates a focus map by placing a sphere of unit intensity and diameter d_MDKA centered at the focus. Multiple focus maps are combined into a study map with the logical OR operator, creating an indicator map showing where one or more foci are found within distance d_MDKA of a given voxel. Multiple study maps are combined into a meta analysis map with the sample mean, providing a map interpretable as the proportion of studies with one or more foci within distance d_MDKA. Monte Carlo resampling is roughly similar in each method, with foci locations randomly shuffled between studies, and meta analysis maps recreated for each realization; see the respective references for details. Traditional mass-univariate statistical inference is carried out, finding either voxel-wise or cluster-wise P-values, corrected by familywise-error methods or the false discovery rate.

While methods like modALE and MKDA are widely used, have freely available implementations, and, for MKDA in particular, have intuitive appeal, we find that they have several shortcomings. Both require spatial kernel parameters (σ_modALE and d_MDKA) that must be fixed; while Eickhoff et al. (2009) propose an algorithm for estimating σ_modALE based on training data, the value is not data adaptive and is assumed to be constant over the brain. Further, while neuroimaging users are familiar with the voxel-wise and cluster-wise inferences generated, these are based on a mass-univariate approach that lacks an explicit spatial model. Specifically, there is no way to infer on spatial dispersion of foci between studies, nor obtain spatial confidence regions on where foci arise in the population of all studies.

In this work we propose a hierarchical spatial point process model (Møller and Waagepetersen 2004; 2007, Illian et al. 2008) and estimate model parameters via the Bayesian paradigm. In particular, we adopt a spatial independent cluster process (van Lieshout and Baddeley 2002). The algorithm used to estimate the posterior distribution of model parameters stochastically searches for clusters of foci. Clusters appear in regions of (relatively) high foci density across studies and thus represent regions where a preponderance of studies reported activation. A cluster’s center represents the most likely location of the foci that define the cluster, and thus represents the “population center” of activation in the particular region of the brain in which the cluster is observed. Thus, a central goal of our modeling is to find clusters of foci and their associated population centers. Furthermore, since we adopt a Bayesian modeling approach, other quantitative information can be extracted from our model that cannot be deduced from current CBMA methods. Such as 1) the variability of the foci about the population center; 2) the variability of the population centers themselves; 3) the probability that there exists at least one population center in any region of interest (ROI) within the brain; 4) the probabilistic comparison of locations of cluster (population) centers of foci across different types of studies (e.g. studies of negative vs. positive emotion); 5) prediction of where a new study will most likely report foci (and hence the most likely locations where activation will be found); and 6) estimation of the proportion of foci that do not cluster with foci from other studies. Specific examples are given in Section 3.

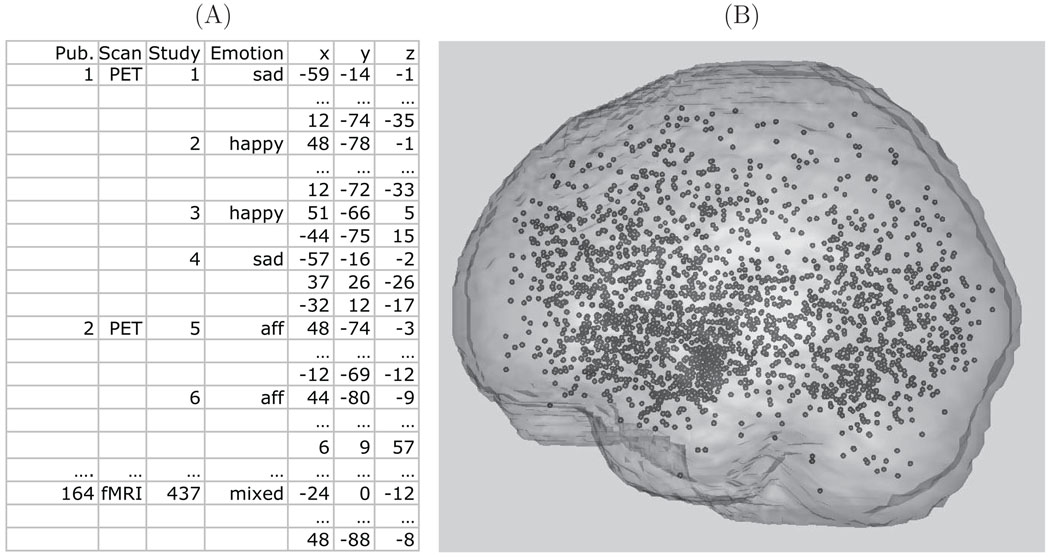
To give an impression of the neuroimaging meta analysis data, Figure 1 shows an extract of the foci data of the emotion meta analysis in both tabular and image form (see Section 3 for more details). Note that both PET and fMRI data are considered, reasonable since, after smoothing, group fMRI studies are similar to PET data in smoothness and interpretation of the signal (Feng et al. 2004). An important facet of the data is the issue of singly reported foci versus multiply reported foci. For a given activation area in the brain, some authors only report a single focus, while others report multiple foci, however this information is rarely provided in the literature. These differences are attributable to how different software packages report results, and simply author preference.

Figure 1.

Panel (A): A subset of the emotion meta analysis data set. Panel (B): All foci, (x,y,z) locations, from all studies plotted in the MNI brain template.

The remainder of this manuscript is organized as follows. In Section 2 we propose our Bayesian hierarchical marked spatial independent cluster process. In Section 3, we apply our model to a meta analysis data set of emotion studies and compare our results from modALE and MKDA. In Section 4 we briefly discuss results from sensitivity and simulation studies. We conclude the paper with a discussion of our model and ideas for future research. We provide supplementary material in a Web Appendix with a brief overview of the spatial point process models we use (see also, Møller and Waagepetersen (2004; 2007) for more details), algorithm details, pseudo code, and details from simulation studies and sensitivity analyses.

2 THE MODEL

2.1 Model Outline and Notation

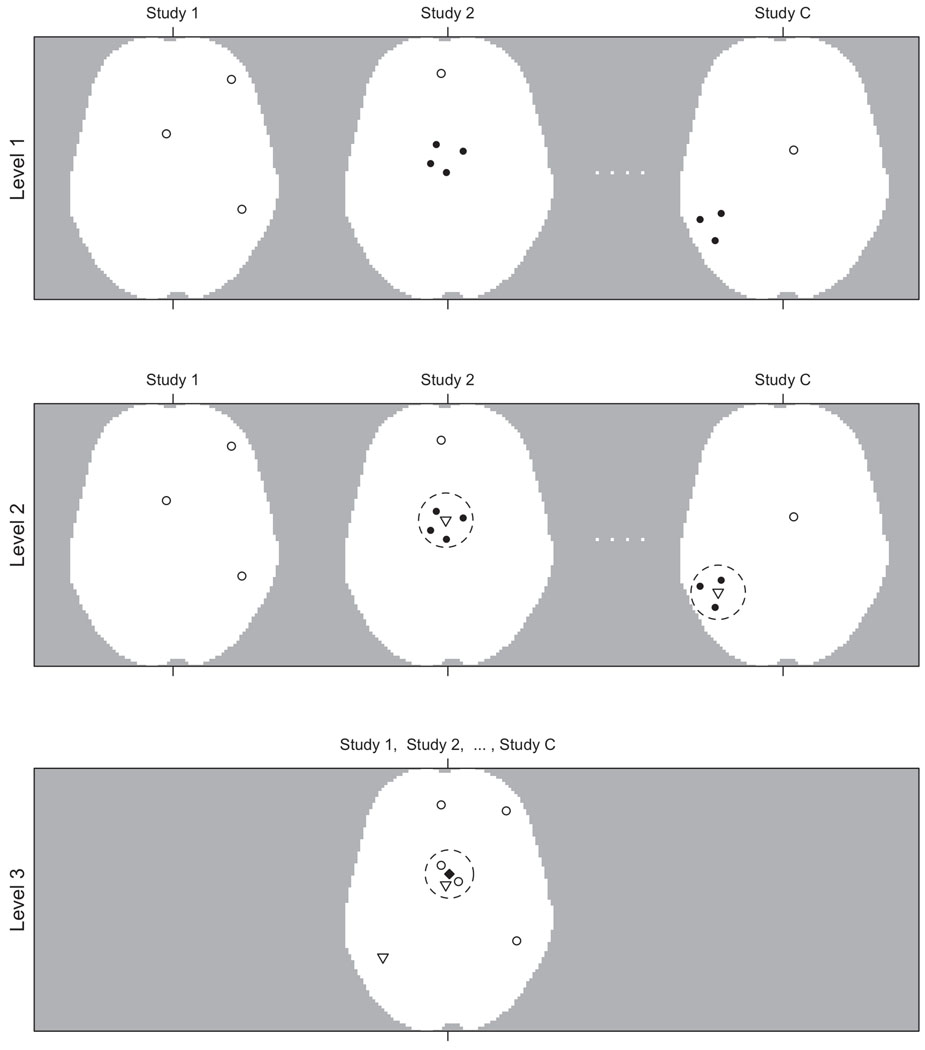
First we outline our model and then present details. The hierarchical model consists of three main levels and is illustrated in Figure 2. At the lowest level, level 1, are the foci (data). For study c, c = 1,…, C, the foci are a realization, x_c, of an independent cluster process, X_c, driven by random intensity function λ_1c and these processes are independent across studies. The process X_c is made up of two types of foci: singly reported foci (type 0) and multiply reported foci (type 1). For a generic point x ∈ x_c denote the missing type indicator, or mark, by δ_x. Let ${\mathbf{X}}_c^d=\{x\in {\mathbf{X}}_c:{\delta }_x=d\}$, d = 0, 1. Conditional on the realization, y_c, of a latent study activation center process, Y_c, we associate with each y ∈ y_c a process, ${\mathbf{X}}_{\mathit{\text{cy}}}^1$, of type 1 foci normally distributed about the study activation center y with covariance Ψ_y and that these processes are independent and their union ${\mathbf{X}}_c^1={\cup }_{y\in {\mathbf{y}}_c}{\mathbf{X}}_{\mathit{\text{cy}}}^1$ forms an independent cluster process driven by random intensity function ${\lambda }_{1c}^1$. Note that Ψ_y is a latent, random mark attached to y ∈ y_c. Also, conditional on the realization, z, of a latent population center process, Z, we associate with each z ∈ z a process, ${\mathbf{X}}_{\mathit{\text{cy}}}^0$, of type 0 foci normally distributed about the population center z with covariance Σ_z (a latent random mark attached to z) and that these processes are independent across studies. We also allow the possibility that type 0 foci do not cluster about any z ∈ z and model them as an independent homogeneous Cox process X_c∅ driven by homogeneous random intensity ε_1c. The union ${\mathbf{X}}_c^0={\cup }_{z\in \mathbf{z}}{\mathbf{X}}_{\mathit{\text{cz}}}^0\cup {\mathbf{X}}_{c\varnothing }$ forms an independent cluster process driven by random intensity function ${\lambda }_{1c}^0$. We note that ${\mathbf{X}}_c={\mathbf{X}}_c^0\cup {\mathbf{X}}_c^1$ and is driven by the random intensity ${\lambda }_{1c}={\lambda }_{1c}^0+{\lambda }_{1c}^1$.

Figure 2.

Hierarchical Model Illustration: Level 1: The foci from each study, x_c, are the observed data, here shown as open and filled circles. The open circles represent singly reported foci, ${\mathbf{X}}_c^0$ , and the solid circles represent multiply reported foci, ${\mathbf{X}}_c^1$. Whether foci are multiply or single reported is a latent property, δ_x. Level 2: Multiple reported foci cluster about latent study activation centers, y_c, (open triangles) with the dashed circles representing Ψ_y. Singly reported foci in level 1 are shown in level 2 as open circles as they, along with the study activation centers, may cluster together in level 3. Level 3: Activation centers, ${\mathbf{X}}_c^0$ from level 1 and y_c from level 2, may cluster about a population center, z (filled diamond) with the dashed circle representing Σ_z or may fail to cluster and are modeled as background scatter and outliers.

At level 2 we model the latent study activation center process for study c, Y_c, as an independent cluster process. Conditional on the (realized) population center process, z, we associate with each z a finite process, Y_cz, with realization y_cz of points normally distributed about the population center z with covariance Σ_z. We assume that the processes Y_cz given z are independent. We allow the possibility that some study activation centers do not cluster about any z ∈ z and model these as an independent homogeneous Cox process Y_c∅ driven by homogeneous random intensity ε_2c. and thus their union Y_c = ∪_z∈zY_cz ∪Y_c∅ forms an independent cluster process driven by the random intensity function λ_2c. (A study activation center is a substitute for the location of the global maximum in a given activation region, which is not reported. This is how we account for multiply reported foci.)

At the highest level, level 3, are the latent population centers. We assume, a priori, that the population centers are a realization, z, of a homogeneous Cox process Z driven by homogeneous random intensity β. Attached to each population center, z ∈ z, is a latent random mark, Σ_z. The points that cluster about the population centers are singly reported foci from level 1 and study activation centers from level 2. We refer to the singly reported foci and the study activation centers collectively as activation centers.

2.2 Model Details

We begin at level 1. We model X_c with an independent cluster process on the brain, ℬ, driven by λ_1c(x; ·). (Throughout, f(x; ·) represents a parametrized function f of x. The ‘·’ is shorthand for all parameters on which f depends.) The conditional likelihood of this process for study c is

$$\pi [{\mathbf{x}}_c|{\lambda }_{1c}(x;·)]\propto \text{exp}\left[-{\displaystyle {\int }_{ℬ}}{\lambda }_{1c}(s;·)\mathit{\text{ds}}\right]{\displaystyle \prod _{x\in {\mathbf{x}}_c}}{\lambda }_{1c}(x;·).$$ (1)

We note here that X_c | λ_1c(x; ·) is a Poisson point process and that the conditional likelihood defined in (1) is the density of X_c | λ_1c(x; ·) with respect to the measure of a unit-rate Poisson process and not to the standard Lesbesgue measure (Møller and Waagepetersen 2004; 2007). The unmarked process X_c is made up of the two types of foci—singly reported, type 0, and multiply reported, type 1. For a generic point x ∈ X_c assume, a priori, that π(δ_x = 0) = p = 1 − π(δ_x = 1). Given these marks the processes ${\mathbf{X}}_c^0\text{ and }{\mathbf{X}}_c^1$ are independent and are driven by intensity functions ${\lambda }_{1c}^0\text{ and }{\lambda }_{1c}^1$, respectively, with ${\lambda }_{1c}={\lambda }_{1c}^0+{\lambda }_{1c}^1$. Let (x, δ)_c = {(x, δ_x) : x ∈ x_c}. The joint density of the data and marks is

$$\pi [{(\mathbf{x},\mathit{\delta })}_c|{\lambda }_{1c}]={\displaystyle \prod _{d=0}^1}\pi [{\mathbf{x}}_c^d|{\lambda }_{1c}]{\displaystyle \prod _{x\in {\mathbf{x}}_c}}{p}^{1-{\delta }_x}{(1-p)}^{{\delta }_x}\propto \text{exp}\left[-{\displaystyle {\int }_{ℬ}}{\lambda }_{1c}^0(s;·)\mathit{\text{ds}}\right]{\displaystyle \prod _{x\in {\mathbf{x}}_c}}{[{\lambda }_{1c}^0(x;·)p]}^{1-{\delta }_x}\times \text{ exp }\left[-{\displaystyle {\int }_{ℬ}}{\lambda }_{1c}^1(s;·)\mathit{\text{ds}}\right]{\displaystyle \prod _{x\in {\mathbf{x}}_c}}{[{\lambda }_{1c}^1(x;·)(1-p)]}^{{\delta }_x}.$$ (2)

Now (2) and (1) are equivalent in the sense that if we marginalize over all possible δ_c = {δ_x : x ∈ x_c} in (2) we get (1). The intensity functions are

$${\lambda }_{1c}^0(x;·)={\epsilon }_{1c}+{\displaystyle \sum _{z\in \mathbf{z}}}{\theta }_{1c}{\varphi }_3(x;z,{\mathbf{\Sigma }}_Z)$$ (3)

$${\lambda }_{1c}^1(x;·)={\displaystyle \sum _{y\in {\mathbf{y}}_c}}{\eta }_c{\varphi }_3(x;y,{\mathbf{\Psi }}_y).$$ (4)

The function ϕ₃(a; b, A_b) represents the density of a 3-D normal random variable with mean b, covariance matrix A_b at location a. The parameter θ_1c multiplied by ∫_ℬ ϕ₃(x; z, Σ_z)dx is the expected number of type 0 foci that cluster about population center z ∈ z, while η_c ∫_ℬ ϕ₃(x; y, Ψ_y)dx is the expected number of type 1 foci that cluster about study activation center y ∈ y_c. The intensity function of the type 0 foci that do not cluster about a population center is ε_1c.

Level 2: Let (y, Ψ)_c = {(y, Ψ_y), y ∈ y_c}. The joint density of the conditional latent study activation center process and the independent marking distribution, for study c, is

$$\pi [{(\mathbf{y},\mathbf{\Psi })}_c|{\lambda }_{2c}]=\pi [{\mathbf{y}}_c|{\lambda }_{2c}(y;·)]{\displaystyle \prod _{y\in {\mathbf{y}}_c}}\pi [{\mathbf{\Psi }}_y]\propto \text{ exp }\left[-{\displaystyle {\int }_{ℬ}}{\lambda }_{2c}(s;·)\mathit{\text{ds}}\right]{\displaystyle \prod _{y\in {\mathbf{y}}_c}}{\lambda }_{2c}(y;·)\pi ({\mathbf{\Psi }}_y).$$

The intensity function of the unmarked process Y_c is given by

$${\lambda }_{2c}(y;·)={\epsilon }_{2c}+{\displaystyle \sum _{z\in \mathbf{z}}}{\theta }_{2c}{\varphi }_3(y;z,{\mathbf{\Sigma }}_z).$$ (5)

In (5), θ_2c ∫_ℬ ϕ₃(y; z, Σ_z)dy is the expected number of study activation centers that cluster about population center z ∈ z. The intensity function of the study activation centers that do not cluster about a population center is ε_2c.

By independence the joint density of the processes ${\mathbf{X}}_c^0$, Y_c, c = 1,…, C, is

$${\displaystyle \prod _{c=1}^C}\pi ({\mathbf{x}}_c^0|{\lambda }_{1c}^0)\mathrm{\pi }({\mathbf{y}}_c|{\lambda }_{2c})\propto \text{ exp }\left(-{\displaystyle {\int }_{ℬ}}\lambda (s;·)\mathit{\text{ds}}\right){\displaystyle \prod _{c=1}^C}{\displaystyle \prod _{x\in {\mathbf{x}}_c^0}}{\lambda }_{1c}^0(x;·){\displaystyle \prod _{y\in {\mathbf{y}}_c}}{\lambda }_{2c}(y;·)$$

where

$$\lambda (y;·)=\left({\displaystyle \sum _{c=1}^C}({\epsilon }_{1c}+{\epsilon }_{2c})\right)+\left({\displaystyle \sum _{c=1}^C}({\theta }_{1c}+{\theta }_{2c})\right){\displaystyle \sum _{z\in \mathbf{z}}}{\varphi }_3(y;z,{\mathbf{\Sigma }}_z)\equiv \epsilon +\theta {\displaystyle \sum _{z\in \mathbf{z}}}{\varphi }_3(y;z,{\mathbf{\Sigma }}_z).$$ (6)

Level 3: At the final level, the latent, unmarked, population center process Z is modeled as a homogeneous Cox process driven by β defined on ℬ. Let |ℬ| denote the volume of ℬ. Let (z, Σ) = {(z, Σ_z), z ∈ z}. The conditional joint density of the population center process and the independent marking distribution is

$$\pi [(\mathbf{z},\mathbf{\Sigma })|\beta ,\mathit{T}]=\pi (\mathbf{z}|\beta ){\displaystyle \prod _{z\in \mathbf{z}}}\pi ({\mathbf{\Sigma }}_z|\mathit{T})\propto \text{exp}(-\beta |ℬ|){\displaystyle \prod _{z\in \mathbf{z}}}\beta \pi ({\mathbf{\Sigma }}_z|\mathit{T})$$

where T is a hyperprior for the distribution of Σ_z.

We now specify prior distributions and begin with level 3 priors and work backwards. For z ∈ Z, Σ_z ~ W⁻¹(T, ν); that is, Σ_z has an inverse Wishart distribution with scale matrix T and ν degrees of freedom. The Σ_z are independent of one another and are independent of the process Z. The inverse of the hyper-parameter T is assigned a Wishart distribution: T⁻¹ ~ W(T₀, ν₀) where T₀ and ν₀ are fixed. The random intensity, β, of Z is assigned, a priori, a gamma distribution: β ~ G(a_β, b_β) with a_β and b_β fixed (values of the fixed hyper-parameters should be problem specific and are discussed below in Section 3). Now at level 2, the marks, Ψ_y, of the study activation center processes are given an inverse Wishart distribution: Ψ_y ~ W⁻¹(S, d). The Ψ_y are independent of one another and independent of the processes Y_c, c = 1,…, C. Both ε and θ defined in (6) are assumed known. In the simulation of the posterior distribution, it is not necessary to estimate the parameters ε_2c and θ_2c, c = 1,…, C and estimates of ε_1c and θ_1c are only needed to impute the missing type indicator (whether a focus is a singly reported focus or a multiply reported focus). We assume the probability that a type 0 focus in study c clusters about a population center z ∈ z and the probability that a study activation center in study c clusters about the same population center are equal. We feel this assumption is quite reasonable as it implies that the study activation centers and the singly reported foci are treated equivalently in level 2 (see the intensity functions in (3), (5) and (6)). Furthermore, we assume that these probabilities are also equal across studies. This assumption also reduces the number of parameters that need to be estimated. In the Web Appendix we show that this probability equivalence assumption implies θ_1c/ε_1c = θ_2c/ε_2c = θ/ε, which, in turn, implies that ε_1c/ε = θ_1c/θ (≡ ρ_1c) and ε_2c/ε = θ_2c/θ (≡ ρ_2c). Thus, ${\displaystyle {\sum }_{c=1}^C({\rho }_{1c}+{\rho }_{2c})=1}$. Define ρ = (ρ₁₁,…, ρ_1C, ρ₂₁,…, ρ_2C). A priori, we assign ρ a Dirichlet distribution: ρ ~ D(α₁,…, α₁, α₂,…, α₂). The prior distribution on ρ induces a prior distribution on the ε_1c, θ_1c, ε_2c and the θ_2c. The last level 1 parameters are the η_c. A priori, we assume that η_c ~ G(a_η, b_η) and are independent of one another.

The posterior distribution of parameters given data is complicated and has no closed form solution. Thus we resort to spatial birth and death processes nested within a Markov chain Monte Carlo simulation algorithm to sample from the posterior distribution. Details of the algorithm and pseudo code are provided in the Web Appendix.

3 APPLICATION

In this section, we apply our model to a neuroimaging meta analysis of emotion first reported in Kober et al. (2008). The meta analysis data set consists of 164 publications of various aspects of emotion. A total of 7 emotions were studied across the different experiments: sad, happy, anger, fear, disgust, surprise and affective. Our goal is to find consistent regions of activation across the different studies and types of emotions. Many papers report results from different statistical comparisons called “contrasts”, which we are calling studies. Following the convention of existing neuroimaging meta analyses, we treat each of these studies as independent. There are a total of 437 studies reporting a total of 2475 foci. Table 1 lists some features and summary statistics of this data set. Consult Kober et al. (2008) for further details.

Table 1.

Data Summaries.

Descriptive statistics
	Min.	Median	Mean	Max.
Studies per publication	1	2	2.67	12
Foci per study	1	4	5.67	47
Subjects per publication	4	11	12.23	40

Frequency of modality and inference method
	Fixed	Random	Total
fMRI	32	74	106
PET	48	10	58
Total	80	84	164

Freqency of study emotion type
Emotions	affective	anger	disgust	fear	happy	mixed	sad	surprise	Total
Number	175	26	44	68	36	41	45	2	437

Frequency of corrected and uncorrected thresholds used (intermediate P thresholds rounded up)
P threshold	0.00001	0.0001	0.001	0.005	0.01	0.05	0.1	Missing	Total
Corrected	0	1	12	5	9	89	1	0	117
Uncorrected	1	15	152	48	47	42	0	0	305
Missing	0	0	3	0	0	1	0	11	15
Total	1	16	167	53	56	132	1	11	437

3.1 Prior Parameters

Several parameters are assigned vague or non-informative prior distributions. We assign a vague prior to the η_c: η_c ~ G(0.001, 0.001), c = 1,…, C, while ρ is assigned the non-informative Jeffrey’s prior: ρ ~ D(0.5,…, 0.5, 0.5,…, .5). All other prior and hyperprior parameters are obtained by elicitation from an expert in the meta analysis of neuroimaging data, and neuropsychologist, Tor Wager. We asked Tor, based on his experience, 5 questions: i) How many population centers do you expect to find in this meta analysis? ii) Given that some studies report multiply reported peaks per activation regions and other do not, on average how many multiply reported peaks per study do you expect? or how many activation centers per study do you expect? iii) What percentage of the activation centers do you expect to cluster about population centers? iv) What is the average spread of multiply reported foci about study activation centers? v) What is the average spread of activation centers about population centers? We note that since we need to match expected numbers, or percentages, given in these responses to the actual data, some prior settings have an empirical Bayesian flavor. Given his responses, we derive the remaining prior distributions as follows.

i) The number of population centers, or clusters, for this particular meta analysis is in the range from 20 to 40. Thus, a priori, we set the expected number of population centers, E [N_Z(ℬ)], to 30. We want to be vague about the range of the number of population centers and thus set β|ℬ| ~ G(0.03, 0.001). Therefore, since [N_Z(ℬ) | β|ℬ|] has a Poisson distribution with mean β|ℬ|, N_Z(ℬ) is, a priori, a negative binomial random variable with mean 30 and variance 30, 030. ii) The mean number of foci reported per study is 5.67 (Table 1). We expect that there will be on average, 5 singly reported foci and study activation centers (collectively, activation centers) per study (for a total of 2185) and that iii) the majority of these will cluster about population centers—80% (for a total of 1748). Let $\mathbf{A}={\cup }_{c=1}^C{\cup }_{z\in \mathbf{z}}({\mathbf{X}}_{\mathit{\text{cz}}}^0\cup {\mathbf{Y}}_{\mathit{\text{cz}}})$, then E(N_A (ℬ)) ≡ θ ∑_z∈z Φ₃(·; z, Σ_z) = θ∑_z∈z ∫_ℬ ϕ₃(ξ; z, Σ_z)dξ is the expected number of activation centers that cluster about population centers; i.e., conditional on θ, z and the marks Σ_z, z ∈ z, N_A(ℬ) is a Poisson random variable with mean θ ∑_z∈z Φ₃(·; z, Σ_z). Equating the latent number of population centers to the mean number of population centers, n_z(ℬ) = E(N_Z(ℬ)) = 30, and assuming Φ₃(·; z, Σ_z) ≈ 1, ∀_z ∈ z, we have E(N_A(ℬ)) ≈ 30θ = 1748 which implies that θ = 1748/30. Also, ε|ℬ| is the expected number of activation centers that do not cluster about population centers; i.e. ${\mathbf{A}}_{\varnothing }\equiv {\cup }_{c=1}^C({\mathbf{X}}_{c\varnothing }\cup {\mathbf{Y}}_{c\varnothing })$ ~ Poisson (ℬ, ε) so that N_A∅ (ℬ) is a Poisson random variable with mean ε|ℬ| = 437. Thus, ε = 437/|B|. iv) The covariances, or marks, Ψ_y ~ W⁻¹(S, 5) where S is the 3 × 3 identity matrix, I. This gives, a priori, E(Ψ_y) = I. v) The covariances Σ_z ~ W⁻¹(T, 5) with T⁻¹ ~ W(T₀, 5) where T₀ = 0.8I which results in, a priori, E(Σ_z) = 4I. We note here that if A ~ W⁻¹(B, d) and A has dimension m × m, that the variance and covariances of the elements of A do not exist when d ≤ m + 3 (Press 1982). Thus, the prior distributions of Ψ_y and Σ_z are heavy-tailed.

A sensitivity analysis of the posterior distribution to the informative prior information in our model (numbers 1 through 5 above; i.e. NZ(ℬ), ε, θ, Ψ_y and Σ_z and hyperprior T) is provided in the Web Appendix, Section D.1. We briefly discuss our findings in Section 4, below. Next, we present results from our modeling of the emotion meta analysis dataset.

3.2 Analysis of the Emotion Meta Analysis Dataset

We approximate the posterior distribution by running the algorithm for 120,000 iterations, discarding the first 20, 000 as a burn-in. We assess convergence of the chain by multiple runs of the algorithm from diverse initial conditions and visually inspect the difference in various posterior mean intensity functions and find only minor differences. Furthermore, we use the method of Gelman and Rubin (1992) to assess convergence on the number of population centers. The mean of the potential scale reduction factor is 1.0 with an upper 0.975 quantile of 1.01. Thus, the number of iterations and burn-in appears to be sufficient and that the chain has converged to stationarity.

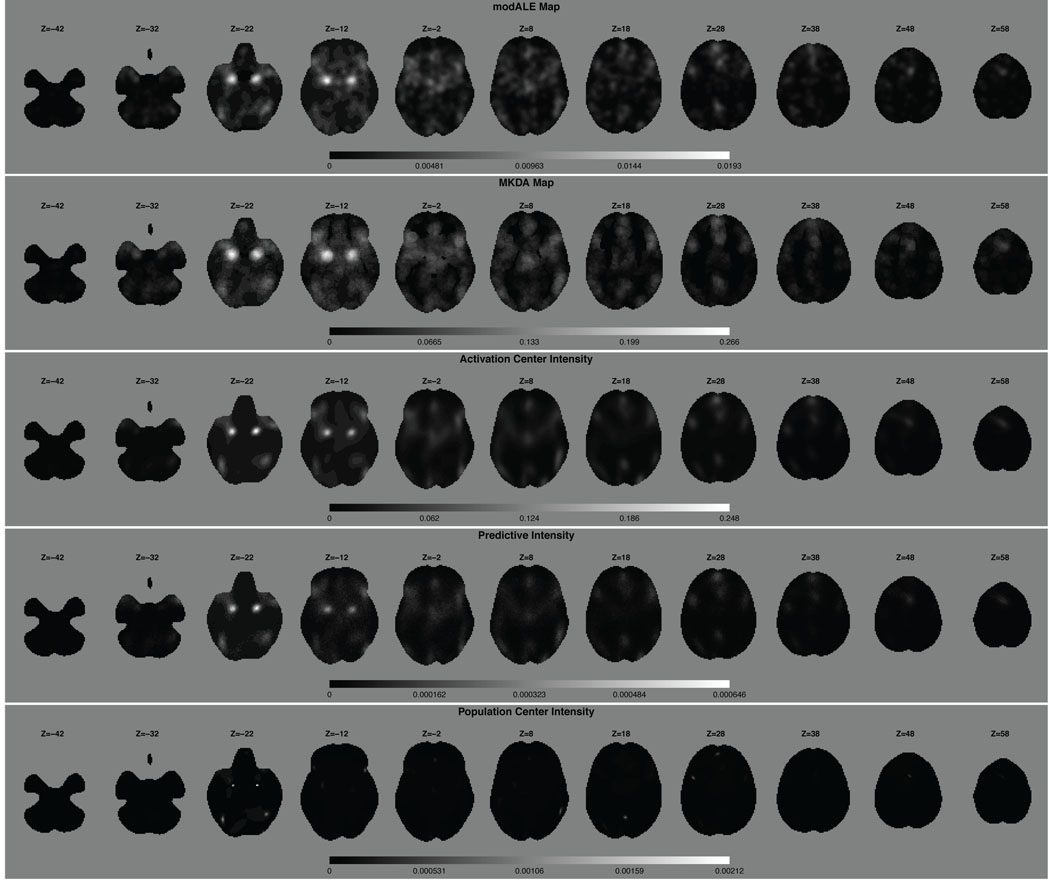
First we compare our results with those from a modALE (Eickhoff et al. 2009) and a MKDA (Wager et al. 2007, Kober et al. 2008) analysis of the same data. Since we do not have an auxiliary data set that can be used to estimate the kernel size used in modALE, we use the default kernel size provided in the software. In fact, the software does not allow the user to define the kernel size. To the best of our knowledge, the kernel size defined in the software is that derived in Eickhoff et al. (2009) and is based on a fist clenching experiment which may not be appropriate for our data. Figure 3 shows a visual, qualitative comparison of the activation center and population center intensity functions and the modALE and MKDA maps for 11 equally spaced, 2 mm axial slices, throughout the brain. Although qualitatively similar, there are visible differences. For instance, in the third column of Figure 3 the activation center intensity from our model appears to be more concentrated than either the modALE or MKDA map. We also note that we have separated out two intensity functions: the activation center intensity function and the population center intensity function.

Figure 3.

Qualitative comparison of the modALE map, MKDA map, the posterior expected activation center intensity function, the posterior predictive intensity for a new study and the posterior expected population center intensity function. We stress here that the gray scale values of the modALE, MKDA and intensity maps are not comparable as their interpretations are not comparable. Qualitatively, the first three rows are similar. The population intensities, however, are much more focused than the activation center intensities, especially in slices Z = −22, 18, 28. This reflects the larger variability of activation centers about the population center than the variability of the population centers, themselves.

We can identify several regions of high intensity, with the highest intensities centered in slice Z = −22mm. These bilateral regions are the amygdalae and the high activation center intensity indicates a preponderance of studies clustering in these regions and that the clustering is tight. Both modALE and MKDA also identify these regions with large statistic values. We find very high, very concentrated intensity in each amygdala in the population center intensity function as well. (The population center intensity function is created by smoothing the posterior histogram of population centers with a Bayesian nonparametric density estimation model. In particular, a mixture of Dirichlet process priors model (Escobar and West 1995).) This indicates that the variability of the population centers is much smaller than the variability of the activation centers about these population centers. Quantitatively, however, it is difficult to compare results between our model and CBMA methods, as they have very different interpretations. At a particular voxel, the value in the modALE map is the probability that at least one focus occurs at said voxel across studies. The value in the MKDA map has the interpretation of a (weighted) proportion of studies that report a focus within a prespecified distance to that voxel. Whereas our posterior intensity functions are interpreted as just that: intensities of activation centers or population centers given the data. Given a voxel, of say volume υ, the integrated intensity over the volume of the voxel (or over any ROI) is interpreted as the expected number of activation centers (or population centers, as the case may be) in that voxel or ROI. Note that if the intensity function is normalized by its integral over the brain, then the normalized intensity function can be interpreted as a spatial density function. The integral of the spatial density function over any ROI is the probability of an activation (population) center occurring in that ROI. There is a distinct difference between this interpretation and that of modALE. In modALE, the probabilities are per voxel so that the probability measure integrates to one at each voxel. Thus, modALE is a massive univariate approach, as is MKDA. Whereas, the spatial density function integrates to one over the entire brain and not at each voxel.

Computationally, modALE takes around 20 minutes, MKDA takes around 2 hours (1000 permutations) and our model takes approximately 20 hours to sample from the posterior (120K iterations), all on a 2.4 GHz iMAC.

Since we use a Bayesian hierarchical model, extra information can be extracted than from current CBMA methods. The information that can be extracted is enumerated in the introduction and we now provide examples.

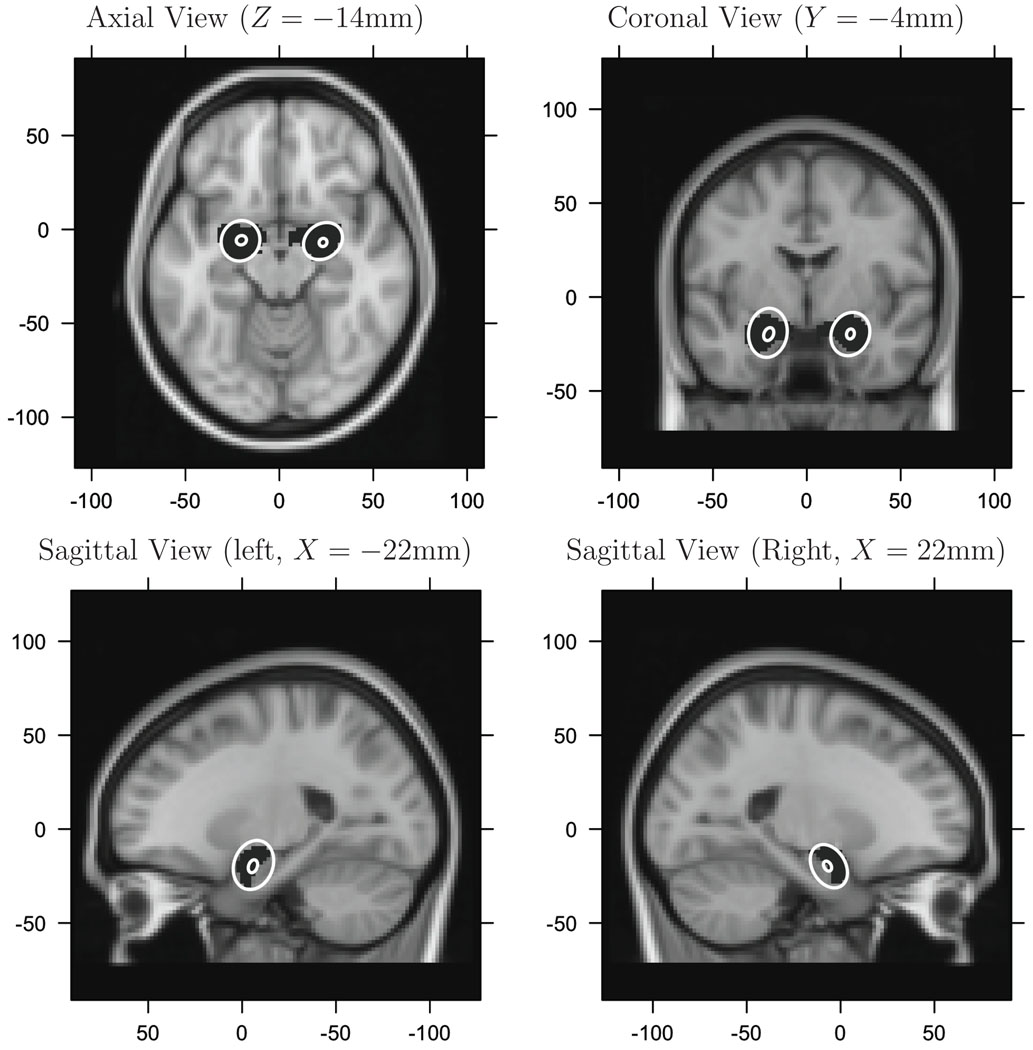
1) and 2). Given any prespecified ROI, our model provides location and variability of location of activation centers about population centers and about the variability of population centers, themselves, within the ROI. We use an amygdala ROI, as over 50 years of research has implicated its role in emotion (see Phelps and LeDoux (2005) for a review). For example, integrating over the z-dimension, the posterior 95% credible ellipses of both population centers and activation centers within the amygdalae are provided in Figure 4. These credible ellipses represent the uncertainty in the location of the population centers that are found in the amygdalae (the gray ellipses) and the variability of activation centers that cluster about the population centers that are found in the these structures (the larger, white ellipses). Note that these latter ellipses are conditional on the event that a single population center occurs in the respective amygdala. A single population center occurred in 69% of the iterations in the left amygdala and 90% in the right.

Figure 4.

The 95% marginal credible ellipses. Large, ellipses are the marginal ellipses of the activation centers. Small, ellipses are the marginal ellipses of the population centers within each amygdala. The black regions (masks), covered by the white ellipses, are the amygdalae.

3) At lease one population center occurred in over 99.9% of the iterations for both amygdalae. In the Web Appendix, Table 4, we provide the probability that at least one population center occurs in various ROIs.

The volumes of the ellipsoids are given in Table 2 and quantify the inter-study variability of activation centers about the population centers and the variability in the locations of the population centers. The location of the maximum statistic value from modALE and MKDA, conditional on being located in each amygdala, are also provided in Table 2 for comparison. Although each activation center ellipsoid is about 3 times the volume of the respective amygdala, any activation center within one of these ellipsoids, is deemed close enough to be associated with the amygdala, irrespective of our model. That is, a neuropsychologist would consider them to be “associated with, or part of, the amygdalae”.

Table 2.

95% credible ellipsoid volumes for population and activation centers.

	Center	Location (mm)			95% Credible Ellipsoid
		x	y	z	Volume (mm3)
Lt. amygdala	Pop.	−20.3	−5.8	−19.8	138.3
	Act.	−20.7	−6.1	−19.1	12473.8
	modALE	−22.0	−6.0	−16.0	NA
	MKDA	−24.0	−4.0	−18.0	NA
Rt. amygdala	Pop.	23.2	−6.9	−19.7	72.8
	Act.	23.2	−6.2	−19.7	8558.8
	modALE	20.0	−4.0	−18.0	NA
	MKDA	22.0	−4.0	−18.0	NA

Note: Volume of a human brain is about 1,450,000 mm³ volume of L./R. amygdala is 3,120/3,192 mm³

The volume of the 95% credible ellipsoids of population centers are roughly 100 times smaller than the corresponding activation center ellipsoids. This demonstrates a key strength of our Bayesian hierarchical model: the ability to quantify the precision of the population locations and to quantify the precision of the activation centers as they cluster about population centers. We note here that there is an identifiability issue with the intensity function defined in (6): it is invariant to permutations of the indices in the summations, and thus the intensity is invariant as well. However, by conditioning on the event that exactly one population center occurs in, say, the right amygdala, we conditionally removed the lack of identifiability.

To the best of our knowledge, our model is the first model of neuroimaging meta analysis data that quantifies these precisions and that separates the precision of the activation centers about population centers and the precision of the location of population centers. CBMA methods, such as ALE and MKDA, provide point estimation of activation regions and do not quantify the associated estimation error. (A bootstrap estimate of standard errors, of the modALE or MKDA map, is conceivable, however the computational cost would be large—for a bootstrap sample of size n, roughly n times longer than a single run—and would not allow separation of sources of variability.)

In Figure 3 we also provide the posterior predictive intensity. This function provides information about where a new, future, study of emotion would most likely report activation centers. For example, the expected number of activation centers in a new study is 5.62. Integrating the predictive intensity over each amygdala results in an expected number of activation centers of 0.090 and 0.092 in the right, left amygdala, respectively.

4) To demonstrate how our model can be used to compare subpopulations of studies, we split our meta analysis into studies based on positive emotions and those based on negative emotions. In particular, there is interest in whether the brain regions that subserve positive and negative emotions are the same. Specifically, is the location of activation the same for both types of emotional stimuli within an amygdala? To address this question we apply our model to the positive and negative emotions subsets. Convergence was assessed visually and by computing the multivariate potential scale reduction factor for both the location of the left (upper bound of reduction factor = 1.02) and right (upper bound = 1.01) amygdala population centers.

There are 522 foci from 95 studies of positive emotions and 1663 foci from 281 studies of negative emotions. For each amygdala, let Z_p and Z_n denote the positive and negative emotions population centers, respectively, located in the amygdala, conditional on the event that there is exactly one population center in the amgydala. The estimated posterior distribution of Z_p and Z_n can be approximated by normal distributions: Z_p ~ N(μ_p, Σ_p) and Z_n ~ N(μ_n, Σ_n), where μ_p and μ_n are the mean locations of the population centers and Σ_p and Σ_n are the covariance matrices, from which we can compute the associated 95% credible ellipsoids (see Figure 5). With the assumption that positive and negative emotions studies are independent, the difference in locations is Z_d = Z_p − Z_n ~ N(μ_p − μ_n, Σ_p + Σ_n). Thus we can compute the 95% credible ellipsoid of Z_d for each amygdala. In both the left and right amygdala, the 95% credible ellipsoid excludes the origin—indicating a substantial difference in location. We also estimate the posterior distribution of the Euclidean distance between Z_p and Z_n, i.e. $E_{\mathit{\text{pn}}}=\sqrt{(Z_p-Z_n)\prime (Z_p-Z_n)}$, from which we can estimate the probability Pr(E_pn > d) for different d’s. For example, in the right amygdala Pr(E_pn > 2mm) > 0.999 and Pr(E_pn > 4mm) = 0.932. For the left amygdala Pr(E_pn > 2mm) = 0.983 and Pr(E_pn > 4mm) = 0.704. This analysis suggests there is strong evidence of a difference in location between the positive and negative emotions population centers located in the right amygdala, and modest evidence for a difference in the left amygdala. To our knowledge, our model is the first one to be able to quantify and draw inferences on differences in population locations between studies.

Figure 5.

The 95% marginal credible ellipses for population centers from positive (dashed ellipses) and negative (solid ellipses) emotion studies. The “x” and the circle represent the centers of the respective ellipses.

5) The posterior predictive intensity of a new study is shown in the fourth row of Figure 3. It is qualitatively similar to the posterior activation center intensity, however some minor differences can be seen.

6) Lastly, the posterior mean of the proportion of activation centers that do not cluster about any population center is 0.22 with a standard deviation of 0.01.

3.3 Model Assessment

We conduct a posterior predictive model assessment using the L function which is a summary statistic for second order properties of a point process (Baddeley et al. 2000, Illian et al. 2009). The L function can indicate aggregation or clustering for a point process. For our model, L(r; ·) = {3K(r; ·)/4π}^⅓, where

$$K(r;{\mathbf{X}}_c,·)=\frac{1}{|ℬ|}{\displaystyle \sum _{x_{1,}{x}_2\in {\mathbf{X}}_c}}\frac{\mathbf{1}[\Vert x_1-x_2\Vert \le r]}{{\lambda }_{1c}(x_1;·){\lambda }_{1c}(x_2;·)}$$

Consider the posterior predictive distribution of the differences ${\Delta }_c(r)=L(r;{\mathbf{X}}_c,·)-L(r;{\mathbf{X}}_c^{*},·)$, where ${\mathbf{X}}_c^{*}$ is a simulated sample from the posterior predictive distribution. As discussed by Illian et al (2009), if zero is an extreme value in the posterior predictive distribution of Δ_c(r) for a range of distances r, then we may question the fit of our model. We estimate the upper and lower boundaries of the 95% posterior intervals for the posterior predictive distributions of Δ_c(r), r > 0, for the 437 studies (c = 1,…, 437). Over ninety percent (395/437) of the studies have 95% posterior intervals of Δ_c(r) that cover zero for r > 0. This implies that the posterior predictive intervals for most studies provide no evidence against our model.

4 SIMULATION STUDIES AND SENSITIVITY ANALYSIS

We briefly discuss our findings of a sensitivity analysis and a study of robustness to model misspecification. Full details are available in the Web Appendix, Section D.

To assess sensitivity to prior specification, we vary several prior and hyperprior values. We investigate nine different prior scenarios. Our conclusion is that the number of population centers is somewhat sensitive to prior specification. This is not surprising as the population centers are latent and partially removed from the data by the second level of our hierarchy. However, our main focus is on the posterior intensity functions, the location and variability of the population centers, and the location and variability of the activation centers about population centers. Specifically, examining the amygdala ROIs, we find that the intensity functions and locations are quite stable, as are the volumes of the 95% credible ellipsoids of the activation centers. However, the volumes of the 95% credible ellipsoids of the (amygdalae) population centers are somewhat sensitive to the prior settings (see Table 3 in the Web Appendix).

To assess robustness to model misspecification we simulate data from three different models. The first two data sets are simulated according to our model hierarchy. The first data set is simulated directly from our model. The second data set is simulated from a Matérn cluster process (Møller and Waagepetersen 2004). Our model is resilient to this model misspecification. The third data set is not simulated according to any hierarchy. Foci are drawn directly from a specific intensity function (Section D.2, simulation C, in the Web Appendix). Here we find that the true activation center process is well approximated by our model. However, in this case, some care is needed in the interpretation of “population centers”.

5 DISCUSSION

In this paper, we present a Bayesian hierarchical spatial cluster modeling approach that is novel for neuroimaging meta analysis. Our model provides extra information and results that previously proposed methods cannot; and, as opposed to all current CBMA methods, our model is not massively univariate. With our modeling approach, we can focus attention on specific regions of interest and provide point estimates of the population centers as well estimates of the precision of the population centers and the precision of the activation centers that cluster about each population center. By introducing latent study centers, our model minimizes the potential bias induced by multiple foci per activation region. Our model also accounts for scatter noise (foci that don’t cluster) by modeling them as a homogeneous process. Furthermore, it is a trivial matter to include study weights into our model that account for differences in publication/study fidelity by weighting the variances of the cluster processes.

One potential drawback of our modeling approach is that practitioners may not be used to thinking in terms of spatial models and their related intensity functions. Rather, they are used to the massive univariate approach (voxel by voxel assessment) of current CBMA methods. Nevertheless, our modeling approach does offer the practitioner important information that other methods, to date, cannot provide (see the list in the Introduction).

Future directions within our modeling approach is to incorporate multiple sources of information into study weights such as sample size, nominal significance level, and whether or not the study adjusted for multiple comparisons, to name a few. These various sources could be combined into a single score via principal components analysis and the score discretized by ranking and thresholding on the n-tiles of the first principal component. Another direction would be to account for publication bias in our model. One potential avenue to pursue is to consider the activation centers as a thinning of a marked point process and model the retention probability as a function of, say, the probability of a negative study (that was not published).