Abstract
Computational maps are of central importance to a neuronal representation of the outside world. In a map, neighboring neurons respond to similar sensory features. A well studied example is the computational map of interaural time differences (ITDs), which is essential to sound localization in a variety of species and allows resolution of ITDs of the order of 10 μs. Nevertheless, it is unclear how such an orderly representation of temporal features arises. We address this problem by modeling the ontogenetic development of an ITD map in the laminar nucleus of the barn owl. We show how the owl's ITD map can emerge from a combined action of homosynaptic spike-based Hebbian learning and its propagation along the presynaptic axon. In spike-based Hebbian learning, synaptic strengths are modified according to the timing of pre- and postsynaptic action potentials. In unspecific axonal learning, a synapse's modification gives rise to a factor that propagates along the presynaptic axon and affects the properties of synapses at neighboring neurons. Our results indicate that both Hebbian learning and its presynaptic propagation are necessary for map formation in the laminar nucleus, but the latter can be orders of magnitude weaker than the former. We argue that the algorithm is important for the formation of computational maps, when, in particular, time plays a key role.
Computational maps (1, 2) transform information about the outside world into topographic neuronal representations. They are a key concept in information processing by the nervous system. Many results point to an ontogenetic development that is critically driven by sensory experience (3). Here we focus on the development of maps of exclusively temporal features (4–10), where the time course of stimuli carries relevant information, in contrast to previous studies that have shown the emergence of orderly representations of spatial or spatiotemporal features. A prominent example is the map of interaural time differences (ITDs) that is used for sound localization (11–13).
Sound localization is important to the survival of many animal species—in particular, to those that hunt in the dark. ITDs often are used as a spatial cue. Because the range of available ITDs depends on the size of the head, ITDs are normally well below 1 ms; they can be measured with a precision of up to a few microseconds. In this article, we address the question of how temporal information from both ears can be transmitted to a site of comparison where neurons are tuned to ITDs, and how those ITD-tuned neurons can be organized in a map. A first step toward a solution was made by Jeffress (1) as early as 1948. He proposed a scheme (Fig. 1A) that combines axonal delay lines from both ears and neuronal coincidence detectors to convert ITDs into a place code where a spatial pattern of neuronal activity codes the ITD. His scheme has had a profound impact on understanding sound localization. Neurons tuned to ITDs and maps resembling the circuit envisioned by Jeffress have been observed in many animals (10–18). However, the mechanism that underlies fine tuning of delays during ontogenetic development has remained unresolved.
Figure 1.
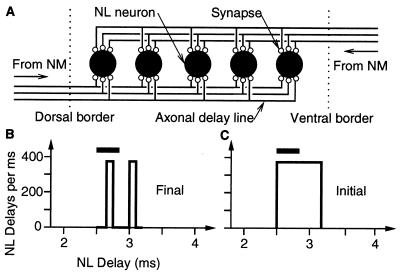
Schematic diagram of the architecture of the nucleus laminaris (NL) as a realization of the Jeffress idea (1, 11) that ITD is mapped along the dorsoventral direction. (A) Part of a single frequency layer. Axonal arbors (full lines) from the contralateral nucleus magnocellularis (NM) enter NL through its ventral border (arrow and dotted line) whereas arbors from the ipsilateral NM enter dorsally. They contact (small open circles) all laminar neurons (large filled circles). Synaptic weights are assumed to be modifiable. We have simulated 30 laminar neurons (5 are shown) and 500 magnocellular afferents, 250 from each side (3 are shown). (B) In adult owls, we propose that, as a result of learning, NL delays (from ear to border of NL) roughly differ by multiples of the best frequency T−1 in the considered NL layer [here T = (3 kHz)−1, horizontal bar]; cf. figure 9 in ref. 13. To this end, we assume that axonal arbors whose synaptic weights vanish are eliminated during development. (C) In young owls, the distribution of NL delays is assumed to be broad with respect to T.
In the barn owl (Tyto alba), an auditory specialist, the first binaural interaction occurs in the third-order nucleus laminaris (NL), where the responses of neurons are tuned to ITDs (10–13). Laminar neurons receive bilateral input from afferents originating from the ipsilateral and contralateral nucleus magnocellularis (NM), which enter the NL at opposite sides (Fig. 1A). Each NL neuron receives input from hundreds of NM cells, each of which is connected to from one to four auditory nerve fibers (19). Within the NL, magnocellular axons run almost parallel to each other and run perpendicular to the NL borders. They act as delay lines, interdigitate, and make synapses mainly on somatic spines of the sparsely distributed laminar neurons (13, 19). The latter act as coincidence detectors (10, 12, 13, 20–22).
NM and NL are tonotopically organized in iso-frequency laminae. Information is conveyed via phase-locked spikes for frequencies as high as 9 kHz. The existence of an oscillatory field potential, the “neurophonic” that arises at the NL borders (12), suggests the almost coincident arrival of volleys of phase-locked spikes in thousands of NM axons (10, 13, 23). In other words, the average conduction times from the inner ear to the NL border (called “NL delays” here) are almost equal. In an NL lamina with best frequency f, NL delays may differ by multiples of the period T = f−1 (Fig. 1B). Because axonal conduction velocities are almost identical within NL (≈4 m/s; ref. 13), spikes are transmitted coherently throughout the nucleus. This is also reflected in the neurophonic measured within the borders of NL.
The above observations on the timing of spikes hold for adult owls. In young owls, e.g., 12 days after hatching (P12), spikes arrive incoherently at laminar neurons (ref. 23; Fig. 1C). In the first weeks after hatching, there is ongoing myelination of NM axons (23). Therefore, no stable temporal cues are available for NL neurons. Results in ref. 13 suggest that the distribution of NL delays has a width of about 1 ms. To summarize, in young owls there is neither an ITD tuning of single neurons nor a neurophonic nor a map, all of which arise during ontogeny. The first ITD-tuned neurophonic responses were recorded from a P21 bird, when myelination is almost finished. How, then, is the selection of NM arbors with appropriate NL delays achieved?
In a previous modeling study (20), it has been shown that spike-based Hebbian learning (refs. 24–31; reviewed in refs. 32 and 33) can lead to a selection of synapses from NM to NL in a competitive self-organized process and to the development of submillisecond ITD tuning of single laminar neurons. Here we go an important step further and explain how an ITD map can be formed in an array of neurons. A coordinated development of ITD tuning requires an interaction mechanism between NL cells. There are several possibilities. We have found that the only feasible interaction mechanism is what is called “axonal propagation of synaptic learning.” This means that spike-based learning is not restricted to the stimulated synapse where it is induced, but that it also gives rise to a factor that propagates intracellularly along the presynaptic axon and affects the properties of synapses of neighboring neurons at the same axon (refs. 34–38; presynaptic lateral propagation reviewed in ref. 39). Long-range cytoplasmic signaling within the presynaptic neuron can be responsible for the propagation of both long-term synaptic depression (35–37) and long-term synaptic potentiation (38). We call this mechanism “nonspecific axonal learning.” Spike-based Hebbian learning in combination with nonspecific axonal learning can result in a selection of NM arbors with proper delays to NL and suffices to explain both map formation and the neurophonic.
Methods
Neuron Model.
We have modeled N = 30 laminar neurons as
integrate-and-fire units that are receiving input from a total of 500
magnocellular (NM) axons, 250 from each side. The mth input
spike arriving at time
t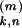 at synapse k (1 ≤ k ≤ 500) of neuron
n (1 ≤ n ≤ N) evokes an
excitatory postsynaptic potential (EPSP) of the form
ɛ
at synapse k (1 ≤ k ≤ 500) of neuron
n (1 ≤ n ≤ N) evokes an
excitatory postsynaptic potential (EPSP) of the form
ɛ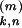 (t)
= Jk,n(t) (t −
t
(t)
= Jk,n(t) (t −
t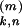 )τ−2
exp[−(t −
t
)τ−2
exp[−(t −
t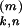 )/τ]
where t >
t
)/τ]
where t >
t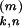 ,
τ = 100 μs, and Jk,n(t) is
the time-dependent synaptic strength. Initially, synaptic strengths are
uniformly distributed between 0.57 and 1.23. The EPSPs (α functions,
half-width 250 μs) from all synapses of a neuron add linearly and
yield the membrane voltage. A neuron fires if the membrane voltage
reaches a threshold that is 96 times the EPSP amplitude for
Jk,n = 1. After firing, the membrane
voltage is reset to zero. Time is discretized in steps of 5 μs.
,
τ = 100 μs, and Jk,n(t) is
the time-dependent synaptic strength. Initially, synaptic strengths are
uniformly distributed between 0.57 and 1.23. The EPSPs (α functions,
half-width 250 μs) from all synapses of a neuron add linearly and
yield the membrane voltage. A neuron fires if the membrane voltage
reaches a threshold that is 96 times the EPSP amplitude for
Jk,n = 1. After firing, the membrane
voltage is reset to zero. Time is discretized in steps of 5 μs.
Neuronal parameters are chosen in accordance with available data. The shape of an EPSP is determined both by the membrane time constant and by the width of the synaptic input current, which have been measured in NM and NL of chicken (40, 41). Data yield membrane time constants near a threshold of about 165 μs, which is caused by an outward rectifying current that is activated above resting potential. Outward rectifying currents are commonly found in phase-locking neurons of the auditory system (40–44). As a result of the short time constants obtained in vitro, the full width at half maximum of single EPSPs in NL neurons in chicken is about 500–800 μs (41). Considering the fact that in chicken phase locking disappears above 2 kHz, whereas neurons in the barn owl exhibit phase locking up to 9 kHz, we assume that NL neurons in vivo in an auditory specialist such as the barn owl are at least twice as fast, and therefore model EPSPs with a width of 250 μs.
Model of an NL Lamina.
N = 30 units are positioned regularly in a row in the dorsoventral direction with a distance of 27 μm between adjoining neighbors, reflecting the topography in NL (refs. 12 and 13; Fig. 1A). The number 30 corresponds to the mean number of neurons contacted by a magnocellular arbor (19). In this way, we simulate part of an iso-frequency lamina of NL.
Input Model.
The input from NM to NL is described by a sequence of phase-locked spikes. We simulate one frequency lamina at a time. It is stimulated by a pure tone of frequency f = T−1 = 3 kHz, unless stated otherwise.
Because of imperfect phase locking, spikes arrive at the borders
of NL with a temporal jitter of σ = 40 μs. The jitter accounts
for internal sources of variability and noise along the auditory
pathway, as well as the bandwidth of frequency tuning (1/3 octave).
The mean conduction time from the ear via NM axon k to the
border where it enters NL is called “NL delay
Δk.” NL delays
Δk (1 ≤ k ≤ 500)
are assumed to be fixed and uniformly distributed in an interval
between 2.5 ms and 3.17 ms; for T = 333 μs,
two periods are covered and, thus, no phase is favored a
priori. The axonal input spike trains are generated independently
for each NM afferent k by an inhomogeneous Poisson process
with intensity Pk(t)
=
νT(σ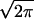 )−1Σ
)−1Σ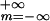 exp[−(t−mT−Δk)2/(2σ2)],
where ν = 2/3 kHz denotes the firing rate of a NM neuron.
exp[−(t−mT−Δk)2/(2σ2)],
where ν = 2/3 kHz denotes the firing rate of a NM neuron.
We have also tested input that was phase locked to 1.5 kHz and 5 kHz as
well as white noise filtered to resemble the tuning of NM fibers. In
the latter case, the amplitude y of the basilar membrane was
obtained by convolving Gaussian white noise with the integral kernel
t3/τ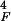 exp(−t/τF)
cos(2πfFt), where
fF = 3 kHz is the center frequency of
the filter and 1/τF = 1 kHz adjusts
the temporal width of the filter kernel to 1 ms. To mimic the behavior
of an inner hair cell, we have fixed its firing rate to
p = 0.2 kHz for y ≤ 0. As soon as
y crosses zero with positive slope we set p
= 1.8 kHz until y drops again below 0 or y has
been positive for more than 0.1 ms, whatever occurs first. In other
words, the width of 1.8-kHz regions is restricted to at most 0.1
ms. The above procedure accounts for the limited resources of the cell.
The spike autocorrelation function is that of the Meddis hair cell
model (45) with time running faster by a factor of 10 to take into
account phase locking for frequencies up to 10 kHz.
exp(−t/τF)
cos(2πfFt), where
fF = 3 kHz is the center frequency of
the filter and 1/τF = 1 kHz adjusts
the temporal width of the filter kernel to 1 ms. To mimic the behavior
of an inner hair cell, we have fixed its firing rate to
p = 0.2 kHz for y ≤ 0. As soon as
y crosses zero with positive slope we set p
= 1.8 kHz until y drops again below 0 or y has
been positive for more than 0.1 ms, whatever occurs first. In other
words, the width of 1.8-kHz regions is restricted to at most 0.1
ms. The above procedure accounts for the limited resources of the cell.
The spike autocorrelation function is that of the Meddis hair cell
model (45) with time running faster by a factor of 10 to take into
account phase locking for frequencies up to 10 kHz.
Besides the NL delay, there is an additional axonal delay of spikes from the NL border to a specific NL neuron. The NL delay (from ear to border) plus the axonal delay within NL (from border to neuron) we call the total delay associated with a synapse. The axonal delay of spikes within NL is the neuron's spatial distance from the border divided by the conduction velocity, which can be assumed to be constant (4 m/s) and identical for all axons within the laminar nucleus, in accordance with experimental data (13). We have also carried out simulations for a distribution of axonal propagation velocities (4 ± 0.5 m/s) and verified robustness.
To take into account changing spatial positions of statistically independent sound sources, we have sampled the applied ITD of a stimulus from the interval [−T/2,T/2] and randomly initialized the mean phase of the stimulating tone every 100 ms.
Model of Spike-Based Learning.
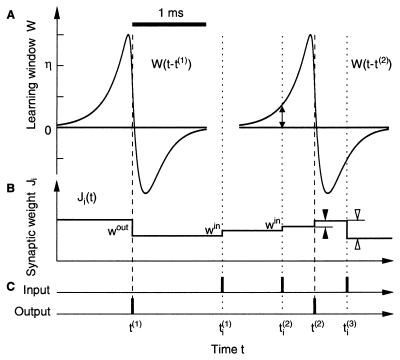
In spike-based Hebbian learning at the level of a single neuron (20, 26–33, 46–49), synaptic strengths are increased or decreased if presynaptic spikes arrive before or after, respectively, the postsynaptic neuron fires. The temporal constraint is implemented by means of a learning window W that is several milliseconds wide (Fig. 2A),
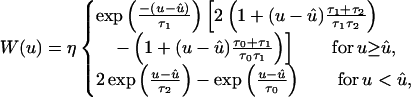 |
1 |
where u denotes the time difference between presynaptic spike arrival and the postsynaptic spike event; τ0 = 0.025 ms, τ1 = 0.15 ms, τ2 = 0.25 ms, η = 5 ×10−4, û = −0.005 ms. The time scale of learning is set by η (46, 49). Existence and form of W have been confirmed by experiment (26–31). Its shape, i.e., the structure near zero, is important because there should be a maximum of W(s) for s < 0, namely, maximal increase of the synaptic strength for a presynaptic spike preceding a postsynaptic spike roughly by the rise time of an EPSP (46, 49). Expanding the tails of the learning window changes the mean output rate of the postsynaptic neuron. Here the width of W is assumed to be reduced when compared with so-called standard cases (26–31) by about an order of magnitude; in this way, it is in agreement with the short time constants of NL neurons (40, 41). We predict that synapses in the auditory system can exhibit a radically faster form of plasticity timing.
Figure 2.
Spike-based learning. (A) Two plots of the learning
window W in units of the learning parameter η as a
function of the temporal difference between spike arrival at time
t at synapse i (e.g., t
=
t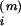 ,
m = 1, 2, 3; dotted lines) and postsynaptic firing
at times t(1) and
t(2) (dashed lines). Scale bar = 1 ms.
(B) Time course of the synaptic weight
Ji(t) evoked through
input spikes at synapse i and postsynaptic output spikes
(vertical bars in C). The output spike at time
t(1) decreases
Ji by an amount
wout. The input at
t
,
m = 1, 2, 3; dotted lines) and postsynaptic firing
at times t(1) and
t(2) (dashed lines). Scale bar = 1 ms.
(B) Time course of the synaptic weight
Ji(t) evoked through
input spikes at synapse i and postsynaptic output spikes
(vertical bars in C). The output spike at time
t(1) decreases
Ji by an amount
wout. The input at
t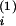 and
t
and
t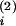 increase
Ji by win
each. There is no influence of the learning window W
because these input spikes are too far away in time from
t(1). The output spike at
t(2), however, follows the input at
t
increase
Ji by win
each. There is no influence of the learning window W
because these input spikes are too far away in time from
t(1). The output spike at
t(2), however, follows the input at
t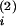 closely enough, so
that, at t(2),
Ji is changed by
wout < 0 plus
W(t
closely enough, so
that, at t(2),
Ji is changed by
wout < 0 plus
W(t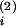 − t(2)) > 0 (double-headed arrow),
the sum of which is positive (filled arrowheads). Similarly, the input
at t
− t(2)) > 0 (double-headed arrow),
the sum of which is positive (filled arrowheads). Similarly, the input
at t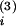 leads to a
decrease win +
W(t
leads to a
decrease win +
W(t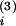 −
t(2)) < 0 (open arrowheads). The
assumption of instantaneous and discontinuous weight changes can be
relaxed to delayed and continuous ones that are triggered by spikes,
provided weight changes are fast when compared with the time scale of
learning (46). If the integral
∫
−
t(2)) < 0 (open arrowheads). The
assumption of instantaneous and discontinuous weight changes can be
relaxed to delayed and continuous ones that are triggered by spikes,
provided weight changes are fast when compared with the time scale of
learning (46). If the integral
∫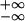 W(s)
ds is sufficiently negative, then one can drop
wout (49).
W(s)
ds is sufficiently negative, then one can drop
wout (49).
To stabilize the mean input to a neuron, we use a weight increment of win = η/50 following every presynaptic spike and a decrement of wout = −η/4 of all synaptic strengths after each postsynaptic spike (9, 39). The particular choice of the non-Hebbian parameters win and wout is not critical for structure formation; they determine the value and stability of the mean firing rate of the postsynaptic neuron (refs. 46, 48, and 49). A stabilization of the output rate is necessary to ensure that the neuron acts as a coincidence detector (21). In addition, there is a lower bound of 0 and an upper bound of 2 for each individual synaptic weight.
We have implemented a nonspecific axonal learning rule (34–39, 50); a weight change ΔJ as described above also induces changes in other synapses of the same magnocellular arbor, which change by an amount ρΔJ. The interaction parameter ρ is small and positive. Nonspecific axonal learning is confined to a magnocellular arbor and does not extend to the whole axon. We have proven that our results still hold, if we restrict the spatial range of the nonspecific component to 200 μm along an arbor. Finally, if all synaptic weights on an axonal arbor are zero, it is assumed to be eliminated.
Delay-Tuning Index.
The degree of T-periodic tuning of a delay
distribution is quantified through a delay-tuning index, which is the
amplitude of the first Fourier component (period T) of the
delay distribution divided by the Fourier component of order zero. It
is a generalization of the “vector strength” (14). For a large
number of random delays, the delay-tuning index is close to its minimum
of 0. For identical delays (modulo T), the delay-tuning
index is at its maximum of 1. We first consider delays from the ear to
the synapses of a single NL neuron. Given the synaptic weights
Jk,n and the total delays
Δk,n through the kth (1
≤ k ≤ 500) magnocellular afferent to the
nth (1 ≤ n ≤ 30) NL neuron, the
Fourier transform of the delay distribution of, e.g., ipsilateral
synaptic weights of neuron n is
x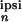 (ω) :=
Σ
(ω) :=
Σ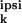 Jk,n
exp(−iωΔk,n), where ω is a
frequency and i =
Jk,n
exp(−iωΔk,n), where ω is a
frequency and i = 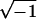 . The sum is
over all magnocellular afferents K from the ipsilateral
side. The delay-tuning index is the ratio
|x
. The sum is
over all magnocellular afferents K from the ipsilateral
side. The delay-tuning index is the ratio
|x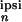 (2π/T)|/x
(2π/T)|/x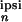 (0),
where T is the period of the stimulating tone. Next, we
consider the delay of magnocellular arbors at the border of NL (NL
delays). The tuning index of NL delays can be used as a measure of the
quality of the map. We define the strength or “axonal weight” of
an NM arbor as the sum of its synaptic weights. One obtains the
delay-tuning index of the distribution of axonal weights similarly to
the single-neuron case above—by replacing both the synaptic weights
Jk,n by the axonal weights
ΣnJk,n
(for axon k) and the total delays
Δk,n to the synapses by the delay
Δk to the NL borders.
(0),
where T is the period of the stimulating tone. Next, we
consider the delay of magnocellular arbors at the border of NL (NL
delays). The tuning index of NL delays can be used as a measure of the
quality of the map. We define the strength or “axonal weight” of
an NM arbor as the sum of its synaptic weights. One obtains the
delay-tuning index of the distribution of axonal weights similarly to
the single-neuron case above—by replacing both the synaptic weights
Jk,n by the axonal weights
ΣnJk,n
(for axon k) and the total delays
Δk,n to the synapses by the delay
Δk to the NL borders.
Results
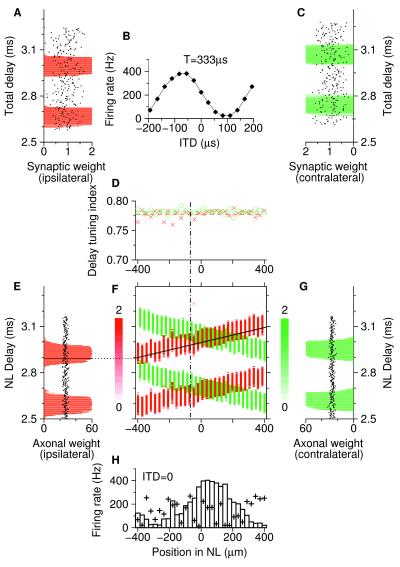
A typical numerical simulation of an array of 30 neurons that belong to the 3 kHz layer in the laminar nucleus (Fig. 1A) is shown in Fig. 3. We have started with a uniform distribution of synaptic weights. After about 1,000 s of learning, the weights have arrived at a stable state where each single neuron exhibits ITD tuning (Fig. 3 A–D). In other words, the cells have learned to detect coincident arrival of ipsi- and contralateral activity. The maximum of the tuning curve in Fig. 3B defines the best ITD of a neuron. It is determined by the delay difference between the ipsi- and contralateral synaptic structure appearing in Fig. 3 A and C. The quality of the periodic synaptic structures, measured by the delay-tuning index (see Methods), saturates at about 0.78 for each individual neuron, regardless of ipsi- or contralateral origin (Fig. 3D).
Figure 3.
Map of ITD-tuned neurons in the laminar nucleus (NL). Ipsi- and contralateral synaptic weights after learning are coded by red and green, respectively. (A) Ipsilateral weights of a single laminar neuron (abscissa) are plotted as a function of the transmission delay (ordinate) from the ear to the synapse, called total delay. Dots denote initial weights before learning. (B) ITD-tuning curve of the neuron in A and C. (C) Same as A but for contralateral afferents. Note the shift of the distribution compared with A. (D) Ipsilateral (crosses) and contralateral (circles) tuning indices of the distributions of total delays (see Methods) as a function of the neuron's spatial position (same scale as in H). Horizontal dashed lines denote mean values. The vertical dot-dashed line indicates the position of the neuron shown in A–C. (E) Distribution of ipsilateral axonal weights (abscissa) as a function of the transmission delay (ordinate) from the ear to the dorsal NL border (NL delay). Dots denote initial weights before learning. (F) Synaptic weights (brightness-coded, scale bars in units of synaptic weights) are a function of the position of the neuron inside NL (abscissa, same scale as in D and H) and of the total delay to a neuron (ordinate, same scale as in E and G). Weights of a specific ipsilateral arbor are represented by the diagonal solid black line with slope 4 m/s, the axonal conduction velocity. Summing synaptic weights along this line, we obtain an axonal weight (horizontal black bar in E). (G) Same as E but for contralateral axons. (H) Dependence of firing rate of laminaris neurons for ITD = 0 on their location (histogram). The maximum firing rate is where the overlap of delay distributions in F is largest. Plus signs indicate rates for ρ = 0 in Fig. 4B; there is no map.
As a result of the presynaptically nonspecific component of synaptic modification (ρ = 0.017; see Methods), best ITDs are spatially ordered along the neuronal array. This means that neighboring neurons give rise to similar best ITDs. The corresponding structure of synaptic weights is shown in Fig. 3F. The slopes of the diagonal red and green stripes, respectively, reflect the axonal conduction velocity (4 m/s). That is to say, the learning rule selects arbors with the right delay Δk from the ear to the NL border (called NL delay in what follows). The sum of the synaptic weights of an NM arbor is called its axonal weight. The ITD map is represented by a T-periodic structure of axonal weights as a function of the NL delay (Fig. 3 E and G). The relative shift of the distributions in Fig. 3 E and G depends on random initial conditions.
The final structure is consistent with Jeffress' proposal (1) of a place code. As the histogram in Fig. 3H shows for stimulation of the array with fixed ITD = 0, the neuron 54 μm to the right of the center of NL fires with highest rate. The reason is that at this position ipsi- and contralateral delay distributions in Fig. 3F largely overlap. Because the cells act as coincidence detectors, their firing rate is maximal when the green and red vertical lanes in Fig. 3F overlap, or, equivalently, when the total delays from right and left ear are equal modulo T = 1/3 ms. As the overlap is less, so the firing rate is lower, with a minimum at about −300 μm in Fig. 3H. If the applied ITD is varied, the place of maximum firing rate shifts proportionally (not shown).
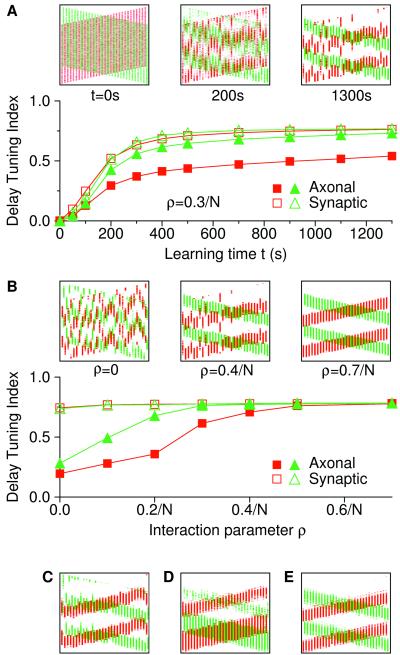
A map's quality, i.e., its degree of global order, depends on the learning time t (Fig. 4A). The global order is quantified by the delay-tuning index of axonal delay distributions (examples in Fig. 3 E and G). Before learning (t = 0), axonal delay-tuning indices (filled symbols in Fig. 4A) are zero and there is no map. As t grows, the global order increases monotonically and saturates, because synaptic weights reach upper or lower bounds. In Fig. 4A, we also have indicated average synaptic delay-tuning indices (open symbols), which measure the map's local order or tuning of individual NL neurons (see also Fig. 3D, horizontal dashed lines). As defined in Methods, the local order is always larger than, or at least equal to, the global order. Large identical values indicate that all neurons are strongly coupled to the same set of axonal arbors. In this case, the best ITD is a linear function of the neuron's position on the dorso ventral axis.
Figure 4.
Dependence of the quality of the map on parameters. Axonal (filled symbols) and synaptic (open symbols) delay-tuning indices (averaged over N = 30 neurons) have been plotted for ipsilateral (red squares) and contralateral (green triangles) NM afferents. Insets (signatures as in Fig. 3F) show the map at different stages. (A) Delay-tuning indices are a function of learning time t. The interaction parameter is ρ = 0.3/N; all other parameters and initial conditions are the same as in Fig. 3. Because alignment is not perfect, synaptic delay-tuning indices exceed the axonal ones. (B) Delay-tuning indices of the final map are a function of the interaction parameter ρ. The same random seed for all simulations gives a smooth dependence on ρ. Restricting the interaction to 8 neighboring neurons (ρ = 0.7/16) (C), filtered white-noise input (D), or a distribution of axonal conduction velocities 4 ± 0.5 m/s (E) hardly changes the final map.
The tuning of the final map (after weights have saturated) depends on the interaction parameter ρ (Fig. 4B). For ρ = 0, the global order is low (filled symbols), although individual neurons are almost perfectly tuned and, thus, the local order is high (open symbols). Nevertheless, a place code in the manner of Jeffress does not exist (plus signs in Fig. 3H). Even for ρ = 0, axonal delay-tuning indices are nonzero, because for a finite number of tuned laminar neurons, there is on the average an accidental global order (here about 0.16). As ρ increases, so does the map's quality. In this way, nonspecific axonal learning is sufficient for map formation, despite the surprising fact that it may be two orders of magnitude weaker than homosynaptic Hebbian plasticity.
Nonspecific axonal learning as it has been used in these simulations is local in the sense that it is restricted to an axonal arbor. It does not apply to the whole axon, which may have many arbors that branch off well outside NL. A local change within an arbor has not been implemented because the range of the interaction reported in refs. 34–38 is of the same order of magnitude as the spatial extension of the laminar nucleus along the dorsoventral axis. We have tested, however, that restricting the nonspecific weight change to, for example, ≈200 μm or the neighboring eight neurons does not change results. For instance, with ρ = 0.7/16, we obtain global tuning indices of 0.72 (ipsi) and 0.67 (contra), or 92% and 86% of the average local indices, respectively (Fig. 4C).
We have also verified that similar results hold for the 1.5-kHz and 5-kHz case (not shown), and we have checked that 3-kHz tonal stimulation and white noise filtered to resemble the tuning of NM fibers (see Methods) yield comparable findings (Fig. 4D; ρ = 0.7/N). In both the noisy and the tonal cases, the autocorrelation functions of the input processes were almost identical on a time scale of 1 ms, which corresponds to the width of the important features of the learning window in Fig. 2. Thus, map formation is robust against variations of the input to NL.
The order of the final map remains basically the same if we start with a distribution of axonal propagation velocities (4 ± 0.5 ms, Fig. 4E). The proposed learning algorithm can select arbors with appropriate conduction velocities. An interaction strength of ρ = 0.7/N yields global tuning indices of 0.76 and 0.75; both are about 97% of the average local indices.
During learning, the ITD is varied randomly every 100 ms to mimic the naturally occurring variation of ITDs. On the much larger time scale of learning, interaural phases within a frequency channel are uncorrelated. Therefore, ipsi- and contralateral synaptic weights evolve almost independently of each other during spike-based learning. Because of this independence, an increase in the range of available ITDs through a growth of the size of the owl's head does not necessarily impair map formation. Owls grow a lot while the map develops (23).
Discussion
In the present article, we offer a solution to the longstanding problem of how a map of ITD-tuned neurons in the barn owl's NL can be formed. Map formation requires a selection of magnocellular arbors with appropriate delays, which can be driven by spike-based Hebbian learning at the level of single synapses and the propagation of spike-based Hebbian learning along the presynaptic axon. Finally, only a subset of the initially present NM arbors provide significant input to NL. Because map formation demands phase-locked input, we predict a delay in the development of an owl's NL if the degree of phase locking is reduced, e.g., by means of an ear occluder (51).
As for the time scale of map formation, the speed of learning slows down if synaptic weight changes are reduced through a reduction of η as it appears in Eq. 1 and Fig. 2. Then, 1,000 s of learning (as in Fig. 4A) may become several days, which is a realistic value for the development of the owl's NL (23) but unrealistic for a computer simulation that cannot work in real time yet.
To explain the neurophonic for which the afferent delay lines are responsible (10, 12, 13, 23), we propose a morphological change accompanying synaptic weight changes, i.e., an elimination of those magnocellular arbors that merely have synapses with vanishing weights. Finally, only axonal arbors survive that have spike latencies (from the ear to the border where the arbors enter NL) roughly differing by multiples of the period T, where T−1 is an NL lamina's best frequency (Fig. 1B, Fig. 3 E and G).
Nonspecific axonal learning is sufficient for map formation in NL, and the strength of the interaction can be orders of magnitude weaker than long-term potentiation at the level of a single neuron. We predict that blocking of nonspecific axonal learning (cf. ref. 50) prevents formation of both map and neurophonic but leaves the development of ITD tuning of single neurons unaffected (Fig. 4B, ρ = 0).
We can rule out other possibilities that have been suggested for map formation in various systems. Factors one might think of are (i) electrical coupling by gap junctions, (ii) electrical crosstalk, (iii) extracellular diffusion of a messenger, and (iv) recurrent synaptic coupling within NL, or (v) recurrent synaptic coupling outside the laminar nucleus. Early in development (P12 or later) gap junctions between almost nonoverlapping dendritic trees are unlikely. The membrane capacitance and resistance of the participating NL neurons, however, would make such junctions act as low-pass filters that delay a signal from one neuron to another by more than 100 μs. The timing constraint for spike-based learning imposed by phase-locked input at 3 kHz, as analyzed in this article, cannot be fulfilled; this is even more true for higher frequencies. Recurrent (multi)synaptic loops are also too slow. Their delays can, in principle, be very accurate (20). This high accuracy would require many lateral connections at the level of the young animal's NL, which are not present either within or outside. The central argument in the analysis of map formation is a mechanism for the selection of axonal arbors. Spatially more or less isotropic interactions such as extracellular diffusion of a messenger and electrical crosstalk can, therefore, be excluded. The only remaining interaction mechanism is nonspecific axonal learning. In the present context, all other interaction mechanisms are unsuitable because of evidence of nonexistence (i, iv), spatial isotropy instead of axonal selectivity (ii, iii), lack of temporal precision of the signal (jitter) (iii, v), and a delay of the order of at least hundreds of microseconds (i, iii, iv, v) that by far exceeds the axonal conductance time between neighboring NL cells and, thus, mixes up the timing between their input and output spikes.
Lateral inhibition is a key ordering factor in many algorithms of map formation. In the laminar nucleus, lateral inhibition is most probably responsible for gain control (52, 53) but is not needed for a diversity of ITD tuning. Diversity is a consequence of the arrangement of laminar neurons along antiparallel axons and a T periodic tuning of their delays (Fig. 1).
Besides our proposed delay-selection mechanism for map formation, an alternative explanation might be the adaptation of conduction velocity of presynaptic axons (47, 54). A possible target for such a learning rule are portions of axons outside the NL, because the conduction velocities within the nucleus are almost identical (13)—which is as it should be to explain the neurophonic. Appropriate changes of conduction velocities outside the NL might have the advantage of making the elimination of certain arbors superfluous because all arbors are retained; their conduction velocity, however, has to be modified specifically. A disadvantage is that it is not known whether and how learning at synapses affects the conduction velocity, and how a map can be stabilized in this way.
In summary, we have studied map formation in a single frequency lamina of NL because we intended to highlight the issue of map formation in the time domain by means of nonspecific axonal learning. The alignment of maps across different frequency layers is an interesting problem but is far beyond the scope of the present article. Furthermore, the NL is tonotopically organized before formation of the ITD map starts (23). In simulating coupled frequency laminae, we would expect no qualitative effect on the development of an ITD map within one lamina.
We have shown that the formation of a temporal-feature map with a submillisecond precision can be based on an interplay of local time-resolved Hebbian learning (20, 24–31, 46–49) and its propagation along a presynaptic axon (34–39, 50). Our results are in agreement with physiological and anatomical data on the barn owl's laminar nucleus, and they explain the formation of a temporal-feature map. It is tempting to apply the proposed mechanisms to other modalities as well. We suggest that presynaptic propagation of synaptic learning is important to the formation of computational maps when, in particular, time plays a key role.
Acknowledgments
We thank A. P. Bartsch, P. H. Brownell, W. Gerstner, C. E. Schreiner, and O. G. Wenisch for useful comments on the manuscript. C.L. holds a scholarship from the state of Bavaria. R.K. has been supported by the Deutsche Forschungsgemeinschaft under Grants Kl 608/10–1 (FG Hörobjekte) and Ke 788/1–1.
Abbreviations
- ITD
interaural time difference
- NL
nucleus laminaris
- NM
nucleus magnocellularis
- EPSP
excitatory postsynaptic potential
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Jeffress L A. J Comp Physiol Psychol. 1948;41:35–39. doi: 10.1037/h0061495. [DOI] [PubMed] [Google Scholar]
- 2.Knudsen E I, du Lac S, Esterly S D. Annu Rev Neurosci. 1987;10:41–65. doi: 10.1146/annurev.ne.10.030187.000353. [DOI] [PubMed] [Google Scholar]
- 3.Berardi N, Pizzorusso T, Maffei L. Curr Opin Neurobiol. 2000;10:138–145. doi: 10.1016/s0959-4388(99)00047-1. [DOI] [PubMed] [Google Scholar]
- 4.Suga N. In: Computational Neuroscience. Schwartz E L, editor. Cambridge, MA: MIT Press; 1990. pp. 213–231. [Google Scholar]
- 5.Schreiner C E. Curr Opin Neurobiol. 1995;5:489–496. doi: 10.1016/0959-4388(95)80010-7. [DOI] [PubMed] [Google Scholar]
- 6.Ehret G. J Comp Physiol A. 1997;181:547–557. doi: 10.1007/s003590050139. [DOI] [PubMed] [Google Scholar]
- 7.Langner G, Sams M, Heil P, Schulze H. J Comp Physiol A. 1997;181:665–676. doi: 10.1007/s003590050148. [DOI] [PubMed] [Google Scholar]
- 8.Schulze H, Langner G. J Comp Physiol A. 1997;181:651–663. doi: 10.1007/s003590050147. [DOI] [PubMed] [Google Scholar]
- 9.Buonomano D V, Merzenich M M. Annu Rev Neurosci. 1998;21:149–186. doi: 10.1146/annurev.neuro.21.1.149. [DOI] [PubMed] [Google Scholar]
- 10.Carr C E. Annu Rev Neurosci. 1993;16:223–243. doi: 10.1146/annurev.ne.16.030193.001255. [DOI] [PubMed] [Google Scholar]
- 11.Konishi M. Trends Neurosci. 1986;9:163–168. [Google Scholar]
- 12.Sullivan W E, Konishi M. Proc Natl Acad Sci USA. 1986;83:8400–8404. doi: 10.1073/pnas.83.21.8400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carr C E, Konishi M. J Neurosci. 1990;10:3227–3246. doi: 10.1523/JNEUROSCI.10-10-03227.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Goldberg J M, Brown P B. J Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- 15.Rubel E W, Parks T N. In: Auditory Function. Neurobiological Bases of Hearing. Edelman G M, Gall W E, Cowan W M, editors. New York: Wiley; 1988. pp. 721–746. [Google Scholar]
- 16.Yin T C T, Chan J C K. J Neurophysiol. 1990;64:465–488. doi: 10.1152/jn.1990.64.2.465. [DOI] [PubMed] [Google Scholar]
- 17.Overholt E M, Rubel E W, Hyson R L. J Neurosci. 1992;12:1698–1708. doi: 10.1523/JNEUROSCI.12-05-01698.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Beckius G E, Batra R, Oliver D L. J Neurosci. 1999;19:3146–3161. doi: 10.1523/JNEUROSCI.19-08-03146.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Carr C E, Boudreau R E. J Comp Neurol. 1993;334:337–355. doi: 10.1002/cne.903340302. [DOI] [PubMed] [Google Scholar]
- 20.Gerstner W, Kempter R, van Hemmen J L, Wagner H. Nature (London) 1996;383:76–78. doi: 10.1038/383076a0. [DOI] [PubMed] [Google Scholar]
- 21.Kempter R, Gerstner W, van Hemmen J L, Wagner H. Neural Comput. 1998;10:1987–2017. doi: 10.1162/089976698300016945. [DOI] [PubMed] [Google Scholar]
- 22.Agmon-Snir H, Carr C E, Rinzel J. Nature (London) 1998;393:268–272. doi: 10.1038/30505. [DOI] [PubMed] [Google Scholar]
- 23.Carr C E. In: Advances in Hearing Research. Manley G A, Klump G M, Köppl C, Fastl H, Oeckinghaus H, editors. Singapore: World Scientific; 1995. pp. 24–30. [Google Scholar]
- 24.Levy W B, Stewart D. Neuroscience. 1983;8:791–797. doi: 10.1016/0306-4522(83)90010-6. [DOI] [PubMed] [Google Scholar]
- 25.Bell C C, Han V Z, Sugawara Y, Grant K. Nature (London) 1997;387:278–281. doi: 10.1038/387278a0. [DOI] [PubMed] [Google Scholar]
- 26.Markram H, Lübke J, Frotscher M, Sakmann B. Science. 1997;275:213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- 27.Debanne D, Gähwiler B H, Thompson S M. J Physiol. 1998;507:237–247. doi: 10.1111/j.1469-7793.1998.237bu.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhang L I, Tao H-z W, Holt C E, Harris W A, Poo M-m. Nature (London) 1998;395:37–44. doi: 10.1038/25665. [DOI] [PubMed] [Google Scholar]
- 29.Bi G-q, Poo M-m. J Neurosci. 1998;18:10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bi G-q, Poo M-m. Nature (London) 1999;401:792–796. doi: 10.1038/44573. [DOI] [PubMed] [Google Scholar]
- 31.Feldman D E. Neuron. 2000;27:45–56. doi: 10.1016/s0896-6273(00)00008-8. [DOI] [PubMed] [Google Scholar]
- 32.Linden D J. Neuron. 1999;22:661–666. doi: 10.1016/s0896-6273(00)80726-6. [DOI] [PubMed] [Google Scholar]
- 33.Paulsen O, Sejnowski T J. Curr Opin Neurobiol. 2000;10:172–179. doi: 10.1016/s0959-4388(00)00076-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bonhoeffer T, Staiger V, Aertsen A. Proc Natl Acad Sci USA. 1989;86:8113–8117. doi: 10.1073/pnas.86.20.8113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cash S, Zucker R S, Poo M-m. Science. 1996;272:998–1001. doi: 10.1126/science.272.5264.998. [DOI] [PubMed] [Google Scholar]
- 36.Fitzsimonds R M, Song H-J, Poo M-m. Nature (London) 1997;388:439–448. doi: 10.1038/41267. [DOI] [PubMed] [Google Scholar]
- 37.Goda Y, Stevens C F. Proc Natl Acad Sci USA. 1998;95:1283–1288. doi: 10.1073/pnas.95.3.1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tao H-z W, Zhang L I, Bi G-q, Poo M-m. J Neurosci. 2000;20:3233–3243. doi: 10.1523/JNEUROSCI.20-09-03233.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fitzsimonds R M, Poo M-m. Physiol Rev. 1998;78:143–170. doi: 10.1152/physrev.1998.78.1.143. [DOI] [PubMed] [Google Scholar]
- 40.Reyes A D, Rubel E W, Spain W J. J Neurosci. 1994;14:5352–5364. doi: 10.1523/JNEUROSCI.14-09-05352.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Reyes A D, Rubel E W, Spain W J. J Neurosci. 1996;16:993–1007. doi: 10.1523/JNEUROSCI.16-03-00993.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Oertel D. J Neurosci. 1983;3:2043–2053. doi: 10.1523/JNEUROSCI.03-10-02043.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Manis P B, Marx S O. J Neurosci. 1991;11:2865–2880. doi: 10.1523/JNEUROSCI.11-09-02865.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Trussell L O. Annu Rev Physiol. 1999;61:477–496. doi: 10.1146/annurev.physiol.61.1.477. [DOI] [PubMed] [Google Scholar]
- 45.Meddis R. J Acoust Soc Am. 1986;83:1056–1063. doi: 10.1121/1.396050. [DOI] [PubMed] [Google Scholar]
- 46.Kempter R, Gerstner W, van Hemmen J L. Phys Rev E. 1999;59:4498–4514. [Google Scholar]
- 47.Eurich C W, Pawelzik K, Ernst U, Cowan J D, Milton J G. Phys Rev Lett. 1999;82:1594–1597. [Google Scholar]
- 48.Song S, Miller K D, Abbott L F. Nat Neurosci. 2000;3:919–926. doi: 10.1038/78829. [DOI] [PubMed] [Google Scholar]
- 49.Kempter, R., Gerstner, W. & van Hemmen, J. L. (2001) Neural Comput., in press. [DOI] [PubMed]
- 50.Ganguly K, Kiss L, Poo M-m. Nat Neurosci. 2000;3:1018–1026. doi: 10.1038/79838. [DOI] [PubMed] [Google Scholar]
- 51.Gold J I, Knudsen E I. J Neurosci. 2000;20:862–877. doi: 10.1523/JNEUROSCI.20-02-00862.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Brughera A R, Stutman E R, Carney L H, Colburn H S. Aud Neurosci. 1996;2:219–233. [Google Scholar]
- 53.Yang L, Monsivais P, Rubel E W. J Neurosci. 1999;19:2313–2325. doi: 10.1523/JNEUROSCI.19-06-02313.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.MacKay D M. In: Self-Organizing Systems. Yovits M C, Jacobi G T, Goldstein G D, editors. Washington, DC: Spartan Books; 1962. pp. 37–48. [Google Scholar]