Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2011 May 19;133(25):9863–9871. doi: 10.1021/ja2019367

Temperature Dependence of Charge Separation and Recombination in Porphyrin Oligomer–Fullerene Donor–Acceptor Systems

Axel Kahnt †, Joakim Kärnbratt †, Louisa J Esdaile ‡, Marie Hutin ‡, Katsutoshi Sawada ‡, Harry L Anderson ‡,✉, Bo Albinsson †,✉
PMCID: PMC3119959  PMID: 21595470

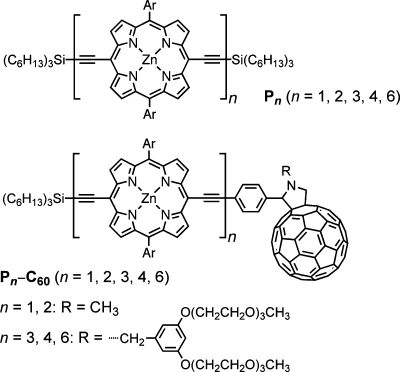
Abstract

graphic file with name ja-2011-019367_0004.jpg

Electron-transfer reactions are fundamental to many practical devices, but because of their complexity, it is often very difficult to interpret measurements done on the complete device. Therefore, studies of model systems are crucial. Here the rates of charge separation and recombination in donor–acceptor systems consisting of a series of butadiyne-linked porphyrin oligomers (n = 1–4, 6) appended to C60 were investigated. At room temperature, excitation of the porphyrin oligomer led to fast (5–25 ps) electron transfer to C60 followed by slower (200–650 ps) recombination. The temperature dependence of the charge-separation reaction revealed a complex process for the longer oligomers, in which a combination of (i) direct charge separation and (ii) migration of excitation energy along the oligomer followed by charge separation explained the observed fluorescence decay kinetics. The energy migration is controlled by the temperature-dependent conformational dynamics of the longer oligomers and thereby limits the quantum yield for charge separation. Charge recombination was also studied as a function of temperature through measurements of femtosecond transient absorption. The temperature dependence of the electron-transfer reactions could be successfully modeled using the Marcus equation through optimization of the electronic coupling (V) and the reorganization energy (λ). For the charge-separation rate, all of the donor–acceptor systems could be successfully described by a common electronic coupling, supporting a model in which energy migration is followed by charge separation. In this respect, the C60-appended porphyrin oligomers are suitable model systems for practical charge-separation devices such as bulk-heterojunction solar cells, where conformational disorder strongly influences the electron-transfer reactions and performance of the device.

Introduction

The production of artificial photosynthetic systems to power solar fuel production is an interesting and promising idea, and to accomplish it, we must rely on molecular and supramolecular assemblies.(1) In natural photosynthesis, cascades of short-range energy-transfer and electron-transfer processes between well-arranged chromophores occur,2−7 and a large variety of super- and supramolecular systems have been studied in order to mimic the natural process. In particular, those systems have been based on chlorophylls,8,9 porphyrins,10−16 or phthalocyanines17−22 as the electron donor and single-walled carbon nanotubes (SWCNTs),23−26 fullerenes,27−30 or graphene31,32 as the electron acceptor. A few systems employing a multiple porphyrin unit as a photoactive electron donor have also been published.33−35 All of these studies were performed at room temperature, but probing the temperature dependence of electron-transfer reactions can give additional information concerning the their mechanism. Because of the experimental difficulties associated with performing temperature-dependent pump–probe experiments, only a few studies of the temperature dependence of fast electron-transfer reactions using femtosecond transient absorption spectroscopy have been reported to date.36−39

Here we present a study of the temperature dependence of the charge-separation and charge-recombination processes in an electron donor–acceptor system based on a series of zinc porphyrin oligomers (Pn, n = 1–4, 6) as electron donors and an appended fullerene as the electron acceptor (Figure 1). The butadiyne links between the porphyrin moieties in the oligomer chain allow for almost barrierless rotation of the individual porphyrins, giving rise to numerous different conformations that vary with respect to their porphyrin–porphyrin dihedral angles. It has previously been shown that these conformations greatly influence the photophysical properties displayed by the system and that the observed absorption spectrum is an average of those for the different conformations.(40) A recent study performed on the fullerene-appended porphyrin dimer P2–C60 showed how selective excitation of twisted or planar conformations could be used to control the rate of electron transfer.(41) It was concluded that charge separation from twisted conformers of P2–C60 resulted in an electron-transfer rate that was 4 times higher than for planar conformers. The main reason for this increase was associated with a stronger electronic coupling to the C60 in the twisted components. This might be because the excitation energy was localized closer to the fullerene in the twisted components than in the planar ones, where the energy is delocalized over both porphyrins.

Figure 1.

Figure 1

Open in a new tab

Molecular structure of the porphyrin oligomer-based donor–acceptor system studied in this work. The aryl substituents (Ar) are 3,5-bis(octyloxy)phenyl groups.

In the present work, we show that excitation of twisted conformers in longer oligomers can have the opposite effect on the electron-transfer rate, as the excitation energy can be localized on a segment of the oligomer that is far away from the electron acceptor. From there, it first must migrate closer to the fullerene before charge separation can occur. Similar behavior has been observed in natural photosynthesis and bulk-heterojunction solar cells. In photosynthetic organisms, excitation can occur at any of the absorbing chromophores, from which the excitation energy is funneled to the reaction center through consecutive energy-transfer reactions before charge separation can occur.(42) Likewise, in bulk-heterojunction (polymer) solar cells, excitation can occur anywhere along the conjugated polymer chain, and the excitation energy migrates along the polymer backbone until it reaches a phase boundary, where charge separation occurs.(43) The system presented here can be seen as a simple model for these important practical charge-separation devices.

The charge separation and recombination were studied using both steady-state and time-resolved emission as well as femtosecond transient absorption in order to probe how these processes depend on the oligomer length. The measurements showed a biexponential behavior of the charge-separation process for all of the oligomers larger than the dimer. To explain this, we have proposed a model wherein both active conformers (which undergo rapid charge separation after excitation) and inactive conformers are excited. The latter must first relax into the active state before charge separation can occur, resulting in delayed charge separation from these conformers. From this model, quantum yields for the charge-separation process were extracted and compared to the values obtained from the quenching of the steady-state fluorescence. In addition, we also explored the temperature dependence of the charge separation and recombination, from which reasonable electron-transfer parameters (electronic couplings and reorganization energies) were extracted.

Experimental Section

Materials

Unless otherwise specified, all of the measurements were made in freshly distilled 2-methyltetrahydrofuran (2MTHF, Sigma-Aldrich) with 1% pyridine (Sigma-Aldrich) added to avoid aggregation of the porphyrin oligomers. The synthesis of compounds P1–C60 and P2–C60 has been reported previously.(44) The synthesis of compounds P3–C60, P4–C60, and P6–C60 is presented in the Supporting Information (SI).

Temperature Studies

For the temperature-dependent ground-state absorption, transient absorption, steady-state emission, and time-resolved emission studies, a temperature-controlled cryostat (Oxford Instruments) cooled with liquid nitrogen was used.

Steady-State Absorption and Emission Spectroscopy

Absorption spectra were measured on a Cary 5000 UV–vis–NIR spectrometer. The spectra were recorded between 350 and 900 nm at 600 nm/min with a 0.5 nm spectral bandwidth. The sample was contained in a 10 mm quartz cuvette. Fully corrected emission spectra were recorded on a Spex Fluorolog 3 spectrofluorometer equipped with a xenon lamp. To avoid aggregation and inner-filter effects, the absorption was adjusted to 0.05 at the excitation wavelength.

Transient Absorption Spectroscopy

A pump–probe setup was used to record transient absorption spectra. A Ti:sapphire oscillator (Tsunami, Spectra Physics) generating pulses with a width of ∼90 fs (fwhm) was used to seed a Ti:sapphire regenerative amplifier (Spitfire, Spectra Physics) that was pumped by a frequency-doubled diode-pumped Nd:YLF laser (Evolution-X, Spectra Physics) and produced pulses of ∼110 fs duration (fwhm) at a repetition rate of 1 kHz. The amplified laser beam (800 nm) was divided by a beamsplitter, and the two beams were subsequently used as the pump and probe beams. The pump beam was manipulated by an optical parametric amplifier (OPA) (TOPAS, Light Conversion Ltd.) to yield a wavelength of 495 nm (450 nm for P1–C60) and was delayed relative to the probe pulse with an optical delay stage (range 0–1.6 ns). The probe beam was obtained by focusing the remaining IR light on a 3 mm sapphire plate, which generated a white-light continuum in the region 500–1000 nm. Alternatively, to generate probe light between 980 and 1040 nm, a TOPAS White OPA (Light Conversion Ltd.) was used. The probe light was subsequently divided into reference and probe beams, and the latter of these was overlapped by the pump at the sample. The probe and reference beams were focused on the entrance slit of a spectrograph and detected by a charge-coupled device (CCD) camera (iXon-Andor) operating synchronously with the 1 kHz laser. The transient spectra were obtained from the difference of the intensities of the probe light (divided by the intensity of the reference) with and without excitation of the sample by the pump beam. Typically 1000 spectra were averaged per delay time.

The transient absorption decays were generally fitted by a triexponential decay function with an offset: I(t) = α1 exp(−t/τ1) + α2 exp(−t/τ2) + α3 exp(−t/τ3) + I0. For every compound at every temperature, two time profiles were fitted: one from the visible part of the spectrum, representing the Q-band bleaching, and one at 1015 nm, where mostly the radical species C60•– and Pn•+ dominate the transient absorption. In the fitting procedure, the two shortest lifetimes (τ1 and τ2) were fixed to the corresponding lifetimes of the first singlet excited state, which were obtained from the fluorescence lifetime measurements (related to charge separation). The two transient absorption decays were fitted individually with the free parameters α1, α2, α3, τ3, and I0 until a reasonable fit was obtained. For P1–C60, a slightly different procedure was employed. Since with our laser system it was not possible to obtain 450 nm pump light and generate probe light at ∼1015 nm in parallel efficiently, only the recovery of the Q-band bleaching was used to determine the lifetime of the charge-separated state. Furthermore, since the fluorescence decay for P1–C60 was monoexponential, the transient absorption decay could be successfully modeled using a biexponential decay function. The fitting parameters α1, α2, and τ2 were free, whereas τ1 was fixed to the corresponding fluorescence lifetime.

Time-Resolved Fluorescence Spectroscopy

Time-resolved emission measurements were performed using a streak camera system. The excitation pulse was provided by a Tsunami Ti:sapphire laser (Spectra-Physics) that was pumped by a Millennia Pro X laser (Spectra-Physics). The Tsunami output was tuned to either 990 or 900 nm and subsequently frequency-doubled to 495 (450 nm for P1–C60). The emitted photons were passed through a spectrograph (Acton SP2300, Princeton Instruments) and finally registered by a streak camera (C5680, Hamamatsu) with a synchroscan unit (M5675, Hamamatsu). Every single frame was measured and stored individually, and the time-resolved fluorescence spectra were obtained from these frames after jitter correction. From these fluorescence spectra, time profiles were extracted by averaging over a selected wavelength region. The fluorescence lifetime decays were fitted with biexponential functions through deconvolution of the instrument response function.

Results and Discussion

Photophysical Studies

The electronic ground-state absorption spectra of the donor–acceptor complexes Pn–C60 are essentially identical with the sum of the corresponding Pn and C60 reference components (Figure 2). The slight red shift in the absorption spectra of the fullerene-terminated oligomers is due to conjugation of the porphyrins with the p-phenylene linking unit. All of the compounds show strong Soret-band absorptions with maxima at 445 nm (P1–C60), 460 nm (P2–C60), 464 nm (P3–C60), 465 nm (P4–C60), and 466 nm (P6–C60) flanked by minor shoulders at ∼495 nm for those compounds containing more than one zinc porphyrin unit. From previous studies it is known that for P2–C60, the absorption at ∼495 nm belongs to the planar conformer (i.e., the conformer in which the porphyrin units are coplanar), whereas the band at 460 nm belongs to a wide distribution of conformers.40,41 This feature allows for nearly exclusive excitation of a planar oligomer in P2 (at 495 nm), but for the longer systems, an increasing number of other conformers are excited at 495 nm because the oligomer contains more subunits. In addition to the Soret-band absorption, sets of Q-bands between 550 and 850 nm (Figure 2) were observed for all systems. The Q-band is red-shifted from 640 to 800 nm and gains intensity as the oligomers get longer.

Figure 2.

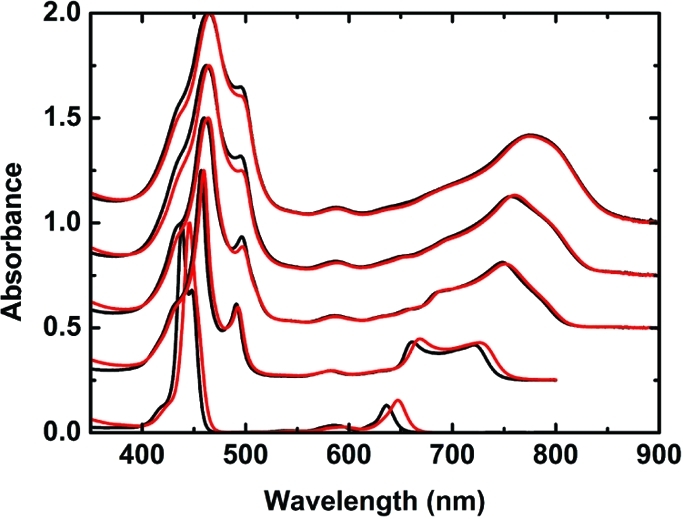
Figure 2

Open in a new tab

Ground-state absorption spectra of Pn (black) and Pn–C60 (red) (n = 1–4, 6) at room temperature. Each spectrum has been normalized and offset by (n – 1) × 0.25 absorbance units.

The influence of temperature on the absorption spectra was investigated for all of the Pn–C60 systems, and only minor changes in the shape of the UV–vis spectra were observed over the temperature range 300–170 K. Below 170 K, the formation of aggregates was observed, as indicated by a sharp absorption band that appeared in the narrow temperature range between 170 and 140 K and was red-shifted relative to the “normal” Q-band absorption. This formation of aggregates was in particular observed for the systems containing more than two porphyrin units (Figures S6.1–S6.5 in the SI), and studies of this phenomenon will be reported in detail elsewhere.(45) In the following, measurements at temperatures where aggregates were expected to form (below 170 K) are presented, but all of the analyses were restricted to temperatures above 170 K to ensure monomolecular behavior.

Charge Separation

Steady-state fluorescence measurements provided information on the overall quenching of the Pn–C60 complexes. Upon excitation at 495 nm (450 nm for P1 and P1–C60), all of the studied donor–acceptor systems showed efficient quenching due to electron transfer from excited Pn to C60.(41) Table 1 shows the calculated quenching efficiencies for the whole series of molecules at temperatures between 140 and 300 K. Except for the two lowest temperatures, where aggregation occurred, the quenching efficiencies varied systematically with both the size of the oligomer and the temperature. The temperature-dependent emission spectra for P3–C60 are shown in Figure 3, and those for the other complexes are presented in Figures S7.1–S7.4 in the SI. While the shapes of the emission spectra for P1–C60 and P2–C60 were unaffected by the temperature change (above 170 K), the corresponding spectra for the longer oligomers exhibited blue shifts, indicative of emission from an increasing number of nonrelaxed conformers as the temperature was lowered. This shows that 495 nm excitation of the longer oligomers produces a mixture of excited conformers, some of which are less prone to undergo charge separation. This behavior was even more evident when the charge-separation process was studied using time-resolved emission.

Table 1. Quenching Efficiencies for the Pn–C60 Compounds Relative to Pna.

T/K P1–C60 P2–C60 P3–C60 P4–C60 P6–C60
140 0.993 0.965 0.858 0.884 0.782
160 0.995 0.973 0.818 0.834 0.770
180 0.994 0.972 0.842 0.688 0.438
200 0.993 0.973 0.868 0.729 0.480
220 0.993 0.975 0.898 0.767 0.519
240 0.993 0.976 0.905 0.799 0.555
260 0.992 0.976 0.909 0.819 0.585
280 0.992 0.975 0.910 0.835 0.602
300 0.990 0.970 0.858 0.840 0.610
Open in a new tab
a

Values at 300 K were calculated as 1 – If(Pn–C60)/If(Pn), where the If’s are the integrated fluorescence intensities from samples of Pn–C60 and Pn with equal absorbances at the excitation wavelength. At lower temperatures, the integrated intensities were related to the intensity recorded at 300 K.

Figure 3.

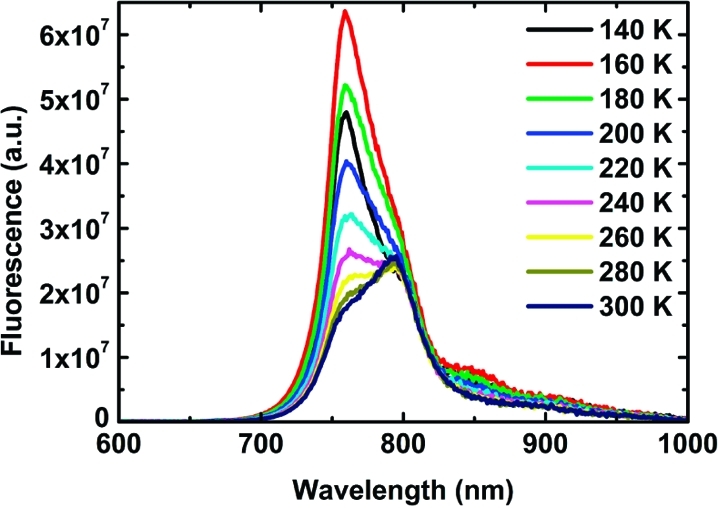
Figure 3

Open in a new tab

Fluorescence spectra of P3–C60 measured at different temperatures.

Measurements of temperature-dependent time-resolved fluorescence and transient absorption based on picosecond and femtosecond laser excitation, respectively, helped provide a more detailed understanding of the electron-transfer processes. Fluorescence decays give the most accurate measurement of the rate constant for charge separation, since the signal is directly related to the quenching process. Except in the case of P1–C60, all of the decays were biexponential at all temperatures (Figure 4 and Figures S8.1–S8.4 in the SI). In general, as shown in Figure 4, the average fluorescence lifetime increased with the length of the porphyrin chain and decreased with increasing temperature. Table 2 presents the lifetimes obtained from fits to the biexponential expression I(t) = α1 exp(−t/τ1) + α2 exp(−t/τ2), in which both the pre-exponential factors (α1 and α2) and the lifetimes (τ1 and τ2) were optimized. The normalized pre-exponential factors were virtually temperature-independent, and their magnitudes scaled with the oligomer length (the average values of α1 were 0.80 for P2–C60, 0.65 for P3–C60, 0.51 for P4–C60, and 0.27 for P6–C60) The first, shorter lifetime (τ1) was slightly temperature-dependent and made a larger contribution for the shorter oligomer systems than for the longer ones. The second, longer lifetime (τ2) also decreased with increasing temperature for the compounds P3–C60, P4–C60, and P6–C60, whereas for P2–C60, no clear trend was seen (Table 2). Since the longer lifetime was significantly shorter than the intrinsic fluorescence lifetime for the corresponding Pn reference system (1450, 1210, 1100, 830, and 650 ps for n = 1–4 and 6, respectively) and the corresponding pre-exponential factor was on the same order of magnitude or even larger than that for the shorter lifetime, the longer-lived component cannot simply be explained as the result of impurities in free Pn.

Figure 4.

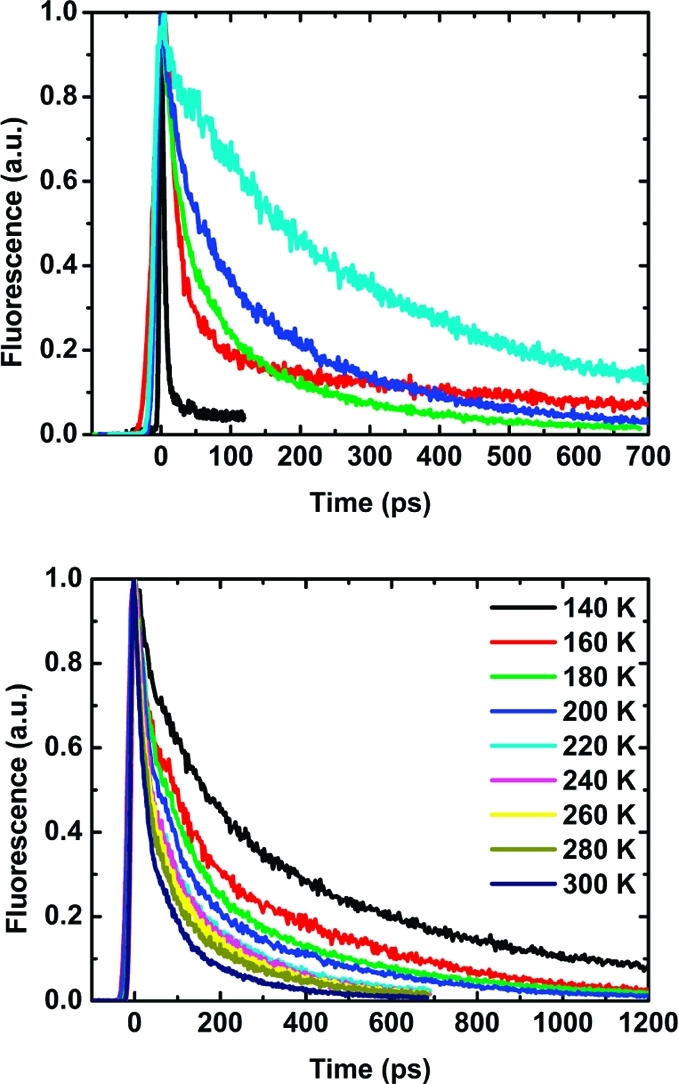
Figure 4

Open in a new tab

(top) Fluorescence decays for the Pn–C60 compounds at 280 K (P1–C60, black; P2–C60, red; P3–C60, green; P4–C60, blue; P6–C60, cyan). (bottom) Fluorescence decays for P3–C60 at different temperatures.

Table 2. Temperature Dependence of the Fitted Lifetimes for P2–C60, P3–C60, P4–C60, and P6–C60 Excited at 495 nm and P1–C60 Excited at 450 nma.

  P1–C60 P2–C60
 P3–C60
 P4–C60
 P6–C60
T/K τ1/ps τ1/ps τ2/ps τ1/ps τ2/ps τ1/ps τ2/ps τ1/ps τ2/ps
140 6.4 37 337 88 536 158 660 269 707
160 6.2 32 311 58 438 101 503 167 650
180 5.9 29 332 51 306 97 447 102 573
200 5.4 23 329 42 310 74 376 76 519
220 5.2 22 361 35 203 52 285 57 471
240 5.0 21 352 29 194 46 254 48 402
260 4.5 20 363 25 181 31 215 36 337
280 4.4 19 445 23 160 29 212 32 300
300 4.4 19 489 20 119 24 216 26 285
Open in a new tab
a

The normalized pre-exponential factors are listed in Table S8.1 in the SI.

Model for Charge Separation

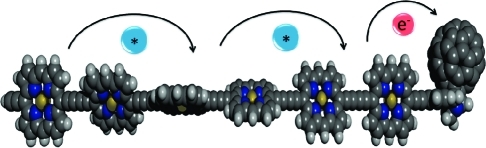
The biexponential fluorescence decay observed for all of the Pn–C60 compounds with n ≥ 2 could be due to several factors, but here we will present a simple model that successfully explains both the oligomer-length dependence and the temperature dependence observed across the whole series of molecules. The fraction of the long-lived decay is larger for the longer oligomers and increases as temperature is lowered (see Figure 4). We know that the porphyrin oligomers have almost free rotation around the butadiyne bridges and that in the ground state all of the conformations are populated even at quite low temperatures. In the case of the longer oligomers, the more twisted conformers dominate the mixture for statistical reasons. In the excited state, the planar structure is stabilized, and if solvent viscosity and/or temperature allow, the excited oligomer planarizes. This process takes ∼100 ps in 2MTHF at room temperature for a single butadiyne bridge (i.e., in P2).(40) Now, upon excitation of Pn–C60, it is possible to localize the excitation energy in one part of the oligomer, as was demonstrated previously for P2.(41) The degree of localization depends on the excitation wavelength or, equivalently, different sets of conformers are selected by tuning the excitation energy. In the experiments presented here, the longest-wavelength peak of the Soret band (495 nm) was selected for excitation. This excites predominantly the planar conformer of P2, but for all of the longer oligomers, this excitation wavelength gives rise to a mixture of conformers, with longer oligomers having broader distributions of excited conformations. Since planarization follows excitation, a thermally activated process occurs in which excitation energy moves from being localized in one part of the oligomer to becoming more delocalized. In the Pn–C60 compounds, where a quencher is attached to one end of the oligomer, it is conceivable that a conformer wherein the excitation energy is localized close to the quencher could undergo rapid electron transfer, whereas another conformer with the excitation energy localized far away from the quencher would first need to transfer its energy to the “active” part of the oligomer before charge separation could occur. In a long oligomer, this could potentially become a very complex process, but in the suggested model shown in Figure 5, we simply divide the molecule into two excited-state populations, an inactive one (Pn*) that is excited “far away” from the quencher and an active one (Pn#) that is excited “close” to the quencher. This simplified model was chosen because a more rigorous treatment of the data involving additional excited-state populations was not needed to fit the measured decays.

Figure 5.

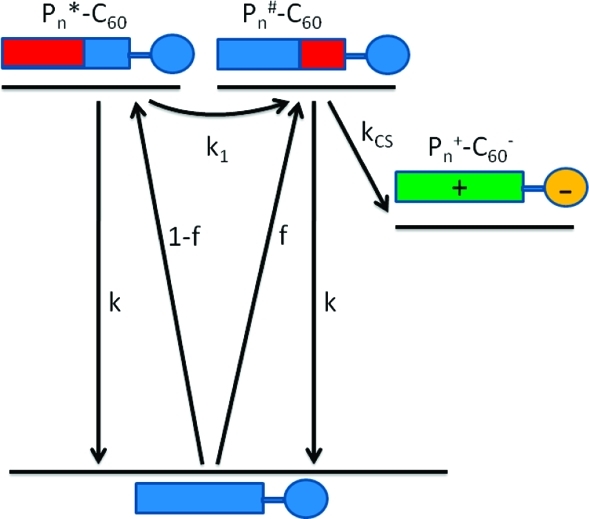
Figure 5

Open in a new tab

Simplified Jablonski diagram showing excitation migration followed by charge separation. Rate constants and symbols are explained in the text.

The kinetic model (Figure 5) is a simple mixture of a consecutive first-order reaction and a first-order quenching. The former contribution stems from the “inactive” population and has a normalized contribution of 1 – f, where f is the fraction of the directly excited “active” population, which undergoes first-order (monoexponential) quenching. Mathematically, this leads to the normalized biexponential fluorescence decay function shown in eq 1:

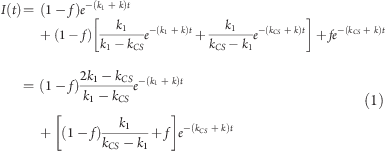graphic file with name ja-2011-019367_m001.gif

where k is the rate constant for unquenched decay of the porphyrin oligomer (assumed to be the same for the active and inactive populations), k1 is the rate constant for transformation of the inactive (*) excited state into the active (#) excited state, and kCS is the charge-separation rate constant (Figure 5). As shown in eq 1, the pre-exponential factors in a biexponential fit of the decays are related to the excited fractions. However, it is only when no transformation between the inactive and active excited states occurs (i.e., when kCS ≫ k1) that the pre-exponential factors directly reflect the excited fractions. Conversely, in a situation where this transformation is much faster than the quenching (k1 ≫ kCS) and faster than the time resolution of the experiment, a monoexponential decay is expected. This latter case corresponds to a donor wherein the excitation energy is fully delocalized over the whole chromophore.

The charge-separation rate constant is thus related to the short lifetime (kCS = τ1–1 – k), and its temperature dependence is expected to follow the Marcus equation (eq 2):

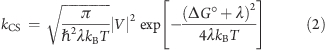graphic file with name ja-2011-019367_m002.jpg

Equation 2 shows that the rate constant for electron transfer is related to several parameters, such as the electronic coupling (V), the reorganization energy accompanying the redistribution of charge (λ), and the thermodynamic driving force for the electron-transfer process (ΔG°). This equation can be rewritten to show that a plot of ln(kCST1/2) versus 1/T should be linear; the electronic coupling V can be obtained from the intercept of this plot, and the slope gives the reorganization energy λ provided that the driving force ΔG° is known. The measured charge-separation rate constants were plotted in this way (Figure 6), and the fits to eq 2 were excellent for all of the oligomers. The two lowest temperatures were excluded from the fit because of the potential for aggregation (see above), although equally good fits were obtained even when these points were included. The data at the lowest temperatures were excluded to ensure that all of the measurements were made on homogeneous samples. The optimized values of the λ and V are found in Table 3. Consistent with our model for charge separation, it was found that the electronic coupling is on the same order of magnitude (20–40 cm–1) for all oligomer lengths. In fact, it was possible to get a reasonable fit of the data by treating V as a common (global) parameter in the fit to all of the oligomers (Figure S8.5 in the SI). This yielded V = 34 cm–1, which is a value consistent with charge separation over short distances. The edge-to-edge distance between the meso carbon of the porphyrin closest to the appended fullerene and the covalent attachment point of the fullerene is ∼9 Å.(46)

Figure 6.

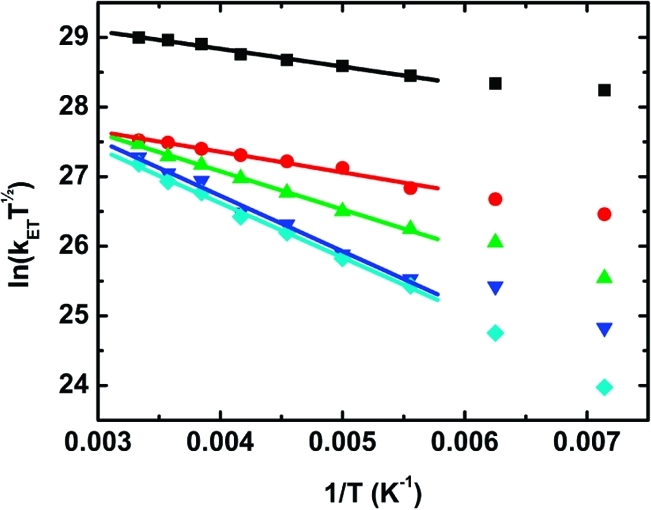
Figure 6

Open in a new tab

Plots of ln(kCST1/2) vs 1/T for P1–C60 (black), P2–C60 (red), P3–C60 (green), P4–C60 (blue), and P6–C60 (cyan). The lines are the individual fits to the linearized form of eq 2.

Table 3. (top) Driving forces (ΔG°),a Reorganization Energies (λ), and Electronic Coupling Values (V) for Charge Separation in Pn–C60 Obtained from Individual Fits of the Curves in Figure 6; (bottom) Reorganization Energies and Electronic Coupling Values for Charge Separation in Pn–C60 Obtained by Treating the Electronic Coupling as a Global Parameter.
  P1–C60 P2–C60 P3–C60 P4–C60 P6–C60
ΔG°/eVa –0.58 –0.38 –0.31 –0.28 –0.25
λ/eV 0.85 0.63 0.66 0.73 0.68
V/cm–1 44 21 31 43 39
  P1–C60 P2–C60 P3–C60 P4–C60 P6–C60
λ/eV 0.78 0.74 0.69 0.69 0.66
V/cm–1 34 34 34 34 34
Open in a new tab
a

ΔG° values for P1–C60, P2–C60, and P4–C60 were taken from ref (44). The values for P3–C60 and P6–C60 were obtained by interpolation and extrapolation of a plot of ΔG° vs 1/n, where n is the number of porphyrin units.

In the suggested charge-separation model, the long-lived fluorescence component (τ2) is assigned to energy transfer from the more distant, charge-separation-inactive domains of the oligomer. As shown in Table 2, this component was also temperature-dependent, and when the energy transfer was treated as an Arrhenius-activated process (Figure S8.6 in the SI), activation energies of 1–2 kcal/mol were obtained for the longer chains containing 3, 4, and 6 porphyrin units. For planarization of the excited perpendicular P2 in 2-MTHF, an activation energy of 2 kcal/mol was found,(40) and since these values have similar magnitudes, it seems likely that the energy-transfer process along the oligomer chain is in part accompanied by planarization. It might seem surprising that the temperature dependence of the long-lived component in P2–C60 did not follow this trend, but since excitation at 495 nm in P2 almost exclusively populates the planar conformer, this minor (<20% at all temperatures) fluorescence decay component might have a different origin than for the longer oligomers.

Quantum Yield for Charge Separation

As a consequence of the restricted delocalization along the longer porphyrin oligomers, the quantum yield for charge separation becomes less than unity and decreases with decreasing temperature. Figure 7 shows the charge-separation quantum yield calculated in two ways: either directly from the quenching efficiencies (Table 1) or from the fitted lifetimes and pre-exponential factors. From the kinetic model (eq 1 and Figure 5), the quantum yield for charge separation can be expressed as

graphic file with name ja-2011-019367_m003.jpg

and since the excited fractions (f and 1 – f) are related to the normalized pre-exponential factors available through fitting the decay, this can be written as

graphic file with name ja-2011-019367_m004.jpg

where α1 is the pre-exponential factor for the decay of Pn* (the long-lived decay component). The agreement between the two ways of calculating the charge-separation quantum yields is reasonable and lends support to the suggested model for charge separation.

Figure 7.

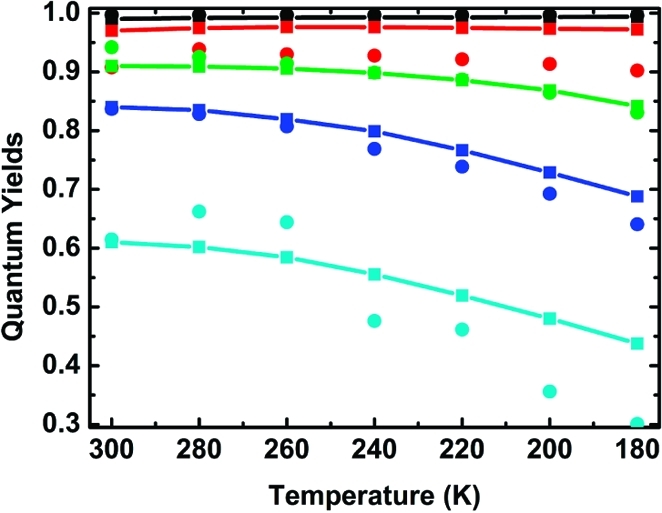
Figure 7

Open in a new tab

Quantum yields for the formation of the charge-separated state based on the steady-state (◼) and time-resolved (●) fluorescence measurements for P1–C60 (black), P2–C60 (red), P3–C60 (green), P4–C60 (blue), and P6–C60 (cyan) at different temperatures. The solid lines between filled squares are guides to the eye.

Charge Recombination

Transient absorption measurements based on femtosecond laser excitation provided evidence for the proposed mechanism for electron transfer between the excited oligoporphyrin and C60. As an example, Figure 8 shows the transient absorption spectrum of P3–C60 75 ps after excitation, which shows characteristic features of the charge-separated state: P3•+ dominates the visible absorption, C60•– and P3•+ both contribute to the NIR absorption,47,48 and Q-band bleaching dominates the negative band in the 700–800 nm region. The kinetic analyses of these bands yielded rates corresponding to the fluorescence decay, showing the expected connection between charge separation and decay of the singlet excited state of the oligoporphyrin. From the decay of the radical absorption and/or the recovery of the Q-band shown in Figure 8, the lifetime of the charge-separated state could be determined (fitting parameters are given in Tables S9.1–S9.5b in the SI). This was done for all systems at temperatures between 140 and 300 K, and the results are collected in Table 4.

Figure 8.

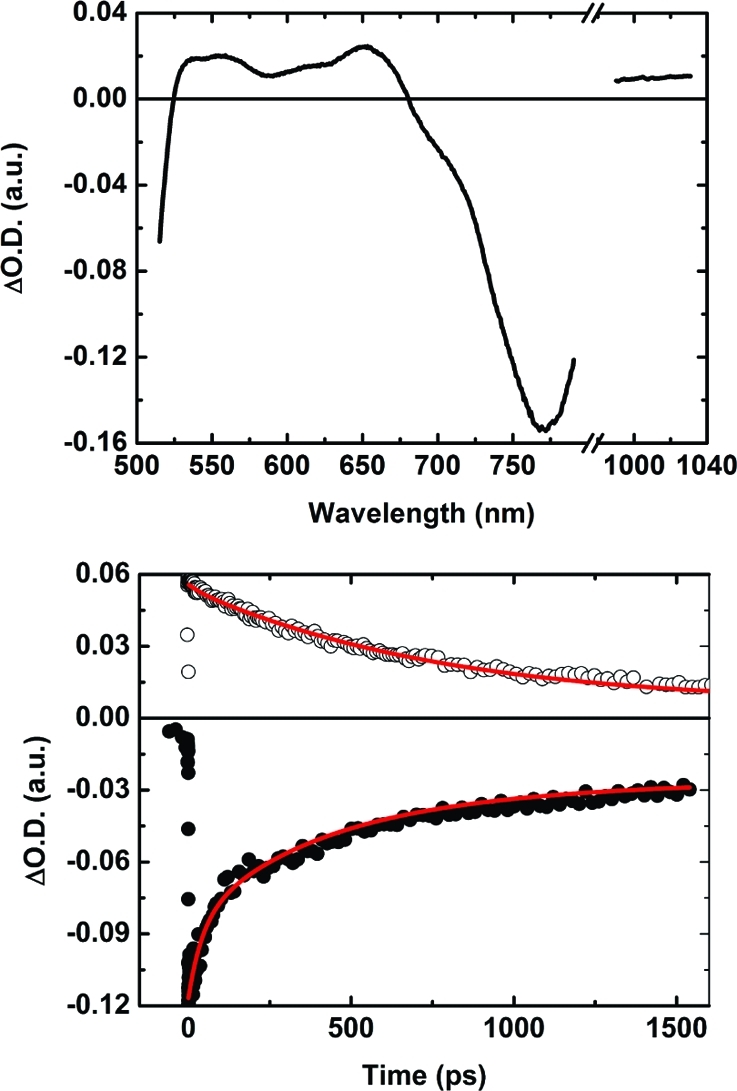
Figure 8

Open in a new tab

(top) Femtosecond transient absorption spectra of P3–C60 at 200 K for a delay time of 75 ps. The NIR part of the spectrum was collected with probe light from an OPA and the visible part with a white-light continuum. (bottom) Transient absorption decay at 1015 nm (○; multiplied by a factor of 5 for better visibility), where the C60•– and P3•+ species dominate the absorption, and at 730 nm (●), showing the recovery of the Q-band absorption. The red solid lines show fits of the transient absorption decays.

Table 4. Lifetimes of the Charge-Separated States for P1–C60, P2–C60, P3–C60, P4–C60, and P6–C60 upon Excitation at 495 nm (450 nm for P1–C60) Obtained from the Transient Absorption Decays at 1015 nm and at the Wavelength of the Q-Band Bleaching Maxima (The Values for P1–C60 Were Found from Q-Band Bleaching at 650 nm).

  τ/ps
T/K P1–C60 P2–C60 P3–C60 P4–C60 P6–C60
140 455 732 904 917 1112
160 349 692 794 846 1005
180 309 640 710 734 951
200 274 584 696 708 903
220 226 493 627 689 821
240 208 454 554 604 786
260 201 373 504 567 748
280 191 290 483 538 658
300 189 276 463 499 643
Open in a new tab

The lifetimes of the charge-separated states have weak temperature dependences for all of the oligomers, spanning from ∼200 ps for P1–C60 at room temperature to 1 ns for P6–C60 at 140 K. More importantly, the lifetimes of the charge-separated states at a given temperature have the same order of magnitude for all of the investigated systems, indicating that the positive charge is either localized close to the fullerene or delocalized over all of the porphyrin units and thus does not need to migrate over a large distance to recombine. Measuring femtosecond transient absorption decays at low temperature (in a liquid nitrogen cryostat) is quite challenging, and the quality of the data did not allow a thorough investigation of potential multiexponentiality arising from a scenario similar to that suggested for charge separation. However, since only almost-planar conformers or excitations localized closest to C60 lead to charge separation, no further structural relaxations are expected during charge recombination. This should lead to a single lifetime for the charge-separated state, and the recombination of the charge separated state was therefore fitted using only one exponential. The whole transient absorption decay was fitted to a triexponential decay function, where the two shortest lifetimes were fixed to the values obtained from the lifetimes of the fluorescence decays (corresponding to the charge separation). The procedure is explained in detail in the Experimental Section.

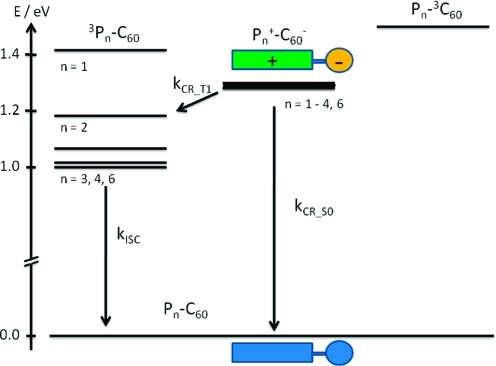
In Figure 9, the rate constants for charge recombination (kCR) are plotted against inverse temperature and fitted to the linearized form of eq 2. Reasonable fits with similar slopes over the whole temperature range (180–300 K) were found for all of the systems except P2–C60, which showed a change in slope above 240 K. Such a temperature dependence might indicate a change in mechanism for the charge recombination. As shown in Table 5, for P2–C60 and the longer systems, charge recombination to the lowest excited triplet state of the porphyrin oligomer is exergonic. From experimental estimates of the triplet energies and oxidation potentials, it is concluded that the driving force increases with increasing size of the oligomer.44,49 This might mean that recombination to the electronic ground state occurs in P1–C60 and recombination to the porphyrin-localized triplet state occurs in P3–C60, P4–C60, and P6–C60. In P2–C60, a combination of charge recombination to the triplet and ground states, with the former dominating at high temperatures, would explain the change in slope. Naturally, it would be desirable to distinguish between these two mechanisms by comparing the residual transient absorption (or bleaching) at long times. However, experimental difficulties combined with quite substantial triplet formation in the longer systems due to the comparably low yield for charge separation (see above) did not allow a precise distinction between the two recombination possibilities. Recombination through the C60 triplet state (experimentally determined to be at 1.5 eV) is endergonic and not expected to contribute to the observed decay.50,51 This is further supported by the absence of the characteristic triplet C60 transient absorption that would have been expected at ∼700 nm if recombination through this channel had been significant.(51) Figure 10 summarizes the recombination processes. The Marcus parameters λ and V for recombination to either the ground state or the triplet state as calculated from the linear fits are summarized in Table 5.

Figure 9.

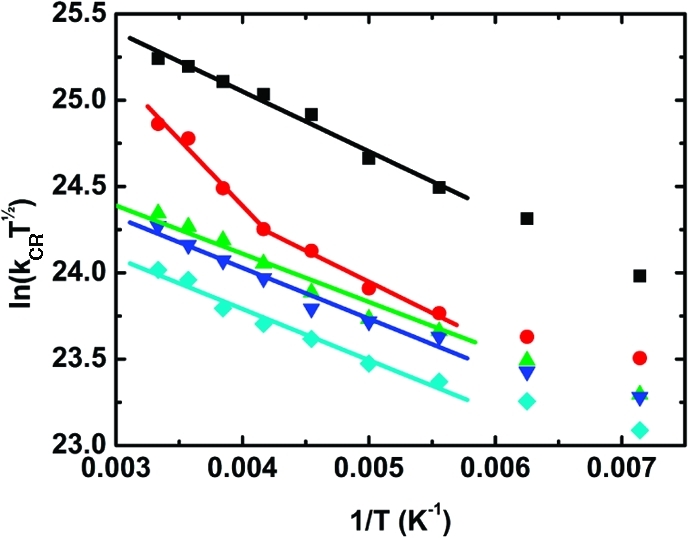
Figure 9

Open in a new tab

Plots of ln(kCRT1/2) vs 1/T for P1–C60 (black), P2–C60 (red), P3–C60 (green), P4–C60 (blue), and P6–C60 (cyan). The samples were excited at 495 nm, and the rate constants were derived from the transient absorption decays (kCR = 1/τ). The lines are fits to the linearized form of eq 2.

Table 5. Driving Forces (ΔG°)a, Reorganization Energies (λ), and Electronic Coupling Values (V) for Charge Recombination in Pn–C60 Obtained from Individual Fits Assuming Recombination to the First Excited Triplet State or Directly to the Ground State.

  P1–C60 P2–C60 P2–C60 P3–C60 P4–C60 P6–C60
parameter   180–240 K 240–300 K      
Assuming Recombination to the First Triplet Excited State
ΔG°/eV +0.12 –0.13 –0.13 –0.24 –0.30 –0.33
λ/eV – 0.33 0.49 0.47 0.53 0.57
V/cm–1 – 4.5 11.5 4.2 3.8 3.52
Assuming Recombination to the Ground State
ΔG°/eV –1.29 –1.30 –1.30 –1.31 –1.31 –1.31
λ/eV 0.95 0.96 0.83 0.98 0.99 0.99
V/cm–1 8.1 5.8 13.1 5.0 4.5 4.0
Open in a new tab
a

ΔG° values for P1–C60, P2–C60, and P4–C60 were taken from refs (44) and (49). The values for P3–C60 and P6–C60 were obtained by interpolation and extrapolation of a plot of ΔG° vs 1/n, where n is the number of porphyrin units.

Figure 10.

Figure 10

Open in a new tab

Energy diagram for the charge-recombination processes. The energy of the charge-separated state is quite insensitive to the oligomer length, whereas for the longer oligomers the lowest triplet state of the oligomer is stabilized enough to become a feasible recombination channel.

Because of the large driving force for recombination to the ground state, the electron-transfer process along this pathway is in the inverted Marcus region (|ΔG°| > λ). For recombination to the triplet excited state, the driving forces are much smaller. Nevertheless, the lifetimes of the charge-separated states are quite short as a consequence of a comparatively large electronic coupling. In comparisons of the electronic couplings for charge separation and recombination, it is notable that these are smaller for the recombination reaction. This might be an additional indication that charge recombination occurs from a more delocalized state than charge separation.

Conclusion

In this study of the temperature dependence of electron-transfer reactions in a series of porphyrin oligomer electron donors appended with a C60 electron acceptor, the following has been learned:

  • 1.

    Charge separation from the excited donor occurs either directly from an active part of the oligomer or through excitation migration along the oligomer chain followed by charge separation.

  • 2.

    Direct charge separation dominates in the short oligomers, while energy migration precedes charge separation in the longer oligomers, particularly at high temperatures.

  • 3.

    Energy migration in the oligomers is thermally activated through dihedral conformational relaxation.

  • 4.

    Factors 2 and 3 limit the yield for charge separation in the longer oligomers. A high quantum yield for charge separation in the longer oligomers requires fast energy migration and, presumably, nearly planar structures with a high degree of excitation-energy delocalization.

  • 5.

    The energy migration model is supported by earlier observations of energy delocalization in porphyrin oligomers through measurements of fluorescence depolarization.(52) Transient fluorescent polarization anisotropy in oligomers such as P6 and P8 shows that light absorption generates an excited state that is initially delocalized over the whole oligomer but contracts rapidly on a time scale of less than 0.5 ps; interporphyrin torsional relaxation then leads to delocalization of the excited state on a time scale of ∼100 ps. The results reported here provide detailed information on the slower delocalization process. They are not sensitive to the initial ultrafast delocalization but demonstrate that exciton self-trapping must be much faster than electron transfer to C60.

  • 6.

    The actual charge-separation and charge-recombination reactions are both temperature-dependent, as predicted by the Marcus theory. Reasonable values for the reorganization energies and electronic couplings were extracted from fits of the temperature variation of the time-resolved fluorescence and femtosecond transient absorption decays.

  • 7.

    Charge recombination occurs directly to the electronic ground state in P1–C60 and through the porphyrin-localized triplet state in P3–C60, P4–C60, and P6–C60. In P2–C60, a combination of charge recombination to the triplet and ground states takes place, with the former dominating at high temperatures.

Acknowledgments

This research was funded by the Swedish Research Council (VR), the Swedish Energy Agency, the Knut and Alice Wallenberg Foundation, the Engineering and Physical Sciences Research Council (EPSRC), and the Swiss National Science Foundation. We thank the EPSRC Mass Spectrometry Service (Swansea) for mass spectra.

Supporting Information Available

Synthesis, NMR spectra, mass spectra, HPLC traces, ground-state absorption spectra, steady-state emission spectra, time-resolved fluorescence decays and fitting parameters, and transient absorption fitting parameters. This material is available free of charge via the Internet at http://pubs.acs.org.

Supplementary Material

ja2019367_si_001.pdf (5.3MB, pdf)

References

  1. Guldi D. Phys. Chem. Chem. Phys. 2007, 9, 1400–1420. [DOI] [PubMed] [Google Scholar]
  2. Deisenhofer J.; Michel H. Annu. Rev. Cell Biol. 1991, 7, 1–23. [DOI] [PubMed] [Google Scholar]
  3. Barter L. M. C.; Durrant J. R.; Klug D. R. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 946–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Windsor M. W. J. Chem. Soc., Faraday Trans. 2 1986, 82, 2237–2243. [Google Scholar]
  5. Boxer S. G.; Goldstein R. A.; Lockhart D. J.; Middendorf T. R.; Takiff L. J. Phys. Chem. 1989, 93, 8280–8294. [Google Scholar]
  6. Huber R. Eur. J. Biochem. 1990, 187, 283–305. [DOI] [PubMed] [Google Scholar]
  7. Clayton R. K. Annu. Rev. Biophys. Bioeng. 1973, 2, 131–156. [DOI] [PubMed] [Google Scholar]
  8. Kelley R. F.; Tauber M. J.; Wasielewski M. R. Angew. Chem., Int. Ed. 2006, 45, 7979–7982. [DOI] [PubMed] [Google Scholar]
  9. Barazzouk S.; Kamat P. V.; Hotchandani S. J. Phys. Chem. B 2005, 109, 716–723. [DOI] [PubMed] [Google Scholar]
  10. Zhang T.-G.; Zhao Y.; Asselberghs I.; Persoons A.; Clays K.; Therien M. J. J. Am. Chem. Soc. 2005, 127, 9710–9720. [DOI] [PubMed] [Google Scholar]
  11. Ohtani M.; Kamat P. V.; Fukuzumi S. J. Mater. Chem. 2010, 20, 582–587. [Google Scholar]
  12. Guldi D. M. Chem. Soc. Rev. 2002, 22–36.12108980 [Google Scholar]
  13. Fukuzumi S.; Honda T.; Ohkubo K.; Kojima T. Dalton Trans. 2009, 3880–3889. [DOI] [PubMed] [Google Scholar]
  14. Rizzi A. C.; van Gastel M.; Liddell P. A.; Palacios R. E.; Moore G. F.; Kodis G.; Moore A. L.; Moore T. A.; Gust D.; Braslavsky S. E. J. Phys. Chem. A 2008, 112, 4215–4223. [DOI] [PubMed] [Google Scholar]
  15. Jakob M.; Berg A.; Rubin R.; Levanon H.; Li K.; Schuster D. I. J. Phys. Chem. A 2009, 113, 5846–5854. [DOI] [PubMed] [Google Scholar]
  16. Harriman A. Angew. Chem., Int. Ed. 2004, 43, 4985–4987. [DOI] [PubMed] [Google Scholar]
  17. Guldi D. M. Phys. Chem. Chem. Phys. 2007, 9, 1400–1420. [DOI] [PubMed] [Google Scholar]
  18. Quintiliani M.; Kahnt A.; Wölfle T.; Hieringer W.; Vázquez P.; Görling A.; Guldi D. M.; Torres T. Chem.—Eur. J. 2008, 14, 3765–3775. [DOI] [PubMed] [Google Scholar]
  19. El-Khouly M. E.; Ito O.; Smith P. M.; D’Souza F. J. Photochem. Photobiol., C 2004, 5, 79–104. [Google Scholar]
  20. Kahnt A.; Guldi D. M.; de la Escosura A.; Martinez-Diaz M. V.; Torres T. J. Mater. Chem. 2008, 18, 77–82. [Google Scholar]
  21. Martinez-Diaz M. V.; de la Torre G.; Torres T. Chem. Commun. 2010, 46, 7090–7108. [DOI] [PubMed] [Google Scholar]
  22. Kahnt A.; Quintiliani M.; Vázquez P.; Guldi D. M.; Torres T. ChemSusChem 2008, 1, 97–102. [DOI] [PubMed] [Google Scholar]
  23. Guldi D. M.; Rahman G. M. A.; Sgobba V.; Ehli C. Chem. Soc. Rev. 2006, 35, 471–487. [DOI] [PubMed] [Google Scholar]
  24. Li H.; Martin R. B.; Harruff B. A.; Carino R. A.; Allard L. F.; Sun Y. P. Adv. Mater. 2004, 16, 896–900. [Google Scholar]
  25. Iurlo M.; Paolucci D.; Marcaccio M.; Paolucci F. Chem. Commun. 2008, 4867–4874. [DOI] [PubMed] [Google Scholar]
  26. D’Souza F.; Ito O. Chem. Commun. 2009, 4913–4928. [DOI] [PubMed] [Google Scholar]
  27. Imahori H.; Sakata Y. Eur. J. Org. Chem. 1999, 2445–2457. [Google Scholar]
  28. Kesti T.; Tkachenko N.; Yamada H.; Imahori H.; Fukuzumi S.; Lemmetyinen H. Photochem. Photobiol. Sci. 2003, 2, 251–258. [DOI] [PubMed] [Google Scholar]
  29. Gust D.; Moore T. A.; Moore A. L. Res. Chem. Intermed. 1997, 23, 621–651. [Google Scholar]
  30. Martin N.; Sanchez L.; Illescas B.; Perez I. Chem. Rev. 1998, 98, 2527–2548. [DOI] [PubMed] [Google Scholar]
  31. Wojcik A.; Kamat P. V. ACS Nano 2010, 4, 6697–6706. [DOI] [PubMed] [Google Scholar]
  32. Guldi D. M.; Sgobba V. Chem. Commun. 2011, 47, 606–610. [DOI] [PubMed] [Google Scholar]
  33. Armaroli N.; Accorsi G.; Song F.; Palkar A.; Echegoyen L.; Bonifazi D.; Diederich F. ChemPhysChem 2005, 6, 732–743. [DOI] [PubMed] [Google Scholar]
  34. Fukuzumi S.; Kojima T. J. Mater. Chem. 2008, 18, 1427–1439. [Google Scholar]
  35. Hasobe T.; Saito K.; Kamat P. V.; Troiani V.; Qiu H.; Solladie N.; Kim K. S.; Park J. K.; Kim D.; D’Souza F.; Fukuzumi S. J. Mater. Chem. 2007, 17, 4160–4170. [Google Scholar]
  36. Goldsmith R. H.; DeLeon O.; Wilson T. M.; Finkelstein-Shapiro D.; Ratner M. A.; Wasielewski M. R. J. Phys. Chem. A 2008, 112, 4410–4414. [DOI] [PubMed] [Google Scholar]
  37. Kuciauskas D.; Liddell P. A.; Lin S.; Stone S. G.; Moore A. L.; Moore T. A.; Gust D. J. Phys. Chem. B 2000, 104, 4307–4321. [Google Scholar]
  38. Kang Y. K.; Duncan T. V.; Therien M. J. J. Phys. Chem. B 2007, 111, 6829–6838. [DOI] [PubMed] [Google Scholar]
  39. Lemmetyinen H.; Tkachenko N. V.; Efimov A.; Niemi M. J. Phys. Chem. C 2009, 113, 11475–11483. [Google Scholar]
  40. Winters M. U.; Kärnbratt J.; Eng M.; Wilson C. J.; Anderson H. L.; Albinsson B. J. Phys. Chem. C 2007, 111, 7192–7199. [Google Scholar]
  41. Winters M. U.; Kärnbratt J.; Blades H. E.; Wilson C. J.; Frampton M. J.; Anderson H. L.; Albinsson B. Chem.—Eur. J. 2007, 13, 7385–7394. [DOI] [PubMed] [Google Scholar]
  42. Sundström V.; Pullerits T.; van Grondelle R. J. Phys. Chem. B 1999, 103, 2327–2346. [Google Scholar]
  43. Halls J. J. M.; Pichler K.; Friend R. H.; Moratti S. C.; Holmes A. B. Appl. Phys. Lett. 1996, 68, 3120–3122. [Google Scholar]
  44. Winters M. U.; Dahlstedt E.; Blades H. E.; Wilson C. J.; Frampton M. J.; Anderson H. L.; Albinsson B. J. Am. Chem. Soc. 2007, 129, 4291–4297. [DOI] [PubMed] [Google Scholar]
  45. Kärnbratt J.; Anderson H. L.; Albinsson B. Manuscript in preparation.
  46. For example, in a porphyrin dimer system with a porphyrin–porphyrin distance of 13 Å, we found V = 19 cm–1. See: ; Pettersson K.; Wiberg J.; Ljungdahl T.; Mårtensson J.; Albinsson B. J. Phys. Chem. A 2006, 110, 319–326. [DOI] [PubMed] [Google Scholar]
  47. Gasyna Z.; Andrews L.; Schatz P. N. J. Phys. Chem. 1992, 96, 1525–1527. [Google Scholar]
  48. Guldi D. M.; Hungerbuhler H.; Janata E.; Asmus K. D. J. Chem. Soc., Chem. Commun. 1993, 84–86. [Google Scholar]
  49. Kuimova M. K.; Hoffmann M.; Winters M. U.; Eng M.; Balaz M.; Clark I. P.; Collins H. A.; Tavender S. M.; Wilson C. J.; Albinsson B.; Anderson H. L.; Parker A. W.; Phillips D. Photochem. Photobiol. Sci. 2007, 6, 675–682. [DOI] [PubMed] [Google Scholar]
  50. Williams R. M.; Zwier J. M.; Verhoeven J. W. J. Am. Chem. Soc. 1995, 117, 4093–4099. [Google Scholar]
  51. Guldi D. M.; Asmus K.-D. J. Phys. Chem. A 1997, 101, 1472–1481. [Google Scholar]
  52. Chang M.-H.; Hoffmann M.; Anderson H. L.; Herz L. M. J. Am. Chem. Soc. 2008, 130, 10171–10178. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja2019367_si_001.pdf (5.3MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES