Combining Disease Models to Test for Gene-Environment Interaction in Nuclear Families

Summary

It is useful to have robust gene-environment interaction tests that can utilize a variety of family structures in an efficient way. This paper focuses on tests for gene-environment interaction in the presence of main genetic and environmental effects. The objective is to develop powerful tests that can combine trio data with parental genotypes and discordant sibships when parents genotypes are missing. We first make a modest improvement on a method for discordant sibs (discordant on phenotype), but the approach does not allow one to use families when all offspring are affected, e.g. trios. We then make a modest improvement on a Mendelian transmission-based approach that is inefficient when discordant sibs are available, but can be applied to any nuclear family. Finally, we propose a hybrid approach that utilizes the most efficient method for a specific family type, then combines over families. We utilize this hybrid approach to analyze a chronic obstructive pulmonary disorder dataset to test for gene-environment interaction in the Serpine2 gene with smoking. The methods are freely available in the R package fbati.

1. Introduction

The interaction between genetic susceptibilities and environmental exposures is thought to play an important role in complex diseases. For example, in chronic obstructive pulmonary disorder (COPD), gene-environment interactions with smoking are thought to be determinants of disease severity (Celedon et al., 2004; Demeo et al., 2006; Vansteelandt et al., 2008). Concern for population substructure and model misspecification warrants robust tests, while utilizing information from all available family structures will increase power.

Case-control methods are used because subjects are easy to recruit and they often have higher power than family-based designs. However, family-based methods can be formulated to be completely robust to population substructure; i.e. a systematic difference in allele frequencies in different groups in a population. For a review of family-based methods see Laird and Lange (2006). We define interaction in a statistical sense here as a departure from additive main effects in a generalized linear model (GLM), which may be different than a biological interaction (Cordell, 2002; VanderWeele, 2009). Here an interaction test is scale dependent, and cannot be made completely model free (Greenland, 1993; Robins et al., 1992). A joint test for gene and gene-environment interaction can be made model-free, but does not distinguish whether the departure from the null involved the main effect or the interaction (Lunetta et al., 2000; Hoffmann et al., 2009). In this paper we consider testing for a gene-environment interaction in the presence of any main genetic or environmental effect.

There are two standard family designs in the literature: triads and discordant sibs. There are also two general methods that have been used to analyze these data, both robust to population substructure. The first set of methods utilizes the information from the Mendelian transmissions of parents to offspring; we will refer to these as transmission-based methods. The second set of methods is based on utilizing the information from the discordant phenotypes of siblings. When we refer to discordant siblings in this paper, we will always be referring to discordant phenotypes.

The transmission-based methods proposed in the literature generally assume a relative-risk based (log-linear) model for disease. They avoid estimating the main effect of the environmental exposure, making less assumptions about the form of the interaction model. However, by not estimating environmental effects, the interaction can be harder to interpret. They also do not use (or need) the environmental exposure of the unaffected offspring. They assume conditional independence of the genotype and environmental exposure given the parents, an assumption first introduced and discussed in detail in Umbach and Weinberg (2000). The assumption fails when the genotype is causal for the environmental exposure; e.g., ALDH2 carriers avoiding alchohol because of discomfort and flushing when drinking (Chen et al., 1998). The approaches proposed by Kistner et al. (2009) and Dudbridge (2008) allow for missing parents by introducing nuisance parameters for them into the likelihood. Dudbridge (2008) shows his approach is not completely robust to population substructure when parents are missing. The Kistner et al. (2009) approach also allows for parent-of-origin effects. Cordell et al. (2004) handles continuous environmental exposures, but is limited to cases when parents are present. The Hoffmann et al. (2009) method extends Lake and Laird (2004) to trios and sibships by stratifying on the sufficient statistic for parental mating type (i.e. the pair of parental genotypes), but is also limited to a single affected offspring. The method we propose based on Mendelian transmissions conditions on the sufficient statistic for parental transmission to handle missing parents, as we explain in the methods section.

The methods based only on discordant phenotypes of offspring (Witte et al., 1999; Siegmund et al., 2000; Weinberg, 2000) have used a logistic model for disease. The conditional logistic regression (CLR) approach proposed by Witte et al. (1999) does not need to assume conditional independence of genotype and exposure, as it does not utilize any transmission information from the parents (Siegmund et al., 2000; Weinberg, 2000). However, it must model the main effect of the environmental exposure, and so makes more assumptions on the disease model than the transmission-based methods previously discussed. A slightly more powerful approach introduced by Chatterjee et al. (2005) for discordant offspring utilizes both the information from the discordant phenotype and from the Mendelian transmissions (we will refer to as CLR-IND); the approach requires a rare disease assumption. The extension we propose of the CLR-IND approach uses the same sufficient statistic for parental transmission that we use in the transmission approach, rather than a pairwise likelihood. The extension offers a modest improvement over the the CLR-IND approach for families with discordant offspring with more than two siblings.

Although applicable to any nuclear family, when applied to discordant offspring, the transmission-based approaches suffer a considerable power loss compared to those that use discordant phenotype information. Chatterjee et al. (2005) suggests combining approaches to utilize the more powerful approach whenever applicable, and a less powerful approach when it is not.

In this paper we propose a hybrid approach to test for gene-environment interaction in the presence of main effects under a rare disease assumption. The hybrid approach utilizes the more efficient method for discordant offspring whenever they are available, and the transmission-based approach when the offspring do not have discordant phenotypes. We test the robustness of the hybrid approach to phenotypic model and rare disease assumptions via simulation. Lastly, we apply the approach to a COPD dataset.

2. Models and Methods

Let i index families and j the offspring in the i^th family. Let g_ij be the respective genotype, Z_ij the environmental exposure, Y_ij the dichotomous phenotype, and C_ij a vector of any potential covariates to adjust for. Let X_ij = X(g_ij) be some coding of the main effect of the genotype. Let X_ge,ij = X_ge(g_ij) be a potentially different coding of the genotype for the interaction; the utility of this approach is explained below. Let g_i, Z_i, C_i, Y_i, and X_i be the corresponding vectors, e.g. of g_ij. A GLM with interaction can be given under the model

$$l\{Pr(Y_{ij}=1\mid {\mathbf{X}}_{ij},Z_{ij},{\mathbf{C}}_{ij},P_i;\mathit{\beta })\}={\alpha }_i+{\mathit{\beta }}_{\text{ge}}^T{\mathbf{X}}_{\text{ge},ij}{Z}_{ij}+{\mathit{\beta }}_{\text{nuis}}^T\mathbf{m}({\mathbf{X}}_{ij},Z_{ij},{\mathbf{C}}_{ij}).$$ (1)

where l is the link function, P_i is the parental genotype, β_nuis = (β_g, β_e, β_c), and $\mathbf{m}({\mathbf{X}}_{ij},Z_{ij},{\mathbf{C}}_{ij})=({\mathbf{X}}_{ij}^T,Z_{ij},{\mathbf{C}}_{ij}^T)$. The intercept α_i will cancel out of all likelihoods in the approaches that we will consider. A term incorporating an arbitrary functional form of the parental mating type and any family factor, μ_i(P_i), could also be added to the model, but is not necessary as it also drops out of the likelihoods that we will consider. In order to test for gene-environment interaction, we test H₀: β_ge = 0. Note that in this model we assume that only Z_ij has an interaction with X_ij, not C_ij.

In this paper, we are focused on testing β_ge. In practice we are rarely testing the true disease susceptibility locus (DSL). Instead we will be testing SNPs that are in linkage disequilibrium (LD), i.e. correlated, with the DSL. In this case the β coefficients do not have a directly meaningful interpretation. To make the test valid when the SNP is only in LD with the DSL, we use score tests with a saturated model for X with dummy variables, i.e. X = X(g) = {I_(g=AA), I_(g=Aa)}, and an empirical variance. To allow for testing specific alternatives, we allow X_ge to be a one degree-of-freedom coding, e.g. additive or recessive.

In all of the following methodology we introduce, when we have multiple offspring, we will make the assumption that

$$Pr({\mathbf{Y}}_i={\mathbf{y}}_i\mid {\mathbf{X}}_i,{\mathbf{Z}}_i,{\mathbf{C}}_i,P_i)=\prod _{j}Pr(Y_{ij}=y_{ij}\mid {\mathbf{X}}_{ij},Z_{ij},{\mathbf{C}}_{ij},P_i).$$ (2)

This assumption could be violated in at least three situations. First it assumes the phenotype of offspring is not affected by siblings’ genotype, even if only in LD to the DSL. Secondly, it assumes phenotype independence within each family. We explore violations of these first two assumptions by simulation. Thirdly, it assumes the environmental exposure or covariates of other subjects in the family have no residual association with the phenotype of other offspring. This is a somewhat more subtle assumption that can be circumvented with more complicated phenotype models, and will be discussed further in the context of the example.

2.1 Transmission-based approach using the conditional genotype distribution for general nuclear families (TX)

The transmission-based approach we will discuss in this section is applicable to any nuclear family, but is less efficient than subsequent approaches when there are discordant offspring, as the phenotype of the unaffected offspring is not used. For the transmission-based approach, we can use a less parametric model for the disease than equation 1 with the model $Pr(Y_{ij}=1\mid g_{ij},Z_{ij},{\mathbf{C}}_{ij},P_i;\mathit{\beta })=Pr(Y_{ij}=1\mid g_{ij}=aa,Z_{ij},{\mathbf{C}}_{ij},P_i)e^{{\mathit{\beta }}_{\text{ge}}^T{\mathbf{X}}_{\text{ge},ij}{Z}_{ij}+{\mathit{\beta }}_{\text{g}}^T{\mathbf{X}}_{ij}}$. This is because individual covariates do not need to be modeled, as they are absorbed into the term Pr(Y_ij = 1|g_ij = aa, Z_ij, C_ij), which will cancel out of the retrospective likelihood proposed below. We still assume there is no interaction between X_ij and C_ij conditioning on the parents. The model allows for an arbitrary functional form of the environmental main effect; we require only that under the null the environmental factor acts multiplicative to the main genetic effect. Thus the test allows for any multiplicative environmental main effect, and a saturated main genetic effect to avoid misspecification.

Assuming Mendel’s laws can be used to specify Pr(X_i|P_i), we use Bayes rule (Schaid, 1996; Cordell et al., 2004; Kistner et al., 2009) to construct a test based on the joint distribution of the genotypes of all of the affected offspring for each family, conditioning on covariates, parental genotypes, and phenotypes:

$${\mathcal{L}}_i^{\text{TX}}=Pr({\mathbf{X}}_i\mid {\mathbf{Y}}_i=1,{\mathbf{Z}}_i,{\mathbf{C}}_i,P_i).$$ (3)

Unaffected offspring only contribute to determining the conditional distribution of affected offspring genotypes when missing one or more parental genotype. In the case of missing parents, there can be several parental genotypes consistent with the observed data. We replace conditioning on P_i by the sufficient statistic for P_i, say S_i. S_i is a function only of the observed genotypes, which may include both offspring and parental genotypes. S_i has the property that $Pr({\mathbf{X}}_i\mid S_i,P_i^{\text{mis}})=Pr({\mathbf{X}}_i\mid S_i)$, where $P_i^{\text{mis}}$ denotes the genotypes of any missing parents. Note that S_i = P_i by definition if both parents are observed, hence we use Pr(X_i|S_i) to denote the conditional distribution regardless of family type. S_i and Pr(X_i|S_i) depend upon the observed family genotypes, but are easily enumerated via the algorithm in Rabinowitz and Laird (2000); see also Knapp (1999). Here we give some examples.

Suppose we observe n_AB offspring with genotype AB and n_BB offspring with BB, where both counts are positive but n_AA = 0, and a parent who is AB. In this case, the observed parental genotype gives no information because it can be inferred from the offspring genotype data. However, the other parent cannot be reconstructed. Further, the two possible mating types, (AB, AB) and (AB, BB), give different probabilities for the observed n_AB and n_BB. In this case, the sufficient statistic is simply the vector of genotype counts (n_AA, n_AB, n_BB). To obtain Pr(X_i|S_i), we permute the individual genotypes among the offspring, fixing S_i. In this way, Pr(X_i|S_i) does not depend upon the unknown mating type.

If instead of the AB parent, we observe a BB parent, the mating type (AB, BB) can be reconstructed exactly (Knapp, 1999). In this case, the sufficient statistic is observing a BB parent and (n_AB > 0 and n_BB > 0), since this information allows us to reconstruct the missing parent. The genotypes AB and BB are randomly assigned to offspring with probability 50/50 (because we know the mating type), but we do not allow outcomes with either n_BB or n_AB equal to zero.

Conditional independence of X_i and Z_i given S_i follows from properties of the sufficient statistic, as shown in Web Appendix A.

The likelihood we use in equation 3 is similar to Cordell et al. (2004), except it conditions on the sufficient statistic for the parents, allowing us to incorporate families with missing parents; for trios the two likelihoods are equivalent. It is also similar to the Kistner et al. (2009) likelihood when parents are present and ignoring parent-of-origin effects.

Using equation 3, the log-likelihood for each family sums over the affected offspring

$${\ell }_i^{\text{TX}}\propto {\mathit{\beta }}_{\text{ge}}^T\sum _j{\mathbf{X}}_{\text{ge},ij}{Z}_{ij}+{\mathit{\beta }}_{\text{g}}^T\sum _j{\mathbf{X}}_{ij}-log\left\{\sum _{{\mathbf{X}}^{★}\in S_i}{e}^{{\mathit{\beta }}_{\text{ge}}^T{\sum }_j{\mathbf{X}}_{\text{ge},j}^{★}{Z}_{ij}+{\mathit{\beta }}_{\text{g}}^T{\sum }_j{\mathbf{X}}_j^{★}}Pr({\mathbf{X}}^{★}\mid S_i)\right\}.$$ (4)

Detailed derivations of this likelihood are provided in Web Appendix B. The derivation assumes that we have conditional independence of the genotype and environment given the parents. In this likelihood, unaffected offspring contribute only to the reconstruction of S_i when parents are missing. Including unaffecteds would require having an estimate of the baseline disease prevalence and modeling the form of the environmental main effect. Thus environmental covariate information is not needed on unaffected offspring, and it does not contribute any information to the test. In this section, because β_g is the only nuisance parameter in the retrospective likelihood, we will define β_nuis = β_g. The derivative of the log-likelihood is given by the following summation over the affected offspring only:

$$\begin{array}{l}{U}_i^{\text{TX}}(\mathit{\beta })={\left\{\begin{array}{cc}{U}_i^{{\mathit{\beta }}_{\text{ge}}}({\mathit{\beta }}_{\text{ge}},{\mathit{\beta }}_{\text{nuis}})& U_i^{{\mathit{\beta }}_{\text{nuis}}}({\mathit{\beta }}_{\text{ge}},{\mathit{\beta }}_{\text{nuis}})\end{array}\right\}}^T\\ =\sum _j\left(\begin{array}{c}{\mathbf{X}}_{\text{ge},ij}{Z}_{ij}\\ {\mathbf{X}}_{ij}\end{array}\right)-E\left\{\sum _j\left(\begin{array}{c}{\mathbf{X}}_{\text{ge},ij}{Z}_{ij}\\ {\mathbf{X}}_{ij}\end{array}\right)|{\mathbf{Y}}_i=1,{\mathbf{Z}}_i,S_i;\mathit{\beta }\right\}.\end{array}$$ (5)

In order to construct a score test for gene-environment interaction, i.e. H₀: β_ge = 0, we first solve for the nuisance parameter β_nuis = β_g from the estimating equation ${\sum }_i{U}_i^{{\mathit{\beta }}_{\text{nuis}}}(\mathbf{0},{\mathit{\beta }}_{\text{nuis}})=\mathbf{0}$. Denote this solution β̂_nuis. Then let the contribution of the i^th family, adjusted for estimating the nuisance parameter, be given by

$$W_i=U_i^{{\mathit{\beta }}_{\text{ge}}}(\mathbf{0},{\widehat{\mathit{\beta }}}_{\text{nuis}})-\widehat{E}\left\{\frac{\partial }{\partial {\mathit{\beta }}_{\text{nuis}}}{U}_i^{{\mathit{\beta }}_{\text{ge}}}(\mathbf{0},{\widehat{\mathit{\beta }}}_{\text{nuis}})\right\}\widehat{E}{\left\{\frac{\partial }{\partial {\mathit{\beta }}_{\text{nuis}}}{U}_i^{{\mathit{\beta }}_{\text{nuis}}}(\mathbf{0},{\widehat{\mathit{\beta }}}_{\text{nuis}})\right\}}^{-}{U}_i^{{\mathit{\beta }}_{\text{nuis}}}(\mathbf{0},{\widehat{\mathit{\beta }}}_{\text{nuis}}).$$ (6)

The derivatives are given in Web Appendix B. Then the test statistic is given using the empirical variance by ${({\sum }_i{W}_i)}^T{({\sum }_i{W}_i{W}_i^T)}^{-}({\sum }_i{W}_i)$. As shown in Web Appendix C, under weak regularity conditions this follows a chi-squared distribution with rank ( ${\sum }_i{W}_i{W}_i^T$) degrees of freedom. We will denote this test by TX (short for transmission), for its use of Mendelian transmission information.

2.2 Using the discordant phenotype and genotype conditional distribution for discordant offspring (CLR-IJ)

As noted by Chatterjee et al. (2005), we can gain more power for discordant sibs using the logit link in equation 1, assuming a rare disease, and assuming conditional independence of genotype and environment given the parents. Note, however, that if the conditional gene-environment independence assumption is violated, especially if there is a strong negative correlation, then the test is not only biased, but is also not necessarily more powerful than CLR (see simulations). We generalize and provide a slightly more powerful test than CLR-IND when there are more than 2 offspring. We can model the likelihood of phenotype and genotype by

$${\mathcal{L}}_i^{\text{CLR}-\text{IJ}}=Pr\{{\mathbf{Y}}_{i,A({\mathbf{Y}}_i)}=\mathbf{1},{\mathbf{Y}}_{i,U({\mathbf{Y}}_i)}=\mathbf{0},{\mathbf{X}}_i\mid {\mathbf{Y}}_{i+},{\mathbf{Z}}_i,{\mathbf{C}}_i,S_i\},$$ (7)

where A(Y_i) indexes the affected offspring, and U (Y_i) indexes the unaffected. The log-likelihood for each family is given by

$${\ell }_i^{\text{CLR}-\text{IJ}}\propto \sum _{j\in A({\mathbf{Y}}_i)}{\mathit{\beta }}_{\text{ge}}^T{\mathbf{X}}_j{Z}_{ij}+{\mathit{\beta }}_{\text{nuis}}^T\mathbf{m}({\mathbf{X}}_j,Z_{ij},{\mathbf{C}}_{ij})-log\left\{\sum _{\begin{array}{c}{\mathbf{X}}^{★}\in S_i,\\ {\mathbf{Y}}^{★}:{\mathbf{Y}}_{+}^{★}={\mathbf{Y}}_{i+}\end{array}}{e}^{{\sum }_{j\in A({\mathbf{Y}}^{★})}{\mathit{\beta }}_{\text{ge}}^T{\mathbf{X}}_j^{★}{Z}_{ij}+{\mathit{\beta }}_{\text{nuis}}^T\mathbf{m}({\mathbf{X}}_j^{★},Z_{ij},{\mathbf{C}}_{ij})}Pr({\mathbf{X}}_i^{★}\mid S_i)\right\},$$ (8)

where Y_i+ = Σ_jY_ij and ${\mathbf{Y}}_{+}^{★}={\sum }_j{Y}_j^{★}$. Detailed derivations are provided in Web Appendix D. The right hand side of equation (8) uses a combination of the conditioning sets of the previous approach in equation 4, (X*∈ S_i), and what would result from conditional logistic regression ( ${\mathbf{Y}}^{★}:{\mathbf{Y}}_{+}^{★}={\mathbf{Y}}_{i+}$) with the set ( ${\mathbf{X}}^{★}\in S_i,{\mathbf{Y}}^{★}:{\mathbf{Y}}_{+}^{★}={\mathbf{Y}}_{i+}$). The likelihood also models the main effect of the environmental exposure, and relies on specifying the main environmental effect correctly. The approach is similar to CLR-IND, except here we condition more generally on S_i and use the joint distribution of the offspring instead of a pseudo-likelihood consisting of all pairs of affected and unaffected offspring in a family. For discordant sibpairs the likelihood ℓ^CLR-IJ is equivalent to CLR-IND, but not for more general families with discordant offspring. The derivative of the log-likelihood for each family is

$$\begin{array}{l}{U}_i^{\text{CLR}-\text{IJ}}(\mathit{\beta })={\left\{\begin{array}{cc}{U}_i^{{\mathit{\beta }}_{\text{ge}}}({\mathit{\beta }}_{\text{ge}},{\mathit{\beta }}_{\text{nuis}})& U_i^{{\mathit{\beta }}_{\text{nuis}}}({\mathit{\beta }}_{\text{ge}},{\mathit{\beta }}_{\text{nuis}})\end{array}\right\}}^T\\ =\sum _{j\in A({\mathbf{Y}}_i)}\left\{\begin{array}{c}{\mathbf{X}}_{\text{ge},ij}{Z}_{ij}\\ \mathbf{m}\text{(}{\mathbf{X}}_{ij},Z_{ij},{\mathbf{C}}_{ij})\end{array}\right\}-E\left[\sum _{j\in A({\mathbf{Y}}_i)}\left\{\begin{array}{c}{\mathbf{X}}_{\text{ge},ij}{Z}_{ij}\\ \mathbf{m}\text{(}{\mathbf{X}}_{ij},Z_{ij},{\mathbf{C}}_{ij})\end{array}\right\}|\begin{array}{c}{\mathbf{Y}}_{i+},{\mathbf{Z}}_i,C_i,\\ S_i;\mathit{\beta }\end{array}\right].\end{array}$$ (9)

The estimating equation here is a combination of both the previous approach (equation 5) and what would come from conditional logistic regression. The resulting score test for H₀: β_ge = 0 is given by following the methodology above for the construction of W_i (equation 6) but using $U_i^{\text{CLR}-\text{IJ}}$. The derivatives are given in Web Appendix D. The resulting test statistic still has a chi-squared distribution with rank ( ${\sum }_i{W}_i{W}_i^T$) degrees of freedom. We refer to this test as CLR-IJ, for both the joint phenotype and genotype conditional distributions, and the conditional independence of genotype and environment given the parent.

2.3 A Hybrid Transmission and CLR-IJ approach (Hybrid)

We will see later in the simulations that the CLR-IJ approach is much more powerful than the TX approach for discordant sibs. Ideally we would like to use the CLR-IJ approach whenever possible, and still obtain some information from families where CLR-IJ does not apply by using the TX approach. We follow the idea of Chatterjee et al. (2005) to combine our approaches under a rare disease assumption. The rare disease assumption is needed at the population level both in the derivation of the ${\mathcal{L}}_i^{\text{CLR}-\text{IJ}}$ likelihood and so that the log and logit scales of the two disease models are approximately the same. The rare disease assumption is not made at the stratum specific nuclear family level, so it is still reasonable to have multiple affected offspring in a family, as will be the case when families are ascertained for affection status. We assess how robust the test is to failures in this assumption in the simulations. We also still require the assumption of conditional independence of the genotype and the environment given the parents. The estimating equations are given by

$$U_i^{\text{Hybrid}}=\{\begin{array}{ll}{U}_i^{\text{CLR}-\text{IJ}},\hfill & \text{discordant}\text{offspring}\hfill \\ U_i^{\text{TX}},\hfill & \text{otherwise}.\hfill \end{array}$$

We construct W_i as before in equation 6, again resulting in a test statistic with rank ( ${\sum }_i{W}_i{W}_i^T$) degrees of freedom. We denote this approach Hybrid, as it is a hybrid of TX and CLR-IJ. Note that the families contributing to $U_i^{\text{CLR}-\text{IJ}}$ estimate more parameters than $U_i^{\text{TX}}$. In the case where there are only a few families with discordant offspring, we may not have enough information to estimate these very well, and the TX method should be used for all of the families. Also note that for cases in which there are always discordant offspring, the Hybrid approach will be equivalent to the CLR-IJ approach. In cases in which all of the offspring are always affected, e.g. trios, the Hybrid approach will be equivalent to the TX approach.

3. Simulations

We used simulations to compare the TX, CLR-IJ, and Hybrid approaches presented in this paper. We also considered the CLR and CLR-IND approaches with an empirical variance.

3.1 Simulation Design

All families were generated by first sampling parental pairs according to the allele frequency p_allele in the population (or subpopulation for scenarios with population stratification), with random genotypes for siblings based on Mendelian transmission. For continuous exposures, a random multivariate normal exposure for Z_i was drawn, with correlation ρ_env. In order to test violations of the gene-environment independence assumption, we also simulated ${\mathbf{Z}}_{ij}\sim N[{\gamma }_{\text{child}}X(g_{\mathit{child}})+{\gamma }_{\text{parent}}\{\frac{1}{2}X(g_{{\mathit{parent}}_1})+\frac{1}{2}X(g_{{\mathit{parent}}_2})\},1]$ in one scenario (with ρ_env = 0). For dichotomous exposures, the normal exposure was dichotomized to have a population prevalence of p_env. Finally, assuming the DSL is the observed marker, the disease status of the offspring was determined by comparing a U(0, 1) draw with the probability the offspring was diseased according to equation 1. In equation 1, we used a log or logit link function, with relative risks or odds rations e^β_e, e^β_g, and e^β_gefor the main environmental effect, main genetic effect, and gene-environment interaction. We kept values of e^β_gand e^β_gebetween 1.2–2, as the main effects of complex diseases are expected to be small (Lohmueller et al., 2003). The value for β₀ was solved for after fixing a certain population prevalence K = Pr(Y = 1). In some scenarios we simulated a rare disease so that the log and logit scales were approximately equivalent so that the different approaches would be comparable. We used five ascertainment criteria: one affected offspring with parents (trios); sibships of size 2, 3, or 4 with no parents, but at least one affected offspring; and sibships of size 3 or 4 with no parents and at least two affected offspring. When LD was simulated, haplotypes were drawn with two alleles of equal frequency with correlation ρ_marker. The probability of alleles crossing over was given by θ_recomb. The first allele in the haplotype was used to generate the data, and the second allele was used to test.

We also simulated data to test general violations of the phenotypic independence assumption described after equation 2. Consider a two by two table for the outcomes of Y_i1 and Y_i2. We first generated the marginal probabilities of this table, Pr(Y_ij = 1|X_ij, Z_ij), as described above. We then induced a correlation in the Y_i by fixing the odds ratio OR_pheno between the pair of offspring in the i^th family, and using this to solve for the distribution of the rest of the two by two table.

3.2 Simulation Parameters

Unless otherwise noted, we simulated 500 of each family structure, e.g. 500 trios, 500 discordant sibpairs (DSP), 500 discordant sibtrios, along with a mixture of 250 sibpairs + 250 trios for some simulations, and case-control having 500 cases and 500 controls. Note that CLR methods will discard trio data in the analysis but the TX method can potentially use all family types. We set p_allele = 0.14. We first tested two type I error situations:

• (1)LD: ρ_marker=0.3, 0.6, 0.9, and 1 (i.e. testing the marker); θ_recomb = 0, 0.3; K = 0.01; log link; p_env = 0.3; dichotomous environmental exposure; ρ_env = 0; e^β_g= e^β_e= 1.5; e^β_ge= 1; various family structures.
• (2)Population substructure: same as (1), but with K₁ = 0.02; K₂ = 0.04; p_afreq1= p_env1= 0.1; and p_afreq2= p_env2= 0.1.

We then tested the robustness to model assumptions:

• (3)Rare disease assumption: varying K ∈ [0.01, 0.1]; log/logit link; p_env = 0.3; dichotomous environmental exposure; ρ_env = 0; e^β_g= 2; e^β_e= 3.
• (4)Sibling conditional phenotype independence: same as (3), but varied OR_pheno = 1/2, 2/3, 1, 1.5, 3.
• (5)Gene-environment independence given the parents assumption: varying γ_child, γ_parent ∈ [−0.1, 0.1]; K = 0.02; log link; continuous environmental exposure; ρ_env = 0; e^β_g= e^β_e= 1.5; e^β_ge= 1, 1.5; discordant sibpairs.

Finally we tested the power of the approaches:

• (6)Comparing to CLR-IND: varied the sibship size from 2–6; 300 families; K = 0.01; log link; p_env = 0.3; dichotomous environmental exposure; ρ_env = 0; e^β_g= e^β_e= 1.5; e^β_ge= 1.4.
• (7)Comparing the Hybrid approach to other family structures, and the effect of sibling environmental correlation: varing ρ_env ∈ [0, 1]; K = 0.01; log link; p_env = 0.3; dichotomous environmental exposure; e^β_g= e^β_e= 1.5; e^β_ge= 1.75; various family structures.

3.3 Findings

3.3.1 Simulation study to assess type I error

(1) LD and (2) Population substructure

We find that the test maintains the correct type I error in Table 1, even if the marker is only in LD with the true DSL (assumption 2, first violation).

Table 1.

Simulation study to assess type I error when there are trios, and sibships (size given by the number in the “family” column) with no parents with different numbers of affected (aff) offspring. In this table we are testing a marker that has correlation ρ_marker with the DSL. Here $e_g^{\beta }=e_e^{\beta }=1.5$. For the results evaluating type I error with no population stratification, 500 families were simulated with K = 0.01, and the allele frequency and environmental exposure was 0.3. For the results evaluating type I error in the presence of population stratification with 2 subpopulations, 250 families were drawn with an allele frequency and environmental exposure of 0.1 along with 250 families with an allele frequency and environmental exposure of 0.9, and K was 0.01 and 0.02 for the two subpopulations. P-values are given in the table, corresponding to each test. Based on 100,000 simulations.

Family Structure	ρmarker	θrecomb	No population stratification				2 Subpopulations
			Avg # Aff	TX	CLR	Hybrid	Avg # Aff	TX	CLR	Hybrid
Trios	0.3	0	1	0.050	–	0.050	1	0.052	–	0.052
		0.3	1	0.051	–	0.051	1	0.053	–	0.053
	0.6	0	1	0.050	–	0.050	1	0.053	–	0.053
		0.3	1	0.051	–	0.051	1	0.051	–	0.051
	0.9	0	1	0.051	–	0.051	1	0.052	–	0.052
		0.3	1	0.050	–	0.050	1	0.050	–	0.050
	1.0	0	1	0.050	–	0.050	1	0.050	–	0.050
		0.3	1	0.050	–	0.050	1	0.051	–	0.051
DSP	0.3	0	1.011	0.051	0.051	0.050	1.010	0.052	0.051	0.051
		0.3	1.011	0.052	0.051	0.050	1.010	0.051	0.052	0.051
	0.6	0	1.011	0.050	0.051	0.050	1.010	0.052	0.050	0.050
		0.3	1.011	0.052	0.051	0.051	1.010	0.052	0.052	0.051
	0.9	0	1.011	0.052	0.051	0.050	1.010	0.052	0.051	0.051
		0.3	1.011	0.052	0.052	0.052	1.010	0.051	0.051	0.051
	1.0	0	1.011	0.051	0.050	0.051	1.010	0.052	0.051	0.052
		0.3	1.011	0.052	0.051	0.051	1.010	0.052	0.052	0.052
Trios + DSP	0.3	0	1.011	0.052	0.051	0.051	1.010	0.052	0.052	0.052
		0.3	1.011	0.051	0.052	0.050	1.010	0.052	0.053	0.053
	0.6	0	1.011	0.052	0.051	0.050	1.010	0.052	0.051	0.052
		0.3	1.011	0.052	0.051	0.052	1.010	0.051	0.052	0.052
	0.9	0	1.011	0.052	0.052	0.051	1.010	0.051	0.051	0.053
		0.3	1.011	0.050	0.051	0.051	1.010	0.052	0.052	0.052
	1.0	0	1.011	0.052	0.051	0.050	1.010	0.052	0.053	0.052
		0.3	1.011	0.052	0.052	0.052	1.010	0.052	0.052	0.051
3, ≥ 1 aff	0.3	0	1.022	0.051	0.049	0.049	1.019	0.052	0.051	0.052
		0.3	1.022	0.051	0.051	0.052	1.019	0.051	0.052	0.051
	0.6	0	1.022	0.051	0.052	0.051	1.019	0.050	0.052	0.053
		0.3	1.022	0.051	0.049	0.050	1.019	0.051	0.053	0.053
	0.9	0	1.022	0.050	0.051	0.051	1.019	0.051	0.053	0.053
		0.3	1.022	0.050	0.052	0.050	1.019	0.050	0.052	0.052
	1.0	0	1.022	0.052	0.051	0.050	1.019	0.051	0.052	0.052
		0.3	1.022	0.051	0.052	0.051	1.019	0.051	0.052	0.053
4, ≥ 1 aff	0.3	0	1.032	0.050	0.050	0.050	1.029	0.051	0.053	0.053
		0.3	1.032	0.050	0.052	0.051	1.029	0.050	0.053	0.053
	0.6	0	1.032	0.052	0.051	0.051	1.029	0.051	0.053	0.052
		0.3	1.032	0.050	0.050	0.051	1.029	0.052	0.053	0.053
	0.9	0	1.032	0.052	0.051	0.051	1.029	0.051	0.053	0.053
		0.3	1.032	0.050	0.050	0.050	1.029	0.051	0.053	0.052
	1.0	0	1.032	0.051	0.050	0.051	1.029	0.051	0.053	0.053
		0.3	1.032	0.050	0.050	0.051	1.029	0.051	0.053	0.052
3, ≥ 2 aff	0.3	0	2.006	0.052	0.051	0.050	2.005	0.050	0.052	0.052
		0.3	2.006	0.050	0.050	0.050	2.005	0.049	0.051	0.051
	0.6	0	2.006	0.049	0.051	0.049	2.005	0.051	0.052	0.052
		0.3	2.006	0.050	0.051	0.050	2.005	0.050	0.052	0.052
	0.9	0	2.006	0.049	0.052	0.050	2.005	0.050	0.052	0.051
		0.3	2.006	0.050	0.050	0.050	2.005	0.050	0.052	0.052
	1.0	0	2.006	0.050	0.051	0.050	2.005	0.050	0.052	0.052
		0.3	2.006	0.049	0.050	0.050	2.005	0.050	0.052	0.051
4, ≥ 2 aff	0.3	0	2.011	0.051	0.051	0.050	2.010	0.049	0.050	0.051
		0.3	2.011	0.050	0.051	0.050	2.010	0.049	0.050	0.050
	0.6	0	2.011	0.050	0.050	0.050	2.010	0.051	0.052	0.051
		0.3	2.011	0.051	0.050	0.050	2.010	0.050	0.049	0.049
	0.9	0	2.011	0.051	0.049	0.051	2.010	0.049	0.050	0.049
		0.3	2.011	0.050	0.050	0.049	2.010	0.050	0.050	0.050
	1.0	0	2.011	0.050	0.050	0.050	2.010	0.049	0.050	0.050
		0.3	2.011	0.050	0.049	0.049	2.010	0.050	0.050	0.050

3.3.2 Robustness to model assumptions

(3) Rare disease assumption

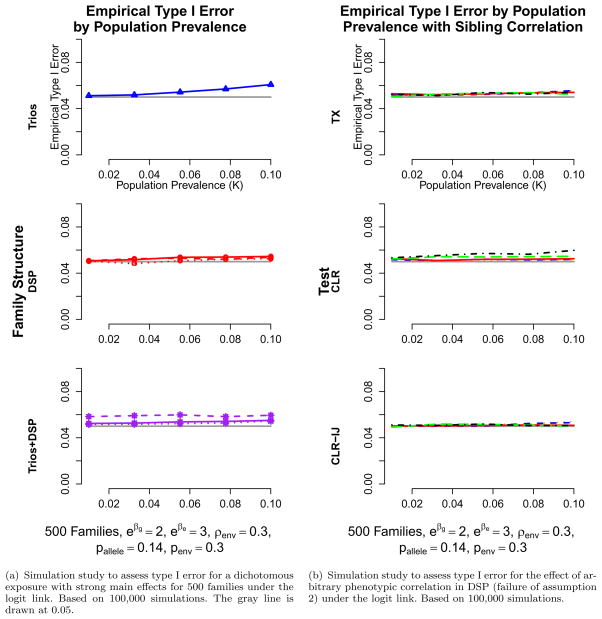
The Hybrid and CLR-IJ extension of the CLR-IND approach all make a rare disease assumption, and only when a disease is rare are the log and logit scales approximately equivalent. The simulation results we present were run with stronger main effects, as deviations are more pronounced in those situations. In Figure 1(a) (logit link) and Web Figure 1 in Web Appendix E (log link) the TX approach shows no deviations from the type I error rate under the RR model, as expected, given it is based on a log link. The CLR-IJ and Hybrid approaches also behave well, likely from their transmission-based components and pieces. The TX, CLR-IJ, and Hybrid also behave well under the logit link, even for high prevalences with a misspecified phenotypic model. The CLR approach shows inflated type I error rates as disease prevalence increases under a misspecified relative risk model, and also for smaller sample sizes, but behaves well under a logit model. Results are similar for a continuous normal environmental exposure and other correlation values between siblings environmental exposure values (results not shown). Results are generally slightly more inflated for higher main effects than those presented in Figure 1(a) (logit link) and Web Figure 1 (log link), and less for lower main effects.

Figure 1.

Type I error and phenotypic model robustness simulations under the logit link.

(4) Sibling conditional phenotype independence assumption

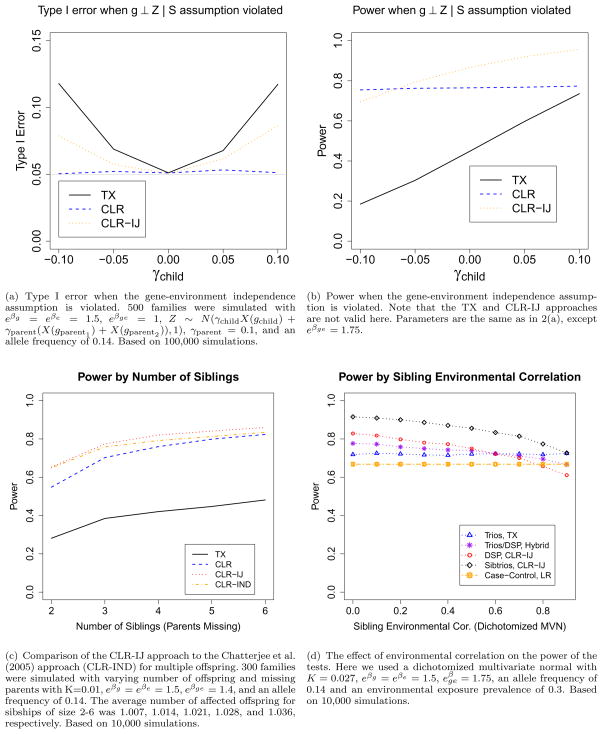
In the best case, when there was either no main environmental effect or no main genetic effect, then the results were not affected by OR_pheno (results not shown, but tested for relative risks up to size 3). In Figure 1(b) we show that the type I error is slightly more inflated when there is an odds ratio > 1 for discordant sibpairs, but only when using CLR and generating under a RR model. CLR-IJ approximately maintains the type I error.

(5) Gene-environment independence given the parents assumption

The CLR approach does not make this assumption, and so completely maintains the type I error. In Figure 2(a), we see that the TX and Hybrid approaches show inflated type I error values when γ_child ≠ 0, i.e. when the gene influences the covariate. Results are only shown for γ_parent = 0.1, as none of the approaches are affected by γ_parent ≠ 0 (i.e., there is population substructure), as expected. Although the TX and the Hybrid approaches have inflated type I error when this assumption is violated, we also compared the power of the approaches in Figure 2(b). We found that when there is a strong enough negative correlation (i.e. γ_child < 0) then the CLR test is more powerful than the CLR-IJ approach. These results are similar to violations of the gene environment independence given the population for case only population genetics designs (Umbach and Weinberg, 1997).

Figure 2.

Type I error and power simulations.

3.3.3 Power

We do not show, but first discuss how our proposed TX approach has similar power to other transmission-based approaches. When we compared it to the Cordell (2002) approach for trios, we found it had the same power, as it is based on an equivalent likelihood, when parents are present. We did not compare it to the Dudbridge (2008) approach, as it is also based on an equivalent likelihood when parents are present, but the Dudbridge (2008) approach is not completely robust to population substructure with missing parents. We also did not compare it to the Kistner et al. (2009) approach, as it too has an equivalent likelihood as TX when parents are present and there are no parent-of-origin effects. Finally, we found the power was essentially the same as the Hoffmann et al. (2009) approach in the case of sibpairs and trios with one affected offspring, and expect it not to be better unless there are a lot of different strata of sufficient statistics (the latter approach estimates a mean within each sufficient statistic, which will be less efficient than a model for the mean, particularly when there are many strata) or more than one affected offspring in a family.

(6) Comparing to CLR-IND

We compared the power of the CLR-IJ, CLR-IND, and TX approaches on discordant sibships, as all methods can be implemented with such a family structure. Recall from the type I error simulations that we found that the type I error rate was preserved in this situation. We found that the main effects typically had little impact on the power (only modest are shown). In Figure 2(c) we first see that the CLR-IJ approach is slightly more powerful than the CLR-IND approach when there are more than 2 offspring. When there are 2 offspring, the CLR-IJ and CLR-IND likelihoods are equivalent, and the power benefit of CLR-IND and CLR-IJ diminishes as the number of sibs increases. We also see it is slightly more powerful than the easily implemented CLR approach. We suspect the power difference is not more dramatic because the largest increase in power is from using discordant phenotypic information, rather than the transmission distribution. Lastly, we also see that the CLR-IJ approach is much more powerful than the RR approach, hence our motivation for constructing the Hybrid approach. In Figure 2(c), there is only 1–1.04 affected offspring per family, but the relative power difference does not change when 2 affected offpsring are ascertained per family.

(7) Comparing the hybrid approach to other family structures, and the effect of sibling environmental correlation

Finally, we compared the power of a situation requiring the hybrid approach (trios + DSP) to the most efficient test for trios, DSP, and also to case-control. Figure 2(d) shows that only for very high environmental correlations is a case-control design or trios more powerful than DSP. This is because DSP is most powerful when the environmental exposures of the offspring are discordant within the family stratum. However it is also important to note that these results are fairly dependent on the population prevalence of the environmental exposure. Web Figure 2 in Web Appendix F shows the power of case-control and trios performing better for a higher population exposure prevalence. Generally the power of trios is fairly comparable to case-control.

4. Application to Serpine2

We applied the gene-environment interaction methods to 127 extended pedigrees from the Boston Early-Onset (age < 53) COPD Study (Silverman et al., 1998) in the Serpine2 gene. The estimated prevalence of COPD is 5.9% (Mannino, 2002). Postbronchodilator measurements of forced expiratory volume at 1 second (FEV1) were measured, as FEV1 is a key intermediate phenotype of COPD. The Serpine2 gene was previously shown to be associated with FEV1 in early-onset COPD families when including a gene-environment interaction with pack-years for the quantitative FEV1 trait (Demeo et al., 2006; Vansteelandt et al., 2008). Here, the trait was obtained by dichotomizing FEV1 percent predicted < 50% and FEV1/FVC < 90%; a stricter definition that is even more appropriate with the rare disease assumption.

We broke the extended pedigrees into 225 nuclear families that would have some potential of contributing to each test statistic. This includes families with parents and at least one affected offspring; or families with one to two missing parents, at least one affected offspring, and two or more offspring. The rest of the informativeness of a family is determined on a SNP by SNP basis with genotype variation. The frequency tabulation of the nuclear family structure is broken down in Table 2. There were a variety of different family structures.

Table 2.

Family structures from the Boston Early-Onset Study.

Offspring	1	2	3	4	5	6	7	8	9	Total
Parents Present	21	23	5	3	2	1	1	0	0	56
Missing 1 Parent	—	43	30	7	2	2	0	0	1	85
Missing 2 Parents	—	35	21	13	8	3	0	3	1	84
Total	21	101	56	23	12	6	1	3	2	225

For the gene-environment interaction test, the environmental exposure was given by pack years of smoking. The estimated intraclass correlation coefficient (ICC) of the environmental exposure was 0.30 (Bliese, 2000). We tested 48 SNPs in this candidate gene using the model

$$log[Pr\{Y=1\mid X(g)\}]={\beta }_0+{\beta }_{g,1}{I}_{(g=aa)}+{\beta }_{g,2}{I}_{(g=Aa)}+{\beta }_{e}Z+{\beta }_{e,2}{Z}^2+{\beta }_{e,3}{Z}^3+{\beta }_{ge}X(g)Z,$$

where X(g) is the additive coding of the SNP, and Z is pack-years, adjusting to the third order term to capture any nonlinear main environmental effect. The results of SNPs with a joint test of gene and gene-environment interaction p-value < 0.15 are shown in Table 3 (chromosome position in Web Figure 3 in Web Appendix G), and are not adjusted for multiple testing. The joint test is from Lunetta et al. (2000), and is a score test of β_g and β_ge from the log-linear model. Although not significant with a Bonferroni adjustment for multiple comparisons, the most promising interaction result is given by the Hybrid approach for rs729631. This marker has a point estimate of 0.041 with 95% bootstrap BCa confidence interval (0.015, 0.092); this means that for each increase in pack-years of smoking, a person has an increased relative risk of 1.042 for each copy of the risk allele.

Table 3.

Data analysis results for the Boston Early-Onset COPD Study in the Serpine2 gene with environmental exposure given by pack-years. SNPs with a joint test of the main effect of the gene and the gene-environment interaction p-value < 0.15 (Lunetta et al., 2000) are displayed (out of 48 SNPs, not corrected for multiple comparisons). The main effects test (Main) is done without modeling the interaction via the FBAT test statistic (Laird and Lange, 2006). The TX, CLR, CLR-IJ, and Hybrid are the approaches presented/discussed in this paper to test explicitly for an interaction. The number of informative families is given in parenthesis. If an entry is not given, it is because the number of informative families is too small.

SNP	Allele Freq	Main (G)	Joint (G, GxE)	Additive Model Interaction (GxE)
				TX	CLR	CLR-IJ	Hybrid
rs729631	0.195	0.424(42)	0.085(43)	0.0311(43)	0.0047(44)	0.0037(47)	0.0030(48)
rs36034130	0.079	0.367(18)	0.104(18)	—	—	—	—
rs7605945	0.230	0.580(49)	0.106(50)	0.0276(51)	0.0115(54)	0.0070(58)	0.0066(59)
rs6738983	0.359	0.325(53)	0.112(55)	0.0433(55)	0.0481(85)	0.0159(87)	0.0140(88)
rs975278	0.204	0.607(41)	0.122(42)	0.0385(43)	0.0060(86)	0.0070(87)	0.0063(88)
rs1371028	0.083	0.832(20)	0.124(20)	—	—	—	—
rs6734100	0.142	0.296(36)	0.136(36)	0.0343(36)	0.0068(89)	0.0152(89)	0.0133(89)
rs6712954	0.075	0.058(21)	0.142(22)	—	—	—	—

In this example, the Hybrid test is usually the most significant test in detecting an interaction, although in a few situations the CLR test is more significant. This may be due in part to the different model scale assumptions of the tests. It may also be due to a lack of phenotypic independence. In this example the TX test is generally the least significant. This might be expected given the low environmental correlation and high number of families with discordant sibships. There is also a slight gain in using the Hybrid approach over the CLR-IJ approach here. In the results, we counted the number of informative families by those that have nonzero $U_i^{{\mathit{\beta }}_{\text{ge}}}$ contributions, i.e. contributed to the interaction term. The number of informative families is often less than the number of families. A family is informative under the TX approach only when at least one parent is heterozygous, or the offspring have at least one differing genotype. A family is informative under the CLR approach only if it has discordant offspring, and requires a discordant genotype or environmental exposure. The hybrid approach utilizes both.

In equation 2 we made the assumption that the environmental exposure of other subjects does not affect the phenotype of the offspring. For example, one way this could be violated is by passive smoking. As COPD is a late onset disease, we expect the assumption to be reasonable in this case. We could alternatively use a more complicated GLM to include information on passive smoking in the same framework.

5. Discussion

We have presented the Hybrid approach that allows us to use a more powerful test for interaction for families with discordant offspring, while still allowing us to use information from families with only affected offspring. The result is a very efficient interaction test for dichotomous traits that can utilize any type of family structure, and dichotomous or continuous environmental exposure, and will be especially advantageous when mostly trios, but some DSPs are available. The test is completely robust to population substructure, and behaves well in situations where the model assumptions are slightly violated and the main effects are not too large. Care should be taken when the main effects or disease prevalence are much larger than those presented in this paper.

The Hybrid approach has limitations as well. It is not applicable in situations with a very common disease, unlike the CLR approach. Like the other tests here, the result is dependent on the true disease model having the form given in equation 1, although it is difficult to avoid assuming a disease model for a general interaction test. This explains the inflated type I error rates in the log and logistic models under the CLR or TX approaches, respectively, for higher population prevalence values. In some cases one way of avoiding assuming a disease model may be through the sufficient cause framework developed by VanderWeele (2009).

In practice, there are several situations where it would be advantageous to use a different test than the Hybrid test. In cases of discordant offspring where one is concerned about violating the assumption that the gene and environment are independent given the parents, the CLR approach does not require this assumption and is nearly as powerful as the Hybrid approach. In cases where one has almost exclusively affected offspring, e.g. trios, it would be advantageous to use the TX approach if there are not enough subjects in discordant sibships to estimate the main effect of the environmental exposure. Finally in cases where the environmental exposure is family specific, TX may be preferred because it does not need to correctly model the main effect of the environment, and loses just a little power.

Software is available in the R (R Development Core Team, 2008) package fbati, available from http://cran.r-project.org/. It uses the package fgui for the graphical interface (Hoffmann and Laird, 2009), and the data loading routines of pbatR (Hoffmann and Lange, 2006).