Repeated Measures Semiparametric Regression Using Targeted Maximum Likelihood Methodology with Application to Transcription Factor Activity Discovery

Abstract

In longitudinal and repeated measures data analysis, often the goal is to determine the effect of a treatment or aspect on a particular outcome (e.g., disease progression). We consider a semiparametric repeated measures regression model, where the parametric component models effect of the variable of interest and any modification by other covariates. The expectation of this parametric component over the other covariates is a measure of variable importance. Here, we present a targeted maximum likelihood estimator of the finite dimensional regression parameter, which is easily estimated using standard software for generalized estimating equations.

The targeted maximum likelihood method provides double robust and locally efficient estimates of the variable importance parameters and inference based on the influence curve. We demonstrate these properties through simulation under correct and incorrect model specification, and apply our method in practice to estimating the activity of transcription factor (TF) over cell cycle in yeast. We specifically target the importance of SWI4, SWI6, MBP1, MCM1, ACE2, FKH2, NDD1, and SWI5.

The semiparametric model allows us to determine the importance of a TF at specific time points by specifying time indicators as potential effect modifiers of the TF. Our results are promising, showing significant importance trends during the expected time periods. This methodology can also be used as a variable importance analysis tool to assess the effect of a large number of variables such as gene expressions or single nucleotide polymorphisms.

1. Introduction

Longitudinal data analysis, or more generally repeated measures analysis, has become increasingly popular in epidemiological and medical studies. Often the main goal of these studies is to determine the effect, or importance, of a particular variable on the outcome over time, for instance the effect of a drug on disease prognosis over the course of a clinical trial. In most cases the repeated measures are observations on subjects at multiple time points or under multiple conditions. More recently, repeated measures analysis has been applied in computational biology, where the experimental unit is now a gene or protein that is observed over time (Gao, Foat, and Bussemaker, 2004, Wang, Chen, and Li, 2007), condition (Conlon, Liu, Lieb, and Liu, 2003, Gao et al., 2004), or even species (Siewert and Kechris, 2009). Similarly, in these analyses the goal is to determine the importance of biological features (i.e. variables) with respect to the observed repeated measures outcome. Here, we present a new tool to estimate variable importance for a repeated measures outcome based on targeted maximum likelihood methodology (van der Laan and Rubin, October 2006) under a flexible semiparametric model. We refer to as this method as tVIM-RM.

In this paper, we propose a semiparametric repeated measures regression model in which the parametric component models the effect of a specific variable of interest and any effect modification by other covariates. We develop the targeted maximum likelihood estimator for the effect parameters of this model using targeted maximum likelihood methodology as presented in van der Laan and Rubin (October 2006). Targeted maximum likelihood estimation (tMLE) focuses estimation on the target parameter of interest, in this case a measure of variable importance. The tMLE method first constructs an initial estimator of the distribution of the data in the semiparametric repeated measures regression model. It then subsequently uses the maximum likelihood estimation (MLE) framework to reduce the bias for the targeted parameter by maximizing the likelihood in a direction that corresponds to fitting the target parameter, while treating the initial estimator as a fixed off-set. Prior applications of tMLE methods have shown great promise and applicability in the epidemiological and medical fields, in particular, for biomarker discovery (Tuglus and van der Laan, 2008). The tVIM-RM method presented here builds upon previous variable importance methodology (Robins, Mark, and Newey, 1992, Robins and Rotnitzky, 2001, Yu and van der Laan, September 2003, van der Laan, 2005), adapting it for repeated measures data and incorporating updates on the methodology to increase efficiency and computational speed.

As indicated above, in repeated measures experimental designs multiple observations are recorded for each subject over a set of conditions and/or time (e.g. longitudinal). Though this experimental design is attractive in that it reduces the variance among observations and can increase the power of the analysis, statistical methods, such as regression, must account for the correlation among the observations on a single subject. Ignoring this dependence can lead to biased standard error estimates for regression parameters (Wang (2003) among others). A popular method to account for the correlation among the observations in parametric regression models is generalized estimating equations (GEE). GEE methods were introduced in 1986 by Zeger and Liang (Liang and Zeger, 1986) and are an extension of generalized linear regression using a quasi-likelihood approach, which weights the residuals according to the correlation structure of the observations on each subject. More flexible semiparametric extensions of the GEE method, such as generalized partially linear models (Zeger and Diggle, 1994, Severini and Staniswalis, 1994, Fan, Huang, and Li, 2007) model covariate effects non-parametrically, but require complicated estimation methods to fit both the parametric and non-parameteric portions of the model. These methods can produce inconsistent and/or inefficient estimates of the model parameters (Lin and Carroll, 2001, Li, Xia, Palta, and Shankar, 2009).

The tVIM-RM semiparametric regression model is a more non-parametric analogue of the standard GEE repeated measures regression model, and the targeted maximum likelihood update is easily implemented using standard GEE software. The tMLE method provides targeted estimation for the parameter of interest and the resulting tVIM-RM estimates are locally efficient in the semiparametric repeated measures regression model: that is, the estimator of the effect of interest is consistent and asymptotically linear if either the mean of the variable of interest as a function of the confounders is correctly modeled (i.e. confounding/treatment mechanism), or if the mean of the outcome as a function of the variables (including variable of interest) is correctly modeled. The tMLE method integrates data-adaptive prediction algorithms such as DSA (Sinisi and van der Laan, March 2004) and super learner (van der Laan, Polley, and Hubbard, July 2007) by using these methods to obtain the initial estimator and the confounding/treatment mechanism used in the targeted update. Details on the method are discussed further in section 2.3.

We present the method with respect to a repeated measures experiment taken over times t = 1, . . ., T, with observed data O = {W^*, Y} ∼ P₀, where P₀ is the true data generating distribution. Here, W^* is a vector of p variables, and Y is the outcome vector of T repeated measures taken over time on a subject, where Y_t represents outcome Y at a specific time point t for a subject. We define the semiparametric regression model for a particular variable $A\hspace{0.17em}=\hspace{0.17em}{W}_j^{*}$ and time, t, controlling for confounders $W\hspace{0.17em}=\hspace{0.17em}{W}_{-j}^{*}$ such that

$$𝔼[Y_t|A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}W]\hspace{0.17em}-\hspace{0.17em}𝔼[Y_t|A\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}W]\hspace{0.17em}=\hspace{0.17em}{m}_t(a,\hspace{0.17em}W|{\beta }_t)$$

We refer to the model m_t(A, W|β_t) as a semiparametric regression model for the effect of A on Y_t. Given estimates of an initial Q_t(A, W) = 𝔼[Y_t|A, W] respecting m_t(0, W|β_t) = 0, and “treatment mechanism” G(W) = 𝔼[A|W], the effect is modeled according to the specified m_t(A, W|β_t) and coefficients β_t are estimated using tMLE. From tMLE theory, it can be shown that this estimate is asymptotically consistent and linear given that either Q_t(A, W) or G(W) is correctly specified, making our estimate doubly robust (van der Laan and Rubin, October 2006). The tVIM-RM estimate is also efficient when both Q_t(A, W) and G(W) are correctly specified (van der Laan and Rubin, October 2006), while it can easily be super-efficient if Q_t(A, W) is correctly specified, and G(W) is misspecified by not incorporating all W (Gruber and van der Laan, 2010). The double robust nature of the tVIM-RM estimate makes the methodology ideal for use in randomized trials when the treatment mechanism (𝔼[A|W]) is known.

The tVIM-RM method is particularly suitable for variable importance analysis. The semiparametric construction not only provides a flexible model, but nicely handles the effect of continuous variables and also allows the incorporation of effect modification of the variable of interest in a straight forward and interpretable manner. This allows the estimation of not only the variable importance averaged over time, but the importance at a particular time (e.g. effect modified by time). Also, the estimation procedure under the semiparametric model does not require inverse weighing by the probability of treatment (i.e. P(A = a|W)), which is required for non-parametric tMLE based variable importance estimation and can be problematic when the probability of treatment approaches one or zero (Bembom, Petersen, Rhee, Fessel, Sinisi, Shafer, and van der Laan, 2009).

This paper is organized as follows. In section 2, we present the tVIM-RM method in detail and outline the basic steps of tMLE based procedures. In section 3, we demonstrate the properties of the tVIM-RM estimator in simulation by comparing it to a standard GEE estimator. We show the tVIM-RM estimator is robust to model mis-specification and provides accurate inference for the parameter of interest. In both simulation and in application, tVIM-RM is implemented using standard software for GEE provided by geepack R library (Yan, Højsgaard, and Halekoh, 2008).

In section 4 we present an application of tVIM to yeast cell cycle expression data. In line with the original analysis done by Bussemaker, Li, and Siggia (2001) and subsequent analysis by Gao et al. (2004), Keles, van der Laan, Dudoit, and Eisen (2002), and others (Liu, Taylor, and Edenberg, 2006, Conlon et al., 2003, Siewert and Kechris, 2009) we apply tVIM-RM to measure the activity of transcription factors with respect to a gene expression profile. In this application, the repeated measures outcome is a time series of yeast gene expression over two cell cycles (Cho, Campbell, Winzeler, Steinmetz, Conway, Wodicka, Wolfsberg, Gabrielian, Landsman, Lockhart, and Davis, 1998). Through this simple application, we demostrate the utility of the tVIM-RM method for this type of analysis and discuss how it may be applied to more sophisticated studies. We end with an overall discussion in section 5.

2. Methods

2.1. Variable Importance

We present the following multivariate extension of the model-based semiparametric variable importance methodology (van der Laan, 2005) for repeated measures data. The variable importance of a specific $A\hspace{0.17em}=\hspace{0.17em}{W}_j^{*}$ controlling for confounders $W\hspace{0.17em}=\hspace{0.17em}{W}_{-j}^{*}$ can be defined generally as follows for a particular time t.

$${\mu }_t\hspace{0.17em}(a)\hspace{0.17em}=\hspace{0.17em}{\text{𝔼}}_W\hspace{0.17em}[m_t\hspace{0.17em}(a,\hspace{0.17em}W|{\beta }_t)]$$

or this can be represented in vector form for all t

$$\mu \hspace{0.17em}(a)\hspace{0.17em}=\hspace{0.17em}{\text{𝔼}}_W\hspace{0.17em}[m(a,\hspace{0.17em}W|\beta )]$$

for a user supplied model m, which models the effect

$$m(A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}W|\beta )\hspace{0.17em}=\hspace{0.17em}𝔼[Y|A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}W]\hspace{0.17em}-\hspace{0.17em}𝔼[Y|A\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}W])$$

under the constraint m(A = 0, W|β) = 0 for all β and W. Analogous to the previously presented tVIM for univariate outcome (Tuglus and van der Laan, 2008), variable A can be binary or continuous. We can also represent this measure in traditional semi-parametric model form

$$𝔼[Y|A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}W]\hspace{0.17em}=\hspace{0.17em}m(A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}W|\beta )\hspace{0.17em}+\hspace{0.17em}g(W)$$

such that m(A = 0, W|β) = 0 for all β and W, and g(W) is unspecified.

2.2. Generalized Estimating Equations

One of the most common approaches for modeling repeated measures data is generalized estimating equation methodology. Introduced by Liang and Zeger in 1986 (Liang and Zeger, 1986), generalized estimating equations uses a quasi-likelihood approach, which weights the residuals in a generalized regression score function according to a working correlation matrix. Specifically, GEE estimates of the parameter β for a Gaussian model are the solution to

$$\sum _{i=1}^n{(D^{(i)})}^T\hspace{0.17em}{(V^{(i)})}^{-1}\hspace{0.17em}(Y^{(i)}\hspace{0.17em}-\hspace{0.17em}Q(W^{*(i)}|\beta ))\hspace{0.17em}=\hspace{0.17em}0$$

where, for subject i in i = 1. . . n, Y⁽ⁱ⁾ is a vector of observations over time t = 1, . . ., T, with T by T covariance matrix, V⁽ⁱ⁾. Here Q(W^*(i)|β) = 𝔼[Y⁽ⁱ⁾|W^*(i)] = β^T W^*(i) is the vector of fitted values for subject i, and $D^{(i)}\hspace{0.17em}=\hspace{0.17em}\left[\frac{dQ(W^{*(i)}|\beta )}{d\beta }\right]$.

The parameter estimates are obtained using iteratively reweighted least squares estimation. More robust estimates are obtained by iterating this with the re-estimation of the covariance parameters in V⁽ⁱ⁾ as a function of β. This robust method is applied in R library geepack (Yan et al., 2008). Standard GEE regression parameter estimates remain consistent given an incorrect correlation structure (Liang and Zeger, 1986).

The GEE approach does not require the specification of the joint distribution of the observations over time for a given subject, only the marginal distribution for each time point and a working correlation matrix. Assuming independence among the subjects and a correctly specified model β^T W, parameter estimates β_n are consistent and given true parameter β₀,

$$n^{1/2}\hspace{0.17em}({\beta }_n\hspace{0.17em}-\hspace{0.17em}{\beta }_0)\hspace{0.17em}\sim \hspace{0.17em}MVN\hspace{0.17em}(0,\hspace{0.17em}{\Sigma }_{\mathit{\text{gee}}})$$

such that given U⁽ⁱ⁾ = (D⁽ⁱ⁾)^T (V⁽ⁱ⁾)^–1 D⁽ⁱ⁾ and R⁽ⁱ⁾ = Y⁽ⁱ⁾ – Q(W^*(i)|β),

$${\Sigma }_{\mathit{\text{gee}}}\hspace{0.17em}=\hspace{0.17em}\underset{n\to \infty }{\text{lim}}\hspace{0.17em}\frac{1}{n}\hspace{0.17em}\sum _{i=1}^n{(U^{(i)})}^{-1}\hspace{0.17em}{\left({(D^{(i)})}^T{(V^{(i)})}^{-1}\hspace{0.17em}{R}^{(i)}\hspace{0.17em}{(R^{(i)})}^T\hspace{0.17em}{(V^{(i)})}^{-1}\hspace{0.17em}{D}^{(i)}\right)}^{-1}\hspace{0.17em}{(U^{(i)})}^{-1}\hspace{0.17em}$$

This is referred to as the sandwich estimator (Hardin, 2003).

In this paper we use the R implementation of GEE in library geepack, function geeglm() (Yan et al., 2008). In simulation we allow GEE to update the correlation parameters. However for computation ease in our application in section 4, we provide a fixed correlation matrix estimate based on the residuals of an initial GEE estimate under independent correlation structure (Hardin, 2003).

2.3. Targeted MLE

The tVIM-RM estimates of parameter vector β are obtained using tMLE methodology (van der Laan and Rubin, October 2006). The tMLE method updates an initial density estimate p⁰(Y|A, W) in the direction which targets the parameter of interest using standard MLE and a “clever covariate” defined such that the tMLE solves the efficient score equation. In the case of repeated measures we define the initial density as the normal density (f^N) such that

$$p^0\hspace{0.17em}(Y|A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}{f}_{Q^0,\sum }^N\hspace{0.17em}(Y|A,\hspace{0.17em}W)$$

where Y is an 1 by T vector and Q⁰ (A, W) = 𝔼[Y|A, W]. Here Σ(A, W) is defined as a T by T covariance matrix corresponding to the conditional covariance among the t = 1. . . T observations for a single subject.

We can decompose Q⁰ (A, W) = m(A, W|β⁰) + Q⁰ (A = 0, W) where the model m(A, W|β⁰) is defined given the constraint m(A = 0, W|β⁰) = 0 for all β⁰ and W. We define the update to the initial density as its hardest submodel in terms of update parameter vector ɛ as follows

$$p(\varepsilon )\hspace{0.17em}(Y|A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}{f}_{Q(\varepsilon ),\sum }^N\hspace{0.17em}(Y|A,\hspace{0.17em}W)$$

where Q(ɛ) (A, W) = m(A, W|β (ɛ)) + Q(ɛ) (0, W) in which β (ɛ) = β⁰ + ɛ, and Q(ɛ) (0, W) = Q⁰ (0, W) + ɛr (W).

We define r(W) such that the score of p(ɛ)(Y|A, W) at ɛ = 0 is equivalent to the efficient score equation for the parameter β in μ (a) = 𝔼_W [m(a, W|β)]. The efficient score equation is presented below. To conserve space, the conditional variance, Σ(A, W), is sometimes simply represented as Σ.

$$D_{h_{\mathit{\text{opt}}},Q,G}\hspace{0.17em}=\hspace{0.17em}{h}_{\mathit{\text{opt}}}\hspace{0.17em}(A,\hspace{0.17em}W)\hspace{0.17em}(Y\hspace{0.17em}-\hspace{0.17em}m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}Q(0,\hspace{0.17em}W))$$

with

$$h_{\mathit{\text{opt}}}\hspace{0.17em}=\hspace{0.17em}{\Sigma }^{-1}\hspace{0.17em}\left(\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}\text{𝔼}{[{\Sigma }^{-1}|W]}^{-1}\text{𝔼}\hspace{0.17em}\left[{\Sigma }^{-1}\hspace{0.17em}\frac{d}{d{\beta }_0}m(A,\hspace{0.17em}W|\beta )|W\right]\right)$$

This is the multivariate extension of the semiparametric tVIM efficient score equation presented in van der Laan (2005) and Tuglus and van der Laan (2008). Further details on the efficient score equation can be found in appendix A.

It follows that the correct form of r(W) is

$$r(W)\hspace{0.17em}=\hspace{0.17em}\text{𝔼}\hspace{0.17em}[\Sigma {(A,\hspace{0.17em}W)}^{-1}|W]\hspace{0.17em}\text{𝔼}\left[\Sigma {\text{(}A,\hspace{0.17em}W)}^{-1}\hspace{0.17em}\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )|W\right]$$

The expectations can be approximated by discretizing A and calculating

$$\text{𝔼}\hspace{0.17em}\left[\Sigma {(A,\hspace{0.17em}W)}^{-1}|W\right]\hspace{0.17em}=\hspace{0.17em}\sum _{a\in A}\Sigma {(a,\hspace{0.17em}W)}^{-1}p(A\hspace{0.17em}=\hspace{0.17em}a|W)$$

and

$$\text{𝔼}\hspace{0.17em}\left[\Sigma {(A,\hspace{0.17em}W)}^{-1}\hspace{0.17em}\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )|W\right]\hspace{0.17em}=\hspace{0.17em}\sum _{a\in A}\Sigma {(a,\hspace{0.17em}W)}^{-1}\hspace{0.17em}\frac{d}{d\beta }m(A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}W|\beta )p(A\hspace{0.17em}=\hspace{0.17em}a|W)$$

Using standard MLE, we solve for ɛ, and calculate the updated regression estimate Q¹ (A, W) = m(A, W|β (ɛ)) + Q⁰ (0, W) + ɛr(W). The procedure is iterated, and at convergence (i.e. ɛ = 0), the final regression estimate is the solution to the robust estimating equation corresponding to the efficient score equation for observed data O = {O⁽ⁱ⁾ : i = 1. . . n}, for n subjects

$$\frac{1}{n}\hspace{0.17em}\sum _{i=1}^n[D_{h_{\mathit{\text{opt}}},Q_n,G_n}\hspace{0.17em}(O^{(i)}|{\beta }_n)]\hspace{0.17em}=\hspace{0.17em}0$$

such that Q_n, G_n, and β_n are the converged estimates of Q, G, and β for the observed data. The tMLE solution therefore inherits the double robust properties of the solution to the efficient score equation and allows us to use the efficient score equation to estimate the correct covariance and inference for our parameter of interest (see section 2.3.1). The double robust property is such that given either a correctly specified form of Q(A, W) = 𝔼[Y|A, W] or G(W) = 𝔼(A|W), the converged estimate for parameter vector, β_n, remains consistent, solving the efficient score equation. Given both are correct, the estimates are also efficient.

2.3.1. Linear case

Given a linear model for m(A, W|β), the update can be written as Q¹ (A, W) = Q⁰ (A, W) + ɛr^* (A, W) where

$$r^{*}\hspace{0.17em}(A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}\left(\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}\text{𝔼}\hspace{0.17em}{[{\Sigma }^{-1}|W]}^{-1}\hspace{0.17em}\text{𝔼}\hspace{0.17em}\left[\hspace{0.17em}{\Sigma }^{-1}\frac{d}{d{\beta }_0}m(A,\hspace{0.17em}W|\beta )|W\right]\right)$$

In the linear case, this update can be achieved using standard software by regressing Y onto the covariate r^* (A, W), setting Q⁰ (A, W) as an offset. The covariate, r^* (A, W) is sometimes referred to as the “clever covariate.”

If we define f_N such that Σ(A, W) = Σ(W), we can simplify h_opt to

$$h_{\mathit{\text{opt}}}^{*}\hspace{0.17em}=\hspace{0.17em}\Sigma {(W)}^{-1}\hspace{0.17em}\left(\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}\text{𝔼}\hspace{0.17em}\left[\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )|W\right]\right)$$

and the “clever covariate” simplifies to

$$r^{*}\hspace{0.17em}(A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}\left(\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}\text{𝔼}\hspace{0.17em}\left[\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )|W\right]\right)$$

Note that if the true covariance is a function of A, estimation using the simplified covariate form will lose efficiency but will still remain double robust. Given the simplified form of the “clever covariate” with linear model for m(A, W|β), the tVIM-RM estimate is a closed form solution and can be calculated without iteration.

The linear semiparametric form allows us to introduce time and/or any additional covariate as effect modifiers of the importance of A in a straight forward interpretable fashion. Consider the following possible model, where we allow effect modification of time indicator variable $t_t^{*}\hspace{0.17em}=\hspace{0.17em}\text{𝕀}\{t^{*}\hspace{0.17em}=\hspace{0.17em}t\}$.

$$m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}=\hspace{0.17em}A({\beta }^T\hspace{0.17em}{t}_1^{*})\hspace{0.17em}+\hspace{0.17em}\dots \hspace{0.17em}+\hspace{0.17em}A\hspace{0.17em}({\beta }^T\hspace{0.17em}{t}_T^{*})$$

When m(.) becomes large it is beneficial to update the coefficient terms sequentially until convergence (i.e. targeting one at a time) instead of completing an update of the full coefficient vector in one step. Updating the model sequentially in this fashion has been shown to improve the overall stability of the updated estimates (see appendix C for details).

2.3.2. Inference

Since the tMLE solution solves the double robust estimating function implied by the efficient score equation (van der Laan and Rubin, October 2006), one can use the influence curve corresponding with this double robust estimating function to provide an estimate of the covariance for tMLE estimated β_n. For this, we use a scaled version of the efficient influence curve which we define for a single subject as

$$IC\hspace{0.17em}(O)\hspace{0.17em}=\hspace{0.17em}{c}^{-1}\hspace{0.17em}{D}_{h_{\mathit{\text{opt}}},Q,G}(O|{\beta }_0)$$

given scale factor

$$c\hspace{0.17em}=\hspace{0.17em}-\text{𝔼}\hspace{0.17em}\left[\frac{d}{d\beta }D(O|{\beta }_0,\hspace{0.17em}{Q}_0)\right]$$

where IC(O) is a T by p matrix for a parameter vector β of length p and β₀ and Q₀ are β and Q under the true data generating distribution.

Given correctly specified estimates for Q(A, W) and G(W), the covariance for parameter vector estimate β_n is asymptotically equivalent to the covariance of IC(O) regardless of the form of Σ(A, W). If Q(A, W) is misspecified, but G(W) is correctly estimated, the above influence curve is known to be conservative (van der Laan, 2005). The empirical estimate of the covariance of β_n is

$${\Sigma }_n\hspace{0.17em}=\hspace{0.17em}\frac{1}{n}\hspace{0.17em}\sum _i\widehat{IC}(O^{(i)})\widehat{IC}{(O^{(i)})}^T$$

so that we can use the normal approximation

$$\sqrt{n}({\beta }_n\hspace{0.17em}-\hspace{0.17em}{\beta }_0)\hspace{0.17em}\sim \hspace{0.17em}N\hspace{0.17em}(0,\hspace{0.17em}{\Sigma }_n)$$

for the purpose of statistical inference. This is analogous to the robust sandwich estimator of GEE.

The covariance can also be estimated by bootstrap estimates of β, but this would require extra computational time and any sampling would need to respect the repeated measures design. If 𝔼[A | W] is estimated consistently, then the variance estimates based on the influence curve are consistent or asymptotically conservative.

Using the estimated p by p covariance matrix, Σ_n, we can test the hypothesis for a single parameter β_n(j), where j = 1, . . ., p, under the null hypothesis H₀ : β_n(j) = 0 using a standard test statistic to obtain p-values, with estimated variance Σ_n(j, j).

$$T_n(j)\hspace{0.17em}=\hspace{0.17em}\frac{\sqrt{n}{\beta }_n(j)}{\sqrt{{\text{Σ}}_n\hspace{0.17em}(j,j)}}\underset{n\to \infty }{\sim }\hspace{0.17em}\mathit{\text{Normal}}\hspace{0.17em}(0,1)$$

Likewise we can also test the hypothesis H₀ : c^T β_n = 0 using a standard Wald test, where the covariance of c^T β_n is c^T Σ_nc. This allows us to obtain inference for μ (a) directly, when m is linear. In practice the parameter of interest may be redefined as the effect at a specific value of effect modifier W, or time t, instead of the mean effect as implied by the definition in section 2.1.

2.3.3. tVIM-RM implementation

Below we outline the basic procedure for implementing tVIM for repeated measures given a fixed correlation matrix and highlight recent improvements in the implementation, which improve efficiency and computational speed of the semi-parametric tVIM method presented previously (Tuglus and van der Laan, 2008).

There are three initial components necessary for applying targeted maximum likelihood methodology to estimate tVIM for repeated measures.

1. Model m(A, W|β) satisfying m(A = 0, W|β) = 0 for any β and W

2. An estimate for G(W) = 𝔼[A|W]: We recommend estimating this data-adaptively.

3. An initial estimate for Q(A, W) = 𝔼[Y | A, W], $Q_n^0(A,W)$, containing valid model m(A, W|β): This provides an initial estimate for the parameter β, ${\beta }_n^0$, and must be defined such that Y|A, W ∼ Normal (Q(A, W), Σ(W)), with an empirically estimated correlation.

The initial regression estimate of proper form may be obtained from semi-parametric methods such as those of Zeger and Diggle (1994), Fan et al. (2007), Wang, Carroll, and Lin (2005) among others, or by using methods such as DSA (Sinisi and van der Laan, March 2004) which allow the user to fix a portion of the model. However, we adopt a more flexible approach which allows us to use a wider range of data-adaptive software, providing that any internal cross-validation respects the repeated measures nature of the data. We obtain an initial regression estimate with proper semiparametric form by updating a data-adaptively estimate for Q(A, W) of general model form using data-adaptive machine learning algorithms such as super learner (van der Laan et al., July 2007) or DSA (Sinisi and van der Laan, March 2004). Given the general model estimate, Q(A, W), for any A, we solve for Q(A = 0, W). Then using standard GEE regression, solve for the initial estimate, Q⁰ (A, W) = m(A, W|β⁰) + αQ(A = 0, W) by specifying model m(.) and treating Q(A = 0, W) as a covariate, which provides us with initial estimates for parameter β. This is an update from the original method outlined in Tuglus and van der Laan (2008). This update improves computational efficiency by only requiring a single data-adaptive estimate for Q(A, W) of general model form for all A.

Using data-adaptive algorithms such as SuperLearner (van der Laan et al., July 2007) and DSA (Sinisi and van der Laan, March 2004) will provide a better estimate for our initial Q(A, W), which improves the performance of the tVIM-RM estimator. We recognize that these methods do not account for the correlation among the repeated measures and only require that any cross-validation within the algorithm respects the repeated measure structure of the data. The asymptotic covariance matrix for the tVIM-RM estimate of β is based on the update of a GEE quasi-likelihood, which allows for the specification of a more accurate covariance structure (i.e., Σ(A, W) in the definition of the efficient score equation). In this manner the targeted MLE can still fully utilize the covariance structure of the repeated measures and potentially be asymptotically linear with efficient influence curve identified by the true Σ(A, W) without a risk of being inconsistent. The overall consistency of the estimator relies on correct specification of either the estimate of G(W) = 𝔼[A|W] or of 𝔼(Y | A, W). This is addressed further in section 2.4.

Additional efficiency in our estimator can also be gained by weighting the initial estimate for Q(A, W) by ${\left(\frac{d}{dB}m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}\text{𝔼}\left[\frac{d}{dB}m(A,\hspace{0.17em}W|\beta )|W\right]\right)}^2$, which effectively reduces the variance of the influence curve (see appendix B). This is also an update from the original method outlined in Tuglus and van der Laan (2008).

Given the three components, tMLE is applied using the following steps. Sample Rcode for a simple example is provided in appendix D.

1. Estimate the “clever covariate” which will allow us to update the initial regression in a direction which targets the parameter of interest. For a linear model the clever covariate is:

   $$r*\hspace{0.17em}(A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}\frac{d}{dB}m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}\text{𝔼}\hspace{0.17em}\left[\frac{d}{dB}m(A,\hspace{0.17em}W|\beta )|W\right]$$

2. Compute the fitted values for your initial estimate, $Q_n^0(A,\hspace{0.17em}W)$

3. Project Y onto r^* (A, W) with $offset\hspace{0.17em}=\hspace{0.17em}{Q}_n^0(A,\hspace{0.17em}W)$, define the resulting coefficient as ɛ . This is done using generalized estimating equations with fixed correlation (geeglm() in R (Yan et al., 2008)) by fitting the model Y ∼ r(A, W) + offset. Note there is no intercept in the model, only the offset value.

4. Update initial estimate ${\beta }_n\hspace{0.17em}=\hspace{0.17em}{\beta }_n^0\hspace{0.17em}+\hspace{0.17em}\varepsilon$ and overall density $Q_n(A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}{Q}_n^0(A,\hspace{0.17em}W)\hspace{0.17em}+\hspace{0.17em}\varepsilon r^{*}(A,\hspace{0.17em}W)$. These are now your single-step targeted estimates. Since this is a simple linear model, the single step solution is the final solution

5. Obtain standard error and inference for β_n using the influence curve as outlined in section 2.3.1.

Given that the number of possible covariates for both Q⁰ (A, W) and G(W) can be quite large and include main effects, interactions among the covariate set W, and interactions with time, we recommend reducing the set of possible covariates using basic univariate linear regression. As in the previous implementation (Tuglus and van der Laan, 2008, Bembom et al., 2009), we can also reduce the instability in our estimate from ETA (Experimental Treatment Assumption) violations, by restricting the covariate set using a δ cut-off based on some measure of dependence between A and W. This removes variables in W which may be highly correlated with A (Bembom, Fessel, Shafer, and van der Laan, March 2008).

2.4. Repeated Measures Estimation of Initial Density Estimate

In the procedure outlined above, the initial density estimate for tVIM-RM is a GEE model with covariate Q(0, W), which is obtained from a data-adaptive fit of Q(A, W) using a data-adaptive prediction algorithm such as DSA (Sinisi and van der Laan, March 2004) or super learner (van der Laan et al., July 2007). Both of these methods respect the repeated measures nature of the data by allowing the user to specify a subject ID to use in sampling and cross-validation, but apply an independent correlation structure for the sake of estimation. If the true correlation structure is not independent, there might be a finite sample loss in efficiency by using this structure. However, by using GEE model with a correlation matrix closer to the truth to carry out the targeted MLE update, this loss is asymptotically negligible. Nevertheless, we wish to propose an alternative initial estimate that potentially already takes into account correlation structure between the repeated measures. Given an outcome of repeated measures, one can transform the observations prior to implementing DSA or Superlearner, and then transform back the predicted values using an estimate of their covariance matrix. This is outlined here.

For a fixed working covariance matrix Σ(A, W), the quasi-likelihood has the equivalent loss function

$$L(O)\hspace{0.17em}=\hspace{0.17em}(Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W))\text{Σ}{(A,\hspace{0.17em}W)}^{-1}\hspace{0.17em}{(Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W))}^T$$

This can be rewritten as the euclidean norm

$$\left|\right|\text{Σ}{(A,\hspace{0.17em}W)}^{-\frac{1}{2}}\hspace{0.17em}(Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W))\left|\right|$$

which can be restructured in the equivalent form

$$\left|\right|\text{Σ}{(A,\hspace{0.17em}W)}^{-\frac{1}{2}}Y\hspace{0.17em}-\hspace{0.17em}\text{Σ}{(A,\hspace{0.17em}W)}^{-\frac{1}{2}}Q(A,\hspace{0.17em}W)\left|\right|$$

Therefore if Y is transformed into $Y_r\hspace{0.17em}=\hspace{0.17em}\sum {(A,\hspace{0.17em}W)}^{-\frac{1}{2}}Y$, then 𝔼[Y_r | A, W] = Q_r(A, W) and the non-transformed predicted values can be regained as follows.

$$Q(A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}\text{Σ}{(A,\hspace{0.17em}W)}^{\frac{1}{2}}\hspace{0.17em}{Q}_r(A,\hspace{0.17em}W)$$

This method can be applied to any machine learning algorithm as long as any sampling or cross-validation respects the repeated measures structure.

3. Simulation Study

In simulation, we demonstrate the robust features of the tVIM-RM method under a known data generating distribution with model mis-specification, confounding, and varying levels of overall noise. We compare our results with those of standard GEE applied using geeglm() R function from library geepack (Yan et al., 2008). The geeglm() function is allowed to update the correlation structure which is simulated and modeled correctly as AR(1). The variable of interest is univariate so sequential updating is not used for the tVIM-RM estimate, but we do apply the pre-weighting of the initial density estimate to improve overall efficiency (See appendix B).

3.1. Data

Simulated data is drawn for n=50, n=100, and n=500 subjects with 4 replicates (e.g. time points) from a linear model Y ∼ 1 – 2A + 0.5W + γ, where Y is a vector {Y_t : t = 1, . . . 4} and the error, γ, is normal with AR(1) covariance structure within replicates for each subject given a true lag-1 correlation of 0.667 and standard deviation σ_Y = 1, 10. Variable A is simulated both independent of W, and as a function of W (e.g. under confounding), where A ∼ N(2, 1) or A ∼ N(W + 2, 1) respectively, with W ∼ N(3, 1).

For each case, the importance parameter for A is measured using both basic GEE methods and tVIM-RM as described in section 2.3, under both correct and incorrect model specification, Y ∼ A +W and Y ∼ A respectively. Note that in all cases the treatment mechanism (𝔼[A|W]) is correctly modeled.

3.2. Results

We show that tVIM-RM estimator remains consistent and efficient under all conditions, with simulations showing that in over 95% of the 500 iterations, tVIM-RM finds that the true parameter value lies inside the 95% confidence interval calculated using the influence curve derived standard error. Simulation results show that in this simple example, GEE estimates are also consistent and efficient, robust to model miss-specification and confounding provided that both are not present at the same time.

4. Application

The biological pathways and mechanisms of an organism are regulated by a network of transcription factors, which control a gene’s expression by binding to specific regulatory motifs upstream of the gene’s coding sequence. Activity of a transcription factor (TF) is reflected in the gene expression profile, and given a TF to gene mapping, this information can be used to determine which transcription factors are active under various stimuli or gene conditions.

The simple approach introduced by Bussemaker et al. (2001) sets the expression profile as an outcome and regresses it onto a set of covariates, representing motif or TF to gene association measures. The association measures are generally determined from the presence of regulatory motifs upstream of the gene’s coding sequence. Often, the association measure is an affinity or matching score that is determined experimentally and/or using algorithms to detect motifs and assign probabilities to each gene-TF pairing (Gao et al., 2004, Wang et al., 2007, Conlon et al., 2003). For this analysis we chose to use a simple binary TF-gene mapping obtained from MacIsaac, Wang, Gordon, Gifford, Stromo, and Fraenkel (2006), which is based on a combination of experimental ChIP-Chip data and algorithm findings. In our covariate matrix a value of one indicates that the TF has been shown to regulate that particular gene according to the strictest conservation and binding thresholds provided by MacIsaac et al. (2006). In the original analysis Bussemaker et al. (2001), the association measure is the number of known binding motif occurrences upstream of the gene. An alternative analysis using similar regression methods focuses on the regulatory motif importance, using the motif-gene mapping as a covariate set to score potential motifs and then relate them back to the transcription network (Keles et al., 2002, Keles, van der Laan, and Vulpe, 2004, Conlon et al., 2003, Liu et al., 2006).

Using this regression approach, tVIM-RM can be used to determine the importance of a specific transcription factor in relation to a set of gene expression profiles. In this case, the repeated measures gene expression outcome is a time series of yeast gene expression over two cell cycles (Cho et al., 1998). The model-based semiparametric nature of tVIM-RM allows us to determine the importance of a TF at specific time points by specifying time indicators as potential effect modifiers of the TF. The goal is to identify the active phases of a given transcription factor during the cell cycle based on the estimated tVIM-RM importance values.

For simplicity in our application, we are using the binary TF-gene mapping provided by MacIsaac et al. (2006). Here, variable A is the binary mapping for a particular TF. This analysis is completed for each TF separately. We use the simple linear model $m_t(A,\hspace{0.17em}W|{\beta }_t)\hspace{0.17em}=\hspace{0.17em}{\beta }_{t}A{t}_t^{*}$ for t = 0, 10, . . ., 160, where $t_t^{*}\hspace{0.17em}=\hspace{0.17em}\text{𝕀}\{t_t^{*}\hspace{0.17em}=\hspace{0.17em}t\}$. Note that the complimentary full model is then $m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}=\hspace{0.17em}{\beta }_{0}A{t}_0^{*}\hspace{0.17em}+\hspace{0.17em}{\beta }_{1}0A{t}_1^{*}0\hspace{0.17em}+\hspace{0.17em}\dots \hspace{0.17em}+\hspace{0.17em}{\beta }_{1}60A{t}_1^{*}60$. For this model, the parameter of interest is ${\mu }_t(A\hspace{0.17em}=\hspace{0.17em}1)\hspace{0.17em}=\hspace{0.17em}{\beta }_{t}P(A_t{t}_t^{*}=1)$. Note that for each time point, $P(A_t{t}_t^{*}\hspace{0.17em}=\hspace{0.17em}1)$ is equivalent. Therefore, the importance of A at time $t_t^{*}$ is represented by the coefficient β_t, and we will only report these coefficients and their inference. Estimates for the initial Q(A, W) and G(W) are obtained using DSA (Sinisi and van der Laan, March 2004).

4.1. Data

In this analysis the outcome is the cell cycle gene expression profile for yeast from Cho et al. (1998). It consists of 17 time points, which is approximately two cell cycles. Data was obtained from the Yeast Cell Cycle Analysis Project website (SGD project). The cell cycle consists of four phases G1, S, G2, M. A brief description of each phase along with its corresponding time points is presented in table 2.

Table 2:

Description of stages of cell cycle. Note there are three major checkpoints at which cell cycle may arrest (Cooper and Hausman, 2007)

Cell Cycle Phase	Description
G1	Growth phase, decision to proceed through division made, checkpoint: Enough nutrients present and cell health
S	DNA synthesis occurs
G2	Checkpoint: Cell is critical size and DNA synthesis and repair are complete
M	Mitosis occurs, checkpoint on chromosome alignment before cell division

Our covariate set consists of 117 binary transcription factor-gene mappings provided by MacIsaac et al. 2006 (MacIsaac et al., 2006). Though the transcription regulatory network for yeast is not completely known, it is widely accepted that the cell cycle involves the following transcription factors: SWI4, SWI6, MBP1, MCM1, ACE2, FKH2, NDD1, and SWI5 (Harbison, Gordon, Lee, Rinaldi, Macisaac, Danford, Hannett, Tagne, Reynolds, Yoo, Jennings, Zeitlinger, Pokholok, Kellis, Rolfe, Takusagawa, Lander, Gifford, Fraenkel, and Young, 2004). Therefore our analysis will focus on these 8 transcription factors. Their known phase associations and reported active time points in Cho et al. (1998) cell cycle data are shown in table 3.

Table 3:

Association of transcription factor with cell cycle phase (Cho et al., 1998)

Transcription Factor	Cell Cycle Phase	Approx. Time Points
SWI4-SWI6, MBP1-SWI6	G1 phase, G1 to S transition	0–30, 80–110
MCM1, (MCM1-ACE2) FKH2, NDD1	G2 phase, G2 to M transition	40–70, 130–150
MCM1, SWI5, (SWI5-MCM1-FKH2-NDD1) ACE2	M phase, M to G1 transition	70–90, 150–160,0

The tVIM-RM method is applied to the 8 TFs listed above, and importance estimates are provided along with standard error derived from the influence curve. It’s important to note that though the current covariate set is binary, this method can also be applied to continuous variables and can be extended to using a score-based mapping of binding motifs such as presented in Keles et al. (2002)

In order to improve computation speed, we have chosen to reduce the yeast gene set by removing genes with variance across time less than 0.10. This reduces the data set to 3135 genes for 17 time points. We also constrain the transcription factor dataset to TFs with at least 10 related genes. TFs with less than 10 related genes are problematic for cross-validation splits used in data-adaptive algorithms. This reduces the number of potential TF confounders to 112. For this application, the initial density estimates are not weighted as discussed in section 2.3.2 and appendix B, however in practice it is possible to apply weighting to improve the overall efficiency.

4.2. Prescreening

Confounders of variable of interest, A, must be significantly related to the outcome, Y, therefore we screen our initial TF data matrix using simple regression which should improve the performance of model selection methods (Bembom et al., March 2008). To determine the set of possible covariates, W, we consider all individual TF effects and all TF:time interactions interactions using univariate regression, where interactions are treated as a single main effect. Our standard cut-off is p-value of less than or equal to 0.05 based on standard t-test. Prescreening in this fashion reduces the potential covariate set to 92 TF main effects and 481 TF:time interactions.

For each TF, separate subsequent individual screening on the covariate set was completed based on the correlation between the covariates and the TF of interest. Any covariates with correlation greater than 0.5 were removed. Such a cut-off aims to reduce bias in our final estimate by excluding variables highly correlated with the variable of interest from the possible covariate set, avoiding ETA (experimental treatment assumption) violations (Bembom et al., March 2008). This cut-off is user supplied. Currently the appropriate cut-off is chosen a priori to the application of tVIM, and in practice results are reported over a range of delta values allowing the researcher to see the full compendium of results (Bembom et al., March 2008). In previous studies it has been shown that tVIM methods remain stable up to correlations of 0.8 (Tuglus and van der Laan, 2008). Here we have chosen a delta of 0.5 based on knowledge from previous studies and computational constraints (Tuglus and van der Laan, 2008, Bembom et al., March 2008).

4.3. Results and Discussion

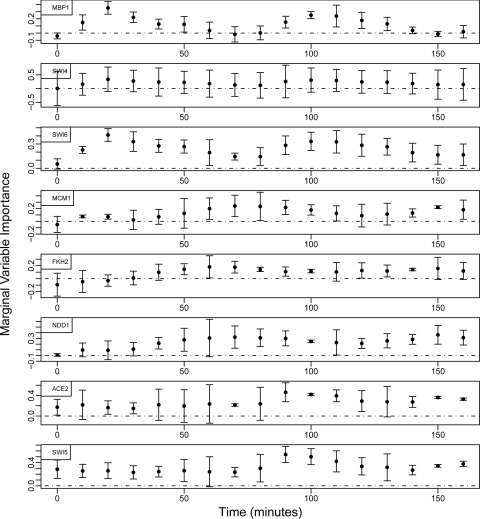
The resulting importance measures (β_t) for the 8 transcription factors are presented in figure 1 for each time point (0 min – 160 min) calculated according to the equation in Section 2.1. Error bars are included, representing the 95% confidence interval for each estimate using the standard error derived from the influence curve as outlined in Section 2.2.1.

Figure 1:

The tVIM-RM importance measures over time with 95 % confidence intervals for (top to bottom) MBP1, SWI4, SWI6, MCM1, FKH2, NDD1, ACE2, and SWI5

Many of the trends in figure 1 coincide well with the expected temporal trends outlined in table 4. MBP1 and SWI6 correspond especially well with a clear periodic trend peaking at 20 and 100 minute within the two G1 phase periods. MCM1 peaks around 70 minutes, then decreases before increasing again around 150 minutes. This approximately corresponds to decreasing during G1 phase, which is the only phase MCM1 is not active. FKH2 and NDD1 peak at 70 and 150 minutes, which corresponds well to G2 phase and G2-M transition, their more active phases.

Table 4:

Average IC-based standard error, n=100

pw	cor(A,W)	with weights	without weights	percent decrease
.1	0.3042	0.3966	0.3967	0.0257
. 2	0.4736	0.2689	0.2730	1.5091
.3	0.4186	0.3075	0.3087	0.3851
.4	0.6005	0.2356	0.2398	1.7828
.5	0.5498	0.2721	0.2738	0.6346
.6	0.5548	0.3211	0.3324	3.3866
.7	0.5733	0.2196	0.2217	0.9594
.8	0.6686	0.1612	0.1634	1.2968
.9	0.8448	0.0534	0.0616	13.4010

ACE2, SWI5, and SWI4 do not correspond as well with their expected behavior. ACE2 and SWI5 have similar trends, which remain fairly constant during the first cell cycle (0–80 minutes) and then increase around 90–100 minutes, at the G1 to S transition of the second cycle. They then slightly decrease only to increase again at 150 minutes before decreasing at the end of the cycle. SWI4 only shows a slight periodic trend with no significant time points.

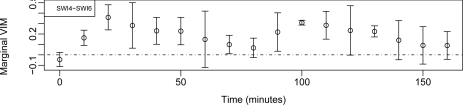
Inconsistencies in the behavior could be due to modeling the effects of the single TF and not the full complex. To explore this briefly we estimate the importance of the SWI4-SWI6 complex using tVIM-RM, allowing for effect modification by time. For this follow-up analysis, we are simply creating a new binary mapping variable where a value of one indicates that both SWI4 and SWI6 are mapped to that gene and zero indicates otherwise. Note that in this model, we still only adjust for single TFs and TF:time interactions and do not include any TF:TF complexes. Results are shown in Figure 2.

Figure 2:

The tVIM-RM importance measures over time with 95 % confidence intervals for SWI4-SWI6 transcription factor composite

In Figure 2, the expected periodic trend is present, with peaks during G1 phases. We also observe that the confidence intervals are smaller than when we measured the importance of SWI6 individually. Additional improvements may be obtained by allowing TF complexes as covariates.

Inconsistencies in our findings may come from a number of sources including the use and accuracy of the binary TF-gene mapping for our covariate set, incomplete knowledge of the yeast cell phases, as well as not providing model selection for our working model, which includes all time interactions. The current application is also fairly simplistic, and though it does show our method has promise for these types of applications, a more extensive and comprehensive study is necessary to obtain more conclusive biological findings. In particular, a thorough study of complexes is of interest, where we allow model selection on the model m(.) in order to choose among possible complexes as well as complex:time interactions. We leave these studies for future papers.

5. Discussion

The tVIM-RM method is a robust and targeted method for variable importance in repeated measures analysis. This semiparametric method requires only model specification for the parameter of interest, making fewer assumptions than a full parametric model while avoiding the need for complicated algorithms to accurately fit non-parametric components of the model. The linear working model form for the parameter of interest is flexible and accommodates both binary and continuous variables of interest while providing a straight-forward and interpretable way to incorporate effect modification of the variable of interest.

The targeted maximum likelihood step in the tVIM-RM method is easily carried out with standard GEE, which allows the user to implement it with standard readily available software. The nature of the update provides a locally efficient and double robust estimate, which remains consistent given that either the initial density estimate (𝔼[Y|A, W]), or treatment mechanism (𝔼[A|W]) is specified correctly. We demonstrated this in simulation, showing the consistency and efficiency of the tVIM-RM method under incorrect model specification and confounding. In general, tVIM-RM performs as well or better than the standard GEE approach assuming a parametric regression model.

The targeted nature of the method makes it ideal for biological studies where the researcher is interested in determining the importance of each variable on a particular outcome. It provides a framework to determine the effect of each individual variable while still adjusting for confounding. It is a especially useful tool in high-dimensional datasets in that each individual variable can be targeted separately and receives its own importance value with accurate inference.

In this paper, we apply tVIM-RM to yeast cell cycle data, measuring the importance of 8 transcription factors with respect to gene expression outcome over two cell cycles. Our results are promising, showing significant importance trends during the appropriate time periods. We follow up the analysis by demonstrating its applicability for TF complexes. Future work will focus on the development of targeted model selection methods which will allow us to select among TF and time effect modifiers for the TF of interest. The analysis is a simple case using a binary TF-gene mapping. However the targeted method can easily be extended for more sophisticated analyses such as binding motif discovery (Keles et al., 2004) and phylogenetic associations (Siewert and Kechris, 2009), where the TF-gene association may be a continuous measures. We also note that in this application we do not account for any error in the TF-gene mapping, which may bias the results. Future work in TMLE is focused on developing methods to address measurement error in A and W.

Our application involved purely observational data in which we rely on the accuracy of the initial fit for 𝔼[Y|A, W] or the fit of the treatment/confounding mechanism, 𝔼[A|W]. This double robust nature of the estimate makes tVIM-RM ideal for application in randomized trials. For instance, a clinical trial for a new AIDS drug would be interested in the average effect of the drug on CD₄ counts over time. In other words, 𝔼[𝔼[CD₄|Drug_A, time] – 𝔼[CD₄|placebo, time]] = 𝔼[β Drug_A], where β represents the effect of drug A over time. Given a randomized experimental design, the tVIM-RM method guarantees a consistent estimate of β.

Targeted Variable importance for repeated measures data provides a powerful new tool for biological studies interested in understanding the driving force behind a mechanism over time and/or experimental condition. This method has a wide range of applicability and will be useful in computational biology as demostrated here, as well as epidemiology and randomized clinical trails, where the tMLE based methods have been shown to be especially powerful (Bembom et al., 2009, Tuglus and van der Laan, 2008).

A. Efficient Influence Curve Derivation Outlined

Given observed data for a single subject O ∼ (W^*, Y = {Y_t : t = 1, . . ., T}) ∼ P₀, where W^* is the set of p covariates and Y is the set of repeated measures outcome taken over time, we define the tVIM-RM importance effect for a particular $A\hspace{0.17em}=\hspace{0.17em}{W}_j^{*}$ and time, t, controlling for confounders $W\hspace{0.17em}=\hspace{0.17em}{W}_{-j}^{*}$ as

$$\text{𝔼}\hspace{0.17em}[𝔼[Y_t|A\hspace{0.17em}=\hspace{0.17em}a,\hspace{0.17em}W]\hspace{0.17em}-\hspace{0.17em}𝔼[Y_t|A\hspace{0.17em}=\hspace{0.17em}0,\hspace{0.17em}W]]\hspace{0.17em}=\hspace{0.17em}\text{𝔼}\hspace{0.17em}[m_t\hspace{0.17em}(a,\hspace{0.17em}W|{\beta }_t)]$$

We propose the following form for the efficient influence curve for the model parameters β of the parameter of interest presented above.

$$D_{h_{\mathit{\text{opt}}},Q,G}\hspace{0.17em}=\hspace{0.17em}{h}_{\mathit{\text{opt}}}\hspace{0.17em}(A,\hspace{0.17em}W)\hspace{0.17em}\text{Σ}{(A,\hspace{0.17em}W)}^{-1}\hspace{0.17em}(Y\hspace{0.17em}-\hspace{0.17em}m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}\theta (W))$$

with the optimal scaling factor

$$h_{\mathit{\text{opt}}}\hspace{0.17em}=\hspace{0.17em}\left(\frac{d}{d\beta }m(A,\hspace{0.17em}W|\beta )\hspace{0.17em}-\hspace{0.17em}r(W)\right)$$

where θ (W) = Q(0, W) and

$$r(W)\hspace{0.17em}=\hspace{0.17em}E\hspace{0.17em}{[\text{Σ}{(A,\hspace{0.17em}W)}^{-1}|W]}^{-1}\hspace{0.17em}E\hspace{0.17em}\left[\text{Σ}{(A,\hspace{0.17em}W)}^{-1}\hspace{0.17em}\frac{d}{d{\beta }_0}m(A,\hspace{0.17em}W|\beta )|W\right]$$

We propose that the multivariate extension of the semiparametric tVIM influence curve (van der Laan, 2005, Tuglus and van der Laan, 2008). is indeed the efficient influence curve for the semiparametric targeted variable importance for repeated measures. Given the following properties (i) it is a score (ii) it is orthogonal to all nuisance scores

• Scores of the form s(W) for tangent space of p(W).

• Scores of the form s(A|W) for tangent space of p(A|W)

• Scores of the form (Y – Q(A, W))Σ(A, W)^–1 (Y – Q(A, W))^T for tangent space of Σ(A, W)

• Nuisance scores of the form r(W)Σ^–1 (Y –Q(A, W)) for tangent space of θ = Q(0, W) given fixed β

Given this, we conclude it is efficient influence curve.

1. It is straightforward to see that the influence curve above is indeed a score in the multivariate normal model space, where the multivariate normal model is defined here as

   $$p(Y|A,\hspace{0.17em}W)\hspace{0.17em}=\hspace{0.17em}{f}_{Q,\text{Σ}}^N\hspace{0.17em}(Y|A,\hspace{0.17em}W)$$

   where f_N is the multivariate normal density with scores of the form

   $$L(O)\hspace{0.17em}=\hspace{0.17em}{h}_{\mathit{\text{opt}}}\hspace{0.17em}(A,\hspace{0.17em}W)\text{Σ}{(A,\hspace{0.17em}W)}^{-1}\hspace{0.17em}(Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W))$$

2. It must be shown that the above form is orthogonal to the above nuisance scores

   • It can be shown that D_hopt,Q,G is orthogonal to scores of the form s(W) in that

     $$E[D_{h_{\mathit{\text{opt}}},Q,G^S}(W)]\hspace{0.17em}=\hspace{0.17em}E[E[D_{h_{\mathit{\text{opt}}},Q,G^S}(W)]|A,\hspace{0.17em}W]]\hspace{0.17em}=\hspace{0.17em}0$$
   • It can be shown that D_hopt,Q,G is orthogonal to scores of the form s(A|W) in that

     $$E[D_{h_{\mathit{\text{opt}}},Q,G^S}(A|W)]\hspace{0.17em}=\hspace{0.17em}E[E[D_{h_{\mathit{\text{opt}}},Q,G^S}(A|W)]|\hspace{0.17em}W]]\hspace{0.17em}=\hspace{0.17em}0$$
   • It can be shown that D_hopt,Q,G is orthogonal to scores of the form

     $$s(\text{Σ})\hspace{0.17em}=\hspace{0.17em}(Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W))\text{Σ}{(A,\hspace{0.17em}W)}^{-1}\hspace{0.17em}{(Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W))}^T$$
     under the assumption of a multivariate normal density model, in that we require E[(Y –Q(A, W))³] = 0. Given this, it follows

     $$E[D_{h_{\mathit{\text{opt}}},Q,G^S}(\text{Σ})]\hspace{0.17em}=\hspace{0.17em}E[E[D_{h_{\mathit{\text{opt}}},Q,G^S}(\text{Σ})|A,\hspace{0.17em}W]]\hspace{0.17em}=0$$

   • It follows that D_hopt,Q,G is orthogonal to scores of the form s(θ) = r(W)Σ^–1 (Y – Q(A, W)) in that r(W) is defined such that E[h_opt (A, W)Σ(A, W)^–1 (Y –Q(A, W))r(W)Σ^–1(Y – Q(A, W))] = 0

B. Weighting of the Influence Curve for Variance Reduction

In addition to the standard targeting of tVIM, steps can be taken to further increase the efficiency of the estimate. We can weigh the initial fit for Q(A, W) = E[Y|A, W] in such a way that reduces the variance of the influence curve. To determine the correct weights we refer to the form of the variance of the influence curve shown below for the linear model m(A, W|β) = Aβ.

$$\mathit{\text{Var}}\hspace{0.17em}((A\hspace{0.17em}-\hspace{0.17em}𝔼[A|W])\hspace{0.17em}(Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W)))\hspace{0.17em}=\hspace{0.17em}{(A\hspace{0.17em}-\hspace{0.17em}𝔼[A|W])}^2\mathit{\text{Var}}\hspace{0.17em}((Y\hspace{0.17em}-\hspace{0.17em}Q(A,\hspace{0.17em}W))$$

Therefore by specifying the weights of (A – 𝔼[A|W])² for our initial fit of Q(A, W) we should be able to effectively increase the efficiency. We show this in practice through a small simulation under increasing levels of ETA violation comparing the efficiency of VIM estimates from the following estimation methods for Q(A, W).

1. Weighted Q(A, W) where weights=(A – 𝔼[A|W])²

2. Unweighted Q(A, W)

3. Unadjusted (and unweighted) Q(A)

Percent of complete ETA violation (i.e. perfect prediction of A by W) was set at p_w = {10, 20, 30, 40, 50, 60, 70, 80, 90}. For percent p_w of the total number of observations of A, A is perfectly predicted by W. For (1 – p_w) percent of the observations A is not a function of W. Here we simulate A,W, and Y as continuous variables. This was completed for 500 simulations with n=500 and 100 observations using perfect confounding between A and W over a set fraction of the observations, p_w.

The data was simulated as follows:

$$\begin{array}{c}W\hspace{0.17em}\sim \hspace{0.17em}\mathit{\text{Normal}}(2,\hspace{0.17em}1)\\ A[W\hspace{0.17em}\ge \hspace{0.17em}{q}_1]\hspace{0.17em}=\hspace{0.17em}2W\\ A[W\hspace{0.17em}<\hspace{0.17em}{q}_1]\hspace{0.17em}\sim \hspace{0.17em}\mathit{\text{Norm}}(5,\hspace{0.17em}1)\end{array}$$

where, q₁ is the $p_w^{th}$ quantile of W. The true treatment mechanism model is A ∼ W + I (W < q₁) – 1, and is fitted using standard lm() function in R. We add an additional covariate W₂ ∼ Norm(2A, 1), which is correlated with A, creating an incorrect model specification for Q(A, W). The true Y is simulated as follows where β₁ = 4, β₂ = 2, β₃ = 2:

$$\begin{array}{c}Y\hspace{0.17em}=\hspace{0.17em}{\beta }_{1}A\hspace{0.17em}+\hspace{0.17em}{\beta }_{2}W\hspace{0.17em}+\hspace{0.17em}{\beta }_3{W}_2\hspace{0.17em}+\hspace{0.17em}\varepsilon \\ \varepsilon \hspace{0.17em}\sim \hspace{0.17em}\mathit{\text{Normal}}(0,\hspace{0.17em}1)\end{array}$$

B.1. Results

The following tables compare the standard error averaged over the 500 simulations.

C. Sequential Targeted Update

Targeted maximum likelihood methodology was initially developed around a low dimensional update of an initial density estimate. For β_n tVIM, which is model based, the dimension of the update increases with the size of the model. This is especially relevant for repeated measures tVIM which can easily have high dimensional model for even a one dimensional A. In an effort to avoid any potential instability in the high dimensional update we propose using a sequential targeted update which updates each component of ɛ sequentially iterating until convergence.

The results of a small simulation show that the sequential update is as good or better than the standard targeted update.

C.1. Simulation

A set of 20 possible covariates, W, is simulated from a multivariate normal with random mean between 0 and 50, a constant variance ρ, and zero correlation. The variable of interest, A, is also simulated from a normal distribution. Three different simulation set ups are used.

1. Uncorrelated: Variables in W and variable of interest, A, are uncorrelated (ρ= 0)

2. Correlated W: Variables in W are correlated with ρ= 0.8 and A is still independent of all variables in W

3. A dependent on W: Variables in W are correlated with ρ= 0.8 and A is still a linear function of two variables from W with mean zero variance 0.1 error

We model the outcome, Y, as a linear function of A : W interactions using 12 different variables from W with normal mean zero variance one error. All interaction terms have coefficients equal to four. The average mean square error for the three scenarios are compared based on 100 simulations and 500 observations.

D. Simple R Code Example

Below is code for implementing tVIM-RM using a simple main effect working model m(A, W|β) = Aβ.

D.1. Simple simulated data

library(geepack) #loads package geepack

nobs<-40 #number of subjects

nt<-4 #number of replicates/time points

visit <- rep(1:nt, nobs)

id <- gl(nobs, nt, nt*nobs)

W <- rnorm(nobs,3,1)

A <- runif(nobs, 0, 1)

#creating AR(1) structure

phi <- 1

rhomat <- 0.667 ^ outer(1:nt, 1:nt, function(x, y) abs(x - y))

chol.u <- chol(rhomat)

noise <- as.vector(sapply(1:nobs, function(x) chol.u %*% rnorm(nt,0,1)))

e <- sqrt(phi) * noise

#True Model

y <- 1+3 * W - 2 * A + e

dat <- data.frame(y, id, visit, W, A)

A=dat[,5] #variable of interest

D.2. tVIM-RM method

D.2.1. Initialization

##Initial fit for Q(A,W) and G(W)

GW<-predict(lm(A∼W,data=dat),newdata=dat)

wts1<-(A-GW)^2 #create weights

fW<-W #Though this can be Q*(0,W) from a data-adaptive fit

AW1<-matrix(A)

dat1 <- data.frame(y, id, visit, fW, AW1)

geeQf<-geeglm(y ∼ AW1+fW, id = id, weights=wts1,data = dat1,

family=gaussian,corstr =“ar1”)

# The above can also include interactions A:W

covY<-cov((matrix(residuals(geeQf),ncol=nt))) #covariance estimate

geeQ<-predict(geeQf,newdata=dat1)

bint<-coefficients(geeQf)[2] #initial parameter est.

D.2.2. tMLE update

##apply tMLE update

Scov<-(A-GW) #solve for simple clever covariate

geeUpQ<-geeglm(y∼Scov+offset(geeQ)-1,id = id, data = dat,

family=gaussian,corstr =“ar1”)#,zcor=zcor1)

bn<-bint+coefficients(geeUpQ) #updated tMLE estimate

geeQn<-predict(geeUpQ)

D.2.3. Covariance estimation

#Calculate standard error est. and p-values using influence curve

Scov1<-array(Scov,dim=c(nt,nobs,1))

Vs<-solve(covY)

VScov1<-Scov1

for(vs in 1:nobs) VScov1[,vs,]<-Vs%*%Scov1[,vs,]

VScov11<-array(VScov1,dim=c(nt*nobs,dim(Scov)[2]))

dDh<-(1/(nt*nobs))*t(VScov11)%*%(AW1)

AY<-(matrix(y)-geeQn) #recently switched from t(bout)

Dh<-as.matrix(VScov11)*AY #apply((VAWmat1),2,function(x){x*AY})

IC<-apply(Dh,1,function(x){x%*%solve(dDh)})

spI<-split(1:(nt*nobs),1:(nt))

ICrep<-array(IC,dim=c(nt,(nobs),1))

for(ic in 1:nt) ICrep[ic,,]=IC[spI[[ic]]]

ICrep1<-apply(ICrep,c(2,3),mean)

SigmaAWn<-(1/nobs)*(1/nobs)*t(ICrep1)%*%(ICrep1)

D.2.4. Simple hypothesis test

###Complete simple hypthesis test

SE<-sqrt(diag(CVest))

tests<-bn/sqrt(diag(CVest))

Pval<-2*(1-pnorm(abs(tests)))

Table 1:

Simulation results comparing GEE and tVIM-RM with n=50, 100, 500 and σ_y = 1, 10: provided are the mean value (μ_β) and standard error (SE_β) for β estimates over the 500 iterations, the mean standard error estimate (μ_SE) for the influence curve based standard error estimate from 500 iterations, and the percent of time the true β value is included in the 95% confidence interval (CI₉₅%) based on the standard error estimate over the 500 iterations.

n=50, σy = 1		tVIM-RM				GEE
Q	Confounding	μβ	SEβ	μSE	CI95% β	μβ	SEβ	μSE	CI95%
true	N	–1.997	0.080	0.075	0.944	–1.997	0.080	0.075	0.942
true	Y	–1.997	0.080	0.076	0.942	–1.997	0.080	0.075	0.942
wrong	N	–2.005	0.079	0.083	0.962	–2.005	0.079	0.083	0.956
wrong	Y	–2.000	0.080	0.078	0.950	–1.735	0.055	0.057	0.002
n=50, σy = 10		tVIM-RM				GEE
true	N	–1.990	0.251	0.238	0.944	–1.990	0.251	0.238	0.942
true	Y	–1.990	0.251	0.241	0.942	–1.990	0.251	0.238	0.942
wrong	N	–1.999	0.250	0.241	0.944	–1.999	0.250	0.241	0.940
wrong	Y	–1.993	0.253	0.242	0.944	–1.734	0.173	0.169	0.622
n=100, σy = 1		tVIM-RM				GEE
true	N	–1.998	0.048	0.051	0.956	–1.998	0.048	0.047	0.936
true	Y	–1.998	0.048	0.052	0.956	–1.998	0.048	0.047	0.936
wrong	N	–2.003	0.049	0.057	0.970	–2.003	0.049	0.052	0.952
wrong	Y	–1.999	0.048	0.053	0.960	–1.760	0.034	0.036	0.000
n=100, σy = 10		tVIM-RM				GEE
true	N	–1.993	0.153	0.162	0.956	–1.993	0.153	0.148	0.936
true	Y	–1.993	0.153	0.164	0.956	–1.993	0.153	0.148	0.936
wrong	N	–1.997	0.154	0.164	0.960	–1.997	0.154	0.150	0.938
wrong	Y	–1.994	0.153	0.164	0.960	–1.756	0.109	0.109	0.364
n=500, σy = 1		tVIM-RM				GEE
true	N	–2.000	0.023	0.023	0.936	–2.000	0.023	0.023	0.934
true	Y	–2.000	0.023	0.023	0.930	–2.000	0.023	0.023	0.934
wrong	N	–1.990	0.024	0.026	0.962	–1.990	0.024	0.025	0.960
wrong	Y	–1.995	0.023	0.023	0.946	–1.746	0.016	0.017	0.000
n=500, σy = 10		tVIM-RM				GEE
true	N	–2.001	0.074	0.074	0.936	–2.001	0.074	0.072	0.934
true	Y	–2.001	0.074	0.072	0.930	–2.001	0.074	0.072	0.934
wrong	N	–1.990	0.074	0.074	0.944	–1.990	0.074	0.073	0.942
wrong	Y	–1.996	0.073	0.072	0.936	–1.747	0.050	0.050	0.000

Table 5:

Average IC-based standard error, n=500

pw	cor(A,W)	with weights	without weights	percent decrease
.1	0.3310	0.1869	0.1872	0.1647
. 2	0.3941	0.1783	0.1812	1.5614
. 3	0.4593	0.1780	0.1796	0.8770
.4	0.5357	0.1527	0.1532	0.3380
.5	0.5546	0.1540	0.1551	0.6753
.6	0.5674	0.1259	0.1260	0.0878
.7	0.6381	0.1004	0.1007	0.3099
.8	0.6981	0.0776	0.0778	0.2872
.9	0.7886	0.0538	0.0551	2.1913

Table 6:

Comparing the average mean square error of scenarios: Uncorrelated, correlated, and A dependent on W using 100 simulations. Percent decrease accounted to using the iterative update over the standard update is also reported.

Scenario	Standard Update	Iterative Update	Percent Decrease
Uncorrelated	0.10950	0.10766	1.7 %
Correlated W	0.01001	0.00917	8.4 %
A dependent on W	0.20454	0.20052	2.0 %