Introducing Knowledge into Differential Expression Analysis

Abstract

Gene expression measurements allow determining sets of up- or down-regulated, or unchanged genes in a particular experimental condition. Additional biological knowledge can suggest examples of genes from one of these sets. For instance, known target genes of a transcriptional activator are expected, but are not certain to go down after this activator is knocked out. Available differential expression analysis tools do not take such imprecise examples into account. Here we put forward a novel partially supervised mixture modeling methodology for differential expression analysis. Our approach, guided by imprecise examples, clusters expression data into differentially expressed and unchanged genes. The partially supervised methodology is implemented by two methods: a newly introduced belief-based mixture modeling, and soft-label mixture modeling, a method proved efficient in other applications. We investigate on synthetic data the input example settings favorable for each method. In our tests, both belief-based and soft-label methods prove their advantage over semi-supervised mixture modeling in correcting for erroneous examples. We also compare them to alternative differential expression analysis approaches, showing that incorporation of knowledge yields better performance. We present a broad range of knowledge sources and data to which our partially supervised methodology can be applied. First, we determine targets of Ste12 based on yeast knockout data, guided by a Ste12 DNA-binding experiment. Second, we distinguish miR-1 from miR-124 targets in human by clustering expression data under transfection experiments of both microRNAs, using their computationally predicted targets as examples. Finally, we utilize literature knowledge to improve clustering of time-course expression profiles.

1. Introduction

High-throughput gene expression measurements provide for a comparison between two experimental conditions. After proper normalization, sets of up- or down-regulated genes (together: differentially expressed) can be determined. Established differential expression analysis tools are based on examining the fold-change of gene expression level and/or performing a t-test (Cui and Churchill, 2003; Slonim and Yanai, 2002, 2009). Typically, a threshold cutting off the differentially expressed genes in the resulting ranked gene list is determined based on the false discovery rate (FDR; Tusher et al., 2001). However, the researcher can often provide examples from the sets of up-/down-regulated, or unchanged genes in the analyzed experiment. The knowledge about the examples is rarely certain and can rather be quantified in distributions over those sets. Given such imprecise information, the problem is to find the threshold that is both stringent enough to select only the significantly changed genes, and permissive enough to include the known examples.

In this work, we propose a novel methodology that systematically incorporates imprecise knowledge into differential expression analysis. We use partially supervised mixture modeling that separates one-dimensional expression data into clusters of differentially expressed and unchanged genes, and profits from imprecise examples to find these clusters. Our partially supervised methodology brings two important benefits to differential expression analysis: First, the use of mixture modeling avoids setting ad-hoc thresholds; the clusters are defined by the model that is most likely, given the data and the examples. Second, partially supervised modeling handles even erroneous examples; such examples may not fit with the rest of the data in their believed cluster and can get “re-clustered” in the output. In this way, modeling tells which of the examples were incorrect according to the data.

The proposed partially supervised approach is implemented using two complementary methods. One extant method, referred to as the soft-label mixture modeling, was recently introduced in machine learning (Côme et al., 2009) and shown to improve model-based clustering of general benchmark datasets. We contribute a partially supervised method that we call belief-based mixture modeling. In the more practical cases when the known examples constitute only a small fraction of all elements in each cluster, the newly introduced method proves to be less susceptible to disproportional representation of examples per cluster than soft-label modeling. If the number of examples is large, the soft-label method better estimates the model parameters. Both methods, as well as other mixture modeling approaches considered in this work, are implemented in an R package bgmm, freely available from http://bgmm.molgen.mpg.de, together with the data used for the analysis presented in this article. The package provides practical support in the application of our methodology to differential data analysis.

Unsupervised mixture modeling was applied to define clusters of differentially expressed and unchanged genes previously (Pan et al., 2002; Garrett and Parmigiani, 2003; Newton et al., 2004; Do et al., 2005). In particular, it is used to define “states” (e.g., up, down or unchanged) of variables in graphical models of biological pathways (Pe'er et al., 2001; Ko et al., 2007). Moreover, numerous applications of multidimensional mixture modeling to clustering of gene expression profiles (Yeung et al., 2001; McLachlan et al., 2002; Ghosh and Chinnaiyan, 2002; Dortet-Bernadet and Wicker, 2008) prove that it is well suited for expression data. In this field, several approaches extend mixture modeling to include prior knowledge. Costa et al. (2007, 2009) and Pan et al. (2006) incorporate pairwise constraints known for a subset of the observations and perform penalized mixture modeling ensuring that the constraints are not violated. Pan (2006) takes into account a grouping of genes, defined by functional relations on top of the clustering. Alexandridis et al. (2004) perform clustering and tumor sample classification using samples whose classes are known precisely. None of these methods, however, can easily be adapted to utilize imprecise examples in differential expression analysis.

Our tests on synthetic data characterize the differences as well as the common features of the belief-based and the soft-label mixture modeling methods. We simulate expression data in two conditions to rigoriously compare our partially supervised methodology to standard differential analysis methods. We show three applications of both partially supervised methods to real gene expression data: first, we identify targets of Ste12 from knockout data in yeast, given knowledge from a Ste12 DNA-binding experiment; second, we distinguish miR-1 from miR-124 human target genes based on expression data from transfection experiments of either microRNAs, with the use of their computationally predicted targets; third, by applying our methodology in the pre-processing step, we improve the clustering of cell cycle genes based on their time-course expression profiles. Our tests show the power of the novel application of the partially supervised methods to differential expression analysis, by comparing to unsupervised and semi-supervised (using precise examples) mixture modeling, the standard p-value threshold-based methods, as well as an extant algorithm called NorDi (Martinez et al., 2007).

2. Methods

In the problem of clustering, a dataset of observations 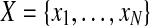is given, and one looks for an assignment of the observations to clusters in 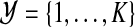. In this article, we assume that the number of clusters K is known, and that the data is one-dimensional. In our application, the clusters correspond to differentially expressed (shortly, differential) or unchanged genes, and data consists of expression ratios comparing two condition measurements. To find the clusters, mixture modeling is applied. Mixture modeling associates each cluster with a model component, which is defined by an underlying distribution estimated from the data.

Mixture modeling variants differ in the way they utilize additional knowledge. We assume the knowledge is available for a subset of first M observations 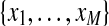, called examples. The knowledge about an example can either be precise and give exactly one cluster the example belongs to, or can be imprecise and described by a probability distribution over the clusters in 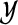. The precisely assigned cluster or the most probable cluster for an example is also called a label, and the examples are also referred to as labeled data.

In the following section, we shortly cover known variants of mixture modeling methods. Sections 2.2 and 2.3 describe the principles of two partially supervised mixture modeling methods: our own, introduced in this article, and one proposed by Côme et al. (2009).

2.1. Mixture modeling

Mixture modeling assumes that the cluster labels are realizations of random variables 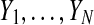that take values in 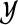and follow a multinomial distribution 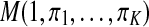, so π_k = P(Y_i = k), for 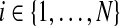and 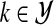. The π_ks are called mixing proportions, or priors, and of course satisfy 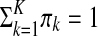. The observations in X are assumed to be generated by continuous random variables with values in and a conditional density function 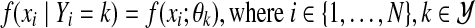, while θ_k denotes the parameters of the density function. We are concerned with Gaussian mixtures, where 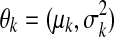. The model parameters, denoted 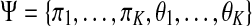, are usually estimated from the data.

In unsupervised mixture modeling, the input is only the data X and no cluster labels are known. In this case, we use the Expectation Maximization (EM) (Dempster et al. (1977) algorithm for parameter estimation. In the semi-supervised mixture modeling case, we know the precise cluster labels for a number of examples, constituting a small subset of all observations. Parameter estimation is obtained via an EM algorithm, where the labels for the examples remain fixed. For more details on these two classical methods, see McLachlan and Peel (2000) and Zhu and Goldberg (2009).

2.2. Belief-based mixture modeling

We propose a partially supervised mixture modeling method that handles imprecise knowledge about the examples. The idea of the method is to set an equivalent of the prior π_k differently for each example x_i (i ≤ M) to the value of our belief, or certainty, about the example belonging to a particular cluster k. The belief is defined as a probability distribution over the clusters in 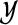, given by a vector b_i, where b_ik = P(y_i = k), satisfying 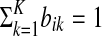. The input set to our method is 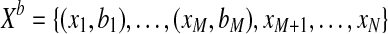. Accordingly, the log likelihood for this dataset reads:

(1)

The maximum likelihood estimate of the parameters Ψ is obtained using the EM algorithm. In the E step of the (q + 1)-th iteration, we compute the posterior probabilities:

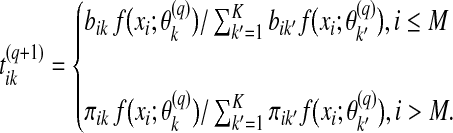(2)

Therefore, in the M step, the update equation for the mixing proportions becomes:

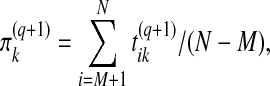(3)

i.e., the examples do not contribute to this estimation. The Gaussian parameters θ_k are updated using the equations:

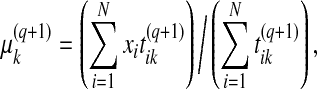(4)

(5)

2.3. Soft-label mixture modeling

Soft-label mixture modeling, introduced by Côme et al. (2009), formulates the given imprecise knowledge with belief functions (Shafer, 1976). In our application, each observation is labeled with a single cluster. In general, the soft-label method allows labels defined as subsets of clusters. Therefore, we consider only a particular case in their approach. In this case, the input dataset is defined as 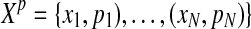, where for an example x_i (i ≤ M), a plausibility p_ik for each cluster k is given, satisfying 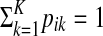. For the remaining observations (i > M), it is assumed that this distribution is uniform, i.e., p_ik = 1/K. Côme et al. (2009) weight the prior for the examples with the plausibilities, obtaining a log likelihood for the input dataset:

(6)

Therefore, in the E step of the EM algorithm, we compute:

(7)

In contrast to belief-based modeling, here the update equation for the mixing proportion in the M step does utilize examples, and reads:

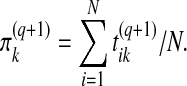(8)

The Gaussian parameters are updated as in Eq. (4) and Eq. (5).

2.4. Key differences

The belief-based and soft-label methods differ in the way they incorporate imprecise knowledge. Belief values should be interpreted as the actual certainties with which the examples belong to each particular cluster. The plausabilities weight the mixing proportions, giving higher weights to more likely clusters. Consider a model with two components of equal proportions and variances, and different means (Fig. 1A). A belief value 0.5 for an example indicates that in the data this example lies exactly in the middle between the two means. The plausability value 0.5 states that there is no certainty about the cluster which the example belongs to, and does not suggest any likely position for the corresponding data point.

Fig. 1.

(A) Model 1 assumed in the first test, with two well-separated components (drawn in black and gray), Gaussian parameters as indicated on the plot, and separated sets of 14 examples per component (marked below). (B) y-axis: average accuracy of belief-based, soft-label and semi-supervised methods in putting data into the same clusters as the true model in A. x-axis: different accuracy bar plots for increasing number of examples that are mislabeled (out of the pool of 14 per component). Both partially supervised methods deal significantly better with mislabeled examples than the semi-supervised method. (C) Model 2 assumed in the second test, with overlapping components and small example sets (14 per component), plotted as in A. (D) The plot as in B, but the x-axis shows the numbers of examples, correctly labeled, used per component (from those indicated in C). The example numbers proportions (from left to right 1:1, 1:2, 1:3, and 1:4) are increasingly biased with respect to the model mixing proportions (1:1). Applied to cluster the data from the model in C, belief-based modeling is more resistant to such bias than both soft-label and semi-supervised modeling. (E) Model 2 with a large number of 450 examples per component assumed in the third test, ploted as in C. (F) The plot as in D, but here the increasing bias is introduced in the proportions of observations that are not used as examples (from left to right 1:1, 2:3, 1:2, and 2:5). Applied to cluster the data from the model in E and given large example numbers, belief-based modeling less acurately estimates the model and is less resistant to such bias than both soft-label and semi-supervised modeling.

The differences in mixing proportion estimation between the belief-based and soft-label modeling (Eq. 3 versus Eq. 8) have a crucial practical consequence. In the case of soft-label modeling, examples with high plausabilities have higher influence on the mixing proportion estimation than the remaining observations. In the case of belief-based modeling, only the remaining observations are used to estimate the mixing proportions. This implies that the soft-label method is susceptible to bias in the proportion of given examples, whereas belief-based modeling is susceptible to bias in the remaining observations' proportions. Consider a dataset with two clusters of 1000 elements each (cluster size proportion 1:1, mixing proportion 0.5). For very low example numbers, it is easy to give biased example proportions affecting the soft-label model estimation. For instance, 10 examples for one and and 100 for the other cluster gives a 1:10 example proportion (and a 99:90 proportion between the remaining observations, close to the desired 1:1). On the other extreme, taking 990 and 900 known examples for the two clusters respectively, hampers the belief-based model estimation in two ways. First, the small number of observations affects proper estimation of the mixing proportion, and in turn, other model parameters in the EM iterations. Second, the remaining observations' proportion 10:1 is biased. Note here that when all examples for a given cluster are known, the belief-based method is not even applicable. To summarize, in comparison to soft-label modeling, belief-based modeling is tailored for the more realistic input sets where the number of examples is small, compared to the amount of unlabeled data required for robust estimation of mixing proportions. However, for high example numbers soft-label modeling should be applied.

2.5. Partially supervised model-based clustering

Once the model is estimated, each observation is assigned to its most probable cluster (from equally probable, one is chosen at random). Note that, by this maximum a posteriori (MAP) criterion, semi-supervised modeling clusters the examples always in the same way as they are labeled in the input (see Section 2.1). In contrast, the partially supervised methods are able to “re-cluster” the examples: an example, although assigned with the highest certainty to a particular cluster k, can have as a result of the EM algorithm the highest posterior probability to belong to a cluster k′ ≠ k. In the case of soft-label modeling, the posterior probability to belong to cluster k can be low for an example x_i if the mixing proportion π_k or the density function f (x_i|θ_k) are small, even if the plausibility p_ik is high (see Eq. 7). Belief-based modeling does not take into account the mixing proportions when deciding the cluster label for a given example. Here the belief about the example “competes” only with the value of the density function (see Eq. 2). In summary, semi-supervised model estimation is most strongly influenced by the examples and, unlike the partially supervised methods, cannot correct for mislabeled examples. Thus, if the data groups into clear clusters, the given examples are in ideal proportions and constitute a representative sample from each component, then the semi-supervised method is expected to perform best in estimating the true model. In the more realistic case, the knowledge is imprecise and uncertain, and both belief-based and soft-label methods are applicable instead.

Note finally, that after assigning to most probable clusters, the clustering is no longer probabilistic but partitional. Thus, when true clustering is available, we evaluate the model-based clustering using standard accuracy (number of correctly labeled observations over the number of all observations) or adjusted Rand index (Hubert and Arabie, 1985). The latter measure takes values in the (0, 1) interval, and for random clusterings gives values close to 0. High values of the Rand index indicate significant agreement of two clusterings.

2.6. The partially supervised methodology applied to differential expression analysis

The methodology takes as input data and imprecise examples of differential and unchanged genes. The data are log expression ratios computed for two conditions, refered to as treatment and control, respectively. When replicate experiments are available, log mean ratios, or t-statistic should be analyzed. Negative observations refer to lower, while positive observations refer to higher expression values in treatment versus control. The differential genes comprise a small fraction of all genes and their observations are expected to lie on the extremes of the data range.

There are two analysis scenarios supported: first, clustering into two clusters of differential and of unchanged genes, and second, clustering into three clusters of down-regulated, up-regulated, and unchanged genes. Practically, in the first scenario, the differential cluster is defined as the one with the higher variance. In the second scenario, we sort the three estimated model components increasingly by their means. The down- and up-regulated clusters have the lowest and the highest mean, respectively. Our implementation provides support for fitting a mixture modeling method of choice in both scenarios. As a result the estimated model parameters, probabilities of belonging to each cluster, and a label of the differential cluster are returned. Additionally, the user can plot the obtained models to verify whether the data clusters as expected. We use the first scenario of two clusters throughout this article.

2.7. Parameter initialization

Both the semi-supervised and partially supervised methods take as input examples with cluster labels. Implicitly, they require that the user assumes an order on the clusters to be found in the data. Each example obtains a label, which is the number of its believed cluster in the assumed order. On the other hand, the EM algorithm estimates the model components (i.e., clusters) in the order of their initial parameters. Consequently, for the EM algorithm to utilize the examples properly, the initial parameters of each component k should correspond to the cluster labeled k by the user, 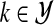. There are various ways of defining the initial parameters. We describe two of them.

One way is to compute the initial parameters from the examples. For a Gaussian mixture model component k one can compute the mean, variance, and proportion of the examples labeled k. Automatically, the initial parameters of component k will correspond to examples from cluster k. However, initialization from examples is not always the best choice, especially when there are only a few of them. Also, for some clusters there might be no example available.

Another common way (used for unsupervised mixture modeling of univariate data by Yeung et al., 2001) is to divide the data into quantiles, returning clusters in an order not necessairly the same as the one assumed by the user. Next, initial parameters for the EM algorithm are obtained from this clustering. Given any such initialization procedure, we run the EM algorithm for all possible permutations of initial parameters, and the estimated model with the highest likelihood is returned.

3. Results

3.1. Validation on synthetic data

We first validate the performance of the belief-based and soft-label mixture modeling methods on synthetic data, where the true labels for all observations are known.

3.1.1. Partially supervised model-based clustering

We first investigate the performance of three methods that utilize knowledge in the general task of model-based clustering. We compare the partially supervised belief-based and soft-label, as well as semi-supervised modeling. We consider two different Gaussian mixture models (Models 1 and 2), with two components each (Fig. 1A, C). In both models the mixing proportions are equal, π = π₁ = π₂ = 0.5. The Gaussian model parameters are denoted 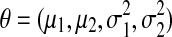. We run three tests on 1000 random samples of 1000 observations each: first, assuming Model 1 and choosing a pool of 14 examples per component; second, Model 2 and 14 examples per component; and third, Model 2 and 450 examples per component. The examples are given belief/plausibility of belonging to their cluster equal to 0.95, and of belonging to the other cluster equal to 0.05. In each test, to generate one sample from the assumed model, we draw the number of observations in the first component from the binomial distribution N₁∼ 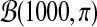, and set the number in the second component to N₂ = 1000 − N₁. Next, we draw N₁ observations from the normal distribution 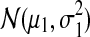and N₂ from 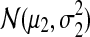. For every observation in the sample a true label is derived: observations are assigned to the most probable cluster under the assumed model (either Model 1 or 2). The compared methods make their predictions of the true labels by first estimating the model of the data sample, given the examples, and next model-based clustering of the data. In each test, the accuracy of assigning true labels to observations that are not used as examples is averaged over the 1000 samples.

The first test (Fig. 1A, B) shows advantage of considering imprecise knowledge. Model 1 (Fig. 1A), with well separated components and sets of examples per component, is easy to estimate. Using all given examples correctly labeled, all methods find true cluster labels accurately (first three bars in Fig. 1B). In contrast to semi-supervised modeling, both partially supervised methods, belief-based and soft-label modeling are highly accurate even when examples are mislabeled by switching their labels to other clusters (remaining bars in Fig. 1B).

Figure 1C–F shows on Model 2 the differences in performance between the belief-based and soft-label modeling (see Section 2.4). The components of Model 2 largely overlap, and we use overlapping subsets of examples per component. In the second test, for small example numbers (Fig. 1C) and equal example proportions the model is well estimated by all methods (first three bars in Fig. 1D). However, when the example number proportions disagree with the assumed model mixing proportions, only belief-based modeling achieves high clustering accuracy (remaining bars in Fig. 1D). In the third test, with large example numbers (Fig. 1E) and equal example proportions, the belief-based method lacks enough observations to estimate the model as good as the soft-label and semi-supervised methods (first three bars in Fig. 1F). Additionally, the larger the bias in representation of observations not used as examples, the poorer the accuracy of the belief-based method (remaining bars in Fig. 1F). In both cases soft-label modeling behaves similarly to semi-supervised modeling.

3.1.2. Partially supervised differential expression analysis

Next, we show the improvement obtained by using our partially supervised approach in differential expression analysis. On synthetic datasets, we compare the partially supervised methods and semi-supervised modeling with standard differential analysis methods: t-test, SAM (Tusher et al., 2001), Cyber-T (Baldi and Long, 2001), and LIMMA (Smyth, 2005). Additionally, we run unsupervised mixture model-based clustering of t-statistic (proposed in a more general setting for differential analysis by Pan et al., 2002).

We generated 100 datasets, each simulating expression of 200 differential and 1800 unchanged genes in the control and treatment conditions. Each dataset consists of two data matrices, control and treatment, with three columns (experimental repeats) and 2000 rows (genes). The basal gene log intensity values in the control matrix are drawn from a normal distribution . The values in the treatment matrix for the unchanged genes come from the same basal distribution, whereas for the differential genes are drawn from 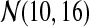. This reflects the biological reality where the differentially expressed genes change their expression between the control and treatment condition, but each to a different extent.

We evaluate the compared methods by their accuracy (measured with the adjusted Rand index; see Section 2.5) of identifying the true differential and unchanged genes. The standard differential analysis aproaches are applied directly to the simulated control and treatment matrices and return p-values of differential expression. Next, we use common p-value thresholds of 0.01 and 0.05 to define the differentially expressed genes. The unsupervised clustering is applied to the t-statistic computed using LIMMA. The partially supervised and semi-supervised methods are applied to log mean treatment versus control intensity ratios (see Section 2.6). Application of those methods to the t-statistic yielded the same results and is thus not reported. Examples for the supervised methods are uniformly drawn at random from the set of differential and unchanged genes and assigned belief/plausability values of belonging to their true clusters equal 0.95.

Figure 2 shows the adjusted Rand index distributions obtained over the 100 synthetic datasets. Given correct examples in true proportions, the partially supervised and semi-supervised methods most accurately classify the differential and unchanged genes by their simulated expression values. Proportional increase in the number of given examples did not change the results; we show performance with 0.04 (eight for the differential and 72 for the unchanged genes) and 0.25 (50 and 450) of all elements in a cluster used as examples. The unsupervised clustering of the t-statistic performs worse, showing the improvement gained with incorporating knowledge in the analysis. Recall that the model-based methods perform MAP clustering (see Section 2.5) and do not require setting cut-off thresholds. In contrast, the accuracy of the standard methods depends on p-value cut-off used. For example, the accuracy obtained by SAM with a p-value cut-off of 0.01 is the highest among standard approaches, but it drops dramatically for the p-value of 0.05. Finally, we show two extreme cases of misleading input example settings that hamper the accuracy of the soft-label, and to a higher extent, the semi-supervised methods (see Section 2.4). First, we give the examples in proportion 9:1, inverted with respect to the actual proportion of cluster sizes. Second, we again give 50 and 450 examples for the differential and unchanged genes (a 0.25 fraction), but we mislabel 25 of them by switching their labels to the other clusters. The belief-based method proves robust to both misleading input settings.

Fig. 2.

Partially supervised differential expression analysis on synthetic data. Given 8 examples of differential and 72 examples of unchanged genes (a 0.04 fraction of all elements in each cluster), the partially supervised belief-based and soft-label methods, as well as semi-supervised modeling achieve superior accuracy (red boxplots) over the standard differential analysis approaches (light blue for the 0.01 p-value cut-off and dark blue for the 0.05 cut-off ). Increasing the number of examples used by the supervised methods to 50 and 450 (a 0.25 fraction; brown boxplots) yields similar results. Belief-based method maintains high performance also when the known examples are given in reversed proportion 9:1 (orange boxplots) or are mislabeled (25 examples switched between the 50 differential and 450 unchanged genes, respectively; violet boxplots).

3.2. Finding Ste12 target genes

Next, we apply the partially supervised methodology to identify pheromone environment-specific target genes of the Ste12 transcription factor (TF) in yeast. We use expression data from four types of cells: untreated wild-type and Ste12 mutants, as well as wild-type and Ste12 mutants treated with 50 nM of α-factor treatment for 30min (Roberts et al., 2000). To focus on transcriptional changes triggered by pheromone stimulation, we limit the analysis to 602 genes that show a 1.5-fold up- or down-regulation upon pheromone treatment of wild-type cells. The analyzed data consists of log₂ expression ratios, pheromone-treated Ste12 mutants versus prehomone-treated wild-type cells. In this dataset, we seek to distinguish the set of differential genes from a set of genes that remain unchanged.

We utilize high-throughput experiments to define examples from the first set of differential genes: we take 42 genes that have their promoter bound by Ste12 in pheromone environment with a p-value <0.0001 (Harbison et al., 2004), and that are at least two-fold up-regulated upon pheromone treatment as compared to wild type (Roberts et al., 2000). We further use the significance of Ste12-DNA binding to reflect the level of certainty about those examples in the belief/plausability values. The Ste12-DNA binding p-values of the example genes correlate with the logarithm of the changes in expression upon Ste12 knockout in pheromone environment (Pearson correlation coefficient 0.42, p-value of 0.0045). We set the belief/plausability of belonging to the set of differential genes accordingly: the belief values lie in the (0.5, 0.95) interval and are proportional to the log binding p-values. We do not use any examples for the second cluster of unchanged genes. All mixture modeling methods are initialized using quantiles (see Section 2.7).

For comparison to the partially supervised belief-based and soft-label modeling, we test also the semi-supervised and unsupervised mixture modeling. All these methods are applied to find two clusters: one for the differential genes and one for the unchanged. Additionally, we compare our methods to the NorDi algorithm (Martinez et al., 2007), which identifies differential genes by normalizing and discretizing gene expression measures. This algorithm first fits the data to a single Gaussian component, removing outliers, and next calculates the up- and down-regulated cut-off thresholds using the z-score methodology (Yang et al., 2002). To compare to the traditional differential expression analysis, we use the p-values for the genes provided by Roberts et al. (2000). We define two sets of differential genes, first with the common p-value threshold 0.01, and second with the threshold 0.05. Using each threshold, we first select only genes that are differential under pheromone treatment in wild-type cells. Next, from those, we select genes that are differential under Ste12 knockout in pheromone-treated cells.

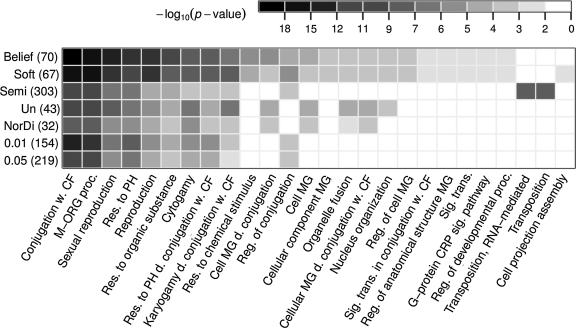
We define the set of Ste12 targets identified by each method as those genes from the obtained set of differential genes, which are down-regulated in the Ste12 mutants (Ste12 is a transcriptional activator; Kirkman-Correia et al., 1993). We evaluate the identified sets of Ste12 targets by testing whether the proteins encoded by the targets take part in Ste12-dependent processes induced by pheromone (Figure 3). To this end, for each target set we computed the p-values for its enrichment in Gene Ontology annotations (GO; Ashburner et al., 2000), using the TermFinder tool by Boyle et al. (2004).

Fig. 3.

Biological validation of identified Ste12 targets. Enrichment p-values (shades of gray) of the sets of Ste12 targets identified by the compared methods (matrix rows; 0.01 and 0.05 denote cut-offs applied to differential expression p-values provided by Roberts et al. [2000]; set sizes are given in brackets) in Gene Ontology (GO) biological process terms (columns). Each presented term is enriched in at least one Ste12 target gene set with a p-value of <0.01 and FDR of <0.01. Significant enrichment represents distinct behavior of the target genes compared with the rest of all genes. The belief mixture modeling identified a set of Ste12 target genes with the lowest product of all p-values. Un, unsupervised; CF, cellular fusion; M-ORG, multi-organism; Res., response; PH, pheromone; MG, morphogenesis; Reg., regulation; CRP, coupled receptor protein; Sig. trans., signal transduction; w., with; d., during.

The set of Ste12 targets identified by the belief-based modeling method has the highest enrichment in the GO annotations related to Ste12 activity upon pheromone stimulation (Herskowitz, 1995): mating and conjugation with cellular fusion. Similarly, strong evidence for the same functionality is shown for the set of Ste12 targets of comparable size, identified by the soft label modeling method.

Unsupervised mixture modeling and the NorDi algorithm identify Ste12 target sets that are smaller than the sets identified by the two partially supervised methods, leaving out many genes that are functionally related to the pheromone-triggered and Ste12-dependent processes (Fig. 3).

Semi-supervised modeling, in contrast, includes all given examples in the cluster of differential genes. As opposed to belief-based modeling, the semi-supervised method shifts this cluster toward low change in expression upon Ste12 knockout (Fig. 4). Therefore, its set of identified Ste12 targets contains half of all analyzed genes, and incorporates most superfluous genes, for example, genes taking part in the transposition process. Also relatively big, the sets of Ste12 targets identified using the two p-value cut-offs have better enrichment scores than the set identified by semi-supervised modeling, but worse than the sets identified by the partially supervised methods (Fig. 3).

Fig. 4.

Different impact of examples on the models estimated by different supervised methods. Model estimated by the partially supervised belief-based (A) and by the semi-supervised mixture modeling (B). The plots are as in Figure 1A.

3.3. Distinguishing miR-1 from miR-124 targets

To further evaluate the performance of the partially supervised mixture modeling methods, we check their accuracy of distinguishing miR-1 from miR-124 target genes in human, based on two expression datasets from transfections of these microRNAs (shortly, miRNAs; Lim et al., 2005) and knowledge from computational miRNA target predictions. We use the subset of the genes measured by Lim et al. (2005), which can be divided into two distinct clusters with rigorous experimental verification: 90 miR-1 targets (Selbach et al., 2008; Zhao et al., 2005) and 35 miR-124 targets (Wang and Wang, 2006; Krek et al., 2005; Karginov et al., 2007). Among them, we use as examples 16 miR-1 and 11 miR-124 target genes that have computationally predicted binding sites of miR-1 and miR-124, respectively. We take only the examples that are predicted as respective targets by both computational methods that we used: MirTarget2 (Wang and El, 2007; Wang, 2008) and miRanda (Betel et al., 2008). The belief/plausibility values for examples to belong to their clusters are set to 0.95.

In both transfection datasets, we expect to see down-regulation of one miRNA's target genes (e.g., miR-1 targets upon miR-1 transfection) and the other target genes unchanged by the transfection. Therefore, for each dataset, we apply the partially supervised modeling methods and, for comparison, the remaining mixture modeling methods to find two clusters. The obtained clusterings are validated with the two true clusters of miR-1 and miR-124 target genes using the adjusted Rand index (see Section 2.5). The examples are not included in computing the index.

The data from the miR-124 transfection is easier to cluster than the data from the miR-1 transfection (for miR-124 the clusters are more separated; data not shown). Accordingly, the estimations of the model are less accurate for the miR-1 transfection data (Fig. 5A, B). As expected (see Section 2.5), in the easier case of miR-124 transfection, the semi-supervised modeling achieves better results than others. On the contrary, in the more difficult case of the miR-1 transfection, the semi-supervised method performs worst, and the partially supervised methods achieve the highest accuracy. The same is observed when randomly chosen sets of examples are used instead of the computationally predicted ones (Fig. 5C, D).

Fig. 5.

Improved accuracy of distinguishing miR-1 from miR-124 targets. (A) The adjusted Rand index (x-axis) indicates whether the different mixture modeling methods (y-axis) clustered the data correctly into true groups of known miR-1 and miR-124 targets. Analyzed expression data comes from the miR-1 transfection experiment. The semi-supervised and partially supervised methods utilized 16 computationally predicted examples of miR-1, and 11 of miR-124 targets. (B) Plot as in A, but for the data obtained under the miR-124 transfection. (C) Box-plots show the adjusted Rand index distribution (x-axis), obtained by the methods (y-axis) in 1000 tests, where 16 examples were drawn from all miR-1 targets, and 11 drawn from all miR-124 targets at random, and the data came from miR-1 transfection. (D) Plot as in C, but for the data from miR-124 transfection.

3.4. Clustering cell cycle gene profiles

Finally, we make use of partially supervised mixture modeling in the task of clustering cell cycle gene expression profiles (Cho et al., 1998). Based on expression measurements over 17 time points, which cover two cell cycles, 384 genes fall into five disjoint clusters. Each cluster contains genes peaking at a particular cell cycle phase: early G₁, late G₁, S, G₂, or M (Cho et al., 1998). Following Yeung et al. (2001), we take this five-phase criterion as the true clustering of genes in this dataset. For each phase cluster, we take seven examples of genes known to be active in this phase (first seven listed for that cluster in Table 1 of Cho et al. [1998], excluding genes active in more than one phase), i.e., all together, 35 examples.

The partially supervised modeling methods, as well as the unsupervised, semi-supervised, and NorDi (Martinez et al. (2007; see Section 3.2) methods are applied to cluster the 384 genes in a two-step procedure:

1. Clustering of data from each time point into two clusters. In the data from each time point t separately, find two clusters, one of which corresponds to the up-regulated genes. Use seven genes known to be active in the phase corresponding to this time point as examples for the up-regulated cluster, with belief/plausibility values of 0.95. Similarly, use the remaining 28 examples for the second cluster of genes that are unchanged or down-regulated. Output the probability 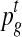of each gene g to belong to the cluster of up-regulated genes (the posterior probability for the mixture modeling methods, and one minus the p-value of differential expression for the NorDi algorithm).

2. Clustering of genes into five clusters. For each cell cycle phase cluster, construct a binary profile reflecting the default “activity” of genes from this cluster over the 17 time points. The activity profile 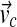of a phase cluster c has a value 1 in entry t if genes from this cluster peak in the time point t. Otherwise, the entries are 0. For each gene g, take the vector of its estimated up-regulation probabilities from step 1, and assign g to the cluster with the most similar activity profile. Formally, we assign gene g to cluster

where 1 denotes a vector of length 17 filled with 1s.

Figure 6 compares the clusterings obtained in the first step by the unsupervised algorithms, to the clusterings obtained by the belief-based method. The examples help to clearly distinguish patterns of genes from each phase cycle peaking at their characteristic time points.

Fig. 6.

Cell cycle gene clustering. The probability of up-regulation estimated for each cell cycle gene (rows; ordered by their true cluster labels), in each time-point (columns) by three methods: NorDi, as well as unsupervised and belief-based mixture modeling, applied to each time point data separately. Belief-based mixture modeling, which uses examples of up-regulated and of unchanged genes in each time-point (marked in pink and green), achieves most clearly visible distinct gene expression profiles, characteristic for the five cell cycle phase clusters.

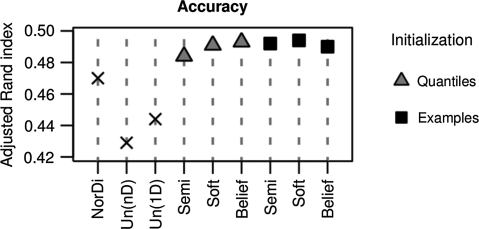
Figure 7 shows that all supervised modeling methods, regardless of the parameter initialization, outperform the unsupervised methods in clustering the cell cycle gene profiles using the two-step procedure. For comparison, we applied also a one-step analysis with multidimensional Gaussian mixture modeling (Yeung et al. (2001), denoted Un(nD)) to separate the entire dataset at once into five clusters. Interestingly, multidimensional clustering obtained the least accuracy, measured with the adjusted Rand index (see Section 3.3). Best results are obtained for the two-step procedure, using either belief-based or soft-label modeling in the first step.

Fig. 7.

The accuracy of cell cycle gene clustering. From all compared methods, the partially supervised have higher accuracy (measured by adjusted Rand index, y-axis) in grouping genes into five cell-cycle gene clusters than the semi-supervised and unsupervised methods. The partially supervised modeling methods were initialized in two ways: either quantile- or example-based (see Section 2.7).

4. Discussion

Mixture modeling is an established technique in machine learning and has proved successful in the field of gene expression analysis. The two partially supervised methods presented in this article extend mixture model-based clustering, adding the ability to utilize imprecise examples. In contrast to other mixture modeling methods that incorporate knowledge, both belief-based and soft-label modeling can be customized for differential expression analysis guided by examples of genes that are believed to be up, down, or unchanged. The known examples usually constitute only a small subset of all genes and are themselves not 100% certain. The presented applications show a rich variety of possible knowledge sources for examples: high-throughput TF-DNA binding experiments, computational predictions of miRNA targets, and literature knowledge of genes active in different cell cycle phases. The known examples are traditionally used to verify experimental outcome after it is defined by differential expression analysis. Our methodology incorporates such prior biological knowledge into the analysis itself, making the outcome more reliable.

Our methodology enables confronting available uncertain knowledge with the data. On the one hand, the partially supervised methods profit from the examples to better cluster the remaining data. On the other hand, they use the entire data to verify the knowledge about the examples. For instance, the signal in the data may contradict the prior belief about a gene to be up-regulated in a knockout experiment. Both partially supervised methods may “re-cluster” the examples with such improbable initial cluster labels. In this way, they are more flexible than semi-supervised mixture modeling, which assumes that the example labels are fixed.

The application of the proposed methodology to the problem of differential analysis imposes two natural restrictions, which could easily be abandoned for the needs of different applications. First, here we analyze only one-dimensional data, but in general the approach can as well be extended to multidimensional clustering given examples with imprecise cluster labels. Similarily, we restrict ourselves only to consider two- or three-component models, although it is common to use tools of model selection to choose out of models with arbitrary numbers of clusters. Here it is also dictated by the nature of the problem: we assume the clusters to be interpreted and the known examples to be assigned to each of the clusters. Intuitively, we expect examples of differential or unchanged genes (two clusters), alternatively, of up-regulated, down-regulated, or unchanged genes (three clusters). It would be difficult to assign those examples to clusters in a model with more than three components.

Acknowledgments

E.S. is thankful to Julia Lassere for insightful discussions and to Florian Markowetz for commens on this manuscript. This work was partly supported by the Polish Ministry of Science and Education (grants N-N301-065236 and PBZ-Minil-2/1/2005) and the Deutsche Forschungsgemeinschaft (DFG) (grant SFB 618).

Disclosure Statement

No competing financial interests exist.