Charge Requirements for Proton Gradient-driven Translocation of Anthrax Toxin

Abstract

Anthrax lethal toxin is used as a model system to study protein translocation. The toxin is composed of a translocase channel, called protective antigen (PA), and an enzyme, called lethal factor (LF). A proton gradient (ΔpH) can drive LF unfolding and translocation through PA channels; however, the mechanism of ΔpH-mediated force generation, substrate unfolding, and establishment of directionality are poorly understood. One recent hypothesis suggests that the ΔpH may act through changes in the protonation state of residues in the substrate. Here we report the charge requirements of LF's amino-terminal binding domain (LF_N) using planar lipid bilayer electrophysiology. We found that acidic residues are required in LF_N to utilize a proton gradient for translocation. Constructs lacking negative charges in the unstructured presequence of LF_N translocate independently of the ΔpH driving force. Acidic residues markedly increase the rate of ΔpH-driven translocation, and the presequence is optimized in its natural acidic residue content for efficient ΔpH-driven unfolding and translocation. We discuss a ΔpH-driven charge state Brownian ratchet mechanism for translocation, where glutamic and aspartic acid residues in the substrate are the “molecular teeth” of the ratchet. Our Brownian ratchet model includes a mechanism for unfolding and a novel role for positive charges, which we propose chaperone negative charges through the PA channel during ΔpH translocation.

Introduction

Transmembrane protein translocation (1–4) and intracellular protein degradation (5) are essential processes that allow the cell to traffic protein, form new organelles, maintain protein quality control, and regulate the cell cycle. Because folded proteins are thermodynamically stable under typical cellular conditions, protein translocation and degradation often require complex, energy-consuming molecular machines to catalyze the required series of unfolding and translocation steps in these pathways. Some of these protein transporters and degradation machines mechanically unfold their protein substrates via an ATP-dependent motor. However, a transmembrane proton gradient (ΔpH) may also be used to generate an appropriate driving force that can unfold (6) and translocate a substrate protein across a membrane (1).

A transmembrane proton gradient forms a proton motive force (PMF)² comprised of two different types of available free energy: an electrical free energy (ΔG^Δψ) dependent on the membrane potential (Δψ) and a chemical potential (Δμ^ΔpH) dependent on the proton concentration gradient (ΔpH). The former ΔG^Δψ can be derived from the charge of the translocating protein, z, and Faraday's constant, F, according to the relation, ΔG^Δψ = ΔG^Δψ° + zFΔψ (1, 6, 7). The latter Δμ^ΔpH is expressed as a chemical potential, Δμ^ΔpH = Δμ^ΔpH° + 2.3 nRT ΔpH (where n is the number of protons involved in the reaction, and R and T are the gas constant and temperature, respectively) (1, 6). Either of these energies can develop enough force under physiological conditions, on the order of tens of pN (6, 8), to unfold a protein during translocation (6, 9). The molecular mechanism of ΔpH-driven translocation, in particular the enforcement of directionality and substrate unfolding, is not well understood.

Anthrax toxin (10) is a useful model system (4) to study ΔpH-driven protein unfolding (11) and translocation (1, 2, 6, 12). The toxin is a key virulence factor secreted by Bacillus anthracis (the causative agent of anthrax). It is comprised of three proteins: the translocase component, protective antigen (PA, 83 kDa); and two enzyme components, lethal factor (LF, 91 kDa) and edema factor (EF, 89 kDa). These secreted proteins must assemble into holotoxin complexes either on the surface of cells or in the blood serum (13). In each assembly mechanism, PA is initially cleaved by a protease, allowing a small 20-kDa portion to dissociate. The remaining 63-kDa PA fragment can then self-assemble into either a ring-shaped homoheptamer, PA₇ (14–16), or homooctamer, PA₈ (12, 13). PA oligomers then bind to LF and EF and form toxic complexes. Binding occurs at the top of the prechannel and in a deep amphipathic cleft, termed the α clamp, which also aids in unfolding the substrate (17).

The complex is then endocytosed by the target host cell, and subsequent acidification of the endosome causes the PA oligomer to convert into a transmembrane channel. Moreover, the ΔpH generated by the acidification of the endosome facilitates the unfolding (11) and translocation of LF and EF through PA (1) into the cytosol. ΔpH-driven translocation is aided by two catalytic active sites: the α clamp (17) and the Φ clamp (2). The Φ clamp is located inside the PA channel (1, 2). It is comprised of a narrowly apposed ring of seven or eight Phe⁴²⁷ residues, where one Phe is contributed by each PA monomer in the oligomer (2). The Φ clamp prefers to make interactions with hydrophobic and aromatic groups, and its activity facilitates translocation (2) by helping to unfold the substrate (6). How the Φ clamp stimulates (1) ΔpH-driven translocation is unclear.

Although a ΔpH can drive translocation, the groups that are protonated and/or deprotonated in the substrate and/or channel are unknown. One clue is provided by the known cation selectivity of the PA channel (18). This selectivity is likely due to the ∼100–150 glutamic and aspartic acid residues (depending upon the oligomeric state of PA) known to be located inside the PA channel (2, 19). This cation selectivity is unusual given the acidic isoelectric points of both LF and EF (1). Thus we previously proposed a ΔpH-driven charge state Brownian ratchet translocation mechanism (1), which is based upon the theoretical work of Feynman et al. (20), Oster and co-workers (21), and Astumian (22). In this mechanism, the large available thermal energy of the translocating protein is biased in a useful and directed way by the proton gradient, thereby supporting productive translocation.

Because the channel is cation-selective and, therefore, anion-repulsive, we expect that anionic residues within the portion of LF or EF passing through the channel must be protonated, thus making the translocating chain net cationic. The segment of LF within the channel is in fact net positive, as shown by Δψ-dependent measurements, which report positive z values (6). Once the Brownian thermal energy of the translocating protein causes the substrate to exit to the higher pH cytosolic side of the membrane, deprotonation to a more anionic state is favored. The resulting charge repulsion can then enforce directionality during translocation by preventing backward movement through the anionic channel. This process then repeats in multiple cycles toward completion. In this report, we investigate how ΔpH-driven translocation depends upon charged residues in the substrate.

EXPERIMENTAL PROCEDURES

Constructs and Proteins

Site-directed mutagenesis was performed using a QuikChange procedure. WT PA was expressed and purified as described (2). PA₇ oligomers were produced as described (12). His₆-LF_N (residues 1–263 of LF) and mutants thereof were purified from overexpressing bacteria using standard Ni²⁺-nitrilotriacetic acid affinity chromatography and Q-Sepharose anion exchange chromatography, when required (GE Healthcare) (1). When indicated, His₆ tags, which are amino-terminal, 17-residue leaders containing a hexahistidine sequence, MGSSHHHHHHSSGLVPR, were removed from His₆-LF_N with bovine α-thrombin treatment (0.5 units/mg of protein) for 30 min at room temperature in 20 mm Tris, 150 mm NaCl, 2 mm CaCl₂, and 1 m glucose at pH 8.0. Note that after thrombin cleavage, an additional GSHM sequence was left at the amino terminus of all cleaved LF_N constructs derived from the pET15b plasmid.

More complex synthetic LF_N constructs were made using a three-step, gene synthesis procedure, according to the following scheme: HM¹AGGHGDVGM¹⁰HVKEKEKNKD²⁰ENKRKDEERN³⁰KTQEEHLKEI⁴⁰MKHIVKIEVK⁵⁰GEEAVKKEAA⁶⁰EKLLEKVPSD⁷⁰VLEMYKAIGG⁸⁰KIYIVD. The underlined pairs of amino acids on either end were encoded by the restriction sites, NdeI and a silent SalI site (Val⁸⁴ and Asp⁸⁵), respectively, which were used for cloning. Superscripted numbers indicate the numbering convention of LF residues in PDB ID 1J7N (23). Overlapping oligonucleotides encoding the desired sequences with the amino-terminal replacement were synthesized (Elim Biopharmaceuticals, Inc., Hayward, CA) and amplified by two rounds of PCR. In Round I, 22 nm of nested oligonucleotides with consistent annealing temperatures of ∼55 °C were amplified in a standard PCR. In Round II, 1 μl of the PCR product made in Round I was amplified with the two outermost PCR primers (1 μm each) to make the synthetic double-stranded DNA fragment. These LF_N synthetic DNA fragments were ligated via a 5′ NdeI site and 3′ SalI site into the pET15b-LF_N(SalI) construct, which contains an in-frame, silent SalI restriction site in LF_N at Val⁸⁴ and Asp⁸⁵. The synthetic LF_N constructs were overexpressed and purified, and their His₆ tags were subsequently removed as described above (when required).

Electrophysiology

Planar lipid bilayer currents were recorded using an Axopatch 200B amplifier (Molecular Devices Corp., Sunnyvale, CA) (6, 12). Membrane bilayers were painted onto a 100-μm aperture of a 1-ml polyethersulfone cup with 3% 1,2-diphytanoyl-sn-glycero-3-phosphocholine (Avanti Polar Lipids, Alabaster, AL) in neat n-decane. Cis (side to which the PA oligomer is added) and trans chambers were bathed in the indicated buffers as required. By convention, Δψ ψ_cis − ψ_trans (ψ_trans 0 V), and ΔpH pH_trans − pH_cis.

Translocation Assays

Translocation experiments were carried out as described (6, 12) generally using a universal pH bilayer buffer system (UBB: 10 mm oxalic acid, 10 mm phosphoric acid, 10 mm MES, 1 mm EDTA). However, for translocations requiring a pH > 7.5, we used an altered UBB (6 mm oxalic acid, 6 mm phosphoric acid, 6 mm MES, 6 mm boric acid, 6 mm TAPS, 1 mm EDTA), which is better at buffering in the 7.5–9 range. We found that these two types of buffers produced consistent translocation results. Generally, an additional 100 mm equivalent of KCl was added to the UBB and maintained symmetrically in most translocation experiments, excepting when translocation kinetics were monitored in the absence of a Δψ. In that case, additional KCl was only added to the cis-side buffer. The pH_cis was generally 5.6 unless indicated otherwise.

In a typical experiment, we first inserted PA₇ channels into a planar bilayer by adding the prechannel oligomeric form to the cis-side of the membrane under a small Δψ of 20 mV. Insertion was observed as an increase in current. Then WT or a mutant LF_N was added also to the cis-side of the membrane, and a decrease in current was observed. Excess LF_N in the cis-compartment was removed by perfusion, and the translocation process was initiated by either raising the Δψ or by creating a ΔpH by raising the pH of the trans chamber. When translocation is initiated by raising the pH of the trans chamber, we set the time when 1% of maximum translocation occurs as t = 0 s to control for different mixing times.

An alternative method of creating a proton gradient was also used and provided similar results: the pH_cis and pH_trans buffers were preadjusted to their final conditions; after substrate binding to the channel was complete, then the cis buffer was perfused at ∼0 mV at pH 5.6 to maintain the ΔpH, and then the voltage was raised to the final voltage upon the completion of perfusion (after ∼30 s).

Single-channel Recordings

Single-channel LF_N docking experiments were performed as described (6, 12). Planar lipid bilayers were bathed in symmetric buffer (100 mm KCl, 1 mm EDTA, 10 mm succinic acid, pH 5.6). PA oligomer was applied directly to membranes at ∼10⁻¹⁶ m. Single channel insertion was observed by a discrete step in current under an applied voltage. Once a single channel had inserted into the membrane, LF_N was added to the cis-side of the membrane at 200 pm. Blocking events were recorded at a constant Δψ of 20 mV for various LF_N mutants with and without their His₆ tag. The data were acquired at 400 Hz using a low pass filter of 200 Hz. For LF_N that stably blocked a PA channel, the voltage was reversed to −80 mV after several minutes of conductance block to clear the substrate from the channel; this procedure verified that the channel was still present. Histograms of the current versus time data were fit to a two or three Gaussian function to obtain the relative percentages of time spent in the open, blocked, and partly blocked states.

RESULTS

Chemical Potential Component of PMF Is Sufficient to Drive Translocation

To study translocation, we used planar lipid bilayer electrophysiology (1, 2, 6) and a model substrate, LF_N, the amino-terminal, 263-residue, PA-binding domain of LF (24). In this assay, a planar lipid bilayer separated two aqueous chambers (called cis and trans). We first inserted PA channels into a planar bilayer by adding the prechannel heptameric form of PA to the cis-side of the membrane under a Δψ of 20 mV (Δψ ψ_cis − ψ_trans, where ψ_trans 0 V). Channel formation, observed as an increase in current, then stabilized, and either wild type (WT) LF_N or an LF_N mutant (MUT) was added also to the cis-side of the membrane. Subsequently, an exponential decrease in current was observed as the amino-terminal presequence of LF_N inserted into the ion-conducting channel and blocked ion flow (25). Excess LF_N in the cis compartment was removed by perfusion, and the translocation process was initiated by either changing the Δψ and/or ΔpH. The ensuing current increase that was generally observed resulted from LF_N translocation to the trans-side of the membrane, as inferred by control experiments (1, 26). Thus two types of parameters can be obtained from translocation records: the time for half of the protein to translocate (t½, measured in seconds) and the efficiency of translocation, which is equivalent to the fraction of LF_N that successfully translocates.

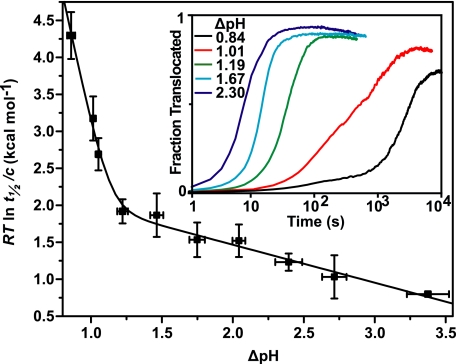
Although a ΔpH can drive substrate translocation in the presence of a small, positive Δψ (1), it has not yet been shown whether a ΔpH alone is sufficient. To test this possibility, we set up the bilayer with a potassium chloride gradient; this procedure allowed current to flow when Δψ is 0 mV. It should be noted that by design, the voltage-clamp amplifier maintained the system at 0 mV even under a ΔpH, which we defined as ΔpH pH_trans − pH_cis. At a Δψ of 0 mV and positive ΔpH values, we found that both the rate and efficiency of LF_N translocation increased with larger positive ΔpH gradients (Fig. 1, inset). We estimated the activation energy of translocation (ΔG‡) using the following relationship, ΔG‡ = RT ln(t½/c), where c is an arbitrary constant of 1 s. The ΔpH dependence of the ΔG‡ for LF_N translocation was biphasic with two different limiting slopes (Fig. 1). This dependence is similar to what has been observed under varying ΔpH conditions with a constant, nonzero Δψ (1, 6). The relationship fits to a two-barrier model,

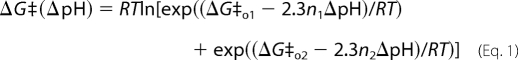where the indexed ΔG‡_o and n values are the activation energy and number of protons required to cross each barrier, respectively (6). The steeper ΔpH dependence of the ΔG‡ on the left-hand side of the graph (less than 1.2 ΔpH, n₁ value of 4.0 (±0.5)) corresponds to a barrier limited by LF_N unfolding (6), whereas the shallower ΔpH dependence on the right-hand side (at higher ΔpH values, n₂ value of 0.22 (±0.03)) may correspond to a barrier limited by a yet uncharacterized translocation process (6) (Fig. 1). We concluded that the chemical potential component of the PMF was sufficient to drive LF_N translocation.

FIGURE 1.

The chemical potential of the PMF is sufficient to drive LF_N translocation. Analysis of LF_N translocations driven purely by a ΔpH. Activation free energies (ΔG‡; expressed as RTlnt½/c) for individual translocations of His₆-LF_N are plotted against their respective ΔpH values and fit to Equation 1. The fit parameters are: ΔG‡_o1 = 12.2 (± 1.1) kcal mol⁻¹, ΔG‡_o2 = 2.5 (± 0.2) kcal mol⁻¹, n₁ = 4.0 (± 0.5), and n₂ = 0.22 (± 0.03). Inset, representative LF_N translocation records normalized as a fraction of the theoretical maximum of translocation under the following ΔpH values at a Δψ of 0 mV: 0.84 (black), 1.01 (red), 1.19 (green), 1.67 (blue), and 2.30 (purple). The universal bilayer buffer was consistently at a pH_cis of 5.6, and pH_trans was adjusted to form the indicated ΔpH values. To control for buffer mixing lag times, t = 0 was set as the time when 1% of maximum translocation occurred. The error bars are the means ± S.D. (n = 2–5).

ΔpH-driven Translocation Depends on Charged Residues in LF_N

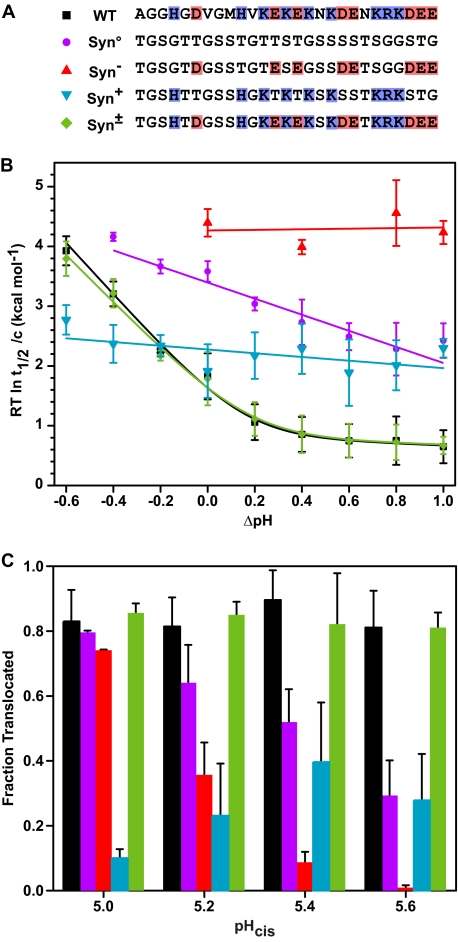
The charge state Brownian ratchet model (1) predicted that negatively charged acidic residues in the substrate are critical to ΔpH-driven translocation. To test this model, we replaced the unstructured amino-terminal presequence of LF_N (residues 1–27) with a randomized neutral/uncharged background comprised of Gly, Ser and Thr residues (Fig. 2A). We call this neutral mutant background LF_N Syn°. This sequence was still polar and flexible but lacked charged residues. We found that LF_N Syn° translocated more slowly than LF_N WT under conditions of ΔpH = −0.6 to 1.0, pH_cis = 5.6, and Δψ = 60 mV (Fig. 2B). Additionally, the construct possessed a significantly reduced ΔpH dependence (LF_N WT: n₁ = 1.9 (±0.2); LF_N Syn°: n = 0.59 (±0.06); Fig. 2B). (It should be noted that we included the amino-terminal His₆ tag in these LF_N constructs because of defects in channel blocking for certain constructs, an effect that we explore more fully below. To our knowledge, the His₆ tag does not obfuscate our results or interpretations, because we were looking at effects relative to similarly His₆-tagged control constructs.) Initially, we predicted that acidic residues alone would be sufficient to restore the defect of LF_N Syn° in translocation rate and its weaker ΔpH dependence; however, we found this was not the case. LF_N Syn⁻, which has acidic residues restored at their WT positions, further reduced the rate and efficiency of translocation relative to LF_N Syn° and had essentially no ΔpH dependence (n value of 0.0 (±0.1); Fig. 2B). Restoring only basic residues in the LF_N Syn⁺ construct increased the translocation rate relative to LF_N Syn° but further reduced the ΔpH dependence (n value of 0.14 (±0.07); Fig. 2B). Only when both the acidic and basic residues are restored in LF_N Syn^± do we see translocation that is identical to the WT substrate (Fig. 2B). Moreover, because LF_N WT and LF_N Syn^± translocated with identical ΔpH dependences, we can safely assume that the noncharged residues in the WT leader sequence are unimportant to ΔpH-driven translocation, as these have been substituted en masse with Gly, Ser, and Thr residues in LF_N Syn^±. Thus acidic residues alone in the presequence of LF_N are not sufficient for efficient ΔpH-driven translocation; instead, a balance of acidic- and basic-charged residues is required.

FIGURE 2.

Efficient ΔpH-driven translocation requires both acidic and basic charged residues. A, design of synthetic LF_N constructs (LF_N Syn) in which the first 27 amino acids are replaced using a sequence containing both acidic and basic residues (Syn^±), neither acidic nor basic residues (Syn°), only acidic residues (Syn⁻), and only basic residues (Syn⁺). The exact sequence compositions of these constructs are shown alongside the LF_N WT sequence. B, translocation activation energy versus ΔpH results for the His₆-LF_N Syn constructs shown in A: His₆-WT (black square), His₆-Syn° (purple circle), His₆-Syn⁻ (red triangle), His₆-Syn⁺ (blue inverted triangle), and His₆-Syn^± (green diamond). These ΔpH-driven translocation experiments were conducted at a ΔpH of −0.6 to 1.0, pH_cis of 5.6, and a Δψ of 60 mV. The error bars are the means ± S.D. (n = 2–5). The fit parameters for His₆-WT and His₆-Syn^± using Equation 1: His₆-WT, ΔG‡_o1 = 1.5 (± 0.2) kcal mol⁻¹, ΔG‡_o2 = 0.8 (± 0.3) kcal mol⁻¹, n₁ = 1.9 (±0.2), n₂ = 0.1 (± 0.2); His₆-Syn^±, ΔG‡_o1 = 1.5 (±0.2) kcal mol⁻¹, ΔG‡_o2 = 0.8 (± 0.3) kcal mol⁻¹, n₁ = 1.7 (± 0.2), n₂ = 0.1 (± 0.2). His₆-Syn°, His₆-Syn⁻, and His₆-Syn⁺ were fit to a single-barrier model (ΔG‡ = ΔG‡_o − 2.3nΔpH), with the parameters: His₆-Syn°, ΔG‡_o = 3.40 (± 0.08) kcal mol⁻¹, n = 0.59 (± 0.06); His₆-Syn⁻, ΔG‡_o = 4.3 (± 0.2) kcal mol⁻¹, n = 0.0 (± 0.1); His₆-Syn⁺, ΔG‡_o = 2.28 (± 0.09) kcal mol⁻¹, n = 0.14 (± 0.07). C, maximum translocation efficiency achieved within 5 min at varying pH_cis values for the His₆-LF_N Syn constructs. These ΔpH-driven translocation experiments were conducted at a ΔpH of 2.0, pH_cis ranging from 5.0 to 5.6, and a Δψ of 0 mV. To control for buffer mixing lag times, t = 0 was set as the time when 1% of maximum translocation occurred. The legend colors are identical to those in B. The error bars are the means ± S.D. (n = 2–8).

To further explore the differences between the Syn constructs, we translocated them under more physiologically relevant conditions (ΔpH = 2, Δψ = 0 mV). Suspecting that difficulties in protonating all of the acidic residues in LF_N Syn⁻ account for its poor translocation, we also varied the cis pH to see whether lower pHs would increase its translocation speed relative to the chargeless LF_N Syn°. Here, we report that the fraction of substrate translocated after 5 min. This is a better method for comparing substrates that display large differences in both translocation efficiencies and rate. Unsurprisingly, LF_N WT and LF_N Syn^± showed no cis pH dependence (Fig. 2C). LF_N Syn°, however, displayed a moderate, linear cis pH dependence, likely because of the increased substrate destabilization at lower pHs. As predicted, LF_N Syn⁻ had a much stronger cis pH dependence. It displayed little translocation within 5 min at cis pH 5.6 (although it does eventually reach 15–20% translocation). By cis pH 5.0, LF_N Syn° and LF_N Syn⁻ translocated similarly to LF_N WT and LF_N Syn^±. When the membrane potential was 0 mV, LF_N Syn⁺ translocated poorly at all cis pH levels. We assume that the comparatively better performance of LF_N Syn⁺ relative to LF_N Syn⁻ under higher voltage conditions (Fig. 2B) is an artifact of the supplemental Δψ-driving force. Thus we conclude that LF_N Syn⁻ is greatly stimulated by a PMF dominated by a ΔpH with lower cis pH conditions, i.e. below ∼pH 5.2.

Cationic Groups in Presequence Allow Anionic Residues to Penetrate Channel

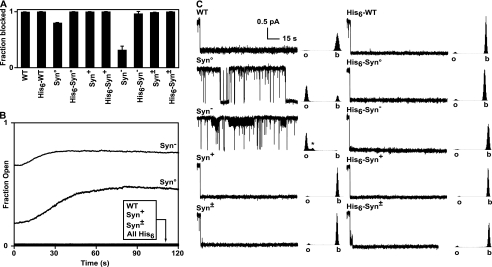
The translocation defect observed for LF_N Syn⁻ at pH 5.6 was surprising and led us to hypothesize that a presequence dominated by acidic groups is unable to traverse the cation-selective PA channel, likely because of electrostatic repulsion, which impeded entry into the channel. To test this possibility, we examined the ability of the His₆-tagged and untagged versions of the LF_N Syn constructs to bind inside the PA channel. In this assay, when the presequence of LF_N bound the PA channel, it blocked ion conductance. In bulk, ensemble channel binding assays, we found that all of the His₆-Syn constructs could fully engage and dock into the PA channel, as evidenced by the complete block the of channel conductance (Fig. 3A). Upon removing the His₆ tag, we found that LF_N Syn° and LF_N Syn⁻ are defective in forming a stable interaction with the PA channel. Moreover, when we tested the ability of these LF_N Syn constructs to remain stably engaged in a blocked conductance state with the PA channel, we found that LF_N Syn° and LF_N Syn⁻ rapidly dissociated from the channel with dissociation lifetimes of ∼30 and ∼10 s, respectively (Fig. 3B). All other Syn constructs showed little dissociation, and the His₆-tagged versions of LF_N Syn° and LF_N Syn⁻ maintained a stable complex with the PA channel. We conclude that uncharged and purely anionic leader presequences are unable to stably engage the PA channel; however, the defects in these constructs may be complemented by a 17-residue His₆ tag.

FIGURE 3.

Charge requirements for LF_N docking. A, ensemble bilayer recordings of PA channel conductance block by LF_N WT and LF_N Syn mutants with and without their His₆ tags were obtained at symmetrical pH 5.6 and saturating concentrations of LF_N (100 nm). The relative fraction of conductance block is given for each Syn mutant construct relative to LF_N WT. The error bars represent the means ± S.D. (n = 2). B, ensemble bilayer recordings of PA channel conductance block by LF_N WT and LF_N Syn mutants at symmetrical pH 5.6 following perfusion of the cis-side of the membrane. Perfusion removes excess LF_N, allowing the channel dissociation kinetics to be recorded. Significant rapid dissociation was only observed with LF_N Syn° and Syn⁻; all His₆-tagged LF_N and the non-His₆-tagged LF_N (including WT and mutants, Syn⁺ and Syn^±) did not dissociate during the recording. C, single-channel blocking events recorded for LF_N WT and LF_N Syn mutants with and without their His₆ tags at symmetrical pH 5.6. Once a single channel inserts into the membrane, LF_N is added under a Δψ of 20 mV. Approximately 2 min of a typical blocking event is shown for each LF_N. The data are acquired at 400 Hz under a low pass filter of 200 Hz. For clarity, the displayed single-channel traces were downsampled by a factor of 10. To the right of each trace is a histogram of the current level for each recording. Gaussian functions fit to these histograms assess the percentage of the time the LF_N-channel complexes spend in the open (o), blocked (b), and partly blocked states (*). The percentages of time in the blocked and partly blocked states are given as follows: all His₆-tagged LF_N constructs as well as untagged LF_N WT, LF_N Syn⁺ and LF_N Syn^± were 100% blocked; untagged LF_N Syn° was 28% blocked; and LF_N Syn⁻ was 1.6% blocked and 3% partly blocked (*). The errors for percentage of the time spent in the block states are all better than ±1%. The partly blocked (*) state is 29 (± 2)% less conducting than the fully open state.

We then examined the channel blocking activity of the LF_N Syn constructs at symmetrical pH 5.6 in single-channel experiments. The His₆-tagged Syn constructs all formed stable, fully blocked complexes with the PA channel, where few opening (or unblocking) events were observed (Fig. 3C). However, for the untagged LF_N Syn° and LF_N Syn⁻ constructs, we again found noticeable defects in channel blocking activity. The two untagged constructs differed notably in their behavior. Untagged LF_N Syn° was able to form transient blockades of the PA channel (which fully block the conductance) for durations of 5–10 s. Untagged LF_N Syn⁻ is not able to form lasting blockades and only blocked 29 (±2)% of the channel conductance. These partly blocked flickering events lasted 10–30 s (Fig. 3C). From these single-channel studies, we concluded that the two defective mutant LF_N presequences (Syn° and Syn⁻) possess distinguishable characteristics; the purely anionic version (Syn⁻) cannot penetrate the PA channel and only produces a partial flickering 30% blocked state, whereas the neutral Syn° presequence can completely penetrate and block the channel, albeit ∼70% less often than WT, Syn⁺, and Syn^±. These results, taken together, imply that anionic residues are effectively repulsed by the channel; however, cationic residues can effectively chaperone anionic residues through the channel.

Acidic Residue Dependence of ΔpH Translocation Extends beyond Presequence

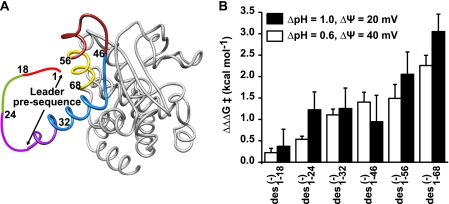
Based upon our initial characterization of the sequence dependence of ΔpH-driven translocation, we determined that acidic residues are responsible for the ΔpH dependence, but counter-balancing positively charged residues can assist passage through the cation-selective PA channel. It should be noted that the requirement of acidic residues on the ΔpH dependence of LF_N translocation exists when all the negative charges are mutated to serine (supplemental Fig. S1A) and when the His₆ tag is cleaved and the negative residues mutated to their uncharged analogs (i.e. Glu → Gln and Asp → Asn; supplemental Fig. S1B). Here we produced a series of amino-terminal LF_N mutants in which successively larger amino-terminal stretches of acidic residues are replaced with serine residues (Fig. 4A). We call these anionic residue replacement constructs LF_N des⁽⁻⁾_x-y, where x and y designate the region of sequence in which the natural Asp and Glu residues were replaced with Ser. Such extensive mutations in LF_N destabilized the substrates to varying degrees, as shown in equilibrium protein folding stability measurements (supplemental Fig. S2A). In fact, our analysis is limited to the first 68 residues of LF_N because removing acidic residues beyond this point resulted in too substantial a loss in protein solubility and stability.

FIGURE 4.

Acidic residues within the folded domain of LF_N are also critical to ΔpH-driven translocation. A, the ribbon depiction of the structure of LF_N is from PDB ID 1J7N (23), where regions of sequence are colored by sequence position. The unstructured leader presequence (residues 1–32) is indicated as a thick colored line. Regions in which acidic residues were replaced with serine residues are colored as follows: residues 1–18 (red), residues 19–24 (green), residues 25–32 (purple), residues 33–46 (blue), residues 47–56 (brown), and residues 57–64 (gold). B, the difference in activation energy ΔΔG‡ for each His₆-LF_N des⁽⁻⁾ series mutant are obtained using two ΔpH-driven conditions (ΔpH = 1.0 and Δψ = 20 mV; ΔpH = 0.6 and Δψ = 40 mV) and one condition in the absence of a ΔpH (ΔpH = 0 and Δψ = 60 mV), where ΔΔG‡ = ΔG‡(ΔpH>0) − ΔG‡(ΔpH = 0). ΔΔG‡ values for each mutant (MUT) are then referenced to that of LF_N WT to give the reported ΔΔΔG‡ values plotted above. ΔΔΔG‡ = ΔΔG‡(MUT) − ΔΔG‡(WT). In all cases, pH_cis = 5.6. The error bars are the means ± S.D. (n = 2).

To normalize for these differences in protein stability, we translocated each His₆-tagged LF_N des⁽⁻⁾ mutant in the presence (i and ii) or absence (iii) of a ΔpH driving force: (i) lower Δψ and higher ΔpH, ΔpH = 1, pH_cis = 5.6, Δψ = 20 mV (supplemental Fig. S2B); (ii) higher Δψ and lower ΔpH, ΔpH = 0.6, pH_cis = 5.6, Δψ = 40 mV (supplemental Fig. S2C); and (iii) higher Δψ and no ΔpH, ΔpH = 0, pH_cis = 5.6, Δψ = 60 mV (supplemental Fig. S2D).

By comparing the translocation rates of a single mutant under two different conditions, we can calculate a ΔΔG‡ value by ΔΔG‡ = ΔG‡(ΔpH>0) − ΔG‡(ΔpH = 0), which normalizes for stability. We then referenced the ΔΔG‡ values for each mutant to that of LF_N WT by determining a ΔΔΔG‡ value, where ΔΔΔG‡ = ΔΔG‡(MUT) − ΔΔG‡(WT). Here, larger ΔΔΔG‡ values indicate a reduced capacity to translocate using a pH gradient compared with LF_N WT. These comparisons revealed a clear trend showing that the more acidic residues that are removed from LF_N, the less it was able to effectively use a pH gradient for translocation (Fig. 4B). Also, we generally found that condition (i), which contains a higher ΔpH, increases ΔΔΔG‡ more so than the lower ΔpH condition (ii), indicating that the effect was specifically due to an inability to use the pH gradient (Fig. 4B). Based on these results, we conclude that acidic residues are critical to the mechanism of ΔpH-dependent translocation both within the presequence region and well into the folded structure of the substrate protein.

Optimal Positions for Acidic Residues in the Presequence

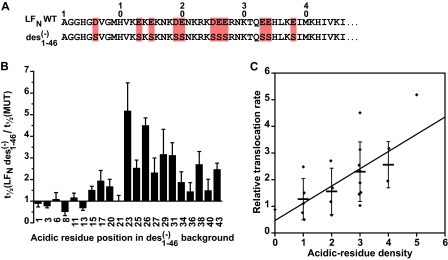
We then asked which acidic residues in the leader presequence were most critical to ΔpH-driven translocation. Using the LF_N des⁽⁻⁾_1–46 construct as our background, we introduced single glutamates at various positions and measured the translocation kinetics of these new constructs under the influence of a ΔpH. We found that little or no gain (and perhaps a small decrease in rate) was observed when introducing a single Glu at positions 1–13 (inclusive; Fig. 5B). A small but reproducible ∼2-fold increase in translocation rate (relative to the LF_N des⁽⁻⁾_1–46 background) was observed when introducing a Glu into positions 15–20 (inclusive; Fig. 5B). The optimal region for the introduction of a Glu residue appeared to occur between residues 23 and 31 (inclusive), where the most optimal site was position 23 (increase of 5-fold; Fig. 5B). More modest increases in the translocation rates were observed at residues 34–43 (the extent of the analysis in this mutant background; Fig. 5B). Similar results were obtained in the LF_N des⁽⁻⁾_1–32 background, and multisite replacements with as few as four of the eight wild-type charges could fully restore the translocation rate to that of LF_N WT (supplemental Fig. S3). We concluded that residues 23–31 in the presequence of LF_N are the most optimal positions to place acidic residues for ΔpH-mediated translocation.

FIGURE 5.

Acidic residue positions in the presequence of LF_N are most critical to ΔpH-driven translocation. Acidic residues were added back into the His₆-LF_N des⁽⁻⁾_1–46 construct background. A, the sequences of the first 46 residues of LF_N WT and LF_N des⁽⁻⁾_1–46 are shown, where acidic residues in the WT sequence are shaded red. B, the relative translocation t½ times for acidic residue introductions into the His₆-LF_N des⁽⁻⁾_1–46 mutant backgrounds are given as the ratio t½(des⁽⁻⁾_1–46)/t½(MUT) for ΔpH-driven translocation. The numbers on the x axis indicate the positions in which acidic residues are reintroduced into the His₆-LF_N des⁽⁻⁾_1–46 mutant background. ΔpH-driven translocation conditions were ΔpH = 0.8, pH_cis = 5.6, and Δψ = 50 mV. The error bars are the means ± S.D. (n = 2–4). C, a correlation of relative translocation rate (given as the ratio t½(des⁽⁻⁾_1–46)/t½(MUT)) for the mutants in B versus the density of acidic residues normally found in the WT sequence. Acidic residue density in this instance is the total number of acidic residues found in the four residues amino- and carboxyl-terminal to the probed site. The linear regression fit to all of the individual measurements (filled diamonds) is significant with a p value of 0.001 for the fit function, y = a + bx, where a = 0.5 (± 0.5) and b = 0.6 (± 0.2). Because multiple observations of particular acidic residue densities were obtained in certain instances, a heavy horizontal bar (mean) and error bars (± S.D.) are also given.

Anionic Charge Density in Presequence Is Optimized for ΔpH-driven Translocation

We then determined whether the natural sequence of LF_N is optimized in terms of the placement of the acidic residues in the presequence. First, we determined the density of various classifications of amino acids: acidic, basic, acidic plus basic, and hydrophobic. Our density metric was calculated as the number of residues in each classification that are ±4 positions, or one turn of an α helix, from the probed site. We then performed linear regression analysis to determine the degree to which the density of these various types of residue classifications correlated with the relative change in translocation rate resulting from the introduction of Glu residues into the LF_N des⁽⁻⁾_1–46 background (Fig. 5B). We find that acidic residue density provides the strongest correlation with a significant p value of 0.001 (Fig. 5C). Although the density of total charges, acidic plus basic, is a fairly good predictor (p = 0.003), this correlation likely reflects the contribution of the negative charge density and not the positive charge density, because the latter correlation is not significant (p = 0.3). The degree of hydrophobicity also poorly correlated (p = 0.09) with the most optimal positions for acidic residues in ΔpH-mediated translocation. We conclude that the natural placement of acidic residues in the presequence of LF_N is optimized for ΔpH-dependent translocation.

Charge-dense Regions Are Optimally Positioned Proximal to Folded Structure

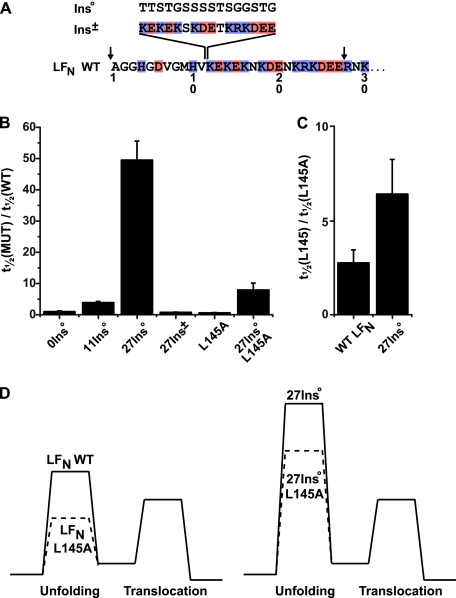
Because we found that when translocating under a ΔpH driving force that the region of highest charge density in the presequence of LF_N (residues ∼15 to 30) is also the optimal region for introducing Glu residues into the LF_N des⁽⁻⁾_1–46 mutant background (Fig. 5), we hypothesized that the location of this cluster of charged residues is only critical in relation to the folded domain of LF_N. That is, if the charged cluster were moved further away from the folded structure of LF_N, then the force generated by the applied ΔpH gradient would not be as fully realized on the folded structure of LF_N. Thus acidic residues more proximal to the folded region of the substrate would better facilitate proper LF_N unfolding. To test this hypothesis, we created the LF_N 27Ins° construct, which inserts a series of 16 random Gly, Ser, and Thr residues between positions 27 and 28 of LF_N WT (Fig. 6A). Despite possessing all of the acidic residues of LF_N WT and only extending the overall length of the substrate by ∼6%, translocation is slowed ∼50-fold under a 1.06 unit ΔpH and no Δψ (Fig. 6B). An identical insertion placed earlier (LF_N 0Ins° and LF_N 11Ins°) in the amino terminus of the LF_N did not appreciably effect ΔpH-dependent translocation. Restoring charges to the inserted region in a pattern matching that of LF_N residues 12–27 (LF_N 27Ins^±) returned translocation speed to that of LF_N WT. Interestingly, all constructs with inserts (regardless of position, charge, or background) displayed a reduction in efficiency of translocation: ∼50–65% that of LF_N WT.

FIGURE 6.

Charged residues must be located immediately before the folded domain of the substrate for efficient translocation. A, sixteen-residue inserts with either no charge (Ins°) or a mix of positive and negative charges (Ins^±) were inserted into LF_N WT or LF_N L145A. The resulting constructs are called yIns^x, where y denotes the last WT residue prior to the insert, and the superscript x represents the charge of the insert. The arrows indicate two other positions (0 and 27) where the Ins° sequence was inserted. B, the relative translocation t½ times of insertion and LF_N L145 mutants (MUT) are given as the ratio t½(MUT)/t½(WT). ΔpH-driven translocation conditions were: ΔpH = 1.06, pH_cis = 5.6, and Δψ = 0 mV. The error bars are the means ± S.D. (n = 2). C, the relative translocation t½ times of the LF_N L145A and LF_N 27Ins° L145A mutants compared with their respective (L145) counterpart given as the ratio t½(L145)/t½(LF_N L145A). Translocation conditions are as in B. D, model energy diagrams depicting the changes in energy barriers caused by the L145A and 27Ins° mutations, wherein we interpret 27Ins° as greatly increasing the unfolding barrier. The L145A mutation reduces the unfolding barrier by the same extent in the WT and 27Ins° backgrounds. However, in the WT background, the rate becomes limited by the translocation barrier, so the relative increase in speed is not as large as that observed for the 27Ins° background.

To test whether the reduction of the translocation rate in the LF_N 27Ins° construct is due to an effective stabilization of the folded substrate, we introduced the destabilizing mutation, L145A (6), into the LF_N WT and 27Ins° backgrounds (Fig. 6C). Under the same conditions described above, the translocation rate of LF_N WT was increased by a factor of 2.3 (±0.7) by the L145A mutation, whereas the rate of 27Ins° L145A increases by 6.4 (±1.9). We posit that 27Ins° greatly increases the height of the unfolding barrier (Fig. 6D). When the L145A mutation is introduced in LF_N WT, a second barrier becomes limiting, but in 27Ins° the unfolding barrier remains limiting. Thus, despite reducing the height of the unfolding barrier to the same extent, the L145A mutation has a greater effect in 27Ins°. We conclude that the highly charged region must be present immediately prior to the folded domain for efficient protein unfolding to take place under a ΔpH.

Intermixed Cationic and Anionic Groups in the Presequence of LF_N are Optimal for ΔpH Translocation

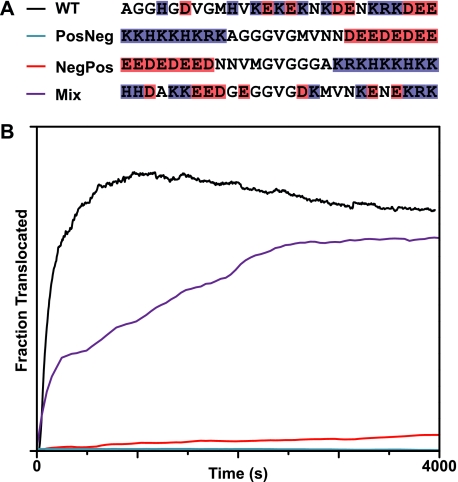
So far we have reported that basic residues are important for the initial insertion into the channel and acidic residues are most important just before the folded domain of LF_N. From these observations, we might predict that translocation would not be inhibited when the presequence of LF_N is rearranged so that all the basic residues are at the beginning and all the acidic residues are at the end. We made such a construct (LF_N PosNeg) along with its inverse (LF_N NegPos) and assayed their abilities to translocate with a proton gradient, ΔpH = 1.06 and Δψ = 0 (Fig. 7A). Both constructs were essentially unable to translocate (Fig. 7B). However, a construct with a randomized amino-terminal presequence (LF_N Mix) was able to translocate much more similarly to LF_N WT (Fig. 7B). Interestingly, none of the positions in this construct share the charge of their WT counterparts. The effectiveness of the LF_N Mix construct suggests that the specific WT arrangement of positive and negative charges is less important than simply maintaining an intermixed arrangement of positively and negatively charged residues. We propose that positively charged residues act locally as ionic chaperones for negatively charged acidic residues.

FIGURE 7.

Proton gradient-driven translocation requires that acidic and basic residues be intermixed in the substrate. A, design of constructs that separate the acidic and basic amino acids in the first 27 residues of LF_N to opposite ends of the presequence. PosNeg has a contiguous stretch of basic residues at the amino-terminal end and a contiguous stretch of acidic residues at the carboxyl-terminal end; NegPos is the inverse sequence of PosNeg. A randomized construct was also prepared (called Mix), in which the acidic and basic residues are intermixed, but no position has the same charge as its WT counterpart. B, translocation records for His₆-LF_N WT (black), His₆-LF_N PosNeg (blue), His₆-LF_N NegPos (red), and His₆-LF_N Mix (purple). ΔpH-driven translocation conditions were: ΔpH = 1.06, pH_cis = 5.6, and Δψ = 0 mV.

DISCUSSION

To perform work, molecular machines and protein translocases in the cell require a source of energy, generally in the form of chemical energy (ATP) or potential energy stored as either a PMF or other ionic gradient. These sources of energy are interchangeable as evidenced by the highly homologous (27) bacterial flagellum (28, 29), F₁F_o-ATP synthase (30, 31), and the vacuolar V_oV₁-ATPase membrane proton pump (32–34). In the former two cases, a PMF is used to drive the rotational motion of the flagellum (29) or the cycles of enzyme reactions (35) that produce ATP in the transmembrane F₁F_o-ATP synthase (36). In the latter system, ATP hydrolysis powers a rotary proton pump to generate a PMF, which is essentially the ATP synthase in reverse. The PMF is also an important driving force for transmembrane protein translocation in mitochondria (37), chloroplasts (38), and the endosomal compartment (1). Proton gradients also exist across the endoplasmic reticulum and other compartments in the cell (39) and in theory may comprise an important driving force for other types of translocases in the cell.

Active Pushing/Pulling Translocation Models

Protein translocation is basically a series of reactions that convert a source of free energy to mechanical work used to drive protein unfolding and unidirectional transport. This process is involved in transmembrane transport, protein degradation, and chaperone activities. Here, either ATP hydrolysis cycles (5, 40–42) or utilization of the PMF (1) can propel polypeptides across membranes or into hydrolytic compartments for degradation. Often the molecular machine that carries out translocation processes contains loop regions with critical aromatic groups at their tips. Also, additional accessory proteins outside the channel may be utilized to engage the polypeptide during translocation. It is thought that cycles of ATP binding, ATP hydrolysis, and ADP and inorganic phosphate release cause these loops/proteins to move like simple linear actuators, which effectively pushes the translocating polypeptide in a particular direction (40, 42–44). This mechanism is supported in part because these Φ-clamp-type structures are found in various conformations for different nucleotide bound states. For anthrax toxin, the utilization of the proton gradient occurs most optimally with an intact aromatic Φ-clamp structure (1, 2), suggesting that these aromatic internal pore loops may push the translocating polypeptide in a similar manner. At present, this active pushing mechanism of translocation is favored in many systems, but it cannot by itself explain all of the mechanochemical coupled mechanisms.

Brownian Ratchet Models for Translocation

An alternative, but potentially complementary view, of mechanochemical coupling should be considered in addition to the active pushing model. The Brownian ratchet model (20–22, 45, 46) suggests that nonequilibrium fluctuations, namely in the form of chemical reactions or thermal gradients, can bias random thermal motion in a productive and directional way. In Feynman's initial conception (20), stochastic fluctuations may be harnessed for useful work using a temperature gradient. Although a thermal gradient is difficult to achieve across a biological membrane, chemical asymmetries and membrane gradients, such as a ΔpH or those created by ATP hydrolysis, are readily available to drive biological Brownian motors.

Ratchet Model of ΔpH-driven Anthrax Toxin Translocation

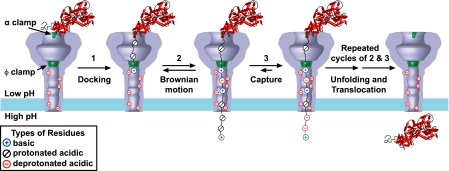
Anthrax toxin activity is most optimal when the endosomal compartment is allowed to naturally acidify (47). Acidification produces a transmembrane PMF that stimulates translocation (1, 2, 6). The chemical potential component of the gradient, Δμ^ΔpH, is sufficient by itself to drive translocation (Fig. 1). How might ΔpH-driven translocation follow a Brownian ratchet mechanism? Brownian fluctuations in the substrate polypeptide chain may be coupled to protonation state changes in the substrate chain or channel (Fig. 8). We infer that acidic residues in the substrates (which have net acidic isoelectric points) are protonated upon entering the PA channel, because the charge dependence, or z value, we observe for translocation is positive. This fact implies that the substrate chain is positively charged at the point of the potential drop in the channel (1, 6). The positive charge dependence also reflects the known fact that the PA channel is cation-selective (18), and a highly anionic polypeptide would be repulsed by the channel as we observe with our LF_N Syn⁻ construct (Fig. 2B). A similar effect has been observed when LF_N is modified with a sulfate group (48). Therefore, a segment of substrate chain with protonated acidic residues will more readily achieve a positive charge enabling its passage through the PA channel under Brownian motion. It can subsequently release protons into the trans-side of the membrane (as favored in the higher pH condition), thus leading to a build-up of anionic charge in the trans-side substrate. The anionic charge in the trans substrate should effectively impede retrograde efflux (under Brownian motion) back into the anion-repulsive channel and enforce proper directionality. Cycles of this charge state Brownian ratchet mechanism would then translocate the remainder of the polypeptide across the membrane.

FIGURE 8.

The charge state Brownian ratchet model for ΔpH-driven translocation of anthrax toxin. At the time of endosome acidification, the substrate is bound to the top of the channel, with its α1 helix in the α clamp. Upon channel conversion, the unstructured amino terminus docks in the Φ clamp. The low pH of the endosomal compartment will protonate most of the acidic residues, whereas positive charges chaperone any remaining deprotonated aspartic or glutamic acids. This ensures that the translocating polypeptide will have a net positive charge, allowing it to move freely through the cation-selective channel. Because of Brownian motion, a portion of the substrate will eventually emerge in the cytosol. There, the higher pH of this region will result in frequently deprotonated acidic residues, thereby giving the emerged portion of the polypeptide a net negative charge and capturing it on the cytosolic side of the membrane. Repeated cycles of emergence from the channel through Brownian motion and capture via deprotonation allow the remaining portion of the substrate to translocate across the membrane.

Acidic Residues in the Substrate Are the Teeth in the ΔpH-driven Brownian Ratchet

One obvious and testable feature of this charge state Brownian ratchet mechanism is the role of acidic residues in the substrate. A previous study using a synthetic peptide attached to the folded domain of LF_N via native chemical ligation showed that chargeless or positive-only presequences are defective in translocation (49). Here we more extensively explored charged residue involvement in ΔpH translocation. By replacing the residues in the presequence en masse with neutral residues and measuring translocation under a variety of ΔpH conditions, we determined the ΔpH dependence of translocation, which is the best indicator of the ability to use a proton gradient as a driving force (Fig. 2). We found that sequences lacking acidic residues had comparatively weak ΔpH dependences (Fig. 2) and the ability to translocate using a ΔpH decreases as more acidic residues are removed (Fig. 4). A more detailed scan, using an anion-less variant, LF_N des⁽⁻⁾_1–46, showed that the region spanning residues 23–31 received the largest gain in translocation kinetics when a single acidic residue was introduced (Fig. 5B). Furthermore, the natural sequence appears to maximize its inherent acidic residue density in this very region to best take advantage of the ΔpH driving force (Fig. 5C). Thus based on this model, we conclude that acidic residues in the substrate form the molecular teeth in the ΔpH-driven Brownian ratchet mechanism.

Novel Role for Positive Charges in the Charge State Ratchet

We identified one other complicating factor in our analysis when we tested for the role of positive charges in the presequence. Using the synthetic presequence Syn series, we find that a Syn⁻ presequence dominated by acidic residues and lacking basic residues is defective in translocation (Fig. 2B). However, this result does not mean that ΔpH-driven translocation requires only positive charges, because presequences engineered to only contain cationic residues tend to have flat ΔpH dependences (Fig. 2B). Various lines of evidence indicate that acidic residues require neutralization either by direct protonation (Fig. 2C) or by proximal positively charged residues (Figs. 3 and 7). This requirement demonstrates that the channel has robust charge selectivity. We propose this selectivity enforces directionality through electrostatic repulsion, thereby making it an integral feature of the charge state Brownian ratchet translocation mechanism.

Can ΔpH-driven Brownian Ratchets Generate Robust Unfoldase Activity?

Some formulations (21, 44), but not all (50), of the Brownian ratchet mechanism imply that unfolding must occur prior to the engagement of the ratcheting process. In the unfolding-limited conceptualization of the Brownian ratchet model, it is suggested that the channel must wait for the protein to unfold and the channel itself is not a participant in the denaturation. In this view, it is thought that the Brownian ratchet mechanism cannot fully explain the large translocation rate accelerations observed for stable substrates, such as dihydrofolate reductase (51), barnase (52), or cytochrome b₂ (53).

This formulation of the Brownian ratchet model requires some updating with more current reports (1, 2, 6, 17). The PA channel, for example, utilizes two principle unfoldase or denaturation sites within the channel, namely the Φ clamp (2, 6) and α clamp (17). The former site is comprised of a ring of seven or eight Phe residues (depending on the oligomerization state of the PA complex), which can clamp onto the amino terminus of LF (2) and drive unfolding (6), presumably by binding to hydrophobic moieties in the substrate in a nonspecific manner (2). The latter α-clamp site is a deep cleft, situated between the twin Ca²⁺ ion-binding sites on the surface of the PA oligomer; this clamp is capable of binding nonspecifically to a ∼10-residue α helix and short ∼5-residue β strand (17). The initial characterization of the α clamp revealed an interesting capability of the site: upon binding to the surface of the PA oligomer, LF_N is partially unfolded. In this unfolding, the first α helix and β strand of LF unfurl and dock into the α-clamp cleft. The α clamp also has broad binding specificity, allowing the site to recognize many types of sequences and making it a general denaturation site on the translocase. The second factor to consider is that ΔpH-driven translocation facilitates unfolding (6). Two different types of barriers have been identified in LF_N translocation. The more force-dependent barrier (as determined by the n value, Equation 1) is also limited by protein unfolding (6). Thus substrate unfolding may not be out of the realm of possibility for a Brownian ratchet powered translocase, because the closely spaced denaturation sites in the channel allow for small displacements of sequence (small fluctuations) to be captured and stabilized via interactions with the channel.

How Might Denatured Protein-binding Sites on the Channel Operate in Conjunction with a ΔpH-driven Ratchet?

Brownian thermal fluctuations are a significant source of energy that, if partially harnessed, could serve to denature a protein. For a polypeptide presequence (30 residues in length), Brownian thermal fluctuations provide ∼6 kcal mol⁻¹ of thermal energy (assuming two degrees of freedom per backbone Φ and Ψ angle/residue). Thus, although the α-clamp structure maintains contact with the sequence carboxyl-terminal to the presequence, the amino-terminal end may move through the channel purely motivated by Brownian thermal fluctuations. Successful excursions require that the presequence region is electrostatically compatible with the cation-selective lumen of the channel. We believe that this is ensured either through the lowered pH of the cis-side of the membrane or by adjacent positive charges, which may act to help chaperone the acidic groups across the membrane. Successful excursions are then anchored or captured on the trans-side of the membrane once the acidic groups further deprotonate in the higher pH medium. The high degree of correlation between the best sites to introduce a Glu residue in LF_N des⁽⁻⁾_1–46 and the naturally high density of negative charges in the presequence of LF (Fig. 5C) suggests that this anchoring step is more favorable with higher acidic residue densities.

Interestingly, we find that the acidic residue-rich sequence is located immediately adjacent to the folded structure. Thus after successful anchoring of the presequence takes place, an entropic tension may be effectively applied to the remaining folded structure. This entropic tension is derived from the fact that a more extended polypeptide chain would have fewer possible conformations, and to relieve this entropic tension, the protein would be driven to unfold. We tested the positional dependence of this acidic residue cluster by creating an artificial gap between this naturally dense region and the folded structure of LF_N. When the gap contains neutral residues, the translocation rate decreases 50 fold, but when the gap contains charged groups, the translocation rate is similar to WT (Fig. 6B). Furthermore, the decrease in the translocation rate coincides with an observed stabilization of the substrate (Fig. 6C). Previous studies show that a larger nucleus of structure unfolds during translocation in a large cooperative unfolding step (6); however, this unfolding occurs after a smaller portion of the amino-terminal structure is unfolded and docked into the α-clamp site (17). Therefore, we expect that the α- and Φ-clamp protein denaturation sites in the channel can reduce the overall unfolding barrier by allowing for small incremental unfolding steps to be stabilized. Effective trapping of Brownian fluctuations may force partially unfolded intermediates to then disengage from the channel, leading ultimately to the larger scale cooperative unfolding event (6) that we observe under a ΔpH.

Finally, the charge requirements we identify for the substrate strongly favor a Brownian ratchet model. However, we cannot rule out the possibility that ΔpH-driven transport also involves coordinated, proton-dependent movement of loops within the PA channel, which helps to push the substrate chain during translocation. A combination of the active pushing and Brownian ratchet models may apply to this system because these models are not mutually exclusive. In fact, other translocases already known to push proteins using ATP-driven loop movements may also use a Brownian ratchet to further drive transport.