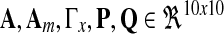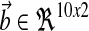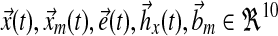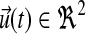Abstract
Robust behavior in metabolic pathways resembles stabilized performance in systems under autonomous control. This suggests we can apply control theory to study existing regulation in these cellular networks. Here, we use model-reference adaptive control (MRAC) to investigate the dynamics of de novo sphingolipid synthesis regulation in a combined theoretical and experimental case study. The effects of serine palmitoyltransferase over-expression on this pathway are studied in vitro using human embryonic kidney cells. We report two key results from comparing numerical simulations with observed data. First, MRAC simulations of pathway dynamics are comparable to simulations from a standard model using mass action kinetics. The root-sum-square (RSS) between data and simulations in both cases differ by less than 5%. Second, MRAC simulations suggest systematic pathway regulation in terms of adaptive feedback from individual molecules. In response to increased metabolite levels available for de novo sphingolipid synthesis, feedback from molecules along the main artery of the pathway is regulated more frequently and with greater amplitude than from other molecules along the branches. These biological insights are consistent with current knowledge while being new that they may guide future research in sphingolipid biology. In summary, we report a novel approach to study regulation in cellular networks by applying control theory in the context of robust metabolic pathways. We do this to uncover potential insight into the dynamics of regulation and the reverse engineering of cellular networks for systems biology. This new modeling approach and the implementation routines designed for this case study may be extended to other systems. Supplementary Material is available at www.liebertonline.com/cmb.
Key words: algorithms, metabolic pathway dynamics, model-reference adaptive control, biochemical regulation, sphingolipid de novo synthesis
1. Introduction
Control theory is a cornerstone of engineering applied to design systems that need to be regulated, or study systems that already are regulated (Kailath, 1980; Luenberger, 1979; Ogata, 1998). Compared to engineering systems, there is arguably more complexity and uncertainty in biochemical systems such as cellular networks and metabolic pathways. Nonetheless, within metabolic limits, such complex systems are capable of maintaining specific behaviors under perturbation, i.e., such systems exhibit robustness that suggests they are controlled autonomously. It follows that we may study existing regulation in biochemical systems in terms of autonomous control using models based on control theory. A more principled understanding of the robustness of biochemical responses to drugs may inform and improve the design and development of drug intervention strategies (Kitano, 2007a) and contribute towards developing a theory of biological robustness (Kitano, 2007b). Recent opinions also express cautious optimism to apply control theory to reverse engineer biological complexity and regulation (Csete and Doyle, 2002; Lauffenburger, 2000; Tomlin and Axelrod, 2005).
1.1. Robustness of cellular networks
The persistence of specific behaviors in cellular networks under constantly changing conditions has attracted much interest (Stelling et al., 2004), not only in attempts to understand biological complexity but also to influence biological performance. To understand biological complexity, for example, in cybernetics it is long posited that behavioral robustness is the result of structural complexity (Wiener, 1965). Recent examples include metabolic networks in Escherichia coli, human hepatocytes, and erythrocytes (Behre et al., 2008), and in adult rat cardiomyocytes and human skeletal muscle (Guzun and Saks, 2010) that have been studied using this bottom-up approach. To influence biological performance, for example, it is shown that sliding mode control can be applied in a generalized bioreactor based on nonlinear model dynamics to specify appropriate nutrient flow rates, in order to achieve and maintain a desired amount of cells (Fossas et al., 2001). Thus, while robustness of cellular networks, or biochemical systems in general, is an undisputed property of biological systems, how it arises or can be manipulated for specific applications remain active areas of research.
1.2. Biochemical systems regulation as autonomous control
Models based on control theory can be used to study existing regulation in biochemical systems that exhibit robustness as a result of autonomous control, e.g., where specific outcomes such as convergence to steady state and stabilizing feedback are assured. For example, exact adaptation of chemotaxis in E. coli is observed to be robust and not affected by changes in protein levels (Alon et al., 1999; Barkai and Leibler, 1997). Subsequently, such robust behavior can be modeled as the result of integral feedback control that ensures convergence to steady state behavior without error (Yi et al., 2000). In another example, the regulation of heat shock response in E. coli can be modeled using open- and closed-loop control to study the costs and benefits to cells in mounting a heat shock response, from the perspective of control (El-Samad et al., 2005). Thus, models based on control theory are useful to gain insight into biochemical systems regulation and robustness from the perspective of autonomous control.
2. Biological Significance of Sphingolipids
2.1. Regulation of de novo sphingolipid synthesis
De novo sphingolipid synthesis is necessary because sphingoid bases present in food are mostly degraded in the intestine (Vesper et al., 1999). Sphingolipids are involved in key eukaryotic cell functions such as membrane structure recognition, signal transduction, intracellular regulation, and cell-cell interaction. Three of the initial enzymes of sphingolipid biosynthesis are thought to be particularly important (Fig. 1b): serine palmitoyltransferase (SPT), which catalyzes the initial step of sphingolipid biosynthesis by condensation of L-serine and palmitoyl-coA (Pal-CoA); (dihydro)ceramide synthase, which adds the amide-linked fatty acid to form dihydroceramide; and dihydroceramide desaturase, which adds the 4,5-trans-double bond of the sphingoid base backbone to form ceramide. At the same time, de novo sphingolipid biosynthesis has also been described as “a necessary, but dangerous, pathway” (Merrill, 2002).
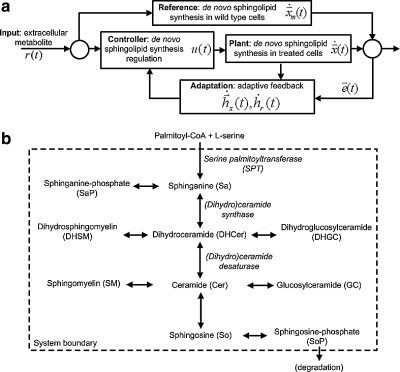
FIG. 1.
Model-reference adaptive control (MRAC) approach to study regulation in de novo sphingolipid synthesis. (a) Block diagram of model-reference adaptive control (MRAC); treated cells (plant) follow wild type cells (reference) to minimize the difference in sphingolipid amounts. (b) De novo sphingolipid synthesis pathway with key enzymes in italics; uni-/bi-directional arrows indicate irreversible/reversible reactions respectively; pathway intermediates, e.g., ceramide, sphingomyelin, are highly bioactive.
Regulation of sphingolipid levels through synthesis is important because pathway intermediates such as ceramide and sphingomyelin are highly bioactive. Alterations in sphingolipid synthesis, storage, and metabolism are implicated in human diseases (Kacher and Futerman, 2006). For example, in synthesis, infantile-onset symptomatic epilepsy is described as a genetic defect in ganglioside GM3 synthase (Simpson et al., 2004); in storage, Tay-Sachs, Sandhoff, and Gaucher disease are characterized by glycosphingolipid accumulation (Kolter and Sandhoff, 2006); in metabolism, ceramide functions as a tumor suppressor in various cancer cells (Ogretmen and Hannun, 2004). Thus, regulation of sphingolipid levels through synthesis is critical to maintain key cell functions, failing which leads to a variety of human diseases. Consequently, we may be able to learn more about the onset and development of these diseases by first studying how de novo sphingolipid synthesis is regulated in living cells, specifically in terms of metabolic pathway dynamics.
2.2. Sphingolipid-omics
Furthermore, the diversity and complexity of sphingolipids require researchers to possess a range of tools to work with these compounds, such as the resources available at LIPIDMAPS (www.lipidmaps.org). The general structure of a sphingolipid comprises a sphingoid base backbone, such as sphinganine that is modified by addition of long-chain fatty acids, double bonds in the sphingoid base (i.e., to make sphingosine), and polar headgroups. When variation in these components is considered, for example, in terms of the number of double bonds and hydroxyl groups in sphingoid bases, chain length in fatty acids, and types and arrangement of headgroups, this is one of the most complex families of biomolecules (Fahy et al., 2005).
As a result, to study dynamic changes in cellular sphingolipid amounts, we require computational methods that couple mass spectrometry with statistical algorithms to analyze the vast number of lipid species from cellular extracts (Forrester et al., 2004). We also require systems-based models that can reveal underlying interactions within these pathway systems that are not apparent. Current approaches in systems biology models, based on more familiar methods of dynamic modeling such as mass action kinetics (Gulberg and Waage, 1986; Lund, 1965), are useful to simulate the dynamics of biochemical reactions between components. So they may be used as a basis to investigate possible underlying dynamics of pathway regulation. Thus, the increasing wealth of quantitative lipidomic data makes the study of sphingolipid biology from a systems-based approach promising and challenging at the same time (Merrill et al., 2007).
3. Research Objectives
Here, we use model-reference adaptive control (MRAC) as a model to study existing regulation in metabolic pathways in a combined theoretical and experimental case study. Specifically, we focus on extracting insight into how de novo sphingolipid synthesis is regulated in serine palmitoyltransferase (SPT) over-expressing human embryonic kidney (HEK) cells. Thus, our goals are:
First, to compare the efficacy of MRAC, to simulate metabolic pathway dynamics, to a standard method of modeling biochemical systems, i.e., mass action kinetics, and
Second, to demonstrate the use and value of MRAC to uncover quantitative and potentially novel insight into metabolic pathway regulation.
Results show that the proposed MRAC approach compares well with using mass action kinetics alone to simulate metabolic pathway dynamics. The goodness-of-fit of the two cases with experimental data differs by only 5% in terms of root-sum-square (RSS) error when all model variables are considered, i.e., all pathway molecules. In addition, the proposed MRAC approach also reveals potential systematic pathway regulation and key molecules in terms of adaptive feedback from individual molecules in continuous time.
3.1. Model-reference adaptive control (MRAC)
Model-reference adaptive control (MRAC) (Osbourne et al., 1961; Whitaker, 1959) is a form of autonomous control, in particular adaptive control, where the objective is to steer the plant to behave identically to the reference. By definition (Fig. 1a), the reference exhibits the desired dynamics in response to an input, and is used as an ideal system for the plant to follow. As a result, the error, i.e., difference between the state trajectory in plant and reference, is a quantity of interest. The controller adapts real-time information about the plant and reference directly in terms of input and error to give adaptive feedback. In addition, the efficiency of feedback adaptation also depends on the choice of suitable parameters. In theory, the dynamics, or state trajectory, of the plant can be influenced to converge with the reference over time (Hahn, 1963; LaSalle, 1964; Lyapunov, 1992).
Readers who are familiar with metabolic control analysis (MCA) (Heinrich and Rapoport, 1974; Kacser and Burns, 1973) should distinguish it from control theory described here. On one hand, MCA is a specialized form of sensitivity analysis where the effect of changes in enzyme activity on the flux of metabolites in a (biochemical) system is correlated to resultant changes in the properties of other system components (Fell, 1992). On the other hand, control theory encompasses a set of broad mathematical theorems collectively stated for the purpose of guiding the dynamics of a (general) system by design. Consequently, various modes of control have been developed to accomplish this objective in a variety of systems, traditionally for engineering applications.
3.2. An MRAC approach to study metabolic pathway regulation
We represent treated HEK cells, i.e., SPT over-expressing, as the plant and wild type HEK cells as the reference (Fig. 1a). We assume that in response to increased metabolite amounts available for de novo synthesis, treated cells attempt to regulate the pathway such that sphingolipid amounts in these cells are similar to the wild type. Experimentally, we add 13C-labeled palmitate, which is converted to PalCoA inside the cells, as the input to elicit and observe a response in terms of normalized sphingolipid amounts.
Specifically, we propose to use an MRAC approach for several reasons:
As a concept framework, adaptive control (Anderson and Dehgani, 2008; Goodwin et al., 1984) is consistent with knowledge that biochemical resources are conserved and metabolic states approach steady state over time in live cells. Furthermore, compared to other modes of autonomous control also consistent with this knowledge, e.g., optimal and robust control, we require less prior knowledge to implement adaptive control in comparison with optimal control (Bryson Jr., 1996; Sussman and Willems, 1997), which requires assuming cost functions, and robust control (van Antwerp and Braatz, 2000; van Antwerp et al., 1999), which requires estimating system performance constraints.
From a biological perspective, we can expect HEK cells to implement a biochemical version of MRAC because treated cells are genetically identical to the wild type. Apart from single gene over-expression (SPT 1/2), the treated cells and wild type are clones from the same cell line. The net effect of SPT 1/2 over-expression increases the amount of PalCoA that enters the pathway, i.e., increased metabolite influx.
From a reverse engineering perspective, we may regard the MRAC approach as a knowledge-based method. In other words, we use the dynamics of the wild-type cells as a knowledge source to learn possible interactions between molecules that serve to regulate pathway dynamics as a result of perturbing the system (in the form of single gene over-expression). Thus, the wild type behavior informs the behavior of treated cells.
Finally, using MRAC, we can define a clear and quantifiable modeling objective, i.e., for pathway regulation in treated cells to minimize the difference between treated and wild-type cells in finite time. Because we use MRAC as a model to study existing pathway regulation, but not to design an autonomous controller to regulate metabolic activity, the difference between treated and wild type cells is only assumed to be minimized but not eliminated.
4. Results and Discussion
The ten molecules of interest in this case study are sphinganine (Sa), sphinganine phosphate (SaP), dihydroceramide (DHCer), dihydroglucosylceramide (DHGC), dihydrosphingomyelin (DHSM), ceramide (Cer), glucosylceramide (GC), sphingomyelin (SM), sphingosine (So), and sphingosine phosphate (SoP). For brevity, we refer to them in four groups: (i) Sa*, i.e., Sa/SaP, (ii) So*, i.e., So/SoP, (iii) DH*, i.e., DHCer/DHGC/DHSM, and (iv) Cer*, i.e., Cer/GC/SM. In addition, Sa*, So* are sphingoid bases, DH* are dihydrosphingolipids, and Cer* are sphingolipids.
4.1. Wild type behavior
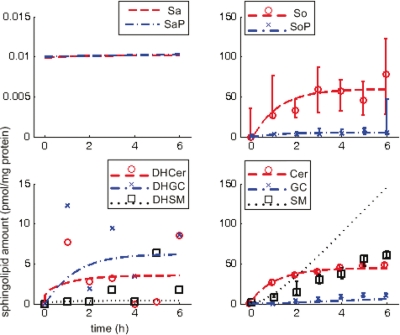
Figure 2 shows the observed data and simulated dynamics in wild type (observed data in scatter plot—median and range of four technical replicates indicated where available; Sa* data not available; simulated results in broken lines). From the observed data, So and Cer increase steadily at first, then settle to constant levels; SoP, DHSM, GC, and SM increase steadily throughout; DHCer and DHGC vary significantly although DHCer also appears to approach a steady level.
FIG. 2.
Sphingolipid dynamics in wild type (reference). Abscissa-time (hours), ordinate-normalized sphingolipid amounts (pmol/mg protein); scatter plots represent observed data (median and range for four technical replicates, indicated where available, i.e., no data for Sa* and limited data for DH*), lines represent simulations.
The simulated dynamics are based on estimated reaction rate constants. Comparing simulation results with observed data, they compare well for four molecules (So, SoP, Cer, and GC), i.e., simulation results fall clearly and consistently within range of the observed data. Simulation results compare fairly with data for three molecules (DHCer, DHGC, and SM) where simulation results either suggest a plausible trend given fluctuations in limited data (DHCer, DHGC) or reflect the general trend over time but at a noticeably different rate (SM). Simulation results compare poorly with data for one molecule (DHSM), which fail to reflect the overall trend of a steady increase.
4.2. Treated cells behavior, without and with MRAC
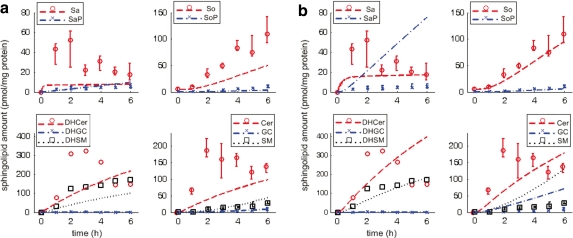
Figure 3 shows the observed data and simulated dynamics in treated cells (observed data in scatter plot—median and range of four technical replicates indicated where available; simulated results in broken lines). From the observed data, Sa, DHCer, and Cer increase transiently before settling to constant levels; DHSM increases steadily and settles to a constant level; SaP, SoP, DHGC, GC, and SM are present at noticeably low levels although SaP, SoP, GC, and SM increase steadily while DHGC remains fairly constant; So increases steadily throughout at relatively high levels.
FIG. 3.
Sphingolipid dynamics in treated cells, without and with MRAC. Abscissa-time (hours), ordinate-normalized amounts (pmol/mg protein); scatter plots represent observed data (median and range indicated for four technical replicates, indicated where available, i.e., limited data for DH*), lines represent simulations. (a) Without MRAC. (b) With MRAC.
In Figure 3a (without MRAC), simulation results consistently underestimate the observed data, specifically for five molecules (Sa, So, DHCer, DHSM, and Cer), although this seems to compare well for the other five molecules present at noticeably low levels (SaP, SoP, DHGC, GC, and SM). In Figure 3b (with MRAC), simulation results compare well for two molecules present at low levels (SoP, DHGC) but not the other three (SaP, GC, and SM); simulation results also compare well for two molecules (So, DHSM), and arguably better for three molecules that increase transiently before settling to constant levels (Sa, DHCer, and Cer).
Table 1 shows the goodness-of-fit of the simulated model dynamics with observed data using root-sum-square (RSS) as a metric. Simulation results compare much better with observed data for all molecules in wild type than treated cells. In treated cells, the most significant impact of MRAC to simulate pathway dynamics is observed in the RSS for Sa*, i.e., 76.9% increase, and So*, i.e., 64.8% decrease over simulations using mass action kinetics alone. For Sa*, the RSS increase using MRAC is due to consistent overestimates of SaP although the trend of a steady increase in the observed data is reflected. For So*, the RSS decrease using MRAC is due to a more accurate estimate of So, compared to without MRAC. The differences in RSS for DH* and Cer* are not as significant, given the limited observed data. If all molecules in the pathway are considered, RSS between data and simulations using the proposed MRAC approach or mass action kinetics alone varies by less than 5%.
Table 1.
Goodness-of-Fit Between Simulated Dynamics and Observed Data
| |
Root-sum-square (RSS) difference between simulations and dataa |
||||
|---|---|---|---|---|---|
| Data | Sa* | DH* | Cer* | So* | All |
| Wild type | n/a | 20.06 | 122.97 | 29.12 | 127.95 |
| Treated, without MRAC | 66.55 | 368.68 | 216.15 | 94.84 | 442.80 |
| Treated, with MRACb | 117.75 (+76.9) | 379.26 (+2.9) | 233.09 (+7.8) | 33.37 (−64.8) | 461.68 (+4.3) |
Root-sum-square (RSS) is calculated using median data across all discrete time points, i.e., 0, 1, 2, … , 6h.
percentage change over RSS difference in treated cells without MRAC is stated in parentheses.
Asterisk (*) indicates similar molecules, e.g., Cer* refers to Cer, GC, and SM.
Based on these results, using the proposed MRAC approach shows improvement for Sa, Cer, DHCer, and So at the expense of SaP, GC, and SM. We revisit what this implies in the next section. Thus, using MRAC to model and simulate pathway dynamics in de novo sphingolipid synthesis is comparable to using a more established biochemical systems model, i.e., mass action kinetics.
4.3. Systematic feedback and key molecules in regulating de novo sphingolipid synthesis
The primary use and value of MRAC as a model to study existing regulation in this case study is to extract insight that was not previously accessed using more familiar models. Such insight may be described more specifically, e.g., to uncover systematic pathway responses to perturbation or to distinguish key molecules from others.
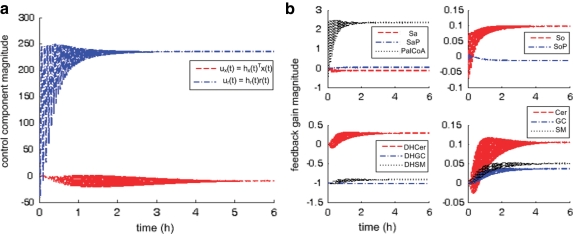
Figure 4a shows controller dynamics in terms of two components due to (a) feedback from pathway molecules, ux(t), and (b) palmitate input, ur(t). ur(t) is significantly and consistently larger than ux(t). Before settling to steady values, ur(t) oscillates with larger amplitude from 0–2 h while ux(t) oscillates with much smaller amplitude from 0–4 h. Furthermore, from the onset, ux(t) lags in response to ur(t). This suggests that in response to excess extracellular palmitate to the pathway, facilitated by SPT over-expression, de novo sphingolipid synthesis is first regulated by modifying palmitate uptake and conversion (to PalCoA) before adjusting for feedback from pathway molecules. In terms of using the least resource to achieve the most direct effect, this observation is consistent with our expectation that in such a regulated pathway, the more economic and effective approach in response to perturbation is to intervene at the source of perturbation before altering the amounts of downstream molecules.
FIG. 4.
Regulatory dynamics in treated cells. Abscissa-time (hours), ordinate-magnitude (dimensionless). (a) Controller comprises two components 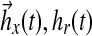 from pathway feedback and input respectively. (b) Detailed pathway feedback in terms of adaptation gain from individual molecules; all gains initialized at zero except for DHGC, DHSM initialized at −1.
from pathway feedback and input respectively. (b) Detailed pathway feedback in terms of adaptation gain from individual molecules; all gains initialized at zero except for DHGC, DHSM initialized at −1.
In Figure 4b, pathway feedback from individual molecules is tracked in terms of adaptive feedback in continuous time, i.e., changes in adaptation gain 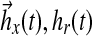 where absolute value indicates magnitude and sign indicates direction. We may interpret intervals of oscillation, plotted as relatively broad swathes in the figure, to mean periods of more frequent or active regulation. For instance, consistent with Figure 4a, palmitate input is regulated quickly from the onset from 0–2 h until it settles to a constant level subsequently.
where absolute value indicates magnitude and sign indicates direction. We may interpret intervals of oscillation, plotted as relatively broad swathes in the figure, to mean periods of more frequent or active regulation. For instance, consistent with Figure 4a, palmitate input is regulated quickly from the onset from 0–2 h until it settles to a constant level subsequently.
When we consider results in Figure 4 together with the known structure of the sphingolipid synthesis pathway (Fig. 1b), we see that feedback from “core” molecules, i.e., along the main artery of the pathway (DHCer, Cer, and So), is regulated (a) more frequently and (b) with greater amplitude than from molecules along the branches (e.g., SaP, DHGC, and DHSM). This observation is consistent with the current understanding that three of the initial enzymes of this pathway, i.e., SPT, (dihydro)ceramide synthase, and (dihydro)ceramide desaturase, are thought to be particularly important. Consequently and significantly, the improvement in simulated dynamics for these “core” molecules at the expense of other molecules at the branches underscores the value of using MRAC to reveal underlying pathway regulation.
In addition, comparing Cer, GC, and SM from 0–4 hours, feedback from Cer is also regulated more frequently. This observation is also consistent with other independent studies that identify ceramide as a key molecule involved in regulating de novo sphingolipid synthesis (Jenkins et al., 2002; Wells et al., 1998). At the same time, feedback from Sa, SaP do not change much throughout. This may also suggest that molecules immediate to the source of perturbation are located too close in the pathway to play as active a role in regulation than molecules further downstream. This presents an interesting hypothesis that may be tested, in future work, directly by moving the location of perturbation, e.g., by altering amounts of SM directly instead. Thus, more active feedback in terms of adaptation dynamics suggests a more prominent role in pathway regulation.
4.4. Limitations and future work
4.4.1. Nonlinear behaviors
The approach in this case study may be limited by a description of plant and reference dynamics using first-order linear ODEs alone. We may be able to improve this in future by including structured nonlinearities to account for possible nonlinear behaviors, e.g., by modifying plant, controller and adaptation dynamics as follows:
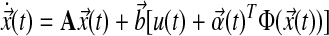 |
(1) |
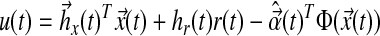 |
(2) |
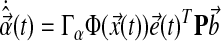 |
(3) |
where  is a set of structured nonlinear terms,
is a set of structured nonlinear terms,  is the true contribution of the nonlinear terms to the system dynamics, and
is the true contribution of the nonlinear terms to the system dynamics, and 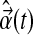 approximates the true contribution of these terms. At the same time, there are two particular challenges in doing so: (a) to avoid data overfitting in case too many nonlinear terms are included, and (b) to inform and justify the choice of some terms over others, e.g., polynomial versus logarithmic, based on a deeper understanding of sphingolipid dynamics in terms of biochemical kinetics. In addition, to complement such computational efforts, the experimental protocol need also be continually optimized to acquire data more frequently and for longer periods so as to try and address possible measurement and biological noise.
approximates the true contribution of these terms. At the same time, there are two particular challenges in doing so: (a) to avoid data overfitting in case too many nonlinear terms are included, and (b) to inform and justify the choice of some terms over others, e.g., polynomial versus logarithmic, based on a deeper understanding of sphingolipid dynamics in terms of biochemical kinetics. In addition, to complement such computational efforts, the experimental protocol need also be continually optimized to acquire data more frequently and for longer periods so as to try and address possible measurement and biological noise.
4.4.2. Molecular mechanisms
Explicit molecular mechanisms are not obvious from the results. In other words, the proposed MRAC approach to study metabolic pathway regulation does not shed light on how cells may implement the suggested feedback. For example, we do not speculate on how (a) treated cells determine that increased amounts of PalCoA available for de novo sphinoglipid synthesis perturbs the pathway system, (b) enzymes and metabolites involved communicate and coordinate their activity to achieve adaptive feedback, or (c) feedback is targeted at individual molecules. To address this issue in future, we may use confocal microscopy to locate enzymes and lipid metabolites conjugated with fluorescent dyes, or use x-ray crystallography on immobilized lipid membranes, to learn more about possible molecular mechanisms through co-localization.
5. Conclusion
The insights uncovered are consistent with existing knowledge of de novo sphingolipid synthesis and contributes directly to it. Specifically, results suggest that several underlying regulatory interactions may explain the observed data, i.e., changes in sphingolipid dynamics in response to increased palmitate levels facilitated by SPT over-expression. From literature, various other aspects of de novo sphingolipid synthesis have been studied, for instance, in terms of (a) sequence of synthesis steps, e.g., the introduction of fatty acids, double bonds and headgroups; (b) donor molecules, e.g., availability and utilization of different fatty acids; (c) regulation, e.g., the rate of production of sphinganine versus its partitioning into different downstream metabolites (Pewzner-Jung et al., 2006); and (d) response to perturbation, e.g., how heat induces ceramide production in yeast (Wells et al., 1998) and mammalian cells (Jenkins et al., 2002). To complement these studies, insights into potential underlying dynamics of pathway regulation from this case study may guide future research in sphingolipid biology by suggesting novel and interesting hypotheses that can be tested directly. Finally, in terms of impact on systems biology, we can also extend implementation routines designed for this study to other cases. Importantly, this combined theoretical and experimental case study demonstrates how models based on control theory may be applied to reverse engineer existing regulation in cellular networks from the perspective of autonomous control.
6. Methods
6.1. Quantifying sphingolipid isotopomers
Sphingolipids, i.e., sphingoid bases and (dihydro)N-acyl species, are extracted from samples of cultured human embryonic kidney (HEK) cells and quantified by liquid chromatography electrospray ionization tandem mass spectrometry (LC-ESI-MS/MS) as described previously (Merrill et al., 2005; Sullards et al., 2007). Measurements from four replicates are taken at hour intervals from 0 to 6 hours for a total of seven time points. To quantify sphingoid bases labeled with [U-13C]-palmitate, additional multiple reaction monitoring (MRM) pairs corresponding to [M + 16] precursor ions and [M + 16] product ions are used. To quantify (dihydro)N-acyl sphingolipids labeled with a single [U-13C]-palmitate, MRM pairs corresponding to [M + 16] precursor ions and both [M + 0] and [M + 16] product ions are used, providing discrimination of labeling on the sphingoid base and N-acyl moieties. These [M + 16] isotopomers are designated BASE and FA respectively. To quantify (dihydro)N-acyl sphingolipids labeled with two [U-13C]-palmitate molecules, MRM pairs corresponding to [M + 32] precursor ions and [M + 16] product ions are used; the [M + 32] isotopomers are designated DUAL. Unlabeled sphingolipids are designated 12C. The peak areas of unlabeled and labeled sphingolipid isotopomers are integrated, converted to picomoles using the peak area of the internal standard, and normalized to the mg of protein in the extracted sample.
6.2. De novo sphingolipid synthesis dynamics
The ten sphingolipids of interest in this case study are sphinganine (Sa), sphinganine phosphate (SaP), dihydroceramide (DHCer), dihydroglucosylceramide (DHGC), dihydrosphingomyelin (DHSM), ceramide (Cer), glucosylceramide (GC), sphingomyelin (SM), sphingosine (So), and sphingosine phosphate (SoP). The input to this system is extracellular palmitate that is converted to palmitoyl-CoA (PalCoA) inside the cells. We define the state space 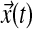 as the set of sphingolipid amounts where
as the set of sphingolipid amounts where
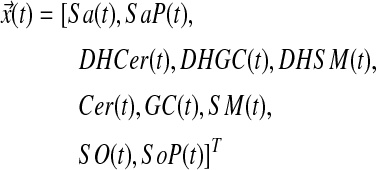 |
(4) |
and simplify the equations of motion, i.e., biochemical reactions, between these molecules as a linear system of ordinary differential equations (ODEs) using mass action kinetics (Gulberg and Waage, 1986; Lund, 1965):
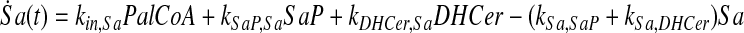 |
(5) |
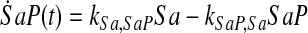 |
(6) |
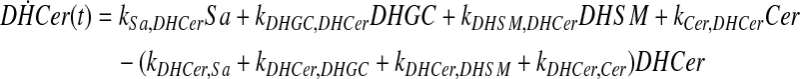 |
(7) |
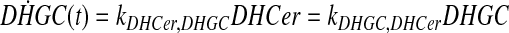 |
(8) |
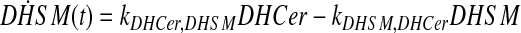 |
(9) |
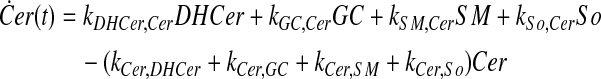 |
(10) |
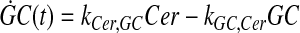 |
(11) |
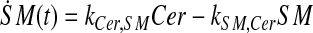 |
(12) |
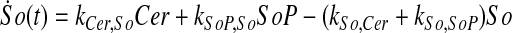 |
(13) |
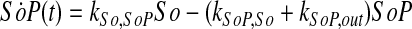 |
(14) |
where ka,b indicates the rate constant for the reaction going from a to b. Experimentally, extracellular palmitate is introduced to the cells in excess. Hence, in our model, we assume the amount of PalCoA as an input remains constant.
Here the reader might expect Michaelis-Menten kinetics (Voet and Voet, 2004) because enzymes play a critical role in de novo sphingolipid synthesis. However, while a small number of key enzymes have been identified and are of active interest in current research, there are many other enzymes in this pathway that are not well-studied whose effects remain difficult to observe and measure. In addition, the Michaelis-Menten algorithm also requires estimating significantly more parameters (Atkins and Ninmo, 1980; Currie, 1982), which detracts from the focus of this case study.
6.3. Estimating reaction rate constants
We designed a genetic algorithm to optimize a modified least-squares error between simulated sphingolipid amounts using ODEs and corresponding experimental data obtained from LC-ESI-MS/MS at discrete times. Reaction rate constants are estimated using only C-16 DUAL species data from both treated and wild-type cells. Additional information may be inferred from each of the labeled/unlabeled combinations of BASE, FA, or 12C species but is not used here so as to reduce complexity. Inputs to the estimation routine include the measured amounts of all sphingolipid species that are determined from four technical replicates. Furthermore, we use only five of seven data points, from 0 to 4 hours, as training data for estimation and leave the final two data points for initial verification.
6.4. Implementation
6.4.1. Symbolic expressions for MRAC
In a single-input direct MRAC system, the dynamics for the plant state 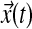 , i.e., treated cells, and reference state
, i.e., treated cells, and reference state 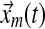 , i.e., wild-type cells, are:
, i.e., wild-type cells, are:
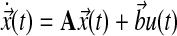 |
(15) |
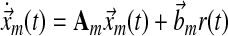 |
(16) |
where A, Am are matrices that contain corresponding rate constants ka,b based on the linear ODEs previously described for specific reactions; 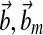 are actuation vectors associated with the plant and reference respectively; u(t) is the scalar controller, and r(t) is the scalar input. The controller u(t) utilizes full state feedback and input r(t):
are actuation vectors associated with the plant and reference respectively; u(t) is the scalar controller, and r(t) is the scalar input. The controller u(t) utilizes full state feedback and input r(t):
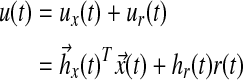 |
(17) |
where ux(t), ur(t) are components of the controller, and 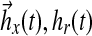 are gains, associated with state feedback and input respectively. Then it follows, by verifying the conditions for stability as described by Lyapunov (1992), that the dynamics of adaptation governed by these gains are:
are gains, associated with state feedback and input respectively. Then it follows, by verifying the conditions for stability as described by Lyapunov (1992), that the dynamics of adaptation governed by these gains are:
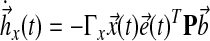 |
(18) |
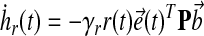 |
(19) |
where the error 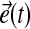 is defined by:
is defined by:
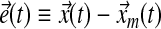 |
(20) |
and Γx, γr are adaptation parameters. Finally, P satisfies the Lyapunov equation:
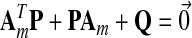 |
(21) |
where Am Hurwitz, P = PT positive definite symmetric and so is Q. In addition, the initial conditions 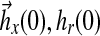 may be specified using the matching conditions:
may be specified using the matching conditions:
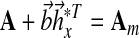 |
(22) |
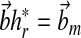 |
(23) |
by setting them to approximate constant ideal gains 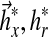 Figure 1a summarizes these symbolic expressions in context of the MRAC block diagram.
Figure 1a summarizes these symbolic expressions in context of the MRAC block diagram.
6.4.2. Verifying Lyapunov stability
First, the error and error dynamics are given by (from equation (20)):
 |
(24) |
where
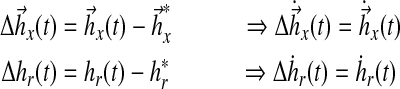 |
Then, we select the candidate Lyapunov function:
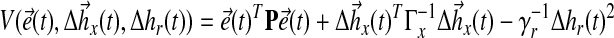 |
(25) |
and take the derivative with respect to time:
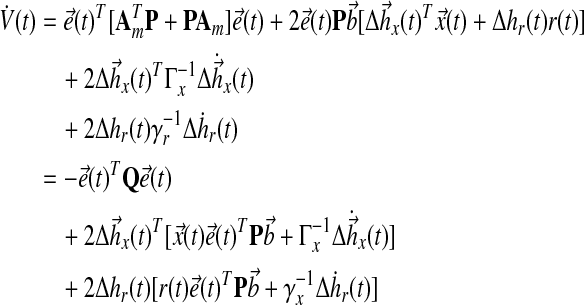 |
(26) |
Thus, the adaptation dynamics in equations (18), (19) ensure we have a negative semidefinite 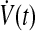 that guarantees uniform stability, i.e.,
that guarantees uniform stability, i.e.,
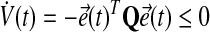 |
(27) |
6.4.3. Numerical details
We numerically integrate the system of ODEs in MATLAB using ode15s() to simulate the complete duration of experimental data acquisition, i.e., 0–6 hours. To do this, we implement the symbolic expressions with some modifications:
Specifically, we design the plant actuation  to supply ux(t), ur(t) separately and choose
to supply ux(t), ur(t) separately and choose  to achieve reasonable goodness-of-fit between simulation results and experimental data. Reaction rate constants ka,b are available (for Supplementary Material, see www.liebertonline.com/cmb). The matrix P is solved in MATLAB using lyap() given Am and Q. All other parameters are defined as follows:
to achieve reasonable goodness-of-fit between simulation results and experimental data. Reaction rate constants ka,b are available (for Supplementary Material, see www.liebertonline.com/cmb). The matrix P is solved in MATLAB using lyap() given Am and Q. All other parameters are defined as follows:
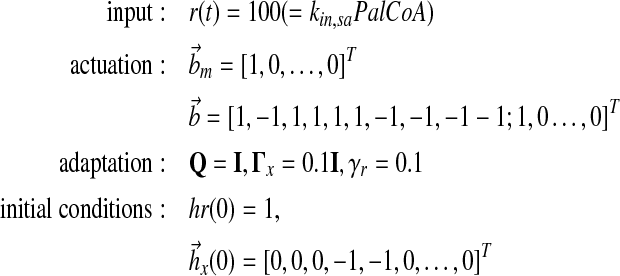 |
Supplementary Material
Acknowledgments
We thank the reviewers for their comments. We also thank Elaine Wang, Christopher Haynes, and Jeremy Allegood for data acquisition; and Neil Shah for programming. This work is supported by grants from the Lipid Metabolites and Pathways Strategy consortium (LIPIDMAPS GM069338), the Parker H. Petit Institute for Bioengineering and Bioscience, Johnson & Johnson, Bio Imaging Mass Spectrometry Initiative at Georgia Tech, National Institutes of Health (BRP R01CA108468, CCNE U54CA119338), Georgia Cancer Coalition (Distinguished Cancer Scholar Award to MDW), and Microsoft Research.
Disclosure Statement
No competing financial interests exist.
References
- Alon U. Surette M.G. Barkai N., et al. Robustness in bacterial chemotaxis. Nature. 1999;397:168–171. doi: 10.1038/16483. [DOI] [PubMed] [Google Scholar]
- Anderson B.D.O. Dehgani A. Challenges of adaptive control—past, permanent, and future. Annu. Rev. Control. 2008;32:123–135. [Google Scholar]
- Atkins G.L. Ninmo I.A. Review: current trends in the estimation of Michaelis-Menten parameters. Anal. Biochem. 1980;104:1–9. doi: 10.1016/0003-2697(80)90268-7. [DOI] [PubMed] [Google Scholar]
- Barkai N. Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- Behre J. Wilhelm T. von Kamp A., et al. Structural robustness of metabolic networks with respect to multiple knockouts. J. Theor. Bio. 2008;252:433–441. doi: 10.1016/j.jtbi.2007.09.043. [DOI] [PubMed] [Google Scholar]
- Bryson A.E., Jr Optimal control—1950 to 1985. IEEE Control Syst. Magazine. 1996;16:26–33. [Google Scholar]
- Csete M.E. Doyle J.C. Reverse engineering of biological complexity. Science. 2002;295:1664–1669. doi: 10.1126/science.1069981. [DOI] [PubMed] [Google Scholar]
- Currie D.J. Estimating Michaelis-Menten parameters: bias, variance and experimental design. Biometrics. 1982;38:907–919. [Google Scholar]
- El-Samad H. Kurata H. Doyle J.C., et al. Surviving heat shock: control strategies for robustness and performance. Proc. Natl. Acad. Sci. USA. 2005;102:2736–2741. doi: 10.1073/pnas.0403510102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahy E. Subramaniam S. Brown H.A., et al. A comprehensive classification system for lipids. J. Lipid Res. 2005;46:839–862. doi: 10.1194/jlr.E400004-JLR200. [DOI] [PubMed] [Google Scholar]
- Fell D. Metabolic control analysis: a survey of its theoretical and experimental development. Biochem. J. 1992;286:313–330. doi: 10.1042/bj2860313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forrester J.S. Milne S.B. Ivanova P.T., et al. Computational lipidomics: a multiplexed analysis of dynamic changes in membrane lipid composition during signal transduction. Mol. Pharmacol. 2004;65:813–821. doi: 10.1124/mol.65.4.813. [DOI] [PubMed] [Google Scholar]
- Fossas E. Ros R.M. Fabregat J. Sliding mode control in a bioreactor model. J. Math. Chem. 2001;30:203–218. [Google Scholar]
- Goodwin G.C. Hill D.J. Palaniswami M. A perspective on convergence of adaptive control algorithms. Automatica. 1984;20:519–531. [Google Scholar]
- Gulberg C.M. Waage P. Studies concerning affinity [Translated] J. Chem. Educ. 1986;63:1044–1047. [Google Scholar]
- Guzun R. Saks V. Application of the principles of systems biology and wiener's cybernetics for analysis of regulation of energy fluxes in muscle cells in vivo. Int. J. Mol. Sci. 2010;11:982–1019. doi: 10.3390/ijms11030982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn W. Theory and Application of Lyapunov's Direct Method. Prentice-Hall; Englewood Cliffs, NJ: 1963. [Google Scholar]
- Heinrich R. Rapoport T.A. A linear steady-state treatment of enzymatic chains. general properties, control and effector strength. Eur. J. Biochem. 1974;42:89–95. doi: 10.1111/j.1432-1033.1974.tb03318.x. [DOI] [PubMed] [Google Scholar]
- Jenkins G.M. Cowart L.A. Signorelli P., et al. Acute activation of de novo sphingolipid biosynthesis upon heat shock causes an accumulation of ceramide and subsequent dephosphorylation of sr proteins. J. Biol. Chem. 2002;277:42572–42578. doi: 10.1074/jbc.M207346200. [DOI] [PubMed] [Google Scholar]
- Kacher Y. Futerman A.H. Genetic diseases of sphingolipid metabolism: pathological mechanisms and therapeutic options. FEBS Lett. 2006;580:5510–5517. doi: 10.1016/j.febslet.2006.08.041. [DOI] [PubMed] [Google Scholar]
- Kacser H. Burns J.A. The control of flux. Sym. Soc. Exp. Biol. 1973;27:65–104. [PubMed] [Google Scholar]
- Kailath T. Linear Systems. Prentice-Hall; Eaglewood Cliffs, NJ: 1980. [Google Scholar]
- Kitano H. A robustness-based approach to systems-oriented drug design. Nat. Rev. Drug Dis. 2007a;6:202–210. doi: 10.1038/nrd2195. [DOI] [PubMed] [Google Scholar]
- Kitano H. Towards a theory of biological robustness. Mol. Syst. Bio. 2007b;3:137. doi: 10.1038/msb4100179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolter T. Sandhoff K. Sphingolipid metabolism diseases. Biochim. Biophys. Acta Biomembranes. 2006;1758:2057–2079. doi: 10.1016/j.bbamem.2006.05.027. [DOI] [PubMed] [Google Scholar]
- LaSalle J.P. Recent advances in liapunov stability theorem. SIAM Rev. 1964;6:1–11. [Google Scholar]
- Lauffenburger D.A. Cell signaling pathways as control modules: complexity for simplicity? Proc. Natl. Acad. Sci. USA. 2000;97:5031–5033. doi: 10.1073/pnas.97.10.5031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luenberger D.G. Introduction to Dynamic Systems: Theory, Models, & Applications. John Wiley & Sons, Inc.; New York: 1979. [Google Scholar]
- Lund E.W. Guldberg and waage and the law of mass action. J. Chem. Educ. 1965;65:548–550. [Google Scholar]
- Lyapunov A.M. In: General Problem of the Stability of Motion. Taylor & Francis Ltd.; London: 1992. [Google Scholar]
- Merrill A.H. De novo sphingolipid biosynthesis: a necessary, but dangerous, pathway. J. Biol. Chem. 2002;277:25843–25846. doi: 10.1074/jbc.R200009200. [DOI] [PubMed] [Google Scholar]
- Merrill A.H. Sullards M.C. Allegood J.C., et al. Sphingolipidomics: high-throughput, structure-specific, and quantitative analysis of sphingolipids by liquid chromatography tandem mass spectrometry. Methods. 2005;36:207–224. doi: 10.1016/j.ymeth.2005.01.009. [DOI] [PubMed] [Google Scholar]
- Merrill A.H. Wang M.D. Park M., et al. (Glyco)sphingolipidology: an amazing challenge and opportunity for systems biology. Trends Biochem. Sci. 2007;32:457–468. doi: 10.1016/j.tibs.2007.09.004. [DOI] [PubMed] [Google Scholar]
- Ogata K. System Dynamics. 3rd. Prentice-Hall, Inc.; Upper Saddle River, NJ: 1998. [Google Scholar]
- Ogretmen B. Hannun Y. A. Biologically active sphingolipids in cancer pathogenesis and treatment. Nat. Rev. Cancer. 2004;4:604–616. doi: 10.1038/nrc1411. [DOI] [PubMed] [Google Scholar]
- Osbourne P.V. Whitaker H.P. Kezer A. New developments in the design of model reference adaptive control systems. Instit. Aeronaut. Serv. 1961;61:39. [Google Scholar]
- Pewzner-Jung Y. Ben-Dor S. Futerman A.H. When do lasses (longevity assurance genes) become cers (ceramide synthases)? Insights into the regulation of ceramide synthesis. J. Biol. Chem. 2006;281:25001–25005. doi: 10.1074/jbc.R600010200. [DOI] [PubMed] [Google Scholar]
- Simpson M.A. Cross H. Proukakis C., et al. Infantileonset symptomatic epilepsy syndrome caused by a homozygous loss-of-function mutation of gm3 synthase. Nat. Genet. 2004;36:1225–1229. doi: 10.1038/ng1460. [DOI] [PubMed] [Google Scholar]
- Stelling J. Sauer U. Szallasi Z., et al. Robustness of cellular functions. Cell. 2004;118:675–685. doi: 10.1016/j.cell.2004.09.008. [DOI] [PubMed] [Google Scholar]
- Sullards M.C. Allegood J.C. Kelly S., et al. Structure-specific, quantitative methods for analysis of sphingolipids by liquid chromatography-tandem mass spectrometry: “inside-out” sphingolipidomics. Methods Enzymol. 2007;432:83–115. doi: 10.1016/S0076-6879(07)32004-1. [DOI] [PubMed] [Google Scholar]
- Sussman H.J. Willems J.C. 300 years of optimal control: from the brachystochrone to the maximum principle. IEEE Control Syst. Magazine. 1997;17:32–44. [Google Scholar]
- Tomlin C.J. Axelrod J.D. Understanding biology by reverse engineering the control. Proc. Nat. Acad. Sci. USA. 2005;102:4219–4220. doi: 10.1073/pnas.0500276102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Antwerp J.G. Braatz R.D. A tutorial on linear and bilinear matrix inequalities. J. Process Control. 2000;10:363–385. [Google Scholar]
- van Antwerp J.G. Braatz R.D. Sahinidis N.V. Globally optimal robust process control. J. Process Control. 1999;9:375–383. [Google Scholar]
- Vesper H. Schmelz E.-M. Nikolova-Karakashian M.N., et al. Sphingolipids in food and the emerging importance of sphingolipids to nutrition. J. Nutru. 1999;129:1239–1250. doi: 10.1093/jn/129.7.1239. [DOI] [PubMed] [Google Scholar]
- Voet D. Voet J.G. Biochemistry. 3rd. John Wiley & Sons, Inc.; New York: 2004. [Google Scholar]
- Wells G.B. Dickson R.C. Lester R.L. Heat-induced elevation of ceramide in Saccharomyces cerevisiae via de novo synthesis. J. Biol. Chem. 1998;273:7235–7243. doi: 10.1074/jbc.273.13.7235. [DOI] [PubMed] [Google Scholar]
- Whitaker H.P. An adaptive system for control of the dynamics performances of aircraft and spacecraft. Instit. Aeronaut. Serv. 1959;59:100. [Google Scholar]
- Wiener N. Cybernetics: or Control and Communication in the Animal and the Machine. 2nd. MIT Press; Cambridge, MA: 1965. [Google Scholar]
- Yi T.-M. Huang Y. Simon M.I., et al. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA. 2000;97:4649–4653. doi: 10.1073/pnas.97.9.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.