An integrated approach to characterize genetic interaction networks in yeast metabolism

Abstract

Intense experimental and theoretical efforts have been made to globally map genetic interactions, yet we still do not understand how gene-gene interactions arise from the operation of biomolecular networks. To bridge the gap between empirical and computational studies, we: i) quantitatively measure genetic interactions between ~185,000 metabolic gene pairs in Saccharomyces cerevisiae, ii) superpose the data on a detailed systems biology model of metabolism, and iii) introduce a machine-learning method to reconcile empirical interaction data with model predictions. We systematically investigate the relative impacts of functional modularity and metabolic flux coupling on the distribution of negative and positive genetic interactions. We also provide a mechanistic explanation for the link between the degree of genetic interaction, pleiotropy, and gene dispensability. Last, we demonstrate the feasibility of automated metabolic model refinement by correcting misannotations in NAD biosynthesis and confirming them by in vivo experiments.

Recent large-scale genetic analyses of yeast have enabled the systematic screening of pairwise genetic interactions and provided valuable insights into the functional organisation of a eukaryotic cell¹ as well as genetic networks underlying specific biological processes^2,3. Despite the rapid growth in quantitative data on genetic interactions, we still have only a limited understanding of the molecular mechanisms through which one mutation modifies the phenotypic effect of another. Furthermore, while the general properties of genetic interaction networks have been explored phenomenologically^1,4, we often lack a mechanistic understanding of these patterns. For example, a recent large-scale study reported that single mutants with severe fitness defects tend to exhibit numerous genetic interactions¹, a phenomenon that still awaits explanation. Finally, the systematic generation of novel biological hypotheses from the welter of phenotypic data produced by interaction screens remains a major challenge. By examining how cellular phenotypes arise from the operation of molecular networks, systems biology offers great promise for meeting these challenges.

Metabolism is one of the best-characterized cellular subsystems and is especially suited for system-level studies of the genotype–phenotype relationship, and hence genetic interactions. First, high-quality metabolic network reconstructions are available that specify the chemical reactions catalysed by hundreds of enzymes and cover the molecular function for a significant fraction of the genome (e.g. 15% in yeast)⁵. Second, these reconstructions can be converted into computational models to calculate the phenotype of both wild-type and mutant cells using constraint-based analysis tools⁶, such as flux balance analysis (FBA). This imposes mass balance and capacity constraints to define the space of feasible steady-state flux distributions of the network and then identifies optimal network states that maximise biomass yield, a proxy for growth. Despite its simplicity and low data requirements, this modelling framework has shown great predictive power and has been successfully applied to various research problems⁷, including predicting the viability of single-gene deletants⁸ and model-driven analysis of high-throughput data^8-10. Although some properties of genetic interaction networks have also been addressed using FBA, these earlier studies were exclusively^11,12 or mainly^13,14 theoretical due to the lack of large-scale genetic interaction data for metabolic genes.

To bridge the gap between theory and experiment, we have systematically measured genetic interactions between pairs of metabolic genes in yeast and combined these data with a detailed metabolic network reconstruction. Quantitative measurement of the fitness of single and double mutants has enabled us to detect both negative (aggravating) and positive (alleviating) interactions (i.e. the double mutant has a lower or higher fitness, respectively, than would be expected from the product of the single-mutant fitnesses). Our integrated approach has three major goals. First, we investigate the distribution of genetic interactions within and across functional modules as defined by classical annotation groups and network-based mathematical methods. Second, we perform constraint-based analysis of the network to simulate mutational effects and predict interactions in silico. We then employ our in vivo interaction data to test the model's ability to capture the general properties of genetic interaction networks and to assess the validity of its specific predictions. Third, we automate the reconciliation of empirical interaction data with model predictions and use discrepancies to update the metabolic network and direct biological discovery.

Results

Constructing a genetic interaction map of yeast metabolism

We selected genes for our genetic interaction map based on an updated reconstruction of the S. cerevisiae metabolic network, which consists of 1412 reactions and accounts for 904 genes¹⁰. Genetic interaction data has been generated by large-scale synthetic genetic array (SGA) technology¹⁵. First, we performed new screens to construct a map that covers all major metabolic subsystems, except for tRNA aminoacylation. The screens involved constructing of high-density arrays of double mutants by crossing 613 query mutants, including 78 hypomorphic alleles of essential genes, against an array of 470 null mutants, producing double mutants for 184,624 unique gene pairs. The fitness of single and double mutants was assessed quantitatively by measuring colony size¹⁶. Interaction scores (ε) were calculated based on the deviation of the double-mutant fitness (f₁₂) from the product of the corresponding single-mutant fitnesses (ε = f₁₂ – f₁·f₂)¹⁷. Second, we supplemented our measurements with data from our recent large-scale genetic interaction screen¹, which employed the same experimental procedure as the present study, but represented genes in all functional categories, including metabolism.

Overall, our combined dataset covers more than 80% of metabolic network genes, including 82 essential genes, and provides interaction scores for 215,907 pairs, 57% of which have been independently screened more than once. Applying a previously defined confidence threshold that proved informative in functional analyses¹, we detected 3,572 negative and 1,901 positive interactions (Online Methods). We have focussed on interactions between null mutations of non-essential genes (176,821 pairs) due to their better coverage and easier interpretation; data on essential genes has only been employed for specific analyses. Additionally, we also defined a high-confidence interaction set based on the reproducibility of replicate experiments and employed it when very low false-positive rates were required.

Genetic interactions are widespread between different functional modules

We took advantage of our quantitative genetic interaction map to empirically test earlier predictions about the distribution of interactions within and between metabolic functional modules. Specifically, a computational study based on FBA suggested that: i) genetic interactions are enriched within metabolic annotation groups, and ii) interactions between different functional groups tend to be either exclusively negative or exclusively positive, a property termed ‘monochromaticity’¹¹.

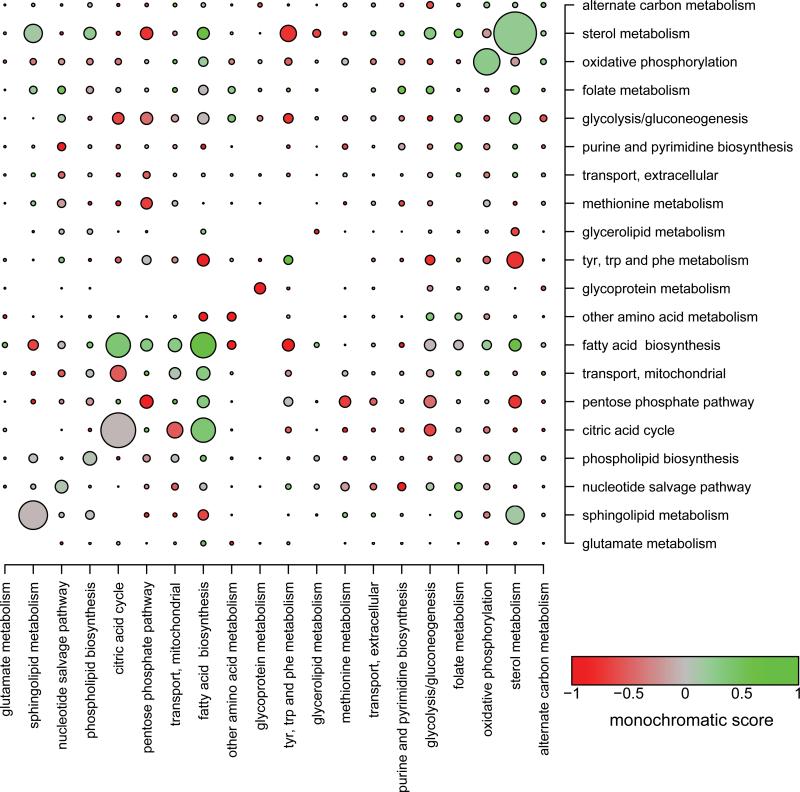
First, we report a modest, but significant, enrichment of both negative (1.6-fold) and positive (2.5-fold) interactions within classically defined functional modules. For example, lipid metabolism is especially enriched in genetic interactions, with sterol metabolism and fatty acid biosynthesis being primarily enriched in positive interactions, while both forms of interactions are overrepresented in sphingolipid metabolism (Fig. 1). Importantly, the enrichments remain after controlling for potential confounding variables, such as paralogy¹⁸, physical interaction³, or single-mutant fitness¹ (Online Methods) and become more pronounced when using the high-confidence interaction set (3.8-fold and 8.7-fold enrichment of negative and positive interactions, respectively). However, as Figure 1 demonstrates, the majority of genetic interactions occur between genes assigned to different metabolic functions (93% of negative and 90% of positive, or 86% and 73%, respectively, when using high-confidence interactions). The fact that even strongly enriched functional groups, such as fatty acid biosynthesis, exhibit numerous interactions with other groups indicates widespread pleiotropy across metabolic subsystems.

Figure 1.

Distribution and monochromaticity of genetic interactions between functional groups. The radii of the circles represent the fraction of screened gene pairs that show genetic interaction within and between functional annotation groups (e.g. sterol metabolism has the highest prevalence of interactions with a value of 0.225). Enrichment of genetic interactions within functional groups is visually apparent and corresponds to larger circles on the diagonal. The colors of the circles reflect the monochromatic score defined as the normalized ratio of positive to all interacting pairs (see Online Methods). Functional groups displaying only positive genetic interactions between each other have a monochromatic score of +1 (green), while those interacting purely negatively have a score of -1 (red). The background ratio of positive to all interactions (0.348) corresponds to a score of 0 (grey). Only the top 20 functional groups with the largest number of screened gene pairs and those genes assigned to only one functional group are included in the plot.

Next, we asked whether interactions between different functional groups tend to be either exclusively negative or positive. In agreement with theoretical predictions, we found a statistically significant excess of monochromaticity among pairs of functional groups in the real data compared to randomized interaction maps (P<10^-4). For example, while sterol metabolism displays almost purely negative interactions with tyrosine, tryptophan, and phenylalanine metabolism, it predominantly interacts positively with fatty acid biosynthesis (Fig. 1). Nevertheless, monochromaticity in our genetic interaction map is modest, only ~24−34% more monochromatic pairs were found than expected by chance, a conclusion that remained qualitatively the same when using high-confidence interactions (Supplementary Table 1).

As an alternative to functional groups defined based on classical biochemical pathways, unbiased mathematical methods have been developed to measure functional relatedness based on coherent usage of reactions in the metabolic network^6,19. In particular, flux coupling²⁰ provides a biochemically sound definition of functional relatedness and has strong physiological and evolutionary significance^21-23. To further investigate the distribution of genetic interactions within and between functional modules, we identified flux-coupled gene pairs computationally (i.e. pairs of reactions where the activity of one reaction implies the activity of the other, either reciprocally or in one direction; Online Methods). In agreement with results obtained using annotation groups, while we find that both negative (2-fold) and positive (2.7-fold) interactions are enriched in flux-coupled pairs (P<10^-6 and P<10^-8, respectively), the overwhelming majority (>97%) of both forms of interactions occur between uncoupled genes, even when only high-confidence interactions are investigated (>93%).

In conclusion, both definitions of functional relatedness reveal that most genetic interactions connect across distinct functional modules, extending an earlier estimate that synthetic lethal interactions are 3.5 times more likely to span pairs of protein-protein interaction pathways than to occur within such pathways²⁴. Furthermore, our finding that both negative and positive interactions tend to occur between metabolic modules is consistent with recent observations that both forms of interactions primarily connect genes belonging to different protein complexes^1,16.

A metabolic model elucidates the degree distribution of genetic interaction networks

To further explore the organizational principles of the genetic interaction network, we next investigated its degree distribution using a computational model of metabolism. A prominent attribute of genetic interaction networks, also shared by other biological networks²⁵, is that the majority of genes display few interactions, while a minority of “hub” genes are highly connected^1,4. Furthermore, a recent study uncovered a strong correlation between the number of genetic interactions a gene exhibits and the fitness defect associated with its deletion (dispensability)¹, a pattern also confirmed by our empirical metabolic interaction map (Supplementary Fig. 1). Nevertheless, the tendency of ‘sick’ single mutants to engage in an especially high number of both negative and positive interactions remains unexplained. Intuitively, one expects that a strongly deleterious single mutation can mask a large number of mildly deleterious mutations in other genes, and hence display numerous positive interactions. However, a similar logic would imply a paucity of negative interactions for sick mutants (i.e. a sick deletant is less likely to be made worse by other mutations), an expectation that is inconsistent with observations¹.

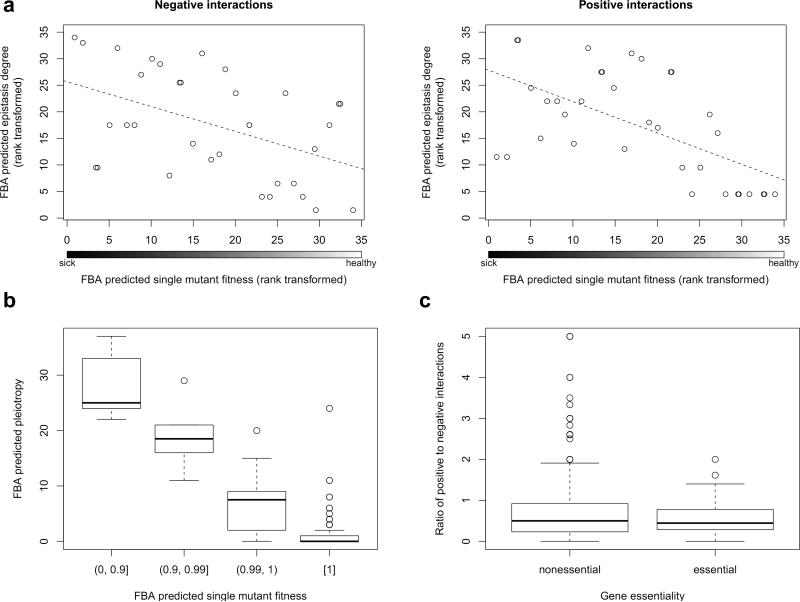
To probe whether a simple structural model of metabolism is able to capture the above properties of genetic interaction networks, we computed in silico interaction degrees and single-mutant fitness employing FBA. Similar to the empirical data, in silico genetic interaction degree is also unevenly distributed, with only ~12% of genes accounting for the majority (~85%) of interactions. Most remarkably, the model predicted a strong negative correlation between single-mutant fitness and genetic interaction degree for both positive and negative interactions, confirming the trend observed in the experimentally-derived genetic interaction network (Spearman's ρ= -0.89 and ρ= -0.66, respectively). Importantly, these trends remained when genes without any in silico fitness contribution were excluded from the analysis (ρ= -0.59, P<10^-3 for positive; ρ= -0.47, P=0.005 for negative interactions, Fig. 2a), demonstrating that the associations are not simply due to the presence of silent reactions in the metabolic model.

Figure 2.

Degree distribution of genetic interaction networks and gene dispensability. (a) Both negative and positive genetic interaction degrees predicted by FBA show negative correlations with predicted single-mutant fitness. Only genes exhibiting non-zero in silico fitness defects are shown and variables are rank transformed. See Online Methods for details on selecting independent data points (genes) for the statistical analysis. To improve the visual representation of coincident data points, we added a small amount of noise over the x-axis for plotting. (b) The FBA-predicted single-gene deletion effect is strongly associated with predicted system-level pleiotropy degree (i.e. the number of biosynthetic processes to which a gene contributes). See Online Methods for details on the gene selection procedure. (c) Comparison of the empirically determined positive to negative genetic interaction ratio between null mutants of non-essential genes and hypomorphic alleles of essential genes reveals no significant difference. Horizontal lines of the boxplots correspond to the medians, the bottoms and tops of the boxes show the 25^th and 75^th percentiles, respectively. Whiskers show either the maximum (minimum) value or 1.5 times the interquartile range of the data, whichever is smaller (higher). Points more than 1.5 times the interquartile range above the third quartile or below the first quartile are plotted individually as outliers.

Having established its ability to capture the high genetic interaction connectivity of sick mutants, we asked the metabolic model to provide mechanistic explanations. One reason why a gene might exhibit numerous genetic interactions is that it contributes to multiple biological processes (i.e. it is highly pleiotropic), hence the phenotypic effect of its deletion may be modulated by a large number of other genes, each of them negatively or positively affecting a different aspect of its functionality. Indeed, it has been reported that genetic interaction hubs often display multifunctionality¹. If highly pleiotropic genes also have (on average) a large fitness contribution, then we would expect a negative correlation between single-mutant fitness and interaction degree. Although pleiotropy is difficult to define empirically, the FBA framework offers a rigorous approach to compute pleiotropy and test this idea. To do this, we determined the number of key metabolites (so-called biomass components, including amino acids, nucleotides, etc.) whose maximal production is affected by the absence of each gene (see Online Methods and ref. ²⁶). In accordance with our hypothesis, we found a strong association between the number of biosynthetic processes to which a gene contributes and the predicted fitness of its deletant (ρ=-0.83, P<10^-9 on raw data for genes with a non-zero deletion effect, see also Fig. 2b). Moreover, pleiotropy correlates with both in silico and in vivo genetic interaction degrees (negative degree: ρ=0.55 and ρ=0.24; positive degree: ρ=0.62 and ρ=0.25, respectively; P<10^-8 in all cases). Given the close association between computationally derived single-mutant fitness and pleiotropy, we next performed partial correlation analyses to disentangle the effects of these factors on in silico interaction degrees. Our multivariate analyses revealed that, while positive interaction degree is determined by single-mutant fitness (a finding consistent with the idea that severe mutations can mask numerous milder mutations), negative interaction degree is driven by pleiotropy (Supplementary Table 2).

Taken together, these computational results suggest that the structure of the metabolic network dictates both the fitness contribution (and hence positive interaction degree) and the functional pleiotropy (and hence negative interaction degree) of genes. Future empirical studies of pleiotropy will help to clarify whether these mechanisms also adequately explain in vivo genetic interaction degrees.

No empirical evidence for prevalent positive interactions in essential genes

A recent FBA study suggested that non-lethal mutations in essential metabolic genes exhibit strikingly different interaction patterns compared to null mutations of non-essential genes¹⁴. Specifically, it was predicted that essential metabolic genes frequently display positive interactions with other metabolic genes, regardless of their function or the latter's essentiality, strongly skewing the ratio of positive to negative interactions. While a small-scale empirical analysis was consistent with this prediction¹⁴, it remained to be seen whether it was supported by large-scale experiments. Accordingly, we mapped genetic interactions between hypomorphic alleles² of a set of essential genes and null mutants of non-essential genes, screening 39,086 pairs. If positive interactions were indeed highly abundant between gene pairs involving an essential reaction, then we should observe a strong bias toward positive interactions for essential genes. Although we found that essential genes have an increased number of positive interactions, they also display more negative interactions, therefore their ratio of positive to negative interactions is virtually identical to those of non-essential genes (Wilcoxon test: P=0.89, Fig. 2c). In sum, we failed to find empirical evidence for the predicted high prevalence of positive genetic interactions for essential metabolic genes. Given that the only experimental study reporting abundant positive interactions investigated only a handful of non-metabolic essential genes¹⁴, we speculate that the discrepancy between the small-scale study¹⁴ and our results could partly be due to sampling bias in the former.

Fine-scale evaluation of predicted genetic interactions

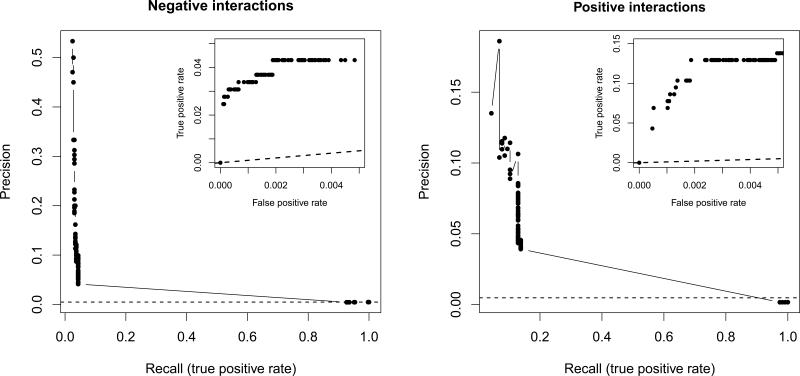
Our comprehensive genetic interaction map provides an unprecedented opportunity to assess the FBA framework's ability to predict individual interactions. To rigorously estimate the fraction of true predicted interactions (precision) and the fraction of experimentally observed interactions that are captured by the model (recall or true-positive rate), we selected a set of high-confidence empirical interactions between non-essential genes (Online Methods) and excluded genes that are associated with poorly characterized network parts (i.e. blocked reactions²⁰). This resulted in 325 negative and 116 positive interactions among 67,517 non-essential gene pairs. We found that experimentally identified interactions are highly over-represented among predicted strong interactions, with up to 100-fold and 60-fold enrichment for negative and positive interactions, respectively (i.e. precision values of 50% and 11%, respectively, see Fig. 3). Although this confirms that the highest predicted interaction scores have high physiological relevance¹³, we find that only a minority of empirical interactions are captured by the model at the same cut-off points (recall values are 2.8% and 12.9% for negative and positive interactions, respectively), a conclusion that remained unchanged when an alternative algorithm²⁷, an alternative interaction score¹¹, or a less compartmentalized metabolic model²⁸ was employed to compute interactions (Supplementary Figures 2a-c). Importantly, only a minority of gene pairs that show negative (7.6%) or positive (3%) interactions in vivo display non-zero interaction scores of the opposite sign in silico, indicating that the low recall of the model stems from missed genetic interactions, not from misclassification of the two forms of interactions.

Figure 3.

Comparison of computationally predicted and empirically determined genetic interactions. Prediction accuracy evaluated by visualizing the trade-off between precision (fraction of predicted interactions that are supported by empirical data) and recall (fraction of empirical interactions that are successfully identified by the model), and true-positive and false-positive rates (partial ROC curves, inset) at different in silico genetic interaction score cut-offs. Dashed lines represent the levels of discrimination expected by chance. Note the different scale of the y-axes for negative and positive interactions.

Why are so many genetic interactions missed by the model? First, as single-mutant fitness predictions are far from perfect^8,10, one might expect that interaction between two non-essential genes could be missed simply because one or the other gene is essential in the model. Indeed, ~24% of negative and ~22% of positive interactions are missed due to misprediction of single-mutant viability. Although the true-positive rate of genetic interaction predictions slightly improves when genes falsely predicted to be essential are excluded, the majority of empirical interactions are still not captured by the model. In particular, FBA predicts strong negative interaction scores for only 3.7% of in vivo negative interactions, indicating that it over-predicts double mutant fitness in the majority of these gene pairs. Second, weak in vivo genetic interactions might be inherently less reproducible by the metabolic model. While this idea is supported by an improved true-positive rate for strong in vivo interactions (~17% for ε ≤ -0.5 and 25% for ε ≥ 0.15), we conclude that even the strongest interactions are frequently missed by the model. Third, FBA predicts optimal metabolic behaviour without incorporating regulatory mechanisms. Consequently, reactions that are down-regulated in vivo could nevertheless compensate deletions in other parts of the network in silico, therefore the model likely underestimates mutational effects. To address this possibility, we used published quantitative transcriptome data²⁹ to identify non-expressed metabolic genes and constrained the corresponding reaction activities to zero in the simulations³⁰. Imposing transcriptional constraints did not noticeably improve predictions (Supplementary Fig. 2d), suggesting that detailed information on other layers of regulation³¹ (e.g. metabolic regulation³²), data on toxic intermediates and more sophisticated modelling frameworks (e.g. regulatory FBA³³) are needed to probe the performance limits of genome-scale models. Finally, aside from the limitations of FBA, some false predictions likely indicate incomplete knowledge or annotation errors in the metabolic network.

Numerous statistical methods have been proposed to predict genetic interactions by combining heterogeneous sources of genomic and functional data (e.g. sequence homology, physical interaction, co-expression, etc.)^34,35. These statistical approaches serve complementary roles to FBA. While biochemical modelling has the advantage of easy interpretability and offers direct mechanistic insights, statistical models may illuminate the amount of information available in large-scale datasets to predict genetic interactions. Thus, we asked whether such methods may substantially improve our knowledge on genetic interactions in the metabolic network.

To assess the performance of statistical modelling, we first compiled a dataset of gene-pair characteristics (following earlier studies^34,35 and based on metabolic network features, but omitting any information on genetic interactions; see Supplementary Note). and employed data-mining methods (random forest³⁶ and logistic regression) to classify genetic interactions based on these features. Although an increased fraction of in vivo interactions can be retrieved, ~70% of negative and ~75% of positive interactions are still predicted with very low (<10%) precision (Supplementary Fig. 3). Thus, we conclude that the majority of genetic interactions are not well understood either in terms of biochemical processes or statistical associations. Importantly, incorporating FBA-derived fitness and genetic interaction scores into statistical models boosts the precision of negative interaction predictions (Supplementary Fig. 3), indicating that biochemical modelling provides unique information that is not captured by purely statistical data integration.

Automated model refinement using genetic interaction data

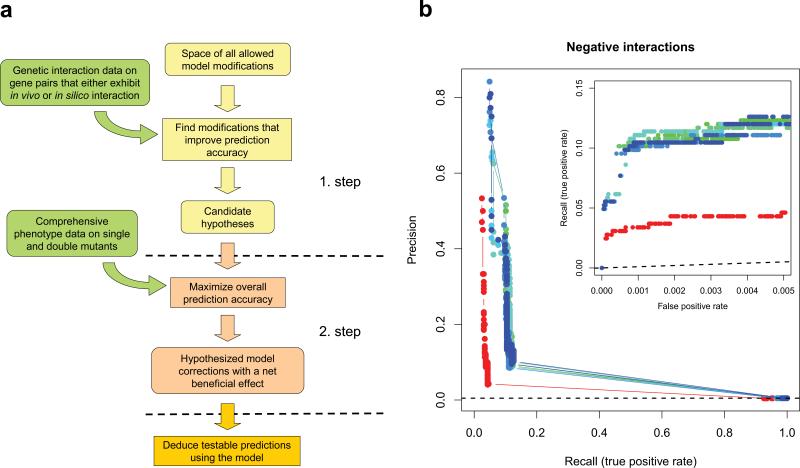
To reconcile discrepancies between empirical and computational genetic interaction maps, we developed a machine-learning method that automatically generates hypotheses to explain in vivo compensation (negative interaction) between genes. In contrast to a previously proposed approach³⁷ that reconciled experimental and computational growth data mutant by mutant, we sought to minimize model mispredictions globally (i.e. using all available data) by employing a two-stage genetic algorithm (Fig. 4a and Supplementary Note). The following types of changes to the model were allowed³⁷: i) modifying reaction reversibility, ii) removing reactions, and iii) altering the list of biomass compounds required for growth (Supplementary Note).

Figure 4.

Automated model refinement procedure. (a) Workflow of the two-stage model refinement method. In the first stage, a coarse-grained search is executed where candidate models are evaluated only for those gene pairs that display interaction either in vivo or in silico, according to the original model. In the second stage, the best models are refined in a restricted search space that is based on the results of the first stage, but now using all available data to evaluate the models. This two-stage approach made it feasible to explore a large space of candidate hypotheses while also making use of all available phenotypic data. (b) Results of 8 independent runs of the model refinement algorithm. Fits of the modified (blue – green) and unmodified original (red) models to our empirical genetic interaction data are visualized by both precision-recall and partial ROC curves (inset). Dashed lines represent the levels of discrimination expected by chance. Note that the same empirical dataset was used for both model refinement and model evaluation, i.e. no unseen test data was used to generate these plots. For a cross-validation estimate of model improvement see main text and Supplementary Note.

Our automated method suggested several modifications (Supplementary Table 3) that, together, considerably improved the fit of the model to our genetic interaction map (100 – 267% increase in recall and 44 – 59% increase in precision, Fig. 4b). Importantly, cross-validation confirmed that our method also significantly improves the model's ability to predict genetic interactions that were not used in model refinement (with recall increased by ~87% on average, P<0.002; Supplementary Note).

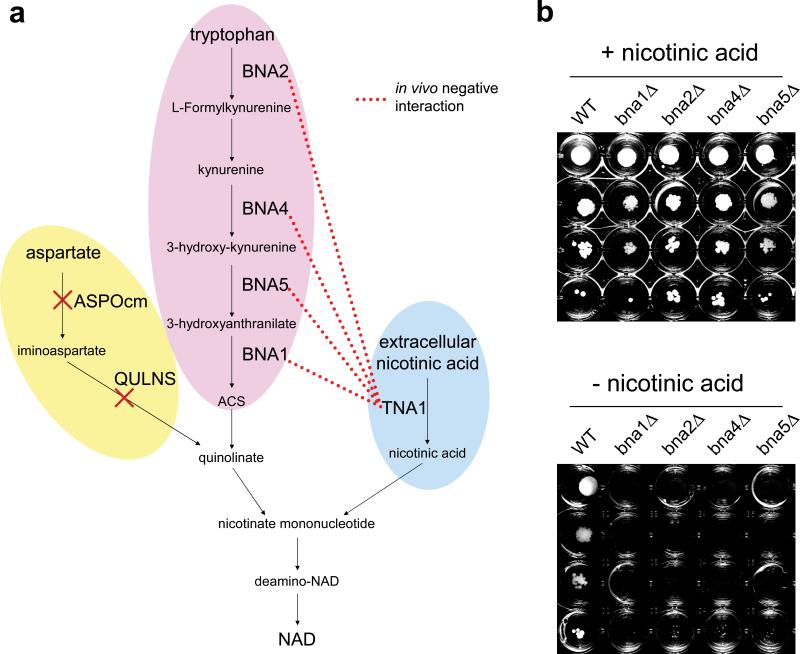
As an example of a modification suggested by our method, it showed that omitting glycogen from the set of essential biomass components corrects two falsely-predicted genetic interactions. This is congruent with glycogen's role as a reserve carbohydrate, which becomes important in nutrient-depleted or stress conditions³⁸. Remarkably, our algorithm also revealed that removal of only one or two reactions from the network corrects the prediction of 4 negative interactions between alternative NAD biosynthesis pathways. In particular, the published network reconstruction¹⁰ contains three biosynthetic routes for NAD, and removing the two-step path from aspartate to quinolinate uncovers pairwise compensation between the other two pathways (Fig. 5a). Importantly, while de novo NAD synthesis from aspartate is present in E. coli³⁹, it has no genes annotated in the yeast network and bioinformatics analyses failed to find yeast homologs of the E. coli enzymes (Supplementary Note). To further investigate whether quinolinate formation from aspartate might be wrongly included in the yeast reconstruction, we interrogated the metabolic model to deduce specific predictions for experimental testing. We found that only the refined model predicts the essentiality of genes in the kynurenine pathway (BNA1, BNA2, BNA4, and BNA5) when nicotinic acid is absent from the medium. Next, we tested these predictions experimentally and confirmed that deletants of all four genes were nicotinic acid auxotrophs (Fig. 5b). Together, these results strongly suggest that the aspartate to NAD pathway is not present in yeast⁴⁰.

Figure 5.

Automated model refinement suggests modifications in NAD biosynthesis. (a) Biosynthetic routes to nicotinate mononucleotide in the yeast metabolic network reconstruction. Genes involved in the de novo pathway from tryptophan show negative genetic interactions with the nicotinic acid transporter gene in vivo, but not in silico due to the presence of a two-step biosynthetic route from aspartate to quinolinate in the reconstruction (ASPOcm, aspartate oxidase; QULNS, quinolinate synthase). (b) Experimental verification of suggested model modifications. Deletion of genes for kynurenine pathway enzymes causes nicotinic acid auxotrophy. Strains deleted for the genes of the kynurenine pathway (bna1Δ bna2Δ bna4Δ, and bna5Δ) along with wild type (WT) were spotted in four serial dilutions on solid SC-His/Arg/Lys medium and incubated at 30 °C for 48 hours in the presence and absence of nicotinic acid as indicated. To prevent diffusion of any substances that would complement nicotinic acid auxotrophy, the strains were grown separately from each other in a 24-well plate. Repeating the experiment using liquid media confirmed the nicotinic acid auxotrophy of the mutants (data not shown). Yeast strains used in the auxotrophy study are derivatives of the BY4741 yeast deletion collection^47,48.

Our automated procedure identified additional erroneous predictions between NAD pathway genes and suggested further modifications (Supplementary Table 3), prompting us to thoroughly revise NAD biosynthesis in the published reconstruction. Based on inspection of interaction data, single-mutant phenotypes, and literature information, we propose a number of changes including modifications of gene-reaction associations and reaction reversibilities (Supplementary Fig. 4). The revised model is not only consistent with literature data, but also improves both interaction (12 corrections) and gene essentiality (1 correction) predictions.

Discussion

A system-level understanding of genetic interactions requires the integration of experimental and theoretical approaches. To progress towards this goal, we experimentally mapped interactions in yeast metabolism and systematically compared empirical data with predictions from a biochemical model. Our approach provides the first glimpse of genetic interactions in small-molecule metabolism and establishes the performance limits of a genome-scale metabolic model. We revealed that a simple structural model of metabolism captures several organizational properties of genetic interaction networks and suggests mechanistic hypotheses.

Importantly, the computational model sheds new light on the relationship between the severity of mutational effects and genetic interactions. The FBA model not only captures the hitherto unexplained relationship between fitness effect and genetic interaction degree, but also suggests a novel mechanistic link between negative interaction degree and functional pleiotropy: the effect of mutations in pleiotropic genes may be modulated by mutations in a large number of other genes, each of them compensating a different aspect of the first gene's functionality.

Although we reported a coarse-grained consistency between model predictions and experiments, evaluation of individual interaction predictions revealed abundant discrepancies. In particular, FBA fails to capture the majority of experimentally determined genetic interactions, an attribute shared with statistical models built via data integration. Furthermore, interaction patterns of hypomorphic alleles of essential genes are grossly mispredicted, resulting in a discrepancy between our empirical data and a previous theoretical expectation about the high prevalence of positive interactions¹⁴.

We can draw several conclusions from these inconsistencies. First, the quality and completeness of the metabolic reconstruction should be improved. Second, while null mutations can easily be represented in the FBA framework, simulation of hypomorphic alleles is inherently problematic as it hinges on assumptions about the relationship of enzyme activity to flux⁴¹. Third, the fact that a large number of in vivo instances of genetic interactions are not explained by the structure of the metabolic network suggests that regulation at both the gene expression and metabolite-enzyme levels should be taken into account in future attempts to realistically model metabolic behavior in genetically perturbed cells⁴².

Most significantly, the comprehensive interaction map can be used to refine the metabolic model. Indeed, reconciling discrepancies between predicted and observed phenotypes is of central importance in developing systems biology models^43,44. We demonstrated the feasibility of an automated method to refine the metabolic model. We anticipate that similar approaches, coupled with high-throughput experimentation, have the potential to close the iterative cycles of generating and testing novel hypotheses, leading to at least partial automation of biological discoveries^45,46.

Online Methods

Experimental mapping of genetic interactions

We employed synthetic genetic array (SGA) methodology, an automated form of genetic analysis, to construct high-density arrays of double mutants (for details, see Refs.^4,15). Quantitative assessment of genetic interactions requires measurements of single- and double-mutant fitness, and an estimate of the double-mutant fitness that would be expected based on the single-mutant phenotypes. Mutant fitnesses were derived from colony sizes after correcting systematic experimental biases (including positional effects, spatial effects, nutrient competition and screen batch effects)¹⁶. Single-mutant fitness was estimated using a set of control SGA screens, where the queries carried a mutation in a neutral genomic locus¹. Double-mutant fitness was estimated by employing the regular SGA protocol. We used the obtained single- (f_i and f_j) and double-mutant fitnesses (f_ij) to derive genetic interaction measures as ε = f_ij – f_i·f_j. A statistical confidence measure (P-value) was assigned to each interaction based on a combination of the observed variation of each double mutant across four experimental replicates and estimates of the background log-normal error distributions for the corresponding query and array mutants^1,16.

To explore the general properties of the metabolic genetic interaction map, we applied a previously suggested¹ confidence threshold of |ε|>0.08 and P<0.05 to define significantly interacting gene pairs. This threshold has been previously shown¹ to yield a good balance between coverage and precision and defines genetic interactions that cover at least ~35% of negative and ~18% of positive interactions deposited in BioGrid⁴⁹ with estimated precisions of ~63% and ~59%, respectively. In the case of replicate screens (e.g. both AB and BA pairs were screened), we applied the following procedure: if replicate screens show opposite interaction signs and at least one of them is significant, both pairs were removed; if they show the same interaction sign (both positive or both negative), the interaction with the lowest P-value was retained and both pairs are reported with that interaction. Comparison of interactions from screens performed in the present study with those from a full-genome study¹ revealed a good correlation (r=0.76) between interaction scores that were identified as significant by both studies. The high cross-study correlation allowed us to merge interaction data from the present study with interaction data on metabolic gene pairs from the genome-scale screens¹.

Additionally, we also defined a smaller high-confidence dataset in which all gene pairs were independently screened at least twice to minimize false interactions. Here, two genes are considered as interacting if at least one screen shows |ε|>0.08 and P<0.05, and another screen shows P<0.05 of the same interaction sign, whereas non-interacting pairs are defined as those not showing |ε|>0.08 and P<0.05 in any of the screens. Any other gene pairs were removed from the high-confidence set. This resulted in 529 negative and 194 positive interactions between 122,875 gene pairs.

Interaction data can be down loaded from http://www.utoronto.ca/boonelab/data/szappanos/.

Analysis of the effect of functional relatedness, paralogy and protein-protein interactions on genetic interactions

We used logistic regression analysis to test the association between genetic interaction and various categorical and continuous features (e.g. paralogy, co-functionality, single mutant fitness etc.). Functional annotation groups were as defined in the published metabolic reconstruction¹⁰ and information on physical interactions between proteins was extracted from the BioGrid 2.0.58 database⁴⁹. Paralog gene pairs were identified by performing all-against-all BLASTP similarity searches⁵⁰ of yeast ORFs. We defined two genes as paralogs if: i) the BLAST score had an expected value E<10^-8, ii) alignment length exceeded 100 residues, iii) sequence similarity was >30%, and iv) were not parts of transposons.

Monochromaticity analysis

To examine the monochromaticity of genetic interactions between pairs of functional annotation groups, we defined a monochromatic score (MC) as follows. Let pr_ij denote the ratio of positive to all genetic interactions between group i and j and bpr denote the background ratio of positive to all interactions:

$$\begin{array}{cc}\hfill \text{if}p{r}_{ij}>bpr& {\mathrm{MC}}_{ij}=\left(p{r}_{ij}\text{-}bpr\right)∕\left(1\text{-}bpr\right)\hfill \\ \hfill \text{if}p{r}_{ij}=bpr& {\mathrm{MC}}_{ij}=0\hfill \\ \hfill \text{if}p{r}_{ij}<bpr& {\mathrm{MC}}_{ij}=\left(p{r}_{ij}\text{-}bpr\right)∕bpr\hfill \end{array}$$

A pair of groups showing purely positive (negative) genetic interactions between each other has an MC-score equal to +1 (-1), while those reflecting the background ratio (bpr) have MC-scores of 0. We computed MC-scores based on those genes that are assigned to one functional group only. A pair of functional groups was considered monochromatic if |MC_ij| > 0.5.

To assess the significance of monochromaticity, we compared the monochromatic score of the experimentally determined genetic interaction network to those of a 10,000 interaction maps that were constructed by randomizing the sign of each genetic interaction while keeping constant the total number of negative and positive interactions and conserving the annotation groups (see ref¹¹). We restricted our analysis to those functional group pairs that show at least 2 or 3 interactions between each other (Supplementary Table 1).

Computing the impact of mutations and genetic interactions by flux balance analysis

The recently reconstructed metabolic network (iMM904)¹⁰ of Saccharomyces cerevisiae was employed to simulate gene deletions. The reconstruction includes 904 genes and 1412 reactions and gives information on the stoichiometry and direction of biochemical reactions, their assignment to subcellular compartments and their associations to protein coding genes (including information on isoenzymes and enzyme complexes). Details of flux balance analysis (FBA) have been described elsewhere⁶. The simulated growth medium was set up to mimic the one used in the experiments, see Supplementary Note for more details. Genes CAN1, LYP1, URA3, LEU2 and MET17 were removed from the iMM904 reconstruction to mimic the strain background used in the experiments.

We employed linear programming to identify the maximum biomass yield of the wild-type network. The impact of gene deletions (null mutations) were calculated by constraining the corresponding reaction fluxes to zero and using either FBA or a linearized version of MOMA²⁷ to compute biomass yields of the mutant networks. Mutant fitness was defined as the biomass yield relative to wild-type and interaction between two mutations was calculated as follows: ε = f₁₂ – f₁·f₂ (where f₁, f₂ and f₁₂ refer to the single and double mutant fitnesses, respectively). To compute the effect of a partial (non-null) mutation in a gene, we constrained the flux of its corresponding reaction to ≤50% of its wild-type level¹⁴.

All calculations were carried out in the custom software package Sybil (Gabriel Gelius-Dietrich and Martin J. Lercher, unpublished), developed in the R statistical environment⁵¹ and using solvers GLPK and CPLEX.

Exploring the general properties of the FBA-derived genetic interaction map

To generate an in silico genetic interaction map based on FBA, we computed interaction scores between all non-essential metabolic gene pairs and considered two genes as interacting if predicted |ε|>10^-4 (using a more stringent cut-off does not qualitatively affect our results). To investigate the relationship between in silico single deletion fitness and other computed network properties (i.e. in silico genetic interaction degree and pleiotropy), we focused only on those genes i) whose reactions are not blocked (i.e. can attain a flux in some steady states of the network) and ii) whose removal affect the reaction content of the network (i.e. do not have isoenzymes) thereby excluding genes that cannot have any single deletion effect in the model. Furthermore, some sets of genes would always produce identical phenotypes in the model simulations and cannot be treated as independent data points in statistical analyses (e.g. genes encoding flux coupled reactions or subunits of the same protein complex). To avoid such a bias in our analysis, we represented each correlated gene set with one randomly chosen gene. These filtering procedures resulted in 193 genes.

Computing system-level functional pleiotropy

We employed the metabolic model to derive a measure of functional pleiotropy for each metabolic gene. The model specifies a list of 54 metabolites that are essential for biomass formation and therefore in silico growth (e.g. amino acids, carbohydrates, fatty acids, etc.). We computed the maximum production yield of each biomass compound in the wild-type network by maximising the flux through a pseudo-reaction representing its secretion²⁶. Next, we deleted each gene and examined whether the knockout showed a reduction in the maximum production of a given compound (i.e. a flux reduction of at least 10^-4 was considered as significant). Finally, for each gene, we counted the number of biomass compounds whose maximal production is affected by its deletion. This number reflects the network-level multifunctionality, hence pleiotropy of a gene.

Identifying flux coupled genes in the network

Coupled genes were identified by applying the flux coupling finder algorithm²⁰ on the metabolic network. We distinguished between coupled and uncoupled relationships between reaction pairs: i) coupled (fully and directionally coupled): activity of one reaction fixes the activity of the other and vice versa or activity of one reaction implies the activity of the other, but not the reverse, and ii) uncoupled: activity of one reaction does not imply the activity of the other and vice versa, indicating that the reactions are not required to operate together. Coupling relationships were calculated without assuming a fixed biomass composition to avoid coupling of a large set of fluxes to the biomass reaction²⁰.