Abstract
Thermal fluctuations cause proteins to adopt an ensemble of conformations wherein the relative stability of the different ensemble members is determined by the topography of the underlying energy landscape. “Folded” proteins have relatively homogeneous ensembles, while “unfolded” proteins have heterogeneous ensembles. Hence, the labels “folded” and “unfolded” represent attempts to provide a qualitative characterization of the extent of structural heterogeneity within the underlying ensemble. In this work, we introduce an information-theoretic order parameter to quantify this conformational heterogeneity. We demonstrate that this order parameter can be estimated in a straightforward manner from an ensemble and is applicable to both unfolded and folded proteins. In addition, a simple formula for approximating the order parameter directly from crystallographic B factors is presented. By applying these metrics to a large sample of proteins, we show that proteins span the full range of the order–disorder axis.
All proteins undergo thermal fluctuations that cause them to sample a variety of different conformations, where the dominant conformations correspond to local minima on the protein’s energy landscape. A conformational ensemble is a description of the protein in terms of these low-energy conformations and their relative stabilities, or population weights. An ensemble of conformations may be homogeneous or heterogeneous, corresponding to folded and unfolded proteins, respectively. The labels “folded” and “unfolded” qualitatively describe the heterogeneity of an ensemble, but this categorical description obscures the fact that protein disorder is a continuous property of an ensemble that can be quantified.
Many recent advances in structural biology have focused on the development of methods for describing biomolecules using ensembles of structures.2−7 For example, intrinsically disordered proteins (IDPs), which possess very heterogeneous ensembles consisting of a diverse set of highly populated conformations, have been indentified.2,3,8−10 In addition, it is now recognized that deviations from the native state often play an important role in protein function and disease, even for proteins that are considered to be well-described by a single conformation under physiological conditions.4,11−14 For instance, non-native structures play a critical role in molecular recognition,(4) enzymatic catalysis,11,12,15 and prion diseases.16,17 In order to understand the role of structural disorder in protein function and disease, it is necessary to be able to measure the disorder of a conformational ensemble. To accomplish this, we define an order parameter derived from information theory to quantify the degree of disorder in an ensemble.
We first unambiguously define our use of the term “ensemble”. An ensemble comprises a set of structures, S = {s1, s2, ..., sn}, and the set of their corresponding weights, W = {w1, w2, ..., wn}, where wi represents the probability that the protein adopts structure si. We propose that an order parameter O for protein ensembles should have the following properties: (1) 0 ≤ O ≤ 1 ; (2) O = 1 if and only if the protein adopts a single conformation (with no conformational fluctuations) throughout its biological lifetime; (3) O = 0 if the protein equally populates an infinite number of structurally dissimilar conformations. Therefore, O should be related to the entropy of the population weights and serve as a measure of structural dissimilarity among the conformations in the ensemble. An order parameter that satisfies these properties is given by
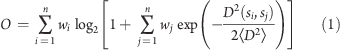 |
where D2(si, sj) is the Cα coordinate mean-square distance (MSD) between structures si and sj and ⟨D2⟩ is the average pairwise MSD due to the fluctuations of a typical protein structure at some prespecified temperature. In the Supporting Information (SI), we provide a derivation of eq 1, discuss some of its properties, and describe how simulations were used to estimate ⟨D2⟩ = 2.75 Å2.
A physical interpretation for O emerges by considering the relationship between the order parameter and the number of conformations in the ensemble. As shown in the SI, O in eq 1 is bounded as log2(1 + 1/n) ≤ O ≤ 1. Since O ≥ log2(1 + 1/n), the minimum number of conformations in the ensemble is n* = (2O – 1)−1. That is, n* is the smallest number of conformations capable of producing the amount of disorder characterized by O.
By definition, an IDP is a protein with a high degree of conformational heterogeneity.(9) Although these proteins are natively unfolded, understanding just how disordered these molecules are is an important question in and of itself. One way to approach this is to compare the order parameter of an IDP ensemble to that of a simple random coil ensemble of the same size. We recently constructed a conformational ensemble for the K18 isoform of Tau, which is a 130-residue peptide that consists of the four microtubule binding repeat regions.(3) Tau protein is an IDP that has been extensively studied because of its proposed roles in a number of human diseases, such as Alzheimer’s dementia, a common neurodegenerative disorder that affects millions of individuals in the United States each year.18,19
The K18 ensemble was constructed by weighting a structurally diverse set of 300 conformations in such a way that observables calculated from the ensemble agreed with experimental data. However, as we have previously shown, agreement with experiment alone is insufficient to ensure that any given ensemble is correct.(3) Therefore, our Bayesian weighting (BW) algorithm, which is based on techniques from Bayesian statistics, provides an additional uncertainty metric called the posterior divergence (or the uncertainty parameter), which quantifies the uncertainty in the resulting ensemble. Moreover, the BW algorithm can be used to compute error bounds for calculated observables arising from the model.
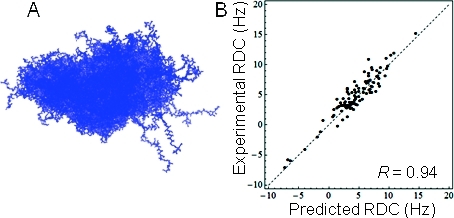
The 300 conformations that make up the K18 ensemble are shown in Figure 1A. As discussed in our prior work, the ensemble has calculated observables that agree with experiment (e.g., Figure 1B), and the calculated uncertainty parameter in the underlying model is relatively low.(3) The order parameter and minimal ensemble size of K18 computed from this ensemble are O = 0.045 ± 0.005 and n* = 32 ± 3, respectively, where the errors correspond to approximate 95% confidence regions. For comparison, we calculated the order parameter for a random coil model of K18 from an ensemble of 300 structures generated using a previously described algorithm that employs sequence-specific backbone dihedral angle statistics and excluded volume interactions.20,21 The order parameter calculated from this random coil model was ORC ≈ 0.005. It is striking that the order parameters for the BW K18 ensemble and the random coil model differ by an order of magnitude, providing an intriguing bit of evidence for residual structure in this IDP. Furthermore, this conclusion can be drawn with a high degree of confidence because the order parameter calculated from the random coil model falls well outside of the 95% Bayesian confidence interval for the order parameter of the BW K18 ensemble. As more ensembles are determined for other IDPs, it will be interesting to see whether there is a similar amount of residual structure for other disordered proteins.
Figure 1.
BW ensemble for K18 Tau. (A) The 300 conformations used to construct the ensemble, aligned via Cα atoms. (B) Residual dipolar couplings (RDCs) predicted from the ensemble using PALES(1) compared to those measured experimentally.
While the data on disordered proteins are sparse, there is a wealth of information about the conformations of proteins that have more homogeneous ensembles (i.e., folded proteins). Because a significant portion of these data were obtained from crystallographic studies, it is useful to have a corresponding formula for the order parameter in terms crystallographic data. Information about ensemble heterogeneity can be obtained from B factors, assuming that the contributions to the B factors from sources of noise (e.g., crystal disorder) are negligible. Kuzmanic and Zagrovic recently derived a relationship between the B factors and the ensemble-averaged mean-square deviation between structures.(22) As discussed in the SI, this relation can be used to derive the following approximation for the order parameter:
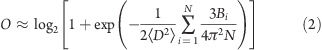 |
where N is the number of Cα atoms with listed B factors. The order parameter computed from a protein’s B factors describes the flexibility of the protein under the particular set of experimental conditions. For example, if the structure was obtained in the presence of a ligand, then the order parameter describes the heterogeneity of the bound form and could potentially be different from what would have been obtained for the protein’s unbound state.
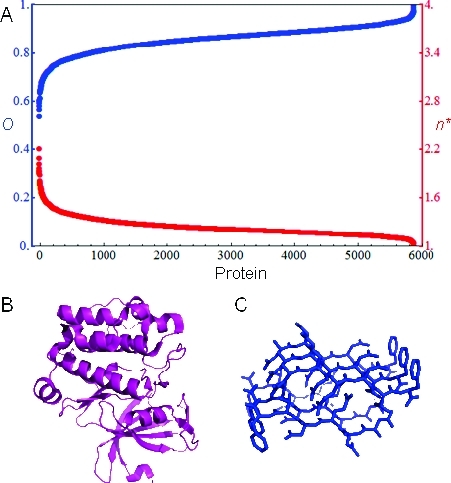
To study the range of order parameters found in folded proteins, we collected X-ray crystallographic structures having a resolution of less than 2.0 Å and an Rfree value less than 0.2 and containing only a single model from the Protein Data Bank (PDB) as of November 22, 2010.(23) We computed the order parameter for each of the resulting 5881 structures from the corresponding B factors using the approximation given by eq 2. As shown in Figure 2A, these values spanned the range from ∼0.5 to ∼1. An important observation is that this range includes a number of proteins with minimum ensemble sizes of two or more conformations. The smallest order parameter (O ≈ 0.5) belonged to PDB code 2BZH, a structure of human Pim-1 kinase complexed with a ruthenium-containing ligand (Figure 2B).(24) It is interesting to note that this corresponds to an effective ensemble size greater than 2 (i.e., the protein is not accurately described by a single structure). Pim-1 is an important drug target because of its role as an oncogenic protein that has been implicated in a number of cancers.25,26 Many candidate drugs bind in the vicinity of a glycine rich P-loop that forms part of the binding pocket for ATP (Pim-1’s natural ligand).(25) It has been suggested that the flexibility of the P-loop region in other kinases is important for ligand binding via an induced-fit mechanism.(25) At the other end of the spectrum, the largest order parameter (O ≈ 1) was obtained for PDB code 3FVA, the NNQNTF segment from elk prion protein, a model of prion fibrils (Figure 2C).(27) This peptide was found to pack into two “steric zipper” polymorphs that are both highly stable and separated by a large energy barrier.(27) In addition, the high degree of order of these fibrils may play an important role in prion-based pathogenesis by sequestering regions of the peptide that would be vulnerable to enzymatic cleavage and thus preventing proteolysis.27,28
Figure 2.
Protein conformational heterogeneity as determined using crystallographic B factors. (A) Plots of order parameters (blue) and minimal ensemble sizes (red) for a large sample of proteins calculated from crystallographic B factors. (B) Structure of human PIM-1 kinase (PDB code 2BZH), which had the smallest order parameter. (C) Structure of a peptide model of prion fibrils (PDB code 3FVA), which had the largest order parameter.
In addition, we computed values of the order parameter from ensembles constructed using simulations obtained from the Dynameomics Project.29−33 The Dynameomics.org database contains molecular dynamics (MD) simulations at 298 K that are at least 31 ns in duration for a selection of proteins corresponding to the 100 most common structural folds. The all-atom simulations were conducted with the in lucem molecular mechanics (ilmm) program using the explicit solvent model F3C.34−36 Each ensemble consisted of 1000 structures taken in evenly spaced 3 ps intervals from a 30 ns MD simulation. While these ensembles were constructed from relatively short trajectories (30 ns), we note that a prior study examined a subset of the trajectories that we used from the Dynameomics database and found that these simulations yielded reasonable agreement with experimental NMR data, including NOEs, chemical shifts, and S2 order parameters.(33) This suggests that these data provide a reasonable representation of each protein’s accessible states in solution. Nevertheless, we recognize the likelihood that additional sampling would yield a more diverse assortment of accessible conformations; therefore, the order parameters calculated from these trajectories likely represent an upper bound on the true value of the order parameter that would be obtained from a trajectory of infinite length.
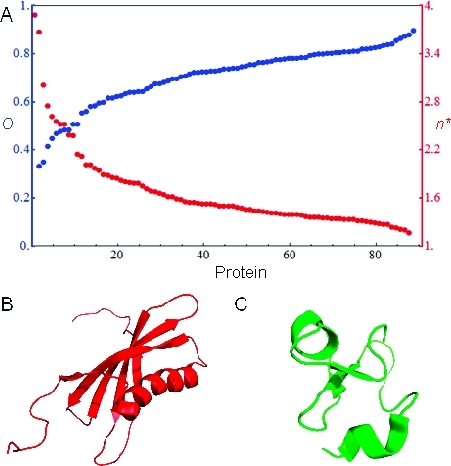
The order parameters were calculated using these structures and eq 1, where the weight of each structure was set to wi = 1/1000. As shown in Figure 3A, the order parameters span the range from ∼0.3 to ∼0.9. The fact that the structures obtained from the MD simulations often yielded lower values for the order parameter suggests that some proteins exhibit more structural heterogeneity in solution than in a crystal (an observation that is consistent with previous studies37−39) and/or that the use of B factors to approximate the order parameter neglects regions with missing electron density that may be highly flexible. Despite the differences between values calculated from the crystallographic B factors and the MD trajectories, the two data sets demonstrate that folded proteins cover a large portion of the order–disorder axis, including regions corresponding to proteins with multiple conformational states.
Figure 3.
Protein conformational heterogeneity as obtained from MD simulations. (A) Plots of order parameters (blue) and minimal ensemble sizes (red) calculated for a sample of protein folds from simulations in the Dynameomics database. The sample corresponded to 88 of the top 100 most common structural folds in the database, for which we were able to obtain the data required to compute the order parameter. (B) NMR structure of oryzacystatin-I (PDB code 1EQK), which had the smallest order parameter. (C) Structure of the antifungal peptide EAFP2 (PDB code 1P9G), which had the largest order parameter.
The smallest order parameter (O ≈ 0.3) belonged to oryzacystatin-I, a cysteine proteinase inhibitor from a species of rice.(40) The structure of the 102 amino acid protein (PDB code 1EQK) was determined by NMR analysis (Figure 3B). Both the N- and C-terminal regions are relatively unstructured, a property that is conserved in cysteine proteinase inhibitors from other species.40−42 Moreover, docking studies of a related protein suggested that the flexibility of the N-terminal region may be important for recognition of the target enzyme.(41) The largest order parameter from the simulation data set (O ≈ 0.9) was obtained for a 41-residue antifungal peptide called EAFP2 that contains 5-disulfide bonds.43−45 The structure of EAFP2 was determined by both NMR analysis(45) and X-ray crystallography(44) (Figure 3C). The highly ordered nature of this peptide is consistent with the fact that it maintains its activity even at 100 °C.(43) Furthermore, this rigidity may be an important functional characteristic, given that similar disulfide bonding patterns have been observed in other antifungal peptides.43−45
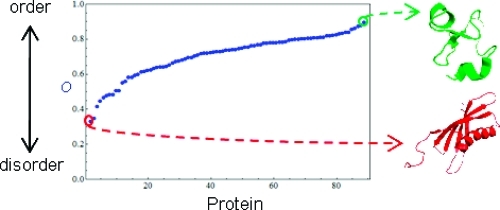
The picture of the protein order–disorder axis that we have obtained from these studies is materially different from the way that conformational heterogeneity is typically discussed. First, we want to re-emphasize that proteins, both folded and unfolded, span a large range of the order–disorder axis and that the ability to quantify the heterogeneity within a given ensemble represents a new way to view (and make quantitative statements about) protein ensembles. Thus, instead of classifying proteins into mutually exclusive “folded” or “unfolded” categories, it is important to quantify the actual extent of heterogeneity within the ensemble. In this sense, our metrics provide a language for describing protein flexibility that will allow thorough studies of protein order and disorder using a multitude of biophysical techniques. From amyloid-like fibrils on one end of the axis to IDPs on the other, it is clear that conformational heterogeneity has important implications for understanding disease states as well as normal protein function.
Acknowledgments
This work was supported by NIH Grant 5R21NS063185-02.
Supporting Information Available
Mathematical derivations and discussion, details of simulation data, and a figure illustrating the quality of the approximations used to derive eq 2. This material is available free of charge via the Internet at http://pubs.acs.org.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Zweckstetter M.; Bax A. J. Am. Chem. Soc. 2000, 122, 3791. [Google Scholar]
- Salmon L.; Nodet G.; Ozenne V.; Yin G.; Jensen M. R.; Zweckstetter M.; Blackledge M. J. Am. Chem. Soc. 2010, 132, 8407. [DOI] [PubMed] [Google Scholar]
- Fisher C. K.; Huang A.; Stultz C. M. J. Am. Chem. Soc. 2010, 132, 14919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange O. F.; Lakomek N. A.; Fares C.; Schroder G. F.; Walter K. F.; Becker S.; Meiler J.; Grubmuller H.; Griesinger C.; de Groot B. L. Science 2008, 320, 1471. [DOI] [PubMed] [Google Scholar]
- Levin E. J.; Kondrashov D. A.; Wesenberg G. E.; Phillips G. N. Jr. Structure 2007, 15, 1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindorff-Larsen K.; Best R. B.; Depristo M. A.; Dobson C. M.; Vendruscolo M. Nature 2005, 433, 128. [DOI] [PubMed] [Google Scholar]
- Korzhnev D. M.; Salvatella X.; Vendruscolo M.; Di Nardo A. A.; Davidson A. R.; Dobson C. M.; Kay L. E. Nature 2004, 430, 586. [DOI] [PubMed] [Google Scholar]
- Turoverov K. K.; Kuznetsova I. M.; Uversky V. N. Prog. Biophys. Mol. Biol. 2010, 102, 73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunker A. K.; Oldfield C. J.; Meng J.; Romero P.; Yang J. Y.; Chen J. W.; Vacic V.; Obradovic Z.; Uversky V. N. BMC Genomics 2008, 9 (Suppl. 2), S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang A.; Stultz C. M. Future Med. Chem. 2009, 1, 467. [DOI] [PubMed] [Google Scholar]
- Bakan A.; Bahar I. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 14349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henzler-Wildman K. A.; Thai V.; Lei M.; Ott M.; Wolf-Watz M.; Fenn T.; Pozharski E.; Wilson M. A.; Petsko G. A.; Karplus M.; Hubner C. G.; Kern D. Nature 2007, 450, 838. [DOI] [PubMed] [Google Scholar]
- Henzler-Wildman K.; Kern D. Nature 2007, 450, 964. [DOI] [PubMed] [Google Scholar]
- Salsas-Escat R.; Stultz C. M. Proteins: Struct., Funct., Bioinf. 2010, 78, 325. [DOI] [PubMed] [Google Scholar]
- Salsas-Escat R.; Nerenberg P. S.; Stultz C. M. Biochemistry 2010, 49, 4147. [DOI] [PubMed] [Google Scholar]
- Venneti S. Clin. Lab. Med. 2010, 30, 293. [DOI] [PubMed] [Google Scholar]
- Sakudo A.; Xue G.; Kawashita N.; Ano Y.; Takagi T.; Shintani H.; Tanaka Y.; Onodera T.; Ikuta K. Curr. Protein Pept. Sci. 2010, 11, 166. [DOI] [PubMed] [Google Scholar]
- Lees A. J.; Hardy J.; Revesz T. Lancet 2009, 373, 2055. [DOI] [PubMed] [Google Scholar]
- Blennow K.; de Leon M. J.; Zetterberg H. Lancet 2006, 368, 387. [DOI] [PubMed] [Google Scholar]
- Bernado P.; Mylonas E.; Petoukhov M. V.; Blackledge M.; Svergun D. I. J. Am. Chem. Soc. 2007, 129, 5656. [DOI] [PubMed] [Google Scholar]
- Bernado P.; Blanchard L.; Timmins P.; Marion D.; Ruigrok R. W.; Blackledge M. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 17002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmanic A.; Zagrovic B. Biophys. J. 2010, 98, 861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. Nucleic Acids Res. 2000, 28, 235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debreczeni J. E.; Bullock A.; Knapp S.; Von Delft F.; Sundstrom M.; Arrowsmith C.; Weigelt J.; Edwards A.. Crystal Structure of the Human Pim1 in Complex with Ruthenium Organometallic Ligands. Protein Data Bank entry 2BZH. DOI: 10.2210/pdb2bzh/pdb. Deposition Date: Aug 18, 2005.
- Doudou S.; Sharma R.; Henchman R. H.; Sheppard D. W.; Burton N. A. J. Chem. Inf. Model. 2010, 50, 368. [DOI] [PubMed] [Google Scholar]
- Shah N.; Pang B.; Yeoh K. G.; Thorn S.; Chen C. S.; Lilly M. B.; Salto-Tellez M. Eur. J. Cancer 2008, 44, 2144. [DOI] [PubMed] [Google Scholar]
- Wiltzius J. J.; Landau M.; Nelson R.; Sawaya M. R.; Apostol M. I.; Goldschmidt L.; Soriaga A. B.; Cascio D.; Rajashankar K.; Eisenberg D. Nat. Struct. Mol. Biol. 2009, 16, 973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupfer L.; Hinrichs W.; Groschup M. H. Curr. Mol. Med. 2009, 9, 826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Kamp M. W.; Schaeffer R. D.; Jonsson A. L.; Scouras A. D.; Simms A. M.; Toofanny R. D.; Benson N. C.; Anderson P. C.; Merkley E. D.; Rysavy S.; Bromley D.; Beck D. A.; Daggett V. Structure 2010, 18, 423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonsson A. L.; Scott K. A.; Daggett V. Biophys. J. 2009, 97, 2958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simms A. M.; Toofanny R. D.; Kehl C.; Benson N. C.; Daggett V. Protein Eng., Des. Sel. 2008, 21, 369. [DOI] [PubMed] [Google Scholar]
- Benson N. C.; Daggett V. Protein Sci. 2008, 17, 2038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck D. A.; Jonsson A. L.; Schaeffer R. D.; Scott K. A.; Day R.; Toofanny R. D.; Alonso D. O.; Daggett V. Protein Eng., Des. Sel. 2008, 21, 353. [DOI] [PubMed] [Google Scholar]
- Beck D. A.; Daggett V. Methods 2004, 34, 112. [DOI] [PubMed] [Google Scholar]
- Levitt M.; Hirshberg M.; Sharon R.; Daggett V. Comput. Phys. Commun. 1995, 91, 215. [Google Scholar]
- Levitt M.; Hirshberg M.; Sharon R.; Laidig K. E.; Daggett V. J. Phys. Chem. B 1997, 101, 5051. [Google Scholar]
- Eastman P.; Pellegrini M.; Doniach S. J. Chem. Phys. 1999, 110, 10141. [Google Scholar]
- Northrup S. H.; Pear M. R.; McCammon J. A.; Karplus M.; Takano T. Nature 1980, 287, 659. [DOI] [PubMed] [Google Scholar]
- Petsko G. A.; Ringe D. Annu. Rev. Biophys. Bioeng. 1984, 13, 331. [DOI] [PubMed] [Google Scholar]
- Nagata K.; Kudo N.; Abe K.; Arai S.; Tanokura M. Biochemistry 2000, 29, 14753. [DOI] [PubMed] [Google Scholar]
- Bode W.; Engh R.; Musil D.; Thiel U.; Huber R.; Karshikov A.; Brzin J.; Kos J.; Turk V. EMBO J. 1988, 7, 2593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsubo S.; Kobayashi H.; Noro W.; Taniguchi M.; Saitoh E. J. Agric. Food Chem. 2005, 53, 5218. [DOI] [PubMed] [Google Scholar]
- Huang R. H.; Xiang Y.; Liu X. Z.; Zhang Y.; Hu Z.; Wang D. C. FEBS Lett. 2002, 521, 87. [DOI] [PubMed] [Google Scholar]
- Xiang Y.; Huang R. H.; Liu X. Z.; Zhang Y.; Wang D. C. J. Struct. Biol. 2004, 148, 86. [DOI] [PubMed] [Google Scholar]
- Huang R. H.; Xiang Y.; Tu G. Z.; Zhang Y.; Wang D. C. Biochemistry 2004, 43, 6005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.