Competing Risks Analysis of Correlated Failure Time Data

Summary

We develop methods for competing risks analysis when individual event times are correlated within clusters. Clustering arises naturally in clinical genetic studies and other settings. We develop a nonparametric estimator of cumulative incidence, and obtain robust pointwise standard errors that account for within-cluster correlation. We modify the two-sample Gray and Pepe–Mori tests for correlated competing risks data, and propose a simple two-sample test of the difference in cumulative incidence at a landmark time. In simulation studies, our estimators are asymptotically unbiased, and the modified test statistics control the type I error. The power of the respective two-sample tests is differentially sensitive to the degree of correlation; the optimal test depends on the alternative hypothesis of interest and the within-cluster correlation. For purposes of illustration, we apply our methods to a family-based prospective cohort study of hereditary breast/ovarian cancer families. For women with BRCA1 mutations, we estimate the cumulative incidence of breast cancer in the presence of competing mortality from ovarian cancer, accounting for significant within-family correlation.

1. Introduction

In epidemiological cohort studies, individuals may be followed for more than one type of event. The survival times are subject to competing risks if the occurrence of one event type prevents other event types from occurring. There are effective methods for analyzing competing risks data when individuals are independent (Moeschberger and Klein, 1995). Furthermore, several approaches have been proposed (Lee, Wei, and Amato, 1992; Cai and Prentice, 1995) that extend the Cox proportional hazards model to correlated survival data. However, little attention has been given to competing risks analysis when event times from different individuals are clustered. Such clustering arises naturally in family-based cohort studies; but clustering may arise due to several other mechanisms. For example, in clinical genetic studies, unrelated individuals may be subject to a cluster effect if they share the same deleterious mutation or if several genes lead to the same clinical syndrome.

This article was motivated by a prospective cohort study of hereditary breast and ovarian cancer (HBOC) conducted by the National Cancer Institute (Kramer et al., 2005). In this study, 451 women from 31 families with multiple cases of breast and/or ovarian cancer in multiple generations were followed for up to 30 years. Entry of a kindred into the cohort was initiated by a single family member (the proband) in the United States. The proband was identified by the diagnosis of either breast or ovarian cancer. The proband and all other cases of breast and/or ovarian cancer that had been diagnosed prior to the time of family's ascertainment were excluded from our analysis. Subsequently, 23 of these families were found to carry a deleterious germ-line mutation in the BRCA1 gene. In these families, there were 98 mutation-positive and 353 mutation-negative women. Competing risks of interest are breast cancer and death from causes other than breast cancer. In mutation-positive women, the latter hazard is substantially elevated due to death from ovarian cancer.

A major objective of the present study is to estimate the cumulative incidence of breast cancer in the BRCA1 mutation-positive women, accounting for competing mortality and the effects of within-family correlation. We develop novel methods to account for the effects of clustering on estimators and test statistics, and we investigate the sensitivity of these estimators and tests to the degree of correlation.

For independent data, nonparametric maximum likelihood estimators of cumulative incidence based on cause-specific hazard functions have been well described (Prentice et al., 1978; Gaynor et al., 1993). In this article, we propose a non-parametric estimator of cumulative incidence that accounts for within-cluster correlation, and we provide a robust estimator for the pointwise variance.

The two-sample tests for competing risks have also been explored for independent data. Gray considers a class of K-sample tests for the cumulative incidence based on weighted averages of subdistribution hazard functions (Gray, 1988). Pepe and Mori develop test statistics using weighted averages of cumulative incidences (Pepe and Mori, 1993). Recently, it is shown that the nonparametric estimator of cumulative incidence obtained from independent data converges weakly to a zero-mean Gaussian process (Lin, 1997). Spiekerman and Lin (1998) extend this result to estimate the cumulative hazard function from clustered data. In this report, we combine these approaches to develop tests for correlated competing risks data. Three tests are proposed for the two-sample problem: extensions of the widely used Gray and Pepe–Mori tests, and a novel pointwise landmark test.

The rest of this article is organized as follows. In Section 2, we adopt counting process tools to derive an estimator of cumulative incidence appropriate for clustered data, and we develop a robust variance estimator that can be incorporated into the test statistics. In Section 3, we consider two-sample tests. In Section 4, we present simulation studies. In Section 5, we apply our methods to the HBOC dataset. In Section 6, we present concluding remarks.

2. Nonparametric Estimation

For concreteness, we introduce the notation for the two-state problem with events “breast cancer” and “death without prior breast cancer.” The notation generalizes to the multistate problem in an obvious manner. We suppose that there are n clusters involved in the study, with n_i individuals in cluster i, and we let $m={\sum }_{i=1}^n{n}_i$ Note that the cluster size n_i may vary with cluster. We also assume that a finite constant M exists such that max_1≤i≤n {n_i} < M for every n. Adopting the notation of cause-specific hazards (Prentice et al., 1978), let (T_ik, J_ik) be the age at breast cancer diagnosis (J_ik = 1), and age at death without prior breast cancer (J_ik = 2) for individual k in cluster i, respectively. For i = 1, …, n, failure times ${\{T_{ik},J_{ik}\}}_{k=1}^{n_i}$ for individuals in different clusters are assumed to be independent random variables. However, individuals within the same cluster may have correlated failure times. We further assume that all failure times T_ik have a common marginal survival function S(t). Let X_ik = min (T_ik, C_ik) be the observed event or censoring time, where C_ik is the independent right-censoring time for T_ik; and let Δ_ik = I (T_ik < C_ik) be the right-censoring indicator. Furthermore, we denote the indicator function for an event type by δ_ik = Δ_ik × J_ik. That is, δ_ik = j for j = 1 and 2 if a type j event occurs, 0 if a censoring event occurs. Therefore, the random vectors that can be observed are ${\{X_{ik},{\delta }_{ik}\}}_{k=1}^{n_i}$, i = 1, …, n. We assume that the marginal distribution (X_ik, δ_ik) is the same for all i, k.

Instead of specifying a complete multivariate distribution for the underlying survival data, we specify the marginal cause-specific hazard function for a type j = 1 and 2 event by

$$h_j(t)=\underset{\mathrm{\Delta }t\to 0}{lim}\frac{Pr\{t\le X_{ik}<t+\mathrm{\Delta }t,{\delta }_{ik}=j|X_{ik}\ge t\}}{\mathrm{\Delta }t},\text{for}j=1\text{and}2,$$ (1)

and let h(t) = h₁(t) + h₂(t). In the setting of competing risks, the cumulative incidence of a type 1 event is given by $F_1(t)={\int }_0^{t}S(u)d{H}_1(u)$, where $H_j(t)={\int }_0^t{h}_j(u)$ du is the cumulative hazard function for a type j event, and S(t) is the overall survival function. Adopting the notation of counting processes (Andersen et al., 1993), for an individual k in cluster i, let

$$\begin{array}{l}{N}_{1ik}(t)=I\left\{X_{ik}\le t\wedge C_{ik},{\delta }_{ik}=1\right\},\text{and}\\ N_{2ik}(t)=I\left\{X_{ik}\le t\wedge C_{ik},{\delta }_{ik}=2\right\},\end{array}$$

be a count of the number of observed type j = 1, 2 events through time t, respectively. Let N_ik (t) = N_1ik (t) + N_2ik (t) be the overall event count, at time t. Let Y_ik (t) = I{t ≤ X_ik} be the indicator function that individual k in cluster i is at risk of either a type 1 event or a type 2 event just prior to time t, and let $Y(t)={\sum }_{i=1}^n{\sum }_{k=1}^{n_i}{Y}_{ik}(t)$ be the total number of individuals at risk at time t −. The risk process Y_ik (t) can be modified to allow left truncation or other general at risk processes. The nonparametric Nelson–Aalen type estimators (Aalen, 1978) for the cause-specific cumulative hazard functions are ${\widehat{H}}_1(t)={\int }_0^{t}d{\widehat{H}}_1(u)$, and $\widehat{H}(t)={\int }_0^{t}d\widehat{H}(u)$, where

$$d{\widehat{H}}_1(t)=\sum _{i=1}^n\sum _{k=1}^{n_i}\frac{d{N}_{1ik}(t)}{Y(t)},\text{and}d\widehat{H}(t)=\sum _{i=1}^n\sum _{k=1}^{n_i}\frac{d{N}_{ik}(t)}{Y(t)}.$$

Even if event times for individuals within a cluster are correlated, the Nelson–Aalen estimators Ĥ₁ (t) and Ĥ (t) still provide consistent estimators of the cumulative hazard functions H₁ (t) and H(t) when the number of clusters m goes to infinity (Spiekerman and Lin, 1998). Here we use the Nelson–Aalen type estimate for the overall survival function Ŝ (t) = exp{−Ĥ (t)} (Nelson, 1972; Aalen, 1978).

The nonparametric estimator of cumulative incidence is obtained by replacing S(t) and H₁(t) with the corresponding estimators

$${\widehat{F}}_1(t)={\int }_0^t\widehat{S}(u)d{\widehat{H}}_1(u).$$ (2)

When failure times are independent, several variance estimators have been proposed for the cumulative incidence function, and a detailed comparison of these variance estimators was recently presented (Braun and Yuan, 2006). Here we construct a novel robust variance estimator for clustered competing risks data. In the Web Appendix, we show that F̂₁ (t) is a consistent estimator of the cumulative incidence F₁ (t), and $\sqrt{m}\{{\widehat{F}}_1(t)-F_1(t)\}$ can be written as the sum of mean zero random variables

$$\sqrt{m}\{{\widehat{F}}_1(t)-F_1(t)\}=\sum _{i=1}^n\sum _{k=1}^{n_i}{Z}_{ik}(t)+o_p(1),$$ (3)

using a technique similar to that of Ghosh and Lin (2000). Because Z_ik (t) only depends on the observation of subject k in cluster i, the between-cluster variance estimator of the simple linear statistic $Z(t)={\sum }_{i=1}^n{\sum }_{k=1}^{n_i}{Z}_{ik}(t)$ is

$$\widehat{V}(t)=\frac{n}{n-1}\sum _{i=1}^n{\{{\widehat{Z}}_i.(t)-\overline{Z}\mathrm{..}(t)\}}^2,$$ (4)

where Ẑ_ik (t) is obtained by replacing the unknown quantities in equation (A.1) with the corresponding estimator, ${\widehat{Z}}_{i\cdot }(t)={\sum }_{k=1}^{n_i}{\widehat{Z}}_{ik}(t)$, and ${\overline{Z}}_{..}(t)=\frac{1}{n}{\sum }_{i=1}^n{\widehat{Z}}_{i\cdot }(t)$. By using results for the clustered linear statistic (Williams, 2000), we show in the Web Appendix that V̂ (t) is an unbiased estimator for the variance of the linear statistic Z(t), or equivalently, $\sqrt{m}\{{\widehat{F}}_1(t)-F_1(t)\}$.

3. Two-Sample Tests

When it is of interest to investigate whether the cumulative incidence of the same event type is equivalent in two groups, say, group 1 and group 0, we have the following null hypothesis:

$$\begin{array}{cc}{H}_0:F_1^{(1)}(t)=F_1^{(0)}(t)& \text{for all}t>0,\end{array}$$

where $F_1^{(g)}(t)$ is the cumulative incidence for cause 1 in group g, for g = 0 and 1. For any fixed time t, a test for the difference in cumulative incidence at t is given by

$${\widehat{Q}}_{LM}(t)=\sqrt{\frac{m_0{m}_1}{m}}\{{\widehat{F}}_1^{(1)}(t)-{\widehat{F}}_1^{(0)}(t)\},$$

where m₀ is the sample size for group 0, m₁ is the sample size for group 1, and m = m₀ + m₁. In practice, t can be set to a clinically relevant landmark time. Under the null hypothesis, test statistic Q̂_LM(t) is asymptotically normally distributed with mean zero and asymptotic variance that can be consistently estimated by

$${\widehat{V}}_{LM}=\frac{1}{m}\times \frac{n}{n-1}\sum _{i=1}^n{\left\{\sum _{k=1}^{n_i}{g}_{ik}{\widehat{Z}}_{ik}(t)-d{\widehat{Z}}_{\mathrm{..}}^{\ast }(t)\right\}}^2,$$ (5)

where $g_{ik}=\sqrt{m_0}$ if individual ik belongs to group 1, otherwise, $g_{ik}=-\sqrt{m_1};$ and ${\widehat{Z}}_{\cdot \cdot }^{\ast }(t)=\frac{1}{n}{\sum }_{i=1}^{n_i}{\sum }_{k=1}^{n_i}{g}_{ik}{\widehat{Z}}_{ik}(t)$. Here individuals from group 0 and group 1 may come from the same cluster. However, when the event times for individuals in groups 0 and 1 are independent, the variance estimator has the following simple form

$${\widehat{V}}_{LM}(t)=\frac{m_0}{m}{\widehat{V}}^{(1)}(t)+\frac{m_1}{m}{\widehat{V}}^{(0)}(t).$$ (6)

where V̂^(g) (t) can be obtained from equation (4) for individuals in group g = 0 and 1. The standardized landmark test is ${\stackrel{\sim }{Q}}_{LM}(t)={\stackrel{\sim }{Q}}_{LM}(t)/\sqrt{{\stackrel{\sim }{V}}_{LM}(t)}$.

To test for an overall difference of the cumulative incidence functions, Gray (1988) considers the difference of the subdistribution hazard function

$${\widehat{Q}}_G^{\ast }=\sqrt{\frac{m_1{m}_0}{m}}\int \widehat{W}\ast (t)\left\{\frac{d{\widehat{F}}_1^{(1)}(t)}{1-{\widehat{F}}_1^{(1)}(t-)}-\frac{d{\widehat{F}}_1^{(0)}(t)}{1-{\widehat{F}}_1^{(0)}(t-)}\right\},$$

where Ŵ (t) is a predictable weight function. With simple algebra, the Gray type test statistic can be rewritten as:

$${\widehat{Q}}_G=\sqrt{\frac{m_1{m}_0}{m}}\int \widehat{W}(t)d\{{\widehat{F}}_1^{(1)}(t)-{\widehat{F}}_1^{(0)}(t)\}.$$

A common choice for Ŵ (t) is the log-rank weight function $\widehat{W}(t)=\frac{Y^{(1)}(t)Y^{(0)}(t)}{Y^{(1)}(t)+Y^{(0)}(t)}$.

Alternatively, Pepe and Mori (1993) consider the following test statistic for the overall difference of the cumulative incidence functions:

$${\widehat{Q}}_{PM}=\sqrt{\frac{m_1{m}_0}{m}}\int \widehat{K}(t)\{{\widehat{F}}_1^{(1)}(t)-{\widehat{F}}_1^{(0)}(t)\}dt,$$

where the weight function K̂(t) converges in probability to a certain function K(t). Some constraints must be imposed on both the weight functions K̂(t) and K(t) to ensure the stability of the test statistics (Pepe and Fleming, 1989). For some positive constants Γ and δ, the constraints are $|\widehat{K}(t)|<\mathrm{\Gamma }{\{\widehat{C^{(g)}}(t)\}}^{\frac{1}{2}+\delta }$ and $|K(t)|<\mathrm{\Gamma }{\{C^{(g)}(t)\}}^{\frac{1}{2}+\delta }$ for g = 0 and 1, where $\widehat{C^{(g)}}(t)$ is the estimator of survival function for the right censoring time in group g. For example, one can use $\widehat{K}(t)=\frac{m\widehat{C^{(0)}}(t)\widehat{C^{(1)}}(t)}{m_0\widehat{C^{(0)}}(t)+m_1\widehat{C^{(1)}}(t)}$, that satisfies the constraints.

In the Web Appendix, we show that under the null hypothesis, the variances for Q̂_G and Q̂_PM can be consistently estimated by ${\widehat{V}}_G=\frac{1}{m}\times \frac{n}{n-1}{\sum ^n}_{i=1}{\{{\sum ^{n_i}}_{k=1}{g}_{ik}\int \widehat{W}(t)d{\widehat{Z}}_{ik}(t)-\int \widehat{W}(t)d\widehat{Z}\ast -(t)\}}^2$ and ${\widehat{V}}_{PM}=\frac{1}{m}\times \frac{n}{n-1}{\sum ^n}_{i=1}{\{{\sum ^{n_i}}_{k=1}{g}_{ik}\int \widehat{W}(t){\widehat{Z}}_{ik}(t)dt-\int \widehat{W}(t)\widehat{Z}\ast -(t)dt\}}^2.$ The null hypothesis is rejected at significance level α when the standardized Gray test statistic ${\stackrel{\sim }{Q}}_G={\widehat{Q}}_G/\sqrt{{\widehat{V}}_G}$ or the standardized Pepe–Mori test statistic ${\stackrel{\sim }{Q}}_{PM}={\stackrel{\sim }{Q}}_{PM}/\sqrt{{\widehat{V}}_{PM}}$ is greater than Φ⁻¹(1 − α/2), where Φ (x) is cumulative distribution function of the standard Gaussian distribution.

4. Simulation Studies

4.1 One-Sample Estimation

For the one-sample estimation problem, we considered total cluster sizes of n = 20 and 40. Clustered survival data ${\left\{X_{ik},{\delta }_{ik}\right\}}_{k=1}^{n_i}$ were generated for n_i individuals per cluster, where Pr{n_i = q} = 0.1, for q ∈ {1, 2, …, 10}. Failure times ${\left\{T_{\mathit{\text{jik}}}\right\}}_{k=1}^{n_i}$ for individuals within the same cluster shared a multivariate log-normal distribution with parameter (μ_j, Σ_j) for type j events, j = 1, 2, respectively. The covariance matrix was Σ₁ = φI + (1 − φ)1_nj×nj and Σ₂ = φI + (1 − φ)1_nj×nj, where 1_nj×nj was a n_j × n_j matrix with all entries equal to 1 and I was a n_j × n_j identity matrix, here we fix φ = 0.3. The right-censoring time followed an exponential distribution with parameter λ_C = 0.05. X_ik was the minimum of the two failure times and the right-censoring time, and δ_ik = 0, 1 or 2, corresponding to right-censored data or to failures of type 1 and 2, respectively.

To evaluate the impact of within-cluster correlation on estimates of cumulative incidence, we considered scenarios with varying φ. We reported the biases b(t) = F̂₁(t) − F₁(t) for the nonparametric approach (equation 2) at times t corresponding to the 10, 20, 30, 40, 50, 60, 70, 80, 90, and 95 percent quantiles of the normalized subdistribution $F_1^{\ast }(t)=\{F_1(t)/F_1(\infty )\}$ (Gaynor et al., 1993), e.g., the time t₉₀ such that $F_1^{\ast }(t_{90})=0.90$. For μ₁ = μ₂ = 0.1, the results based on 10,000 replications for φ = 0.0, 0.3, 0.6, and 0.9 (corresponding to independence, and low, moderate, and strong within-cluster correlations, respectively, among survival times for type 1 events) are shown in Figure 1. The overall absolute biases are small, less then 0.02 in all scenarios considered. As the number of clusters increased, the bias decreased. Indeed, for a study with n = 40 clusters, the absolute biases are all less than 0.01, even with very heterogeneous clusters.

Figure 1.

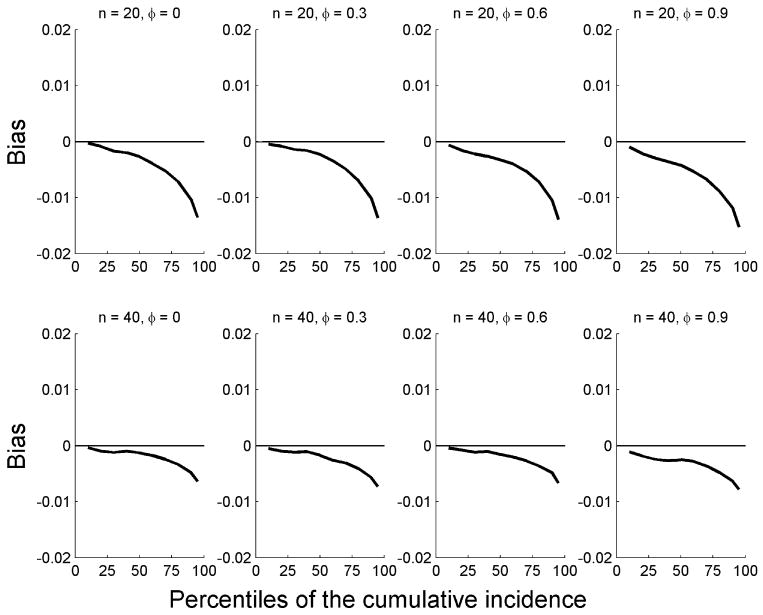
Biases for the cumulative incidence functions by percentile of the standardized cumulative incidence function $F_1^{\ast }(t)$ when μ₁ = 0.1 and μ₂ = 0.1 for different cluster sizes m and correlation coefficient φ. Results were based on 10,000 replications.

Figure 2 shows the empirical standard error (ESE), the robust standard error (RSE) that accounts for correlation of clustered individuals, and the naïve standard error (NSE) that ignores correlation of clustered individuals, under the same parameter configuration as shown in Figure 1. The ESEs were obtained from 10,000 Monte Carlo replications and are an accurate approximation of the true standard errors. The RSEs closely track the ESEs at all time points in each scenario. However, the NSEs tend to underestimate the true standard errors, substantially so for times beyond the conditional median. Other hazard curves (e.g., data were generated from the Weibull distribution with a shared Gamma random effect variable) were examined, and all gave broadly similar results in terms of bias and standard error estimations (data not shown).

Figure 2.

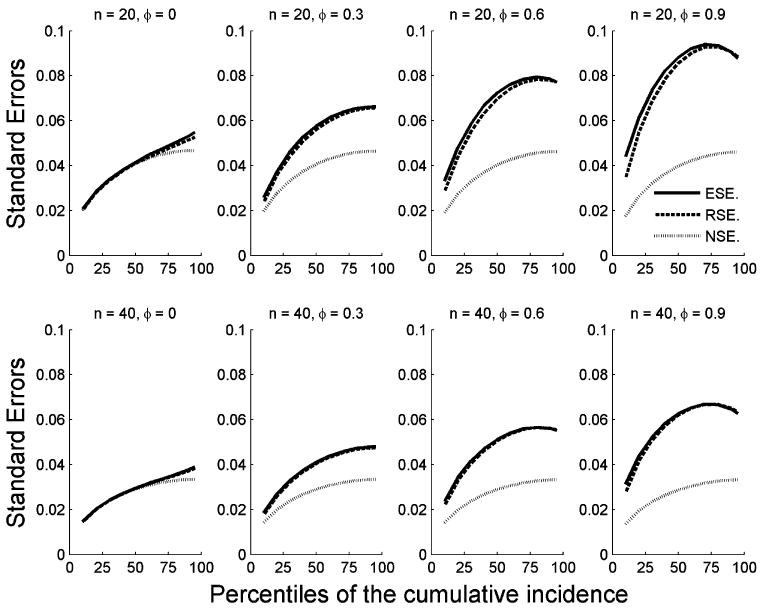
ESEs, RSEs, and NSEs by percentile of the standardized cumulative incidence function $F_1^{\ast }(t)$. Results were based on 10,000 replications.

4.2 Two-Sample Testing

For the two-sample testing problem, we investigated the type I error rates under the null hypothesis and the power under alternative hypotheses. Under the null, we considered cluster size m₀ = m₁ = 20 and 40, and simulated data using the same settings of the one-sample study for both group 0 and group 1. The test procedures developed in Section 3 were applied. The Type I errors are reported in Table 1. In all settings considered, the three test procedures have Type I errors close to the nominal level of α = 0.05. These data suggest that the variance estimator for each test statistic is asymptotically consistent for large cluster size. When within-cluster correlations were ignored and the naïve variances were used to construct the test statistics, similar simulations found that the Type I errors increased to as large as 0.25, substantially above the nominal level of 0.05.

Table 1. Empirical Type I errors for two-sample tests of correlated competing risks data.

Number of clusters	$${\mu }_1^{\text{a}}$$ a	φb	Landmark test	Gray test	Pepe–Mori test
20	0.05	0.0	0.0574	0.0541	0.0618
20	0.05	0.3	0.0510	0.0497	0.0563
20	0.05	0.6	0.0500	0.0529	0.0606
20	0.05	0.9	0.0525	0.0534	0.0625
20	0.10	0.0	0.0546	0.0514	0.0576
20	0.10	0.3	0.0533	0.0523	0.0642
20	0.10	0.6	0.0497	0.0493	0.0594
20	0.10	0.9	0.0510	0.0515	0.0538
40	0.05	0.0	0.0524	0.0499	0.0552
40	0.05	0.3	0.0519	0.0492	0.0602
40	0.05	0.6	0.0496	0.0489	0.0626
40	0.05	0.9	0.0506	0.0471	0.0639
40	0.10	0.0	0.0512	0.0490	0.0495
40	0.10	0.3	0.0462	0.0476	0.0526
40	0.10	0.6	0.0520	0.0489	0.0463
40	0.10	0.9	0.0489	0.0551	0.0458

^aμ₁ is the mean parameter of the log-normal distribution for the event of interest.

^bφ is the correlation coefficient parameter for the event of interest.

Results for all empirical type I errors are based on 10,000 replications.

To study the power of these tests under alternative hypotheses, we considered failure times with Weibull distributions using hazard functions for event type 1 of $h_1^{(g)}(t)={\upsilon }_{1g}{\lambda }_{1g}{t}^{p_{1g}}$ in groups g = 0 and 1, where υ_1g ∼ Gamma(φ, φ ⁻¹). Again, the hazard rates for type 2 events were set to a constant function $h_2^{(g)}(t)=0.1$ in groups g = 0 and 1. Figure 3 shows the powers of selected scenarios of alternative hypotheses for the landmark test at t₉₀, the Gray test, and the Pepe–Mori test for φ = 0.5, 1.0, 1.5, 2.0, 3.0, and 4.0. Panel A shows the power to detect distinct cumulative incidence functions when the baseline hazards for event type 1 are parallel constant lines. In panels B, C, and D, the two baseline hazards cross, with the hazards in group 0 being constant and the hazards in group 1 increasing over time at different rates. The performance of the test statistics depended on the shapes of the hazard functions and the degree of homogeneity among clusters. Power decreased for all three test statistics when hazards in different clusters became more heterogeneous, corresponding to a large random effects variance or small φ The Pepe–Mori test dominated when the cumulative incidence of one group was consistently greater then the other, while the Gray test tended to have higher power when the cumulative incidence functions had a different shape (Ghosh and Lin, 2000). Although all three test statistics were sensitive to within-cluster correlation, the effect of correlation on each test was variable. The landmark test performance depended on the time that was selected to conduct the test and could be underpowered in some scenarios, for example, in panel C, when the landmark time of interest is located at a point where the cumulative incidence curves are similar.

Figure 3.

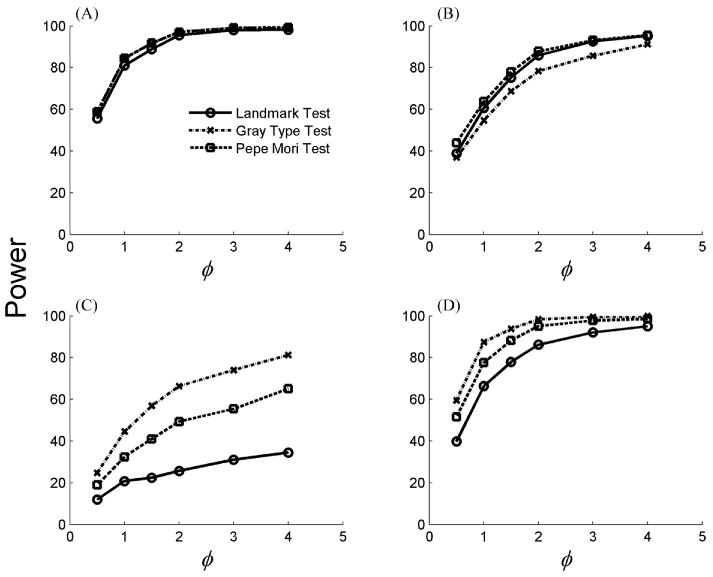
Power of the landmark test at t₉₀ (the 90% quantile of the normalized subdistribution function), the Gray test, and the Pepe–Mori test for value of the frailty parameter φ. Results were based on 10,000 replications. The baseline hazard rates are: (A) $h_1^{(0)}(t)=0.10$ and $h_1^{(1)}(t)=0.25$, (B) $h_1^{(0)}(t)=0.10$ and $h_1^{(2)}(t)=0.20\times \sqrt{t}$, (C) $h_1^{(0)}(t)=0.10$ and $h_1^{(2)}(t)=0.02\times t$, and (D) $h_1^{(1)}(t)=0.15$ and $h_1^{(2)}(t)=0.02\times t$.

5. Application to HBOC Data

We applied the proposed methods to the HBOC study. Age is the natural time scale. Prospective follow-up for family members began at the time that the proband was enrolled (the ascertainment date). For individuals who were less than 20 years old at the time of enrollment of the family, the starting date was deferred until their 20th birthday. The left-truncation times for siblings could depend on each other, but this should not affect our analysis. It is reasonable to assume that the left-truncation times are independent of the event times (time of breast cancer or death) for any given family, because the follow-up that is stipulated in the protocol does not depend on the age at diagnosis of breast or ovarian cancer of the proband, or the number of affected relatives at any point of time. We extended our methods in Section 2 to accommodate left truncation by modifying the at-risk processes as Y_ik (t) = I{E_ik < t ≤ X_ik } where E_ik is the left-truncation time. All individuals alive without developing breast cancer at the study closing date (June 30, 2003) were considered as right censored. The censoring times are independent of the event times. Thirty-three individuals among 98 mutation-positive women, and 5 individuals among 353 mutation-negative women, developed breast cancer during up to 30 years of follow-up. There were 17 and 14 deaths without prior breast cancer in the BRCA1 mutation-positive and mutation-negative groups, respectively.

We estimated the cumulative incidence of breast cancer for women in BRCA1 mutation-positive and mutation-negative women, treating death without breast cancer as a competing risk and taking within-family correlation into account. The lifetime cumulative incidence of breast cancer in the non-carriers was 6.4% with 95% confidence interval 0.3–12.5%, which is similar to that observed in the general population. Both the NSEs and the RSEs were 0.031. We also used a Gamma frailty model (Andersen et al., 1993) to investigate the within-cluster correlation of failure times. The generalized likelihood ratio tests showed no evidence of family effects for either breast cancer or death without breast cancer in the 353 BRCA1 mutation-negative women, with variance for the frailty variable modulating time to breast cancer estimated as ${\widehat{\mathit{\sigma }}}_1^2=4.1\times {10}^{-5}$ (p-value for ${\widehat{\mathit{\sigma }}}_1^2=0$. is 0.999) and the variance for the frailty variable modulating time to death estimated by ${\widehat{\mathit{\sigma }}}_2^2=0.4$ (p-value for ${\mathit{\sigma }}_2^2=0$ is 0.122).

The cumulative incidence of breast cancer by age 80 in the BRCA1 mutation-positive group was 62.3%, with 95% robust confidence interval 43.8–80.1%. The corresponding RSE was 9.4%, compared with 6.5% for the NSE that ignored within-cluster correlation. The cumulative incidence of breast cancer in the mutation-positive women and the corresponding pointwise 95% confidence intervals are shown in Figure 4 using the nonparametric approach. The Gamma frailty model showed significant within-family correlation for the breast cancer outcome, with ${\widehat{\mathit{\sigma }}}_1^2=0.60$. The generalized likelihood ratio test of the null hypothesis $H_{10}:{\widehat{\sigma }}_1=0$ yielded a p-value 0.029. However, a family effect was not present for the mortality event, with ${\widehat{\mathit{\sigma }}}_2^2=1.2\times {10}^{-4}$, and generalized likelihood ratio test p-value equal to 0.958.

Figure 4.

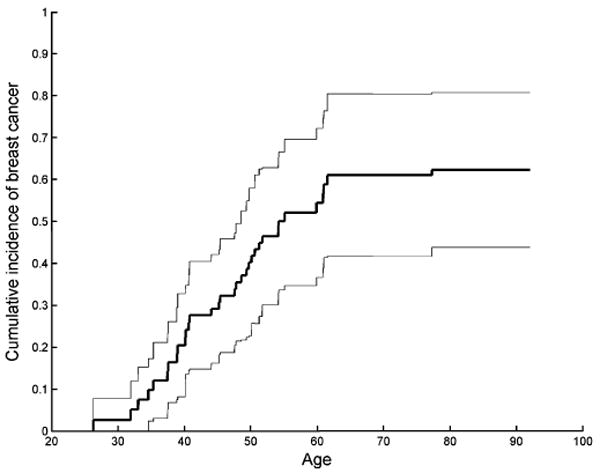
Cumulative incidence of breast cancer in BRCA1 mutation-positive women, and corresponding pointwise 95% confidence intervals.

The landmark test statistic for the null hypothesis of no difference between these two groups at age 80 is Q_LM = 0.559 (S.E. 0.100), with standardized value Q̃_LM = 5.59, and corresponding p-value of 2.3 × 10⁻⁸. The Gray test statistic is Q_GT = 14.27 (S.E. 2.74), with standardized value Q̃_GT = 5.21, and p-value of 1.9 × 10⁻⁷. The Pepe–Mori test statistic is Q_PM = 20.04 (S.E. 4.07), with Q̃_PM = 4.92, and p-value 8.7 × 10⁻⁷. As expected, each test is highly significant. Although the standardized test statistics are similar, the landmark test is readily interpreted as a 56% difference between the cumulative risks at age 80 in carriers versus noncarriers from the same family.

6. Discussion

The competing risks problem for cluster-correlated failure times is frequently encountered in clinical genetics studies. The HBOC study described here provides an illustrative example with familial clustering. It has been pointed out by several investigators (Gaynor et al., 1993; Pepe and Mori, 1993) that use of the Kaplan–Meier method can be misleading in the presence of competing risks. Therefore, cumulative incidence estimators may be more appropriate. The goal of our analysis was to develop general methods to estimate cumulative incidence accounting for cluster correlation, and to develop appropriate test statistics comparing cumulative incidence curves in the two-sample setting. Our simulation studies and example suggest that naïve estimators and tests may overestimate precision and suffer from inflated type I errors. Therefore, our new methods may be broadly applicable and more appropriate for clinical genetics studies. Our specific finding of a significant family effect for breast cancer among BRCA1 mutation-positive women is biologically plausible and should be followed up in other studies.

The methods developed in this article provide asymptotically consistent point estimates of the cumulative incidence. Simulation studies show that the finite sample biases of the cumulative incidence curves appear to be small, and diminish as the sample size increases, even in settings where individuals within the same cluster are highly correlated with each other. As individuals from different clusters become homogeneous and within-cluster correlation disappears, the robust variance estimate still provides a consistent estimate for the true variance, although it may not be as efficient as the naïve variance estimate.

Left truncation can occasionally introduce computational difficulties. If the risk set includes only a single individual who fails then the Kaplan–Meier curve equals zero beyond that time even if other individuals enter later. Fortunately, the Nelson–Aalen estimator does not have computational difficulties in this situation. A second problem is that the risk sets can be very small, often for early times, and this can result in very large standard errors associated with estimates of cumulative hazards or cumulative incidence.

For two-sample testing problems, we examined the empirical size of a landmark test, Gray test, and Pepe–Mori test under the null hypothesis, and we evaluated the empirical power of these tests under selected alternative hypotheses. All tests controlled the type I error. The respective powers depended on the extent of within-cluster correlation. The landmark test is simple to interpret but it may be underpowered if the data are not informative at the landmark time of interest. Both the Gray and the Pepe–Mori tests can have higher statistical power over the other; the Gray test is more powerful when the shapes of the two cumulative incidence curves are different, while the Pepe–Mori test is more powerful when one cumulative curve is consistently higher than the other curve. Therefore, both can be useful in practice.

Our methodology can be extended in several settings. In Section 5, we extended it to accommodate left-truncation by modifying the at-risk processes Y_ik (t). For the general K-sample problem, one might design a global test by constructing the optimal linear combination of results from two-sample test statistics. The Gray and Pepe–Mori tests have been generalized to the setting of recurrent events (Ghosh and Lin, 2000) and multivariate recurrent events (Chen and Cook, 2004) in the presence of the competing risk of a terminal event (death). The robust variance estimator for the regression coefficients has been studied for clustered recurrent events in the settings of semiparametric models (Schaubel, 2005). However, it remains to extend those nonparametric tests to cluster-correlated recurrent events.

In conclusion, we develop estimates and tests for cumulative incidence curves when event times for individuals from the same cluster are correlated. Such an approach is useful when interest lies in investigating the absolute risks, as we see from the HBOC study. The HBOC dataset is available through Dr MHG (greenem@mail.nih.gov). The simulation studies and data analysis for this article were conducted using Matlab (MathWorks, 2006). Programs are available from BEC (bingshu@chenstat.com) upon request.