Abstract
The distribution of contractile forces generated in cytoskeletal stress fibers (SFs) contributes to cellular dynamic functions such as migration and mechanotransduction. Here we describe a novel (to our knowledge) method for measuring local tensions in SFs based on the following procedure: 1), known forces of different magnitudes are applied to an SF in the direction perpendicular to its longitudinal axis; 2), force balance equations are used to calculate the resulting tensions in the SF from changes in the SF angle; and 3), the relationship between tension and applied force thus established is extrapolated to an applied force of zero to determine the preexisting tension in the SF. In this study, we measured tensions in SFs by attaching magnetic particles to them and applying known forces with an electromagnetic needle. Fluorescence microscopy was used to capture images of SFs fluorescently labeled with myosin II antibodies, and analysis of these images allowed the tension in the SFs to be measured. The average tension measured in this study was comparable to previous reports, which indicates that this method may become a powerful tool for elucidating the mechanisms by which cytoskeletal tensions affect cellular functions.
Introduction
Forces generated by the cytoskeleton in cells are believed to contribute to the dynamic processes of cells. For example, such forces cause cells to move, resulting in cell migration. During cell migration, the lamellipodial membrane protrudes at the leading edge of the cell, the cell adheres to the substratum, and the cell body translocates forward. In the translocation step, contraction of stress fibers (SFs), which are actomyosin bundles, retract the rear part of the cell, resulting in forward propulsion of the cell body. Inhibition of actomyosin-based tension generation results in inhibition of lamellipodia formation (1), indicating that the tension in SFs has a major role in moving a cell during cell migration. In a previous study using traction force microscopy, which determines the stress distribution rather than the force in a cell by measuring the deformation of extracellular substrates (2,3), Iwadate and Yumura (4) demonstrated that the stress distribution in cells changes during migration. Therefore, it is important to understand how the force distribution in SFs affects the motility of migrating cells by measuring the magnitude and distribution of tensions in SFs.
In addition to the direct effects of cytoskeletal forces on cell functions such as cell migration, recent studies have shown that changes in cytoskeletal forces may indirectly regulate cell functions. For example, vascular endothelial cells exposed to fluid shear stresses align their long axis with the direction of the flow (5,6) and exhibit a variety of cellular responses, including cell proliferation (7), expression of adhesive molecules (8), and changes in cytoskeletal structure and morphology (9). As cells respond to changes in cytoskeletal forces, they transduce the external forces into chemical signals in a process called mechanotransduction. A previous study suggested that forces acting on the cell surface are transmitted through the cytoskeleton to the nucleus and focal adhesion sites in the mechanotransduction process (10). In a more recent study, Hayakawa et al. (11) directly demonstrated force transmission through SFs by pulling the SFs and observing a calcium influx at the focal adhesion sites. This result indicates that changes in the tension in SFs cause changes in cellular responses. To ascertain whether this is indeed the case, it is necessary to measure both the tension and its distribution in SFs during the force-transmitting process.
Because of the important influence of cytoskeletal forces on cell functions, several studies have sought to determine the tension in SFs. Sabass et al. (12) and Schwarz et al. (13) reconstructed traction forces at focal adhesion sites of cells seeded on an elastomeric gel with embedded microbeads from the displacement field of the beads by solving an inverse problem. Focal adhesion sites anchor the SFs in cells; therefore, this method enables us to indirectly estimate the tension in SFs from the traction forces. Deguchi et al. (14,15) estimated the tension in SFs by first measuring the average preexisting strain in a collection of SFs on a dish and then determining the average tension-strain relationship from tensile tests on isolated SFs. Key requirements for the next advances in cytoskeletal force analysis are 1), the ability to measure tensions in SFs using the SFs themselves as the measuring tools, without using intermediate substances or subcellular objects as proxies; and 2), the ability to measure local tensions within SFs in a cell.
In this study, we developed and tested a novel (to our knowledge) method to measure the local tensions generated in SFs. The method uses the principle of force balance. Here we describe the principles of the proposed method and present an example of measurement of tension in SFs.
Materials and Methods
Principle of tension measurement
The method developed in this study uses the force balance between the tension in a filament (e.g., an SF) and an externally applied force. A schematic illustration of the principle used to measure tension is depicted in Fig. 1. Here, we consider an example in which a tension, T, is generated within a filament in the original filament direction (Fig. 1 A). When a known external force, F, is applied to the filament, it deforms such that a balance is achieved among F and the tensions in the filament to the left and right of the force application point (TL, TR). When these three forces are balanced, two equations are obtained that describe the force balance in the original filament direction and the perpendicular direction as follows:
| (1) |
| (2) |
where β is the angle between the external force and the direction perpendicular to the original filament direction, and θL and θR are the angular changes of the left and right segments of the filament, respectively. If the external force is applied from a direction perpendicular to the original filament direction, i.e., β ≈ 0, Eqs. 1 and 2 can be written as
| (3) |
and
| (4) |
respectively. Thus, TL and TR can be calculated by measuring the angles θL and θR. The tensions in the original filament direction, TL′ and TR′, are written as:
| (5) |
| (6) |
Figure 1.
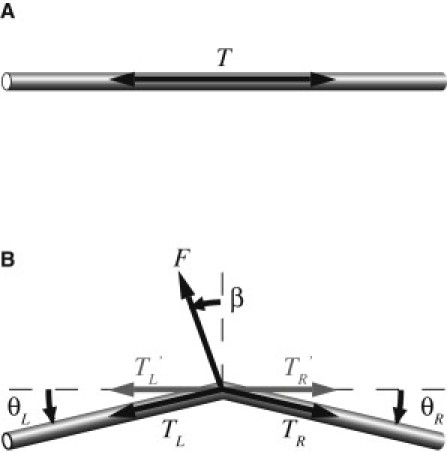
Schematic illustration of force balance within a fiber (A) before and (B) after application of an external force, F. T: Tension before application of F. β: Angle from the direction perpendicular to the direction of the original filament. TL, TR: Tension of the filament during force application. θL, θR: Changes in the angle of the filaments before and after application of F. TL′, TR′: Element of the tension in the direction of the original filament. Subscripts L and R indicate the left and right parts of the filament, respectively, as determined by the force application point.
To eliminate the effect of the applied force F and determine the preexisting tension in the filament, TL′ and TR′ are measured for applied forces of different magnitudes, and the relationship between tension and applied force is plotted. Extrapolating this relationship to an applied force of zero then yields the preexisting tension in the filament. It is obvious that the tension T does not depend on the angle β in this process. To minimize any differences between TL′ and TR′, the force F is applied under the condition where β ≈ 0.
Preparation of magnetic particles
Because the tension in SFs has been reported to be several nanonewtons (14,16), we used an electromagnetic needle and magnetic particles to apply external forces to the cytoskeletons. Two properties were required for the magnetic particles in this study: a narrow size distribution and a spherical shape. A narrow size distribution was required because we calibrated the force acting on the particles in a separate experiment by measuring the drag force of the particles, and then applied this calibration to all tension measurements. A spherical shape was necessary because we used a Stokes equation for the force calibration. For these reasons, 2.8-μm-diameter spherical magnetic particles (Dynabeads M-280 Streptavidin; Invitrogen, Carlsbad, CA) were selected. First, 0.25 mg of the particles were washed three times with 0.1% bovine serum albumin (BSA) in phosphate-buffered saline (-) (PBS(-)) solution and suspended in 25 μL of the same solution. Then, 50 μL of bio-XX-phalloidin (B7474, 0.5 U; Invitrogen) were added to the suspension and this mixture was incubated with shaking at room temperature for 30 min. Finally, the phalloidin-coated magnetic particles were washed three times with 0.1% BSA in PBS(-) solution.
Application of magnetic force
The electromagnetic needle was fabricated as described previously (17,18). A schematic illustration of the experimental setup is depicted in Fig. 2. The electromagnetic needle was attached to a hydraulic 3D micromanipulator (MMN-1 and MMO-203; Narishige, Tokyo, Japan) on a microscope (IX-81; Olympus, Tokyo, Japan). A direct current driver provided electrical current for the electromagnetic needle. The current was switched on and off with a mechanical relay, which was controlled by a trigger signal generated from a custom LabVIEW 8.6 program (National Instruments, Austin, TX) via a multifunction data acquisition unit (USB-6009; National Instruments). To synchronize image capture with force application, the trigger signals were also sent to an electron-multiplying charge-coupled device camera (iXonEM + DU-888 EM CCD; Andor Technology, Belfast, UK). To prevent overheating of the electromagnetic needle, a silicone tube was wrapped around the coil of the needle, and cooling water was supplied to the tube with a syringe pump.
Figure 2.
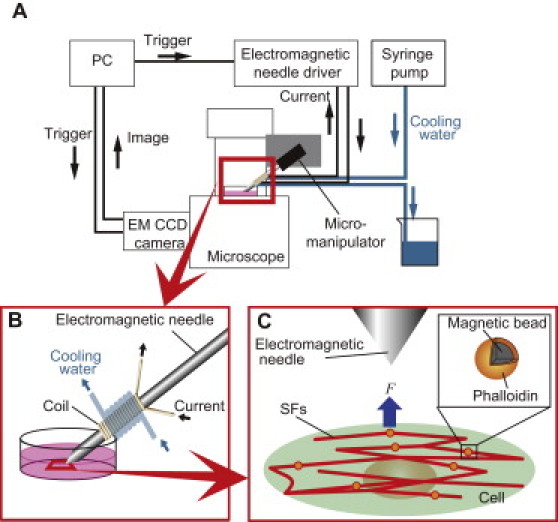
Schematic illustration of the experimental method. (A) Overall experimental setup. Trigger signals sent from a PC apply current to the coil, resulting in the generation of strong magnetic force at the tip of the electromagnetic needle. The heated coil is cooled with a water-based cooling system. Images of SFs and magnetic particles are captured on the EM-CCD when the trigger signals are sent from the PC. (B) A magnified view of the region marked by the thick-line rectangle in panel A. Cells are incubated on a culture dish, the dish is then set on a microscope, and the electromagnetic needle is directed to the dish. (C) A magnified view of the region marked by the thick-line quadrangle in panel B. The tip of the electromagnetic needle is positioned perpendicular to the fiber axis. A magnetic particle bound to an SF is pulled to the tip of the electromagnetic needle.
To calibrate the distance dependence of the force applied to the particles by the electromagnetic needle, the velocity, V, of the magnetic particles driven by a magnetic force in a viscous solution was measured. The magnetic particles were dispersed in a low-viscosity solution (379.5 mPaċs at 22.0°C; JS500; Nippon Grease, Osaka, Japan) or a high-viscosity solution (9270 mPaċs at 22.0°C; JS14000; Nippon Grease) and their velocity was measured for distances of 20–80 μm or 10–20 μm, respectively, from the tip of the electromagnetic needle. The actual viscosity was determined from a temperature-viscosity table obtained from the manufacturer of the product. In each experiment, temperature changes were within ±0.5°C, resulting in a maximum viscosity change of ±3%. The velocity was measured from the captured images with the use of image analysis software (ImageJ 1.42i; National Institutes of Health, Bethesda, MD). Because the fluid force acting on a magnetic particle balances the magnetic force, the magnetic force was calculated from the Stokes equation:
| (7) |
where A is the diameter of the magnetic particles and η is the viscosity of the solution. Force-distance curves under 50, 100, 200, 300, and 450 mA of electric current were obtained in this manner.
Preparation of cells
Xenopus laevis cells derived from tadpoles (XTC-YF, RCB0771; RIKEN BioResource Center, Tsukuba, Japan) were cultured in a mixture of 60% L-15 medium (11415; Invitrogen), 10% fetal bovine serum (12483; Invitrogen), and 30% distilled deionized water supplemented with penicillin-streptomycin (P4333; Sigma-Aldrich, St. Louis, MO). For the experiments, cells were seeded onto a glass-bottom culture dish (P35G-0-14-C; MatTek, Ashland, MA) coated with 0.1% fibronectin (354008; BD, Franklin Lakes, NJ). The cells were incubated until they were subconfluent, and the dish was then immersed in various solutions according to the modified method of Katoh et al. (19) to easily attach magnetic particles to the SFs. The cells were washed three times with buffer A (1 μg/mL leupeptin (4041; Peptide Institute, Osaka, Japan), 1 μg/mL pepstatin (4397; Peptide Institute) in PBS(-)) and then incubated in a low-ionic-strength solution (2.5 mM of 2,2′,2″-nitrilotriethanol (145-05605; Wako, Osaka, Japan), 1 μg/mL leupeptin, and 1 μg/mL pepstatin in distilled deionized water) for 10 min. This solution was replaced every 1.5 min. The cells were sequentially treated with Extraction Buffer I (0.05% Nonidet-P40 octylphenoxypolyethoxyethanol (E109; Amresco, Solon, OH) in buffer A) for 5 min and Extraction Buffer II (0.05% Triton-X100 in buffer A) for 5 min, followed by three washes with buffer A.
The obtained SFs were incubated in a solution containing 50 μg/mL of the magnetic particles coated with phalloidin for 1 h. To visualize the SFs, we further incubated them for 30 min in a solution containing myosin II antibodies (GTX11087; GeneTex, Irvine, CA) conjugated with fluorescent dye (Z25302; Invitrogen) according to the product manual. Finally, the SFs were washed three times with buffer A. All processes described in this section that followed incubation in the low-ionic-strength solution were performed on ice.
Force application to SFs
The SFs were observed under an epifluorescent microscope through a 100× oil immersion lens (NA = 1.4, UPlanSApo; Olympus). An SF bound to a magnetic particle was located in the field of view and the binding was first confirmed by applying a weak magnetic force. When several SFs overlapping a magnetic bead moved together, or magnetic beads were apparently bound to multiple SFs, these SFs were not analyzed. When a single bead bound to an SF was seen to be close to other SFs, a weak magnetic force was applied to the bead, and the movements of the nearby SFs were checked to confirm that the bead was not bound to them.
After the electromagnetic needle was positioned perpendicular to the longitudinal axis of the SF, a square wave current with a frequency of 0.5 Hz and a duty cycle of 50% was applied to the coil of the electromagnetic needle for 12 s to record six images under both application and removal of force. Fluorescent images of the myosin signal and bright-field images of the magnetic particles and needle were captured by the CCD camera every second. Magnetic forces with five different magnitudes were sequentially applied to a single magnetic particle using electric currents of 50, 100, 200, 300, or 450 mA.
Analysis
The captured fluorescent and bright-field images were analyzed with the use of image analysis software (ImageJ). From the bright-field images, the distance between the tip of the electromagnetic needle and the center of mass of the magnetic particles were measured, and the magnetic force was determined from the force-distance relationship.
Displacement of the SFs was measured from fluorescent images of SFs bound to magnetic particles (Fig. 3 A) as follows: Images were captured every second for 12 s and averaged for noise reduction (Fig. 3 B). The center positions of the myosin signals were then determined with a plug-in available with ImageJ (Particle Tracker (20); Fig. 3 C). We grouped the myosin points on the SF into the left or right side of the SF by drawing a line through the tip of the electromagnetic needle and center of mass of the magnetic particle (Fig. 3 D). For each side of the SF, we fitted a regression line to the center positions of the myosin signals using a least-squares method (Fig. 3 E). We then calculated the angles between lines fitted in the presence or absence of the magnetic force from the slopes of the lines.
Figure 3.
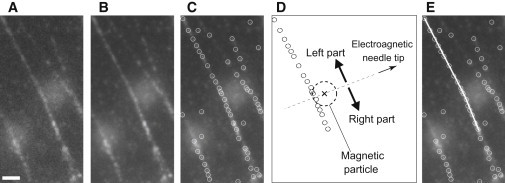
Procedure for measuring displacement of an SF. Raw fluorescent images (A) were captured six times and then averaged (B). (C) The fluorescently labeled myosins were then detected (circles) with an image analysis tool. For the left and right parts of the SF in the image (D), straight lines were fitted using the least-squares method (E), and finally the angle between lines before and after application of external forces was calculated. Bar = 2 μm.
The tension in the SF during the application of the magnetic force was then calculated based on Eqs. 3–6.
Results
To investigate the time required for the magnetic particles to complete their movement after an external force was applied, we measured the change in the displacement of the particles over time. Fig. 4 A shows a typical bright-field image of a magnetic particle bound to an SF. After applying an external force of 570 pN, we measured the displacement of the magnetic particle every 43 ms for 10 s. The time variation of the displacements of magnetic particles bound to different SFs is shown in Fig. 4 B. Particles moved quickly in response to the magnetic force, and their displacements rapidly reached a plateau level. The magnified view of the chart (Fig. 4 C) shows that within 0.20 s after the application of force, all of the particles completed ≥80% of their displacement and remained at this plateau for a further 10 s. We also calculated the time constant of the displacement-time relationship by applying a standard linear model. Because the tip of the electromagnetic needle started to move toward the bead due to the heating caused by the electric current, we calculated the time constant from the data before movement occurred, i.e., 2.5–5.0 s after force application. As a result, the damping time constant was calculated to be 0.08 ± 0.08 s (mean ± standard deviation (SD)), which was sufficiently small. Fluorescent and bright-field images were acquired 0.60 s after the application of force in the experiments described below.
Figure 4.
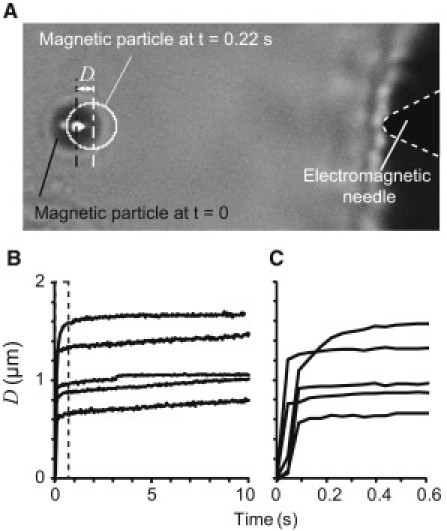
Changes in displacement of the magnetic particles over time after the application of magnetic force (570 pN). (A) A raw bright-field image of a magnetic particle and tip of the electromagnetic needle before application of the external force. The white circle shows the position of the particle at t = 0.22 s after application of the force. The displacement D was measured from the position of the center of the mass of the particle. (B) Changes in the displacement D of the particles after application of the external force. Each line was obtained from different particles on different SFs. Displacement D was measured from images captured every 43 ms. (C) An enlarged view of the box-shaped region in panel B.
Fig. 5 A shows a bright-field image of magnetic particles in a cultured cell, and Fig. 5 B shows a fluorescent image of the same region. In Fig. 5 B, SFs identified with fluorescent myosin II antibodies were clearly evident (arrows). Even after washing with PBS(-), many magnetic particles, which were apparently unbound to any SFs, were also clearly seen. To confirm whether a magnetic particle was bound to an SF, we applied a weak magnetic force to the particle. One particle within this field of view was confirmed to be bound to an SF (arrowhead in Fig. 5, A and B).
Figure 5.
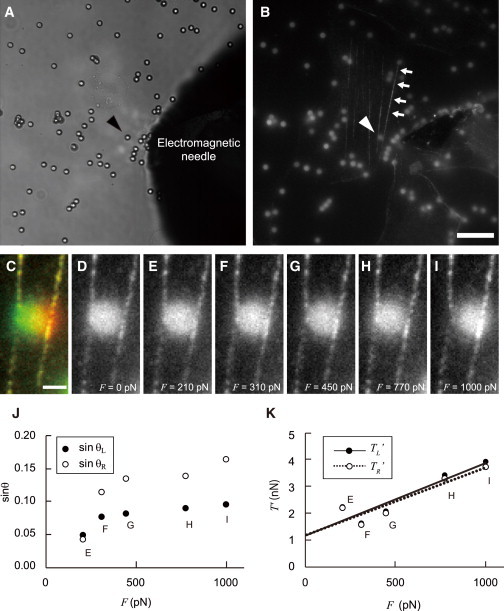
A typical example of the measurement of tension in an SF. (A) A bright-field image was used to track the electromagnetic needle and the particles. (B) A fluorescent image of the myosin II (arrows) label in the same field of view shown in panel A. Magnetic particles were also found in this fluorescent image perhaps because the particles were autofluorescent. Arrowheads in panels A and B show a magnetic particle that was confirmed to be bound with the SF. Bar = 10 μm. (C–I) Enlarged views of the area around the magnetic particle indicated by the arrowheads in panels A and B when external forces were applied. (C) Merged image of images at F = 0 (green) and 1000 pN (red). Bar = 1 μm. The applied forces were (D) F = 0, (E) F = 210, (F) F = 310, (G) F = 450, (H) F = 770, and (I) F = 1000 pN. (J) The relationship between external force, F, and displacement of the SFs. The displacement increased with an increase in F. (K) Calculated tensions (TR′, TL′) from Eqs. 3–6, and data for displacement and F. Fitted linear and dotted lines to plots were obtained by least-squares regression (TL′ = 2.7 F + 1.2, R2 = 0.86; TR′ = 2.5F + 1.2, R2 = 0.85). (In color online.)
When the magnetic force was applied, the SF bound to the magnetic particle moved toward the tip of the electromagnetic needle. Fig. 5 C shows merged images of an SF and a bound particle when a 0 pN (green) or 1000 pN (red) external force was applied. It can be seen that both the particle and the SF moved toward the tip of the electromagnetic needle, confirming that the magnetic force was applied to the particle and the SF. However, the displacement of the magnetic particle (1.02 μm) was greater than that of the SF (400 nm) in the direction of the applied force, indicating that the magnetic particle may have rotated about the axis of the SF under the influence of the magnetic field. Therefore, it is necessary to measure the displacement of the SF instead of the particle. Images of an SF subjected to external forces corresponding to electric currents of 0, 50, 100, 200, 300, or 450 mA are shown in Fig. 5, D–I. The magnitudes of the applied forces determined from the calibrated force-distance curves were 0, 210, 310, 450, 770, and 1000 pN, respectively. Fig. 5 J shows plots of the sine of the angles θL and θR versus the applied force (F). These results demonstrate that the angles increased with the magnitude of the applied force.
Plots of the calculated tensions, TL′ and TR′, for each applied force are shown in Fig. 5 K. It can be seen that there is a general increase with the magnitude of the force. The best-fit lines for TL′ and TR′ were found to be TL′ = 2.7F + 1.2 (R2 = 0.86) and TR′ = 2.5F + 1.2 (R2 = 0.85), respectively. Therefore, the tension in this SF was determined to be 1.2 nN from the intercept of the fitted lines on the y axis of the chart.
Fig. 6 shows a histogram of the measured tensions in the SFs. These measurements were obtained from different SFs in different cells, and were found to be distributed in the range of 0–4 nN, with an average value of 1.6 ± 1.0 nN (mean ± SD, n = 19). The average tension is comparable to estimated values reported in previous studies (several tens of nanonewtons (16) and 4 nN (14)), indicating that the method developed in this study is useful for measuring tension in SFs.
Figure 6.
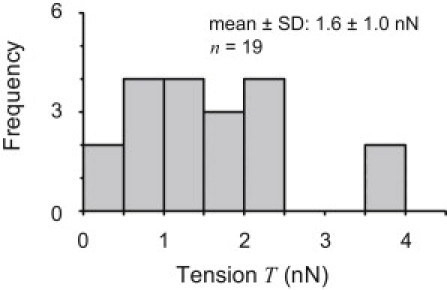
Histogram of measured tensions in SFs. Multiple measurements of tensions were made for many SFs; the distribution of these tensions is shown in this graph. The measured tensions were all obtained from SFs in different cells.
Discussion
We have described a novel (to our knowledge) method for measuring the local tension in SFs using their displacements under an applied magnetic force in the presence of magnetic particles. Techniques that accurately measure local tension are important for determining the distribution of tension in cells. Such information may prove useful in future studies to investigate the effect of the force distribution on the motility of migrating cells. We developed our method for measuring tension by analyzing the simple force balance between tension and a known external force applied to the SF. When an external force is applied to an SF, the displacement of the SF depends on its tension. In other words, perturbation due to the mechanical force application enables us to measure the tensions present in SFs before force application.
The method uses an electromagnetic needle and particles, and enables us to measure tensions in cells in a noncontact manner. Therefore, this method may be used to measure cytoskeletal forces in live cells if magnetic particles are injected into them, allowing changes in the tension of filaments over time to be measured. Because this is central to understanding the mechanisms of mechanotransduction and cell migration, the proposed method is expected to be a powerful tool for the investigation of these mechanisms.
We measured tensions in SFs in XTC-YF cells to demonstrate the feasibility of the proposed method. The principle is applicable not only to SFs but also other filaments that generate tension. We used an electromagnetic needle in part because the estimated tension of nanonewtons in SFs (14,16) is comparable to the typical forces generated by an electromagnetic needle (i.e., from a few piconewtons (21) to several nanonewtons (22)). One can adapt the method to filaments with tensions smaller or larger than those associated with SFs simply by changing the magnitude of the applied force. For example, for relatively small tensions, optical tweezers, which normally produce forces of up to several tens of piconewtons, would be suitable.
During the tension measurements in this study, other (undesired) forces acted on the SFs due to stretching and bending. This occurred because the external force was applied in the direction perpendicular to the original filament direction. As shown in Fig. 1 B, deformation of SFs under an applied force lengthens and stretches them. This stretching generates an internal force, resulting in an overestimation of the measured tension. Bending of the SFs may also occur, giving rise to a repulsive force that opposes the applied force, again resulting in an overestimation of the tension. However, these overestimations were found to be within a few percent of the measured values (see Supporting Material), indicating that the effects of stretching and bending were negligible. Furthermore, the values of tension presented here were determined by extrapolation to a theoretical point with zero applied force, as shown in Fig. 5 K. Presumably, bending and stretching do not affect the tension at F = 0; therefore, their effects on the measured tension are likely to be insignificant. It should be noted that although the force applied to the bead might cause it to rotate to balance the angular moment generated from the applied force and the tensions, no change in the force balance occurs, i.e., no additional forces are generated due to the rotation (see Supporting Material). Therefore, such a rotation does not have a significant effect on the measurement of tension in SFs.
In Fig. 5, only very local bending of the SF is observed close to the bead. The typical length of SFs, which was obtained from images of cells transfected with GFP-actin, was 12.9 ± 6.5 μm (mean ± SD, n = 33; data not shown). This indicates that very thin SFs, which can barely be observed under a fluorescent microscope, exist between the clearly visible SFs. In this case, SFs far from a bead should undergo less bending during the application of magnetic force. However, we confirmed that even though such thin invisible SFs may exist, tension measurements on the visible SFs are still valid when the SFs are observed to be straight (see Supporting Material) because the forces on the thin SFs should be negligibly small. Therefore, in this analysis we used only those myosin points that were close to the bead, i.e., in the region where the SFs appeared to be straight.
It is possible that labeling of the SFs with antibodies might affect their tensions and mechanical properties. However, we believe that these effects were negligible, for the following reasons: First, we used nonmuscle myosin IIA antibodies to label the SFs, and their antigen is at the tail of the myosin, at the C-terminal. Therefore, the antibody is not likely to have a critical effect on the tension in SFs. Second, in our preliminary experiments, we confirmed that the tension in SFs labeled with quantum dots conjugated with phalloidin, which labels f-actin in SFs, was comparable to the results presented here (1.9 and 3.3 nN; data not shown). Because the separation between the quantum dots on the SFs was ∼1 μm, labeling with quantum dots should have no significant effect on the mechanical properties and tensions of the SFs. A similarly small influence would be expected for myosin II labeling.
In this study, forces were applied under the condition β ≈ 0. If this were not the case, the regression lines in Fig. 5 K would cross each other at F = 0. Although for β ≠ 0, it might be possible to measure the force more reliably, such a situation could lead to other concerns. For a large applied force F, it is possible for one side of the SF to become compressed. In this situation, a linear relation would not exist between the measured tension T and F, and it would be difficult to recognize those situations from the acquired images. To avoid this situation, we decided that it was better to apply the forces with β ≈ 0.
The differences between the fitted and measured results in Fig. 5 K are thought be due to errors in the determination of the center of the myosin. We simulated the effect that this would have on the measured tensions (for details, see Supporting Material). We determined the SD associated with errors in the myosin positions to be ∼0.1 pixel using a method that assumes a Poisson pixel noise distribution (20). The myosin positions were then statistically varied based on a normal error distribution with an SD of 0.1 pixel, and the resulting changes in the SF angles were calculated. The results indicated a distribution of SF angles with an SD of 0.57°. In this study, the applied magnetic force caused a change of 4.1° in the SF angle. An angular error of 0.57° thus corresponds to an error of ∼13% in the measured tension. Because this is comparable to the value of 11% obtained for the SD of the tension errors, it may partially explain the discrepancy between the fitted and measured results shown in Fig. 5 K.
One possible limitation of the method developed in this study is the response of cells to applied external forces. The applied forces would increase tension in SFs by causing them to stretch. Changes in tensions in the cytoskeleton may cause unintended responses in cells. Because the responses of vascular endothelial cells to external forces are dose-dependent (23) and exhibit thresholds (24), reducing the magnitude of the applied force might reduce these unwanted effects. However, if smaller forces are used, improvements in image capture and analysis methods may be necessary to detect the smaller changes in the bending angles of SFs. For example, labeling SFs with brighter dyes will be useful because measurement of angle θL and θR depends on the accuracy of the position of the myosin, which depends on the signal/noise ratio of the light point of myosins (25).
In summary, we have developed what is to our knowledge a novel and unique method to measure tensions in SFs by applying external forces to the cytoskeleton and analyzing the force balances. The method enabled us to measure local tensions in SFs. Furthermore, the magnetic particles and electromagnetic needle system employed in this method allowed us to obtain these measurements without contacting the cells. Tensions measured in SFs in XTC-YF cells were found to be comparable to reported values, indicating that this method is accurate and reliable. The principle of this method can be applied widely to fibrous substances other than SFs, regardless of the tension they generate, indicating that it will be a useful tool for analyzing a wide range of cell functions affected by cytoskeletal forces.
Acknowledgments
The authors thank Dr. Yutaka Yamagata and Ms. Junko Sunaga at RIKEN for their technical support.
This study was supported in part by Grants-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology of Japan (Nos. 20001007 and 21-3835).
Supporting Material
References
- 1.Parker K.K., Brock A.L., Ingber D.E. Directional control of lamellipodia extension by constraining cell shape and orienting cell tractional forces. FASEB J. 2002;16:1195–1204. doi: 10.1096/fj.02-0038com. [DOI] [PubMed] [Google Scholar]
- 2.Oliver T., Dembo M., Jacobson K. Traction forces in locomoting cells. Cell Motil. Cytoskeleton. 1995;31:225–240. doi: 10.1002/cm.970310306. [DOI] [PubMed] [Google Scholar]
- 3.Dembo M., Wang Y.L. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Iwadate Y., Yumura S. Actin-based propulsive forces and myosin-II-based contractile forces in migrating Dictyostelium cells. J. Cell Sci. 2008;121:1314–1324. doi: 10.1242/jcs.021576. [DOI] [PubMed] [Google Scholar]
- 5.Dewey C.F., Jr., Bussolari S.R., Davies P.F. The dynamic response of vascular endothelial cells to fluid shear stress. J. Biomech. Eng. 1981;103:177–185. doi: 10.1115/1.3138276. [DOI] [PubMed] [Google Scholar]
- 6.Davies P.F., Dewey C.F., Jr., Gimbrone M.A., Jr. Influence of hemodynamic forces on vascular endothelial function. In vitro studies of shear stress and pinocytosis in bovine aortic cells. J. Clin. Invest. 1984;73:1121–1129. doi: 10.1172/JCI111298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Levesque M.J., Nerem R.M., Sprague E.A. Vascular endothelial cell proliferation in culture and the influence of flow. Biomaterials. 1990;11:702–707. doi: 10.1016/0142-9612(90)90031-k. [DOI] [PubMed] [Google Scholar]
- 8.Morigi M., Zoja C., Remuzzi A. Fluid shear stress modulates surface expression of adhesion molecules by endothelial cells. Blood. 1995;85:1696–1703. [PubMed] [Google Scholar]
- 9.Galbraith C.G., Skalak R., Chien S. Shear stress induces spatial reorganization of the endothelial cell cytoskeleton. Cell Motil. Cytoskeleton. 1998;40:317–330. doi: 10.1002/(SICI)1097-0169(1998)40:4<317::AID-CM1>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- 10.Davies P., Barbee K. Endothelial cell surface imaging: insights into hemodynamic force transduction. News Physiol. Sci. 1994;9:153–157. [Google Scholar]
- 11.Hayakawa K., Tatsumi H., Sokabe M. Actin stress fibers transmit and focus force to activate mechanosensitive channels. J. Cell Sci. 2008;121:496–503. doi: 10.1242/jcs.022053. [DOI] [PubMed] [Google Scholar]
- 12.Sabass B., Gardel M.L., Schwarz U.S. High resolution traction force microscopy based on experimental and computational advances. Biophys. J. 2008;94:207–220. doi: 10.1529/biophysj.107.113670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schwarz U.S., Balaban N.Q., Safran S.A. Calculation of forces at focal adhesions from elastic substrate data: the effect of localized force and the need for regularization. Biophys. J. 2002;83:1380–1394. doi: 10.1016/S0006-3495(02)73909-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Deguchi S., Ohashi T., Sato M. Evaluation of tension in actin bundle of endothelial cells based on preexisting strain and tensile properties measurements. Mol. Cell. Biomech. 2005;2:125–133. [PubMed] [Google Scholar]
- 15.Deguchi S., Ohashi T., Sato M. Tensile properties of single stress fibers isolated from cultured vascular smooth muscle cells. J. Biomech. 2006;39:2603–2610. doi: 10.1016/j.jbiomech.2005.08.026. [DOI] [PubMed] [Google Scholar]
- 16.Tan J.L., Tien J., Chen C.S. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc. Natl. Acad. Sci. USA. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ueki Y., Sakamoto N., Sato M. Cyclic force applied to FAs induces actin recruitment depending on the dynamic loading pattern. Open Biomed. Eng. J. 2010;4:129–134. doi: 10.2174/1874120701004010129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Matthews B.D., LaVan D.A., Ingber D.E. Electromagnetic needles with submicron pole tip radii for nanomanipulation of biomolecules and living cells. Appl. Phys. Lett. 2004;85:2968–2970. [Google Scholar]
- 19.Katoh K., Kano Y., Fujiwara K. Isolation and contraction of the stress fiber. Mol. Biol. Cell. 1998;9:1919–1938. doi: 10.1091/mbc.9.7.1919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sbalzarini I.F., Koumoutsakos P. Feature point tracking and trajectory analysis for video imaging in cell biology. J. Struct. Biol. 2005;151:182–195. doi: 10.1016/j.jsb.2005.06.002. [DOI] [PubMed] [Google Scholar]
- 21.Strick T.R., Allemand J.F., Croquette V. The elasticity of a single supercoiled DNA molecule. Science. 1996;271:1835–1837. doi: 10.1126/science.271.5257.1835. [DOI] [PubMed] [Google Scholar]
- 22.Bausch A.R., Ziemann F., Sackmann E. Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 1998;75:2038–2049. doi: 10.1016/S0006-3495(98)77646-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ando J., Ohtsuka A., Kamiya A. Wall shear stress rather than shear rate regulates cytoplasmic Ca++ responses to flow in vascular endothelial cells. Biochem. Biophys. Res. Commun. 1993;190:716–723. doi: 10.1006/bbrc.1993.1108. [DOI] [PubMed] [Google Scholar]
- 24.Lawrence M.B., Kansas G.S., Ley K. Threshold levels of fluid shear promote leukocyte adhesion through selectins (CD62L,P,E) J. Cell Biol. 1997;136:717–727. doi: 10.1083/jcb.136.3.717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yildiz A., Forkey J.N., Selvin P.R. Myosin V walks hand-over-hand: single fluorophore imaging with 1.5-nm localization. Science. 2003;300:2061–2065. doi: 10.1126/science.1084398. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


