Abstract
The actin regulatory protein, cofilin, increases the bending and twisting elasticity of actin filaments and severs them. It has been proposed that filaments partially decorated with cofilin accumulate stress from thermally driven shape fluctuations at bare (stiff) and decorated (compliant) boundaries, thereby promoting severing. This mechanics-based severing model predicts that changes in actin filament compliance due to cofilin binding affect severing activity. Here, we test this prediction by evaluating how the severing activities of vertebrate and yeast cofilactin scale with the flexural rigidities determined from analysis of shape fluctuations. Yeast actin filaments are more compliant in bending than vertebrate actin filaments. Severing activities of cofilactin isoforms correlate with changes in filament flexibility. Vertebrate cofilin binds but does not increase the yeast actin filament flexibility, and does not sever them. Imaging of filament thermal fluctuations reveals that severing events are associated with local bending and fragmentation when deformations attain a critical angle. The critical severing angle at boundaries between bare and cofilin-decorated segments is smaller than in bare or fully decorated filaments. These measurements support a cofilin-severing mechanism in which mechanical asymmetry promotes local stress accumulation and fragmentation at boundaries of bare and cofilin-decorated segments, analogous to failure of some nonprotein materials.
Introduction
Cofilin is an actin filament severing protein that contributes to overall assembly dynamics and motility by increasing the number of free filament ends from which free subunits associate and dissociate (1–4). Severing occurs without coupling to energy sources such as ATP hydrolysis. Severing is instead driven by cofilin binding and linked reactions (5).
Cofilin alters the helical structure of filaments (6,7) and increases the conformational dynamics of subunits such that they are more compliant in bending (8–10) and twisting (11). These changes in filament mechanical properties suggest that alterations of filament mechanics and dynamics could promote their fragmentation. The observed surface tethering-dependence of cofilin severing activity (12) is consistent with filament mechanics playing a critical role in severing.
We proposed that a local asymmetry in actin filament (bending-and-twisting) mechanics and discontinuity in topology localizes stress at boundaries and promotes severing, analogous to fatigue fractures of nonprotein materials (8,13,14). Consistent with this model, cofilin severing is maximal at substoichiometric binding densities (12,15) and scales with the density of boundaries between bare and cofilin-decorated segments (14), for some (16,17) but not all (12,15,18) cofilactin isoforms. In cases where severing activity peaks at cofilin binding densities smaller than those yielding the maximum number of boundaries (12,15,18), surface tethering sites could potentially act as mechanical barriers to filament fluctuations, similar to boundaries, thereby promoting severing (12).
This mechanical asymmetry model also predicts that cofilin-linked changes in filament elasticity influence severing. To evaluate whether alteration of filament elasticity by cofilin scales with filament severing, we measured the severing activities and bending mechanics from thermal fluctuations in shape of various cofilactin isoforms. Cofilin isoforms that alter weakly the actin filament bending stiffness display weak severing activity. In addition, imaging thermally driven fragmentation of fluctuating filaments indicates that severing at boundaries of bare and cofilin-decorated segments occurs at smaller filament deformations than fragmentation of homogenous (bare or cofilin-saturated) filaments. These results support a model in which cofilin-linked stress accumulation and severing occur at bare and cofilin-decorated boundaries possessing a local mechanical asymmetry.
Materials and Methods
Protein purification
All reagents were the highest purity commercially available and came from Sigma-Aldrich (St. Louis, MO), unless otherwise noted. Rabbit skeletal muscle actin was purified and labeled with pyrenyl iodoacetamide (Molecular Probes, Eugene, OR (13)), Alexa 488 succinimidyl ester (Molecular Probes (8)) for flexibility and steady-state length assays, or biotin-maleimide (Sigma-Aldrich) and Cy3b-maleimide (GE Healthcare, Waukesha, WI) for real-time severing assays by using a method similar to that used for pyrene labeling yeast actin (19). The material was then gel-filtered over Sephacryl S300 (Sigma-Aldrich) at 4°C in G-buffer (5 mM Tris (pH 7.5), 0.2 mM ATP, 0.2 mM CaCl2, 0.5 mM DTT, 1 mM NaN3). Saccharomyces cerevisiae actin was purified and labeled with pyrene maleimide or similarly labeled with biotin-maleimide (Sigma-Aldrich) and Cy3b-maleimide (GE Healthcare) for real-time severing assays as described in Northrop et al. (19) or Alexa 488 succinimidyl ester (Molecular Probes (8)) for flexibility and steady-state length assays.
The labeling efficiency was ∼0.8–1.0 pyrene and ∼0.8 Alexa 488 fluorophores per actin monomer. Ca2+-actin monomers were converted to Mg2+-actin monomers with 0.2 mM EGTA and 50 μM MgCl2 then polymerized with 0.1 vol 10× polymerization buffer yielding KMI6.8 buffer (50 mM KCl, 2 mM MgCl2, 2 mM DTT, 0.2 mM ATP, 20 mM imidazole, pH 6.8). Recombinant human nonmuscle cofilin-1, Schizosaccharomyces pombe ADF/cofilin, and actophorin were purified as described in De La Cruz (13). S. cerevisiae cofilin was purified as described in Grintsevich et al. (20). S. cerevisiae cofilin (D34C, C62A mutant) was labeled with Alexa-488 as described in Suarez et al. (21).
Equilibrium binding to actin filaments
Equilibrium binding of cofilin and pyrene actin filaments was monitored by fluorescence with a Quantamaster fluorimeter (Photon Technologies International, South Brunswick, NJ) thermostatically controlled at 25(±0.1)°C. Samples were excited at 366 nm and the observed fluorescence intensities at 407 nm were converted to filament binding densities (ν) as described (5,13,22). Equilibrium binding isotherms were fitted to the numerical solutions of an implicit bimolecular binding equation (23) with the stoichiometry and binding affinity as unconstrained fitting parameters. Fit parameters are subject to large experimental error due to stoichiometric binding limitations. Measurements were made in KMI6.8 buffer at total concentrations of 2 μM for vertebrate and 1.6 μM for yeast actin.
Determination of filament flexural rigidity
Images of individual labeled bare and fully cofilin-decorated fluorescently-labeled actin filaments in supplemented KMI6.8 buffer (KMI6.8 buffer supplemented with 15 mM dextrose, 100 mM DTT, 0.1 mg mL−1 glucose oxidase, and 20 μg mL−1 catalase) were acquired using an Eclipse TE300 microscope (Nikon, Melville, NY) equipped with a Coolsnap HQ-cooled charge-coupled device camera (Roper Scientific, Tucson, AZ) and MetaMorph image acquisition software (Molecular Devices, Downingtown, PA) as described in McCullough et al. (8). The bending persistence length (Lp) was determined by fitting the average angular (θ) cosine correlation of a segment of length s to the following two-dimensional correlation function:
| (1) |
Analysis of filaments undergoing thermal fluctuations and those adsorbed to poly-L-lysine-treated slides using Eq. 1 yielded comparable results.
Real-time severing assay
Direct visualization of filament severing by total internal reflectance fluorescence microscopy was performed essentially as described in Pavlov et al. (12) except filaments (comprised of 1% biotinylated and 15% Cy3b-labeled subunits) were tethered to the coverslip surface with neutravidin (24) and cofilin was added to the flow cell with a chamber volume of 18 μL. Final conditions were KMEI6.8 buffer supplemented with 15 mM dextrose, 100 mM DTT, 0.1 mg mL−1 glucose oxidase, and 20 μg mL−1 catalase and the indicated cofilin concentration. We assessed severing from the average filament length after a minute upon the addition of cofilin to the flow cell.
Equilibrium length severing assay
Samples of 6 μM Alexa-488 labeled actin and cofilin concentrations yielding a range of binding densities were equilibrated for 60 min, serial-diluted to 100–200 nM total actin in buffer containing cofilin concentrations to not alter the binding density, adsorbed to poly-L-lysine treated slides, and imaged as done for the determination of filament flexural rigidity. The average filament length, Lavg, at different cofilin binding densities was measured to estimate the apparent boundary-severing rate, using equations describing the relationship between Lavg and severing (25,26) that were modified as follows.
The total filament number (N) depends on severing and annealing events according to the reaction scheme
| (2) |
where dN > 0. The rate of change in filament number (dN/dt; normalized by the total number of filament subunits, n) is given by the apparent normalized second-order annealing rate constant (kanneal, in units of subunits s−1 filament−1) and the apparent normalized filament severing rate (ksever, in units of filaments s−1 subunit−1) according to
| (3) |
The average filament length (Lavg) is equivalent to the total population of filament subunits divided by the total number of filaments (Lavg= n/N). The values of n, N, and Lavg do not change (dn/dt = 0, dN / dt = 0, and dLavg / dt = 0) under steady-state conditions, such that
| (4) |
and Lavg simplifies to the following function of kanneal and ksever:
| (5) |
Therefore, an increase in ksever yields shorter average filament lengths (when changes in kanneal are small).
To distinguish between severing at boundaries and symmetric sites, we express ksever in terms of the normalized fraction of subunits at boundaries of bare and cofilin-decorated segments (b) as
| (6) |
where ksever,sym (filaments s−1 symmetric subunit−1) is the boundary-independent apparent rate for actin filament severing at symmetric sites; ksever,boundary is the apparent severing rate for cofilin-induced actin filament severing at boundaries (filaments s−1 boundary subunit−1). The fraction of occupied sites at boundaries (b) is a function of the cofilin binding density (ν) according to
| (7) |
for noncooperative binding or
| (8) |
for cooperative binding, where ω is the thermodynamic cooperativity parameter (13,22). Note that all sites are symmetric when no boundaries are present (b = 0 when ksever,sym = ksever).
This model assumes that the severing probability, and therefore ksever, is equivalent at identical filament sites (e.g., unoccupied, isolated, singly-contiguous, doubly-contiguous, as defined by a one-dimensional lattice of binding sites (13,22)). Long filaments sever more readily than shorter filaments because they have more potential sites at which to sever. This length-dependence of the severing process is explicitly accounted for in Eq. 3.
To estimate the apparent severing rate at boundaries, we fit Lavg as a function of binding density (Eqs. 6–8) with the cooperativity parameter (ω) for cooperative human cofilin binding constrained to experimentally determined values obtained under comparable conditions (13). The rate of spontaneous (i.e., cofilin-independent) actin filament severing (ksev = 1 × 10−6 filaments s−1 subunit−1; see Fig. 2 (25,27)) was constrained during the fitting procedure. The fits yielded an apparent annealing rate of 4.6 ± 0.2 and 5.7 ± 0.2 subunits s−1 filament−1 for vertebrate and yeast actin filaments, respectively.
Figure 2.
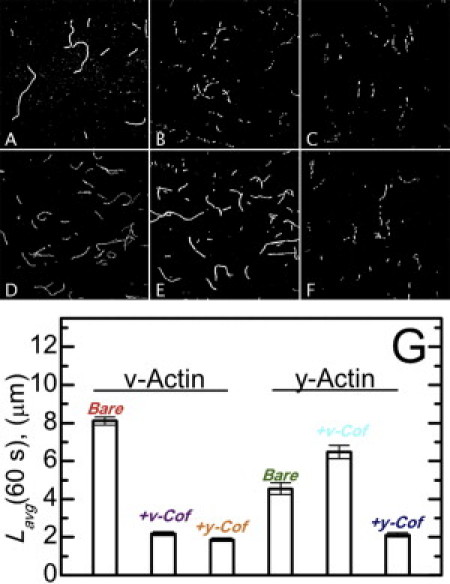
Real-time actin filament severing by cofilin. Fluorescent images of vertebrate muscle (A–C) or yeast (D–F) actin filaments 1 min after the addition of buffer (A and D), 250 nM vertebrate cofilin (B and E), or 250 nM yeast cofilin (C and F). (G) The average filament length of samples shown in panels A–F for sample sizes (number of filaments) of 393 (bare v-actin), 443 (v-actin + v-cofilin), 402 (v-actin + y-cofilin), 1647 (bare y-actin), 1466 (y-actin + v-cofilin), and 417 (y-actin + y-cofilin).
Determination of the critical severing angle
Individual, thermally fluctuating Alexa-488-labeled actin (100–200 nM total actin) and cofilactin (addition of 1.4 μM total cofilin) filaments in supplemented KMI6.6 buffer were imaged as done for determination of filament flexural rigidity. Irreversible filament severing events were identified, cropped, and digitally processed to enhance resolution (8). Severing at boundaries of bare and cofilin-decorated segments was observed by imaging Alexa-488 labeled S. cerevisiae yeast cofilin (D34C, C62A mutant) binding to Alexa568-labeled actin filaments using total internal reflectance fluorescence (21). The angle between filament segments before severing was determined from two consecutive, post- and pre-severing, frames (n = 10 for bare actin and saturated cofilactin filaments; n = 20 for fragmentation at boundaries of partially decorated filaments). The acquisition rate was 10 frames per second in experiments using fluorescently-labeled cofilin, which is well below the observed (see Fig. 4) or predicted (8) bending relaxation time, indicating adequate temporal sampling of the bending angle before severing. Individual measurement errors were within 95% confidence for all events.
Figure 4.
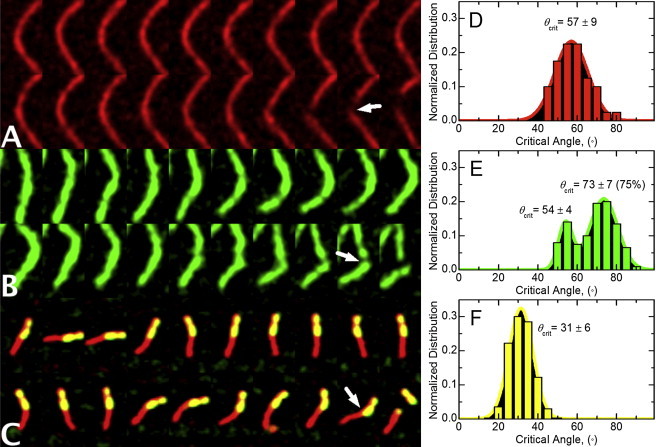
Modulation of the critical actin filament severing angle by cofilin. Subsequent fluorescent images acquired at 100-ms intervals of a thermally fluctuating vertebrate muscle (A) actin or (B) cofilactin filament conformations before fragmentation. (C) Subsequent fluorescent images acquired at 5 s intervals of a thermally fluctuating vertebrate muscle actin filament partially decorated with yeast cofilin (21) before fragmentation. (Arrows) Bending vertex from hingelike motion. The average critical angle for severing of (D) bare vertebrate actin (n = 10), (E) vertebrate cofilactin (n = 10), or (F) at boundaries of bare and cofilin-decorated segments (n = 20). (Solid lines) Best fits of the data to normal distributions. Unimodal and bimodal random fitting distributions of the cofilactin severing angles evaluated using the ANOVA F-test indicate that a bimodal distribution is statistically warranted with >99.9% confidence. Using Satterthwaites's approximation, the statistical probability that we observed a difference between populations by chance is <0.1%.
Energy, forces, and internal work in elastic filaments
The equilibrium equations for an inextensible actin filament segment subject to a bending deformation (28) were used to estimate the net shear force associated with filament conformations. We used the classical Euler bending (θ, ϕ) and twisting (ψ) angles to parameterize the orientation of the filament with arc-length (s) to derive the total elastic free energy function (H, normalized by kBT) with inextensibility constraints,
| (9) |
where Fx, Fy, and Fz are the three components of the internal force associated with the inextensibility condition; LB and LT are the bending and twisting persistence lengths, respectively. We introduce the three moments (A1, A2, and A3) associated with the three Euler angles θ, ϕ, ψ,
| (10) |
to simplify the energy function
| (11) |
and obtain the equilibrium equations for the filament (28)
| (12) |
supplemented with the inextensibility conditions
| (13) |
where X(s), Y(s), and Z(s) are the spatial coordinates of s. In absence of an externally applied force, the internal force components (Fx, Fy, Fz) are constants determined from the solution to Eq. 10.
We solve Eq. 11 with boundary conditions at the ends (s = 0, s = L) of a filament segment of length, L. Both filament ends are constrained to bend with zero elevation (Z(0) = Z(L) = 0; θ(0) = θ(L) = π/2) and to not twist (ψ(0) = ψ(L) = 0). The azimuthal angle, ϕ, is set to 0 and varied at s = L so that the angle between the two unit tangent vectors is ϕ (L). These conditions deal with position (X, Y, and Z) or orientation (θ, ϕ, ψ) variables only. Therefore, the internal force (Fx, Fy, Fz) and moments (A1, A2, A3) are determined by solving Eq. 12 with the above boundary conditions. The shear force, Fshear, is calculated from the projection of the internal force on a plane orthogonal to the tangent vector at one-half of the segment length,
| (14) |
where F is the vector of components (Fx, Fy, Fz), t is the unit tangent vector expressed at s = L/2, and I the identity matrix. The shear work done by the shear force over a distance of one actin filament diameter was calculated by multiplying the shear force by the filament diameter of 6 nm and converting to thermal energy (kBT).
Results
Yeast actin filaments are more compliant in bending than vertebrate actin filaments
The bending persistence length (Lp) of a semiflexible polymer such as an actin filament is determined by the bending stiffness, or (apparent) flexural rigidity (κ), according to
| (15) |
Lp is the characteristic length over which angular correlations of filaments undergoing thermally (kBT)-driven shape fluctuations diminish (stiff filaments have longer Lp lengths than flexible ones). Thus, the filament Lp is determined from the average angular correlation along the contour length of individual filaments undergoing thermally driven fluctuations in shape (Fig. 1).
Figure 1.
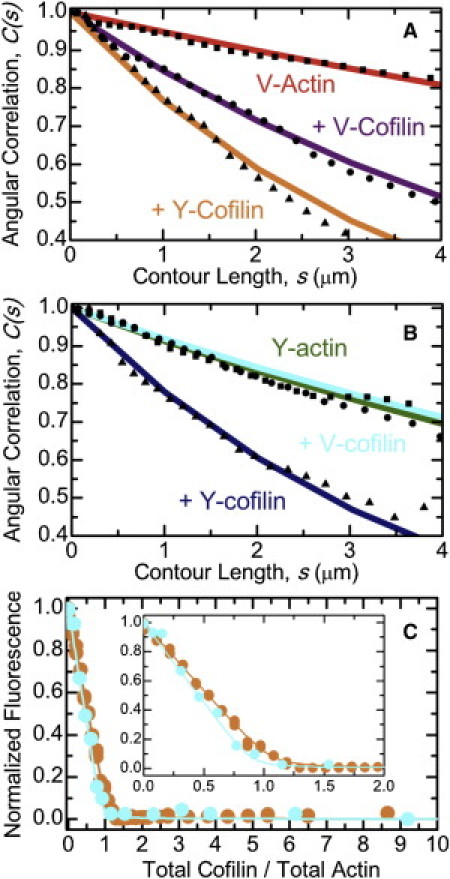
Bending flexibility of yeast and vertebrate cofilactin filaments. (A) The best fits of the average angular correlation of vertebrate muscle actin filaments to the two-dimensional persistence length function (Eq. 1): bare (red), fully decorated human cofilin-1 (violet), or yeast cofilin (orange). (B) The best fits of the average angular correlation of yeast actin filaments to the two-dimensional persistence length function (Eq. 1): bare (green), fully decorated human cofilin-1 (blue), or yeast cofilin (cyan). (C) Equilibrium binding of cofilin and actin filaments: yeast cofilin and vertebrate muscle actin filaments (orange), vertebrate cofilin and yeast actin filaments (blue). (Solid line through the data) Best fit to the numerical solutions of an implicit bimolecular binding isotherm (23), yielding binding affinities <50 nM (52).
Vertebrate muscle actin filaments have an Lp of 9.4 μm (Fig. 1 A; Table 1), in agreement with previous determinations made under slightly different buffer conditions (8,29,30), and as predicted from normal mode analysis (31) and all-atom molecular dynamics simulations (32,33). S. cerevisiae (herein referred to as “yeast”) actin filaments are more flexible in bending than vertebrate filaments, displaying an Lp of 5.5 μm (Fig. 1 B; Table 1), in accord with greater conformational dynamics (34–36) and instability (37,38).
Table 1.
Summary of actin and cofilactin filament bending parameters
| Actin | Cofilin | Lp (μm) |
|---|---|---|
| Vertebrate | — | 9.4 (± 0.7) |
| Vertebrate | Human-1 | 3.0 (± 0.2) |
| Vertebrate | Yeast | 1.9 (± 0.3) |
| Vertebrate | Yeast (S. pombe) | 2.2 (± 0.1) |
| Vertebrate | Actophorin | 2.8 (± 0.3) |
| Yeast | — | 5.5 (± 0.5) |
| Yeast | Human-1 | 5.9 (± 0.4) |
| Yeast | Yeast | 2.0 (± 0.2) |
Conditions are KMI6.8 buffer, 25°C. Yeast is S. cerevisiae unless noted.
Vertebrate cofilin does not increase the flexibility of yeast actin filaments
Vertebrate cofilactin filaments bend more readily than bare filaments (Fig. 1 A (8,10)), as indicated by the reduction in their persistence length from 9.4 to 3.0 μm (Table 1). Similarly, yeast cofilactin filaments are approximately threefold more compliant in bending than their bare filament counterparts, displaying a persistence length of 2.0 μm compared to 5.5 μm (Fig. 1 B; Table 1). Yeast cofilin increases the flexibility of vertebrate actin filaments approximately fivefold (Table 1); the persistence length of saturated filaments is 1.9 μm (Fig. 1 A; Table 1).
In contrast, vertebrate cofilin does not significantly affect the bending flexibility of yeast actin filaments. Yeast filaments saturated with human cofilin have a persistence length of 5.9 μm, comparable to that of bare filaments (5.5 μm; Fig. 1 B; Table 1). Fluorescence quenching of pyrene-labeled yeast actin (Fig. 1 C) and cosedimentation of Alexa-488-labeled yeast actin (data not shown) confirm strong binding under our experimental conditions (Kd = 16 ± 4 nM), revealing that vertebrate (human cofilin-1) cofilin binds yeast actin filaments but does not significantly alter their overall filament flexural rigidity.
Cofilin severing efficiency correlates with linked changes in filament elasticity
It was previously demonstrated that (vertebrate) cofilin increases the bending flexibility of (vertebrate) actin filaments (8), and suggested that local asymmetry in filament mechanics at boundaries of bare and cofilin-decorated segments promotes stress accumulation and severing (8,14). This model leads to two notable predictions that can be experimentally tested: 1), human cofilin severs weakly yeast actin filaments, because its binding does not alter appreciably their elasticity; and 2), combinations of cofilactin displaying enhanced filament flexibility promote severing.
We evaluated these predictions through direct imaging of severing events (Fig. 2) and the [cofilin]-dependence of the average filament length distribution at steady state (Fig. 3). Vertebrate actin filaments are severed readily by vertebrate and yeast cofilin in real-time severing assays (Fig. 2), as previously reported (12,15). Similarly, yeast actin filaments are severed efficiently by yeast cofilin (Fig. 2 (39)). In contrast, no detectable severing of yeast actin filaments is observed upon addition of vertebrate cofilin (Figs. 2 and 3).
Figure 3.
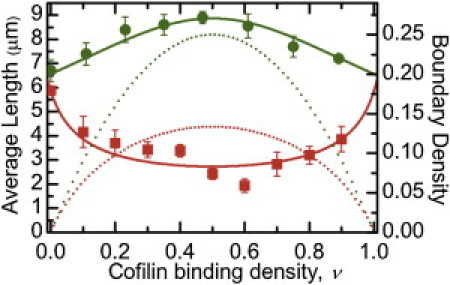
Dependence of average actin filament length on cofilin binding density. The vertebrate cofilin binding density-dependence of the average vertebrate (red) and yeast (green) actin filament steady-state length. (Dotted lines) Density of boundaries between bare and cofilin-decorated filament segments along vertebrate (red) and yeast (green) actin filaments calculated from the binding density and equilibrium binding constants (13,14). The sample size ranged from 100 to 200 filaments at each binding density. Uncertainty bars represent standard errors of the mean.
Filament severing by cofilin scales nonmonotonically with the binding density and is maximal when filaments are partially saturated (12,14,15). These real-time severing measurements were made at identical conditions [cofilin] for all cofilactin isoforms, raising the possibility that the observed severing efficiencies reflect differences in cofilin binding and boundary density on the approach to equilibrium (22) during an experiment, because the affinities and cooperativities differ among the isoforms. We therefore evaluated the yeast and vertebrate filament steady-state length distribution over a range of vertebrate [cofilin] and binding densities (Fig. 3). We did not evaluate severing by yeast cofilin in a similar way because thorough characterization of that process, including the [cofilin]-dependence, has been previously reported (12).
Vertebrate actin filaments have a mean length, Lavg, of ∼7 μm at steady-state (Fig. 3), as previously reported (25,40). Severing decreases the steady-state Lavg (26). Vertebrate cofilin shortens the Lavg for vertebrate actin filaments in a manner that scales with the density of bare and cofilin-decorated boundaries (peak at a binding density of ∼0.5; Fig. 3 (14)), indicative of an increased actin filament severing rate. To assess the severing rate at boundaries of bare and cofilin-decorated segments, we modified equations for Lavg from severing-dependent actin polymerization models (25,26) to yield expressions relating Lavg to the dependence of severing activity on the cofilin-binding density (Eqs. 6–8; see Materials and Methods). The best fit of the binding density-dependence of Lavg to Eqs. 6 and 8 indicates that the severing rate at vertebrate cofilin boundaries along vertebrate filaments is 10-fold greater than within bare or cofilin-decorated clusters (ksever,sym = 1 × 10−6 filaments s−1 symmetric subunit−1; ksever,boundary = 2.7 (± 0.5) × 10−5 filaments s−1 boundary subunit−1). Analysis of severing rates in real-time assays (Fig. 2) yields a comparable severing rate (ksever = 2.6 (± 0.1) × 10−5 filaments s−1 subunit−1).
In contrast to its effect on vertebrate actin, vertebrate cofilin does not shorten the average length of yeast actin filaments (Fig. 3) over a broad range of binding densities, indicating attenuated severing activity as observed in real-time severing assays (Fig. 2). The apparent severing rate at bare and cofilin-decorated boundaries estimated from the binding density-dependence of Lavg (Eqs. 6 and 7) yields comparable severing rates at boundaries and within clusters (ksever,sym = 1 × 10−6 filaments s−1 symmetric subunit−1; ksever,boundary = −8 (±1) × 10−7 filaments s−1 boundary subunit−1; the negative value of ksever,boundary obtained from the best fit of the data results from a reduced severing activity). The overall apparent severing rate, accounting for contributions from both symmetric and boundary subunits, is 5.5 (±1) × 10−7 filaments s−1 subunit−1 at the peak boundary density, comparable to the severing rate determined in real-time assays (Fig. 2; ksever = 6.1 (± 4.1) × 10−7 filaments s−1 subunit−1) and suggest that vertebrate cofilin partially protects yeast actin from fragmentation at intermediate binding densities (Figs. 2 and 3), the molecular basis of which requires further investigation. More importantly, these data reveal that there is a correlation between changes in filament elasticity and cofilin severing activity, consistent with the hypothesis that stress accumulation at boundaries of mechanical asymmetry promotes filament fragmentation (8,12).
Cofilin alters the reversibility of filament bending deformations
We measured the bending deformation at breakage sites of freely-fluctuating filaments (Fig. 4). Observed severing events are associated with a localized bending at the site of fragmentation (Fig. 4). The angle at which local deformation becomes irreversible and filaments sever (i.e., critical bending angle), depends on bound cofilin, such that cofilactin filaments sever at higher critical angles than bare actin filaments (θcrit = 73 ± 7° versus 57 ± 9°; Fig. 4, D and E). The critical severing angle is lowest for severing events at boundaries between bare and cofilin-decorated segments (θcrit = 31 ± 6°; Fig. 4 F) and hingelike motions are observed before severing ((21); Fig. 4 C).
The internal shear force and work resulting from a given filament bending deformation were estimated through simulation of the elastic free energy function of a filament segment constrained by a bending angle (see Materials and Methods, and Eqs. 9–14). We assume that the internal force orthogonal to the tangent vector reflects the shear force. Compliant cofilactin filament bending introduces less shear force than equivalent bending of stiffer bare actin filaments. As a result, they sever at larger bending angles than bare filaments; cofilactin filaments must bend more to introduce comparable shear forces (Fig. 5).
Figure 5.
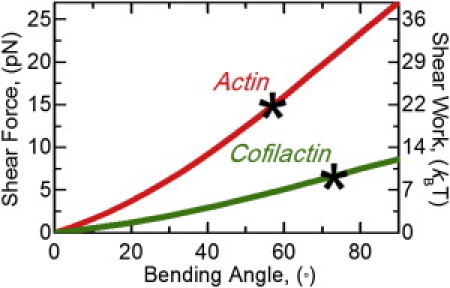
Calculated applied shear force from bending of actin and cofilactin filaments. Simulations of the equilibrium equations for an inextensible elastic filament with ends constrained by an applied bending angle are used to determine internal forces and moments. The projection of the internal force expressed at one-half the arc-length is the applied shear force (left axis) for a bare (red) or fully cofilin-decorated (green) actin filament from a bending angle. The applied shear force over the diameter of a filament (6 nm) is the applied shear work (right axis) from a bending angle and is an estimate of the energy required to sever a filament. (Asterisks) Estimated shear force and work associated with the critical severing angles (Fig. 4) for bare and fully cofilin-decorated actin filaments.
To estimate the shear energy required to sever a filament, the shear work across the filament diameter (d = 6 nm) was calculated from the shear force at the critical severing angle. We estimate the shear energy associated with severing of an actin filament to be ∼20 kBT (Fig. 5), comparable to the standard free energy change associated with phalloidin-stabilized filament fragmentation (ΔG° = 28.5 kBT (27)). The shear energy for cofilactin filament severing is estimated to be ∼10 kBT (Fig. 5), assuming a comparable shear displacement. In this study, filaments are constrained to fluctuate in two dimensions, so filament elastic free energy contributions (Eq. 9) originating from twist-bend coupling (41) are minimized and therefore not considered in the calculations. The mechanical properties of filaments partially decorated with cofilin are uncertain, so we did not attempt to calculate the shear force and work associated with bending at boundaries.
Discussion
Isoform-dependent actin filament flexibility
Biochemical studies indicate that despite being 86% identical (94% homologous), yeast and vertebrate muscle actin filaments display distinct functional properties that have physiological significance, as substitution of yeast actin with vertebrate muscle actin is lethal (42). Yeast actin polymerizes (36,38), exchanges nucleotide (43), and releases Pi more rapidly (44) than vertebrate muscle actin. Yeast actin filaments “breathe” and bind phalloidin between adjacent subunits more rapidly (35), twist more readily (34), and fragment more easily (38) than vertebrate muscle actin filaments. Analysis of the bending fluctuations in this study (Fig. 1) indicates that yeast actin filaments are also more compliant in bending than vertebrate actin filaments, consistent with previous reports that they appear qualitatively less rigid (37). The enhanced yeast actin filament bending and twisting flexibility, structural dynamics, and susceptibility to fragmentation result from weaker inter- and intrasubunit filament contacts than in vertebrate actin filaments (41,45,46).
Enhanced filament compliance promotes severing by cofilin
Cofilin severing activity correlates with its effect on actin filament flexibility. Vertebrate cofilin binds but has minimal effects on yeast actin filament bending stiffness (Table 1) and does not sever them to an appreciable extent (Figs. 2 and 3). Yeast (S. cerevisiae and S. pombe) cofilin severs vertebrate actin filaments more efficiently than vertebrate cofilin—as determined by a decrease in the average filament length (Fig. 2 G; see (15,18) for S. pombe cofilin severing analysis)—and also increases the filament bending flexibility to a greater extent (Table 1). Yeast cofilin severs yeast actin filaments similarly to vertebrate actin filaments (Fig. 2 G) and yields comparable filament elasticities (Table 1).
Cofilin binding increases the radial mass of filaments. One would expect decorated filaments to be more stiff than bare ones because they have a larger geometric moment (47). However, cofilin lowers the filament stiffness, indicating that the apparent elastic modulus is lower and that the strength of filament inter- and intrasubunit contacts are compromised (8). The observation that vertebrate cofilin binds yeast actin filaments without altering their overall stiffness suggest that the mass contributions to the geometric moment are balanced by changes in the apparent elastic modulus.
Stress accumulation promotes severing at boundaries of bare and cofilin-decorated segments
We hypothesized that a local asymmetry in filament mechanics localizes stress from thermally driven shape fluctuations and promotes preferential severing at the boundaries of bare and cofilin-decorated segments along filaments (8,14). Bending vertex and hingelike motions are observed at breakage sites (Fig. 4), particularly at boundaries between bare and cofilin-decorated segments (Fig. 4 C). Consistent with stress accumulation promoting filament severing, severing at boundaries coincides with a smaller critical angle for breakage (Fig. 4). That is, bending deformations at boundaries are irreversible at smaller angles than within homogenous (bare or fully decorated) filament segments.
The critical severing angle distribution of cofilactin filaments is bimodal (Fig. 4 E). A small fraction (∼25%) of cofilactin severing events occurs with a critical angle comparable to bare actin (54 ± 4°); the majority of cofilactin severing events are at a larger critical angle (73 ± 7°). This bimodal distribution suggests that a fraction of cofilactin adopts a conformation with mechanical properties like that of native actin (7,48,49), and is consistent with multiple, isoenergetic cofilactin equilibrium conformations identified from spectroscopic (11) and kinetic (22,50) studies. A larger severing angle for cofilactin filaments is expected because enhanced elasticity will allow them to bend more under an equivalent load.
The shear force and work introduced by bending a bare actin filament is greater than on a cofilactin filament because the former is stiffer (Fig. 5). Consequently, cofilactin filaments bend more than bare filaments before severing (Fig. 4). We note that the shear work (∼10 kBT) at the cofilactin filament critical angle (73°) is approximately equal to that of a bare filament bent to the critical severing angle at boundaries of partially decorated filaments (31°). This observation suggests that boundaries have bare and cofilactin-like properties, namely the energetic stability (i.e., shear work needed to sever) of cofilactin and the stiffness (deformation needed to introduce a given shear force) of bare actin filaments.
Collectively, these measurements favor a mechanism in which enhanced filament elasticity with cofilin binding introduces a local asymmetry in filament topology and mechanics at boundaries of bare and cofilin-decorated segments that generates the accumulation of stress, thereby promoting filament severing (8,14,21). According to this mechanism, any mechanical barrier such as that introduced by myosin motors and cross-linking proteins (provided the filament binding densities do not completely inhibit cofilin binding (51)) would promote stress accumulation and severing by cofilin. In this manner, mechanical discontinuities along filaments act as stress accumulators, analogous to mechanical defects in nonprotein materials (Fig. 6 (14)).
Figure 6.
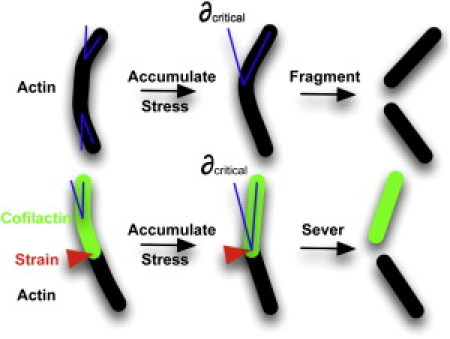
Model for cofilin-dependent actin filament severing. The strain required to fragment a filament is reached at a critical bending angle. A local gradient in filament bending mechanics localizes mechanical stress from thermal fluctuations at boundaries between bare and cofilin-bound segments which accumulates, thereby promoting the severing of filaments.
Acknowledgments
We thank John A. Cooper (Washington University in St. Louis) for providing yeast cofilin and yeast actin used in the early stages of this work.
This work is supported by the American Heart Association (grant No. 0940075N awarded to E.M.D.L.C.), the National Institutes of Health (grant No. GM071688 and No. GM071688-03S1 awarded to E.M.D.L.C.), the Agence Nationale de la Recherche (grant No. ANR-08-Blanc-0012 awarded to L.B.), and the United States Public Health Service (grant No. USPHS GM077190 awarded to E.R.). B.R.M. was supported by American Heart Association predoctoral award No. 09PRE2230014. E.M.D.L.C. is an American Heart Association Established Investigator, and is a recipient of the National Science Foundation CAREER Award No. MCB-0546353 as well as being a Hellman Family Fellow.
Footnotes
Arnon Henn's present address is Faculty of Biology, Technion - Israel Institute of Technology, Haifa, Israel.
References
- 1.Condeelis J. How is actin polymerization nucleated in vivo? Trends Cell Biol. 2001;11:288–293. doi: 10.1016/s0962-8924(01)02008-6. [DOI] [PubMed] [Google Scholar]
- 2.Michelot A., Berro J., Blanchoin L. Actin-filament stochastic dynamics mediated by ADF/cofilin. Curr. Biol. 2007;17:825–833. doi: 10.1016/j.cub.2007.04.037. [DOI] [PubMed] [Google Scholar]
- 3.Roland J., Berro J., Martiel J.L. Stochastic severing of actin filaments by actin depolymerizing factor/cofilin controls the emergence of a steady dynamical regime. Biophys. J. 2008;94:2082–2094. doi: 10.1529/biophysj.107.121988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Oser M., Condeelis J. The cofilin activity cycle in lamellipodia and invadopodia. J. Cell. Biochem. 2009;108:1252–1262. doi: 10.1002/jcb.22372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cao W., Goodarzi J.P., De La Cruz E.M. Energetics and kinetics of cooperative cofilin-actin filament interactions. J. Mol. Biol. 2006;361:257–267. doi: 10.1016/j.jmb.2006.06.019. [DOI] [PubMed] [Google Scholar]
- 6.McGough A., Pope B., Weeds A. Cofilin changes the twist of F-actin: implications for actin filament dynamics and cellular function. J. Cell Biol. 1997;138:771–781. doi: 10.1083/jcb.138.4.771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Galkin V.E., Orlova A., Egelman E.H. Actin depolymerizing factor stabilizes an existing state of F-actin and can change the tilt of F-actin subunits. J. Cell Biol. 2001;153:75–86. doi: 10.1083/jcb.153.1.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.McCullough B.R., Blanchoin L., De la Cruz E.M. Cofilin increases the bending flexibility of actin filaments: implications for severing and cell mechanics. J. Mol. Biol. 2008;381:550–558. doi: 10.1016/j.jmb.2008.05.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pfaendtner J., De La Cruz E.M., Voth G.A. Actin filament remodeling by actin depolymerization factor/cofilin. Proc. Natl. Acad. Sci. USA. 2010;107:7299–7304. doi: 10.1073/pnas.0911675107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sharma S., Grintsevich E.E., Gimzewski J.K. Atomic force microscopy reveals drebrin induced remodeling of F-actin with subnanometer resolution. Nano Lett. 2011;11:825–827. doi: 10.1021/nl104159v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Prochniewicz E., Janson N., De la Cruz E.M. Cofilin increases the torsional flexibility and dynamics of actin filaments. J. Mol. Biol. 2005;353:990–1000. doi: 10.1016/j.jmb.2005.09.021. [DOI] [PubMed] [Google Scholar]
- 12.Pavlov D., Muhlrad A., Reisler E. Actin filament severing by cofilin. J. Mol. Biol. 2007;365:1350–1358. doi: 10.1016/j.jmb.2006.10.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.De La Cruz E.M. Cofilin binding to muscle and non-muscle actin filaments: isoform-dependent cooperative interactions. J. Mol. Biol. 2005;346:557–564. doi: 10.1016/j.jmb.2004.11.065. [DOI] [PubMed] [Google Scholar]
- 14.De La Cruz E.M. How cofilin severs an actin filament. Biophys. Rev. 2009;1:51–59. doi: 10.1007/s12551-009-0008-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Andrianantoandro E., Pollard T.D. Mechanism of actin filament turnover by severing and nucleation at different concentrations of ADF/cofilin. Mol. Cell. 2006;24:13–23. doi: 10.1016/j.molcel.2006.08.006. [DOI] [PubMed] [Google Scholar]
- 16.Yeoh S., Pope B., Weeds A. Determining the differences in actin binding by human ADF and cofilin. J. Mol. Biol. 2002;315:911–925. doi: 10.1006/jmbi.2001.5280. [DOI] [PubMed] [Google Scholar]
- 17.Bobkov A.A., Muhlrad A., Reisler E. Cooperative effects of cofilin (ADF) on actin structure suggest allosteric mechanism of cofilin function. J. Mol. Biol. 2006;356:325–334. doi: 10.1016/j.jmb.2005.11.072. [DOI] [PubMed] [Google Scholar]
- 18.Chan C., Beltzner C.C., Pollard T.D. Cofilin dissociates Arp2/3 complex and branches from actin filaments. Curr. Biol. 2009;19:537–545. doi: 10.1016/j.cub.2009.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Northrop J., Weber A., Walsh T.P. Different calcium dependence of the capping and cutting activities of villin. J. Biol. Chem. 1986;261:9274–9281. [PubMed] [Google Scholar]
- 20.Grintsevich E.E., Benchaar S.A., Reisler E. Mapping the cofilin binding site on yeast G-actin by chemical cross-linking. J. Mol. Biol. 2008;378:540–550. doi: 10.1016/j.jmb.2007.12.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Suarez C., Roland J., Blanchoin L. Cofilin tunes the nucleotide state of actin filaments and severs at bare and decorated segment boundaries. Curr. Biol. 2011;21:862–868. doi: 10.1016/j.cub.2011.03.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.De La Cruz E.M., Sept D. The kinetics of cooperative cofilin binding reveals two states of the cofilin-actin filament. Biophys. J. 2010;98:1893–1901. doi: 10.1016/j.bpj.2010.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cao W., Coman M.M., De La Cruz E.M. Mechanism of MSS116 ATPase reveals functional diversity of dead-box proteins. J. Mol. Biol. 2011;409:399–414. doi: 10.1016/j.jmb.2011.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ha T., Rasnik I., Chu S. Initiation and re-initiation of DNA unwinding by the Escherichia coli Rep helicase. Nature. 2002;419:638–641. doi: 10.1038/nature01083. [DOI] [PubMed] [Google Scholar]
- 25.Sept D., Xu J., McCammon J.A. Annealing accounts for the length of actin filaments formed by spontaneous polymerization. Biophys. J. 1999;77:2911–2919. doi: 10.1016/s0006-3495(99)77124-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Carlsson A.E. Stimulation of actin polymerization by filament severing. Biophys. J. 2006;90:413–422. doi: 10.1529/biophysj.105.069765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kinosian H.J., Selden L.A., Gershman L.C. Actin filament annealing in the presence of ATP and phalloidin. Biochemistry. 1993;32:12353–12357. doi: 10.1021/bi00097a011. [DOI] [PubMed] [Google Scholar]
- 28.Berro J., Michelot A., Martiel J.L. Attachment conditions control actin filament buckling and the production of forces. Biophys. J. 2007;92:2546–2558. doi: 10.1529/biophysj.106.094672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Isambert H., Venier P., Carlier M.F. Flexibility of actin filaments derived from thermal fluctuations. Effect of bound nucleotide, phalloidin, and muscle regulatory proteins. J. Biol. Chem. 1995;270:11437–11444. doi: 10.1074/jbc.270.19.11437. [DOI] [PubMed] [Google Scholar]
- 30.Greenberg M.J., Wang C.-L.A., Moore J.R. Modulation of actin mechanics by caldesmon and tropomyosin. Cell Motil. Cytoskel. 2008;65:156–164. doi: 10.1002/cm.20251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.ben-Avraham D., Tirion M.M. Dynamic and elastic properties of F-actin: a normal-modes analysis. Biophys. J. 1995;68:1231–1245. doi: 10.1016/S0006-3495(95)80299-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chu J.W., Voth G.A. Allostery of actin filaments: molecular dynamics simulations and coarse-grained analysis. Proc. Natl. Acad. Sci. USA. 2005;102:13111–13116. doi: 10.1073/pnas.0503732102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pfaendtner J., Branduardi D., Voth G.A. Nucleotide-dependent conformational states of actin. Proc. Natl. Acad. Sci. USA. 2009;106:12723–12728. doi: 10.1073/pnas.0902092106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Prochniewicz E., Thomas D.D. Differences in structural dynamics of muscle and yeast actin accompany differences in functional interactions with myosin. Biochemistry. 1999;38:14860–14867. doi: 10.1021/bi991343g. [DOI] [PubMed] [Google Scholar]
- 35.De La Cruz E.M., Pollard T.D. Kinetics and thermodynamics of phalloidin binding to actin filaments from three divergent species. Biochemistry. 1996;35:14054–14061. doi: 10.1021/bi961047t. [DOI] [PubMed] [Google Scholar]
- 36.Kim E., Miller C.J., Reisler E. Polymerization and in vitro motility properties of yeast actin: a comparison with rabbit skeletal α-actin. Biochemistry. 1996;35:16566–16572. doi: 10.1021/bi9623892. [DOI] [PubMed] [Google Scholar]
- 37.Kron S.J., Drubin D.G., Spudich J.A. Yeast actin filaments display ATP-dependent sliding movement over surfaces coated with rabbit muscle myosin. Proc. Natl. Acad. Sci. USA. 1992;89:4466–4470. doi: 10.1073/pnas.89.10.4466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Buzan J.M., Frieden C. Yeast actin: polymerization kinetic studies of wild type and a poorly polymerizing mutant. Proc. Natl. Acad. Sci. USA. 1996;93:91–95. doi: 10.1073/pnas.93.1.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bergeron E.W., Wedemeyer R., Bartlett H.L. Allele-specific effects of thoracic aortic aneurysm and dissection (TAAD) {α}-smooth muscle actin mutations on actin function. J. Biol. Chem. 2011;286:11356–11369. doi: 10.1074/jbc.M110.203174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Xu J., Casella J.F., Pollard T.D. Effect of capping protein, CapZ, on the length of actin filaments and mechanical properties of actin filament networks. Cell Motil. Cytoskeleton. 1999;42:73–81. doi: 10.1002/(SICI)1097-0169(1999)42:1<73::AID-CM7>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- 41.De La Cruz E.M., Roland J., Martiel J.L. Origin of twist-bend coupling in actin filaments. Biophys. J. 2010;99:1852–1860. doi: 10.1016/j.bpj.2010.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McKane M., Wen K.-K., Rubenstein P.A. Effect of the substitution of muscle actin-specific subdomain 1 and 2 residues in yeast actin on actin function. J. Biol. Chem. 2006;281:29916–29928. doi: 10.1074/jbc.M602251200. [DOI] [PubMed] [Google Scholar]
- 43.Chen X., Cook R.K., Rubenstein P.A. Yeast actin with a mutation in the “hydrophobic plug” between subdomains 3 and 4 (L266D) displays a cold-sensitive polymerization defect. J. Cell Biol. 1993;123:1185–1195. doi: 10.1083/jcb.123.5.1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yao X., Rubenstein P.A. F-actin-like ATPase activity in a polymerization-defective mutant yeast actin (V266G/L267G) J. Biol. Chem. 2001;276:25598–25604. doi: 10.1074/jbc.M011797200. [DOI] [PubMed] [Google Scholar]
- 45.Orlova A., Chen X., Egelman E.H. Modulation of yeast F-actin structure by a mutation in the nucleotide-binding cleft. J. Mol. Biol. 1997;271:235–243. doi: 10.1006/jmbi.1997.1163. [DOI] [PubMed] [Google Scholar]
- 46.Stokasimov E., Rubenstein P.A. Actin isoform-specific conformational differences observed with hydrogen/deuterium exchange and mass spectrometry. J. Biol. Chem. 2009;284:25421–25430. doi: 10.1074/jbc.M109.013078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gittes F., Mickey B., Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Orlova A., Shvetsov A., Reisler E. Actin-destabilizing factors disrupt filaments by means of a time reversal of polymerization. Proc. Natl. Acad. Sci. USA. 2004;101:17664–17668. doi: 10.1073/pnas.0407525102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kozuka J., Yokota H., Yanagida T. Dynamic polymorphism of single actin molecules in the actin filament. Nat. Chem. Biol. 2006;2:83–86. doi: 10.1038/nchembio763. [DOI] [PubMed] [Google Scholar]
- 50.Kueh H.Y., Brieher W.M., Mitchison T.J. Dynamic stabilization of actin filaments. Proc. Natl. Acad. Sci. USA. 2008;105:16531–16536. doi: 10.1073/pnas.0807394105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schmoller K.M., Semmrich C., Bausch A.R. Slow down of actin depolymerization by cross-linking molecules. J. Struct. Biol. 2011;173:350–357. doi: 10.1016/j.jsb.2010.09.003. [DOI] [PubMed] [Google Scholar]
- 52.Bobkov A.A., Muhlrad A., Reisler E. Structural effects of cofilin on longitudinal contacts in F-actin. J. Mol. Biol. 2002;323:739–750. doi: 10.1016/s0022-2836(02)01008-2. [DOI] [PubMed] [Google Scholar]


