A model of cytoplasmically driven microtubule-based motion in the single-celled Caenorhabditis elegans embryo

Abstract

We present a model of cytoplasmically driven microtubule-based pronuclear motion in the single-celled Caenorhabditis elegans embryo. In this model, a centrosome pair at the male pronucleus initiates stochastic microtubule (MT) growth. These MTs encounter motor proteins, distributed throughout the cytoplasm, that attach and exert a pulling force. The consequent MT-length-dependent pulling forces drag the pronucleus through the cytoplasm. On physical grounds, we assume that the motor proteins also exert equal and opposite forces on the surrounding viscous cytoplasm, here modeled as an incompressible Newtonian fluid constrained within an ellipsoidal eggshell. This naturally leads to streaming flows along the MTs. Our computational method is based on an immersed boundary formulation that allows for the simultaneous treatment of fluid flow and the dynamics of structures immersed within. Our simulations demonstrate that the balance of MT pulling forces and viscous nuclear drag is sufficient to move the pronucleus, while simultaneously generating minus-end directed flows along MTs that are similar to the observed movement of yolk granules toward the center of asters. Our simulations show pronuclear migration, and moreover, a robust pronuclear centration and rotation very similar to that observed in vivo. We find also that the confinement provided by the eggshell significantly affects the internal dynamics of the cytoplasm, increasing by an order of magnitude the forces necessary to translocate and center the pronucleus.

Proper nuclear positioning is crucial to the successful progression of early development in animal cells and depends on active and passive mechanisms. In many types of cells, nuclear positioning has been shown to depend on the microtubule (MT) cytoskeleton, and several mechanisms for such MT-based motion have been proposed (1). One type of MT-based motion occurs in WT Caenorhabditis elegans where the male pronucleus is tightly associated with two centrosomes that act as MT organizing centers (MTOCs) to nucleate MTs. In sand dollar embryo, it was observed that a male pronucleus will move in the direction of its longest MTs until it is centered within the region allowing MT growth (2). This led to the proposal of cytoplasmically based length-dependent forces, with the molecular basis being minus-end directed motor proteins such as dynein distributed and anchored in the cytoplasm (2). Despite the appeal of such a model, one is left to identify the cytoplasmic substrate able to anchor the motor proteins and thus counteract the drag on the MTOC and its associated structures and lead to nuclear motion. Recently, Kimura and Kimura showed that endosomes, lysosomes, and yolk granules may act as such substrates in C. elegans (3).

Although pronuclear motion under a length-dependent MT-based force model was studied in ref. 4, the effect of forces on the cytoplasm was not considered and forces in the model were not fully balanced. Here, we present a simple yet mechanically balanced model that yields nuclear motion via MT-based forces actively generated within a viscous cytoplasm. The cytoplasm is contained within an ellipsoidal egg periphery and is modeled as a highly viscous Newtonian fluid. The male pronucleus is a spherical body bound to two MTOCs from which MTs emanate. We include a model of MT growth and shrinkage where growth is limited by the egg periphery. This yields a coupled system for the fluid and structure dynamics, which we solve using an immersed boundary formulation. For simplicity, a uniform density of cytoplasmic motor proteins is assumed, and at each point along an MT a motor protein load-velocity relationship is satisfied whereby the relative local velocity of the fluid and MT is related to equal and opposite forces acting on the fluid and MT, acting in concert with the overall balance of forces within the system. We demonstrate through simulations that this model is sufficient to propel the pronucleus through the cytoplasm while at the same time dragging cytoplasmic fluid particles toward the minus ends of MTs. Here, viscous resistance of the cytoplasmic fluid to these motions acts as a counterbalance to drag on the pronucleus. We do not model additional anchoring substrates within the cytoplasm, although such structures may be present in vivo (3) and could supply greater resistance.

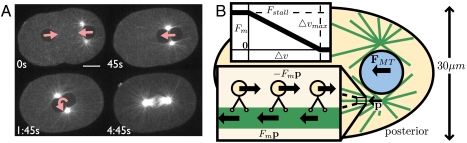
We demonstrate numerically how the proposed mechanism might contribute to several processes in the single-celled C. elegans embryo. Shortly after fertilization, the male pronucleus becomes tightly associated with two centrosomes and migrates from the cell posterior toward the anterior. Simultaneously, the female pronucleus migrates from the anterior toward the male pronucleus, possibly assisted by cortically driven cytoplasmic flows directed toward the posterior (5). Pronuclear meeting between the female and male takes place in the posterior of the cell. At meeting, the centrosomes dynamically center between the male and female pronucleus, and the resulting nuclear centrosome complex (NCC) migrates toward the cell center (centration) and rotates 90° to align with the anterior–posterior (AP) axis of the cell (rotation). These events are depicted in Fig. 1A in a live C. elegans embryo expressing GFP-tagged β-tubulin (see also Movies S1 and S2). Our simulations show pronuclear motion such as the early male pronuclear migration, as well as geometry-dependent centration and rotation. Our model also explains the observed fast motion of yolk granules along MTs toward the center of asters as the motion of minus-end directed motor proteins under small load. Although the fast-moving yolk granules are visually prominent in live systems, our model predicts that there are also more heavily loaded, slower-moving components of the cytoplasm exerting larger forces on MT-bound structures and that these forces are sufficient for propulsion of pronuclei.

Fig. 1.

(A) MT-based dynamics in a live single-celled C. elegans embryo visualized with GFP-tagged β-tubulin (Movie S1). (Left to Right, Top to Bottom) Migration of the male and female pronuclei, pronuclear meeting, NCC centration, and spindle orientation following NCC rotation. Scale bar, 10 μm. (B) Schematic of the biophysical model, with an ellipsoidal cell boundary encapsulating the cytoplasm (yellow), pronucleus (blue), and associated MTs (green). Asymmetric lengths of MTs due to cessation of growth at the cortex creates a force imbalance 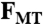favoring centration. (Upper Inset) The relationship between load F_m and velocity Δv for a single motor protein. (Lower Inset) Motor proteins embedded in the cytoplasm exert equal and opposite forces ± F_mp on the cytoplasm and MT, resulting in their relative motion.

Here we do not model cortically based active flows, nor asymmetric mechanisms that arise from polarity and play a role in asymmetric spindle elongation during anaphase (6).

Biophysical Model

The biophysical model is depicted in Fig. 1B. We model the egg periphery as a fixed ellipsoid with a major AP axis of length 50 μm and minor axes of length 30 μm. The male pronucleus is modeled as a sphere with radius R = 5 μm. For simplicity, we do not include the female pronucleus, whose motion is influenced by cortically driven cytoplasmic flow (5), as well as by tracking of the astral MTs by motor proteins anchored in its nuclear envelope (1). Note that beyond its early migration away from the posterior, the single pronucleus in the model is taken to represent the NCC after pronuclear meeting. We model the MTs as rigid, one-dimensional rods, rigidly fixed to the pronucleus at the poles of a pronuclear axis initially transverse to the AP axis of the cell.

Model of Cytoplasm and Pronucleus.

We model the cytoplasm as an incompressible, viscously dominated, Newtonian fluid. The cytoplasmic velocity, u, and pressure, q, satisfy

[1]

where Σ = -qI + μ(∇u + ∇u^T) is the stress tensor for a Newtonian fluid and μ is the viscosity. Here, g_MT is the MT-based force density (Eq. 4) that drives the flow. Assuming a Newtonian fluid response agrees with ref. 7, which measured in vivo the extent and time lag of mean squared displacements of 100-nm particles to infer the viscoelastic properties of single-celled C. elegans cytoplasm. Their results indicate that the cytoplasm behaves like a liquid of high viscosity μ ∼ 10³ cP (water at 20 °C has a viscosity μ ∼ 1 cP) and negligible elasticity. Mechanical properties can be scale dependent; at the smaller scales experienced by proteins, cytoplasmic viscosity is near that of water (8). It is possible that at larger scales, such as that of the pronuclei, the viscoelastic properties differ again (9), but there is no such evidence as yet for this in C. elegans embryo. Inertial effects in the cytoplasm are ignored as is appropriate here (the Reynolds number is < 10^-5). We also ignore thermal fluctuations in the fluid.

The egg periphery is assumed to be of fixed shape and the no-slip boundary condition is applied there. This ignores cortical motions investigated by others (10). The pronucleus is assumed to be a solid body moving under rigid body translation and rotation with velocity V and angular velocity Ω. A no-slip condition matches the fluid velocity at the boundary of the pronucleus to that of the pronucleus. Without any applied force, the pronucleus remains stationary. Here, the applied force arises from the action of motor protein pulling forces acting on the attached MTs. The consequent force, F_MT, and torque, T_MT, on the pronucleus are balanced by the total fluid force and torque on the pronucleus:

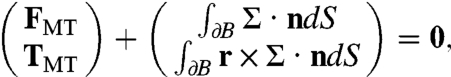[2]

where ∂B is the surface of the pronucleus, with n its outward unit normal and r its position relative to the center of mass of the pronucleus. Given F_MT and T_MT, solution of the Stokes equations (1) under these boundary conditions and force balances (2) yields V and Ω. However, F_MT and T_MT must themselves be determined as part of the dynamics problem.

At an MT, the cytoplasmic fluid can slip along the direction of the MT and satisfies a no-slip condition in the directions transverse to the MT. We exclude the latter from the computations due to the difficulty of resolving that boundary condition with the computational method. Inclusion of the no-slip boundary condition would result in increased drag on the NCC, which could be compensated for by increasing the motor density parameter D (discussed below), while maintaining D within a biophysically plausible range. The geometric effects produced here are expected to be similar.

Microtubule Dynamic Instability.

The MTs are polar structures with their minus ends anchored in the centrosome and plus ends emanating radially out from the centrosome (Fig. 1B). The growth and shrinkage of MTs due to polymerization and depolymerization of their constituent tubulin dimers is described by the model of dynamic instability (11). As in refs. 4 and 12, we use a simple version of this model specified by four constant parameters: the growth velocity, shrinkage velocity, catastrophe frequency, and rescue frequency. The transition of an MT from growth to shrinkage (shrinkage to growth) is described by a Poisson process with rate parameter equal to the catastrophe (rescue) frequency (13). MTs that would otherwise extend beyond the cell boundary are shortened so that their plus ends lie on the boundary.

Pulling Force Model.

In the present model, minus-end directed motor proteins move along the length of polar MT tracks, transporting cargo while exerting a pulling force on the MT and its associated structures. Our model is based on the models described in refs. 4 and 12, with the important difference that we locally model the interaction of the active fluid and the MT and can thus model the relationship between motor protein load and local relative velocity of the motor protein and MT. Because the pulling is actuated along the lengths of MTs (as opposed to, e.g., special sites at the cortex), the resulting forces are length-dependent. Consequently, the NCC will assume a favored position and orientation within the cell.

The force density at distance s along the MT is given by G_MT(s) = D(s)F_m(s)p, where D(s) is the density per unit length of motor proteins, F_m is the force exerted on the MT by a single motor protein, and p is the direction vector for the MT. We take D(s) to be constant, and 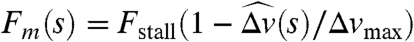, where 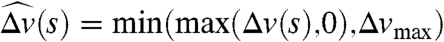and Δv(s) is the relative velocity of the MT and the motor protein at s projected onto the direction p (Fig. 1B, plot). An expression of this form was used in ref. 4, but there the velocity was the absolute velocity of the MT, yielding a different value of F_m (especially where fluid is fast moving) and hence different dynamics. The MT-based force and torque on the associated pronucleus is given by

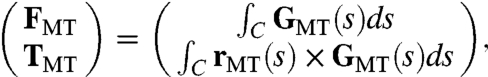[3]

where C represents the one-dimensional MT with position X_MT(s), anchored in a centrosome at s = 0 and of length L, and r_MT(s) = X_MT(s) - X₀ is position on C relative to the center of mass X₀ of the pronucleus. To express the equal and opposite force on the fluid due to the motor proteins, the Lagrangian force density G_MT is converted to a Eulerian force density g_MT through the relation (14)

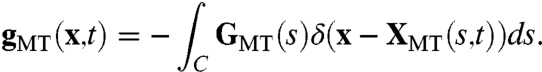[4]

Parameters in the Biophysical Model.

Parameters in the model include the cytoplasmic viscosity μ, the number of MTs associated with each centrosome, the MT growth and shrinkage velocities and rescue and catastrophe frequencies, motor protein stall force, and maximum motor protein velocity. We use the parameter values given as the standard condition in ref. 4, table 1. See ref. 4 and the references therein for the sources of these parameters. Note that ref. 4 tuned the motor protein density parameter D so that centration occurred at observed time scales. We did not tune parameters. Force magnitudes increase linearly with D and hence we expect velocities to increase and time scales to decrease linearly with D as well. Thus, such quantities in the results are meaningful in relative terms only. Similar to ref. 4, we find the qualitative aspects of the motion to be robust to variations in the parameter values.

Results

Pronuclear Translation and Cytoplasmic Flow due to a Bundled, Parallel Array of MTs.

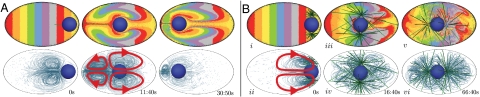
To begin, we study a simplified configuration of our model that illustrates that the pronucleus can be propelled by pulling directly on the viscous cytoplasm and that a counterflow of cytoplasm is generated (Fig. 2A). We emphasize that we are not modeling any additional structures in the cytoplasm. A pronucleus located at the posterior is attached to a bundle of 10 parallel MTs (represented in the model by one MT with a force multiplier of 10) directed toward the anterior and oriented along the AP axis. From a three-dimensional simulation of this model, Fig. 2A shows how cytoplasmic material is displaced, and the associated flow structures (Movie S3). Under the action of cytoplasmic pulling on the growing MT bundle, the pronucleus translates toward the anterior, while cytoplasm is pulled along the MT bundle toward the posterior. Flow streamlines show the appearance of two toroidal vortices, one about the MT and the other about the pronucleus. This flow structure is associated with a “puller” type microswimmer (15) as the tangential active stresses along the MT create fluid slip along the MT, while cytoplasm is dragged with the body due to the no-slip condition. Although this simple model illustrates nicely how cytoplasmic pulling can translate the pronucleus, the model lacks a proper balance of MT-induced pulling forces. Hence, the pronucleus overshoots the center and shows neither centration nor subsequent rotation for proper positioning.

Fig. 2.

Frames from simulations of two example scenarios. A slice through the three-dimensional volume is shown. (Top) Colored passive tracer particles have been added for visualization. (Bottom) Streamlines of the flow. (A) A simple example demonstrating the propulsion mechanism (Movie S3). A filament is pulled along its length by motor proteins embedded in the cytoplasm. The attached pronucleus moves toward the anterior while the cytoplasm along the filament moves to the posterior. The flow structure consists of two toroidal vortices, one centered at the filament and one centered at the pronucleus. (B) The full WT model (Movie S4). The NCC starts at the posterior (Left). Asymmetric lengths of MTs due to cessation of MT growth at the cortex leads to centration of the NCC (Middle). Fluctuations in the MT lengths initiate a rotation of the NCC, which continues until it is aligned with the AP axis (Right).

Centration of the Nuclear Centrosome Complex.

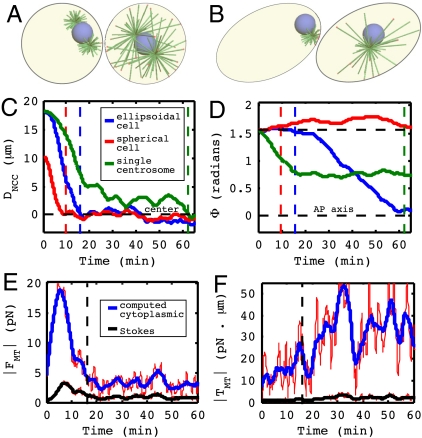
We now simulate our full three-dimensional model of NCC motion under cytoplasmically driven MT-based pulling forces. This model of WT embryo assumes an ellipsoidal periphery containing a spherical NCC with two MTOCs located at poles whose axis is initially transverse to the AP axis. Fig. 2Bi shows the two MT arrays shortly after growth is initiated, whereas Fig. 2Bii shows the early-time flow structure set up by cytoplasmic pulling. MTs that reach the cell periphery are prevented from growing further. Thus, by the NCC being initially at the posterior, MTs grow preferentially toward the anterior and this AP length imbalance drives centration. Fig. 3C (blue) plots the evolution of NCC position D_NCC(t) along the AP axis (0 indicates the cell center), showing that the NCC stops migrating upon reaching the center but remains subject to random perturbations due to the stochastic MT dynamics. Fig. 2Biii–vi shows that the flows associated with the MTs are very complex, with continual cytoplasmic streaming along MTs toward the centrosomes (Movie S4).

Fig. 3.

(A) The initial and final configuration for a spherical embryo. The NCC centers but fails to rotate. (B) The initial and final configuration for an embryo with a single centrosome (Movie S6). NCC positioning and orientation are disrupted. (C) Position of NCC along the AP axis. (D) Angle of NCC to the AP axis. The vertical dashed line indicates time of centration. (E and F) Net cytoplasmic drag force/torque computed in the present model (accounting for the enclosing cell geometry) compared with drag/torque estimated by Stokes law (assuming an open geometry). Red lines are the raw data, and the blue and black lines are moving averages, shown for clarity.

Rotation of the Nuclear Centrosome Complex.

Although the NCC is stably positioned at the cell center, it is unstable to rotation away from the centrosomal (CS) axis being transverse to the AP axis. Random fluctuations in orientation provide the perturbations that again lead to an imbalance in MT length, though in this case involving MTs that are exerting forces tangential to the pronucleus. This yields a developing rotational torque. Consequently, the NCC undergoes a 90° rotation as it nears the center and assumes a stable orientation aligned with the AP axis as seen in Fig. 2 Bv and vi. Fig. 3D (blue; dashed vertical lines indicate time of centration) plots the evolution of the angle Φ(t) between the CS axis and the AP axis. The NCC begins slowly rotating somewhat before centration and continues until it is aligned with the AP axis (Movies S4 and S5).

Such centering and rotation are a consequence of the length dependence of the forces and the cell geometry. In particular, a full model of the fluid is not required to see these qualitative effects, and they were also demonstrated with the simpler model of ref. 4 and in a subsequent work by the same authors (16).

The Confining Geometry of the Ellipsoidal Cell Increases the Necessary Pulling Forces.

We now consider the forces and torques associated with centration and rotation. Fig. 3 E and F show the total force and torque (blue curves), respectively, exerted upon the NCC by MT-based pulling forces, which is exactly balanced and opposed by fluid drag upon the NCC (Eq. 2). In the epoch leading up to centration, the rise of total force is associated with the MT-length imbalance initiated by MT growth. The length imbalance disappears as the NCC centers and the total force drops. The total torque grows up to and through centration and is associated with the rotation of the CS axis toward alignment with the AP axis.

In ref. 4, male pronuclear migration was studied under both cortical pushing and length-dependent cytoplasmic pulling force models against cytoplasm whose drag was modeled using Stokes law. Stokes law follows from computing the motion of a sphere in an infinite fluid with no boundaries. However, for viscous flow, the presence of a confining geometry such as the eggshell has a significant impact on both the magnitude of viscous drag forces and on the resulting flow structure. By including a flow model for the cytoplasm, we can more accurately compute the dynamics. Fig. 3 E and F (black curves) also show drag force and torque estimates based on the instantaneous velocity and angular velocity using Stokes law F_d = 6πμRV and T_d = -8πμR³Ω, respectively. Note that Stokes law estimates are significantly smaller than the computed values that account for cell geometry.

Two Perturbations of the Model.

We now consider two interesting perturbations from the full WT model. In the first, the ellipsoidal periphery is replaced by a spherical one of the same volume, corresponding to an embryo with its shell removed as studied in ref. 6. In the second, we model NCC motion, again in the ellipsoidal geometry, but with only one centrosome corresponding to a zyg-1 mutant where centrosome duplication fails (4, 17) (Movie S6). The NCC dynamics of these two cases are shown in Fig. 3 A–D.

In both cases the NCC is initially at the posterior and MT growth is biased toward the interior of the cell. This again leads to migration toward the center. In the spherical case, this yields stable centration, though the rate of initial displacement from the periphery is steeper than in the ellipsoidal cases (Fig. 3C). This is due to the fact that the spherical boundary is flatter than the ellipsoidal boundary near NCC initial position, making it easier to draw in cytoplasmic fluid behind the NCC as it moves away from the posterior. In the single centrosome case, the MTOC approaches the cell center (at D_NCC ≈ 3.5 μm) on a time scale comparable to that in the WT case (Fig. 3C, green), despite the NCC having 50% fewer force-generating MTs. This is because competing MT forces toward the posterior are reduced as the NCC rotates toward the anterior. Note, however, that positioning of the NCC is significantly affected and is more sensitive to MT fluctuations.

In the spherical case, no single orientation is favorable over another, and the NCC angle exhibits random drift from its initial value (Fig. 3D, red). In the single centrosome case, the initial force imbalance between the two poles of the nucleus is large due to the absence of one MTOC, and thus the NCC begins rotation immediately as the single MTOC is pulled toward the cell center (Fig. 3D, green). However, this rotation does not lead to proper alignment with the AP axis. Rather, the NCC angle approaches an intermediate value of approximately π/4.

Discussion

Pulling on Microtubules by Cytoplasmic Components.

Cytoplasmically driven MT-based forces have been considered as a possible mechanism for nuclear and spindle positioning (1, 2). It was proposed that minus-end directed motor proteins anchored in the cytoplasm exert pulling forces on MTs, resulting in motion of MT-bound structures. MT-based force models were studied in ref. 4, where it was concluded that qualitative aspects of male pronuclear migration in vivo were consistent with a length-dependent pulling mechanism rather than a pushing mechanism. Recently, Kimura and Kimura (3) identified a protein in C. elegans that may be involved in anchoring dynein to cytoplasmic components. They showed that motion of small organelles was correlated to centrosome motion during centration (3) and that knockdown of the protein simultaneously disrupted both minus-end directed organelle motion and centration. Their work suggests that endosomes, lysosomes, and yolk granules serve as anchoring substrates in a cytoplasmic pulling force mechanism. Structures such as the actin cytoskeleton and endoplasmic reticulum have also been suggested [(18), box 1]. Our model could be used to compute forces from measured velocities to more precisely test for correlation between predicted net forces and NCC movement.

We assume that the motion of a motor protein along an MT creates a minus-end directed force in the fluid, perhaps by the motor protein carrying a payload. We assume also a constant and uniform distribution of minus-end directed motor proteins, more generally representing the balance of minus-end directed motors over opposing mechanisms such as plus-end directed motors. In one-celled C. elegans, dynein is present throughout the cytoplasm in a punctate manner (19).

Experiments in sand dollar eggs provide direct evidence for cytoplasmically based forces driving pronuclear motions. In ref. 2, eggs were treated with the MT depolymerizing drug colcemid. The effect of the drug was then selectively inhibited through localized UV irradiation. When a circular region containing the sperm aster, but not the female pronucleus nor the cortex, was irradiated, the sperm aster migrated in the direction of its longest MTs until it centered within the irradiated region. These experiments showed that MT contact with the cortex was unnecessary for pronuclear motion and centering, suggesting that it was driven by components in the cytoplasm.

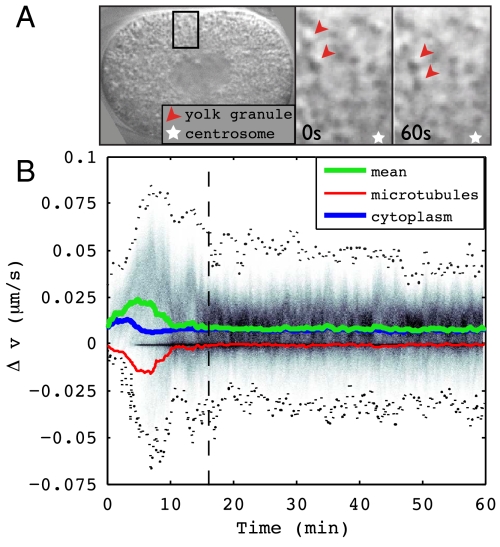
Fast movement of yolk granules toward aster centers has been observed in sand dollar (2) and C. elegans (3, 19). Fig. 4A shows two yolk granules moving toward the centrosome. Dynein was shown to be responsible for similar motion of droplets along MTs in Drosophila embryos (20). Such movements indicate the presence of cytoplasmic pulling forces on MTs. Indeed, a positive correlation between minus-end directed organelle motion and centrosome motion in the opposite direction was recently demonstrated (3).

Fig. 4.

(A) Differential interference contrast imaging of a live embryo shows linear motion of yolk granules along the lengths of MT filaments toward the centrosome (Movie S2). (B) The background density shows the distribution of motor protein velocities along the lengths of MTs throughout the simulation of the WT case, with its mean (green) and boundaries (dotted lines). The mean MT velocity (red) and cytoplasm velocity (blue) along MTs, directed toward minus ends, are also shown.

A motor protein moving under smaller load exhibits faster motion than one moving under larger load (Fig. 1B, Upper Inset). A yolk granule under small drag in turn exerts a small pulling force on the MT, whereas a yolk granule under larger drag exerts a larger pulling force. The latter granule would not be visually prominent as it would not be fast-moving. Our model explains the fast movement of yolk granules and predicts that slower-moving, more highly loaded cytoplasmic components can generate sufficient force to position the pronuclei. The average speeds of experimentally observed fast-moving yolk granules in anaphase were plotted in ref. 19, Fig. 3B. The maximum granule speeds of approximately 1.9 μm/s are very close to measurements of 2 μm/s for the maximum in vivo velocity of dynein reported in ref. 20 for early Drosophila embryos. In analogy to that figure, Fig. 4B plots all velocities along MTs throughout the simulation. This plot shows that on average, motor proteins and cytoplasm move along MTs toward minus ends, whereas MTs move toward plus ends. The spike in density of motor protein velocities near zero occurs close to the pronuclear body, as cytoplasm cannot flow freely into the centers of MTOCs due to incompressibility.

Additional Mechanisms for Nuclear and Spindle Positioning.

Several mechanisms for nuclear and spindle positioning have been proposed (1, 18, 21), and we briefly discuss these here.

Pushing forces due to MT polymerization against a resisting barrier were investigated as a possible mechanism of male pronuclear migration in ref. 4 and found to be less significant than a pulling mechanism. It was also noted in ref. 19 that the male pronucleus fails to move away from cortex in dynein heavy chain mutants, although the mechanisms underlying the pushing model were presumably intact.

There is evidence that direct pulling between the male and female pronuclei plays a significant role in pronuclear motion up to pronuclear meeting. In the colcemid/UV experiments of ref. 2, male pronuclear migration was 2–4 times faster when the female pronucleus was in the irradiated region than when it was outside the region, and the female pronucleus also migrated in this case. Plots of male and female pronuclei position vs. time in sand dollar [(2), figure 7] and C. elegans [(22), figure 3] show an acceleration of the motion as the bodies approach one another, possibly due to their association through a larger number of MTs interacting with the nuclear envelopes, where dynein is enriched (19).

The prevailing model for spindle positioning appears to be cortically driven pulling forces (23), where cortical force generators are balanced during symmetric positioning and unbalanced during asymmetric positioning, and control of positioning is achieved through regulation of cortical force generators. Possible mechanisms include capture and depolymerization of MTs at special sites on the cortex (24), as well as actin-based translocation of MTs along the cortex. Because of the rounded shape of the C. elegans embryo and the stiffness of MTs, these cortical interactions are presumed to be end-on. In flatter cells, such as the fission yeast, MTs can interact with the cortex along their lengths (25, 26). Application of the colcemid/UV experimental methodology of ref. 2 to the C. elegans embryo would be instructive in differentiating between cytoplasmically and cortically driven MT-based forces. Other approaches allowing spatial control of MTs, such as laser ablation (25), could also be used to test the present model.

Although the above mechanisms are likely involved in nuclear and spindle positioning, they cannot be fully responsible for the centering phenomenon demonstrated in the colcemid/UV study of ref. 2, as the areas of UV radiation were spatially isolated from the cortex in those experiments. Furthermore, unlike the cytoplasmically based model, pushing or cortical pulling models do not predict the observed movement of cytoplasmic components toward the center of asters.

Geometry-Dependence of Microtubule-Based Forces in the Centering and Rotation of the NCC.

Following pronuclear meeting, the NCC migrates to the center of the ellipsoidal cell and rotates 90° so that the spindle is aligned with the AP axis (27). Although spindle position and orientation in the single-cell C. elegans embryo have been shown to be coupled to polarity cues (for a recent review, see ref. 28), experiments interfering with such cues demonstrate the dependence of spindle positioning and orientation on extrinsic geometry (6).

In our pulling model, minus-end directed motor proteins are assumed to be uniformly distributed and anchored throughout the cytoplasm. Therefore, a longer MT can associate with more motor proteins, resulting in a force that is directly proportional to the MT length. When the NCC is offset from the center of the cell an MT-length imbalance favoring the direction of the cell center develops, and the net MT-based force on the NCC is directed toward the cell center (Fig. 1B). Our simulations reproduce this centering within a symmetric geometry, as depicted in Fig. 2B. The NCC position is stable in the cell center under the present model, and once in the cell center, it undergoes only small fluctuations due to randomness in the MT forces.

In our simulations, we observed that the NCC began to passively rotate as it approached the cell center and once centered continued to rotate until it aligned with the AP axis (Fig. 3D). That orientation was stable to continuing perturbations due to fluctuations in MT forces. The passive rotation results from symmetry breaking in the geometric positioning or orientation of the NCC, which in the cell could be due to a number of factors such as constitutive variations within the cell, the dynamics of the finite number of MTs, etc.

In the simulated spherical case, rotation failed due to the absence of orientational asymmetries in the forces. Experimentally, rotation is observed in otherwise unaltered spherical embryos (6, 29). However, this observed rotation depends on molecular mechanisms downstream of the par proteins (6). In par-3 mutants, rotation in spherical embryos failed, whereas in normally shaped oblong par-3 mutants, rotation was observed (6). Thus polarity-related mechanisms in the cell appear to induce intrinsic geometric asymmetries even in the absence of extrinsic geometric asymmetries. Because we do not model polarity in the cell, our results concerning rotation of the NCC are more consistent with embryos where polarity is disrupted. Interestingly, it was noted in ref. 29 that actin microfilaments may be required for rotation to occur in a spherical geometry whereas they may not be required in an ellipsoidal geometry.

Conclusion

We have presented a simplified model of MT-based motion transduced through interaction of MTs with active elements in the cytoplasm. We have demonstrated the feasibility of pronuclear and NCC motion through direct interaction with active elements in the cytoplasm along the length of MTs without assuming the presence of additional structures for anchoring motor proteins. We have illustrated that geometry-dependent centration and rotation can result passively as a consequence of the MT force model and the cell shape. We have shown that the inclusion of the cytoplasmic hydrodynamics in simulations of pronuclear migration significantly affects the cytoplasmic drag forces on the pronucleus. When MTs are aligned, this process can generate strong cytoplasmic flows, as illustrated in the simplified, bundled MT example. Thus, this model is applicable to other phenomena, for example, cytoplasmic streaming in other organisms and axonal transport of organelles. More generally, it is applicable to the interaction of motor proteins and polar filaments in a fluidic environment.