Abstract
A fundamental feature of information processing in neocortex is the ability of individual neurons to adapt to changes in incoming stimuli. It is increasingly being understood that cortical adaptation is a phenomenon that requires network interactions. The fact that the structure of local networks depends critically on cortical layer raises the possibility that adaptation could induce specific effects in different layers. Here we show that brief exposure (300 ms) to a stimulus of fixed orientation modulates the strength of synchronization between individual neurons and local population activity in the gamma-band frequency (30–80 Hz) in macaque primary visual cortex (V1) and influences the ability of individual neurons to encode stimulus orientation. Using laminar probes, we found that although stimulus presentation elicits a large increase in the gamma synchronization of rhythmic neuronal activity in the input (granular) layers of V1, adaptation caused a pronounced increase in synchronization in the cortical output (supragranular) layers. The increase in gamma synchronization after adaptation was significantly correlated with an improvement in neuronal orientation discrimination performance only in the supragranular layers. Thus, synchronization between the spiking activity of individual neurons and their local population may enhance sensory coding to optimize network processing across laminar circuits.
A fundamental issue in our understanding of brain circuits is how networks in different layers of the cerebral cortex encode information. Cortical layers are ubiquitous structures throughout neocortex (1, 2) that consist of highly recurrent local networks that communicate among each other to possibly influence the information encoded in population activity. In recent years, significant progress has been made in our understanding of the differences in response properties of neurons across cortical layers (3, 4), yet there is still a great deal to learn about whether and how neuronal populations encode information in a layer-specific manner. A measure of the activity of a local population (or ensemble) of neurons (5) is captured by local field potentials (LFPs), which are composed of low-frequency extracellular voltage fluctuations, including local excitatory and inhibitory intracortical inputs (6) believed to originate from within 250–500 μm of the recording site (7, 8). In visual cortex, it has been found that neuronal groups exhibit strong responses in the gamma-band frequency (30–80 Hz) (9–11) and that single neurons synchronize their responses with the local population activity (12, 13). Synchronization in visual cortex, particularly in the gamma-band, has been found to be critically involved in sensory processing (9, 11, 14), grouping (9, 11; but see refs. 15–17), attention (10, 18–20), working memory (5), and behavioral reaction times (20). The results of these studies support the hypothesis that efficient information transmission would occur whenever two networks are synchronous in their excitability peaks, which could constitute an energy-efficient mechanism for temporal coordination. In addition, selective activation of fast-spiking interneurons and their phase relationship with excitatory pyramidal cell activity has been shown to enhance the gamma rhythm (14, 21, 22). This inhibition-based mechanism is also consistent with anatomical results indicating that both the density of interneurons and the distribution of GABAb receptors, known to be involved in gamma oscillations, favor superficial layers of cortex (23–25). This raises the possibility that the capacity of individual neurons to exhibit gamma synchronization with their local population activity could depend on cortical layer.
We investigated this issue in the context of rapid, adaptation-induced plasticity in macaque primary visual cortex (area V1), where neurons have been shown to exhibit plasticity of feature coding even after brief exposure (at the time scale of visual fixation) to a stimulus of fixed structure (26–30). We focused on rapid adaptation because this phenomenon has been previously demonstrated to depend on the local network context in which neurons are embedded (31, 32), thus raising the possibility that the adaptive capacity of individual neurons may exhibit cortical layer dependency. Surprisingly, adaptation has never been directly investigated in relation to neuronal synchronization, particularly in the gamma frequency range. Indeed, although gamma synchronization has been found to be involved in a variety of conditions (9–11, 14, 18–20), whether a fundamental feature of individual neurons, such as the capacity to exhibit adaptive changes or plasticity, is influenced by synchrony in the gamma frequency band remains unclear. Recently, several studies have addressed the relationship between neuronal synchronization and adaptation-induced cortical changes during learning and memory (33–35). However, these studies have focused on longer forms of plasticity while ignoring plastic changes occurring at more rapid time scales.
We demonstrate that despite the fact that stimulus presentation is accompanied by pronounced gamma synchronization between individual neurons and their local population in the input (granular) layers of V1, rapid adaptation causes an increase in neuronal synchronization specifically in the cortical output (supragranular) layers. Importantly, the increase in gamma synchronization after adaptation may influence neuronal signaling because it is significantly correlated with an improvement in neuronal orientation discrimination performance (26–30) specifically in the supragranular layers.
Results
We used multicontact laminar electrodes (Plextrode U-Probe; Plexon Inc.; Fig. S1) to record neuronal activity at 20 V1 recording sites, each measured at 16 different depths, while two monkeys (W: 13; P: 7) performed a rapid adaptation fixation task (Fig. 1A). While animals fixated on a white dot at the center of a screen, an adapting stimulus was flashed for 300 ms in the center of the neurons’ receptive field. After a 100-ms blank, a test stimulus of random orientation (eight equally spaced orientations spanning 0–180°) was presented for 300 ms. The adapting stimulus was either a random dot patch (control condition) or a sine-wave grating with spatial characteristics identical to those of the test stimulus, but fixed in orientation within 45° of each cell's preferred orientation (adaptation condition). All stimuli were static and consisted of 5° circular sine-wave gratings of 1.4 cycles/degree spatial frequency and 50% contrast level presented binocularly. The orientation range of the adapting stimulus was chosen on the basis of our previous orientation adaptation experiments (28, 32) reporting strong effects when the adaptor is relatively close to the cell's preferred orientation.
Fig. 1.
Rapid adaptation across cortical layers in V1. (A) Schematic description of the orientation adaptation protocol. (B) Multicontact laminar electrodes (Left) were used to record neuronal activity across cortical depth. Cortical layers we identified using CSD. In this example, the current sink (blue) represents the granular layer and spans ≈400 μm. This analysis served as a reference to assign electrode contacts above and below the granular layer. (C) Example of LFP responses across cortical layers for a single penetration during control (blue) and adaptation (red). Each trace represents the average response across all trials and test orientations in each condition (a 45° adaptor). (D) Raster plots represent the spike times of three example V1 neurons across cortical layers responding to the adapting and test stimuli in the control (blue) and adaptation (red) conditions. The horizontal lines mark the 300-ms time windows during which the adapting (first line) and test stimuli (second line) were presented.
Identification of Cortical Layers.
To identify cortical layers, we measured the evoked response potentials (ERPs) of LFPs across laminar contacts during the presentation of a full-field white flashed stimulus. We then computed the current-source density (CSD; Fig. 1B) of the LFP time-series to identify the polarity inversion accompanied by the sink-source configuration at the base of layer 4; the sink (blue region) is inside layer 4, subsequently referred to as the granular layer (36, 37). Fig. 1B also illustrates the stability of our CSD analysis in identifying cortical layers across cortical depth as a function of time—the position of the granular, supragranular, and infragranular layers remained stable even after 4 h after the end of the adaptation task (Fig. S2). Using CSD analysis, we assigned electrode contacts above and below the granular layers to supragranular and infragranular layers, respectively (the contact with the largest sink center of mass served as the granular layer reference at 0 μm).
Adaptation Increases Spike–LFP Gamma Synchronization.
For each recording session, we recorded spike and LFP responses across all cortical layers during control and adaptation. The traces in Fig. 1C show the mean LFP amplitude as a function of time produced by the stimuli evoking an increase in the response to the adaptor (45° in this example), as well as the test (Fig. S3). Fig. 1D shows representative spike responses recorded in the same session spanning all cortical layers. Single unit isolation on the laminar electrode was performed manually, and distinct clusters were identified according to spike waveform properties, such as the weight of the first and second principal components (Fig. S4 A and B) spike width, valley, and peak. Overall, for the population of 77 cells (supragranular = 33, granular = 24, and infragranular = 20), we found that adaptation significantly reduces the peak firing rate irrespective of cortical layer (P = 0.0003, Wilcoxon signed-rank test) (consistent with previous results (26, 28, 29).
Therefore, we examined the effect of rapid adaptation on the degree of synchronization between individual neurons and LFPs in different frequency bands by computing spike-field coherence (SFC; 38, 39) during the presentation of the test stimulus for our population of 986 pairs that exhibited significant response modulation by stimulus orientation. We computed the mean SFC by averaging, for each recording site, the coherence values for pairs of single units and LFPs within 300 μm of cortical space.
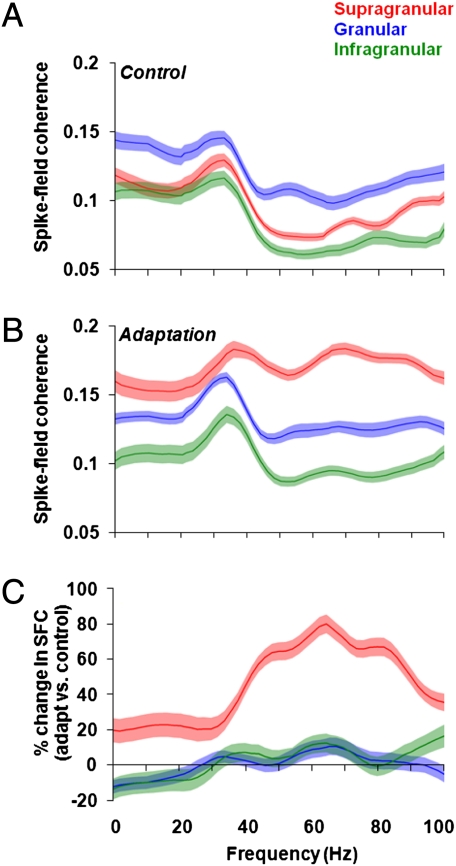
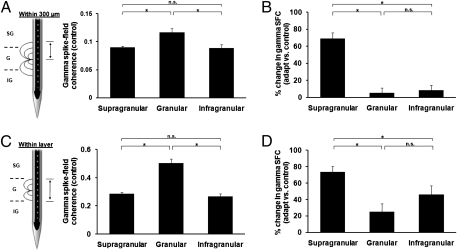
In control trials, the presentation of the test stimulus led to pronounced synchronous activity across all cortical layers, with the most significant increase in gamma synchronization in the granular layers (Fig. 2 A and B, Left). However, after adaptation, there was a significant increase in gamma synchronization specifically in the supragranular layers (Fig. 2 A and B, Right). Our population analysis confirms these results: before adaptation we found spike-LFP gamma synchronization across all layers (mean ± SEM; supragranular: 0.08 ± 0.002; granular: 0.12 ± 0.007; infragranular: 0.08 ± 0.006) with the largest SFC level in the granular layers [Figs. 3A and 4A; one-way ANOVA, F(2,74) = 8.75, P = 0.0004; post hoc multicomparison, Tukey's least significant difference]. However, despite the high gamma synchronization in the granular layers during control, adaptation significantly increased SFC only in the supragranular layers (Fig. 3B), whereas the granular and infragranular layers exhibited only a weak increase in synchronization.
Fig. 2.
Examples of synchronization across cortical layers during control and adaptation. (A and B) Two examples illustrating SFC across cortical depth during control and adaptation as a function of frequency. During the presentation of the control stimuli there is an increase in gamma activity in the granular layer. Adaptation increases SFC across cortical layers, with the largest increase in the supragranular layer. Dashed lines equal the granular layer.
Fig. 3.
Adaptation influences synchronization between individual neurons and local populations in a layer-specific manner. (A) Population analysis during the presentation of the control stimulus results in a significant increase in SFC between 30 and 80 Hz in the granular layer. (B) Adaptation increases SFC in the supragranular layer for all frequency bands between 0 and 80 Hz, with the largest increase in the gamma-band (30–80 Hz; shaded regions represent SEM). (C) We calculated the percentage change between adaptation and control across the entire frequency range and observed a significant increase in gamma-band SFC for the supragranular layer (shaded regions represent SE for percentage change).
Fig. 4.
Adaptation increases gamma synchronization in supragranular layer. (A) “Within 300 μm” pooling scheme: to compute SFC, we pooled the spike-field pairs within a 300-μm window around each isolated unit. Population mean gamma-band SFC (30–80 Hz) shows a significant increase in the granular layer during control [mean ± SEM; supragranular: 0.08 ± 0.002; granular: 0.12 ± 0.007; infragranular: 0.08 ± 0.006; one-way ANOVA, F(2,74) = 8.75, P = 0.0004]. (B) Although adaptation significantly increases the population mean SFC in the supragranular layer, it does not significantly alter SFC in the granular and infragranular layers [one-way ANOVA, F(2, 74) = 35.24, P = 1.77 10−11]. The mean percentage change in SFC was calculated by computing the percentage change in SFC for each spike-field pair, and then we averaged the calculated percentages to obtain the data shown in the figure. (C and D) “Within-layer” pooling scheme: restricting the coherence analysis to those contacts within an identified layer does not alter the results shown in A and B. Although the population mean SFC in the gamma-band showed an overall increase across all layers, the main result of an increase in granular SFC during control [C; mean ± SEM; granular: 0.50 ± 0.02, F(2,74) = 44.1, P = 2.45 10−13] and a postadaptation increase in synchronization in the supragranular layers [D; one-way ANOVA, F(2,74) = 8.22, P = 0.0006] was unchanged for this more restrictive analysis.
It is important to note that although our adaptation paradigm did not yield a spectrally significant gamma peak in the SFC, we observed a pronounced increase specifically in the supragranular layers. We also calculated the percentage change in gamma SFC between adaptation and control (ΔSFC) across the entire frequency range and found a significant increase in synchronization for the supragranular layer [68.91% ± 6.75%; Fig. 3C and 4B; one-way ANOVA, F(2,74) = 35.24, P = 1.77 10−11; post hoc multicomparison, Tukey's least significant difference]. The postadaptation increase in gamma SFC in the supragranular layers was observed only when both recording sites were stimulated with test stimuli within 45° of the cells’ preferred orientation (Fig. S5; P = 1.12 10−12, Wilcoxon signed-rank test). Nonoptimal test orientations reduced spike rates, LFP amplitudes, and SFC in the control condition; adaptation at these orientations did not result in a significant increase in gamma SFC (P = 0.20, Wilcoxon signed-rank test). Of note, although rapid adaptation caused an increase in gamma synchronization in the supragranular layer, we also noticed a significant increase in synchronization for lower frequencies, such as alpha (8–14 Hz; Fig. S6A) and beta (14–27 Hz; Fig. S6B). However, over the entire low-frequency range (0–30 Hz), we found only a 24% SFC change in adaptation vs. control (Fig. S6C). Overall, adaptation increased low-frequency SFC across all layers, with the largest increase occurring in supragranular layers.
In principle, the 300-μm pooling of LFP inputs used for our calculation of mean SFC might have overestimated the spatial extent of the LFP inputs attributable to the same cortical layer. To control for this possibility, we recomputed SFC for each recording site by pooling only those LFPs located within the same cortical layer, irrespective of the distance between LFPs and the single unit site. Nonetheless, our main results remained unchanged: an increase in gamma-band SFC in the granular layer during the control condition [0.50 ± 0.02, mean ± SEM; Fig. 4C; one-way ANOVA, F(2,74) = 44.1, P = 2.45 10−13] and an improvement in gamma synchronization after adaptation that is specific to the supragranular layers [Fig. 4D; one-way ANOVA, F(2,74) = 8.22, P = 0.0006].
Relationship Between Gamma Synchronization and Neuronal Discrimination.
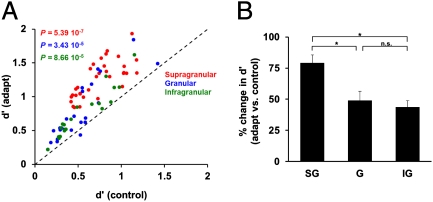
We further investigated whether the ability of neurons in different cortical layers to discriminate stimulus orientation is influenced by the postadaptation change in synchronization between individual cells and their local population. We addressed this issue by examining the relationship between the postadaptation change in gamma-band SFC and the change in neurons’ capacity (d′) (40, 41) to discriminate nearby orientations (22.5° apart). In agreement with previous studies (28, 29, 32), we found a significant increase in d′ after adaptation across the population of neurons (P = 3.65 10−14; Fig. 5A; supragranular: P = 5.39 10−7; granular: P = 3.43 10−5; infragranular: P = 8.86 10−5; Wilcoxon signed-rank test). As expected, the changes in d′ in each layer were accompanied by an increase in response slope (response difference at the two nearby test orientations: supragranular: 29.33%, P = 5.39 10−7; granular: 19.98%, P = 4.91 10−4; infragranular: 28.33%, P = 1.89 10−4, Wilcoxon signed-rank test) and a decrease in response variance (supragranular: −25.87%, P = 5.39 10−7; granular: −27.71%, P = 1.02 10−4; infragranular: −21.56%, P = 1.89 10−4, Wilcoxon signed-rank test). Importantly, the increase in discriminability after adaptation depends on cortical layer—neurons residing in the supragranular layer showed the largest postadaptation increase in d′ [Fig. 5B one-way ANOVA, F(2,74) = 7.66, P = 0.0009].
Fig. 5.
Postadaptation layer-specific changes in neuronal discrimination performance. (A) Scatter plot showing the effects of adaptation on neuronal discrimination performance (d′) at the population level across cortical layers. Each dot represents the mean d′ during control and adaptation, whereas the different colors indicate the layer in which the neuron was isolated. Across the total population of cells (SG = 33; G = 24; IG = 20), adaptation significantly increases orientation discriminability. (B) Although adaptation significantly increases d′ across all cortical layers, the largest increase occurred in the supragranular layer.
The increase in neuronal discriminability after adaptation has been suggested (26, 42) to emerge from changes in firing rates (both suppressive and facilitatory) across the population of cells, mainly due to the depression of excitatory and inhibitory synapses originating from neurons tuned to the adapting stimulus. We thus explored whether the postadaptation increase in gamma synchronization in the supragranular layers might have contributed to the larger increase in neuronal discriminability found in supragranular neurons after adaptation.
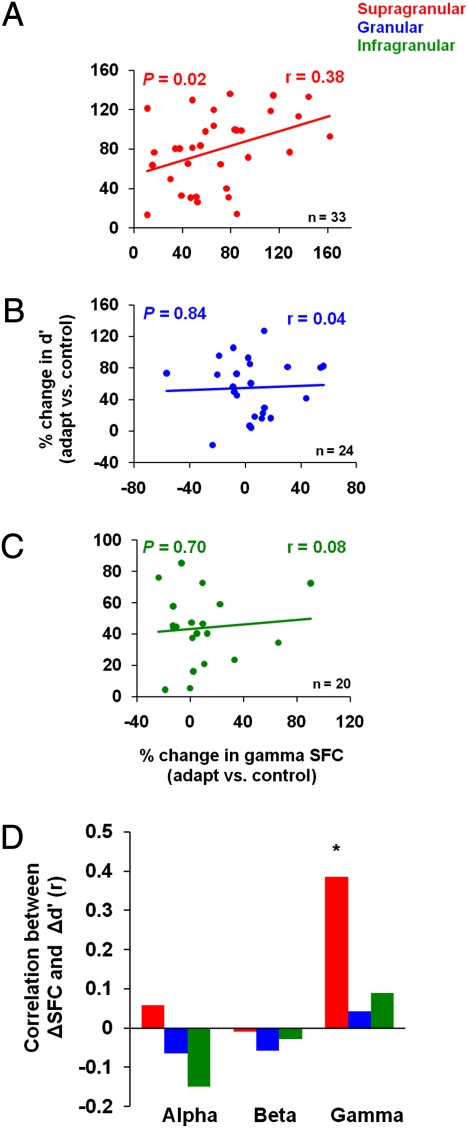
We measured the correlation between the changes in gamma-band SFC in each cortical layer and the adaptation-induced changes in neuronal discrimination performance. We found a significant correlation between the postadaptation change in d′ and the corresponding change in SFC only for the recording sites in the supragranular layers (Fig. 6A, r = 0.38, P = 0.02, Pearson correlation). In contrast, neurons in granular and infragranular layers exhibited postadaptation changes in discriminability that were independent of the changes in gamma SFC (Fig. 6 B and C; granular: r = 0.04, P = 0.84; infragranular: r = 0.08, P = 0.70, Pearson correlation).
Fig. 6.
The relationship between gamma synchronization and neuronal discrimination performance. (A–C) Postadaptation change in gamma-band SFC influences the neurons’ ability to discriminate small changes in orientation. There is a significant and positive correlation between the gamma-band SFC after adaptation and the change in d′ that is specific to the supragranular layers. The color lines represent the linear regression fits associated with each cortical layer. (D) Analysis of lower frequency bands (<30 Hz) does not reveal a statistically significant correlation between the postadaptation change in SFC and the change in d′.
We further observed that adaptation increases SFC in the supragranular layers to enhance response slope (correlation between changes in gamma SFC and changes in response slope, r = 0.36, P = 0.03, Pearson correlation) and decrease response variability (correlation between changes in gamma SFC and changes in response SD, r = −0.34, P = 0.04) to enhance orientation coding by supragranular neurons. However, for the granular and infragranular layers we did not find any significant correlation between postadaptation SFC and response slope (granular: r = −0.17, P = 0.42; infragranular: r = −0.13, P = 0.58) or response variability (granular: r = −0.09, P = 0.64; infragranular: r = −0.15, P = 0.51, Pearson correlation). The laminar-specific relationship between the postadaptation changes in SFC and d′ was preserved when LFPs were pooled according to the “within layer” scheme (compare Fig. 4 C and D; Fig. S7 A–C). The relationship between neuronal synchronization and the enhancement in neuronal discrimination after adaptation in the supragranular layers was specific to the gamma band (see also coefficient of variations analysis, Fig. S8 A–C). Changes in coherence in lower-frequency bands, such as alpha and beta, showed no significant correlation with the postadaptation changes in d′ (Fig. 6D).
One possible explanation for the result shown in Fig. 6A is that the increase in d′ after adaptation in supragranular layers might simply reflect a change in firing rate rather than an increase in gamma synchronization. Therefore, we performed multiple least-squares regression in which we modeled the change in d′ as a linear combination of the postadaptation change in peak firing rate and the change in gamma-band SFC: Δd′ = β0 + β1 ΔFR + β2 ΔSFCγ. We combined data from all of the neurons in our population by calculating the percentage change in peak firing rate and gamma SFC after adaptation corresponding to each neuron as a function of layer. The postadaptation decrease in firing rate was significant across all layers (supragranular: P = 0.0068; granular: P = 0.01; infragranular: P = 0.02), indicating that changes in firing rate are an important factor that could potentially influence d′. However, we found that incorporating the changes in gamma SFC after adaptation resulted in a significant improvement in the regression fit only in the supragranular layer (P < 0.05). This implies that although changes in firing rates after adaptation can explain in part the improvement in neuronal discriminability, the increase in gamma-band SFC after adaptation further increases neuronal discrimination performance specifically in the supragranular layers.
Discussion
The laminar structure of the visual cortex has been known for a long time, yet whether there are differences in the way in which neuronal populations across cortical layers encode information is just beginning to be understood (3, 4, 43). Aside from a study in anesthetized cat V1 (32) reporting pronounced adaptive effects irrespective of cortical depth, whether adaptation influences sensory coding in a layer-specific manner has never been investigated. The fact that neurons in the supragranular layers exhibit the largest increase in gamma synchronization after adaptation and the highest correlation with the postadaptation improvement in feature coding has functional implications for models of cortical function. Indeed, neurons in the supragranular layers of V1 provide the only cortical input to downstream visual areas. Infragranular layers also constitute output layers, but they target deep subcortical structures, such as the thalamus and superior colliculus. Therefore, neurons in higher-order cortices would benefit most if cells in the supragranular layers would exhibit a large increase in stimulus coding after adaptation.
The relationship between the postadaptation change in gamma synchronization and neuronal discriminability described here should be interpreted cautiously. Thus, we and others have previously shown that incorporating synaptic depression in recurrent models of cortical adaptation may be sufficient to explain the increase in neuronal discrimination performance of individual neurons and networks (26, 44). Indeed, we found that a large percentage of neurons in our population exhibited an increase in d′ even in the absence of a corresponding increase in gamma coherence (in the granular and infragranular layers). However, our analysis implies that the pronounced increase in gamma SFC after adaptation in the supragranular layers contributes to the larger change in neuronal discriminability shown by supragranular neurons.
The possible relationship between gamma synchronization and neuronal performance has been indirectly suggested by attention studies in midlevel cortical areas (10, 19). Experimental and theoretical studies have both suggested that gamma oscillations of spiking neuronal populations can enhance signal discrimination by decreasing the variance of the responses (45, 46) and that synchronization could enhance the response gain of neurons (47). In addition, recent evidence indicates that selective activation of fast-spiking interneurons and their phase relationship with excitatory pyramidal cell activity enhances the gamma rhythm and controls sensory responses (14, 21, 22) This raises the possibility that an increase in local inhibition due to adaptation (42) could subsequently cause an increase in gamma synchronization possibly to improve neuronal discrimination performance. This inhibition-based mechanism is consistent with our finding that the relationship between the adaptation-induced changes in gamma synchronization and neuronal discriminability is more prominent in the supragranular layers of V1. Indeed, anatomical results indicate that both the density of interneurons and the distribution of GABAb receptors (known to be involved in gamma oscillations) are highest in the supragranular layers of V1 (23–25). At the same time, one cannot entirely exclude the fact that our effects may be due to extrastriate feedback that exclusively targets the superficial layers of V1. For instance, it has been found that neuronal responses in superficial layers of V1 are increased via attentional mechanisms, which are known to be mediated by acetylcholine (Ach) acting through muscarinic receptors (48). The fact that superficial layers contain a higher density of cholinergic fibers than deep layers (49) and that one way by which Ach influences attention is through changes in oscillatory activity (10) raises the possibility that the increase in spike–LFP gamma synchronization could be mediated by Ach. However, future experimental and theoretical work is needed to determine precisely the mechanism underlying laminar changes in neuronal synchronization after adaptation and its relationship with neuronal performance.
Methods
Adaptation Paradigm.
All experiments were performed in accordance with protocols approved by the US National Institutes of Health Guidelines for the Care and Use of Animals for Experimental Procedures. Two rhesus monkeys (Macaca mulatta) performed an orientation adaptation task. Monkeys were trained to fixate on a small spot (0.1°) presented on a video monitor placed at a distance of 57 cm from each monkey's eye. Stimuli were generated with Psychophysics Toolbox from MATLAB and presented on a cathode ray tube 19” color video monitor (Dell, 60-Hz refresh rate). All stimuli were static and consisted of 5° circular sine-wave gratings of 1.4 cycles/degree spatial frequency and 50% contrast level presented binocularly. Monkeys triggered the trial by holding a bar, and after 300 ms of fixation an adapting stimulus was flashed for 300 ms in the center of the neurons’ receptive fields. After 100 ms blank, a 300-ms test stimulus of random orientation (eight equally spaced orientations spanning 0–180°; random spatial phase for each test orientation) was flashed at the same visual location. The adapting stimulus was either a 5° random dot patch (control condition) or a sine-wave grating of identical characteristics as the test stimulus (5° circular sine-wave grating of 1.4 cycles/degree spatial frequency and 50% contrast level) but fixed in orientation (0°, 45°, 90°, or 135°; adaptation condition). Both the adaptor and test stimuli had the same mean luminance. Each test orientation was randomly presented 50 times in each of the control and adaptation conditions.
Multicontact Electrophysiological Recordings.
We conducted 20 recording sessions in two monkeys using laminar electrodes. On average, we were able to identify 14–16 LFPs and five to eight single units per recording session for each electrode. Each laminar electrode consisted of a linear array of 16 equally spaced contacts (100 μm intercontact spacing) positioned to sample from all cortical layers simultaneously (Plextrode U-Probe; Plexon Inc; Fig. S1). In half of the recording sessions, the electrodes were treated with carbon nanotube coating that gave impedance between 0.3 and 0.5 MΩ at each contact. Real-time neuronal signals recorded from multiple contacts along the electrode shaft were analyzed using a Multichannel Acquisition Processor system (Plexon Inc). Single unit recordings were amplified, filtered, and viewed on an oscilloscope and heard through a speaker. The spike waveforms were sorted using Plexon’s Offline Sorter program that implemented waveform clustering based on parameters such as principal components, spike width, valley, and peak. Before the adaptation experiment, when a unit was isolated, its receptive field was mapped using a reverse correlation stimulus. Recording sites were selected on the basis of the quality of the signal (signal-to-noise ratio) and their receptive field position. Using home-made scripts in MATLAB and Plexon’s Offline Sorter we analyzed the unit's waveform characteristic (e.g., width and peak), firing rate, and orientation selectivity. Only single units with stable firing rate and orientation selectivity were included in the analysis.
Supplementary Material
Acknowledgments
We thank Diego Gutnisky and Ye Wang for discussions; and Sorin Pojoga for behavioral training. This study was supported by the National Institutes of Health (NIH) Exceptional, Unconventional Research Enabling Knowledge Acceleration (EUREKA) Program, the National Eye Institute, the Pew Scholars Program, the James S. McDonnell Foundation (V.D.), and an NIH Vision training grant (to B.J.H.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1102017108/-/DCSupplemental.
References
- 1.Hubel DH, Wiesel TN. Receptive fields and functional architecture of monkey striate cortex. J Physiol. 1968;195:215–243. doi: 10.1113/jphysiol.1968.sp008455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nassi JJ, Callaway EM. Parallel processing strategies of the primate visual system. Nat Rev Neurosci. 2009;10:360–372. doi: 10.1038/nrn2619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lakatos P, et al. The leading sense: Supramodal control of neurophysiological context by attention. Neuron. 2009;64:419–430. doi: 10.1016/j.neuron.2009.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Maier A, Adams GK, Aura C, Leopold DA. Distinct superficial and deep laminar domains of activity in the visual cortex during rest and stimulation. Front Syst Neurosci. 2010;4:1–11. doi: 10.3389/fnsys.2010.00031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- 6.Logothetis NK. The underpinnings of the BOLD functional magnetic resonance imaging signal. J Neurosci. 2003;23:3963–3971. doi: 10.1523/JNEUROSCI.23-10-03963.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Katzner S, et al. Local origin of field potentials in visual cortex. Neuron. 2009;61:35–41. doi: 10.1016/j.neuron.2008.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kruse W, Eckhorn R. Inhibition of sustained gamma oscillations (35-80 Hz) by fast transient responses in cat visual cortex. Proc Natl Acad Sci USA. 1996;93:6112–6117. doi: 10.1073/pnas.93.12.6112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Engel A, Konig P, Kreiter A, Singer W. Interhemispheric synchronization of oscillatory neuronal responses in cat visual cortex. Science. 1991;252:1177–1179. doi: 10.1126/science.252.5009.1177. [DOI] [PubMed] [Google Scholar]
- 10.Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- 11.Gray CM, König P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- 12.Freiwald WA, Kreiter AK, Singer W. Stimulus dependent intercolumnar synchronization of single unit responses in cat area 17. Neuroreport. 1995;6:2348–2352. doi: 10.1097/00001756-199511270-00018. [DOI] [PubMed] [Google Scholar]
- 13.Tsodyks M, Kenet T, Grinvald A, Arieli A. Linking spontaneous activity of single cortical neurons and the underlying functional architecture. Science. 1999;286:1943–1946. doi: 10.1126/science.286.5446.1943. [DOI] [PubMed] [Google Scholar]
- 14.Cardin JA, et al. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Palanca BJ, DeAngelis GC. Does neuronal synchrony underlie visual feature grouping? Neuron. 2005;46:333–346. doi: 10.1016/j.neuron.2005.03.002. [DOI] [PubMed] [Google Scholar]
- 16.Roelfsema PR, Lamme VA, Spekreijse H. Synchrony and covariation of firing rates in the primary visual cortex during contour grouping. Nat Neurosci. 2004;7:982–991. doi: 10.1038/nn1304. [DOI] [PubMed] [Google Scholar]
- 17.Thiele A, Stoner G. Neuronal synchrony does not correlate with motion coherence in cortical area MT. Nature. 2003;421:366–370. doi: 10.1038/nature01285. [DOI] [PubMed] [Google Scholar]
- 18.Chalk M, et al. Attention reduces stimulus-driven gamma frequency oscillations and spike field coherence in V1. Neuron. 2010;66:114–125. doi: 10.1016/j.neuron.2010.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gregoriou GG, Gotts SJ, Zhou H, Desimone R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science. 2009;324:1207–1210. doi: 10.1126/science.1171402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Womelsdorf T, Fries P, Mitra PP, Desimone R. Gamma-band synchronization in visual cortex predicts speed of change detection. Nature. 2006;439:733–736. doi: 10.1038/nature04258. [DOI] [PubMed] [Google Scholar]
- 21.Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Traub RD, Whittington MA, Stanford IM, Jefferys JG. A mechanism for generation of long-range synchronous fast oscillations in the cortex. Nature. 1996;383:621–624. doi: 10.1038/383621a0. [DOI] [PubMed] [Google Scholar]
- 23.Eickhoff SB, Rottschy C, Zilles K. Laminar distribution and co-distribution of neurotransmitter receptors in early human visual cortex. Brain Struct Funct. 2007;212:255–267. doi: 10.1007/s00429-007-0156-y. [DOI] [PubMed] [Google Scholar]
- 24.Fitzpatrick D, Lund JS, Schmechel DE, Towles AC. Distribution of GABAergic neurons and axon terminals in the macaque striate cortex. J Comp Neurol. 1987;264:73–91. doi: 10.1002/cne.902640107. [DOI] [PubMed] [Google Scholar]
- 25.Whittington MA, Traub RD, Jefferys JG. Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature. 1995;373:612–615. doi: 10.1038/373612a0. [DOI] [PubMed] [Google Scholar]
- 26.Dragoi V, Sharma J, Miller EK, Sur M. Dynamics of neuronal sensitivity in visual cortex and local feature discrimination. Nat Neurosci. 2002;5:883–891. doi: 10.1038/nn900. [DOI] [PubMed] [Google Scholar]
- 27.Felsen G, et al. Dynamic modification of cortical orientation tuning mediated by recurrent connections. Neuron. 2002;36:945–954. doi: 10.1016/s0896-6273(02)01011-5. [DOI] [PubMed] [Google Scholar]
- 28.Gutnisky DA, Dragoi V. Adaptive coding of visual information in neural populations. Nature. 2008;452:220–224. doi: 10.1038/nature06563. [DOI] [PubMed] [Google Scholar]
- 29.Müller JR, Metha AB, Krauskopf J, Lennie P. Rapid adaptation in visual cortex to the structure of images. Science. 1999;285:1405–1408. doi: 10.1126/science.285.5432.1405. [DOI] [PubMed] [Google Scholar]
- 30.Yao H, Dan Y. Stimulus timing-dependent plasticity in cortical processing of orientation. Neuron. 2001;32:315–323. doi: 10.1016/s0896-6273(01)00460-3. [DOI] [PubMed] [Google Scholar]
- 31.Dragoi V, Rivadulla C, Sur M. Foci of orientation plasticity in visual cortex. Nature. 2001;411:80–86. doi: 10.1038/35075070. [DOI] [PubMed] [Google Scholar]
- 32.Dragoi V, Sharma J, Sur M. Adaptation-induced plasticity of orientation tuning in adult visual cortex. Neuron. 2000;28:287–298. doi: 10.1016/s0896-6273(00)00103-3. [DOI] [PubMed] [Google Scholar]
- 33.Masquelier T, Hugues E, Deco G, Thorpe SJ. Oscillations, phase-of-firing coding, and spike timing-dependent plasticity: An efficient learning scheme. J Neurosci. 2009;29:13484–13493. doi: 10.1523/JNEUROSCI.2207-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rutishauser U, Ross IB, Mamelak AN, Schuman EM. Human memory strength is predicted by theta-frequency phase-locking of single neurons. Nature. 2010;464:903–907. doi: 10.1038/nature08860. [DOI] [PubMed] [Google Scholar]
- 35.van Wingerden M, Vinck M, Lankelma JV, Pennartz CM. Learning-associated gamma-band phase-locking of action-outcome selective neurons in orbitofrontal cortex. J Neurosci. 2010;30:10025–10038. doi: 10.1523/JNEUROSCI.0222-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mitzdorf U. Current source-density method and application in cat cerebral cortex: Investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65:37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- 37.Schroeder CE, Mehta AD, Givre SJ. A spatiotemporal profile of visual system activation revealed by current source density analysis in the awake macaque. Cereb Cortex. 1998;8:575–592. doi: 10.1093/cercor/8.7.575. [DOI] [PubMed] [Google Scholar]
- 38.Jarvis MR, Mitra PP. Sampling properties of the spectrum and coherency of sequences of action potentials. Neural Comput. 2001;13:717–749. doi: 10.1162/089976601300014312. [DOI] [PubMed] [Google Scholar]
- 39.Mitra PP, Pesaran B. Analysis of dynamic brain imaging data. Biophys J. 1999;76:691–708. doi: 10.1016/S0006-3495(99)77236-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Green DM, Swets JA. Signal Detection and Psychophysics. New York: John Wiley & Sons; 1966. [Google Scholar]
- 41.Macmillan NA, Creelman CD. Detection Theory: A User's Guide. 2nd Ed. Mahwah, NJ: Lawrence Erlbaum Associates; 2005. [Google Scholar]
- 42.Chelaru MI, Dragoi V. Asymmetric synaptic depression in cortical networks. Cereb Cortex. 2008;18:771–788. doi: 10.1093/cercor/bhm119. [DOI] [PubMed] [Google Scholar]
- 43.Sun W, Dan Y. Layer-specific network oscillation and spatiotemporal receptive field in the visual cortex. Proc Natl Acad Sci USA. 2009;106:17986–17991. doi: 10.1073/pnas.0903962106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Teich AF, Qian N. Learning and adaptation in a recurrent model of V1 orientation selectivity. J Neurophysiol. 2003;89:2086–2100. doi: 10.1152/jn.00970.2002. [DOI] [PubMed] [Google Scholar]
- 45.Masuda N, Doiron B. Gamma oscillations of spiking neural populations enhance signal discrimination. PLoS Comput Biol. 2007;3:e236. doi: 10.1371/journal.pcbi.0030236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Murthy VN, Fetz EE. Oscillatory activity in sensorimotor cortex of awake monkeys: synchronization of local field potentials and relation to behavior. J Neurophysiol. 1996;76:3949–3967. doi: 10.1152/jn.1996.76.6.3949. [DOI] [PubMed] [Google Scholar]
- 47.Salinas E, Sejnowski TJ. Impact of correlated synaptic input on output firing rate and variability in simple neuronal models. J Neurosci. 2000;20:6193–6209. doi: 10.1523/JNEUROSCI.20-16-06193.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Herrero JL, et al. Acetylcholine contributes through muscarinic receptors to attentional modulation in V1. Nature. 2008;454:1110–1114. doi: 10.1038/nature07141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Voytko ML, Kitt CA, Price DL. Cholinergic immunoreactive fibers in monkey anterior temporal cortex. Cereb Cortex. 1992;2:48–55. doi: 10.1093/cercor/2.1.48. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.