Systematic variation in the temperature dependence of physiological and ecological traits

Abstract

To understand the effects of temperature on biological systems, we compile, organize, and analyze a database of 1,072 thermal responses for microbes, plants, and animals. The unprecedented diversity of traits (n = 112), species (n = 309), body sizes (15 orders of magnitude), and habitats (all major biomes) in our database allows us to quantify novel features of the temperature response of biological traits. In particular, analysis of the rising component of within-species (intraspecific) responses reveals that 87% are fit well by the Boltzmann–Arrhenius model. The mean activation energy for these rises is 0.66 ± 0.05 eV, similar to the reported across-species (interspecific) value of 0.65 eV. However, systematic variation in the distribution of rise activation energies is evident, including previously unrecognized right skewness around a median of 0.55 eV. This skewness exists across levels of organization, taxa, trophic groups, and habitats, and it is partially explained by prey having increased trait performance at lower temperatures relative to predators, suggesting a thermal version of the life-dinner principle—stronger selection on running for your life than running for your dinner. For unimodal responses, habitat (marine, freshwater, and terrestrial) largely explains the mean temperature at which trait values are optimal but not variation around the mean. The distribution of activation energies for trait falls has a mean of 1.15 ± 0.39 eV (significantly higher than rises) and is also right-skewed. Our results highlight generalities and deviations in the thermal response of biological traits and help to provide a basis to predict better how biological systems, from cells to communities, respond to temperature change.

Investigation of the thermal response of diverse biological processes should reveal general mechanisms by which life responds to Earth's complex and rapidly changing thermal landscape (1). General patterns of how temperature affects biological systems can be deduced in at least two ways. First, physiological and ecological traits (e.g., metabolic rate, encounter rate) can be measured for each species at its optimal temperature and plotted together to construct a single curve across species (2, 3). This interspecific approach has been used extensively (2–8), including studies of how climate affects biological systems (8–11). Second, a curve can be constructed by measuring trait values across a range of temperatures for a single species (intraspecific) (12, 13). In both intra- and interspecific cases, each curve can be characterized by its Q₁₀ value or activation energy (4, 6). These parameters, along with optimal temperature and response breadth for intraspecific responses, can be contrasted to explore effects of taxa, traits, and habitats. Indeed, for nearly a century, intraspecific studies have been conducted on a huge diversity of physiological and ecological traits (3, 6, 12, 14–17). Comparative studies of these intraspecific data have tended to focus on a subset of available data (16, 18–21). A broad-scale comparative analysis of intraspecific thermal responses has not been performed previously because of a lack of a comprehensive database. As we now show, this approach provides new insights into the general features of thermal responses not accessible with interspecific studies.

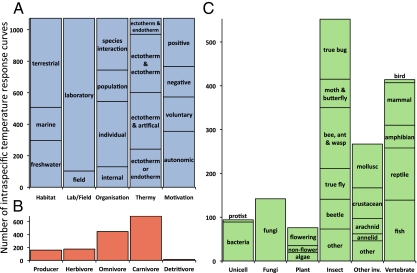
We construct from the literature a database containing 2,445 intraspecific temperature responses. Our ecoinformatics approach allows us to: (i) combine these data into a single database with consistent measurement units and trait definitions and (ii) describe patterns that suggest mechanisms responsible for generalities and deviations in the thermal dependence of biological traits. We compile data on both physiological and ecological traits but focus on those central to species interactions (SI Appendix, Table S1). The thermal response of interaction traits can be strongly influenced by organismal behavior (22–25), so we focus on how biological processes are executed (e.g., attack body velocity, handling rate) and not on decisions (e.g., attack probability, defense behavior probability) about whether to execute them. Requiring each response to have nonzero measurements at a minimum of four distinct temperatures that cover a range of at least 5 °C yields 1,072 responses. Our ontology categorizes these responses into 112 distinct traits that span levels of biological organization from internal physiology to species interactions (Fig. 1 and Materials and Methods). Traits were measured in marine, freshwater, and terrestrial habitats for 309 species of plants, microbes, and animals.

Fig. 1.

Diversity of intraspecific temperature responses analyzed in our study. Total number of thermal response data for habitat, laboratory/field, level of biological organization, and thermy of predator or prey (traits involving single species) or predator and prey (traits involving interactions between two species) (artificial taxa are shown in SI Appendix, Table S3) as well as motivation (main text) (A), trophic group (B), and taxonomic group (C). B and C sum to more than 1,072 (the total number of responses) because species interactions include multiple species. Further details on trait categories and data sources are provided in SI Appendix.

Thermal responses are typically unimodal over the full temperature range, but many studies only record measurements for a restricted temperature range over which responses typically rise or fall monotonically (3, 4, 8). Consequently, we analyze three components of the thermal response: the initial increase in the trait value with temperature (rise), its ultimate decrease at higher temperatures (fall), and the transition between the rise and fall components (unimodal) (SI Appendix, Fig. S1). After combining pseudoreplicates (SI Appendix, SI Materials and Methods), this process yields 374 rise, 70 fall, and 240 unimodal responses (minimum temperature range was increased to 10 °C for unimodals to capture both the rise and fall components).

Results

Our analyses of these data reveal four novel aspects of the thermal responses of biological traits.

Mean Activation Energy of Trait Rises.

We find a general pattern in the rise component, which covers the temperature range over which organisms commonly operate under natural conditions (3, 26). The metabolic theory of ecology (MTE) suggests that the Boltzmann–Arrhenius model from chemical reaction kinetics can be used to predict the rise of many biological rates and times, including systematic effects on metabolic rate (2–5, 8, 27–29). According to the MTE, the scaling of a biological rate, R, with body temperature, T, is

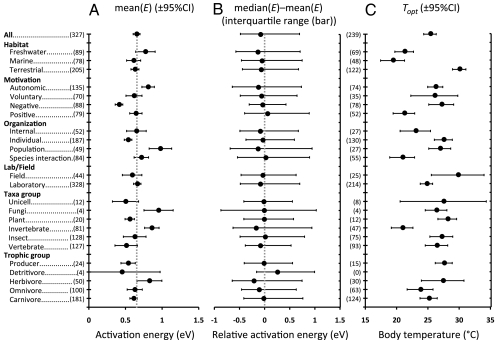
where E is activation energy, k is Boltzmann's constant, and R_o is an organism- and state-dependent scaling coefficient. Interspecific studies have found that the activation energy, E, of most rises centers at or near 0.65 eV (2, 4, 18). However, activation energies for important metabolic reactions vary from ∼0.2–1.2 eV (4, 18, 27), with 0.65 eV being near the middle of this range. Some variation around this value is therefore expected. This range corresponds to Q₁₀ values (change in trait value when temperature is changed by 10 °C) of about 1.31–5.13 when averaged over 0–40 °C (SI Appendix, Table S2). Of the 374 intraspecific rises we analyze, 87% are consistent (R² ≥ 0.5, P < 0.05) with the Boltzmann–Arrhenius model. The mean activation energy, E, of these responses is 0.66 ± 0.05 eV [mean ± 95% confidence intervals (CIs) used throughout our paper] (Fig. 2A). The 95% CIs include the value of 0.65 eV reported across species for the MTE. The generality of this result across traits, taxa, trophic groups, levels of organization, and habitats (Fig. 1) may be attributable to the influence of metabolic rate on a wide range of biological processes (2, 30). Indeed, for rises that are significant, the vast majority (88%) of activation energies are between 0.2 and 1.2 eV, corresponding to the range observed for metabolic reactions (4). Even at the population level, where variance is largest, 80% of all activation energies fall between this range (Fig. 2A). Of trait rises whose relationship to metabolic rate is more obvious (i.e., rates, times), a higher proportion (281 of 319) are significantly fit by the Boltzmann–Arrhenius model than those less clearly linked to metabolism (41 of 55), such as conversion efficiencies, optimal muscle strain, and angle of body turning during escape. Of all rises well fit by the Boltzmann–Arrhenius model, about a quarter have residuals with curvature, the vast majority of which are concave (downward). Such deviations from the Boltzmann–Arrhenius model have been observed previously in growth rate data (31, 32) (Discussion).

Fig. 2.

Analysis of activation energies, E, for rise responses and temperatures for optimum trait values, T_opt. (A) Mean E (±95% CI) of intraspecific rise responses calculated from the Boltzmann–Arrhenius model. Responses are grouped by habitat, motivation, level of biological organization, laboratory or field measurements, taxa, and trophic group. The vertical dotted line marks 0.65 eV, as reported for interspecific studies within the MTE. (B) Relative activation energy [median (E) − mean (E)] of intraspecific rise responses bounded by the interquartile range. Symmetrical distributions have an equal mean and median, and thus a relative activation energy of zero (vertical dotted line). Most medians lie below zero, indicating right skew. (C) Mean T_opt (±95% CI) of intraspecific unimodal responses. All values in parentheses are sample sizes with pseudoreplicates combined. Trait categorizations, definitions, treatment of pseudoreplicates, and data sources are provided in SI Appendix.

Distribution of Activation Energy for Trait Rises.

We find systematic deviations around the mean activation energy of 0.66 eV for rise responses. The most noticeable deviation is strong right skewness (Figs. 2 A and B and 3), which is consistent across levels of organization, taxa, habitats, and trophic groups. For unconstrained random processes, this right skewness indicates deviations from normality and random error (SI Appendix, SI Materials and Methods). In principle, right skewness for the rises can be produced by a random diffusion process constrained by a reflective boundary (33) at 0 eV. However, this mechanism does not explain our results because (i) there should be more activation energies close to the boundary (0 eV) than are observed (Fig. 3), indicating the boundary effect is either nonexistent or negligible, and (ii) different degrees of skewness, including lack of skewness, are observed in certain traits (Fig. 2B) (18). The right skewness we observe therefore represents a real and unexplained biological signal.

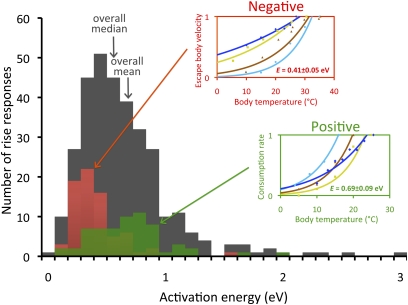
Fig. 3.

Histograms of intraspecific activation energies. Gray columns are the total number of rise responses, red columns are the subset of these responses that correspond to negative motivation, and green columns are the subset of these responses that correspond to positive motivation. (Insets) Examples of responses of traits corresponding to positive (green) and negative (red) motivations, respectively. OLS regressions based on the Boltzmann–Arrhenius model (Eq. 1) were fitted to the rise component of each response. Trait values are normalized relative to the maximum trait value in each data series to present multiple responses on the same scale. Values of E for insets are mean values for all negative and positive motivation traits. Escape body velocities (m/s) (negative motivation) of the northern desert iguana (light blue circle, E = 0.96 ± 0.52 eV), western fence lizard (brown triangle, E = 0.63 ± 0.28 eV), African clawed frog (dark blue diamond, E = 0.25 ± 0.06 eV), and wandering garter snake (yellow square, E = 0.36 ± 0.14 eV) are shown. Consumption rates [consumed prey/(predator * s)] (positive motivation) of river perch preying on phantom midge larvae (light blue circle, E = 0.99 ± 0.25 eV), back-swimmer preying on culex mosquito larvae (brown triangle, E = 1.09 ± 0.46 eV), dampwood termite feeding on eucalyptus tree (dark blue diamond, E = 0.65 ± 0.40 eV), and atlantic oyster drill preying on eastern oysters (yellow square, E = 1.18 ± 0.83 eV) are shown. Trait definitions, data fitting methods, and data sources are provided in SI Appendix.

Independent of mechanism, this right skewness means that the majority of trait responses have activation energies below 0.66 eV (median of 0.55 eV) (Figs. 2B and 3). The MTE does not predict and cannot currently explain why the distribution of activation energies is right-skewed, and thus why the majority of rise responses have activation energies lower than 0.65 eV. Therefore, the MTE needs to be assessed to determine whether or not it can be extended to explain the full form of the distribution of activation energies and its biological consequences.

One possible mechanism driving skewness in rise activation energies is trait motivation. We define autonomic traits as those that largely act below the level of consciousness, such as basal metabolic rate, whereas somatic traits are largely under conscious control (34). We further classify somatic traits as negative (defense or movement away from a stimulus), positive (consumption or movement toward a stimulus), or voluntary. Body velocity, for example, can be negative (e.g., escape body velocity), positive (e.g., attack body velocity), or voluntary (e.g., voluntary body velocity). Analysis of trait rises reveals that negative motivation traits have significantly lower mean activation energies (0.40 ± 0.05 eV) than do positive (0.69 ± 0.09 eV), voluntary (0.64 ± 0.12 eV), or autonomic (0.76 ± 0.08 eV) traits (Figs. 2A and 3). Because negative motivation traits make up 23.4% of all rises and typically have lower activation energies, they contribute substantially to the right skewness observed across taxa and habitats (Fig. 3).

This difference in activation energies means that traits with negative motivation are less sensitive to temperature than traits that are positive or voluntary, and thus supports the hypothesis that stronger selection pressure on prey to escape capture and death [the life-dinner principle (35–37)] results in maintenance of nearly optimal performance across a range of temperatures. That is, although it is energetically costly to maximize effort at low temperature (3), individuals under attack may do so for survival. Prey presumably increase their performance at lower temperatures rather than decrease their performance at higher temperatures, which would more likely result in being captured by a predator. This differential performance is consistent with physiological limitations (38) or shifts in motivation at low vs. high temperatures (22–25). Moreover, diurnal and seasonal variation in temperature could allow the evolution of differences in, for example, the thermal response of attack and escape velocities needed for an individual to alternate between being both a predator and a prey.

By focusing only on body velocities, we can directly test the life-dinner principle. Consistent with the principle, rises for escape body velocity (0.39 ± 0.05 eV) have lower activation energies than do voluntary velocities (0.52 ± 0.09 eV). Moreover, we can quantify how much faster the mass-corrected coefficient (R_o in Eq. 1) at 20 °C for escape body velocity (2.61 m/s) is than for voluntary body velocity (0.31 m/s) (SI Appendix, SI Materials and Methods). These values represent averages across diverse taxa and are qualitatively similar to previous results for lizards that do not examine thermal effects (39, 40). For this analysis, we only included responses for which the individual was clearly and continually moving at a nearly constant velocity, thus precluding other effects and explanations related to behavior and shifts in motivation or strategy (Materials and Methods). Because escape or attack velocity is largely anaerobic and is governed by different biochemical pathways than voluntary velocity (41, 42), it may experience different selection pressures, contributing to differences in activation energies for thermal responses.

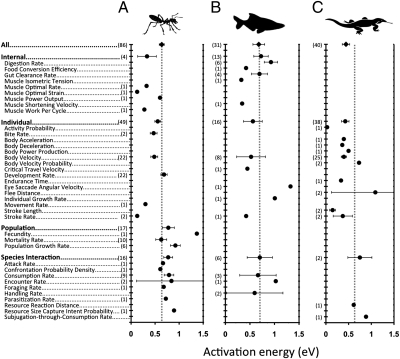
ANOVA of all rises shows that level of organization is also a strong predictor of mean rise activation energies (SI Appendix, Table S4), with internal (0.65 ± 0.13 eV) and individual (0.54 ± 0.05 eV) having a much lower mean E than population (0.98 ± 0.15 eV) (Fig. 2A). Fig. 4 shows rise activation energies for three major taxonomic lineages—terrestrial insects, fish, and lizards—categorized by level of organization. For all taxa, mean rise activation energies averaged across all traits are, again, very close to 0.65 eV (Fig. 4). Although data are too sparse to draw general conclusions, activation energies of trait rises are more variable and tend to increase from internal and individual traits to population and species interaction traits for insects and lizards (Fig. 4 and SI Appendix, Table S4).

Fig. 4.

Mean activation energies, E (±95% CI), of intraspecific rise responses calculated using the Boltzmann–Arrhenius model are categorized by different levels of organization for terrestrial insects (A), marine and freshwater fish (B), and terrestrial lizards (C). The vertical dotted lines mark 0.65 eV reported for interspecific studies (2, 4, 18). All values in parentheses are sample sizes with pseudoreplicates combined. Trait definitions, treatment of pseudoreplicates, and data sources are provided in SI Appendix.

Trait Falls.

Few data or theories exist for the decline of trait performance at higher temperatures, and the data that do exist are often not of high quality. Protein degradation is considered a likely mechanism for falls of some traits (7, 38, 43), and in those cases, activation energy can be interpreted as the energy of degradation processes. Of the 70 fall responses we analyze, the mean E of the 31 significant falls is 1.15 ± 0.39 eV and the median is 0.65 eV, indicating strong right skewness as found for trait rises. Falls have much higher activation energies than rises, consistent with the left skew typically observed in temperature responses (3, 5, 7, 26). We also find that several trait falls are conversion efficiencies (SI Appendix, Table S3), contradicting the common tacit assumption of their temperature invariance (2, 9, 30, 44).

Optimal Temperature and Unimodal Responses.

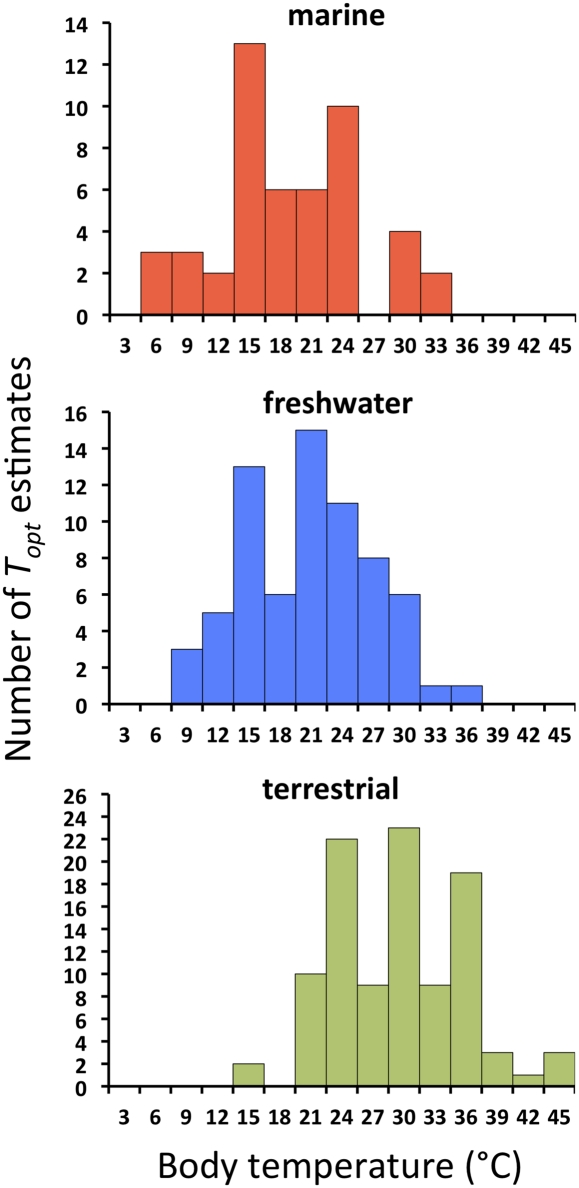
For the 240 unimodal responses, the mean temperature at which optimal trait values occur (T_opt) is 25.3 ± 1 °C. Although temperature fluctuates more in terrestrial habitats than in freshwater or marine habitats, we find no evidence that T_opt is more variable for terrestrial taxa (Fig. 5). Our results cannot be attributed to factors such as the more homogeneous thermal landscape of aquatic habitats (45–49), because most of our data were measured in experimental arenas with constant temperatures (Materials and Methods). Therefore, organisms were not able to thermoregulate behaviorally, effectively eliminating differences between body and ambient temperature. Habitat is by far the strongest determinant of mean T_opt (Figs. 2C and 5 and SI Appendix, Table S5). Traits for terrestrial organisms have a higher mean T_opt (30 °C) than those in freshwater (21 °C) or marine organisms (19 °C). These differences correspond to environmental temperatures (50), indicating a matching between environmental temperatures and those for near-optimal performance (3, 51).

Fig. 5.

Histograms of T_opt categorized by habitat. The optima at 15 °C, 20 °C, 25 °C, 30 °C, and 35 °C likely represent overrepresentation of these temperatures in experimental studies. Data sources are provided in SI Appendix, Tables S3 and S6.

Discussion

Our ecoinformatics analysis illuminates previously unrecognized generalities and deviations in how biological systems respond to temperature. We show that almost 90% of our intraspecific rise responses are well fit by the Boltzmann–Arrhenius model. Across all traits, the mean activation energy is 0.66 eV, close to the value of 0.65 eV reported for interspecific responses and indicating that metabolic rate potentially affects a wide range of biological processes (2, 4, 8, 28, 30). Nonetheless, we find systematic and substantial patterns in the variation of activation energies around this canonical value, including persistent right skewness in the distribution. Notably, the median value of activation energies is 0.55 eV, indicating that most activation energies are lower than 0.65 eV. Our results highlight limitations in the precision, power, and utility of the MTE as it currently stands. We conclude that the MTE requires reassessment and modification to discover whether it can explain these novel features of thermal responses.

The persistent right skewness in the distribution of activation energies raises important questions about whether to interpret the mean or median as the most biologically relevant measure. We expect that processes involving individuals or single species may be more affected by the median, because most individuals and species will have activation energies close to this value. In contrast, ecosystem processes may be determined more by the mean value because they represent an average over many individuals, species, and processes.

Folding the Boltzmann–Arrhenius model into a more realistic unimodal model (7, 13, 52) should prove insightful in this regard and may help to explain recently observed deviations of growth rate data fit to the model, including effects of the values and range of chosen experimental temperatures (32). Further elucidation of these effects requires more high-quality experimental data. Detailing the response of traits over the entire temperature range has been central to understanding and making predictions about the effects of climate change (53). We therefore encourage experimentalists to measure the response of a greater diversity of traits over the full temperature range, thus allowing characterization of the entire unimodal response.

The right skewness we observe in the distribution of activation energies persists across nearly all trait categories. Detailed analyses of these and similar patterns suggest dominant selection pressures and novel biological mechanisms. Differences between negative and positive motivation can be explained by a thermal version of the life-dinner principle (35–37), which predicts systematic differences in the thermal responses of organisms when they are acting as either a predator or a prey. Collecting more high-quality data for the thermal dependence of attack velocity is a high priority for more sensitive tests of the life-dinner principle.

We find that activation energies for rises are generally more variable and tend to increase as one moves from internal and individual traits to population and species interaction traits. This increase represents enhanced thermal sensitivity of populations and species interactions, potentially reflecting density or frequency dependence. These patterns probably have important consequences for species interactions and community stability, and their identification suggests that scaling constraints can be shifted or relaxed by evolutionary or behavioral processes. Data on multiple traits within single species will also help to resolve our understanding of how temperature influences the interaction and integration of traits across different levels of biological organization (54). Investigation of the distribution of activation energies at the lowest level of organization, biochemical reactions, may reveal baseline variation that could be amplified across biological levels. For example, the distribution of activation energies based on a small sample of 11 biochemical reactions (table 3.1 in ref. 27) is right-skewed and may also contribute to the pervasive right skewness observed in our data.

Our trait ontology is a first categorization of thermal response curves and allows us to identify novel patterns and propose new mechanisms, such as right skewness and the life-dinner principle. Alternative categorization of the traits in our database will likely reveal other biological mechanisms. Because life evolves and operates across a complex thermal landscape, it is essential to synthesize empirical knowledge and to deduce general mechanisms for shifts in the thermal responses of biological traits. Our work is an important step along this path and should aid research on how species, communities, and ecosystems respond to changes in temperature.

Materials and Methods

Data Acquisition.

We searched the literature for studies that measured the intraspecific temperature response of biological traits, with a focus on those central to species interactions (main text). We found 273 data sources, including journal articles, published reports, and books. When possible, we contacted authors directly to obtain raw data. Otherwise, we extracted data directly from tables and text or from figures using DataThief (55). This process yielded 2,445 intraspecific temperature responses and 20,394 data points. We primarily selected studies where environmental conditions, such as precipitation, light, and prey density, were either controlled or standardized. Consequently, most responses (92.5%) were measured in the laboratory, where body temperature of ectotherms was known to be close to ambient (based on direct measurement and extended times at test temperatures). The 192 sources from which data were described and analyzed in this paper are listed in SI Appendix, Table S6 and in the raw data in SI Appendix, Table S3.

Trait Ontology.

We constructed an ontology that allowed us to classify biological traits in a way that permits subsets of data to be easily isolated and analyzed, and that defined categories of data closely tied to ecological measurements, intuition, and mechanisms. Construction of a universally accepted trait ontology is currently not achievable, and although our ontology (SI Appendix, Table S1) captures important patterns in the data, categorization of traits in other ways will likely reveal additional biological mechanisms. In this paper, we describe two main components of our ontology: level of biological organization and trait motivation. Levels of biological organization we define are internal (processes internal to the organism), individual (processes at the level of individual organisms that include mechanical interactions with the external environment), population (processes for a group of conspecific individuals), and species interaction (processes involving interaction between two or more species). Trait response can be strongly influenced by the motivation of an organism. For example, how fast an organism moves through the landscape depends not only on its morphological capacity and how this capacity interacts with the environment but on its motivation (36, 39, 40). We therefore also categorize trait motivation, which we define in the main text. SI Appendix, Tables S1 and S3 detail the classification of each data series into this ontology.

Unit Conversions.

Definitions and measures of many traits are inconsistent throughout the literature, so we identified equivalent traits and converted them to comparable definitions and units. All times were converted to rates to ensure a single currency. For consistency, and because of the counterintuitive nature of many mass-specific traits (e.g., detection distance), mass-specific units were converted to per number of individuals (i.e., per capita). Activation energies were the same whether traits were expressed per mass or per capita. Scaling coefficients were mass-corrected. Further discussion of intercept coefficients and their analysis, and a description of how species wet mass was estimated, are provided in SI Appendix, SI Materials and Methods.

Data Quality and Classification.

To be included in our analysis, trait responses must have had (i) nonzero measurements at four or more distinct temperatures (thermal response models require a minimum of two free parameters) and (ii) a temperature range spanning at least 5 °C (it is difficult to differentiate statistically between linear and Boltzmann–Arrhenius model fits over smaller temperature ranges). For responses that satisfied these two criteria, we used ordinary least squares (OLS) regression to fit quadratic functions and then classified responses based on statistically significant coefficients as being rising, falling, or unimodal. For responses not fit well by a quadratic function, we calculated the correlation coefficient to categorize it as either rise or fall, or if our criterion for biological significance (R² ≥ 0.5, P value < 0.05) was not met, it was excluded (8.3% of responses). Because unimodal responses include both rise and fall components, the minimum temperature range for inclusion was doubled to 10 °C for unimodals. Responses classified as being unimodal were further subdivided into rise (fall) components by iteratively removing trait measurements at upper (lower) terminal temperatures until monotonicity was observed in a contiguous subset of the response (SI Appendix, Fig. S1). After each data point removal, we reassessed whether a quadratic or cubic model fit better than a linear model. The model selection was done using the small-sample Akaike Information Criterion (AIC) value (56). In cases where only four points remained after removal of terminal points, an F test was used instead. The original unimodal responses were retained after their monotonic portions were extracted. Thus, we obtained three separate categories of temperature responses: rise (802), fall (239), and unimodal (536). These numbers include pseudoreplicates (SI Appendix, SI Materials and Methods), and rise and fall categories include responses that were extracted from the unimodal set. The MATLAB (MathWorks) code used for this procedure is available on request.

Data Analysis of Monotonic Rise and Fall Temperature Responses.

We assessed fits and calculated E of both trait rises and falls for the Boltzmann–Arrhenius model in the same way. The fit of each response to the Boltzmann–Arrhenius model (Eq. 1) was assessed by OLS regression of log-transformed trait values on the reciprocal of temperature (in Kelvin). OLS regression was appropriate because temperatures are typically measured with much less error than trait values. The Boltzmann–Arrhenius model predicts that the transformed data would be best fit by a straight line. We considered the Boltzmann–Arrhenius model to fit a response if R² ≥ 0.5 and the F test P value is <0.05. These relatively liberal criteria allowed us to use a larger set of responses to analyze deviations from the Boltzmann–Arrhenius model. We assessed how many responses showed concave upward or downward deviations by analyzing the residuals of the fits from above. Using OLS regression, we fit the residuals with a quadratic model using the same R² and P values as above to determine significance. The direction and magnitude of the curvature of residuals were recorded (values of the coefficient of the quadratic term). We could not use the small-sample AIC here to differentiate between a quadratic and linear fit to the residuals because most of our data consist of four points, for which the small-sample AIC cannot be calculated. To estimate the activation energies of trait rises, we calculated both ordinary and weighted averages of measured activation energies, E. Weights were calculated as the ratio of the total number of data points in each response to the total number of data points in all responses within a category (e.g., trait, taxon, habitat, level of organization, motivation). Weighted and unweighted 95% CIs were calculated for the respective means. We also calculated medians, skewness, and quartiles of the E in each category. We used ANOVA to detect differences in mean E between categories of rise responses, such as level of organization or habitat (SI Appendix, Table S4), but not for falls because of an inadequate sample size. We also tested whether the distribution of intercept coefficients (Eq. 1) was normal (SI Appendix, SI Materials and Methods).

Data Analysis of T_opt.

For unimodal responses, we estimated T_opt as the temperature at which the maximum trait value was recorded. For responses with multiple maximal values (within 5% of each other), we calculated their average temperature (SI Appendix, SI Materials and Methods). As described above for activation energies of rise and fall responses, values of T_opt across trait categories were compared using ANOVA (SI Appendix, Table S5).