S K-edge XAS and DFT Studies of High and Low Spin {FeNO}⁷ Thiolate Complexes: Exchange Stabilization of Electron Delocalization in {FeNO}⁷ and {FeO₂}⁸

Abstract

S K-edge XAS is a direct experimental probe of metal ion electronic structure as the pre-edge energy reflects its oxidation state, and the energy splitting pattern of the pre-edge transitions reflects its spin state. The combination of sulfur K-edge XAS and DFT calculations indicates that the electronic structures of {FeNO}⁷ (S=3/2) (S^Me2N₄(tren)Fe(NO), complex I) and {FeNO}⁷ (S=1/2) ((bme-daco)Fe(NO), complex II) are Fe^III(S=5/2)-NO^-(S=1) and Fe^III(S=3/2)-NO^-(S=1), respectively. When an axial ligand is computationally added to complex II, the electronic structure becomes Fe^II(S=0)-NO• (S=1/2). These studies demonstrate how the ligand field of the Fe center defines its spin state and thus changes the electron exchange, an important factor in determining the electron distribution over {FeNO}⁷ and {FeO₂}⁸ sites.

Introduction

Mononuclear non-heme iron centers are present in a wide range of enzymes that carry out reactions involved in oxygen activation.^{1, 2} To obtain molecular insight into the mechanisms of these enzymes, it is important to have a detailed description of the electronic structure of the non-heme iron-dioxygen adducts.³ However, these oxygen intermediates often rapidly react and are therefore not amenable to experimental study. NO has been shown to reversibly bind to the ferrous center of many mononuclear non-heme iron enzymes and model complexes, forming stable Fe-NO complexes that can be spectroscopically studied.^4-9 These Fe-NO complexes can serve as analogs of dioxygen intermediates and provide insight into the electronic structures of the intermediates and the mechanisms of oxygen activation.^{3, 10, 11} In addition to being an analog, non-heme Fe-NO complexes are active in biological processes such as the nitric oxide reductases¹².

The Fe-NO complexes considered here are of the {FeNO}⁷ type according to the Enemark and Feltham notation,¹³ i.e. the total number of valence electrons in the Fe d and NO π* orbitals is seven. The spin state of these {FeNO}⁷ complexes is either S=3/2 or S=1/2. The electronic structures of {FeNO}⁷ complexes have been controversial.^{3, 6-8, 10, 11, 14-31} Plausible descriptions are presented in Scheme 1A and 1B. For {FeNO}⁷(S=3/2), reference 11 presented spectroscopic evidence and calculations which strongly support an electronic description of a high spin Fe^III (S=5/2) antiferromagnetically coupled to NO^- (S=1). For {FeNO}⁷(S=1/2), a number of studies^{7, 17-20} invoke a description of low spin Fe^II (S=0) coupled to NO•(S=1/2), while references 21 and 24 proposed a description of intermediate spin Fe^III (S=3/2) antiferromagnetically coupled to NO^- (S=1).

Scheme 1.

Scheme 1A. Plausible descriptions of {FeNO}⁷ S=3/2 spin states.

Scheme 1B. Plausible descriptions of {FeNO}⁷ S=1/2 spin states.

We have developed sulfur K-edge X-ray absorption spectroscopy (XAS) as a direct experimental probe of the electronic structure and bonding in metal complexes.^32-34 The K-edge X-ray absorption spectrum of a sulfur ligand bound to a transition metal ion can have an intense pre-edge feature, which is assigned as a sulfur 1s to metal 3d transition. The intensity of this transition (i.e. I(S_1s→ Ψ*_d) in eq. 1, below) is directly proportional to the % sulfur np character (α²) mixed into unoccupied or half-occupied valence metal d orbitals Ψ*_d = (1- α²)^1/2|M_d> - α|S_3p> of a transition metal complex.^{32, 35}

$$I({\text{S}}_{1\text{s}}\to \Psi {\ast }_{\text{d}})={\alpha }^{2}I({\text{S}}_{1\text{s}}\to {\text{S}}_{3\text{p}})$$ (1)

Here I(S_1s→S_3p) is the intrinsic intensity of a sulfur 1s→3p transition. Thus the pre-edge intensity provides a direct measure of sulfur-metal bond covalency (α²).

The energy of the pre-edge transition reflects the energy difference between the metal d and sulfur 1s orbital. For the same type of sulfur ligand (i.e. thiolate, sulfide, dithiolene) the energy of the sulfur 1s orbitals is fairly constant³⁴. Therefore, the pre-edge energy reflects the energy of the metal d electron acceptor orbital, which is dependent on the ligand field and, more strongly, the effective nuclear charge (Z_eff) of the metal, which in turn is determined by its oxidation state. In addition, the pre-edge energy splitting pattern reflects the half-occupied and unoccupied d orbitals, hence the spin state of the metal center.³⁶ Therefore, S K-edge XAS is a direct experimental probe of metal ion electronic structure.

In the present study, (S^Me2N₄(tren))Fe(NO) (complex I, S=3/2 determined by EPR and SQUID)³⁷ and (bme-daco)Fe(NO) (complex II, S=1/2 determined by EPR)³⁸ are examined since complex I is an SOR (superoxide reductase) analog while complex II is the only reported {FeNO}⁷ (S=1/2) model complex that contains sulfur ligands. Both complexes are structurally defined by x-ray crystallography and have a bent Fe-N-O unit. (The structures are shown in Figure 1; bond lengths and angles are given in Table 1.) Complex I is six-coordinate with one thiolate, one imine and three amine ligands while complex II is a five-coordinate complex with two thiolate ligands and two amine ligands, in addition to the NO moiety.

Figure 1.

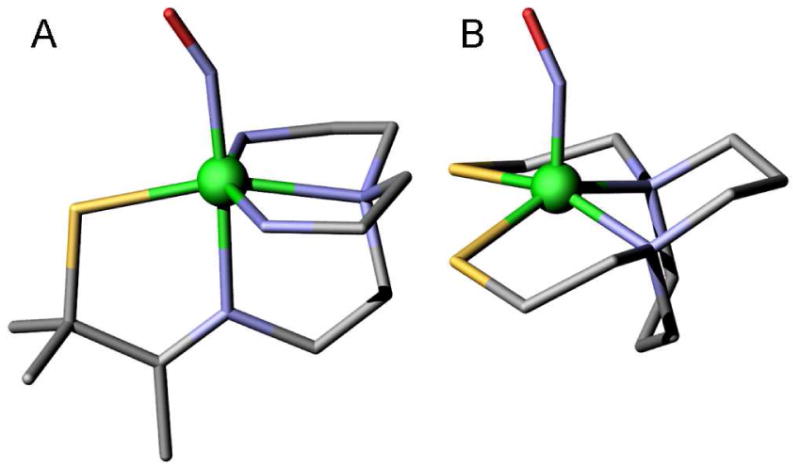
Molecular structures of A) complex I and B) complex II, from x-ray crystallography³⁷,³⁸. (Fe atoms are in green, S atoms are in yellow, C atoms are in grey, and N atoms are in blue. H atoms are omitted for clearity).

Table 1.

Geometric parameters, spin densities, and S covalencies from crystal structures, experimental data, and calculations.

Fe(trenS)NO (complex I)			Fe(daco)NO (complex II)
	Exp.	B3LYP		Exp.	B3LYP
Fe-S	2.28	2.28	Fe-S1	2.24	2.26
Fe-N1	2.12	2.21	Fe-S2	2.25	2.26
Fe-N3	2.2	2.34	Fe-N1	2.07	2.15
Fe-N2A	2.21	2.32	Fe-N2	2.08	2.15
Fe-N2B	2.21	2.29
Fe-NO	1.76	1.8	Fe-NO	1.70	1.73
N-O	1.15	1.16	N-O	1.17	1.19
Fe-N-O	152.6	161	Fe-N-O	151.4	149.8
O-N-Fe-S	0	-14.3	O-N-Fe-S1	20.3	46
Spin density on Fe		3.67	Spin density on Fe		2.16
Spin density on NO		-1.13	Spin density on NO		-1.15
S covalency	43 a	39	S covalency	55 a	40

^aFrom the covalency in Table 2.

A combination of sulfur K-edge XAS and DFT calculations is used to elucidate the electronic structures of {FeNO}⁷(S=3/2) (complex I) and {FeNO}⁷(S=1/2) (complex II). The experimentally validated computational results are further used to explore the factors determining the electron distribution over the {FeNO}⁷ unit. These studies are also relevant to {FeO₂}⁸ intermediates (see Discussion) as they demonstrate how the metal ion spin state (a result of its ligand field) influences the electron distribution over FeNO and FeO₂ sites.

Experimental Details

Sample preparation

The complexes (S^Me2N₄(tren))Fe(NO) and (bme-daco)Fe(NO) were synthesized according to procedures in the literature.^37-40 For complex I, SQUID data gave a good fit (R²=0.999) over the temperature range T = 5 - 265 K, with μ_eff=4.12 BM, and the elemental analysis of the solid isolated compound is good (Anal. Calcd for FeC₃₅H₄₃N₅O₁S₁: C, 64.74%, H, 6.62%; N, 10.79%. Found: C, 64.67%; H, 6.53%; N, 10.29%). Spin quantitation of the EPR signal (vs Fe^IIIEDTA) indicated 96% purity.³⁷ For complex II, the samples studied were in pure crystalline form (ground into powder). The analytical data for the crystals can be found in ref 38. For S K-edge XAS experiments, the samples were ground into a fine powder and dispersed as thinly as possible on sulfur-free Mylar tape in a N₂-filled inert atmosphere glovebox. This procedure has been verified to minimize self-absorption effects. The samples were then mounted across the window of a 1 mm thick aluminum plate. A 6.3 μm polypropylene film window protected the solid samples from exposure to air during transfer from the glovebox to the experimental sample chamber.

Data Collection and Analysis

All sulfur K-edge data were measured at the Stanford Synchrotron Radiation Lightsource using the 54-pole wiggler beam line 6-2 under ring conditions of 3 GeV and 60–100 mA. Details of the experimental configuration for low-energy studies have been described previously.³⁴ The photon energy was calibrated to the maximum of the first pre-edge feature of Na₂S₂O₃•5H₂O at 2472.02 eV. A total of 3-5 scans were measured per sample to ensure reproducibility. Raw data were calibrated and averaged using EXAFSPAK.⁴¹ Using the PySpline program,⁴² the background was removed from all spectra by fitting a second-order polynomial to the pre-edge region and subtracting it from the entire spectrum. Normalization of the data was accomplished by fitting a flat second-order polynomial or straight line to the post-edge region and normalizing the edge jump to 1.0 at 2490 eV. The intensities of the pre-edge features were quantified by fitting the data with pseudo-Voigt line shapes with a fixed 1:1 ratio of Lorentzian to Gaussian contributions, using the EDG_FIT program.⁴¹ The reported intensity values are based on the average of 10-12 good fits. In addition to the error resulting from the background correction and fitting procedure (∼2%), normalization procedures can introduce 1-3% error in the total pre-edge peak areas. The uncertainty in pre-edge energy is ∼0.1 eV.⁴³

DFT Calculations

Geometry optimization and single point calculations were performed on dual-CPU Intel Xeon workstations using the Gaussian 03 package.⁴⁴ The optimizations were performed using the unrestricted B3LYP hybrid functional^{45, 46} for both complexes. For complex I, the 6-311+G(3df) basis set was used for Fe, S, N, and O atoms and 6-311+G* was used for C and H atoms. For complex II, the 6-311+G* basis set was used for Fe, S, N, and O atoms and 6-311G* was used for C and H atoms⁴⁷. The initial coordinates for the geometry optimization were obtained from the crystal structures.^{37, 38} Single point calculations were performed for both complexes using the unrestricted B3LYP functional and a 6-311+G(3df) basis set on the Fe, S, N, and O atoms and a 6-311+G* basis set on the C and H atoms with tight convergence. The molecular orbitals were plotted using the Gaussview v.3.0 software, and Mulliken population analyses^48-51 were performed using the QMForge program.⁵² TD-DFT calculations were performed with the electronic structure program ORCA^{53, 54} with the same basis sets and functional as the single point calculations. The {FeO₂}⁸ complexes in different configurations were calculated using the Gaussian 09 package.⁵⁵

Results

A. S K-Edge X-ray Absorption Spectroscopy

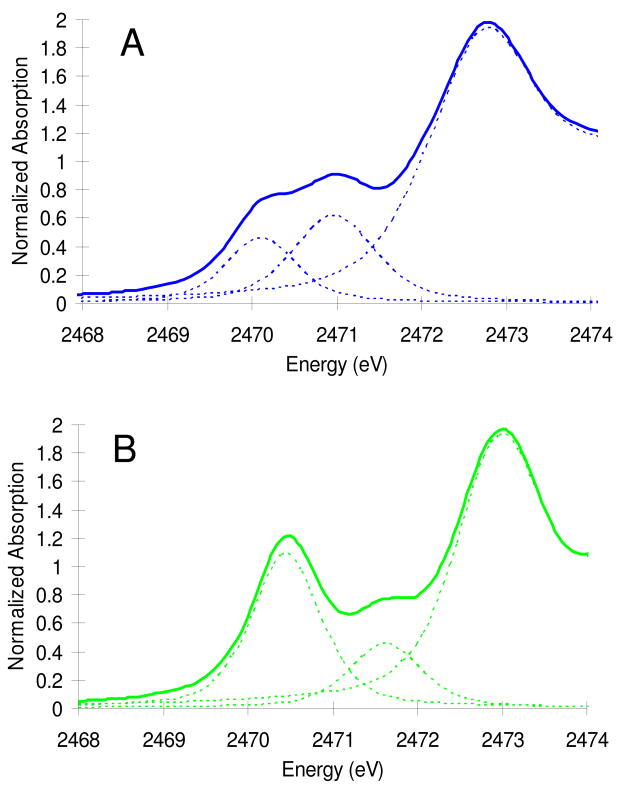
The S K-edge XAS data for (S^Me2N₄(tren))Fe(NO) (complex I, S=3/2, blue) and (bme-daco)Fe(NO) (complex II, S=1/2, green) are presented in Figure 2. The resolved pre-edge fits are shown on an expanded scale in Figure 3, with fit results given in Table 2. Complex I shows two pre-edge features, at 2470.1 eV and 2471.0 eV, respectively, split by 0.9 eV. Complex II also shows two pre-edge features, at 2470.5 eV and 2471.6 eV, split by 1.1 eV with a different intensity pattern.

Figure 2.

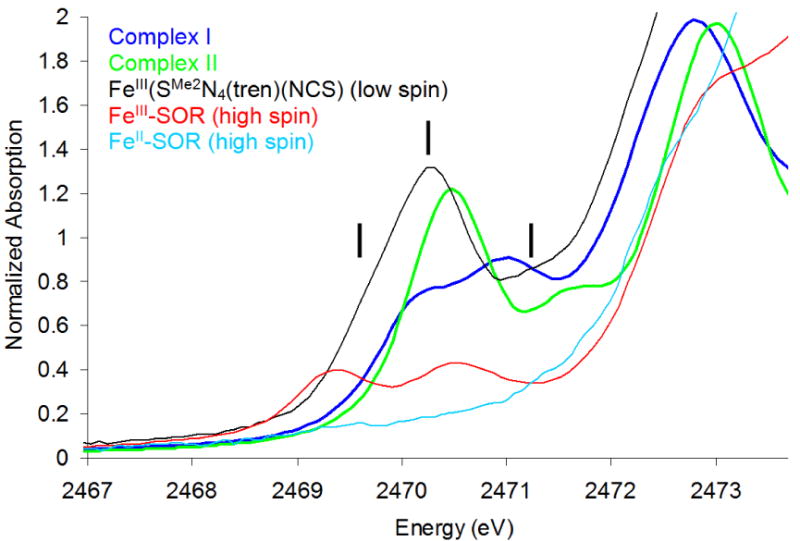
S K-edge XAS spectra of complex I ({FeNO}⁷, S=3/2, blue), complex II ({FeNO}⁷, S=1/2, green), Fe^III-SOR (high spin, red), Fe^III(S^Me2N₄(tren))(NCS) (low spin, black) and Fe^II-SOR (high spin, light blue). The vertical lines indicate the three pre-edge features associated with transitions to ¹A₁, to ³T₁, ³T₂ and ¹T₁, and to ¹T₂ states for Fe^III(S^Me2N₄(tren))(NCS).

Figure 3.

Fits of the pre-edge features of complex I (A) and complex II (B).

Table 2.

Pre-edge peak energies (E, eV), intensities (D₀) and covalencies.

Complex	E (eV)	D0	Covalencya	Total covalency
I	2470.1	0.44	17	43
	2471.0	0.70	26
II	2470.5	1.05	39	55
	2471.6	0.42	16

^aQuantitation was based on the expression D₀=Aα²I(S)/3n, where α² is the S character in each orbital, A is the ground state degeneracy, n is the normalization factor (i.e., number of S atoms contributing to the pre-edge feature, n=1 for complex I and n=2 for complex II) and I(S) is the transition dipole integral (I(S)=8.05 for thiolate³⁴).

To elucidate the electronic structures of complex I and II, data of three reference complexes are also included in Figure 2. Fe^III(S^Me2N₄(tren))(NCS) (black) is a six-coordinate low spin ferric complex⁵⁶ which shows three pre-edge features associated with transitions to ¹A₁, to ³T₁, ³T₂ and ¹T₁, and to ¹T₂ states, respectively⁵⁷ (vertical lines in Figure 2); Fe^III-SOR (red) is a six-coordinate high spin ferric protein site, which has two pre-edge features of comparable intensity, assigned to S 1s→Fe d(t₂) and S 1s→Fe d(e)⁵⁸ transitions; Fe^II-SOR (light blue) is a six-coordinate high spin ferrous complex, whose pre-edge feature is higher in energy and obscured by the S 1s transition to the S-C σ* orbital at ∼2472.5 eV.⁵⁸

Both complex I and complex II show distinct pre-edge features in the same energy region as the Fe^III reference complexes, showing that their Z_eff reflects an Fe^III site. The shape of the complex I pre-edge feature (blue in Figure 2) resembles that of Fe^III-SOR (red, two peaks of comparable intensity split by ∼1.2eV), suggesting that complex I is a high spin Fe^III complex. However, the pre-edge feature of complex II (i.e. two peaks with intensity ratio of 2.5 : 1, split by ∼1.1 eV) differs from that of Fe^III-SOR as well as from that of the low spin reference complex Fe^III(S^Me2N₄(tren))(NCS) (black in Figure 2), which shows three pre-edge features (with the intensity ratio of 1.1 : 4.8 : 1). This indicates that while complex II has an Fe^III site, it is neither high nor low spin, raising the possibility of an intermediate spin ground state. This is supported by TD-DFT calculations in section B.

Since there is a linear relationship between oxidation state and effective nuclear charge⁵⁹, and the pre-edge transition energy reflects the Z_eff (for the same type of S ligand), we can estimate the oxidation states of the iron in complex I and II based on their pre-edge transition energies relative to those of the Fe^IIISOR and Fe^IISOR references60. Using the Slater-Zener rules,^{59, 61} the oxidation state is estimated to be 2.75 for complex I and 2.67 for complex II (see Supporting Information). These results indicate that both complexes I and II have oxidation states close to the oxidation state of the Fe^III reference complex defined as 3.0.

B. DFT Modeling

Geometry optimizations were performed using the spin unrestricted B3LYP functional, starting from the crystal structures^{37, 38} for both complexes. The optimized geometric parameters for complexes I and II are listed in Table 1 for comparison to the parameters from the crystal structures. For both complexes, the optimized bond lengths and angles agree well with those of the crystal structures, with the main differences being that for complex I the calculated Fe-amine bond lengths are longer than in the crystal structure by ∼0.1 Å and for complex II the O-N-Fe-S dihedral angle is calculated to be larger than in the crystal structure. However, the total energy change is only 0.56 kcal/mol for the bond length change in complex I and 0.13 kcal/mol for the angle change in complex II relative to the crystallographic values.

The calculated wavefunctions for both complexes were found to be stable using the stability check option in Gaussian 03. From the Mulliken spin densities⁵⁰ in Table 1, both complexes are determined to have the Fe and NO antiferromagnetically coupled.

The calculated MO diagrams for both complexes are presented in Figure 4A and B. Only the lowest seven unoccupied orbitals that have significant Fe d or NO π* character are included in the diagram and are analyzed further.⁶² From the MO diagram, complex I has two unoccupied alpha orbitals that are composed mainly of NO π* character (π_h* denotes the orbital in the Fe-N-O plane; π_v*denotes the orbital perpendicular to the Fe-N-O plane) and five unoccupied beta orbitals that are composed mainly of Fe d character. Complex II has three alpha and four beta unoccupied orbitals, all of which have both Fe and NO character. Two alpha orbitals are mainly NO π*, while one alpha and the four beta orbitals are mainly Fe d.

Figure 4.

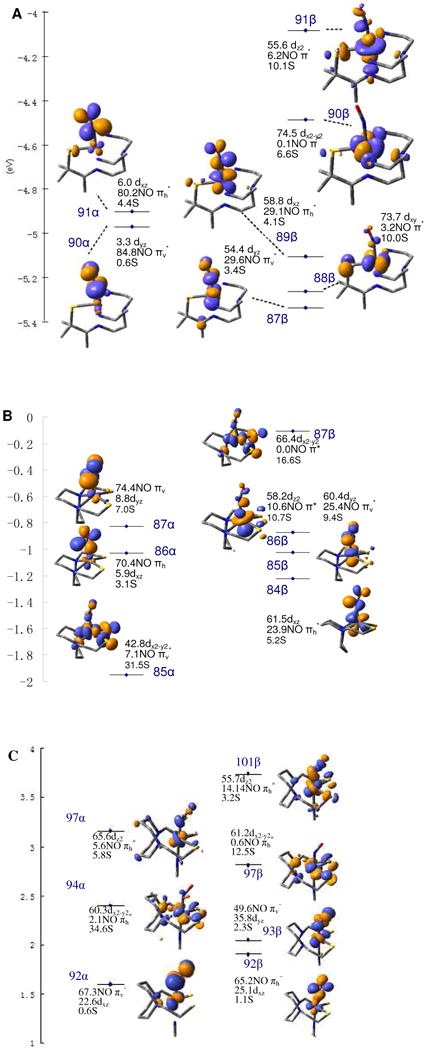
MO diagrams of complex I (A), complex II (B) and complex II + axial L (C). (Only unoccupied orbitals are shown. Occupied orbitals are in Figure S1-S3.) Numbers shown are the percentage of Fe d, NO_2p and S_3p orbitals in each MO. α contours are shown on the left and β contours on the right.

Total S covalencies were calculated by summing the S p component in the orbitals shown in the MO diagram. The calculated S covalencies are listed in Table 1 (bottom). For both complexes, the calculated total S covalencies are lower than the experimental values from S K-edge XAS in Table 2 by 4% for complex I and 15% for complex II.⁶³

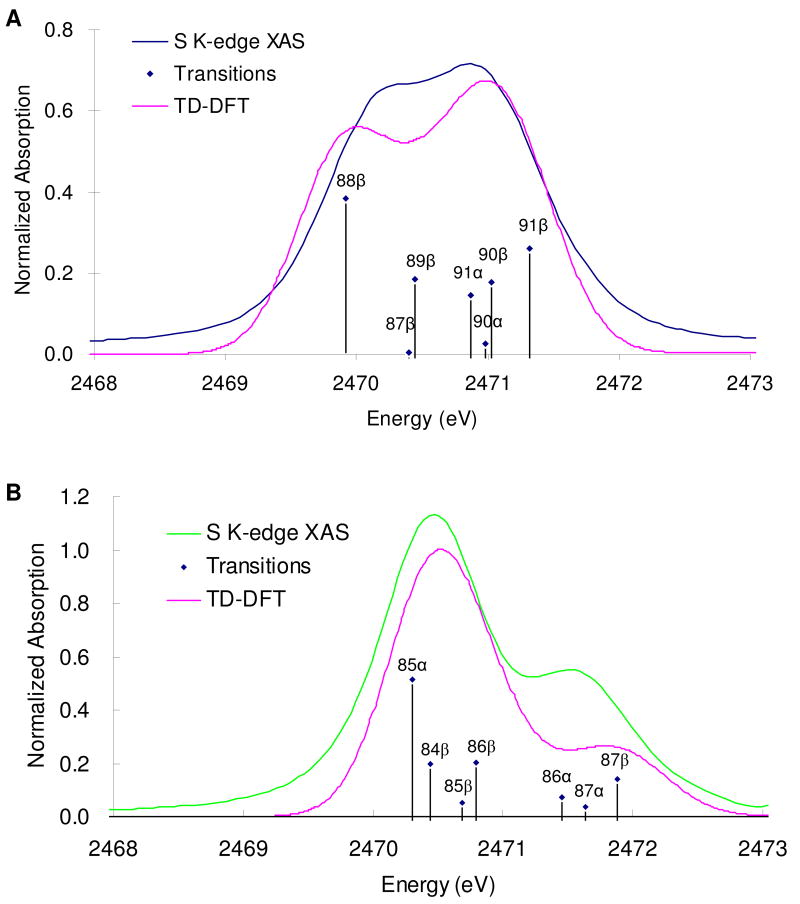
To further test the results of these electronic structure calculations, TD-DFT calculations were performed to simulate the S K-edge XAS data. In Figure 5 the energy is shifted up by 57.3 eV to compensate for relativistic effects that are not included in the calculation and the intensity is scaled down by 0.024 to compensate for the intensity normalization of the experimental data.⁶⁴ For both complexes, the calculated S K-edge XAS spectra reproduce the split pre-edge in the experimental spectra, supporting the accuracy of the calculated descriptions of the bonding. From these TD-DFT calculations, for complex I (Figure 5A) the pre-edge feature at 2470.1 eV is assigned to transitions to the Fe t₂ (β) orbitals (d_yz (87β), d_xy (88β), and d_xz (89β)) and that at 2471.0 eV is assigned to transitions to Fe e (β) (d_x2-y2 (90β) and d_z2 (91β)) and NO π* (α) (90,91α) orbitals. For complex II the pre-edge feature at 2470.5 eV is assigned as transitions to Fe d_xz (β) (84β), d_yz (β) (85β), d_z2 (β) (86β) and d_x2-y2 (α) (85α) orbitals⁶⁵ while that at 2471.6 eV has contributions from the transitions to Fe d_x2-y2 (β) (87β) and NO π* (α) (86,87α) orbitals.

Figure 5.

TD-DFT calculated (pink) and experimental (blue for complex I and green for complex II) S K-edge XAS spectra for complex I (A) and complex II (B). The transitions have been convolved with a pseudo-Voigt function of 0.5 eV half-width to account for experimental and core-hole broadening.

Analysis

A. Electronic Structure of Complex I (S=3/2)

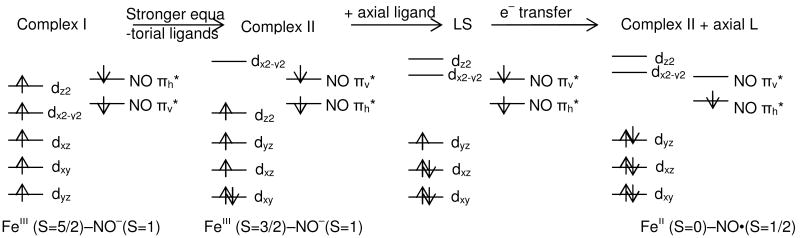
For complex I {FeNO}⁷ (S=3/2) in Figure 4A, the two unoccupied α orbitals 90 and 91 are NO π* orbitals and the five unoccupied β orbitals 87-91 all have dominant Fe d character, i.e. the Fe d orbitals have five α electrons while the NO π* orbitals have two beta electrons. Therefore, complex I is described as a high spin Fe^III (S=5/2) antiferromagnetically coupled to triplet NO^- (S=1) (Scheme 2, left). This is electronic description is consistent with the experimental S K-edge XAS result that complex I has a high spin ferric center very similar to that in Fe^III-SOR. It is also consistent with our earlier studies.^{3, 11}

Scheme 2.

Descriptions of {FeNO}⁷ complexes with different ligand fields.

We also note that the wavefunctions in Figure 4A are significantly delocalized between the Fe d orbitals (especially d_xz and d_yz) and the NO π* orbitals. The delocalization in the β unoccupied orbitals between d_xz and NO π_h* and between d_yz and NO π_v* reflects the amount of electron donation from the occupied NO^- π* to the Fe d orbital while the delocalization in the α unoccupied orbitals between NO π* and d_xz/d_yz reflects the backbonding of the occupied Fe d character into the NO π* orbitals. Because the amount of electron donation from NO π* to Fe d (total ∼66%) is much larger than that from Fe to NO (total ∼9%), the net delocalization somewhat decreases the Z_eff of the Fe^III center. This is consistent with the fact that the oxidation state estimated from S K-edge data is 2.75, which is lower than the oxidation state of the Fe^III-SOR reference complex of 3. Rodriguez et al.¹⁴ have drawn a similar conclusion from the isomer shifts in the Mössbauer spectra and from DFT calculations for nitrosyl derivatives of deoxy hemerythrin.

B. Electronic Structure of Complex II (S=1/2)

For complex II, the MO diagram in Figure 4B shows that there are two α holes in NO π* (86, 87) and one α (85) and four β holes (84-87) in Fe d orbitals, i.e. the Fe d orbitals have four α electrons and one β electron while the NO π* orbitals have two β electrons. Therefore, complex II is described as an intermediate spin Fe^III(S=3/2) antiferromagnetically coupled to triplet NO^-(S=1) (Scheme 2, middle left). This description is consistent with the experimental results from the S K-edge data that complex II has an intermediate spin ferric center.

Complex II also has the seven valence electrons partially delocalized within the {FeNO} unit. The electron delocalization of the four unoccupied β orbitals reflects the amount of electron donation from the NO π* into the Fe d orbitals (∼60% total), while the delocalization of the unoccupied α orbitals 86 and 87 reflects the backbonding from the occupied Fe d_xz/d_yz into the NO π_h*/π_v* orbitals (∼15% total). As in complex I, the net NO^- donation in complex II decreases the Z_eff of the Fe^III center. This is consistent with the Z_eff estimated from the S K-edge data, that it is lower in complex II relative to the Fe^III-SOR reference.⁶⁶

C. Correlation of the Electronic Structure Description of Complex II (S=1/2) to Descriptions in the Literature

From the S K-edge XAS spectra and DFT calculations, complex II is described as Fe^III(S=3/2)-NO^-(S=1) S=1/2, i.e. an intermediate spin state ferric center antiferromagnetically coupled to a triplet NO^-. However, in the literature, most {FeNO}⁷(S=1/2) complexes have been described as Fe^II(S=0)-NO•(S=1/2), i.e. a low spin ferrous center coupled to a NO radical^{7, 17-20}, with the exception of reference 21 and 24, in which an Fe^III(S=3/2)-NO^-(S=1) description is proposed.

There are two possible explanations for this discrepancy: 1) the method used here to determine the electronic structure is different from that used in the literature; 2) the electronic structure of complex II is different from that of the other complexes studied, reflecting its different geometric structure. The first possibility can be ruled out because B3LYP was also used in the previous studies^{7, 17, 18, 20} and the description of complex II does not change when the basis sets used in literature were examined (See Table S1), indicating that the electronic structure difference may be due to the specific geometric structure of complex II.

The structure of complex II is different from the structures in the literature^{7, 17-20} in two ways: 1) there are two cis thiolate ligands; 2) complex II is five-coordinate with a pseudo-square pyramidal geometry (similar to the complex in reference 24) while the other complexes in the literature all have six ligands and are pseudo-octahedral. To investigate the effects of these structural differences, we performed calculations on three models: A) the thiolate ligands in complex II were replaced by amines; B) a N coordinated axial CN^- ligand was added to the original structure, trans to the NO; C) the thiolate ligands were replaced by amines and an axially N-coordinated CN^- ligand was added.

From the calculations (Table S2 and S3), model A gives the same electronic structure description as the original structure of complex II (Fe^III(S=3/2)-NO^-(S=1)) while models B and C both give a low spin ferrous (S=0) center coupled to an NO radical (Scheme 2 right), equivalent to most of the descriptions in the literature. The MO diagram for complex II + axial L is given in Figure 4C. There are two α and two β holes in the d σ orbitals (i.e. a (t_2g)⁶ configuration on the Fe) and one α and two β holes in the NO π* orbitals (i.e. an NO• configuration). These results indicate that it is the lack of an axial ligand that changes the electronic structure of complex II relative to that of most of the complexes studied previously.

D. Ligand Field Contributions to Spin States of {FeNO}⁷

It is interesting that in going from complex I to complex II to complex II + axial L, the {FeNO}⁷ moiety changes from Fe^III(S=5/2)-NO^-(S=1) to Fe^III(S=3/2)-NO^-(S=1) to Fe^II(S=0)-NO•(S=1/2). From the analysis in section C, the ligand field of the Fe can affect its spin state and thus the electronic structure of the {FeNO}⁷ site.

From the MO diagrams in Figure 4, complex I has a high spin ferric center with one α electron in each d orbital, while complex II has an intermediate spin ferric center with an electron pair in the d_xy orbital and an unoccupied d_x2-y2 orbital. The Fe^III center in complex II is intermediate spin rather than high spin because the energy gap between the d_x2-y2 and d_xy orbitals is large enough to overcome the electron repulsion increase associated with electron pairing in the d_xy orbital. From DFT calculations, the energy difference between the d_x2-y2 and d_xy orbitals in complex I is 1.2 eV while the energy difference between d_x2-y2 and d_xy in complex II is 2.3 eV⁶⁷. This large energy gap between d_x2-y2 and d_xy orbitals in complex II reflects its square pyramidal geometry with stronger σ donating equatorial ligands (Figure 6).

Figure 6.

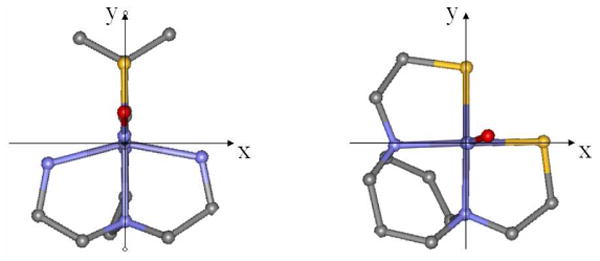
Equatorial ligand field of complex I (left) and complex II (right). Note complex II has two strongly donating cis thiolates and four equal L-Fe-L angles (L=S or N) of 86(±2)° while complex I has one thiolate, two N-Fe-N angles of 53° and two S-Fe-N angles of 101°.

When the axial ligand is computationally added to complex II, the ligand field along the z axis becomes stronger and shifts the d_z2 orbital higher in energy. This would result in a shift of the d_z2 electron of complex II into the d_xz orbital to spin pair, producing a low spin Fe^III state (Scheme 2 center-right). However, the computed electronic structure description of complex II + axial L is a low spin Fe^II. This means that upon going low spin due to the strength of the ligand field, one electron also transfers from the NO^- π_v* orbital into the Fe d_yz orbital, resulting in a low spin Fe^II and NO• (Scheme 2, far right). The driving force for this electron transfer is investigated below.

E. Exchange Contributions to the Electron Distribution over {FeNO}⁷

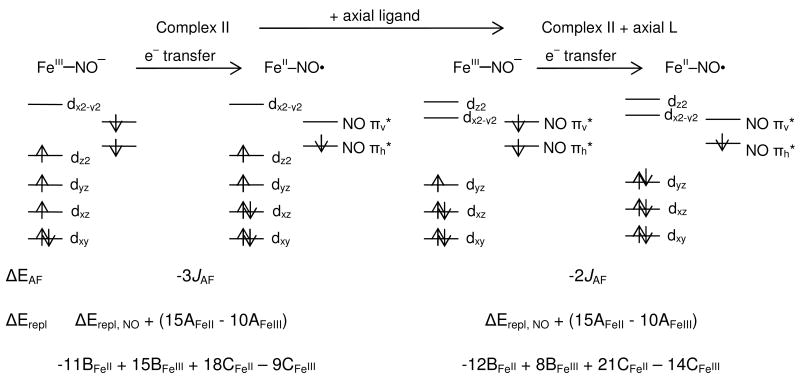
Normally adding an axial ligand would stabilize the oxidized Fe^III state, however, the computed electronic structure for complex II + axial L is Fe^II-NO•. This indicates that the total energy of the Fe^II-NO• configuration is lower than that of the Fe^III-NO^- configuration, i.e. the total energy change in going from Fe^III-NO^- to Fe^II-NO• (ΔE_tot) is negative for complex II + axial ligand. In contrast, for complex II (without an axial ligand), ΔE_tot is positive since the ground state is Fe^III-NO^-.

In going from the Fe^III-NO^- to the Fe^II-NO• configuration for complex II (Scheme 3 left half) and complex II+axial L (scheme 3 right half) an electron is transferred from the NO π* orbital to the acceptor Fe d orbital. Since the NO π* orbital is higher in energy than the Fe d orbital in both complexes, the Fe^II-NO• configuration is favored (i.e. the one electron orbital energy difference, ΔE_orb, is negative). Since there is one more donor ligand on the Fe in complex II + axial L, the Z_eff^Fe is less positive and the d manifold should be higher in energy, its ΔE_orb should be less negative. Therefore, this term will stabilize Fe^II-NO• configuration more in complex II than in complex II + axial L, the reverse of what is found in the DFT calculations and experiments for complex II.

Scheme 3.

Correlation between descriptions for complex II and complex II + axial L (contributions to energy difference between Fe^III–NO⁻ and Fe^II–NO• for each complex at bottom).

However, two additional contributions have to be considered in evaluating the relative stability of the two electronic configurations for the two complexes: 1) the decrease in the stabilization energy due to the antiferromagnetic exchange coupling between the spins on the Fe and NO, ΔE_AF, and 2) differences in the e^--e^- repulsion interaction between the two configurations for each of the two complexes, ΔE_repl.

1) ΔE_AF

This term has an energy contribution to the stabilization of the ground state of each configuration for each complex in Scheme 3, which is given by equation 2 (for H = -2JS₁•S₂, where J is the antiferromagnetic exchange coupling constant):

$${\text{E}}_{\text{AF}}=-\text{J}({\text{S}}_{\text{tot}}({\text{S}}_{\text{tot}}+1)-{\text{S}}_1({\text{S}}_1+1)-{\text{S}}_2({\text{S}}_2+1).$$ (2)

For complex II, the Fe^III(S=3/2)-NO^-(S=1) S_tot=1/2 configuration has E_AF of 5J, the Fe^II(S=1)-NO•(S=1/2) S_tot=1/2 configuration has E_AF of 2J and thus ΔE_AF=-3J, assuming similar J values for both configurations. For complex II + axial L (Scheme 3 right half), the Fe^III(S=1/2)-NO^-(S=1) S_tot=1/2 configuration is stabilized by 2J while the Fe^II(S=0)-NO•(S=1/2) S_tot=1/2 configuration has no exchange stabilization, so ΔE_AF=-2J.

Since the J's are negative (i.e. antiferromagnetic coupling), for both complexes the Fe^IIINO^- configuration is stabilized by the increase in the number of its exchange pathways. The Fe^IIINO^- configuration is more stabilized in complex II by ∼ J_AF (see bottom of Scheme 3). This is qualitatively consistent with the above DFT calculations where complex II has an Fe^IIINO^- ground configuration, however this term is expected and calculated to be small (∼ 0.14 eV).^68-71

2) ΔE_repl

In going from the Fe^IIINO^- to the Fe^II-NO• configuration for both complexes in scheme 3, electron repulsion on the NO moiety is lost while the e^--e^- repulsion on the Fe is increased. For ΔE_repl,NO, the NO^- loses J(π_v*, π_h*) − K(π_v*, π_h*) repulsion, where J is the two electron Coulomb and K the two electron exchange integral. For ΔE_repl,Fe, this change in e^--e^- repulsion must be obtained for each of the two configurations (for complex II: Fe^III(S=3/2) and Fe^II(S=1); for complex II + axial L: Fe^III(S=1/2) and Fe^II(S=0)) in terms of J and K integrals, which can be then rewritten in terms of the Racah parameters A, B, and C.^{72, 73} These expressions are given in Table 3. The difference in the repulsion between the two configurations for each complex, ΔE_repl, is given at the bottom of Scheme 3. The first two terms, ΔE_{repl NO} + (15A_Fe^II − 10A_Fe^III) are common in both and will be positive (i.e. favor the Fe^III-NO^- configuration) as the e^--e^- repulsion is higher on the metal iron than the NO. However, it is important to focus on the difference of the differences in configurational repulsion between the two complexes, equation 3.

Table 3.

E_{repl, Fe} for complex II and for complex II + axial L in terms of Coulomb, and exchange integrals, and their conversion to Racah parameters.

		Expressions in J and K	Expressions in A, B and C
Complex II	FeIII	J(dz2, dyz) + J(dz2, dxz) + 2J(dz2, dxy) + J(dyz, dxz) + 2J(dyz, dxy) + 2J(dxz, dxy) + J(dxy, dxy) − K(dz2, dyz) − K(dz2, dxz) − K(dyz, dxz)	10A−15B+9C
	FeII	J(dz2, dyz) + 2J(dz2, dxz) + 2J(dz2, dxy) + 2J(dyz, dxz) + 2J(dyz, dxy) + J(dxz, dxz) + 4J(dxz, dxy) + J(dxy, dxy) − K(dz2, dyz)	15A−11B+18C
Complex II + axial L	FeIII	2J(dyz, dxz) + 2J(dyz, dxy) + J(dxz, dxz) + 4J(dxz, dxy) + J(dxy, dxy)	10A−8B+14C
	FeII	J(dyz, dyz) + 4J(dyz, dxz) + 4J(dyz, dxy) + J(dxz, dxz) + 4J(dxz, dxy) + J(dxy, dxy)	15A−12B+21C

$$\Delta \Delta {\text{E}}_{\text{repl}}={{\text{B}}_{\text{Fe}}}^{\text{II}}+7{{\text{B}}_{\text{Fe}}}^{\text{III}}-3{{\text{C}}_{\text{Fe}}}^{\text{II}}+5{{\text{C}}_{\text{Fe}}}^{\text{III}}$$ (3)

Since C_Fe^III is larger than C_Fe^II, this term is positive, indicating that the Fe^III-NO^-configuration is favored in complex II relative to complex II + axial L by this difference in electron repulsion. The magnitude of this term can be estimated from the Racah parameters. For Fe^III, B = 1015 cm^-1, C = 4800 cm^-1, and for Fe^II, B = 917 cm^-1, C = 4040 cm^-1. Their nephelauxetic reductions due to covalency in π backbonding complexes are found to be β=0.65 (Fe^III), and β=0.4 (Fe^II).^74-76 These give a calculated estimate that the Fe^III-NO^- configuration is stabilized in complex II by 1.95 – 2.5 eV (depending on the nephelauxetic reduction) relative to this configuration in complex II + axial L due to differences in e^--e^- repulsion. From table 3 a significant contribution to this is the exchange given by K(d_z2,d_xz) + K(d_yz,d_xz), estimated to be 1.1 – 1.7 eV (dependent on the covalent reduction of the B and C) only present for the electronic configurations for complex II.

In summary, the difference in energy between the two configurations of each complex is:

$$\Delta {\text{E}}_{\text{tot}}+\Delta {\text{E}}_{\text{orb}}+\Delta {\text{E}}_{\text{AF}}+\Delta {\text{E}}_{\text{repl}}$$ (4)

The orbital term favors the Fe^II-NO• configuration, while the antiferromagnetic coupling (which is small) and the change in e^--e^- repulsion favor the Fe^IIINO^- configuration. For complex II, the electron exchange for Fe^III(S=3/2) dominates and the ground configuration is Fe^IIINO^- with the LMCT excited state (corresponding to the Fe^II-NO• configuration) calculated to be at 1.8 eV higher energy from TD-DFT. For complex II + axial L, in the low spin Fe^III(S=1/2)NO^-(S=1) configuration the two electron exchange is eliminated and the ground configuration is found to be Fe^II-NO• with the MLCT excited state (i.e. Fe^IIINO^- configuration) calculated (from TD-DFT) to be at 1.3 eV.

Discussion

A. Ligand Field and two e^- Exchange

The range of electronic structure descriptions of {FeNO}⁷ complexes ^{3, 6-8, 10, 11, 14-31} is at least partially due to the different ligand environments of the different complexes. Most {FeNO}⁷ (S=1/2) species studied in the literature^{7, 17-20} are described as Fe^II(S=0)-NO•(S=1/2) complexes. Interestingly, all such complexes are six coordinate. The complex of Franz et al.²⁴ is five coordinate and is described as Fe^III(S=3/2)-NO^-(S=1), consistent with complex II in the present study. The complex of Hauser et al.²¹ is also described as Fe^III(S=3/2)-NO^-(S=1), but has an additional axial Cl^- ligand. However, Cl^- is a relatively weak field ligand and when replaced by a stronger carboxylate ligand, the resultant complex is described as Fe^II(S=0)-NO•(S=1/2)²⁰. Praneeth et al.¹⁸ and Radoń et al.³¹ also found that the axial ligand affects the electronic structure of {FeNO}⁷ species.

The electronic structure descriptions of complex I, complex II and complex II + axial L determined in this study are Fe^III(S=5/2)-NO^-(S=1), Fe^III(S=3/2)-NO^-(S=1) and Fe^II(S=0)-NO•(S=1/2), respectively. In going from complex I (S=3/2) to complex II (S=1/2), the equatorial ligand field becomes stronger. As a result, the high spin Fe^III in complex I becomes an intermediate spin Fe^III in complex II. Complex II still has significant stabilization of the Fe^III-NO^- electronic configuration relative to the Fe^II-NO• configuration and thus Fe^III-NO^- is the experimentally determined electronic structure description. When an axial ligand is computationally added to complex II, the 10Dq on the Fe^III becomes large enough to stabilize low spin Fe^III which, in turn, leads to electron transfer from the NO^- to the Fe. This electron transfer is due to the relatively low two-electron exchange stabilization of the low spin Fe^III (and the fairly limited antiferromagnetic exchange coupling between the Fe^III and the NO^- in the Fe^III(S=1/2)-NO^-(S=1) configuration). The NO π* orbital is at higher energy relative to the redox active Fe d orbital and thus transfers an electron to reduce the Fe, leading to the Fe^II(S=0)-NO•(S=1/2) description of the ground state. In summary, the ligand field defines the spin state of the ferric center. This changes the electron exchange and thus the electron distribution over the {FeNO}⁷ unit.

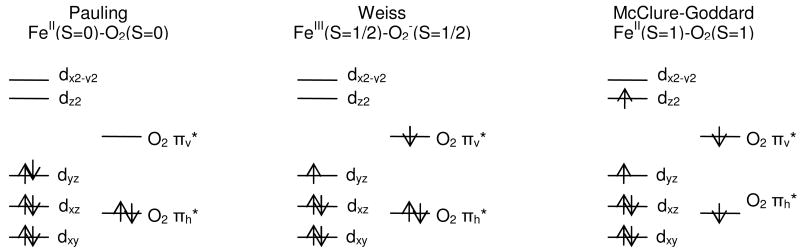
B. Extension to {FeO₂}⁸ Systems

At least three electronic structure descriptions have been considered for {FeO₂}⁸ (S=0) sites, such as in hemoglobin: the Pauling description Fe^II(S=0)-O₂(S=0)⁷⁷, the Weiss description Fe^III(S=1/2)-O₂^-(S=1/2)⁷⁸ and the McClure-Goddard description Fe^II(S=1)-O₂(S=1)^{79, 80} (Scheme 4). The model developed here for {FeNO}⁷ can be extended to {FeO₂}⁸ complexes to consider the contributions that would stabilize each configuration. Using the approach described in the Analysis section E, the contribution to the relative E_orb, E_AF and E_repl for the three descriptions of {FeO₂}⁸ are listed in Table 4. For E_orb, the three descriptions follow the order: Pauling < McClure-Goddard < Weiss; for the antiferromagnetic coupling (E_AF), the order is: McClure-Goddard < Weiss < Pauling; for E_{repl, O2} and E_repl,Fe, the orders, respectively, are: McClure-Goddard < Pauling < Weiss and Weiss < McClure-Goddard < Pauling. Since the Coulombic repulsion between electrons in Fe d orbitals is larger than that in O₂ π* orbitals, the total E_repl follows the order: Weiss < McClure-Goddard < Pauling. The electronic distribution that has the lowest total energy is again determined by the net effect of E_tot = E_orb + E_AF + E_repl.

Scheme 4.

Three electronic structure descriptions of {FeO₂}⁸

Table 4.

Expressions of relative E_orb, E_repl and E_AF for the three descriptions of {FeO₂}⁸

	Pauling	Weiss	McClure-Goddard
Eorb1	0	${\text{E}}_{{\pi }_{\text{v}}^{\ast }}-{\text{E}}_{d_{yz}}$	${\text{E}}_{d_{z2}}-{\text{E}}_{d_{yz}}+{\text{E}}_{{\pi }_{\text{v}}^{\ast }}-{\text{E}}_{{\pi }_{\text{h}}^{\ast }}$
EAF	0	-3/2JAF	-4JAF
Erepl,Fe	J(dyz,dyz) + 4J(dyz,dxz) + 4J(dyz,dxy) + J(dxz,dxz) + 4 J(dxz,dxy) + J(dxy,dxy)	2J(dyz,dxz) + 2J(dyz,dxy) + J(dxz,dxz) + 4 J(dxz,dxy) + J(dxy,dxy)	J(dz2,dyz) + 2J(dz2,dxz) + 2J(dz2,dxy) + 2J(dyz,dxz) + 2J(dyz,dxy) + J(dxz,dxz) + 4 J(dxz,dxy) + J(dxy,dxy) - K(dz2,dyz)
Erepl
Erepl,O2	J(πh*, πh*)	J(πh*, πh*) + 2J(πv*, πh*)	J(πv*, πh*) - K(πv*, πh*)

¹E_orb (Pauling) defined as 0.

Compared with the Pauling description, the Weiss configuration is favored by E_repl,Fe and E_AF but disfavored by E_{repl, O2} and E_orb (Scheme 4, Table 4). In going from the Weiss to the Pauling configuration, the change in E_{repl, Fe} is the same as ΔE_{repl, Fe} in going from Fe^III(S=1/2)-NO^-(S=1) to Fe^II(S=0)-NO•(S=1/2) for complex II + axial L (Scheme 3, Table 3). The change in E_AF (-1.5J_AF) is smaller than ΔE_AF for complex II + axial L (-2 J_AF, Scheme 3), by -0.5J_AF assuming similar J_AF values. The change in E_{repl, O2} in going from Weiss to Pauling (-2J(π_v*, π_h*)) is larger in magnitude than ΔE_{repl, NO} (−[J(π_v*,π_h*) − K(π_v*,π_h*)]) by J(π_v*,π_h*) + K(π_v*,π_h*), due to the extra electron in π_h*and the lack of two electron exchange in O₂^- (S=1/2). The change in E_orb in going from the Weiss to the Pauling configuration is expected to be smaller in magnitude than ΔE_orb in {FeNO}⁷ due to the higher electronegativity of the oxygen atom. Therefore, compared with the {FeNO}⁷ complex II + axial L where the electronic structure of the ground configuration is defined above as Fe(II)-NO•, for the {FeO₂}⁸ complex the Pauling description (Fe^II(S=0)-O₂(S=0)) is favored by the E_{repl, O2} contribution (and a small contribution from E_AF) while the Weiss description is favored by the decreased E_orb contribution. To evaluate the resultant effects of these differences in e^--e^- repulsion, E_AF and relative ligand and metal orbital energies, we have also calculated complex II + axial L as an {FeO₂}⁸ S=0 system in both the Pauling (Fe^II(S=0)O₂(S=0)) and Weiss (Fe^III(S=1/2)-O₂^-(S=1/2)) configurations. Since complex II + axial L is a computation model, we have also calculated complex I and complex II which have been studied experimentally above as {FeO₂}⁸ systems to calibrate this approach. These results are given in supporting information (Figure S4) and show their ground electronic configurations to be Fe^III(S=5/2)O₂^-(S=1/2) for complex I and Fe^III(S=3/2)-O₂^-(S=1/2) for complex II, consistent with their corresponding {FeNO}⁷ ground electronic structures. However, for complex II + axial L the {FeO₂}⁸ S=0 complex is calculated to have a Weiss like Fe^III(S=1/2)O₂^-(S=1/2) ground configuration with the Fe^II(S=0)-O₂(S=0) configuration at 16 kcal/mol higher energy. This is in contrast to the {FeNO}⁷ species in complex II + axial L, which has an (Fe^II(S=0)-NO•) ground configuration. Thus, the lower energy of the O₂ π* valence orbitals appears to be the key feature in shifting from the Fe^II-NO• to an Fe^IIIO₂^- ground state. In fact, calculations of an {FeNO}⁸ model of complex II + axial L give a ground configuration of Fe^II(S=0)-NO^-(S=0).⁸¹

Since E_orb is strongly impacted by the ligand field of Fe and the E_repl and E_AF are affected by the covalent delocalization of the MOs which affect 2e^- repulsion and antiferromagnetic coupling, the resultant effect of this combination of contributions in specific cases, in particular oxy-hemoglobin and oxy-picket fence porphyrin⁸², is best determined by experiment. The most recent computational study of oxy-myoglobin favors the Weiss description⁸³.