Systems biology of stem cells: three useful perspectives to help overcome the paradigm of linear pathways

Abstract

Stem cell behaviours, such as stabilization of the undecided state of pluripotency or multipotency, the priming towards a prospective fate, binary fate decisions and irreversible commitment, must all somehow emerge from a genome-wide gene-regulatory network. Its unfathomable complexity defies the standard mode of explanation that is deeply rooted in molecular biology thinking: the reduction of observables to linear deterministic molecular pathways that are tacitly taken as chains of causation. Such culture of proximate explanation that uses qualitative arguments, simple arrow–arrow schemes or metaphors persists despite the ceaseless accumulation of ‘omics’ data and the rise of systems biology that now offers precise conceptual tools to explain emergent cell behaviours from gene networks. To facilitate the embrace of the principles of physics and mathematics that underlie such systems and help to bridge the gap between the formal description of theorists and the intuition of experimental biologists, we discuss in qualitative terms three perspectives outside the realm of their familiar linear-deterministic view: (i) state space (ii), high-dimensionality and (iii) heterogeneity. These concepts jointly offer a new vista on stem cell regulation that naturally explains many novel, counterintuitive observations and their inherent inevitability, obviating the need for ad hoc explanations of their existence based on natural selection. Hopefully, this expanded view will stimulate novel experimental designs.

1. Introduction

The very concept of ‘regulatory pathways’ is the default, taken-for-granted paradigm of explanation in our quest for understanding biological phenomena in molecular terms. In stem cell biology, understanding how stem cells maintain multi-potency, resolve their state of indeterminacy and make cell-fate decisions accordingly relies almost exclusively on this unquestioned epistemic principle of molecular causation. However, the surge of data for genome-wide gene expression and molecular interactions for stem cells [1–4] associated with these cellular processes is mounting insidious pressure to confront this custom of biological understanding [5–7]. But old habits die hard.

Molecular pathways, typically schematized in the form of an arrow–arrow diagram (A→ B→ C→ etc., top of figure 1a), represent biochemical cascades and are seen as the molecular embodiment of chains of causation, thereby providing comfortable explanation for many cell phenotypes. However, such linear pathways are in reality embedded in complex, genome-wide networks and the flood of ‘omics’ data undermine this familiar notion of linear causation. The unfathomable complexity of molecular networks that broad genome-scale analyses has produced and whose ubiquitous graphical representations are often derided as ‘fuzzball’ because of their impenetrable density, obviously defy the clarity and the simplicity of the linear logics of causation that has satisfied our minds used to the arrow–arrow schemes of molecular pathways. Yet, the blind hope that by mapping out the entire ‘road map’ or ‘wiring diagram’ of the genomic network of regulatory interactions, one day we will fully comprehend how stem cells maintain multi-potency and make decisions continues to drive the collection of genome-wide information and its integration into networks. Despite calls for a ‘systems’ or ‘integrative’ approach [8–10], the desire to discover within the fuzzball networks simple causal relationships, for instance ‘pluripotency genes’ [11] and their molecular targets to explain ‘pluripotency’, has promoted the brute-force genome-wide characterization of all the molecular parts while obviating the development of rigorous formal concepts for understanding the collective action of the parts. Entirety of analysis has trumped analysis of entirety [8].

Figure 1.

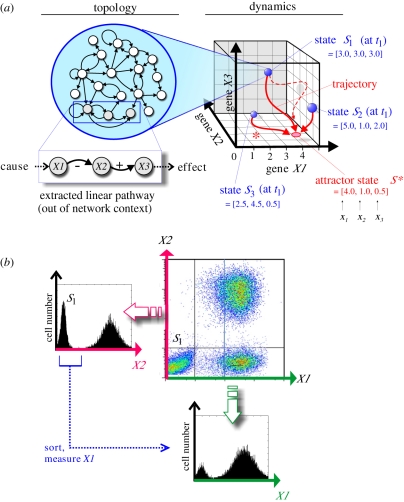
Schematic of the three perspectives discussed in this paper. (a) From gene-regulatory network topology to dynamics in the state space (§2). The traditional paradigm of a linear pathway as a chain of causation consisting of genes X1, X2, X3 extracted out of the network context is shown as a contrast underneath the network topology map. On the right, a three-dimensional state space capturing the dynamics of a hypothetical three-gene network (genes X1, X2 and X3) is shown. Any point in this space represents a (theoretical) network state S at time t, defined by the expression values x of the sub-network's three genes, S = (x₁, x₂, x₃) (gene-expression pattern) at time t. Three arbitrary states (blue balls), S₁, S₂ and S₃ are shown. Their gene-expression patterns (x₁, x₂, x₃) are indicated and, by acting as the space coordinates, define the position of the states in the state space. Since, as most states, they do not represent stable network states, they are driven by the network interactions to seek a stable state; hence they move in state space along trajectories (red solid lines) that lead to the stable attractor state. The trajectory denoted by asterisk (*) best represents the movement of the state discussed in the main text that manifests the regulatory relationship ‘X1 inhibits X2’—however, it is modulated by other inputs from the network. The dashed trajectory represents an example of a trajectory that has been perturbed (e.g. by drugs that affect expression of genes X1, X2 and X3) away from its natural course defined by the network interactions into regions of the state space that are even less stable, and hence quickly returns to the trajectory that leads to the attractor. In summary, the states, S1, S2, S3 and the perturbed trajectory all lie within the state-space region that ‘drain’ to the particular attractor S*, hence they all lie within its basin of attraction. (b) Illustration of both neglected (‘hidden’) dimensions (§3) and heterogeneity of clonal populations (§4). A typical two-dimensional flow cytometry dot-plot output (for hypothetical proteins X1 and X2) with three subpopulations is shown, along with the separate histograms of the projection on the two individual dimensions X1 and X2 (schematic, from simulations). Note that subpopulation S₁ (which may represent an attractor with respect to protein X2) when sorted and probed for protein X1 is actually bimodal with respect to the latter.

It is obvious to many biologists that increasing the density of the molecular fuzzball by ceaseless discovery of new regulatory relationships, now accelerated by genome-wide chromatin immunoprecipitation (ChIP) assays [12,13], is inapt for providing an intuitive grasp of the observable, emergent stem cell behaviours that are actually quite simple and readily described in few words, such as the decision of an embryonic stem cell to either stay pluripotent or to commit to either the trophoectoderm or the inner cell mass lineage [14,15]. The conceptual simplicity of such nested binary choices at the cell behaviour level stands in stark contrast to the vastly complicated molecular network with countless circular control loops which, one naively hopes, may offer linear causal explanations when carefully combed.

An explanation of a phenomenon that exceeds in complexity the phenomenon itself that it seeks to explain will not afford a natural, satisfactory understanding. There is no understanding without simplification [16]. Thus, we propose that any efforts to achieve satisfactory explanation for how a cell-fate decision ultimately results from the collective action of the molecular interactions must be dedicated to the identification of more abstract, generalizable patterns or principles that are simple enough to be grasped by the human mind notwithstanding the complexity of the impenetrably entangled network of molecular interactions.

Granted, there has been no shortage of attempts to cast stem cell behaviour in some kind of simple governing principles to satisfy our intuitive comprehension. However, such simplification attempts tend to resort to ad hoc concepts, using metaphoric terms, such as ‘blank state’, ‘ground state’ [17], ‘multi-lineage priming’ [18], ‘collapse’ of the pluripotency network [3] or ‘occlusion’ of lineage-inappropriate genes [19]. Such mental images are perhaps a bit more hand-waving than serving to convey deep principles rooted in formal concepts. However, they are certainly convenient and useful in that they assign a label to abstract phenomena and thus may offer a starting point for our quest to more formally define general concepts that ultimately must be deducible from or at least be consistent with physical and mathematical principles.

We are fortunately moving towards establishing such theoretical foundations [10,20] although such efforts still linger beneath the radar screen of mainstream stem cell biologists since the discovery and description of new phenomena are still prevalent in the young discipline [9]. Yet we have so far collected a sufficient set of coherent facts concerning emergent stem cell behaviours that can indeed readily be derived from the molecular networks that we have assembled to date using well-known ‘first principles’ of mathematics and physics of dynamical systems. Hence, time is ripe to take a first step from describing facts to defining basic principles. Whatever stem cells do, the fundamental laws governing the underlying regulatory systems must be obeyed. These, in turn, impose constraints on cell behaviour that cannot be conceived in the ad hoc schemes of causal arrows or through metaphors, for the latter are malleable and not anchored in mathematical principles. In contrast, if explanations are rooted in a set of first principles, then the very existence of particular stem cell behaviours, such as the robustness of multi-potency and its destabilization preceding cell-fated decisions, the binary nature of the latter, etc., will follow as inevitable, necessary consequence from the mathematics and physics of gene-regulatory networks. Such features and capacities need not by default be viewed as product of Darwinian evolution that serves a functional purpose.

This is important because the only mode of explanation in biology beyond the currently dominating ‘proximate explanation’ [21] that uses molecular pathways as chains of causation is one that holds that interesting features of living systems have been generated and optimized by natural selection to meet some functional requirement. This evolutionary explanation is indeed based on general principles but does not consider constraints by mathematical laws [22–25] as organizing force. By viewing evolution as a powerful tinkerer who seeks the optimal solution in the engineer's sense, even if only by trial and error [26], one inadvertently invokes some purposeful design. Replace the ‘intelligent designer’ in the teaching of opponents of evolution by the term ‘natural selection’ (the tinkerer)—and the parallels in the argumentation logics between these two explanations of the biosphere are exposed, for, deeply, they share the very concept of purposefulness—by divine design or by evolution's tinkering. While Darwinian adaptation of course has its place in shaping living systems, the key to explaining system behaviours and why they are the way they are, however, is to first establish, as the null hypothesis, the fundamental constraints immanent to the system that make a particular biological phenomenon inevitable (given some initial conditions). The broader goal of this paper is to demonstrate the utility of such explanatory philosophy using the concrete questions of cell-fate regulation.

This paper cannot provide a detailed account of the physical principles of genomic regulatory networks that impose the constraints. We refer to more extensive (but still introductory) reviews [10,20,27,28]. However, the paucity of stem cell biologists who embrace these principles points to a lack of awareness of useful intellectual perspectives that exist outside of the realm of the current monolithic pathway-based thinking. Hence, the specific goal of this piece is to introduce three perspectives that have barely entered the conscience of experimental stem cell biologists: (i) the state space perspective, which shall replace the biologists' pathway-based causality scheme, (ii) the perspective of high-dimensionality, which shall extend the notion of low-dimensional systems (i.e. consisting of a handful of variables), and finally (iii) the perspective of heterogeneity, which shall take the place of the biologists' tacit assumption of homogeneity of cell populations and of determinism of processes. These three distinct views will offer a new optic to biologists through which the mathematical principles of gene networks as dynamical systems, presented here in a permissively simplified form, and their relevance to stem cells can be readily comprehended. This will hopefully offer protection from resorting to ad hoc metaphoric explanations when facing with the daunting task of extracting a crisp explanatory meaning from complex networks of thousands of genes.

2. Perspective 1: from pathway and networks to state space

Networks of regulatory pathways are viewed as some kind of wiring diagrams or maps [29,30]—hence the occasional depiction of a cellular pathway network in the form of a subway map [31]. Within this metaphoric concept, a change of the cellular phenotypic state, such as loss of pluripotency, is then explained by the ‘collapse’ of the ‘pluripotency network’ that obviously encompasses genes involved in maintaining pluripotency [3]. This example illustrates the thoughtless propagation of a false metaphor of which Stephen J. Gould has warned us [32]. More precisely, it demonstrates the widespread failure to distinguish formally between network architecture (which includes the topology of the ‘wiring’) and network dynamics [27,30]. The former is not directly explanatory; only the latter can link a gene network to emergent biological behaviour.

The topology of networks, as part of the entire network architecture, is often studied for its own sake. Herein a network as the object of study is defined as consisting of a static collection of nodes (=genes, proteins) and connecting arrows (=regulatory or physical interactions). One is then concerned with the structural aspects of the network as a mathematical graph (figure 1a): for instance, the average connectivity of each node (how many target and upstream regulators), the presence of a power-law distribution thereof (or not) [29,30], or local network motives, such as the number of feedback loops [33], etc. The network topology together with the information of how the individual interactions modulate the expression of a target gene (e.g. modality, such as inhibition/activation and logical function, such as ‘AND’ function to describe the necessity of two upstream positive regulators for activation) form the network architecture that governs cell behaviour. Naturally, the architecture of the genome-wide regulatory network that encompasses all the genes of a genome is ‘hardwired’ in the genomic DNA sequence through the structure of interaction domains of regulatory proteins and the DNA sequence of cis-regulatory elements.

By contrast, network dynamics is the key concept for linking network architecture and cell behaviour [27]. Arrows connecting genes can still serve as symbols of causation to explain a particular event, such as the induction of a lineage-specific gene (e.g. gene X1 activates gene X2 that encodes an observable phenotype, hence gene X1 causes that phenotype). However, such linear interpretation of network connections as causation [34] fails to consider the context of the entire network in which all the causal interactions are embedded. Here is where the explanatory utility of network topology or even network architecture ends. Yet, many stem cell biologists still persevere in using static gene network architecture as explanatory principle while agnostic of network dynamics.

The state space is a general tool for dealing with the dynamics of a network [20,27,35]. But what is network dynamics? Life is breathed into the static network structure if we consider that every node i (gene i) of the network can change its expression level x_i (for simplicity, we lump transcription and translation and post-translational protein activation into the quantity ‘expression level’ x). Then the collective change in time of all the expression levels x_i over all the N genes of the network is referred to as network dynamics. (This change does not involve change of the architecture of the network, which remains invariant!). It is immediately obvious that the individual expression levels x_i change in a particularly coordinated way because the genes influence each others' expression via the ‘arrows’ in the network. With N in the thousands of genes that change their expression level, one will quickly lose track. Here is where the state space perspective becomes indispensable. First, we introduce a network state S(t) at time t, which is collectively defined by the expression levels x_i of all the N genes i of the network at time t: S(t) = [x₁, x₂, x_3, … x_n]. The state S(t) (depicted as blue balls in figure 1a) is a point in the continuous, N-dimensional space, the state space, which contains all possible states S, that is, all the possible combinations of expression levels x_i, each located at a characteristic position that is defined in the following way. The state space is spanned by the N axes, each representing a gene. The position of a state S(t) in this space is then determined by the value of the expression levels of each gene x_i that act as the respective coordinates in each of the N dimensions, x₁, x₂, x₃, … x_n. (Technically, the expression profile (x₁, x₂, x_3, … x_n) acts as a state vector.) Figure 1 (right panel) shows the state space of a three-gene (sub-)network (n = 3), thus the state space has three dimensions (which still allows for a graphical representation of the position of S in this space), affording a visual intuition of how the network state S is defined by the levels of expression of the three genes it contains. In summary, an abstract network state S(t) = (x₁, x₂, … x_n) at time t, which also represents a particular gene-expression profile, hence the state of a cell, is mapped into a point object characterized by its position.

Now, where is the dynamics? The execution of all regulatory interactions between the genes, as defined by the network, will change the network state S(t)—or the gene-expression profile, in a particularly coordinated manner. For instance, let us for clarity's sake focus on the X1–X2 plane (and ignore X3 dimension for a moment): if the network architecture determines that gene X1 inhibits gene X2 (figure 1a), then increasing x₁ will lead to a decrease in the value of x₂ and S(t) will move according to the corresponding change of its coordinates, for instance from a spot with (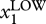, 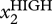) to the position (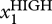, 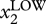) in state space. (This is most prominently seen in the trajectory in figure 1a for the movement of S_3, whose trajectory is denoted by an asterisk (*).) In other words: S moves along trajectories in the state space as the genes exert their regulatory action onto each other. The movement of the state S in state space manifests the coordinated change of all the genes of the network. Its journey is predestined by the ‘laws of motion’ (of a different kind) encoded in the architecture of the genomic network. Thus, the genome, via the regulatory network that it encodes, constrains the movement of the state S of each cell. We have now arrived at a first step in formalizing how genomic information translates into rule-governed cell behaviour.

Thus, it is important to note that the network architecture encoded in the genome (which, again, encompasses the topology of the interaction network and the modalities of all the individual regulatory interactions) does not change in a lifetime—except when somatic mutations occur [35]. The network architecture is essentially a static entity in the time scale of an individual life. What is dynamic, i.e. what changes and causes changes in cell phenotype, is the constrained alterations in the expression values of the genes, x_i. This in turn shifts the position of the state S = (x₁, x₂, x₃ … x_n). Such changes in S can be caused by: (i) network intrinsic processes owing to either the execution of regulatory interactions given an unstable initial state (see below) or to spontaneous, noisy fluctuations in gene expression (see §4); (ii) external influences from outside the cell that via signal transduction affect the expression values x_i of a set of genes. These changes push S = (x₁, x₂, x₃ … x_n) around along the trajectories in state space that are allowed under the constraints of the genomic regulatory network.

In summary, an entire network and its state S at a time t maps into one point in state space. The trajectory in state space captures the coordinated change in gene expression as dictated by the gene-regulatory network. Since the network state S also represents a gene-expression profile, which in turn determines the cell phenotype, a trajectory tracks the cell's phenotype change. The state space trajectory is thus a directed curve that truly represents a developmental process, such as differentiation. Unlike an arrow in a network diagram or a ‘pathway’, which is merely a shorthand symbol that has been over-interpreted as a causal explanation in biology, the arrow in state space or trajectory (figure 1a, red arrows) is a formal physical entity and represents a biological process in its entireness; it is a true ‘path’.

We have now established the general conceptual framework. A central idea is that the movement of S is constrained to particular trajectories (that depend on the position of S) by the regulatory network of the genome—much as the laws of motion limit planetary movements to orbits. Development and homeostasis take place within these constraints. But what is their precise nature? What is the specific course of the trajectories of S allowed by the gene-regulatory network?

Now it turns out that biological networks have a network architecture such that they typically drive trajectories emanating from distinct points within a particular region of the state space towards equilibrium states of the network [27,36] where all the gene-regulatory interactions are harmoniously satisfied. For instance, reusing the above example: if gene X1 inhibits gene X2, then both genes cannot be simultaneously highly expressed: the state, S = [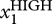, 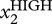] is unstable, as exemplified by the states S₁ and S₂, and to a lesser extent S₃, in figure 1a. Instead it will move to an equilibrium state, where we will necessarily have the [, 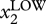] configuration (at a particular ratio x₁/x₂). At such an equilibrium point, the network state S does not experience any driving force anymore, it is in a stationary (=‘not changing’) or steady state. An equilibrium point is not only stationary but also stable if trajectories from its state space environment converge to it. Such stable stationary states are so-called attractor states (because they ‘attract’ nearby states). An attractor state, denoted S*, is exemplified in figure 1a. (But note that other interactions and genes of the network play a role in the existence and precise position of the attractor state, for instance, we have in the network in figure 1a a feedback loop such that X2 also inhibits X1. Such mutual inhibition between two regulators (X1 and X2) is frequently found in gene-regulatory networks controlling cell fates and is necessary for establishing a system consisting of two sister attractor states (‘bistability’)—for more details, see [10,20,37].)

Attractor states have long been proposed to represent discernible stable cell states, such as differentiated states, cell lineages or cell types (reviewed in [27]). They are characterized by stable gene-expression profiles that are robust to small perturbations since they would ‘attract’ all unstable points in their neighbourhood (that may have been reached in response to perturbations) until again all regulatory interactions are satisfied. Since a whole set of ‘initial states’ (e.g. S₁, S₂ and S₃ in figure 1a) can end up in the same attractor state, there are many ways to reach a particular attractor—a hallmark of stability. The set of initial states (points in state space) that ‘end up’ in the attractor state forms its ‘basin of attraction’. The robustness of attractors is manifest in the size of its basin. Perturbations of trajectories (e.g. by drugs that alter gene-expression levels, hence the state space coordinates), if not too large, will only cause a state to deviate transiently from the attractor or trajectories leading to it. The perturbed state will, if it did not leave the basin of attraction, eventually return to the attractor state and re-establish the associated specific gene-expression pattern (dashed trajectories in figure 1a).

The emergent dynamics of stem cells, that is, the observable behaviours to be explained, is played on the stage of this structured state space with trajectories, attractors and its basins and boundaries. These structures emanate from the constraints on network dynamics jointly imposed by all the gene-regulatory interactions.

Briefly, as an important corollary of the thesis that cell types are attractors, the state of multi-potency is then naturally represented by ‘metastable states’ in state space: states that are located on the boundary between two attractors, perhaps locally stabilized because they are in a shallow attractor [38]. This central position between two cell-fate attractors naturally predicts the ‘multi-lineage priming’ of stem cells and their access to two sister lineages, which underlies the binary decision. The metastability is also consistent with the local and temporal stabilities of pluri/multipotent states under particular conditions as well as their overall instability, epitomized in the natural proclivity of stem cells to differentiate (reviewed in [20,39]). On this basis, fate decisions have been mathematically modelled as the destabilization of the metastable stem cell attractor and/or as noise-induced exit of that attractor which forces the multi-potent stem cell to ‘choose’ either one of the two adjacent attractors [15,20,38,40–42].

A recent extension of the concept of state space and its attractors has been introduced to compare the relative stability of attractors in a multi-attractor system [43]. This consideration of ‘global dynamics’ [44,45] goes beyond conventional dynamical systems theory that is mostly concerned about local (linear) stability. Global dynamics introduces the idea of a potential landscape [45,46]. Very roughly, one assigns to each state S in state space the probability P(S) to find the system in that particular state S (at the system's steady state). Invoking probability is sensible if we assume that a system is noisy and the position of S can thus be determined only in terms of ‘likelihoods’. In fact, real systems are noisy owing to random fluctuations of gene-expression levels x_i such that the point S actually ‘wiggles’ (locally) in state space even under stationary conditions (discussed in §4). Moreover, without noise and perturbations, there is no spontaneous transition between attractors—the ontological condition sine qua non for comparing stabilities between distinct attractor states. Then, without dealing with formal details, it is intuitively conceivable that the more stable an attractor state, the greater is the probability P(S) (when the system is in a global equilibrium) to find a state S in that attractor state in a noisy system. Thus, P(S) is (loosely) related to its ‘stability’. As in other domains of physics and chemistry, stability (corresponding here to high P(S)) is graphically represented as low elevation (valleys, potential wells) and instability as high elevation (hill tops). Therefore, P(S) is inversely related to the notion of ‘potential energy’. One thus often defines a quasi-potential energy U as the inverse of P(S) and scales it by the logarithm: U =−ln[P(S)]. One then computes the elevation U(S) for each state S, which results in a landscape over the state space S. This of course is only visually intuitive for two-dimensional systems in which S is a location in the XY-plane and U would be represented by the Z-axis (figure 2). For formal accuracy, it is important to note here that U is not a ‘true’ potential energy in classical mechanics and, therefore, gradients of U (‘steepness’ of the landscape at position) cannot be interpreted as an accurate measure of the driving force for the movement of a given S in state space. This is because of the non-integrability of the ‘laws of motion’ of the network mentioned earlier and has to do with the fact that the network is a so-called non-equilibrium system [47].

Figure 2.

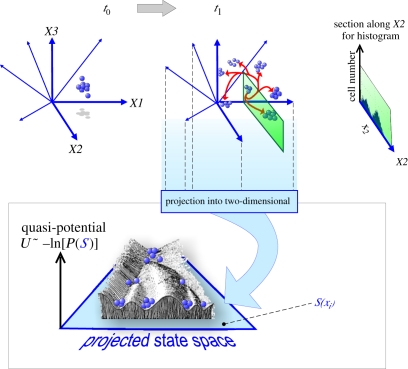
Integration of the three perspectives, state space, high-dimensionality and heterogeneity of populations, into a systems dynamics picture and its relationship to Waddington's [48] ‘Epigenetic Landscape’ (see text). State-space dimensions are represented by the blue arrows/axes. Using the same notation as in figure 1, a starting population of cells (t₀) is shown expanding, owing to gene-expression noise and proliferation, into predestined clusters (t₁). Histogram for dimension X2 is shown, obtained from the information contained in a state-space section parallel to X2 (green). Projection of the high-dimensional state space into a two-dimensional plane (light blue) and plotting the values of the inverse natural logarithm (ln) of the steady-state probability P(S) to find a cell at each position S, as the ‘quasi-potential’ U (the z-axis) generates the landscape. Note that the z-axis, U = −ln(P) does not represent the ‘true’ energy potential that drives the development (rolling down of the balls)—see text. As above, each blue ball represents a cell and its network state S.

Nevertheless, the landscape picture intuitively captures (for not too densely wired networks) the global dynamics in a system with multiple attractors. In such a landscape, the embryonic stem cells would start in a metastable state in the ‘high mountainous’ region, follow trajectories that ‘bifurcate’ at watersheds separating two valleys (representing binary cell-fate decisions), flowing downwards to ultimately end up in the deep attractors that represent the terminally differentiated cell types [20]. This is precisely what Waddington envisioned with his metaphoric ‘epigenetic landscape’ [48,49] (figure 2, bottom). For once, a metaphor is actually formally reducible to fundamental principles of mathematics and physics [20,27]. Although in his latest work [50], Waddington more explicitly expressed awareness of the link between metaphor and dynamical systems theory, perhaps as a result of his interaction with Stuart Kauffman (S. Kauffman 2009, personal communication), and despite the re-emergence of his landscape picture in the modern stem cell literature, the connection between Waddington's landscape that actually dates back to the 1940s [51,52] and systems biology is rarely acknowledged.

The embodiment as a landscape of the fundamental laws that govern how genes cooperate through regulatory interactions leading to the emergence of elementary properties of cell behaviour, including the stability of distinct states in deep valleys (attractors), the instability of multi-potent states on the hills separating the valleys, the binary fate decisions imposed by the hills, the directionality and branching nature of cell differentiation, etc., lucidly demonstrates that these basic cell behaviours are mathematical consequence of the collective action of interacting elements that form a network. They are intrinsic to the network, and neither the result of purposeful design by an intelligent being nor the product of natural selection dictated by the purpose of maximizing fitness [53]. In fact, as Kauffman showed [36], a broad class of complex networks with random topologies would naturally produce ‘reasonable’ landscapes with valleys and hills, not too flat and not to rugged, serving as a stage for ‘interesting’ cell behaviours. Then, natural selection during evolution of increasingly complex metazoans would have performed only the fine sculpting of the landscape to optimize the developmental trajectories, for instance in ensuring smooth descent to the attractors of mature cell types in order to prevent cells from getting stuck in unused attractors in immature regions of the state space near that of stem cells. Such accidental block of differentiation could lead to cancer [35].

3. Perspective 2: from low-dimensionality to high-dimensionality

The notion of high-dimensionality, the second neglected perspective to be discussed, pertains to the dimensionality of the state space just introduced. While conventional dynamical systems theory typically deals with systems consisting of two, three or a handful of nodes (genes), the genome-wide gene-regulatory network comprises thousands of genes (transcription factors that target other genes, including transcription factors) such that the corresponding state space of the network spans thousands of dimensions. Obviously this cannot be visually represented as in the case of our pedagogical three-gene circuit above (figure 1a) and escapes the realm of intuitive grasp. Yet, the above principles of dynamical systems, such as trajectories that may converge to stable attractor states, still hold. Valuable lessons in high-dimensional thinking were elegantly obtained by the model of gene-regulatory networks introduced by Kauffman in which genes take binary ON–OFF values for their expression level x_i and are connected by Boolean networks. The sacrifice of some details in favour of high-dimensionality is another example of wise abstraction to remove details that interfere with human comprehension. It has opened a new window to the exploration of high-dimensional dynamics by computer simulations and theoretical analysis [54,55].

Based on such analysis of large hypothetical (generic) gene networks [36], we can safely assume that the mammalian genomic network, given the set of network topology features and interaction modalities found so far, belongs to the class of not too densely connected networks that produce ‘reasonable’ dynamics. Thus, it can be expected to generate thousands of stable attractor states [27]. Then, the attractor state S_attr represents a discretely distinct, robust (self-stabilizing) genome-wide gene-expression profile of a cell type, or any distinct, observable cell state, such as a pluripotent/multi-potent state, as well as a terminally differentiated state. Thus, in a simplified picture, the entire state space of the human genomic network is partitioned into thousands of domains defined by attractor states and their surrounding ‘basins of attraction’ (potential wells). These high-dimensional attractor states represent the stable gene-expression profiles that we now can measure, to some approximation, as the characteristic transcriptomes. They encode the cellular programmes that map into distinct cell fates or, more generally, observable cell phenotypes.

In stark contrast to the high-dimensionality of cell states, human imagination and thinking covers only low-dimensional systems—as is manifest in our habit to operationally define a cell type by a just handful of molecular markers. This has practical implications. For instance, in daily experimental practice, such as in flow cytometry measurement and fluorescence-activated cell sorting (FACS), murine haematopoietic stem cells can be identified and separated based on the expression of the marker configuration Sca-1+, c-kit+ and the absence of lineage-specific markers [56]. More generally speaking, assume now a homogeneous cluster of (lineage-negative) cells expressing the markers X1 and X2 (figure 1b), e.g. Sca1+ and c-kit+ , in the two-dimensional flow cytometry dot plot in the X1–X2 graph. This plane obviously corresponds to a projection of a state space into a two-dimensional plane. Although the functional heterogeneity of these FACS-sorted populations has repeatedly been pointed to by Bryder et al. [56], a uniformly looking dense cloud of points in the two-dimensional dot plot or even just in a histogram (subpopulation S₁ in figure 1b) sometimes tempts investigators to interpret it as sign of ‘purity’ because of the absence of outlier dots in that plane or because of the smooth looking bell-shaped histogram. With our notion of high-dimensional state space, it is now obvious that such measurements are but a projection of a high-dimensional state space into a lower-dimensional one and that a uniform cluster or peak actually may stretch over wide ranges in the other, not observed dimensions. Of course, the use of additional markers, i.e. extending the perspective to expose additional dimensions, readily uncovers multiple clusters (multimodality) with respect to these other non-observed dimensions, as discussed below under the perspective of heterogeneity [57] (figure 1b). While such loss of information owing to projection appears conceptually trivial, in experimental practice and with thousands of state-space dimensions, there are biological consequences of high-dimensionality that could be missed.

One less trivial implication of the habitual neglect of ‘hidden’ dimensions in the study of dynamics is the following. From theoretical studies of higher-dimensional dynamical systems [58], it is known that the typical time scales of their dynamics, that is, the ‘speed’ of movement of S in state space, can differ dramatically between different dimensions: S may move vastly faster or slower when projected in one or another dimension, not unlike a rain droplet that moves fast in the vertical direction compared with the much slower drift in the horizontal direction owing to wind as it falls. This coexistence of distinct time scales for movement of S in different dimensions enriches the dynamics in ways that we only begin to appreciate. For instance, a cell may be stable in an attractor S₁ with respect to gene X1, while moving slowly along the dimension spanned by another gene X2. The level of X2 may dictate the extent to which a cell characterized by the relatively uniform and stable expression of a particular level of gene X1 (for instance, stem cell marker Oct4) is prone to leave the attractor with respect to dimension X1 (i.e. to differentiate in the case of Oct4). X2 thus is a factor that stratifies the apparently homogeneous population with respect to X1 levels into those that are more or less prone to differentiate into a particular direction. The transcription factor Nanog, for example, when present at low levels, marks those cells (within an otherwise apparently homogeneous population—see below) which have the proclivity to lose pluripotency [59,60]. Similarly, in apparently uniform bipotent haematopoietic progenitor cells, those that exhibit above average levels of the surface marker Sca-1 harbour a higher tendency to commit to the myeloid than the erythroid lineage [61]. Thus, stratification of a population that appears uniform in dimension X1 by considering another dimension X2 is a manifestation of high-dimension heterogeneity (see §4) and of practical importance for stem cell investigators.

A lucid illustration of our neglect of higher dimensionality beyond those dimensions that we measure is offered by experiments in which a bimodal distribution of the expression of a differentiation marker Z, as seen in flow cytometry, is interpreted as manifesting the presence of two subpopulations (figure 1b, see legend). For instance, in a common scenario, the treatment of a stem cell culture with submaximal doses of a differentiating cytokine will yield a differentiated (Z+) and a non-differentiated (Z−) subpopulation if Z is a marker of differentiation. However, assume now that we have two distinct differentiation inducers, A and B that both cause only partial differentiation, hence each leaving its own (Z−) subpopulation, (Z−)_A and (Z−)_B when stem cells are treated with the respective inducer. In this scenario, one can show that these two (Z−) subpopulations are distinct. When after the treatment of two stem cell cultures with either A or B, respectively, the two (Z−) subpopulations in these two cultures, (Z−)_A and (Z−)_B, are sorted out and their transcriptome compared, one observes quite significant differences in the genome-wide gene-expression profiles of the two subpopulations, (Z−)_A and (Z−)_B. Thus, these two (Z−) subpopulations do not simply represent the same, ‘non-responsive cells’ but instead, these (Z−) cells have responded distinctly to condition A versus B with respect to a high-dimensional space—but in both cases did not (yet) induce the marker Z (H. Chang & S. Huang, unpublished observation).

The above observations indicate a broad but hidden spectrum of all kinds of degrees of intermediate stages of differentiation that are not yet manifest in the expression levels of the monitored marker(s) [57]. Thus, differentiation is not simply a discrete switch from one state (attractor) to another that can be distinguished by the two levels of expression status (X^low versus X^high, or X− versus X+) of a single marker as commonly assumed. Instead, it is a convoluted, multi-step journey in multiple state-space dimensions. This stepwise nature and high-dimensionality of developmental trajectories contribute to a heterogeneity of cell populations that is further accentuated by the stochastic asynchrony of the individuals cell's progression in the long, multi-step journey [62]. Moreover, cells can, depending on the stimulus, take different trajectories to move from one state to another. After all it is now appreciated that, because the destination state represents a high-dimensional attractor, multiple paths (state space trajectories) converge in attractor states [63]. While from the state-space perspective this is not surprising, the discovery of new, rarely used or of artificially induced developmental trajectories continues to stun stem cell biologists [20]. The intermediate states hidden in non-monitored state-space dimensions during phenotype conversion [57] are also encountered in induced pluripotent stem cells reprogramming [64,65] and are thought to contribute to the low rate and frequency of the desired state transition [20]. The advent of single-cell, high-dimensional expression profiling [4,66–68] will extend single-cell resolution measurements of gene expression, which is currently the domain of low-dimensional flow cytometry, by many dimensions, and will enable us to explore new dimensions —mathematically and metaphorically—of cell-fate dynamics.

4. Perspective 3: from homogeneity to heterogeneity

The discussion on hidden intermediate states in non-monitored dimensions of the state space illustrates not only the two perspectives, state space and high-dimensionality, but already leads to the third neglected perspective that is inseparably linked to the former two: the non-genetic heterogeneity of a putatively uniform population of cells, notably, stem cells. This ‘heterogeneity’ is ‘non-genetic’ because it refers to the fact that in a clonal (isogenic), hence nominally uniform, population of cells tacitly assumed to be phenotypically identical to each other, the individual cells in reality are quite distinct from each other (reviewed in [28]). The population thus displays cell-to-cell variability. Accordingly, the cells display cell-individuality—a phenomenon that has long been observed in single-cell organisms [69–71]. If the property X (e.g. abundance level of protein X) is measured for every cell j, one could plot the results as a histogram that displays the number of cells observed as a function of the value of X that each cell displays (figure 1b). However, putting this familiar output format of flow cytometry in the perspective of high-dimensional state space, we now can more formally state that such histograms represent the statistical distributions of the cells' positions in state space projected to the dimension of X. As mentioned above, if two variables are measured, X and Y, then each cell can be represented as a dot on the two-dimensional XY-plane, the projection of the state space in two dimensions. A heterogeneous population is thus manifest by a cluster of points that appear as a ‘cloud’ in this state space [28] (figure 1a,b).

By contrast, measurement of expression of X by traditional biochemical analysis, such as Western blots, RT-PCR and microarrays, provides only a singular value that represents the physical average of the entire population [28]. The key additional information offered by a statistical distribution includes the variance of the distribution (‘diversity’ of the population) and the presence or absence of partitioning into discrete (‘quantized’) subpopulations, as discussed above. The presence of two subpopulations in a putatively homogeneous population, manifest as two (often overlapping) ‘peaks’ in the histogram, centred around two values, X^high and X^low, would go unnoticed in population averaging methods. While it appears trivial that such a bimodal distribution indicates the presence of two discretely distinct subpopulations, as discussed in the previous section in detail, in the light of the high-dimensional state space, a bimodal distribution is highly indicative (but not proof) of the presence of two possibly high-dimensional attractor states—projected to the state space dimension of X [57], so that each ‘peak’ may itself represent multiple discrete subpopulations (figure 2).

‘Heterogeneity’ describes not only such discretely distinct subpopulations (which we refer to as ‘macro-heterogeneity’) but also can refer to a continuous range of a varying property in a unimodal distribution (‘micro-heterogeneity’) [28,72]. In fact, the two tails of a single bell-shaped curve distribution consist of cells that can be biologically distinct, notably in terms of their priming (reversible pre-commitment) to a particular fate. Intriguingly, even cells in the various intermediate regions of a uniformly looking distribution could behave vastly differently because of the ‘missed dimensions’, as discussed in the previous section. Cell sorting experiments with multi-potent cells indicate that fractions of a distribution, e.g. the tails of a one-dimensional histogram or sub-regions of a cloud of points of the two-dimensional state space (in a two colour flow cytometry) contain cells with distinct proclivities to commit to various lineages (reviewed in [28,72]). Thus, the dispersion in state space of a heterogeneous population is tightly associated with differential priming of multi-potent stem or progenitor cells [61,73–76].

Heterogeneity of cell populations is also increasingly appreciated in studies with new digital microscopy techniques and computational image analysis of cell cultures that integrate the information of entire populations rather than view individual cells as mere replicates of each other [76,77].

Awareness of cell population heterogeneity offers a new dimension of biological exploration. The fact that in flow cytometry measurements the values of x_i are ‘distributed around a mean’ (broad ‘peak’ in the histogram) has for a long time been tacitly dismissed as measurement noise by cell biologists. Then, in the past decade, such broad dispersion of single-cell measurement values has been interpreted as ‘gene-expression noise’ by physical scientists [78,79]—an interesting physico-chemical phenomenon that is caused by the stochasticity (randomness) inherent in the thermal nature of chemical reactions, which is not ‘averaged out’ when involving only a small number of molecules. This is certainly the case, for instance, in transcriptional initiation (where a few thousand copies of a given transcription factor bind to just one or two copies of its cognate responsive DNA motif in the regulatory region that is accessible).

Evidently, the spread of the peak in cytometry histograms does not simply reflect the measurement error in the determination of X in individual cells since such error contributes only approximately 10 per cent of the observed variance [61]. However, nor is the spread a pure manifestation of elementary chemical stochasticity—or gene-expression noise. We have recently learned that reality is more complex. Measurement of the dynamics of X in individual cells or in population fractions has revealed that the variance of X in the histograms is not due to fast temporal fluctuations of X that are frozen in time in histograms when the population snapshot for the histogram was taken. Instead, individual mammalian cells have some memory of their individuality in X that can last across several cell generations and only slowly decays [61,80]. For instance, a cell that within the heterogeneous population has extreme high levels of X might maintain its ‘outlier’ status for quite a while (days–weeks)—over a much longer time scale than what would be expected from low-dimensional, purely thermal (stochastic) fluctuations. But the presence of memory by definition is not consistent with pure stochasticity, where events are not influenced by the past. By contrast, the level of X of a given cell appears to fluctuate rather slowly as a cell wanders randomly and aimlessly in state space within the attractors state, spending most time in the vicinity of the centre of the attractor (mean value of X)—hence producing a ‘peak’ there. Outliers with extreme values of X only fully relax back to the mean values with considerable delay. Thus, cells do not jump erratically from one spot to another as one would expect if the spread is governed by pure noise only. In other words, the apparent ‘gene-expression noise’ manifest in broad distributions of X in population snapshots is not pure thermal noise but heavily constrained by the complexity of the process of protein expression that involves multiple layers of regulation and regulatory inputs from the network.

Since the cloud in a flow cytometry dot-plot output or the iconic ‘salt-and-pepper’ appearance in microscopy images of the distribution of regulatory factors in individual cells of early embryos [81–83], which both epitomize non-genetic heterogeneity, represent snapshots in time, they do not permit the distinction of slow fluctuations (or in the extreme case, cell-to-cell variability of stable, i.e. time invariant properties) from purely stochastic, rapid fluctuations owing to gene-expression noise. Discerning between these two scenarios will require knowing the rate at which the individual points in the cloud move around (speed and trajectory) in state space. This can be achieved by observation in real-time digital microscopy of fluorescent reporters for the expression of genes X of interest [84]. Knowledge of the average persistence time of the expression status of key transcription factors (autocorrelation time of fluctuation) is important to address the question to what extent the history (previous states in regard to other dimensions that may have been influenced by external signals) of an individual cell biases lineage choice when otherwise no underlying pattern is visible for fate commitment [85].

While fast fluctuations would be attributed to thermal noise that is unconstrained except for a mean-reverting force (owing to the attractor), the physical basis for the relatively slow fluctuations of X in individual cells is currently debated [28]. Given the complex high-dimensional gene-regulatory network that constrains the movement of the states and the multiple layers and players that participate in the very process of initiating a gene expression, including slow processes, such as chromatin reorganization, it is not surprising that the apparent noise is rich in structure, stretching fluctuations into the time scales of long enduring cell individuality.

This so-called ‘non-ergodicity’ [28] allows random variability to carry biological significance, for it grants sufficient time to random outliers with particular expression levels of a gene X to exert their regulatory activity, leading to coherent genome-wide fluctuations of entire network states as recently observed [61,85]. Since the high-dimensional trajectory of the genomic network is constrained, this may explain the observed priming of stem cells for specific fates as a function of their position in a multi-colour flow cytometry dot plot (representing a low-dimensional projection of the state space) because the entire genome-wide state of a cell may swing back and forth between state-space regions (in the high-dimensional state space) that encode states pre-committed for particular fates [86].

5. Integration and conclusion

In the three new views presented here, the elementary properties of dynamical systems that underlie cell-fate behaviours spring to eye. These three perspectives are natural in the physical sciences. They are not constructed to explain a particular biological phenomenon like many of the mechanistic, ad hoc explanations in biology but instead help expose the fundamental constraints rooted in the laws of physics of complex dynamical systems. These constraints give rise to biological phenomena, such as the instability of undecided states or the stability of committed states. By integrating the three new vistas into one, we arrive at the following self-consistent model of development of multi-cellularity [86] (figure 2).

Cell-type diversification starts with the totipotent zygote that occupies a single point in the high-dimensional state space of the genomic regulatory network that governs development. Then, development of the wide spectrum of cell types that provide the building blocks of the organisms consists of both the multiplication of cells and the diversification of cell types. Thus, as the zygote divides, its daughter cells and their progenies, if we think in state space rather than physical space, represent points in state space that multiply and swarm out from the initial point of the zygotic state as their gene-expression profiles change, primarily driven by gene-expression noise but constrained by the trajectories that lead to attractors. This results in an uneven expansion of a cloud of states in state space. Local fluctuations owing to gene-expression noise generate micro-heterogeneity represented by the size of individual clouds and the partitioning of the state space into multiple clouds produces macro-heterogeneity, manifesting the cell-type attractors [28].

This picture resembles the expansion of a gas of molecules into the three-dimensional (physical) space driven by thermal energy (entropy)—with the formal differences that the cells also multiply in this process—which accelerates the ‘space filling’ and that they expand in the abstract state space, not in physical space (figure 2). The very fundamental, essential difference between gas expansion and development in state space however, is that in the latter case, the movement of particles (points) that represent cell states is highly constraint, channelled towards the local clouds representing attractors. The ensemble of all cell states cannot simply uniformly fill a space as one would expect of gas molecules. This unique vantage point tells us that the wonderful diversity of cell types in a living organism is perhaps not achieved by an active process but instead the result of the limitation of ‘entropy’ maximization that would have filled the entire gene-expression state space, if the constraints owing to gene–gene-regulatory interactions did not exist. Thus, the apparent high degree of ‘organization’ that we associate with complex living systems may actually simply reflect the deficit, or frustration, owing to internal constraints, of the noise-driven process in maximizing (a kind of) ‘entropy’ that seeks to realize all mathematically possible gene-expression configurations. The diversity of cell types may thus be, to paraphrase the biologist and philosopher Stuart Kauffman, just a form of ‘order for free’, or more bluntly, simply ‘inevitable’ [36]. On top of this fundamental, inevitable and hence robust process, everything else that is required to build a functioning organism, such as the correct relative proportions of cell types and their relative positions in the body as well as the array of other mechanisms needed in tissue morphogenesis, can in this view be attributed to further constraints at the level of cell–cell communication networks whose detailed design would have been accomplishment by natural selection during metazoan evolution. But the elementary process of diversification of cell types in metazoans is likely to be given by the physics of dynamical systems and not to be fully credited to natural selection.

The three perspectives presented here introduce a conceptual framework that helps explain the fundamental inevitability of stem cell features. But this is more than a mere academic exercise. It is of course still necessary to work out the molecular details of the specific pathways that were faulted as not being explanatory in the opening of this paper. Knowledge of the precise molecular pathway diagrams with specific details is still indispensable for designing methods to interfere with cell-fate regulation in order to steer their development into a particular, useful state. If characterization of specific pathway diagrams provides a road map, the study of the state space will one day reveal the topography, exposing the valleys in hidden dimensions and the possibly surmountable hills between them. Such information on the structure of the epigenetic landscape will be needed for harnessing the natural forces and constraints that drive cell state changes in order to reprogramme cell fates.