Fluid dynamics and noise in bacterial cell–cell and cell–surface scattering

Abstract

Bacterial processes ranging from gene expression to motility and biofilm formation are constantly challenged by internal and external noise. While the importance of stochastic fluctuations has been appreciated for chemotaxis, it is currently believed that deterministic long-range fluid dynamical effects govern cell–cell and cell–surface scattering—the elementary events that lead to swarming and collective swimming in active suspensions and to the formation of biofilms. Here, we report direct measurements of the bacterial flow field generated by individual swimming Escherichia coli both far from and near to a solid surface. These experiments allowed us to examine the relative importance of fluid dynamics and rotational diffusion for bacteria. For cell–cell interactions it is shown that thermal and intrinsic stochasticity drown the effects of long-range fluid dynamics, implying that physical interactions between bacteria are determined by steric collisions and near-field lubrication forces. This dominance of short-range forces closely links collective motion in bacterial suspensions to self-organization in driven granular systems, assemblages of biofilaments, and animal flocks. For the scattering of bacteria with surfaces, long-range fluid dynamical interactions are also shown to be negligible before collisions; however, once the bacterium swims along the surface within a few microns after an aligning collision, hydrodynamic effects can contribute to the experimentally observed, long residence times. Because these results are based on purely mechanical properties, they apply to a wide range of microorganisms.

Collective behavior of bacteria, such as biofilm formation (1), swarming (2), and turbulence-like motion in concentrated suspensions (3, 4), has profound effects on foraging, signaling, and transport of metabolites (5, 6), and can be of great biomedical importance (7, 8). Large-scale coherence in bacterial systems typically arises from a combination of biochemical signaling (9) and physical interactions. Recent theoretical models that focus on physical aspects of bacterial dynamics identify pairwise long-range hydrodynamic interactions (10–16) as a key ingredient for collective swimming. Such ‘‘microscopic” approaches underpin continuum theories that aim to describe the phenomenology of microbial suspensions (17–23). An assumption underlying many of these theories is that a self-propelled bacterium can be modeled as a force dipole; its body exerts a drag force F on the fluid that is balanced by the rearward flagellar thrust -F. The leading-order fluid velocity field at distance r is therefore a dipolar ‘‘pusher” flow of magnitude u ∝ Fℓ/ηr² (see streamlines in Fig. 1B), where η is the viscosity, and ℓ the distance between the forces (24, 25). While higher order corrections may be due to force-quadrupole contributions (26), the hypothesis that the leading-order flow field around a bacterium is dipolar has not yet been verified experimentally.

Fig. 1.

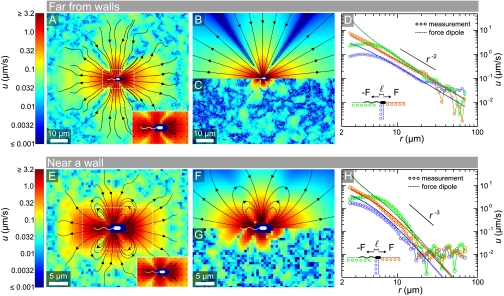
Average flow field created by a single freely swimming bacterium far from surfaces (A–D) and close to a wall (E–H). Streamlines indicate the local direction of flow, and the logarithmic color scheme indicates flow speed magnitudes. (A) Experimentally measured flow field in the bacterial swimming plane, with the inset showing the anterior-posterior asymmetry close to the cell body. (B) Best-fit force dipole flow. (C) Residual flow field, obtained by subtracting the best-fit dipole model from the measured field. (D) Radial decay of the flow speed u in different directions, with r = 0 corresponding to the center of the cell body. For distances r ≲ 6 μm the dipole model overestimates the flow field behind and to the side of the cell body. (E) Experimentally measured flow field in the bacterial swimming plane, for bacteria swimming parallel to a wall at a distance of 2 μm. (F) Best-fit force dipole flow, where the presence of the wall causes inward and outward streamlines to join. (G) Residual flow field. (H) The flow speed decays much faster for bacteria swimming close to a wall, as the fluid velocity must vanish on the surface.

A closely related, controversially discussed issue (27–30) is the relevance of long-range hydrodynamic interactions in the scattering of bacteria with surfaces, a phenomenon intimately linked with surface accumulation and biofilm formation. Cell–surface scattering is very similar to cell–cell scattering, because, by analogy with image charges in electrostatics, a bacterium that swims near a surface induces an ‘‘image bacterium” on the opposite side of the wall to yield the no-slip boundary condition on the surface (27, 31); bacterium–surface scattering can therefore be analyzed as the interaction of a bacterium with its hydrodynamic image. Several recent calculations for microswimmers near surfaces have found that pusher-type organisms (those with thrust generated behind the cell body) should display a passive stable alignment of the swimming direction with the wall (27, 32–35). However, direct measurements of the three-dimensional swimming tracks of bacteria near surfaces suggest that they simply collide with the surface (28, 36). This raises the question: Is this discrepancy between experiment and theory due to incomplete knowledge of the bacterial flow field, or is the magnitude of the flow so small that fluid-mediated interactions are irrelevant?

The need for experimental tests of the force dipole assumption and, more generally, of the relevance of fluid-mediated interactions for bacteria, is further illustrated by recent measurements on Chlamydomonas reinhardtii (37, 38), the archetypal ‘‘puller” microorganism (thrust generation in front of the cell body) that was thought to generate a simple force dipole flow with opposite sign to the bacterial one (25). Surprisingly, these experiments showed that while such a dipolar flow exists at large distances from the organism, in regions where the flow magnitudes are significant (greater than 1% of the swimming speed), the flow topology is qualitatively different and more accurately described in terms of a triplet of force singularities (one for the cell body and one for each flagellum) (37). Here we present direct measurements of the flow field around individual freely swimming bacteria, using Escherichia coli as a model. We find that the pusher force dipole provides a good approximation to the flow field both when the organism is far from surfaces and close to a no-slip boundary, yet the magnitude of the flow is very low in both cases. Using the experimentally determined flow field parameters, the hydrodynamic interaction of two E. coli can be calculated, and it is found to be washed out by rotational diffusion of the swimming direction for closest encounter distances ≳3 μm—a result that should hold for many other bacterial species due to the similarity of motility parameters. Similarly, analysis of cell–surface encounters suggests that hydrodynamics plays a negligible role, except when a bacterium swims along a surface at a small distance (less than a few microns) after an inelastic aligning collision. In this case, hydrodynamic effects can contribute to the observed long residence times near surfaces.

Results

Flow Field Far from Surfaces.

To resolve the miniscule flow field created by bacteria, individual gfp-labeled, nontumbling E. coli were tracked as they swam through a suspension of fluorescent tracer particles (see Materials and Methods). Measurements far from walls were obtained by focusing on a plane 50 μm from the top and bottom surfaces of the sample chamber, and recording approximately 2 terabytes of movie data. Within this data we identified approximately 10⁴ rare events when cells swam within the depth of field (2 μm thick) for > 1.5 s. By tracking the fluid tracers during each of the rare events, relating their position and velocity to the position and orientation of the bacterium, and performing an ensemble average over all bacteria, the time-averaged flow field in the swimming plane was determined down to 0.1% of the mean swimming speed V₀ = 22 ± 5 μm/s. As E. coli rotate about their swimming direction, their time-averaged flow field in three dimensions is cylindrically symmetric. The present measurements capture all components of this cylindrically symmetric flow except the azimuthal flow due to the rotation of the cell about its body axis. In contrast with the flow around higher organisms such as Chlamydomonas (37, 38) and Volvox (37), the topology of the measured bacterial flow field (Fig. 1A) is that of a force dipole (shown in Fig. 1B). Yet, there are some differences between the force dipole flow and the measurements close to the cell body, as shown by the residual of the fit (Fig. 1C).

The decay of the flow speed with distance r from the center of the cell body (Fig. 1D) illustrates that the measured flow field displays the characteristic 1/r² form of a force dipole. However, the force dipole model significantly overestimates the flow to the side and behind the cell body, where the measured flow magnitude is nearly constant over the length of the flagellar bundle. The force dipole fit to the far field (r > 8 μm) was achieved with two opposite force monopoles (Stokeslets) at variable locations along the swimming direction. As r = 0 corresponds to the center of the cell body in Fig. 1D, and not the halfway point between the two opposite Stokeslets, the fit captures some of the anterior–posterior asymmetry in the flow magnitude u. From the best fit, which is insensitive to the specific algorithms used, we obtained the dipole length ℓ = 1.9 μm and dipole force F = 0.42 pN. This value of F is consistent with optical trap measurements (39) and resistive force theory calculations (40). It is interesting to note that in the best fit, the cell drag Stokeslet is located 0.1 μm behind the center of the cell body, possibly reflecting the fluid drag on the flagellar bundle.

Flow Field Near a Surface.

Having found that a force dipole flow describes the measured flow around E. coli with good accuracy in the bulk (far from boundaries), we investigated whether this approximation is also valid when E. coli swim close to a wall. Focusing 2 μm below the top of the sample chamber, and applying the same measurement technique as before, we obtained the flow field shown in Fig. 1E. This flow decays much faster than that in the bulk due to the proximity of a no-slip surface (Fig. 1H), and the inward and outward streamlines are now joined to produce loops (Fig. 1E). However, both of these differences are consistent with a simple force dipole model and are therefore not due to a change in bacterial behavior. In particular, closed streamlines are known to be a rather general feature of point singularities near no-slip surfaces (41). Using the solution of a Stokeslet near a wall (31) to obtain that of a force dipole near a wall yields streamlines (Fig. 1F) and a decay (Fig. 1H) of the flow field that is consistent with the data. The best-fit force dipole in this geometry yields F = 0.43 pN and ℓ = 2.2 μm, consistent with the values obtained far from walls, but less accurate than those values due to the much faster decay of u(r) near a wall.

Spectral Flow Analysis.

To analyze systematically the angular flow structure even at distances r < 6 μm, where the force dipole model overestimates the flow magnitudes, it is useful to decompose the flow field into vector spherical harmonics. The resulting spectra are useful “fingerprints” of the flow field that can be compared among many different organisms, and against theoretical models. Such a spectral analysis is described in the SI Text.

Rotational Diffusion.

Even bacteria that do not display tumbles, such as those studied here, do not swim in completely straight lines. Random changes in swimming direction due to thermal effects and intrinsic noise in the swimming apparatus lead to rotational diffusion, which can be characterized by a coefficient D_r. From the swimming data recorded for E. coli far from surfaces, we measured D_r = 0.057 rad²/s (see Materials and Methods). Even organisms that are too large to have significant thermal rotational diffusion, such as the 10-μm sized alga Chlamydomonas reinhardtii, can have a significant D_r due to noise in the swimming mechanism (42). From swimming data previously recorded for Chlamydomonas (37), we found D_r = 0.4 rad²/s.

Discussion

Our measurements show that, independently of whether E. coli swim near or far from a surface, their flow field can be described to good accuracy by a simple force dipole model whose parameters we determined. We now proceed to discuss the implications of this flow field for cell–cell and cell–surface interactions. Based on the measured parameters and the force dipole approximation, we calculate the effect of long-range hydrodynamics for these two scattering phenomena and evaluate the importance of fluctuations in the swimming direction.

Hydrodynamics vs. Rotational Diffusion in Cell–Cell Scattering.

Fluid-mediated long-range interactions are thought to play an important role in collective motion in bacterial suspensions (17–23). These deterministic interactions, however, compete with rotational diffusion of the swimming direction. To infer the importance of longe-range hydrodynamics in the bulk, we consider the change in swimming direction of a bacterium due to hydrodynamic scattering with another bacterium. This can be done by fixing one bacterium at the origin and examining the trajectory of the other. The flow field around the bacterium at the origin is approximated by that of a point force dipole (31)

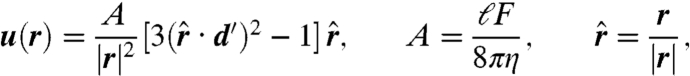[1]

where d^′ is the unit vector in the swimming direction, and r is now the distance vector relative to the center of the dipole. The evolution of the position x and swimming direction d of the second swimmer in this field obeys (43)

[2]

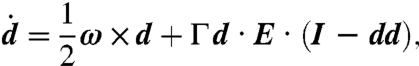[3]

where I is identity matrix, and the central swimmer leads to an advective flow u, a vorticity ω, and a strain-rate tensor E at the position x (see SI Text for exact expressions of these quantities). By examining the evolution of d(t) in a scattering process that begins at -t/2, reaches a minimal encounter distance r at t = 0, and ends at t/2, the mean squared angular change of orientation during a time interval t can be computed as

[4]

where 〈·〉_H indicates an average over all possible orientations and positions of encounters. Assuming that the interaction time scale of the two bacteria τ is small, and using the force dipole model from Eq. 1 we obtain (see derivation in SI Text)

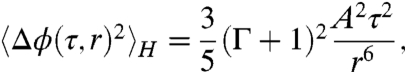[5]

where Γ ∼ 1 is a geometric factor for E. coli. Intuitively, this form arises from the fact that Δϕ ∼ ωτ, where the vorticity magnitude ω falls off as A/r³. To evaluate the importance of hydrodynamic interactions relative to random fluctuations, we compare 〈Δϕ(τ,r)²〉_H with the angular diffusion due to Brownian motion and intrinsic swimming variability in three dimensions, given by 〈Δϕ(t)²〉_D = 4D_rt. Balancing the effects of hydrodynamics and noise,

[6]

defines an effective hydrodynamic horizon r_H, beyond which noise dominates over hydrodynamics. For scattering events with closest encounter distances r > r_H hydrodynamics is therefore practically irrelevant. From this definition of r_H and Eq. 5, we find

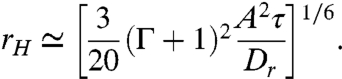[7]

Due to the τ^1/6-dependence, the hydrodynamic horizon r_H is rather insensitive to the particular value used for the interaction time scale τ and, similarly, to changes in the other parameters. Using the measured values D_r = 0.057 rad²/s, V₀ = 22 μm/s, A = 31.8 μm³/s, and adopting τ = a/V₀ ≃ 0.1 s, where a = 3 μm is the length of the cell body, we obtain r_H ≃ 3.3 μm for E. coli. This value of r_H is an upper bound, because the dipolar flow model overestimates u for r ≲ 6 μm (Fig. 1D). At such small separations, however, steric repulsion, flagellar intertwining, and lubrication forces dominate the physical cell–cell interactions (44, 45). For the mean distance between E. coli to reach r_H, the volume fraction needs to be as high as 5–10%. Using our measured parameters in a recent theoretical calculation (46) of the critical volume fraction for the onset of collective swimming due to hydrodynamic interactions leads to an even higher value, implying that a complete analysis of collective behavior in bacterial suspensions must account for steric and near-field interactions.

More generally, we expect similar results to hold for various types of swimming bacteria (e.g., Pseudomonas aeruginosa, Vibrio cholerae, Salmonella typhimurium), as the parameters (a,τ,D_r,Fℓ) are similar across many genera. Larger organisms may display even stronger rotational diffusion due to enhanced intrinsic swimming stochasticity (42). For example, the alga Chlamydomonas (a ≃ 10 μm, V₀ ≃ 100 μm/s) has D_r ≃ 0.4 rad²/s. Although the flow topology around Chlamydomonas is more complicated than that around bacteria, Chlamydomonas still produces a 1/r² field (37), so that our previously calculated result for the bacterial hydrodynamic horizon may be used to give an estimate of r_H ∼ 7.5 μm, again on the scale of the organism. Thus, collisions, rather than long-range hydrodynamics, can also govern scattering events of higher microorganisms. However, for organisms that produce fast flows, have a long interaction time τ, and a negligible D_r, like the alga Volvox, long-range hydrodynamic interactions are significant (47).

Cell–Surface Scattering.

The accumulation of bacteria near surfaces is a key step during the initial stages of biofilm formation, and it has been suggested that long-range hydrodynamics plays an important role in bacteria–surface interactions (27). Because our measurements show that the flow field has a small amplitude, it is plausible that bacterial cell–surface scattering events could be described instead by nearly straight-line swimming interrupted by collisions with the wall that lead to alignment with the surface due to near-field lubrication and/or steric forces during the collision (28). Our experimental results establish the key microscopic parameters required for a systematic investigation of whether long-range hydrodynamic interactions are relevant to bacteria–surface scattering.

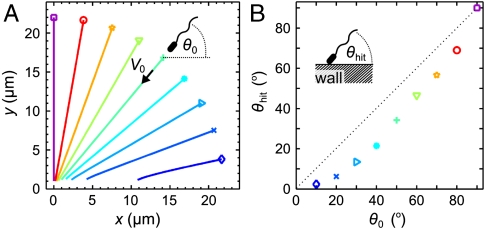
As a first step in our analysis, we performed numerical scattering studies by simulating the deterministic equations of motion for an E. coli-like pusher force dipole swimmer in the presence of an infinite no-slip surface. The equations of motion of the swimmer position x and unit orientation vector d are simply those used above (Eqs. 2 and 3) except that now u, ω, and E are quantities arising from the hydrodynamic image system in the wall (exact expressions for these quantities are given in the SI Text). By restricting ourselves to simulations of the deterministic dynamics at this stage, we overestimate the relevance of hydrodynamic long-range interactions between the swimmer and the wall, because rotational diffusion of the swimming direction further diminishes hydrodynamic effects. However, even without rotational diffusion our simulations show that long-range interactions of swimmers with the wall have little effect on the swimming dynamics (Fig. 2). The trajectories of force dipole swimmers that swim toward the wall from different initial angles θ₀ are depicted in Fig. 2A. The initial distance was chosen such that the swimmer would reach the wall plane (y = 0) after 1 s if hydrodynamic interactions were absent. Each simulation is stopped when a volume around the swimmer (a bacterial shape of length 3 μm and diameter 0.8 μm) crosses the wall. Fig. 2B displays the impact angle θ_hit as a function of the initial angle θ₀, illustrating that the difference between incidence and collision angles is small unless the swimmer already has a small angle of incidence. These simulations indicate that hydrodynamic long-range interactions are not likely to play an important role in cell–surface scattering for E. coli. Because the swimming parameters are similar for many bacterial species, we again expect this result to apply more generally.

Fig. 2.

Simulated dynamics of an E. coli-like force dipole swimmer near a wall. (A) Deterministic swimming trajectories towards a wall at y = 0, numerically simulated from Eqs. 2 and 3, where u, ω, and E are due to the hydrodynamic image system. Simulations used a time step Δt = 10^-5 s and the experimentally determined parameters A = 31.8 μm³/s, V₀ = 22 μm/s and Γ = 0.88 for the force dipole swimmer. The initial distance is chosen such that the swimmer would reach the wall after 1 s if hydrodynamic interactions were not present. (B) Incidence angle θ₀ vs. collision angle θ_hit with the wall for the trajectories in A, using the same symbols and colors. The dotted line indicates θ_hit = θ₀. Both panels illustrate that hydrodynamic long-range interactions can be regarded as small perturbations for typical wall scattering events of E. coli.

Trapping by Surfaces.

When E. coli swim very close to a surface (approximately 1–3 μm), we observed that individual bacteria spend an average of 64 s (standard error 4 s) next to the wall (within the focal plane). Effective trapping by electrostatic attraction is unlikely, because both the E. coli outer cell wall and the chamber walls (bovine serum albumin coated onto PDMS) (48) are negatively charged in our liquid medium (we observed similarly long residence times on simple glass surfaces). However, the surprisingly long residence times could be caused by the suppression of rotational diffusion due to geometric constraints on the orientation of the cell body and flagella near a surface. Although we showed in the previous section that hydrodynamics has a very small effect on the swimming direction before collisions with the surface, hydrodynamic attraction by the surface (27) could contribute to the observed trapping periods when a bacterium is already very close to the surface. Considering only hydrodynamic attraction counteracted by rotational diffusion, we now derive approximate expressions for the mean escape time t_e and escape height above the surface h_e, by mapping the underlying escape process onto a Kramers problem (49, 50) for the noise-induced escape over a potential barrier. The main arguments and implications are summarized below, while a detailed derivation is given in the SI Text.

We again approximate the E. coli flow field by the dipole model, because a force dipole placed close to a wall accurately captures the measured flow field parallel to the surface (see Fig. 1 E–H). Thus, Eq. 1 is modified to account for the presence of the wall (31), as discussed in the SI Text, and near-field hydrodynamic lubrication effects are neglected. A bacterium is able to escape from the surface, if its swimming velocity component perpendicular to the surface, V₀ sin θ, exceeds the attraction from its hydrodynamic image (see SI Text), which yields the defining relation for the escape angle θ_e,

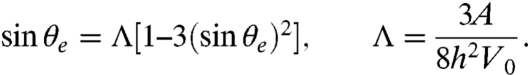[8]

For E. coli swimming at distances h > 1.5 μm from the wall, the escape angles are small, θ_e(h) < 11° ≪ 1 rad so that linearization of Eq. 8 is a good approximation, giving θ_e ≃ Λ.

After colliding with the wall, a bacterium may have a small positive angle θ < θ_e with the surface. The equation of motion for θ can then be rewritten as a Langevin equation (49) in terms of the derivative of an effective “potential” U(θ), and a diffusion term with Gaussian white noise ξ(t),

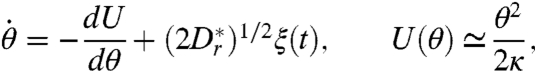[9]

where the approximation θ ≪ 1 reduces U(θ) to a harmonic potential, yielding a time scale κ = 16h³/(9A) that characterizes hydrodynamic realignment. 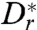is the rotational diffusion constant close to the surface in the direction perpendicular to the surface, which is expected to be smaller than our measured value D_r = 0.057 rad²/s far from boundaries, due to geometric constraints on the bacterial orientation near a surface. The generic form of this Langevin equation means that finding the residence time for a bacterium near a wall is a Kramers problem (49, 50) for the escape over a barrier ΔU. Because the organism can escape if θ > θ_e, we have ΔU = U(θ_e).

By considering the height at which 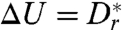—i.e., the distance at which the hydrodynamic torque barrier is comparable to the diffusion “temperature”—we can obtain an expression for the escape height

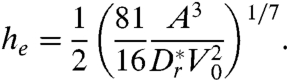[10]

Using our measured values for E. coli, we find 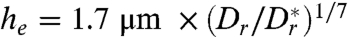, illustrating that hydrodynamics is practially negligible if E. coli are more than a cell length away from the wall.

As long as the torque exerted by the hydrodynamic image is small () the typical escape time is set by the rotational diffusion time scale 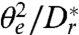. For high barriers 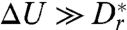[in practice, 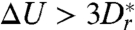often suffices, yielding 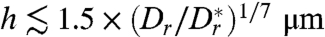], transition state theory (49) implies that the mean escape time is modified by an Arrhenius-Kramers factor, so that approximately

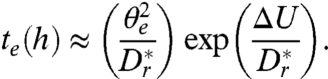[11]

Using the quadratic approximation for ΔU, and Eq. 10 to express 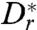in terms of h_e, we find that t_e ∝ exp(h_e/h)⁷. This dramatic scaling arises from the fact that the dipole model overestimates the flow field close to the bacterium but generally hints at the possibility of a strong, hydrodynamically induced increase of t_e when the cells get closer to the surface. We may also evaluate Eq. 11 at a height h = 1.5 μm, where both the Arrhenius–Kramers factor and the approximation θ_e(h) ≪ 1 are valid, to give

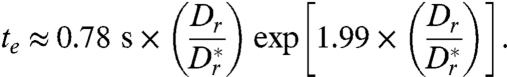[12]

The latter estimate suggests that hydrodynamic effects can possibly explain the experimentally observed long residence times near a wall, even for values of 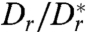that are only moderately larger than 1. It is, however, important to note that this expression for t_e presents an upper bound, because the dipole model overestimates the actual flow field at distances < 6 μm from the bacterium (Fig. 1H), even though the model still correctly captures the flow topology.

The considerations above show that hydrodynamics is negligible if a bacterium is more than a body length away from the wall but that hydrodynamic effects may contribute to the experimentally observed long residence times of bacteria close to no-slip surfaces. A more detailed understanding of the escape problem remains an important future challenge, requiring new methods for measuring 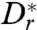and further theoretical studies of the near-field interactions between bacteria, their flagella, and surfaces. However, even if a more accurate description of the hydrodynamics should become available in the future, one can still expect the mean escape time to follow an Arrhenius–Kramers law (as in Eq. 11) with a suitably adapted effective potential U and additional prefactors that account for the curvature at the potential barrier (49).

Conclusions

We have presented direct measurements of the flow field generated by individual freely swimming bacteria, both in bulk fluid and close to a solid surface. For distances ≳6 μm, the experimentally measured flow field is well-approximated by a force dipole model; at smaller distances the dipole model overestimates the flow. Generally, the flow field of E. coli differs markedly from those created by higher microorganisms, such as Chlamydomonas (37, 38) and Volvox (37). With regard to the future classification of flow fields of microorganisms, a decomposition in terms of vector spherical harmonics can provide a useful systematic framework, similar to the classification of the electronic orbital structures in atoms or molecules.

Theories of collective behavior in bacterial suspensions identify as a fundamental process the pairwise interaction of bacteria, often assumed to be dominated by long-range fluid flows established by the action of swimming (25). Our analysis suggests that noise, due to orientational Brownian motion and intrinsic swimming stochasticity, drowns out hydrodynamic effects between two bacteria beyond a surprisingly small length scale of a few microns. This implies that hydrodynamic effects will be relevant only in sufficiently dense bacterial suspensions. However, under such conditions, the flow structure close to the bacterial body and contact interactions (e.g., flagellar bundling, steric repulsion) will be more important than the asymptotic long-range details of individual microswimmer flow fields.

Insights into the biochemical and physical interactions between bacteria and surfaces are crucial for understanding the dynamics of biofilm formation, the emergence of collective bacterial behavior in boundary layers, and, thus, more generally the evolution from unicellular to multicellular, cooperative forms of life. Our results suggest that long-range hydrodynamic effects play a negligible role in the scattering of E. coli with surfaces before collisions. However, hydrodynamic effects can, at least partially, account for the observed trapping of bacteria within a few microns of the surface. The analysis presented herein lends support to the hypothesis (51) that turbulent swarming patterns in bacterial films arise primarily due to steric repulsion and other near-field interactions.

Our experimental and theoretical results favor collision-dominated models (28–30) for the accumulation of bacteria at surfaces over models based on long-range hydrodynamics (27). To obtain a more complete dynamical picture of biofilm formation, future efforts should focus on developing more precise measurement methods and advanced models that include lubrication effects and biochemical bacteria–surface interactions. While our combination of measurements, simulations, and theory shows that long-range physical interactions are negligible for bacterial cell–surface scattering, fluid-mediated coupling could become important for organisms swimming against or in contact with a surface, because the organism is then no longer force-free, resulting in a substantially longer range of hydrodynamic interactions (47, 52).

However, the main implication of the present study is that short-range forces and noise are likely to dominate the interactions between swimming bacteria, so that collective motion in bacterial suspensions, thin films (4, 53), and thin wetting layers (54) relates closely to that seen in driven granular systems (55), assemblages of biofilaments (56), and animal flocks (57, 58). This suggests that many of the principles that determine flocking and self-organization in higher animals should also govern the collective motion of the smallest organisms.

Materials and Methods

A detailed description of the mathematical models is provided in the SI Text. The experiments are summarized below.

Culture Conditions.

We used E. coli strain HCB437 carrying the plasmid pEGFP (Clontech, BD Biosciences), kindly supplied by Douglas B. Weibel (University of Wisconsin-Madison) and Howard C. Berg (Harvard University). Cells were streaked on 1.5% agar plates containing T-broth (1% tryptone, 0.5% NaCl) and 100 μg/mL ampicillin. A single-colony isolate from an overnight plate was used to innoculate 10 mL of T-broth containing ampicillin and 0.1 mM isopropyl β-D-1-thiogalactopyranoside (IPTG, Sigma), which was then grown for 7 h on a rotary shaker (200 rpm) at 33 °C. This culture was diluted 1∶1 with fresh T-broth containing ampicillin and IPTG as above, 0.2% bovine serum albumin, and 0.2 μm fluorescent microspheres (505/515, F8811, Invitrogen) at concentration 9 × 10⁹ beads/mL. This bacterial suspension (approximately 1.6 × 10⁷ cells/mL) was loaded into a polydimethylsiloxane (PDMS) microfluidic device consisting of cylindrical measurement chambers (height 100 μm, radius 750 μm) connected by thin channels. After filling the device, it was sealed to reduce background fluid motion.

Measurement of the Flow Field.

Using a Zeiss Axiovert inverted microscope with a 40× oil objective (NA 1.3), we simultaneously imaged bacteria and microspheres under fluorescence conditions at 40 fps (Pike, Allied Vision Technologies) and at a temperature of 24 ± 1 °C. To measure the flow field far from walls, we focused on a plane 50 μm inside the chamber to minimize surface effects. To measure the flow field close to a no-slip surface, we focused on a plane 2 μm below the top surface of the sample chamber. Each movie was analyzed with custom Matlab software that precisely tracked bacteria by fitting an ellipsoidal two-dimensional Gaussian shape. For each cell swimming along the focal plane for > 1.5 s, we collected the instantaneous velocity of all fluorescent tracers up to a distance of 75 μm, using standard particle tracking algorithms. The resulting approximately 5 × 10⁹ tracer velocity vectors were binned into a 0.63 μm square grid (shown in Fig. 1 A and E). The mean of the well-resolved Gaussian distribution in each bin was taken as a local measure of the flow field. To measure the mean residence time of bacteria near a surface, we used the movies that were recorded for measuring the flow field near the wall.

Measurement of the Rotational Diffusion.

From the tracks of E. coli that swam in the focal plane for > 1.5 s, at a distance of 50 μm from the top and bottom surfaces, we determined an average swimming direction at time t by using the direction between the bacterial positions at t - 0.05 s and t + 0.05 s. Computing the change in average swimming direction Δϕ revealed diffusive scaling, so that we obtained D_r from the equation for two-dimensional orientational diffusion, 〈|Δϕ|²〉 = 2D_rΔt, over a time interval Δt. We measured D_r for Chlamydomonas with the same procedure, using cell-tracking data described earlier (37).