Microscopic events in β-hairpin folding from alternative unfolded ensembles

Abstract

We have performed the first unbiased folding simulations of the GB1 hairpin in explicit solvent, using hundreds of microsecond-long molecular dynamics simulations (total time: 0.7 ms). Our simulations are initiated from two sets of structures. Starting from an equilibrium unfolded state, we obtain single-exponential folding kinetics with rate coefficients in good agreement (T = 350 K) or within an order of magnitude (T = 300 K) of the experimental values. However, simulations initiated from unfolded configurations lacking secondary structure result in biexponential kinetics with an additional fast nanosecond kinetic mode. This mode can strongly bias the folding rate estimated from the mean first passage time, when the trials are much shorter than the folding time. We find that the mechanism of the hairpin folding is insensitive to the details of the initial unfolded ensemble and is initiated by correct formation of the turn of the hairpin, followed by the formation of the native hydrogen bonds and hydrophobic contacts, consistent with experimental ϕ-value analysis. Subsequent native interactions can be formed either from the turn or from the hairpin termini, helping to explain an apparent discrepancy in experimental results. From our simulations, we also obtain the transition path durations, a critical parameter for single molecule experiments aiming to resolve events along folding pathways. The lengths of transition paths span a wide range, from 50 ps to 140 ns, at 300 K.

A large body of both experimental and theoretical work on protein folding has led to a consensus view of the principles by which protein sequences fold efficiently. Energy landscape theory provides a basis for understanding how proteins fold fast (e.g., based on a “funneled” landscape), as well as providing coarse predictions of folding mechanism and rate (1–7). Experiments have shown that many small proteins fold in a highly cooperative, often two-state fashion (8). These studies have provided insights into the regions of structure that are formed in the folding transition state (9, 10) and are consistent with landscape theory predictions (11).

Elucidating the microscopic pathways by which proteins fold, at atomic resolution, remains a major challenge, requiring accurate atomistic simulations as well as experiments with high spatial and time resolution. Two directions are especially promising: single molecule experiments that can be compared directly with simulation without the need for ensemble averaging (12); and the folding of miniproteins, which are amenable to computer simulation and can be studied by ultrafast kinetics experiments (13, 14). Fast-folding proteins may also provide insights into the nature of the folding energy landscape (15–17).

The GB1 hairpin (18), the C-terminal β-hairpin of protein G (19), is the prototypical example of an autonomously folding β-hairpin with a folding time of 6 μs at 300 K (20), consistent with theoretical predictions (21). Despite its small size, it has many of the features of a real protein, such as two-state folding thermodynamics and kinetics, backbone hydrogen bonding, and a hydrophobic cluster (22–27), making it ideal for comparison with simulation. The mechanism of folding of the hairpin has been controversial: Mutation studies by Gai and co-workers (25) showed that strengthening hydrophobic interactions stabilizes the hairpin primarily by reducing the unfolding rate; similarly, ϕ-values (9) for the related Trpzip4 hairpin are near zero for hydrophobic mutations, but ϕ = 0.77 for a mutation in the turn (27). These results together with the Ising-like model used to interpret the original experiments (20, 22) support a “zipper” mechanism where native hydrogen bonds and hydrophobic contacts form sequentially starting at the turn. However, Andersen and co-workers found that mutations introducing charges at the termini affect the folding rate, suggesting a role for terminal interactions in the transition state (26). The hairpin has also been the subject of many simulation studies (28–52), which tend to give a greater importance to “hydrophobic collapse” over turn formation and hydrogen bonding as a key event in the folding mechanism, although the conclusions vary widely. In none of these studies was the GB1 hairpin folded in unbiased equilibrium simulations in explicit solvent, as it is usually necessary to use enhanced sampling methods such as replica exchange molecular dynamics (REMD) (53) to sample folding events. These biased simulations provide the correct equilibrium distribution, but indirect methods are usually needed to obtain reaction mechanism and kinetics (54).

Long time scale all-atom folding simulations, while computationally expensive, enable the mechanism to be identified unequivocally (55). However, in these unbiased simulations, the starting configurations are often not obtained from an equilibrium ensemble—determining this ensemble is in itself a demanding task. Implicit in the use of nonequilibrium initial conditions is the assumption that equilibration of unfolded configurations is fast relative to the folding time, yet recent experimental and computational studies have suggested several exceptions to this description of the unfolded state (56, 57). Therefore it is important to test the possible effects of using different initial conditions on the folding kinetics and mechanism (58, 59).

We perform long all-atom molecular dynamics simulations of GB1 hairpin folding in explicit solvent to determine the folding mechanism, and folding rate as a function of initial unfolded structures and temperature. Starting folding trajectories from an equilibrium distribution in the unfolded state results in exponential kinetics, as expected, and the estimated folding time is either in good agreement (T = 350 K) or within an order of magnitude of experiment (T = 300 K). However, when a further condition of low helix content is placed on the initial configurations, we obtain biexponential kinetics, with an additional nanosecond phase, reminiscent of a “kinetic partitioning” mechanism (60). Although the total amplitude of this phase is small, it strongly biases the results when the duration of the simulations is short relative to the folding time, leading to a much smaller estimate of the mean first passage time for folding. Nonetheless, we find that the folding mechanism itself is independent of the starting unfolded structures and the folding is always initiated by correct turn formation and native hydrogen bond formation precedes or coincides with that of the hydrophobic cluster.

Results

Initial Conditions.

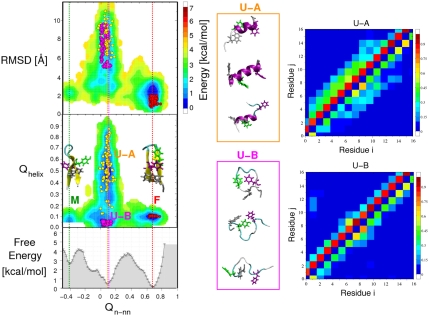
We use a well-equilibrated distribution of the unfolded state determined from 16 μs REMD simulations (51) in order to initialize our folding runs. We obtain a fraction folded of approximately 0.6 at 300 K with the force field used (Amber ff03* with TIP3P water), close to the experimental estimate of approximately 0.45. Free energy surfaces for the hairpin are shown at 303 K projected onto pairs of coordinates in Fig. 1. The chosen global progress coordinate Q_n-nn was based on the fraction of native contacts (see SI Appendix), modified to separate a native-like off-pathway intermediate in which one strand of the hairpin is “flipped” (51): This intermediate is visible at Q_n-nn ≈ -0.45, with the native state at Q_n-nn ≈ 0.7 and most unfolded states near Q_n-nn ≈ 0.1. Fig. 1 shows that this coordinate clearly separates native from nonnative states, in contrast to the frequently used radius of gyration or backbone root-mean-square deviation from the native state, which is found to be approximately 2 Å for the misfolded state. The apparent folding barrier is approximately 3.5 kcal/mol, higher than the 0.5–1.0 kcal/mol from previous projections onto other coordinates (28, 33, 34, 45); the only coordinate showing a comparable free energy barrier was the sum of hydrogen bond distances (44). We chose three sets of initial conditions: an equilibrium folded ensemble “F,” an equilibrium unfolded ensemble “U-A,” and a second equilibrium unfolded ensemble subject to the additional constraint of low helicity “U-B,” illustrated in Fig. 1 (definitions in Simulation Methods). As shown by the representative snapshots and contact maps in Fig. 1, U-A contains a significant number of nonnative helical contacts, whereas U-B is mostly coil-like.

Fig. 1.

Initial conditions for folding/unfolding simulations. Free energy surfaces for the GB1 hairpin at 303 K are shown as a function of global fraction of native contacts Q_n-nn and (Top Left) backbone rms distance (RMSD) from the folded state or (Middle Left) fraction of helical contacts (Q_helix); (Lower Left) the one-dimensional free energy F(Q_n-nn). The structures of the native F (Q_n-nn ≈ 0.7) and misfolded M (Q_n-nn ≈ -0.4) states are shown (Middle Left). Three initial conditions are superimposed (circles): folded F (red), equilibrium unfolded U-A (gold), and equilibrium unfolded with no helix U-B (magenta). (Middle) Structures representative of the unfolded initial conditions for U-A (Top) and U-B (Bottom). (Right) Average contact maps for U-A and U-B, with backbone/sidechain contacts (i.e., a backbone/side-chain atom each from residues i, j within 4.5 Å) shown above/below the diagonal.

Folding Trajectories.

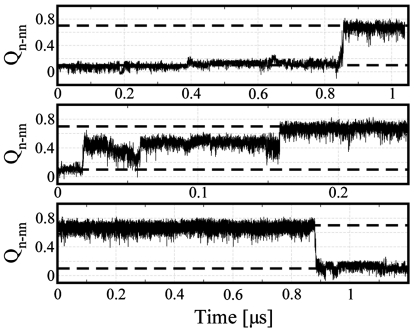
We initiated several sets of long trajectories from each set of initial conditions, with the length of each between 0.25 and 1.5 μs, as detailed in Simulation Methods. Different sets initialized from the same initial configurations used a different random seed for initial velocities. We monitor folding using the coordinate Q_n-nn, with the criteria for folding and unfolding being Q_n-nn > 0.7 and Q_n-nn < 0.1, respectively. Most of the trajectories do not result in folding or unfolding events, as expected from the experimental folding time of 6 μs (approximately equal to the unfolding time at 300 K). In Fig. 2, we plot Q_n-nn(t) for a few representative trajectories that do fold or unfold. Sharp, cooperative transitions between the unfolded and folded states (Fig. 2, Top and Bottom), as well as extended transitions with a transient intermediate (Middle), are observed. In some of the 350-K runs, we also observe unfolding events after folding, as the folding midpoint is 316 K in this force field (51).

Fig. 2.

Folding trajectories. Two representative folding trajectories and one unfolding trajectory at 300 K, projected onto the global coordinate Q_n-nn. Broken horizontal lines indicate the definitions of the folded and the unfolded states for identifying transition paths.

Folding Kinetics.

Folding simulations at 300 K initiated from the equilibrium unfolded distribution, U-A (sets 1–3), resulted in few folding events (5 in a total of 300 μs of simulation time). The resulting maximum likelihood estimate of mean first passage time (MFPT) 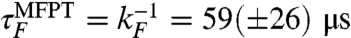is within an order of magnitude of the experimental folding time of approximately 7.5 μs (Table 1). Similarly, only one unfolding trajectory was observed in 50 unfolding simulations, each 1.5 μs long, implying an unfolding time within an order of magnitude of the experimental value of approximately 6.2 μs. To investigate the influence of nonnative secondary structure in the equilibrium unfolded state, we also started folding simulations at 300 K from an alternate unfolded ensemble, U-B, lacking secondary structure (sets 7–9) and observed nine folding events in a total of 75 μs of simulation time. The folding time in this case is 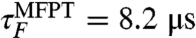, apparently in very good agreement with experiment, 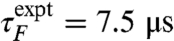. We have also estimated folding times at 325 and 350 K by a similar protocol (Table 1). Although the experimental folding rate is almost temperature-invariant, the folding rate in simulations varies by a factor of approximately 10 for the U-A initial conditions and approximately 2 for U-B between 300 and 350 K. The unfolding time is 3.1 μs at 350 K, compared with an experimental value of approximately 0.5 μs.

Table 1.

Folding and unfolding times (μs) and stabilities (kcal/mol) from simulation and experiment

Param.	Source	300 K		325 K		350 K
τF	expt	7.5		6.5		6.3
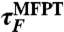	sim:U-A	59.0	(26.0)	12.4	(12.0)	5.3	(1.0)
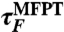	sim:U-B	8.2	(3.0)	4.8	(2.0)	4.6	(1.0)
τF,1	sim:U-B	29.2	(8.0)	—		6.3	(1.0)
τF,2	sim:U-B	0.08	(0.1)	—		0.01	(0.02)
A1	sim:U-B	0.977	(0.005)	—		0.974	(0.004)
τU	expt	6.2		1.3		0.4
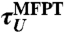	sim:F	25.0	(14.4)	—		3.1	(1.1)
ΔGUF	expt	−0.11		−1.07		−1.95
ΔGUF	sim:τF/τU	−0.52	(0.44)	—		−0.48	(0.55)
ΔGUF	sim:REMD	0.28	(0.43)	—		−0.66	(0.56)

U-A and U-B refer to the initial conditions for folding time calculations; stabilities are calculated either from REMD simulations (51) or the ratio of folding times from U-A. Folding/unfolding times are estimated by maximum likelihood from first passage times, either by assuming single-exponential (τ^MFPT) or double-exponential kinetics p(t) = A₁ exp(-t/τ_F,1) + (1 - A₁) exp(-t/τ_F,2) (see SI Appendix).

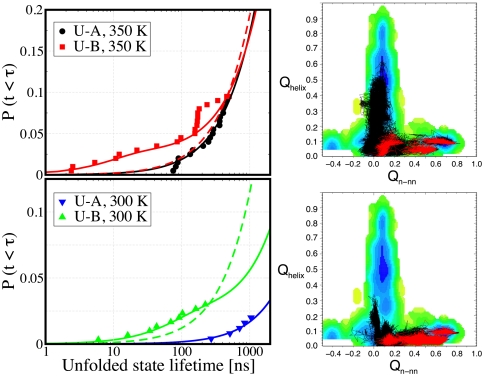
To understand the strong dependence of folding times on initial conditions, we have calculated the cumulative distribution of first passage times at 300 and 350 K as shown in Fig. 3. We find that the distribution is single-exponential for folding simulations starting from U-A at both temperatures but, surprisingly, requires a double-exponential fit for U-B (SI Appendix). The slow and dominant mode from the U-B-initiated simulations occurs on the same time scale, within uncertainties, as the one initiated from U-A. The additional nanosecond kinetic phase arises from a competition between direct folding and rapid formation of nonnative helical states (see SI Appendix, Fig. S6). Because the latter process is much faster, the fraction of trajectories that fold by the direct route is small. In Fig. 3 we present examples showing how fast-folding (red) trajectories reach the native state directly, whereas slow-folding (black) trajectories first form stable nonnative contacts. The reason that the fast phase, despite its small overall amplitude, dominates the cumulative distribution shown in Fig. 3 is the short duration of the trajectories. On a longer time scale the contribution from the fast phase would be much less important. In SI Appendix we present a simple kinetic scheme that explains the observed rates and amplitudes without the need to fit any new parameters.

Fig. 3.

Folding kinetics. (Left) The cumulative distribution of unfolded state lifetimes, defined as the time before the peptide makes a transition to the folded state, are shown by symbols (see legend). The solid lines are the distributions arising from single- and double-exponential fits of the data, for starting initial conditions U-A and U-B, respectively. The dashed line is a single-exponential distribution fit to the simulations data for initial condition U-B. (Right) Typical examples of fast (red) and slow (black) folding trajectories are shown superimposed on the free energy surface.

Transition Path Durations.

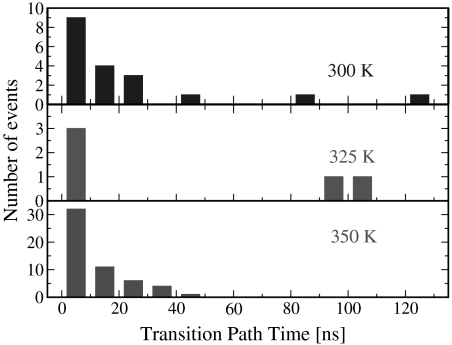
A very useful piece of information accessible from these simulations is the duration of the transition paths, defined here as the minimal segments of a trajectory that cross between Q_n-nn = 0.1 and Q_n-nn = 0.7. For an ideal two-state system that can be represented by a one-dimensional potential with two stable minima separated by a barrier, this quantity is predicted from theory (61, 62) and simulation (63) to be much smaller than the first passage time for crossing the barrier from one state to the other. Moreover, the success of methods such as transition path sampling to generate reaction paths within reasonable time depends on this transition path time being short for transitions between chosen pairs of metastable states (64). This is also a parameter of great interest to single molecule experimentalists, because it defines the necessary sampling frequency to resolve events along transition paths (62): The ability to monitor such transitions directly is a unique property of single molecule techniques. The transition path durations plotted in Fig. 4 span a range from tens of picoseconds to 140 ns, with an average of 22.5 ns at 300 K and 17 ns at 350 K. A comparison of average TP times from simulation with predictions from a theory by Szabo (62), approximately 71 ns at 300 K and 31 ns at 350 K, is in reasonable agreement (further details in SI Appendix).

Fig. 4.

Transition path durations. The distribution of times taken for trajectories to cross between Q_n-nn = 0.1 and Q_n-nn = 0.7, compiled from folding and unfolding trajectories at 300, 325, and 350 K. Additionally, we observe one transition path time of 245 ns for a 350-K trajectory.

Folding Mechanism.

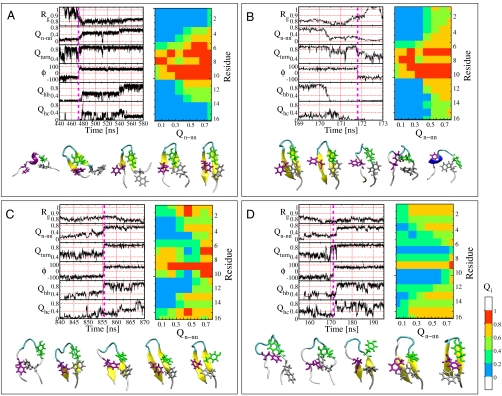
We analyze folding mechanism by following several order parameters, specifically, the fraction of contacts in the turn (residues DATK), Q_turn, the fraction of seven native hydrogen bonds, Q_hb, defined based on a 0.25-nm donor H-acceptor distance cutoff, the fraction of contacts, Q_hc, between hydrophobic side chains (residues WYFV), radius of gyration, R_g, and the backbone dihedral angle ϕ for residue Lys 10. These order parameters are plotted for four trajectories starting from folded and unfolded states at 300 K in Fig. 5.

Fig. 5.

Folding mechanism. (A–D) Four representative folding/unfolding trajectories at 300 K have been projected onto a set of six progress variables: (i) Radius of gyration R_g, (ii) the global coordinate Q_n-nn, (iii) the fraction of native contacts in the turn DATK, (iv) the ϕ-torsion angle of Lys 10, (v) the fraction of native hydrogen bonds Q_hb, and (vi) the fraction of hydrophobic side-chain contacts Q_hc. The vertical magenta line indicates the time at which the ϕ-torsion angle of residue 10 changes, a key event in the folding mechanism. For each trajectory, a sequence of configurations along the transition path is shown below to illustrate the folding mechanism. On the right of each panel is the corresponding ACF matrix (see text).

Although the spacing of events along the folding pathway is often close in time with respect to folding times, the relevant time scale for events in the folding mechanism is set by the length of the transition paths connecting unfolded and folded states. Careful examination of these transition paths reveals that the turn contacts are formed first during folding and are broken last during unfolding events; the importance of correct turn formation has been recognized in previous theoretical studies on the src-SH3 domain (65). The folding and unfolding events are almost exclusively concomitant with a switch in Lys 10 backbone ϕ dihedral angle. This suggests that a key event in the hairpin folding is the formation of the correct backbone dihedral for this particular residue (indicated by magenta vertical line in Fig. 5), which is in the α_L basin in the native state. This is consistent with the importance of stable turn formation established in studies on a variety of engineered β-hairpin systems (66). Interestingly, the hydrophobic contacts show quite significant fluctuations, and we find a weak correlation between Q_hc and folding/unfolding transitions, although on average more hydrophobic contacts are formed in the folded state (SI Appendix, Fig. S7).

We obtain a statistical description of the folding pathways using average contact formation (ACF) matrices, in which the average number of native contacts formed by each residue is given as a function of the global order parameter Q_n-nn, discretized into bins of width 0.1 (Fig. 5) (67). We find many cases in which the native contact formation starts from the turn toward the termini, in a zipper mechanism (Fig. 5 A and B). However, an alternative “pincer” mechanism involves formation of native contacts from the termini back toward the turn (Fig. 5 C and D); note that correct turn formation is always the initial step. By clustering the trajectories using the Euclidean distance between ACF matrices, we obtain two predominant clusters corresponding to these two mechanisms. It appears that the termini-first cluster is favored at low temperature (13 events vs. 6 for turn-first), whereas the turn-first cluster is more frequent at high temperature (37 events vs. 21 for termini-first). This is consistent with the expectation that sequence-local interactions will be more important at high temperature. A complete set of ACF matrices can be found in SI Appendix.

Concluding Remarks

We have obtained a significant number of folding events in serial folding simulations of the GB1 hairpin. By analyzing the order of events along folding paths, we find that hairpin formation is initiated at the turn, followed by the formation of native hydrogen bonds and hydrophobic contacts. Many simulation results have suggested a collapsed intermediate (“H” state) in which the hydrophobic cluster is partially formed (28, 29, 33, 34, 36–38, 43, 44). However, this was inferred either from an analysis of free energy projections onto various progress variables (28, 33, 34, 43), which can be misleading for imperfect coordinates (41, 68) or from high temperature unfolding trajectories (29, 37, 44). We would interpret such collapsed states to be the predominant unfolded state (relative to extended conformations), rather than a folding intermediate, because there is a large free energy barrier between these states and the folded conformation, when projected onto the Q_n-nn coordinate, a conclusion that is supported by experiment (27). Although there is a clear order of contact formation in any given folding event, folding itself is cooperative, with formation of all the contacts usually occurring in a single, concerted transition without stable intermediates—a conclusion that had been reached by some other previous studies (34, 35, 40). Our proposed folding mechanism is consistent with the one derived from the Ising-like model (20, 22) as well as with the results of Φ-value studies on the hairpin (25, 27). In addition, our finding that there are two classes of folding mechanism may explain the apparently contradictory findings from Gai and co-workers (25, 27) and Andersen and co-workers (26) that the turn or the termini, respectively, are structured in the transition state.

We estimate that transition path durations are up to the order of 100 ns. Although still too short to resolve in current single molecule experiments, this value suggests that, for larger proteins, with appropriately chosen experimental conditions, a transition path time on the microsecond time scale may be achievable.

A remarkable finding of our study is the dependence of the folding time on the initial conditions, with unstructured initial conditions giving an estimated mean first passage folding time that is too fast relative to starting from an equilibrium unfolded state. This underestimation highlights the importance of initial conditions when estimating folding times from short simulations (58, 59). Initializing from only extended structures (55) might therefore be expected to give a folding time that is too fast (for a given force field), because the protein is then more likely to fold quickly than if it were stabilized by nonnative interactions (58, 59). The slowing of folding due to nonnative interactions present in the equilibrium unfolded state demonstrates the important role that these can play in the overall folding dynamics. Several recent studies have also suggested that nonnative structure in the unfolded state may play an important role in folding dynamics (69, 70), yet the experimental evidence so far is ambiguous. Therefore, quantitative studies of the unfolded state, integrating both experiment and simulation, will be vital to ensure the accuracy of future protein folding simulations. In future work, we also plan to address the question of how mutations may affect the folding rate and the partitioning between the two observed folding pathways.

Simulation Methods

The Amber ff03* force field [Amber ff03 (71) with a modified Ψ-torsion potential (72)] was used to represent the protein [as this force field was recently shown to alleviate known biases toward a particular type of secondary structure (73)] with the TIP3P model for water (74). The structure of the 16 residue GB1 hairpin was taken from residues 41–56 of the full-length GB1 protein (PDB ID code 1GB1), and solvated in a truncated octahedron simulation cell with 3.5 nm between the nearest faces, containing 984 water molecules, 6 sodium ions, and 3 chloride ions to neutralize the charge. The termini of both peptides were unblocked as in the experiments (20). Molecular dynamics simulations were performed at constant volume with long-range electrostatics calculated using PME with a 1.2-Å grid spacing and 9-Å cutoff. The system was propagated using Langevin dynamics with a friction of 1 ps^-1 for the durations listed in Table 2. The initial conditions are drawn from the equilibrium distribution at 303 K subject to the constraints U-A: Q < 0.2, RMSD > 5 Å; U-B: Q < 0.2, RMSD > 5 Å, Q_h < 0.1; F: Q > 0.7, RMSD < 2 Å.

Table 2.

Sets of folding trajectories

Set	Initial	Temp K	# Traj	Length μs	Folding events	Unfolding events
1	U-A	300	50	1.50	1	0
2	U-A	300	100	1.25	3	0
3	U-A	300	100	1.00	1	0
4	U-A	325	50	0.25	1	0
5	U-A	350	100	0.50	12	0
6	U-A	350	100	0.50	6	3
7	U-B	300	100	0.25	3	0
8	U-B	300	100	0.25	3	0
9	U-B	300	100	0.25	3	0
10	U-B	325	100	0.25	5	0
11	U-B	350	100	0.50	9	2
12	U-B	350	100	0.50	11	2
13	F	300	50	1.50	2	3
14	F	350	100	0.25	2	8