Approximate Methods for State-Space Models

Abstract

State-space models provide an important body of techniques for analyzing time-series, but their use requires estimating unobserved states. The optimal estimate of the state is its conditional expectation given the observation histories, and computing this expectation is hard when there are nonlinearities. Existing filtering methods, including sequential Monte Carlo, tend to be either inaccurate or slow. In this paper, we study a nonlinear filter for nonlinear/non-Gaussian state-space models, which uses Laplace’s method, an asymptotic series expansion, to approximate the state’s conditional mean and variance, together with a Gaussian conditional distribution. This Laplace-Gaussian filter (LGF) gives fast, recursive, deterministic state estimates, with an error which is set by the stochastic characteristics of the model and is, we show, stable over time. We illustrate the estimation ability of the LGF by applying it to the problem of neural decoding and compare it to sequential Monte Carlo both in simulations and with real data. We find that the LGF can deliver superior results in a small fraction of the computing time.

1 Introduction

The central statistical problem in applying state-space models is that of filtering, i.e., estimating the unobserved state from the observations. For nonlinear or non-Gaussian models, considerable effort has been devoted to devising approximate solutions to the filtering problem, based mainly on simulation methods such as particle filtering and its variants (Kitagawa 1987; Kitagawa 1996; Doucet, de Freitas and Gordon 2001). In this article we study a deterministic approximation based on sequential application of Laplace’s method which we call the Laplace Gaussian filter (LGF), and we illustrate the approach in the context of real-time neural decoding (Brockwell, Schwartz and Kass 2007; Eden, Frank, Barbieri, Solo and Brown 2004; Serruya, Hatsopoulos, Paninski, Fellows and Donoghue 2002). In this context we find the LGF to be far more accurate, for equivalent computational cost, than particle filtering.

Suppose we have a stochastic state process {x_t}, t = 1, 2, … and a related observation process {y_t}. Filtering consists of estimating the state x_t given a sequence of observations y₁, y₂, … y_t ≡ y_1:t, i.e., finding the posterior distribution p(x_t|y_1:t) of the state, given the sequence. It is common to assume that the state x_t is a first-order homogeneous Markov process, with initial density p(x₁) and transition density p(x_t+1|x_t), and that y_t is independent of states and observations at all other times given x_t, with observation density p(y_t|x_t). Bayes’s Rule gives a recursive filtering formula,

$$p(x_t|y_{1:t})=\frac{p(y_t|x_t)p(x_t|y_{1:t-1})}{{\displaystyle \int }p(y_t|x_t)p(x_t|y_{1:t-1}){\mathit{\text{dx}}}_t},$$ (1)

where

$$p(x_t|y_{1:t-1})={\displaystyle \int }p(x_t|x_{t-1})p(x_{t-1}|y_{1:t-1}){\mathit{\text{dx}}}_{t-1}$$ (2)

is the predictive distribution, which convolves the previous filtered distribution with the transition density. In principle, Equations (1) and (2) give a complete, recursive solution to the filtering problem for state-space models: the mean-squared optimal point estimate is simply the mean of the posterior density given by Equation (1). When the dynamics are nonlinear, non-Gaussian, or even just high-dimensional, however, computing these estimates sequentially can be a major challenge.

One approach to Bayesian computation is to attempt to simulate from the posterior distribution. Applying Monte Carlo simulation to Equations (1)–(2) would let us draw from p(x_t|y_1:t), if we had p(x_t|y_1:t−1). The insight of particle filtering is that the latter distribution can itself be approximated by Monte Carlo simulation (Kitagawa 1996; Doucet et al. 2001). This turns the recursive equations for the filtering distribution into a stochastic dynamical system of interacting particles (Del Moral and Miclo 2000), each representing one draw from that posterior. While particle filtering has proven itself to be useful in practice (Doucet et al. 2001; Brockwell, Rojas and Kass 2004; Ergün, Barbieri, Eden, Wilson and Brown 2007), like any Monte Carlo scheme it can be computationally costly; moreover, the number of particles (and so the amount of computation) needed for a given accuracy grows rapidly with the dimensionality of the state-space. For real-time processing, such as neural decoding, the computational cost of effective particle filtering can quickly become prohibitive.

The primary difficulty with the nonlinear filtering equations comes from their integrals. We use Laplace’s method to obtain estimates of the mean and variance of the posterior density in Eq. (1), and then approximate that density by a Gaussian with that mean and variance. This distribution is then recursively updated in its turn when the next observation is taken.

There are several versions of Laplace’s method, all of which replace integrals with series expansion around the maxima of integrands. An expansion parameter, γ, measures the concentration of the integrand about its peak. In the simplest version, the posterior distribution is replaced by a Gaussian centered at the posterior mode. Under mild regularity conditions, this gives a first-order approximation of posterior expectations, with error of order O(γ⁻¹). Several papers have applied some form of first-order Laplace approximation sequentially (Brown, Frank, Tang, Quirk and Wilson 1998; Eden et al. 2004). In the ordinary static context, Tierney, Kass and Kadane (1989) analyzed the way a refined procedure, the “fully exponential” Laplace approximation, gives a second-order approximation for posterior expectations, having an error of order O(γ⁻²). In this paper we provide theoretical results justifying these approximations in the sequential context. Because state estimation proceeds recursively over time, it is conceivable that the approximation error could accumulate, which would make the approach ineffective. Our results show that, under reasonable regularity conditions, this does not happen: the posterior mean from the LGF approximates the true posterior mean with error O(γ^−α) uniformly across time, where α = 1 or 2 depending on the order of the LGF.

We specify the LGF in Section 2, and give our theoretical results in Section 3. Section 4 introduces the neural decoding problem and reports comparative results both in simulation studies and with real data. We provide additional comments in Section 5. Proofs and implementation details are collected in the appendix.¹

2 The Laplace-Gaussian filter (LGF)

Throughout the paper, x_t|t and υ_t|t denote the mode and variance of the true filtered distribution at time t given a sequence of observations y_1:t, and similarly x_t|t−1 and υ_t|t−1 are those of the predictive distribution at time t given y_1:t−1, respectively. Hatsˆand tildes˜on variables indicate approximations; in particular, x̂ denotes the approximated posterior mode, and x̃ the approximated posterior mean. The transpose of a matrix A is written A^T. Bold type of a small letter indicates a column vector.

2.1 Algorithm

The LGF procedure for a one-dimensional state is as follows. (The multi-dimensional extension is straightforward; see below.)

1. At time t = 1, initialize the predictive distribution of the state, p(x₁).

2. Observe y_t.

3. (Filtering) Obtain the approximate posterior mean x̃_t|t and variance υ̃_t|t by Laplace’s method (see below), and set p̂(x_t|y_1:t) to be a Gaussian distribution with the same mean and variance.

4. (Prediction) Calculate the predictive distribution,

   $$\widehat{p}(x_{t+1}|y_{1:t})={\displaystyle \int }p(x_{t+1}|x_t)\widehat{p}(x_t|y_{1:t}){\mathit{\text{dx}}}_t.$$ (3)

5. Increment t and go to step 2.

We consider first- and second- order Laplace’s approximations. In the first-order Laplace approximation the posterior mean and variance are x̃_t|t = x̂_t|t ≡ argmax_xt l(x_t) and υ̃_t|t = [−l″(x̂_t|t)]⁻¹, where l(x_t) = log p(y_t|x_t)p̂(x_t|y_1:t−1).

The second-order (fully exponential) Laplace approximation is calculated as follows (Tierney et al. 1989). For a given positive function g of the state, let k(x_t) = log g(x_t)p(y_t|x_t)p̂(x_t|y_1:t−1), and let x̄_t|t maximize k. The posterior expectation of g for the second order approximation is then

$$\widehat{E}[g(x_t)|y_{1:t}]\approx \frac{{|-k″({\overline{x}}_{t|t})|}^{-\frac{1}{2}}\text{exp}[k({\overline{x}}_{t|t})]}{{|-l″({\widehat{x}}_{t|t})|}^{-\frac{1}{2}}\text{exp}[l({\widehat{x}}_{t|t})]}.$$ (4)

When the g we care about is not necessarily positive, a simple and practical trick is to add a large constant c to g so that g(x) + c > 0, apply Eq. (4), and then subtract c. The posterior mean is thus calculated as x̃_t|t = Ê[x_t + c] − c. (In practice it suffices that the probability of the event {g(x_t) + c > 0} is close to one under the true distribution of x_t. Allowing this to be merely very probable rather than almost sure introduces additional approximation error, which however can be made arbitrarily small simply by increasing the constant c. See Tierney et al. (1989) for details.) The posterior variance is set to be υ̃_t|t = [−l″(x̂_t|t)]⁻¹, as this suffices for second-order accuracy (see Remark 1 in Appendix A).

To use the LGF to estimate a state in d-dimensional space, one simply takes the function g to be each coordinate in turn, i.e., g(x_t) = x_t,i + c for each i = 1, 2, …, d. Each g is a function of ℝ^d → ℝ, and $|-l″({\widehat{x}}_{t|t}){|}^{-\frac{1}{2}}\text{ and }|-k″({\overline{x}}_{t|t}){|}^{-\frac{1}{2}}$ in Eq. (4) are replaced by the determinants of the Hessians of l(x̂_t|t) and k(x̄_t|t), respectively. Thus, estimating the state with the second-order LGF takes d times as long as using the first-order LGF, since posterior means of each component of x_t must be calculated separately.

In many applications the state process is taken to be a linear Gaussian process (such as an autoregression or random walk) so that the integral in Eq. (3) is analytic. When this integral is not done analytically, either the asymptotic expansion (23) or a numerical method may be employed. To apply our theoretical results, the numerical error in the integration must be O(γ^−α), where γ is the expansion parameter, to be discussed in section 3.1, and α = 1 or 2 depending on the order of the LGF.

2.2 Smoothing

The LGF can also be used for smoothing. That is, given the observation up to time T, y_1:T, smoothed state distributions, p(x_t|y_1:T), t ≤ T, can be calculated from filtered and predictive distributions by recursing backwards (Anderson and Moore 1979). Instead of the true filtered and predictive distributions, however, we now have the approximated filtered and predictive distributions computed by the LGF. By using these approximated distributions, the approximated smoothed distributions can be obtained as

$$\widehat{p}(x_t|y_{1:T})=\widehat{p}(x_t|y_{1:t}){\displaystyle \int }\frac{\widehat{p}(x_{t+1}|y_{1:T})p(x_{t+1}|x_t)}{\widehat{p}(x_{t+1}|y_{1:t})}{\mathit{\text{dx}}}_{t+1}.$$ (5)

We address the accuracy of LGF smoothing in Theorem 5.

2.3 Implementation

Two aspects of the numerical implementation of the LGF call for special comment: maximizing the likelihood and computing its second derivatives. One key point is that the Hessian in Eq. (4) may be computed by careful numerical differentiation. Avoiding analytical derivatives saves substantial time when fitting many alternative models. See Appendix B for a brief description of our numerical procedure for computing the Hessian matrix, and Kass (1987) for full details.

The log-likelihood function can be maximized by an iterative algorithm (e.g. Newton’s method), in which x̂_t|t−1 and x̂_t|t would be chosen as a reasonable starting point for maximizing l(x_t) and k(x_t), respectively. The convergence criterion also deserves some care. Writing x⁽ⁱ⁾ for the value attained on the i^th step of the iteration, the iteration should be stopped when ‖x⁽ⁱ⁺¹⁾ − x⁽ⁱ⁾‖ < cγ^−α, where c is a constant and γ is the expansion parameter, to be discussed in section 3.1, and α is the order of the Laplace approximation. The value of c should be smaller than that of γ (c = 1 is a reasonable choice in practice).

3 Theoretical Results

For simplicity, we state the results for the one dimensional case. The extension to the multi-dimensional case is notationally somewhat cumbersome but conceptually straightforward. Let p and p̂ denote the true density of a random variable and its approximation, and let h(x_t) be

$$h(x_t)=-\frac{1}{\mathrm{\gamma }}\text{log}p(y_t|x_t)p(x_t|y_{1:t-1}),$$ (6)

where γ is the expansion parameter, whose meaning will be explained later in this section.

3.1 Regularity conditions

The following properties are the regularity conditions that are sufficient for the validity of Laplace’s method (Erdélyi 1956; Kass, Tierney and Kadane 1990; Wojdylo 2006).

• (C.1) h(x_t) is a constant-order function of γ as γ → ∞, and is five-times differentiable with respect to x_t.

• (C.2) h(x_t) has an unique interior minimum, and its second derivative is positive (the Hessian matrix is positive definite for multi-dimensional cases)

• (C.3) p(x_t+1|x_t) is four-times differentiable with respect to x_t.

• (C.4) The integral

  $${\displaystyle }\int p(x_{t+1}|x_t)\text{ exp }[-\mathrm{\gamma }h(x_t)]{\mathit{\text{dx}}}_t$$

  exists and is finite.

We also assume the following condition which prohibits ill-behaved, “explosive” trajectories in state space:

• (C.5) Derivatives of h(x_t) up to fifth-order and those of p(x_t+1|x_t) with respect to x_t up to third-order are bounded uniformly across time.

Strictly speaking, h(x_t) is a random variable, taking values in the space of integrable non-negative functions of ℝ. This random variable is measurable with respect to σ(y_1:t). Therefore, the stated regularity conditions only need to hold with probability 1 under the distribution of y_1:t (Kass et al. 1990).

In the following section we will state the theorems that ensure that, under conditions (C.1)–(C.5), the LGF does not accumulate error over time, but first we explain the meaning of the expansion parameter.

Meaning of γ

As seen in Eq. (6) and the regularity condition (C.1), for a given state-space model, γ is constructed by combing the model parameters so that the log posterior density is scaled by γ as γ → ∞. In general, γ would be interpreted in terms of sample size, the concentration of the observation density, and the inverse of the noise in the state dynamics; we will describe how γ is chosen for a neural decoding model in section 4. From the construction of γ, the second derivative of the log posterior density, which determines the concentration of the posterior density, is also scaled by γ. Therefore, the larger γ is, the more precisely variables can be estimated, and the more accurate Laplace’s method becomes. When the concentration of the posterior density is not uniform across state-dimentions in a multidimensional case, a multidimensional γ could be taken. Without a loss of approximation accuracy, however, a simple implementation for this case is taking the largest γ as a single expansion parameter.

3.2 Main theoretical results

Theorem 1 (accuracy of predictive distributions) Under the regularity conditions (C.1)–(C.4), the α-order LGF approximates the predictive distribution as

$$\widehat{p}(x_t|y_{1:t-1})=p(x_t|y_{1:t-1})+O({\mathrm{\gamma }}^{-\beta }),$$

for t ∈ ℕ, where β = 1 for β = 1 and β = 2 for α ≥ 2. Furthermore, if condition (C.5) holds, the error term is bounded uniformly across time.

The error bound can also be established for the posterior (filtered) expectations in the following theorem.

Theorem 2 (accuracy of posterior expectations) Under the regularity conditions (C.1)–(C.4), the α-order LGF approximates the filtered conditional expectation of a four-times differentiable function g(x),

$$\widehat{E}[g(x_t)|y_{1:t}]=E[g(x_t)|y_{1:t}]+O({\mathrm{\gamma }}^{-\beta }),$$

for t ∈ ℕ, with β as in Theorem 1. Here E[· |y_1:t] and Ê[· |y_1:t] denote the expectation with respect to p(x_t|y_1:t) and p̂(x_t|y_1:t), respectively. Furthermore, if condition (C.5) holds, the error term is bounded uniformly across time.

Note that the order of the error is γ⁻² even for α ≥ 2 both in Theorem 1 and Theorem 2. That is, even if higher than the second-order Laplace approximation in Step 3 of the LGF is employed, the resulting approximation error does not go beyond the second-order accuracy with respect to γ⁻¹. This fact leads to the following corollary.

Corollary 3 The second-order approximation is the best achievable for the LGF scheme.

The following theorem refers to stability of the LGF. It states that minor differences in the initially-guessed distribution of the state tend to be reduced, rather than amplified, by conditioning on further observations, even under the Laplace’s approximation.

Theorem 4 (stability of the algorithm) Suppose that two approximated predictive distributions at time t satisfy

$${\widehat{p}}_1(x_t|y_{1:t-1})-{\widehat{p}}_2(x_t|y_{1:t-1})=O({\mathrm{\gamma }}^{-\nu }),$$

where ν > 0. Then, under the regularity conditions (C.1)–(C.4), applying the LGF u(> 0) times leads to the difference of two approximated predictive distributions at time t + u as

$${\widehat{p}}_1(x_{t+u}|y_{1:t+u-1})-{\widehat{p}}_2(x_{t+u}|y_{1:t+u-1})=O({\mathrm{\gamma }}^{-\nu -u}).$$

Theorem 5 Under the regularity conditions (C.1)–(C.4), the expectation of a four-times differentiable function g(x) with respect to the approximated smoothed distribution Eq. (5) is given by

$$\widehat{E}[g(x_t)|y_{1:T}]=E[g(x_t)|y_{1:T}]+O({\mathrm{\gamma }}^{-\beta }),$$

for t = 1, 2, …, T, with β as in Theorem 1. Furthermore, if condition (C.5) is satisfied, the error term is bounded uniformly across time.

3.3 Computational cost

Assuming that the maximization of l(x_t) and k(x_t) is done by Newton’s method, the time complexity of the LGF goes as follows. Let d be the number of dimensions of the state, T the number of time steps, and N be the sample size. The bottleneck of the computational cost in the first-order LGF comes from maximization of l(x_t) at each time t. In each iteration of Newton’s method, evaluation of the Hessian matrix of l(x_t) typically costs O(Nd²), as d² is the time complexity for matrix manipulation. Over T time steps, the time complexity of the first-order LGF is O(TNd²). In the second-order LGF, the time complexity of calculating the posterior expectation of each x_t,i is still O(Nd²), but calculating it for i = 1, …, d results in O(Nd³). Repeating over T time steps, the complexity of the second-order LGF is O(TNd³).

For comparison, take the time complexity of a particle filter (PF) with M particles. It is not hard to check that the computational cost across time step T of the particle filter is O(TMNd). For the computational cost of the particle filter to be comparable with an LGF, the number of particles should be M = O(d) for the first-order LGF and M = O(d²) for the second-order LGF.

4 Application to neural decoding

The problem of neural decoding consists in using an organism’s neural activity to draw inferences about the organism’s environment and its interaction therewith — sensory stimuli, bodily states, motor behaviors, etc. (Rieke, Warland, de Ruyter van Steveninck Rob and Bialek 1997). Scientifically, neural decoding is vital to studying neural information processing, as reflected by the many proposed decoding techniques (Dayan and Abbott 2001). Its engineering importance comes from efforts to design brain-machine interface devices, especially neural motor prostheses (Schwartz 2004) such as computer cursors, robotic arms, etc. The brain-machine interface devices must determine, from real-time neural recordings, what motion the user desires the prosthesis to have. Such considerations have led to many proposals, emanating from Brown et al. (1998), for neural decoding based on state-space models (Brockwell et al. 2007).

In the rest of this section, we introduce a standard model setup for neural decoding tasks, and identify its Laplace expansion γ. We then simulate the model and apply the LGF, confirming the applicability of our theoretical results, and comparing its performance to particle filtering. Finally, we apply the model and the LGF to experimental data.

4.1 Model setup

We consider the problem of decoding a “state process” from the firing of an ensemble of neurons. Here we suppose that neurons respond to a x_t ∈ ℝ^d, where d is the number of dimensions. x_t may be interpreted as two- or three-dimensional hand kinematics for motor cortical decoding (Georgopoulos, Schwartz and Kettner 1986; Ketter, Schwartz and Georgopoulos 1988; Paninski, Fellows, Hatsopoulos and Donoghue 2004), or hand posture (about 20 degrees of freedom) for dexterous grasping control (Artemiadis, Shakhnarovich, Vargas-Irwin, Donoghue and Black 2007). We consider N such neurons, and assume that the logarithm of the firing rate of neuron i is (Truccolo, Eden, Fellows, Donoghue and Brown 2005)

$$\text{log}{\mathrm{\lambda }}_i({\mathit{x}}_t)={\alpha }_i+{\mathit{\beta }}_i·{\mathit{x}}_t.$$ (7)

We let y_i,t be the spike count of neuron i at time-step t. We assume that y_i,t has a Poisson distribution with intensity λ_i(x_t)Δ, where Δ is the duration of the short time-intervals over which spikes are counted at each time step. We also assume that firing of neurons is conditionally independent with each other given x_t. Thus the probability distribution of y_t, the vector of all the y_i,t, is the product of the firing probabilities of each neuron. We assume that the state model is given by

$${\mathit{x}}_t={\mathit{\text{Fx}}}_{t-1}+{\mathit{\epsilon }}_t,$$ (8)

where F ∈ ℝ^d×d and ε_t is a d-dimensional Gaussian random variable with mean zero and covariance matrix W ∈ ℝ^d×d.

The expansion parameter γ for this model is identified as follows. The second derivative of l(x_t) = log p(y_t|x_t)p̂(x_t|y_1:t−1) is

$$l″({\mathit{x}}_t)=-\mathrm{\Delta }{\displaystyle \sum _{i=1}^N}{\mathit{\beta }}_i\text{exp}({\alpha }_i+{\mathit{\beta }}_i·{\mathit{x}}_t){\mathit{\beta }}_i^T-{\mathit{V}}_{t|t-1}^{-1},$$

where V_t|t−1 is the covariance matrix of the predictive distribution at time t. Then, from the Cauchy-Schwarz inequality,

$$\Vert l″({\mathit{x}}_t)\Vert \le \mathrm{\Delta }{\displaystyle \sum _{i=1}^N}\text{exp}({\alpha }_i+{\mathit{\beta }}_i·{\mathit{x}}_t){\Vert {\mathit{\beta }}_i\Vert }^2+\Vert {\mathit{V}}_{t|t-1}^{-1}\Vert .$$

Since $\Vert {\mathit{V}}_{t|t-1}^{-1}\Vert$ is scaled by ‖W⁻¹‖, we can identify the expansion parameter:

$$\mathrm{\gamma }=\mathrm{\Delta }{\displaystyle \sum _{i=1}^N}{e}^{{\alpha }_i}{\Vert {\mathit{\beta }}_i\Vert }^2+\Vert {\mathit{W}}^{-1}\Vert .$$ (9)

We see that γ combines the number and the mean firing rate of the neurons, the sharpness of neuronal tuning curves and the noise in the state dynamics.

Given our assumptions, the observation model p(y_t|x_t) and the state transition density p(x_t+1|x_t) are strictly log-concave and have an unique interior maximum in x_t, and their derivatives up to fifth-order are uniformly bounded if the state is bounded. Furthermore, h(x_t) is a constant-order function of γ as γ → ∞, which can be seen from the construction of γ. Thus, the regularity conditions (C.1)–(C.5) are satisfied if the initial distribution satisfies them.

In what follows, we took the initial value for filtering to be the true state at t = 0. Note that when there is no information about the initial distribution, we could use a “diffuse” prior density whose covariance is taken to be large (Durbin and Koopman 2001). Either type of initial condition would satisfy the regularity conditions. We can thus construct LGFs according to section 2.

4.2 Simulation study

We performed numerical simulations to study first and second-order LGF (labeled by LGF-1 and LGF-2, respectively) approximations under conditions relevant to the neural decoding problems we are working on. We also compared LGF to particle filtering. We judged performance by accuracy in computing the posterior mean (which was determined by particle filtering with a very large number of particles). However, the posterior mean contains statistical inaccuracy (due to limited data). We also evaluated the accuracy with which the several alternative methods approximate the underlying true state.

Simulation Setup

In each simulation run, we generated a state trajectory from a d-dimensional AR process, Eq. (8), with F = 0.94I and W = 0.019I, I being the identity matrix, over T = 30 time-steps of duration Δ = 0.03 seconds. We examined different number of state-dimensions, d = 6, 10, 20, 30. Regardless of d, we observed neural activity due to the state through N = 100 neurons, with α_i = 2.5 + 𝒩(0, 1) and β_i uniformly distributed on the unit sphere in ℝ^d. Finally, the spike counts were drawn from Poisson distributions with the firing rates λ_i(x_t) given by Eq. (7) above.

Methods

To compare LGF state estimates to the posterior mean we first needed a high-accuracy evaluation of the posterior mean itself. We obtained this by averaging results from ten independent realizations of particle filtering with 10⁶ particles; the resulting approximation error in the mean integrated squared error (MISE) is O(10⁻⁷), and so negligible for our purposes. We also applied the particle filter (PF) for comparison. The number of particles in the PF was chosen by consideration of computational cost; as discussed in subsection 3.3, a LGF-1 is comparable in time complexity to a PF with O(d) particles, and a LGF-2 is comparable to a PF with O(d²) particles. For the case of d ≤ 30, 100 particles (PF-100) was about the least number at which the PF was effective and was not much more resource-intensive than the LGF-1. In order that the computational time of a PF matchs that of the LGF-2, we chose 100, 300, 500 and 1000 particles for d = 6, 10, 20 and 30, respectively. (We label it PF-scaled.) See also Table 2.

Table 2.

Time (seconds) needed to decode

Method	Number of dimensions, d
	6	10	20	30
LGF-2	0.24	0.43	1.0	2.0
LGF-1	0.018	0.024	0.032	0.056
PF-100	0.18	0.18	0.18	0.19
PF-scaled	0.18	0.50	0.81	1.8

NOTE: All values are means from 10 independent replicates. The simulation standard errors are all smaller than the leading digits in the table.

We implemented all the algorithms in Matlab, and we ran them on Windows computer with Pentium 4 CPU, 3.80GHz and 3.50GB of RAM.

Results

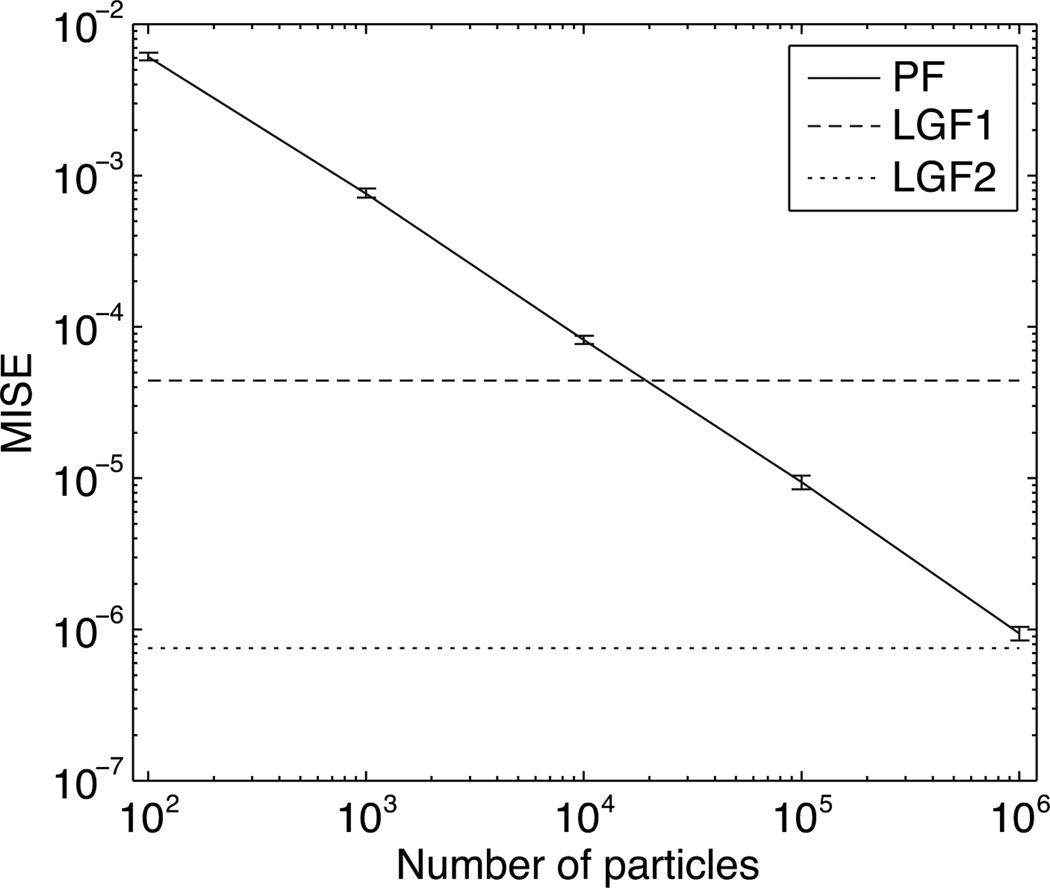
The first four rows in Table 1 show the four filters’ MISE in approximating the actual posterior mean. LGF-2 gives the best approximation, followed by LGF-1; both are better than PF-100 and PF-scaled. Note that LGF-1 is much faster than PF-100, and the computational time of LGF-2 is approximately the same as that of PF-scaled (Table 2). Figure 1 displays the MISE of particle filters in approximating the actual posterior mean as a function of the number of particles, for d = 6. PF needs on the order of 10⁴ particles to be as accurate as LGF-1, and about 10⁶ particles to match LGF-2. Furthermore, since the computational time of the PF is proportional to the number of particles, the time needed to decode by PF with 10⁴ and 10⁶ particles are expected to be about 20s and 2,000s, respectively (from Table 2). Thus, if we allow the LGFs and the PF to have the same accuracy, LGF-1 is about 1, 000 times faster than the PF, and LGF-2 is expected to be about 10, 000 times faster than the PF.

Table 1.

MISEs for different filters

Method	Number of dimensions, d
	6	10	20	30
LGF-2	0.0000008	0.000002	0.00001	0.00006
LGF-1	0.00003	0.00004	0.0001	0.0002
PF-100	0.006	0.01	0.03	0.04
PF-scaled	0.006	0.007	0.01	0.02
posterior	0.03	0.04	0.06	0.07

NOTE: The first four rows give the discrepancy between four approximate filters and the optimal filter (approximation error). The fifth row gives the MISE between the true state and the estimate of the optimal filter, i.e., the actual posterior mean (statistical error). All values are means from 10 independent replicates. The simulation standard errors are all smaller than the leading digits in the table.

Figure 1.

Scaling of the MISE for particle filters. The solid line represents the MISE (vertical axis) of the particle filter as a function of the number of particles (horizontal axis). Error here is with respect to the actual posterior expectation (optimal filter). The dashed and dotted horizontal lines represent the MISEs for the first- and second-order LGF, respectively.

The value of γ for this state-space model is γ ≈ 100 (Eq. (9)). From Theorem 2, the MISEs of LGF-1 and LGF-2 are, respectively, evaluated as $c_1^2{\mathrm{\gamma }}^{-2}\text{ and }{c}_2^2{\mathrm{\gamma }}^{-4}$, where c₁ and c₂ are constants depending on the model parameters. If c₁ and c₂ were in the range 1 to 10, then the MISEs of LGF-1 and LGF-2 should be 10⁻⁴ to 10⁻⁶, roughly matching the simulation results.

The fifth row of Table 1 shows the MISE between the true state and the actual posterior mean. The error in using the optimal filter, i.e., the actual posterior mean, to estimate the true state is statistical error, inherent in the system’s stochastic characteristics, and not due to the approximations. The statistical error is an order of magnitude larger than the approximation error in the LGFs, so that increasing the accuracy with which the posterior expectation is approximated does little to improve the estimation of the state. The approximation error in the PFs, however, becomes on the same order as the statistical error when the state dimension is larger (d = 20 or 30). In such cases the inaccuracy of the PF will produce comparatively inaccurate estimates of the true state.

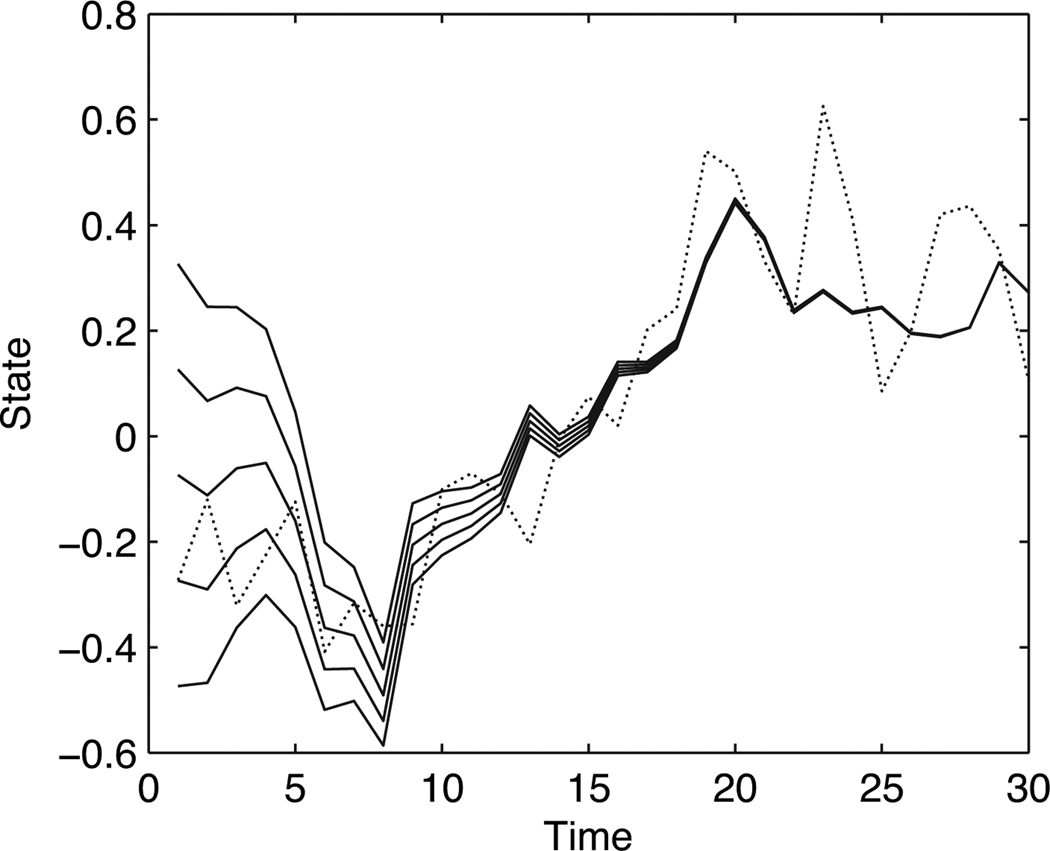
Finally, we examined how the choice of initial prior density affects the filtering result. Figure 2 shows five estimated trajectories started with different initial values. These five trajectories converged to the same state as the time evolves, as expected from Theorem 4.

Figure 2.

The solid lines represent the estimated trajectories with five different initial values by LGF-1. The dashed line represents the true state trajectory.

4.3 Real data analysis

Experiment setting and data collection

We used LGF to estimate the hand motion from neural activity. A multi-electrode array was implanted in the motor cortex of a monkey to record neural activity following procedures similar to those described previously in Velliste, Perel, Spalding, Whitford and Schwartz (2008). In all, 78 distinct neurons were recorded simultaneously. Raw voltage waveforms were thresholded and spikes were sorted to isolate the activity of individual cells. A monkey in this experiment was presented with a virtual 3-D space, containing a cursor which was controlled by the subject’s hand position, and eight possible targets which were located on the corners of a cube. The task was to move the cursor to a highlighted target from the middle of the cube; the monkey received a reward upon successful completion. In our data each trial consisted of time series of spike-counts from the recorded neurons, along with the recorded hand positions, and hand velocities found by taking differences in hand position at successive Δ = 0.03s intervals. Each trial contained 23 time-steps on average. Our data set consisted of 104 such trials.

Methods

For decoding, we used the same state-space model as in our simulation study. Many neurons in the motor cortex fire preferentially in response to the velocity υ_t ∈ ℝ³ and the position z_t ∈ ℝ³ of the hand (Wang, Chan, Heldman and Moran 2007). We thus took the state x_t to be a 6-dimensional concatenated vector x_t = (z_t, υ_t). The state model was taken to be

$${\mathit{x}}_t=\left(\begin{array}{cc}\hfill \mathit{I}\hfill & \hfill \mathrm{\Delta }\mathit{I}\hfill \\ \hfill \mathit{O}\hfill & \hfill \mathit{I}\hfill \end{array}\right){\mathit{x}}_{t-1}+\left(\begin{array}{c}\hfill \mathbf{0}\hfill \\ \hfill {\mathit{\epsilon }}_t\hfill \end{array}\right),$$ (10)

where ε_t is a 3-D Gaussian random variable with mean zero and covariance matrix σ²I, I being the identity matrix. 16 trials consisting of 2 presentations of each of the 8 targets, were reserved for estimating the parameters of the model. The parameters in the firing rate, α_i and β_i, were estimated by Poisson regression of spike counts on cursor position and velocity, and the value of σ² was determined via maximum likelihood. The time-lag between the hand movement and each neural activity was also estimated from the same training data. This was done by fitting a model over different values of time-lag ranging from 0 to 3Δs. The estimated optimal time-lag was the value at which the model had the highest R². Having estimated all the parameters, cursor motions were reconstructed from spike trains for the other 88 trials, and it is on these trials we focused. For comparison, we also reconstructed the cursor motion with a PF-100 and a widely-used population vector algorithm (PVA) (Dayan and Abbott 2001, pp. 97–101) (see also Appendix D).

Results

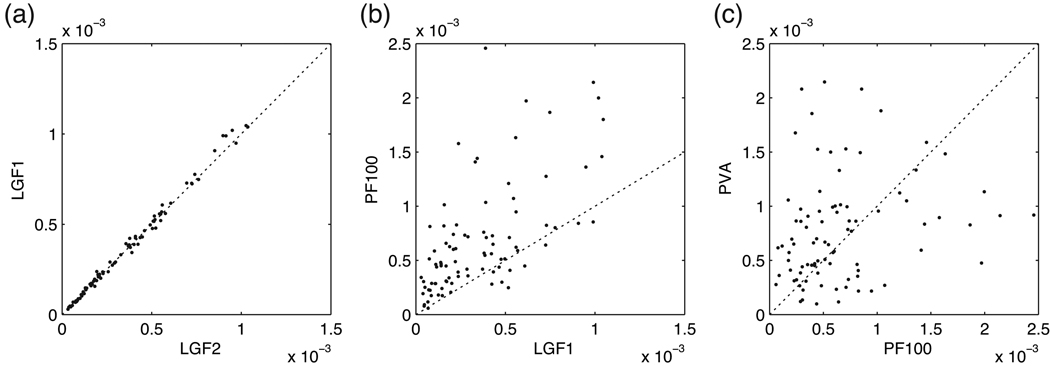
Figure 3 compares MISEs for different algorithms in estimating the true cursor position. Figure 3 (a) compares the MISE of LGF-1 with that of LGF-2. Just like in the simulation study, there is no substantial difference between them since the statistical error is larger than the LGFs’ approximation errors. Figure 3 (b) compares LGF-1 to PF-100: the former estimates the true cursor position better than the latter in most trials. Also (Table 2), LGF-1 is much faster than PF-100. Figure 3 (c) shows that the numerical error in the PF-100 is of the same order as the error resulting from using PVA. (Plots of the true and reconstructed cursor trajectories are shown in Appendix E.)

Figure 3.

Algorithm comparisons. The horizontal and vertical axes represent the MISE of different algorithms in estimating the true cursor position. Each point compares two different algorithms for a trial. Overall, 4 algorithms (LGF-1, LGF-2, PF-100 and PVA) were compared for 88 trials. (a) LGF-2 vs. LGF-1, (b) LGF-1 vs. PF-100, and (c) PF-100 vs. PVA.

5 Discussion

In this paper we have shown that, under suitable regularity conditions, the error of the LGF does not accumulate across time. In the context of a neural decoding example we found the LGF to be much more accurate than the particle filter with the same computational cost: in our simulation study the first-order and second-order LGFs had MISE of about 1/200 to 1/7,500 the size of the particle filter. We also found that for 6-dimensional case, about 10,000 particles were required in order for the particle filtering to become competitive with the first-order LGF; and the second-order LGF remained as accurate as the particle filter with 1,000,000 particles. In many situations (such as some neural decoding applications), implementation needs to be easy so that repeated refinements in modeling assumptions may be carried out quickly. With this in mind, it might be argued that the simplicity of the particle filter gives it some advantages. We have, however, noted how numerical methods may be used to supply the necessary second-derivative matrices (see Appendix B, and Kass (1987)), and these, together with maximization algorithms, make it as easy to modify the LGF for new variations on models as it is to modify the particle filter. Nor does the use of the LGF interfere with diagnostic tests and model-adequacy checks, such as the time-rescaling theorem for point processes (Brown, Barbieri, Ventura, Kass and Frank 2002). The obvious conclusion is that the LGF is likely to be preferable to the particle filter in applications where the posterior in Eq. (1) becomes concentrated.

We should note that the validity of the LGF is guaranteed only when the posterior distribution is uni-modal and has a log-concave property. On the other hand, the particle filter is a distribution-free method and can be used in a multi-modal case.

It is perhaps worth emphasizing the distinction between the LGF and other alternatives to the Kalman filter. The simplest non-linear filter, the extended Kalman filter (EKF) (Ahmed 1998), linearizes the state dynamics and the observation function around the current state estimate x̂, assuming Gaussian distributions for both. The error thus depends on the strength of the quadratic nonlinearities and the accuracy of preceding estimates, and so error can accumulate dramatically. The LGF makes no linear approximations—every filtering step is a (generally simple) nonlinear optimization—nor does it need to approximate either the state dynamics or the observation noise as Gaussians.

In our simulation studies, the second-order LGF was always more (in some cases much more) than 20 times as accurate as the first-order LGF in approximating the posterior, but this translated into only small gains in decoding accuracy. The reason is simply that the inherent statistical error of the posterior itself was much larger than the numerical error of the first-order LGF in approximating the posterior. We would expect this to be the case quite generally. Thus, our work may be seen as supporting the use of the first-order LGF, as applied to neural decoding in Brown et al. (1998).

Finally, an interesting idea is to use a sequential approximation to the posterior based on some well-behaved and low-dimensional parametric family, and to apply sequential simulation based on that family. The Gaussian could again be used (e.g., (Azimi-Sadjadi and Krishnaprasad 2005; Brigo, Hanzon and LeGland 1995; Ergün et al. 2007)), and our results would provide new theoretical justification for such procedures. However, it is well-known that Gaussian distributions, with their very thin tails, are poorly suited for importance sampling, so that heavier-tailed alternatives often work better (e.g., (Evans and Swartz 1995)). Sequential simulation schemes with approximating Gaussians replaced by multivariate t, or other heavy-tailed distributions, may be worth exploring.

APPENDIX A. Proofs of theorems

We begin by proving a lemma and a proposition needed for the main theorems. To simplify notation we introduce the symbols $h_t^{(l)}\equiv {\partial }^{l}h(x_t)/\partial x_t^l{|}_{x_t=x_{t|t}}\text{ and }{q}^{(l)}(x_{t+1})\equiv {\partial }^{l}p(x_{t+1}|x_t)/\partial x_t^l{|}_{x_t=x_{t|t}}$.

Lemma 6 Let ĥ(x_t) be

$$\widehat{h}(x_t)=-\frac{1}{\mathrm{\gamma }}\text{log}p(y_t|x_t)\widehat{p}(x_t|y_{1:t-1}),$$ (11)

${\widehat{h}}_t^{(l)}\equiv {\partial }_{x_t}^l\widehat{h}({\widehat{x}}_{t|t})$, and x̂_t|t the minimizer of ĥ(x_t). Then, under the regularity conditions, the order-α Laplace approximation of the posterior mean and variance have series expansions as

$${\tilde{x}}_{t|t}={\displaystyle \sum _{j=0}^{\alpha -1}}{A}_j(\{{\widehat{h}}_t^{(l)}\}){\mathrm{\gamma }}^{-j},$$ (12)

and

$${\tilde{\upsilon }}_{t|t}={\displaystyle \sum _{j=1}^{\alpha -1}}{B}_j(\{{\widehat{h}}_t^{(l)}\}){\mathrm{\gamma }}^{-j},$$ (13)

where the coefficients, A_j and B_j, are functions of $\{{\widehat{h}}_t^{(l)}\}$.

Proof (Lemma 6) The expectation of a function g(x_t) with respect to the approximated posterior distribution is

$$\widehat{E}[g(x_t)|y_{1:t}]=\frac{{\displaystyle \int }g(x_t)\text{ exp }[-\mathrm{\gamma }\widehat{h}(x_t)]{\mathit{\text{dx}}}_t}{{\displaystyle \int }\text{ exp }[-\mathrm{\gamma }\widehat{h}(x_t)]{\mathit{\text{dx}}}_t},$$ (14)

where g(x_t) = x_t for the mean and $g(x_t)=x_t^2$ for the second moment. We get the coefficients A_j and B_j by applying Laplace’s method, an (infinite) asymptotic expansion of a Laplace-type integral (Theorem 1.1 in (Wojdylo 2006); see Appendix C for a brief summary), to both the numerator and the denominator of Eq. (14); those formulae also show that the coefficients are functions of $\{{\widehat{h}}_t^{(l)}\}$, l = 1, 2, ․ ․ … For example, the coefficients of up to first-order terms are obtained as $A_0(\{{\widehat{h}}_t^{(l)}\})={\widehat{x}}_{t|t},A_1(\{{\widehat{h}}_t^{(l)}\})=-{\widehat{h}}_t^{‴}/(2{({\widehat{h}}_t^{″})}^2),\text{ and }{B}_1(\{{\widehat{h}}_t^{(l)}\})={({\widehat{h}}_t^{″})}^{-1}$.

Remark 1 Lemma 6 guarantees that the choice of x̃_t|t = x̂_t|t and ${\tilde{\upsilon }}_{t|t}={(\mathrm{\gamma }{\widehat{h}}_t^{″})}^{-1}$ provides the first-order approximation of posterior mean and variance. As proved in Tierney et al. (1989), Eq. (4) achieves the second-order expansion of the posterior mean ${\tilde{x}}_{t|t}={\widehat{x}}_{t|t}+A_1(\{{\widehat{h}}_t^{(l)}\}){\mathrm{\gamma }}^{-1}$. Thus Eq. (4) and ${\tilde{\upsilon }}_{t|t}={(\mathrm{\gamma }{\widehat{h}}_t^{″})}^{-1}$ provide the second-order approximation.

Proposition 7 Suppose that the regularity conditions (C.1)–(C.4) hold, and that the approximated predictive distribution of time t satisfies

$$\widehat{p}(x_t|y_{1:t-1}=p(x_t|y_{1:t-1})+{\displaystyle \sum _{j=\nu }^N}{ℰ}_{t,j}(x_t){\mathrm{\gamma }}^{-j}+O({\mathrm{\gamma }}^{-N-1}),$$ (15)

where ℰ_t,j(x_t) is a constant-order function of γ and 0 < ν < N for ν, N ∈ ℕ. Replacing the filtered distribution at time t with a Gaussian with α-order Laplace approximated mean and variance leads to the approximate predictive distribution at time t + 1,

$$\widehat{p}(x_{t+1}|y_{1:t})=p(x_{t+1}|y_{1:t})+{\displaystyle \sum _{j=\beta }^N}{ℰ}_{t+1,j}^{*}(x_{t+1}){\mathrm{\gamma }}^{-j}+{\displaystyle \sum _{j=\nu }^N}{ℰ}_{t+1,j+1}(x_{t+1}){\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-N-1}),$$ (16)

where β = 1 for α = 1 and β = 2 for α ≥ 2. Here ${ℰ}_{t+1,j}^{*}(x_{t+1})$ does not depend on {ℰ_t,k(x_t)}_{k=ν,ν+1,…} and

$${ℰ}_{t+1,j+1}(x_{t+1})={\frac{q\prime (x_{t+1})}{h_t^{″}}\frac{\partial }{\partial x_t}\left(\frac{{ℰ}_{t,j}(x_t)}{p(x_t|y_{1:t-1})}\right)|}_{x_t=x_{t|t}}+O({\mathrm{\gamma }}^{-1}),$$ (17)

for j = ν, ν + 1, …, N. Furthermore, if the condition (C.5) is satisfied, the coefficients of the expansion terms in Eq. (16) are bounded uniformly across time.

Proof (Proposition 7) The proof works by comparing the asymptotic expansions of the true and approximated predictive distributions. To do this, we must find those asymptotic expansions; once this is done the remaining steps are fairly straightforward.

(i) We begin by evaluating the true predictive distribution at time t + 1. From Eqs. (1) and (2), this is

$$p(x_{t+1}|y_{1:t})=\frac{{\displaystyle \int }p(x_{t+1}|x_t)\text{ exp }[-\mathrm{\gamma }h(x_t)]{\mathit{\text{dx}}}_t}{{\displaystyle \int }\text{ exp }[-\mathrm{\gamma }h(x_t)]{\mathit{\text{dx}}}_t}.$$

Applying Laplace’s method (Theorem 1.1 in (Wojdylo 2006), see also Appendix C) to both the numerator and the denominator of above equation leads to

$$p(x_{t+1}|y_{1:t})=\frac{{\displaystyle {\sum }_{s=0}^N}\mathrm{\Gamma }(s+\frac{1}{2}){(\frac{2}{h_t^{″}})}^s{c}_{2s}^{*}{\mathrm{\gamma }}^{-s}+O({\mathrm{\gamma }}^{-N-1})}{{\displaystyle {\sum }_{s=0}^N}\mathrm{\Gamma }(s+\frac{1}{2}){(\frac{2}{h_t^{″}})}^s{\overline{c}}_{2s}^{*}{\mathrm{\gamma }}^{-s}+O({\mathrm{\gamma }}^{-N-1})},$$ (18)

where

$$c_s^{*}={\displaystyle \sum _{i=0}^s}\frac{q^{s-i}(x_{t+1})}{(s-i)!}{\displaystyle \sum _{j=0}^i}\left(\begin{array}{c}\hfill -\frac{s+1}{2}\hfill \\ \hfill j\hfill \end{array}\right){𝒞}_{i,j}(A_1,\dots ),$$ (19)

and

$${\overline{c}}_s^{*}={\displaystyle \sum _{j=0}^s}\left(\begin{array}{c}\hfill -\frac{s+1}{2}\hfill \\ \hfill j\hfill \end{array}\right){𝒞}_{s,j}(A_1,\dots ).$$ (20)

Here 𝒞_s,j(A₁, …) is a partial ordinary Bell polynomial, which is the coefficient of x_i in the formal expansion of (A₁x + A₂x² + ⋯)^j, and $A_i\equiv A_i(\{h_t^{(l)}\})$ is the coefficient which appeared in Lemma 6. Expanding with respect to γ⁻¹, we obtain the asymptotic expansion of p(x_t+1|y_1:t) as

$$p(x_{t+1}|y_{1:t})=q(x_{t+1})+{\displaystyle \sum _{j=1}^N}{C}_j(x_{t+1}){\mathrm{\gamma }}^{-j}+O({\mathrm{\gamma }}^{-N-1}),$$ (21)

where q(x_t+1) was earlier defined as p(x_t+1|x_t), and where C_j(x_t+1) depends on q^(k)(x_t+1) and $h_t^{(l)}(k,l=1,2,\dots )$. C_j(x_t+1) is directly calculated by Eqs. (18)–(20).

(ii) We next consider the approximated predictive distribution of time t+1,

$$\widehat{p}(x_{t+1}|y_{1:t})={\displaystyle \int }p(x_{t+1}|x_t)\widehat{p}(x_t|y_{1:t}){\mathit{\text{dx}}}_t,$$ (22)

where p̂(x_t|y_1:t) is the Gaussian distribution whose mean and variance are given by Eq. (12) and (13), respectively. Eq. (22) can be re-written as

$$\widehat{p}(x_{t+1}|y_{1:t})=\frac{1}{\sqrt{2\pi {\tilde{\upsilon }}_{t|t}}}{\displaystyle \int }p(x_{t+1}|x_t)\text{ exp }\left[-\frac{{(x_t-{\tilde{x}}_{t|t})}^2}{2{\tilde{\upsilon }}_{t|t}}\right]{\mathit{\text{dx}}}_t.$$

Applying Laplace’s method again,

$$\widehat{p}(x_{t+1}|y_{1:t})=\tilde{q}(x_{t+1})+{\displaystyle \sum _{j=1}^N}\frac{{\tilde{q}}^{(2j)}(x_{t+1})}{2^j\mathrm{\Gamma }(j+1)}{\tilde{\upsilon }}_{t|t}^j+O({\tilde{\upsilon }}_{t|t}^{-N-1}),$$ (23)

where Γ(j + 1) is the Gamma function and

$${\tilde{q}}_t^{(l)}\equiv {\frac{{\partial }^{l}p(x_{t+1}|x_t)}{\partial x_t}|}_{x_t={\tilde{x}}_{t|t}}.$$ (24)

Now we compare Eqs. (23) and (21), via a series of substitutions. We want to re-write Eq. (23) with q^(k)(x_t+1) and $h_t^{(l)}$. Substituting Eq. (15) into Eq. (11),

$$\begin{array}{cc}\widehat{h}(x_t)\hfill & =-\frac{1}{\mathrm{\gamma }}\text{log}p(y_t|x_t)\left[p(x_t|y_{1:t-1})+{\displaystyle \sum _{j=\nu }^N}{ℰ}_{t,j}(x_t){\mathrm{\gamma }}^{-j}+O({\mathrm{\gamma }}^{-N-1})\right]\hfill \\ \hfill & =h(x_t)-{\displaystyle \sum _{j=\nu }^N}{ℱ}_{t,j}(x_t){\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-N-2}),\hfill \end{array}$$ (25)

where

$${ℱ}_{t,j}(x_t)=\frac{{ℰ}_{t,j}(x_t)}{p(x_t|y_{1:t-1})}+O({\mathrm{\gamma }}^{-\nu }).$$

is a collection of terms which depend on ℰ_t,j(x_t).

Suppose x̂_t|t = x_t|t + ε and ε ≪ 1. Taking the derivative both sides of Eq. (25) and evaluating it at x_t|t, we obtain

$$\epsilon ={\displaystyle \sum _{j=\nu }^N}\frac{{ℱ}_{t,j}^{\prime }}{h_t^{″}}{\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-N-2}).$$

Then we get

$${\widehat{x}}_{t|t}=x_{t|t}+{\displaystyle \sum _{j=\nu }^N}\frac{{ℱ}_{t,j}^{\prime }}{h_t^{″}}{\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-N-2}).$$ (26)

Inserting Eq. (26) into Eq. (25) gives

$${\widehat{h}}_t^{(l)}=h_t^{(l)}-{\displaystyle \sum _{j=\nu }^N}\left[{ℱ}_{t,j}^{(l)}-\frac{{ℱ}_{t,j}^{\prime }{h}_t^{(l+1)}}{h_t^{″}}\right]{\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-N-2}).$$ (27)

Substituting Eq. (26) and Eq. (27) into Eq. (12) leads to

$${\tilde{x}}_{t|t}=x_{t|t}+{\displaystyle \sum _{j=1}^{\alpha -1}}{A}_j{\mathrm{\gamma }}^{-j}+{\displaystyle \sum _{j=\nu }^N}\frac{{ℱ}_{t,j}^{\prime }}{h_t^{″}}{\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-N-2}).$$ (28)

Inserting Eq. (28) into Eq. (24) and expanding with respect to γ⁻¹,

$${\tilde{q}}^{(l)}(x_{t+1})=q^{(l)}(x_{t+1})+{\displaystyle \sum _{j=1}^{\alpha -1}}{A}_j{q}^{(l+1)}(x_{t+1}){\mathrm{\gamma }}^{-j}+{\displaystyle \sum _{j=2}^{\alpha }}\left[{\displaystyle \sum _{k=2}^j}\frac{1}{k!}{q}^{(l+k)}(x_{t+1}){𝒞}_{j,k}(A_1,\dots )\right]{\mathrm{\gamma }}^{-j}+{\displaystyle \sum _{j=\nu }^N}\frac{{ℱ}_{t,j}^{\prime }}{h_t^{″}}{q}^{(l+1)}(x_{t+1}){\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-\alpha -1}).$$ (29)

Substituting Eqs. (13), (27) and (29) into Eq. (23), we obtain the final asymptotic expansion of p̂(x_t+1|y_1:t),

$$\widehat{p}(x_{t+1}|y_{1:t})=q(x_{t+1})+{\displaystyle \sum _{j=1}^{\alpha }}{R}_j(x_{t+1}){\mathrm{\gamma }}^{-j}+{\displaystyle \sum _{j=\nu }^{N-1}}\frac{{ℱ}_{t,j}^{\prime }}{h_t^{″}}q\prime (x_{t+1}){\mathrm{\gamma }}^{-j-1}+O({\mathrm{\gamma }}^{-\alpha -1}),$$ (30)

in which

$$R_j(x_{t+1})=\{\begin{array}{cc}{G}_j(x_{t+1})+A_{j}q\prime (x_{t+1})\hfill & 1\le j\le \alpha -1\hfill \\ G_j(x_{t+1})\hfill & j=\alpha \hfill \end{array}$$

and

$$G_j(x_{t+1})={\displaystyle \sum _{s=2}^j}\frac{1}{s!}{𝒞}_{j,s}(A_1,\dots )q^{(s)}(x_{t+1})+{\displaystyle \sum _{s=1}^j}\frac{{𝒞}_{j,s}(B_1,\dots )q^{(2s)}(x_{t+1})}{2^s\mathrm{\Gamma }(s+1)}+{\displaystyle \sum _{s=1}^{j-1}}{\displaystyle \sum _{k=s}^{j-1}}\frac{A_{j-k}{𝒞}_{k,s}(B_1,\dots )q^{(2s+1)}(x_{t+1})}{2^s\mathrm{\Gamma }(s+1)}+{\displaystyle \sum _{s=1}^{j-2}}{\displaystyle \sum _{k=s}^{j-2}}{\displaystyle \sum _{n=2}^{j-k}}\frac{{𝒞}_{j-k,n}(A_1,\dots ){𝒞}_{k,s}(B_1,\dots )q^{(2s+n)}(x_{t+1})}{2^s\mathrm{\Gamma }(s+1)n!},$$

where $B_j\equiv B_j(\{h_t^{(l)}\})$ appeared in Lemma 6.

(iii) Now we compare Eqs. (21) and (30). The coefficients, up to second order terms, in the former are

$$C_1(x_{t+1})=\frac{q″(x_{t+1})}{2h_t^{″}}-\frac{h_t^{‴}q\prime (x_{t+1})}{2{(h_t^{″})}^2},$$ (31)

and

$$C_2(x_{t+1})=\frac{q^{(4)}(x_{t+1})}{8{(h_t^{″})}^2}-\frac{5h_t^{‴}q‴(x_{t+1})}{12{(h_t^{″})}^3}+\left[\frac{5{(h_t^{‴})}^2}{8{(h_t^{″})}^4}-\frac{h_t^{(4)}}{4{(h_t^{″})}^3}\right]q″(x_{t+1})+\left[\frac{2h_t^{‴}{h}_t^{(4)}}{3{(h_t^{″})}^4}-\frac{5{(h_t^{‴})}^3}{8{(h_t^{″})}^5}-\frac{h_t^{(5)}}{8{(h_t^{″})}^3}\right]q\prime (x_{t+1}).$$ (32)

For the first-order Laplace approximation (α = 1), the coefficient of order γ⁻¹ in Eq. (30) is

$$R_1(x_{t+1})=\frac{q″(x_{t+1})}{2h_t^{″}},$$ (33)

which does not correspond to C₁(x_t+1), and hence Eq. (16) holds.

For α ≥ 2, R₁(x_t+1) is as

$$R_1(x_{t+1})=\frac{q″(x_{t+1})}{2h_t^{″}}-\frac{h_t^{‴}q\prime (x_{t+1})}{2{(h_t^{″})}^2},$$ (34)

which corresponds to C₁(x_t+1), and the first-order error term in Eq. (16) is canceled.

The second-order error term in Eq. (30) is calculated as

$$R_2(x_{t+1})=\frac{q^{(4)}(x_{t+1})}{8{(h_t^{″})}^2}-\frac{h_t^{‴}q‴(x_{t+1})}{4{(h_t^{″})}^3}+\left[\frac{5{(h_t^{‴})}^2}{8{(h_t^{″})}^4}-\frac{h_t^{(4)}}{4{(h_t^{″})}^3}\right]q″(x_{t+1}),$$ (35)

for α = 2, and

$$R_2(x_{t+1})=\frac{q^{(4)}(x_{t+1})}{8{(h_t^{″})}^2}-\frac{h_t^{‴}q‴(x_{t+1})}{4{(h_t^{″})}^3}+\left[\frac{5{(h_t^{‴})}^2}{8{(h_t^{″})}^4}-\frac{h_t^{(4)}}{4{(h_t^{″})}^3}\right]q″(x_{t+1})+\left[\frac{2h‴h_t^{(4)}}{3{(h_t^{″})}^4}-\frac{5{(h_t^{‴})}^3}{8{(h_t^{″})}^5}-\frac{h_t^{(5)}}{8{(h_t^{″})}^3}\right]q\prime (x_{t+1}),$$ (36)

for α ≥ 3. Thus R₂(x_t+1) ≠ C₂(x_t+1) and second-order error term in Eq. (16) remains for α ≥ 2.

From (31)–(36), the leading error term introduced by the Gaussian approximation is

$${ℰ}_{t+1,1}^{*}(x_{t+1})=R_1(x_{t+1})-C_1(x_{t+1})=\frac{h_t^{‴}q\prime (x_{t+1})}{2{(h_t^{″})}^2}$$

for α = 1, and

$$\begin{array}{cc}{ℰ}_{t+1,2}^{*}(x_{t+1})\hfill & =R_2(x_{t+1})-C_2(x_{t+1})\hfill \\ \hfill & =\frac{h_t^{‴}q‴(x_{t+1})}{6{(h_t^{″})}^3}-\left[\frac{2h_t^{‴}{h}_t^{(4)}}{3{(h_t^{″})}^4}-\frac{5{(h_t^{‴})}^3}{8{(h_t^{″})}^5}-\frac{h_t^{(5)}}{8{(h_t^{″})}^3}\right]q\prime (x_{t+1})\hfill \end{array}$$

for α = 2, and

$${ℰ}_{t+1,2}^{*}(x_{t+1})=R_2(x_{t+1})-C_2(x_{t+1})=\frac{h_t^{‴}q‴(x_{t+1})}{6{(h_t^{″})}^3}$$

for α ≥ 3. Thus if the condition (C.5) is satisfied, the leading error term is bounded uniformly across time. We can confirm in the same way that the other error terms are also bounded uniformly.

There are two sources of error in Eq. (16): first, that due to the replacement of the true filtered distribution at time t by a Gaussian, ${\displaystyle {\sum }_{j=\beta }^N}{ℰ}_{t+1,j}^{*}(x_{t+1}){\mathrm{\gamma }}^{-j}$, and, second, that due to propagation from time t, ${\displaystyle {\sum }_{j=\nu }^{N-1}}{ℰ}_{t+1,j+1}(x_{t+1}){\mathrm{\gamma }}^{-j-1}$. At each step, the Gaussian approximation introduces an O(γ^−β) error into the predictive distribution, where β = 1 for α = 1 and β = 2 for α ≥ 2. However, the errors propagated from the previous time-step “move up” one order of magnitude (power of γ). Applying Eq. (17) repeatedly, we find that the leading error term, ${ℰ}_{t,\beta }^{*}(x_t){\mathrm{\gamma }}^{-\beta }$, which is generated at time-step t, is propagated, by a strictly later time-step u, to be ℰ_u,u−t+β(x_u)^{−(u−t+β)} where

$${ℰ}_{u,u-t+\beta }(x_u)=q\prime (x_u){\displaystyle \prod _{k=t+1}^{u-1}}\left[\frac{1}{h_k^{″}}\frac{\partial }{\partial x_k}\left(\frac{q\prime (x_k)}{p(x_k|y_{1:k-1})}\right){|}_{x_k=x_{k|k}}\right]\times \left[\frac{1}{h_t^{″}}\frac{\partial }{\partial x_t}\left(\frac{{ℰ}_{t,\beta }^{*}(x_t)}{p(x_t|y_{1:t-1})}\right){|}_{x_t=x_{t|t}}\right].$$

The compounded error in time-step u is then given by the summation of the propagated errors from t = 1 to u − 1 as

$$S_u={\displaystyle \sum _{t=1}^{u-1}}{ℰ}_{u,u-t+\beta }(x_u){\mathrm{\gamma }}^{-(u-t+\beta )}<C^{-\beta }{\displaystyle \sum _{t=1}^{u-1}}{(C{\mathrm{\gamma }}^{-1})}^{(u-t+\beta )},$$

where the inequality holds under the condition (C.5), C < γ is a constant which is independent of time t. The right hand side in this equation converge on O(γ^−β−1) as u → ∞, so that the compounded error after infinite time-step remains O(γ^−β−1). The result is that the whole error term in the predictive distribution becomes O(^γ−β), even if it started out smaller, but it does not grow beyond that order. Theorem 1 is then proved from Proposition 7 immediately:

Proof (Theorem 1) The LGFs start with an initial predictive distribution which does not involve any errors. Thus, from Proposition 7 it is proved inductively that the error in the approximated predictive distribution is O(γ^−β) and uniformly bounded for t ∈ ℕ.

Proof (Theorem 2) (Sketch) Since the predictive distribution,

$$p(x_{t+1}|y_{1:t})={\displaystyle \int }p(x_{t+1}|x_t)p(x_t|y_{1:t}){\mathit{\text{dx}}}_t$$

is the posterior expectation of p(x_t+1|x_t) with respect to x_t, Theorem 2 is proved in the same way as Theorem 1 (replacing p(x_t+1|x_t) by g(x_t) in the proof of Theorem 1).

Proof (Theorem 4) From Proposition 7, the two predictive distributions at time t are given by

$${\widehat{p}}_1(x_t|y_{1:t-1})=p(x_t|y_{1:t-1})+{\displaystyle \sum _{j=\nu }^N}{ℰ}_{t,j}^{(1)}(x_t){\mathrm{\gamma }}^{-j}+O({\mathrm{\gamma }}^{-N-1}),$$

and

$${\widehat{p}}_2(x_t|y_{1:t-1})=p(x_t|y_{1:t-1})+{\displaystyle \sum _{j=\nu }^N}{ℰ}_{t,j}^{(2)}(x_t){\mathrm{\gamma }}^{-j}+O({\mathrm{\gamma }}^{-N-1}),$$

where ${ℰ}_{t,j}^{(1)}(x_t)\ne {ℰ}_{t,j}^{(2)}(x_t)$. Applying the LGF to both predictive distributions introduces the same errors at time t + 1, ${\displaystyle {\sum }_{j=\beta }^N}{ℰ}_{t+1,j}^{*}(x_{t+1}){\mathrm{\gamma }}^{-j}$, which are canceled, while propagated errors from time-step t to t + 1 in both predictive distributions, ${\displaystyle {\sum }_{j=\nu }^{N-1}}{ℰ}_{t+1,j+1}^{(1)}(x_{t+1}){\mathrm{\gamma }}^{-j-1}\text{ and }{\displaystyle {\sum }_{j=\nu }^{N-1}}{ℰ}_{t+1,j+1}^{(2)}(x_{t+1}){\mathrm{\gamma }}^{-j-1}$ are not canceled. Then we get p̂₁(x_t+1|y_1:t) − p̂₂(x_t+1|y_1:t) = O(γ^−ν−1). Applying this procedure u times completes the theorem.

Proof (Theorem 5) Assume that the expectation at time t + 1 satisfies

$$\widehat{E}[g(x_{t+1})|y_{1:T}]=E[g(x_{t+1})|y_{1:T}]+O({\mathrm{\gamma }}^{-\beta }).$$ (37)

From Theorem 1 and Eq. (37), we obtain

$${\displaystyle \int }\frac{\widehat{p}(x_{t+1}|y_{1:T})p(x_{t+1}|x_t)}{\widehat{p}(x_{t+1}|y_{1:t})}{\mathit{\text{dx}}}_{t+1}={\displaystyle \int }\frac{p(x_{t+1}|y_{1:T})p(x_{t+1}|x_t)}{p(x_{t+1}|y_{1:t})}{\mathit{\text{dx}}}_{t+1}+O({\mathrm{\gamma }}^{-\beta }).$$

Using Theorem 2, the expectation at time t is

$$\begin{array}{cc}\widehat{E}[g(x_t)|y_{1:T}]\hfill & ={\displaystyle \int }g(x_t)\widehat{p}(x_t|y_{1:t}){\displaystyle \int }\frac{p(x_{t+1}|y_{1:T})p(x_{t+1}|x_t)}{p(x_{t+1}|y_{1:t})}{\mathit{\text{dx}}}_{t+1}{\mathit{\text{dx}}}_t+O({\mathrm{\gamma }}^{-\beta })\hfill \\ \hfill & ={\displaystyle \int }g(x_t)p(x_t|y_{1:t}){\displaystyle \int }\frac{p(x_{t+1}|y_{1:T})p(x_{t+1}|x_t)}{p(x_{t+1}|y_{1:t})}{\mathit{\text{dx}}}_{t+1}{\mathit{\text{dx}}}_t+O({\mathrm{\gamma }}^{-\beta })\hfill \\ \hfill & =E[g(x_t)|y_{1:T}]+O({\mathrm{\gamma }}^{-\beta }).\hfill \end{array}$$

The initial smoothed distribution of the backward recursion is given by the filtered distribution p̂(x_T|y_1:T), which satisfies Ê[x_T|y_1:T] = E[x_T|y_1:T]+O(γ^−β) by theorem 2. Then, the theorem is proved inductively.

APPENDIX B. Numerical Computation for second derivatives

We describe the numerical algorithm for computing the Hessian matrix, as promised in Section 2.3.

The Laplace approximation requires the second derivative (or the Hessian matrix) of the log-likelihood function evaluated at its maximum. However, it is often difficult, and even more often tedious, to get correct analytical derivatives of the log-likelihood function. In such cases accurate numerical computations of the derivative may be used, as follows. Consider calculating the second derivative of l(x) at x₀ for the one-dimensional case. For n = 0, 1, 2, … and c > 1, define the second central difference quotient,

$$A_{n,0}=[l(x_0+c^{-n}{h}_0)+l(x_0-c^{-n}{h}_0)-2l(x_0)]/{(c^{-n}{h}_0)}^2,$$

and then for k = 1, 2, …, n compute

$$A_{n,k}=A_{n,k-1}+\frac{A_{n,k-1}-A_{n-1,k-1}}{c^{2(k+1)}-1}.$$ (38)

When the value of |A_n,k − A_n−1,k| is sufficiently small, A_n,k+1 is used for the second derivative.

This algorithm is an iterated version of the second central difference formula, often called Richardson extrapolation, producing an approximation with an error of order O(h^2(k+1)) (Dahlquist and Bjorck 1974).

In the d-dimensional case of a second-derivative approximation at a maximum, Kass (1987) proposed an efficient numerical routine which reduces the computation of the Hessian matrix to a series of one-dimensional second-derivative calculations. The trick is to apply the second-difference quotient to suitably-defined functions f of a single variable s as follows.

1. Initialize the increment h = (h₁, …, h_d).

2. Find the maximum of l(x), and call it x̂.

3. Get all unmixed second derivatives for each i = 1 to d, using the function

   $$\begin{array}{cc}\hfill x_i& ={\widehat{x}}_i+s\hfill \\ \hfill x_j& ={\widehat{x}}_j\text{ for }j\text{ not equal to }i\hfill \\ \hfill f(s)& =l(\mathit{x}(s)).\hfill \end{array}$$

   Compute the second difference quotient; then repeat and extrapolate until the difference in successive approximations meets a relative error criterion, as in (38); store as diagonal elements of the Hessian matrix array, $l_{i,i}^{″}=f″(0)$.

4. Similarly, get all the mixed second derivatives. For each i = 1 to d, for each j = i + 1 to d, using the function

   $$\begin{array}{cc}\hfill x_i& ={\widehat{x}}_i+s/\sqrt{l_{i,i}^{″}}\hfill \\ \hfill x_j& ={\widehat{x}}_j+s/\sqrt{l_{j,j}^{″}}\hfill \\ \hfill x_k& ={\widehat{x}}_k\text{ for }k\text{ not equal to }i\text{ or }j\hfill \\ \hfill f(s)& =l(\mathit{x}(s)).\hfill \end{array}$$

   Compute the second difference quotient; then repeat and extrapolate until difference in successive approximations is less than relative error criterion as in (38); store as off-diagonal elements of the Hessian matrix array, $l_{i,i}^{″}=(f″(0)/2-1)\sqrt{l_{i,i}^{″},l_{j,j}^{″}}$.

In practice, the increment for computing the Hessian at time t would be taken to be $h_i=0.1\times \sqrt{{\upsilon }_{t|t-1}^{(i,i)}}$, i = 1, 2, …, d, where ${\upsilon }_{t|t-1}^{(i,i)}$ is the (i, i)-element of the covariance matrix of the predictive distribution at time t.

APPENDIX C. Laplace’s Method

Here, we briefly describe Laplace’s method, especially the details used in the proofs of Lemma 6 and Proposition 7.

We consider the following integral,

$$I(\mathrm{\gamma })={\displaystyle \int }g(x)e^{-\mathrm{\gamma }h(x)}\mathit{\text{dx}},$$ (39)

where x ∈ ℝ; γ, the expansion parameter, is a large positive real number; h(x) and g(x) are independent of γ (or very weakly dependent on γ); and the interval of integration can be finite or infinite. Laplace’s method approximates I(γ) as a series expansion in descending powers of γ. There is a computationally efficient method to compute the coefficients in this infinite asymptotic expansion (Theorem 1.1 in (Wojdylo 2006)). Suppose that h(x) has an interior minimum at x₀, and h(x) and g(x) are assumed to be expandable in a neighborhood of x₀ in series of ascending powers of x. Thus, as x → x₀,

$$h(x)~h(x_0)+{\displaystyle \sum _{s=0}^{\mathrm{\infty }}}{a}_s{(x-x_0)}^{s+2},$$

and

$$g(x)~{\displaystyle \sum _{s=0}^{\mathrm{\infty }}}{b}_s{(x-x_0)}^s,$$

in which a₀, b₀ ≠ 0.

Let us introduce two dimensionless sets of quantities, A_i ≡ a_i/a₀ and B_i ≡ b_i/b₀, as well as the constants ${\alpha }_1=1/a_0^{1/2}\text{ and }{c}_0=b_0/a_0^{1/2}$. Then the integral in 39) can be asymptotically expanded as

$$I(\mathrm{\gamma })~c_0{e}^{-\mathrm{\gamma }h(x_0)}{\displaystyle \sum _{s=0}^{\mathrm{\infty }}}\mathrm{\Gamma }(s+\frac{1}{2}){\alpha }_1^{2s}{c}_{2s}^{*}{\mathrm{\gamma }}^{-s-\frac{1}{2}},$$

where

$$c_s^{*}={\displaystyle \sum _{i=0}^s}{B}_{s-i}{\displaystyle \sum _{j=0}^i}\left(\begin{array}{c}\hfill -\frac{s+1}{2}\hfill \\ \hfill j\hfill \end{array}\right){𝒞}_{i,j}(A_1,\dots ),$$

where 𝒞_i,j(A₁, …) is a partial ordinary Bell polynomial, the coefficient of xⁱ in the formal expansion of (A₁x + A₂x² + ⋯)^j. 𝒞_i,j(A₁, …) can be computed by the following recursive formula,

$${𝒞}_{i,j}(A_1,\dots )={\displaystyle \sum _{m=j-1}^{i-1}}{A}_{i-m}{𝒞}_{m,j-1}(A_1,\dots ),$$

for 1 ≥ j ≥ i. Note that 𝒞_0,0(A₁, …) = 1, and 𝒞_i,0(A₁, …) = 𝒞_0,j(A₁, …) = 0 for all i, j > 0.

APPENDIX D. The Population Vector Algorithm

The population vector algorithm (PVA) is a standard method for neural decoding, especially for directionally-sensitive neurons like the motor-cortical cells recorded from in the experiments we analyze (Dayan and Abbott 2001, pp. 97–101). Briefly, the idea is that each neuron i, 1 ≤ i ≤ N, has a preferred motion vector θ_i, and the expected spiking rate λ_i varies with the inner product between this vector and the actual motion vector x(t),

$$\frac{{\lambda }_i(t)-r_i}{{\mathrm{\Lambda }}_i}=\mathit{x}(t)·{\mathit{\theta }}_i,$$ (40)

where r_i is a baseline firing rate for neuron i, and Λ_i a maximum firing rate. ((40) corresponds to a cosine tuning curve.) If one observes y_i(t), the actual neuronal counts over some time-window Δ, then averaging over neurons and inverting gives the population vector

$${\mathit{x}}_{\text{pop}}(t)={\displaystyle \sum _{i=1}^N}\frac{y(t)-r_i\mathrm{\Delta }}{{\mathrm{\Lambda }}_i\mathrm{\Delta }}{\mathit{\theta }}_i,$$

which the PVA uses as an estimate of x(t). If preferred vectors θ_i are uniformly distributed, then x_pop converges on a vector parallel to x as N → ∞, and is in that sense unbiased (Dayan and Abbott 2001, p. 101). If preferred vectors are not uniform, however, then in general the population vector gives a biased estimate.

APPENDIX E. Real data analysis

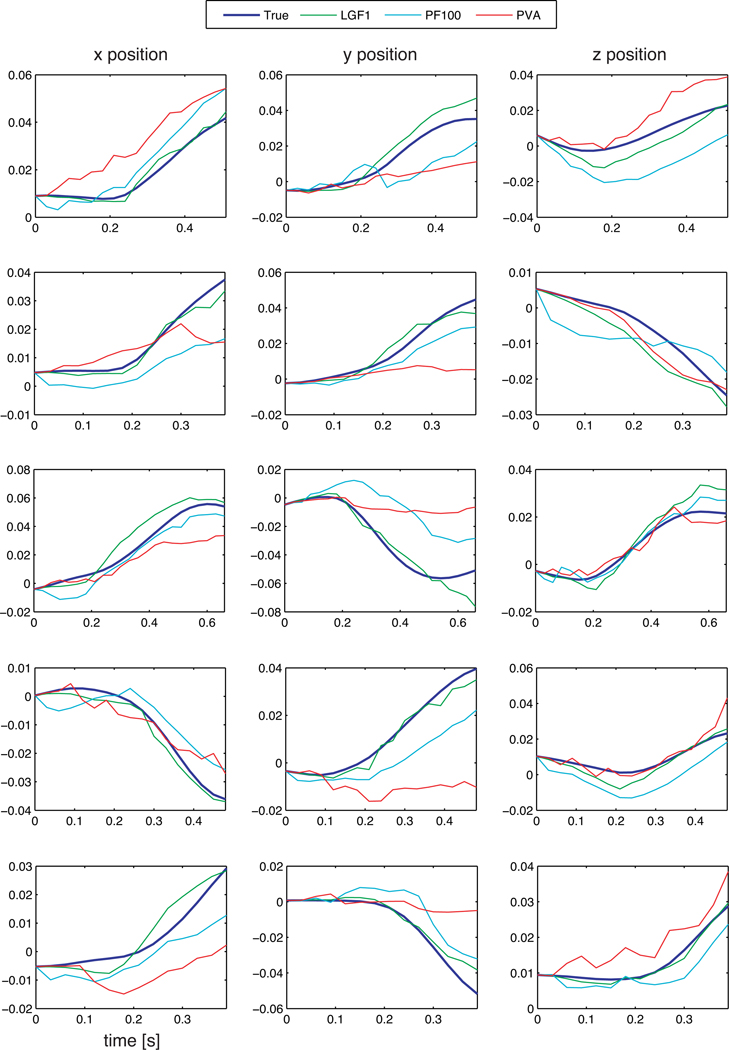
Figure 4 shows trajectories of the true and estimated (by LGF, PF-100 and PVA) cursor position of the real data analysis. It is seen that the LGF provides better estimation than either the PF-100 or the PVA.

Figure 4.

The trajectories of the cursor position. “True”: actual trajectory. “LGF1”: trajectories estimated by first-order LGF, respectively. “PF100”: trajectory estimated by the particle filter with 100 particles. “PVA”: trajectory estimated by the population vector algorithm. The trajectories estimated by the LGF2 are not shown; they are similar to those estimated by the LGF1.