Simulations of the confinement of ubiquitin in self-assembled reverse micelles

Abstract

We describe the effects of confinement on the structure, hydration, and the internal dynamics of ubiquitin encapsulated in reverse micelles (RM). We performed molecular dynamics simulations of the encapsulation of ubiquitin into self-assembled protein∕surfactant reverse micelles to study the positioning and interactions of the protein with the RM and found that ubiquitin binds to the RM interface at low salt concentrations. The same hydrophobic patch that is recognized by ubiquitin binding domains  in vivo is found to make direct contact with the surfactant head groups, hydrophobic tails, and the iso-octane solvent. The fast backbone N-H relaxation dynamics show that the fluctuations of the protein encapsulated in the RM are reduced when compared to the protein in bulk. This reduction in fluctuations can be explained by the direct interactions of ubiquitin with the surfactant and by the reduced hydration environment within the RM. At high concentrations of excess salt, the protein does not bind strongly to the RM interface and the fast backbone dynamics are similar to that of the protein in bulk. Our simulations demonstrate that the confinement of protein can result in altered protein dynamics due to the interactions between the protein and the surfactant.

INTRODUCTION

The cellular environment is a crowded environment with high concentration (up to 400 grams per liter) of macromolecules, including proteins, nucleic acids, and complex sugars, which can take up to 40% of the total cellular volume and significantly reduce the available volume for proteins.¹ This is called the excluded volume effect, which has been shown to influence protein folding rates and stability.^{2, 3, 4, 5} Macromolecular crowding can also reduce protein diffusion rate,⁶ enhances the folding of marginally stable proteins,⁷ changes protein shape and structure,^{8, 9, 10} and affects protein dynamics.^{11, 12} In particular, confinement has been widely used to study crowding effects. Two common methods to introduce confinement include using sol-gel silica glass and reverse micelles.^{13, 14, 15}

Reverse micelles (RM) have been used to study confinement effects because of their many advantages. RMs are thermodynamically stable, nanometer-scale structures that can be formed spontaneously by many kinds of amphiphilic surfactants, such as Sodium bis(2-ethylhexyl) sulfosuccinates (AOTs). RMs have the ability to encapsulate biomolecules into their water pool. Confined waters in RMs have been proposed to mimic confined waters in biological systems.¹⁶ The size of RMs depends on the water to surfactant ratio, w₀, which can be well controlled to alter the confinement and hydration level.¹⁷ Depending on the choice of surfactant, the protein may not maintain the folded structure when encapsulated in a RM.¹⁸

Here, we study the confinement of ubiquitin in a self-assembled AOT reverse micelle. Ubiquitin is a 76 amino acid protein, which is ubiquitously expressed in the eukaryotes. Ubiquitin is highly conserved among eukaryotes and is involved in many cell processes and one prominent function is labeling proteins for ATP-dependent protein degradation.¹⁹ Its functionality is highly dependent on its dynamics and conformational changes. Ubiquitin motions have been extensively characterized over a range of time-scales by nuclear magnetic resonance (NMR) and molecular dynamics (MD) simulation.^{20, 21, 22, 23} Recently, the spin relaxation dynamics of ubiquitin confined in AOT RMs has been studied. In these experiments the AOT RMs are dissolved in low-viscosity solvent, in order to increase the tumbling speed of the confined protein.^{24, 25} Proof-of-principle studies have shown that the structure of ubiquitin does not change significantly upon encapsulation, although there are some changes in the dynamics.

We performed extensive MD simulations in order to understand the nature of the interactions of ubiquitin with RMs, the location of ubiquitin inside RM under various salt conditions, and identify the source of the observed altered ubiquitin dynamics in the confined environment. Self-assembled protein-RM system has been previously studied for an alpha-helical peptide by us²⁶ and a Trp-cage protein by Chaitanya et al.²⁷ In our studies, the reverse micelles are self assembled in the presence of the folded protein, and the dynamics and hydration of the protein are compared with ubiquitin in bulk water. To our knowledge, at this time, our calculations are the longest and most comprehensive simulation studies of self-assembled protein-RM systems. It is found that the protein in the RM is partially dehydrated relative to bulk conditions. We find that the protein dynamics are similar in both environments, and differences are restricted to specific regions of the protein. Interestingly, we found that the protein prefers to be close to the RM interface at low excess salt and for an idealized neutral head group RM. However, at high excess salt, the protein prefers the water phase of the RM. The free-energy of the positioning of ubiquitin relative to the center of mass of the RM, calculated using the adaptive biasing force algorithm,²⁸ show that at low salt (0.187 M NaCl) there is a significant force driving the system toward the AOT headgroups. This force is significantly weaker at higher salt concentration (1 M NaCl). In unbiased simulations it is found that ubiquitin binds to the AOT surfactants through the hydrophobic patch formed by residues Leu 8, Ile 44, and Val 70, which is the same patch that interacts with ubiquitin-binding-domains in vivo. In turn, this hydrophobic patch is surrounded by positively charged residues Lys 6, Lys 11, Arg 42, Lys 48, His 68, Arg 72, and Arg 74. The position of ubiquitin inside a RM is found to be correlated to the structure of water around the protein backbone.

METHODS

Simulations of ubiquitin-AOT RM Self assembly

The self-assembled protein-RM system simulated consists of 3562 water molecules, 286 AOTs, 16 691 isooctanes, 297 sodium ions, 12 chloride ions, and a single folded ubiquitin protein. The total number of atoms is 164 345 and the overall water to surfactant ratio w₀ is 12.5. The system has a high constitutive salt concentration because of the high sodium counter-ion concentration. In the self-assembled system the water pool within an AOT RM has as high as 4M of sodium ions. In addition to the 286 sodium ions added to balance AOT head group charges, 11 sodium ions and 12 chloride ions are added, giving one counter-ion for each charged amino acid in the protein. The NMR structure (PDB ID 1G6J) of ubiquitin is used as starting configuration for the protein. The His 68 residue is protonated and the net charge of the protein is +1. We used the AOT parameters described by Abel et al.,²⁹ the Amber ff99SB force field³⁰ for ubiquitin, and the united atom force field of Siepmann³¹ for isooctane. The AOT parameters that we use have been previously used in RM with iso-octane.²⁹ Experiments in RM are conducted with different solvents.^{14, 17, 18} However, to maintain consistency in the force field and with previous simulations,^{26, 29, 32, 33} we use iso-octane as the organic solvent. Simulations are conducted with the parallel molecular dynamics program NAMD.³⁴ In the initial configuration, one folded ubiquitin molecule with one layer of hydration waters is added to the system, and other components are randomly distributed within the simulation box, while avoiding inter atomic overlaps. The whole system is first energy minimized and then slowly heated up to 300 K using the NVT ensemble over 50 ps, after that the system was simulated under isobaric and isothermal conditions of 1 atm and 300 K. The Nose-Hoover Langevin piston is used for the pressure coupling and Langevin dynamics is used for the temperature coupling.^{35, 36} Van-der-Waals interactions are treated with a 1.0 nm cutoff distance, with a smooth switching to zero for distances between 0.9 and 1.0 nm. Full electrostatic interactions are considered using particle-mesh-Ewald (PME) with a 1.0 nm cutoff distance for direct interactions and grid size of 0.10 nm for the Fourier space interactions.³⁷ All bonds involving hydrogen atoms are constrained using SHAKE (Ref. ³⁸) and SETTLE,³⁹ thus allowing a 2 fs integration time step to be used. Configurations are saved every 10 ps for later analysis. To examine the reproducibility of the results and reduce dependence on the initial conditions, five independent simulations are performed starting from the same random arrangement of components but with different initial velocities: one for 400 ns and four for 100 ns each. All calculations are done at 300 K and 1 atm.

Simulations of ubiquitin in bulk water

To compare the protein dynamics in the RM with the protein in bulk water, the same protein configuration is solvated with 10070 TIP3P water molecules in a unit box of dimensions of 7.133 , 6.573 , and 6.839 nm. We also added 11 sodium ions and 12 chloride ions, giving one counter-ion for each of the charged amino acids in the protein. This makes the sodium concentration of 60 mM and chloride concentration of 66 mM for the system. The total number of atoms is 31 465. This system is equilibrated and heated up using the same process as for protein-RM system and simulated for 200 ns. We denote the protein-RM system URM and the protein bulk water system UBK.

Simulations of ubiquitin in pre-assembled RM

To separate fluctuations in shape of the RM from the dynamics of the protein, pre-assembled protein-RM systems are used for conventional MD (CMD) simulations aimed at studying the translation and rotation of the protein within the RM, and for the calculation of the potential of mean force (PMF) of ubiquitin location inside the RM. The shape of the RM is maintained by applying harmonic restraints to the position of the sulfur atoms in the AOT head groups. All other atoms are unconstrained. We have studied the system under different conditions: low excess salt (0.187 M NaCl), high excess salt (1.0, 1.5, 2.0, and 2.5 M NaCl) and in a RM composed by idealized neutral head group surfactants. In all cases, a pre-assembled spherically shaped RM with a total of 298 AOT surfactants is used. The system has box dimensions of 14.9 nm, 15.0 nm, 15.0 nm, with the RM placed at the center of the box and 10 264 iso-octanes outside the RM in the unit box. The radius of the water pool formed by the RM is 3.35 nm. The number of water molecules is chosen to make the density of water in the water pool to be close to bulk water density. In the initial configurations, each of the systems has one folded ubiquitin in the center of the water pool. In the low excess salt simulation, there are enough sodium ions to neutralize the system and an additional 11 sodium ions and 12 chloride ions, giving one counter-ion for each of the charged amino acids.

Simulations of ubiquitin in pre-assembled neutral surfactant RM

We simulated an idealized neutral-head group surfactants RM system, where we artificially modified the head group charges of the surfactant so that the net charge of the head group is zero although there are still partial charges for different atoms in the head group. (See supplementary material describing the partial charges for the neutralized AOT headgroups.⁴⁰) In the idealized neutral head group surfactants RM, no counter-ions are needed to neutralize the system, and we added 11 sodium ions and 12 chloride ions as excess salt. Four CMD simulations are performed for the idealized neutral head group surfactant RM, each of the simulations is 100 ns long. Three CMD simulations are performed for the high excess salt, each 50 ns long. One 25 ns CMD simulation is performed for the low excess salt concentration.

Potential of mean force calculations of ubiquitin positioning in RM

Potential of mean force calculations for the protein location inside the RM for the three conditions are conducted using the adaptive biasing force (ABF) algorithm contained in the NAMD program.²⁸ The reaction coordinate ζ used here is the distance between the center of mass of ubiquitin and the center of mass of RM. In the ABF algorithm, the force F_ζ acting along the reaction coordinate ζ is evaluated and progressively refined during the simulation to get the average force <F_ζ>. A biasing force is applied to counter this, so that the net force along the reaction coordinate is zero and the evolution of the system along ζ is mainly governed by its self-diffusion properties. The average force <F_ζ> obtained from this process is integrated to give the corresponding potential of mean force with the relationship,

$$\frac{dA\left(\zeta \right)}{d\zeta }=-⟨F_{\zeta }⟩,$$ (1)

where

$$A\left(\zeta \right)=\frac{1}{\beta }ln\left[P\left(\zeta \right)\right]+A_0$$ (2)

is the free energy of the state defined by the reaction coordinate ζ. The free energies are determined within an additive constant, A₀. For all the calculations, 0.01 nm wide windows are used and the average force is evaluated for each window. The convergence of the PMF calculation is determined by the convergence of the average force. The simulation time required for convergence of the average force on each window depends on the specific system. In our calculations, good convergence was achieved within 200 ps in each window. Each window has been sampled for at least 100 000 times before the construction of PMF.

Analysis of trajectories

We characterize the dynamics and hydration of ubiquitin in URM and UBK systems by calculating rmsd, water coordination number, water excess chemical potential, and the backbone order parameters. We calculate the backbone N-H relaxation data using a general framework named isotropic reorientation eigenmode dynamics (iRED) that enables the calculation of relaxation order parameters without the need to align all configurations to a reference structure.⁴¹ For a molecular dynamics simulation with a total of N configurations, we get orientational angle θ_kl between the k_th and l_th internuclear dipolar vectors for each pair of the n dipolar interactions of interest. Then a symmetric n × n covariance matrix C is constructed with each element,

$$C_{lk}=⟨P_2\left(cos\left({\theta }_{kl}\right)\right)⟩,$$ (3)

where P₂(x) is the second order Legendre polynomial. C is averaged over all saved configurations, N. The eigenvectors and corresponding eigenvalues of this matrix are principal modes of concerted motions in the protein and the corresponding motions amplitude, where the concerted motions include both global tumbling (5 largest modes) and internal motions (the rest n−5 modes). The Lipari-Szabo (LS) model free S² order parameters^{42, 43} can be calculated when the global modes and internal modes are separable with

$$S_l^2=\sum _m{S}_{l,m}^2.$$ (4)

The summation is for all the internal n − 5 modes and

$$\delta S_{l,m}^2={\lambda }_m\left(\right|m⟩{⟨m\left|\right)}_{l,l},$$ (5)

where |m> is the eigenvector and λ_m is the eigenvalue of matrix C. The separability between the internal modes and global modes is defined as

$$g_L=\frac{{\sum }_{m=1}^n{\lambda }_m}{{\sum }_{m=1}^{n-5}{\lambda }_m},$$ (6)

where the numerator corresponds to the sum of all eigenvalues and denominator corresponds to the sum of eigenvalues for all internal modes. In a system with large separability, the internal fluctuations and rotational motions are well separated.

In addition to the iRED calculation of the order parameters, all internal auto-correlation functions C_int(t) of backbone N − H internuclear vectors are calculated. First a reference structure of ubiquitin is set to be the average structure of all sampled configurations. Then all sampled configurations are aligned and superimposed to the reference structure using the backbone heavy atoms. Finally the auto-correlation function is calculated using

$$C_{\mathrm{int}}\left(t\right)=⟨P_2(a(\tau -t)\times a\left(\tau \right)⟩,$$ (7)

where a(τ) is the orientation of N − H vector and P₂(x) is the second Legendre polynomial. The autocorrelation function converges if |C_int(∞) − C_tail| ⩽ 0.005. C_tail is the mean value of the tail of the internal auto-correlation function and order parameter S² is extracted as the convergence value.⁴⁴ Density profiles of ubiquitin heavy atoms (hydrogen atoms excluded) and water oxygen atoms to the geometrical center of ubiquitin in URM and UBK are calculated using

$$\rho \left(r\right)dr=\sum _i\frac{m_i}{4\pi r^2}\delta (r-r_i).$$ (8)

The distance r is measured from the geometrical center of ubiquitin. The sum is over all the atoms of component a, m_i is taken as 1 for all atoms calculated here, and <⋯> represents the ensemble average over the last 150 ns of the simulations. The water coordination number is defined by using a 3.5 Å cutoff for water∕water and water∕protein interactions.^{45, 46} In each configuration, we define as bulk waters those waters that are not coordinated to protein atoms; penetrating waters as those that do not have any coordination to bulk water, and solvation waters as those that are coordinated to bulk waters and protein atoms.^{45, 46, 47, 48}

The water excess chemical potential is calculated using a simple Gaussian model. In this model μ_ex depends on the chemical potential of inserting a hard sphere into the cavity, ${\mu }_{ex}^0$, and the chemical potential contribution due to the binding energy of the water in the environment, Δμ_ex. We assume ${\mu }_{ex}^0$ to be the same in URM and UBK systems. The Δμ_ex is calculated with the Gaussian model and depends on the average binding energy, u, of water molecule in that environment and the width σ of the distribution of binding energy,^{47, 49, 50}

$${\mu }_{ex}={\mu }_{ex}^0+⟨u⟩+\frac{1}{2}\frac{{\sigma }^2}{{\kappa }_{B}T},$$ (9)

where σ² = 〈(u − 〈u〉)²〉.

RESULTS AND DISCUSSION

Self-assembly process and ubiquitin encapsulation

For the URM system, surfactants and waters are initially randomly distributed in the unit cell. Surfactants and ubiquitin are first solvated by water molecules, then solvated surfactants aggregate to form small RMs and finally large RMs come into shape with small RMs colliding and fusing together. The solvation process occurs within a few hundred picoseconds and small RMs form within several tens of nanoseconds. During the simulations ubiquitin maintained the secondary and folded structures, with backbone rmsd fluctuations of 0.12 nm from the starting configurations for both the URM and UBK systems (see Figs. s1 and s2 (Ref. ⁴⁰)). At the end of 30 ns, the system contains 16 small RMs, with an average of 18 surfactants in each RM. The formation of large RM through the collision and fusion of small RMs is a relatively slow process in our calculations. On average, during the first 200 ns, fusion-events are observed every 20 ns. At later stages in the simulation, the number of events is reduced as the number of RM decreases. In the 400 ns simulation, the last fusion event occurred at 350 ns. We do not observe events with fusion of more than two RMs. At the end of the simulation, there are six RMs remaining, with an average of 48 surfactants in each RM. The w₀ for five out of the six RMs is about 10, and the largest RM formed has 80 surfactant molecules, with w₀ = 17.8. The largest RM formed at 70 ns and remained stable for the remaining 330 ns. Ubiquitin is contained within the largest RM during this self-assembly process. These calculations indicate that the water to surfactant ratio of the protein containing RM is different (larger) than for the RM without protein and for the overall system (12.5). Figure 1 shows the position of ubiquitin inside the RM, which contains the ubiquitin at the end of the 400 ns URM simulation. The RM has two interfaces, one between the organic solvent and the AOT tails, another between the AOT headgroups and water in the interior of the RM. Ubiquitin locates at the AOT headgroup∕water interface of the RM, with the hydrophobic patch making direct contacts with the surfactant. Ubiquitin inside the RM is located at the AOT-solvent interface, with its hydrophobic patch, composed of Leu 8, Ile 44, and Val 70 in close contact with surfactant head groups of the RM. A positive face of the protein (Lys 6, Lys 11, Arg 42, Lys 48, His 68, Arg 72, and Arg 74) faces the negatively charged RM interface. There are a few water molecules and Na ions between the protein and the RM interface. Interactions between the protein hydrophobic patch and iso-octane molecules are also observed when a patch forms in RM interface and ubiquitin makes part of the RM surface.

Figure 1.

Structure of a RM containing ubiquitin. (a) Position of the protein (in CPK) inside a self-assembled RM. (b) Exterior surface view of the RM. Water molecules are shown as a red surface, AOT molecules are shown as a gray surface, Na ions are shown as orange spheres. The protein is shown in a CPK model. Ubiquitin binds to the AOT surfactants through the hydrophobic patch formed by residues Leu 8, Ile 44, and Val 70(green). This hydrophobic patch is surrounded by positively charged residues Lys 6, Lys 11, Arg 42, Lys 48, His 68, Arg 72, and Arg 74 (white). (c) Interior view of the ubiquitin∕AOT interface. The protein is shown in a ribbon model, except for sidechains that interact directly with AOT molecules. The N- (Met 1) and C- (Gly 76) termini amino acids are labeled. The figure was prepared using the VMD (Ref. ⁵¹).

More details about the position of ubiquitin in the RM are shown in Fig. 3s.⁴⁰ Four additional, 100 ns long, self-assembly simulations were conducted to verify the reproducibility of the self-assembly process and to verify the location of ubiquitin inside RM. In all four simulations, ubiquitin is encapsulated into the largest RMs formed during the self-assembly process and is located at the interface of RM with the hydrophobic patch making contact with surfactants. In Table 1, we show the detailed content for the RM which contains the protein formed at the end of the four 100 ns simulations and the 400 ns simulation. The w₀ for the RM containing ubiquitin in all four simulations is larger than the system average value of 12.5.

Table 1.

Final Composition of self-assembled RMs that contains an ubiquitin molecule.

	tsim	N			N	N	Net
System	(ns)	AOT	Nw	w0	Na	Cl	Charge
URM	400	80	1425	17.8	85	5	+1
SA-RMa	100	46	973	21.2	51	5	+1
SA-RMb	100	68	1298	19.1	73	6	+1
SA-RMc	100	84	1415	16.8	88	5	0
SA-RMd	100	37	877	23.7	38	2	0

Backbone N-H relaxation

The dynamics of ubiquitin in a RM (containing pentane as the organic solvent) have been characterized by NMR relaxation analysis.^{52, 53} Here we are interested in comparing the MD simulation results with available NMR data.^{52, 53} NMR spin relaxation measurements detect motions from picoseconds to nanoseconds, which is below or about the timescale of the global protein tumbling time. The motions measured are averaged over the ensemble of conformations covering time scales up to milliseconds. Long-time MD simulations are necessary to obtain good sampling of a protein native state ensemble in order to extract spin relaxation information. The self-assembled protein-RM system has been simulated for 400 ns, and we use the last 330 ns for analysis. During this period ubiquitin has been encapsulated and the size and shape of the RM encapsulating the protein are stable. The UBK system has been simulated for 200 ns and we use the last 150 ns for analysis. The comparison between the NMR data and the simulations is done by comparing the modeled Lipari-Zsabo^{42, 43} order parameters obtained from the experimental relaxation data with the calculated LS order parameters.

We calculated the LS model free S² order parameter using iRED for 72 N-H internuclear dipolar vectors for the URM system, plotted in Fig. s4 for different sampling times.⁴⁰ We assume that the principal axis of the dipole-dipole tensor is parallel to the N-H bond.⁵⁴ The order parameters for residues Leu 8 ∼Thr 12, Glu 18 ∼Thr 22, Gly 47∼ Gln 49 decrease as we increase the sampling time. Those regions are mainly loop regions which connect beta-sheets and helix. The order parameters for the remaining residues appear to be well converged as a function of sampling time. The decrease of the S² order parameters with sampling time is due to slow local motions. To show this, all internal auto-correlation functions C_int(t) of N-H were calculated and the order parameter were extracted as $S_{\mathrm{Ct}}^2$ (see Analysis). The agreement between the iRED and C_int order parameters indicate that the internal auto-correlation functions for most residues were converged within a few nanoseconds, except for residues Gly 10, Lys 11, Glu 18, Ser 20, Asp 21, Thr 22, Gly 47, and Lys 48, whose C_int(t) do not converge up to 100 ns, indicating the presence of slow local motions. The overall tumbling time of the protein in the simulations is approximately 3 ns. This value is smaller than the measured value, since the Tip3p water model exhibits faster dynamics than water by a factor of 2–3. The S² order parameter is extracted from the converged value of the auto-correlation function. Slow internal local motions with timescales longer than the global tumbling time will be undetected by the standard LS model free analysis.²¹ MD simulation calculations give the same weight to slow motions and fast motions and cause the extracted order parameters to be artificially smaller if a long sampling window is adopted.²⁰ In our calculations, 10 ns blocks are used to calculate order parameters and they are averaged over all the available blocks when we apply the iRED method. By doing so, we get good sampling of the fluctuations in the native state ensemble, without overweighting the effect of slow motions. S² order parameters derived using these two methods are compared with measured order parameters,⁵² (shown in Fig. 2). The calculated parameters compare well with the experimental parameters, except for residues Gln62, Arg72, and Gly75. The Pearson correlation coefficient between the two sets (using amino acids 2-71) is 0.6, the pairwise correlation is 0.5. The low correlation is in part due to the small dynamic range of the order parameters in the encapsulated system. The average differences between experiment and simulation values are 0.03 for both methods with the standard deviation of differences 0.03. We compare S² from iRED with the S² from experimental data, and the average difference is 0.04, with standard deviation of differences 0.02. These calculations show that the modified Amber99SB force field can reproduce well the observed backbone dynamics of ubiquitin in URM and provide a way of validating our simulations.

Figure 2.

LS model free S² Order parameters calculated using iRED, $S_{\text{iRED}}^2$, and internal correlation function, $S_{\mathrm{Ct}}^2$, for URM compared with experimental data, $S_{\exp }^2$. The black circle is from Simorellis and Flynns NMR experiments, the upper part red triangles are S² calculated from iRED using 10 ns blocks and the blue triangles are S² calculated using internal correlation function, and the low parts are the corresponding difference between simulation and experimental data. The inset shows a scatter plot of the experimental and simulation order parameters. The dashed line represents y = x curve, with intercept zero and slope 1.

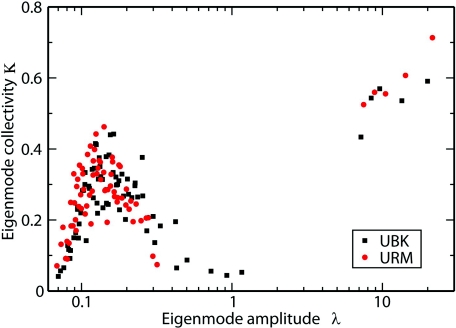
In Fig. 3 we compare the S² order parameters for URM and UBK. The changes in order parameters in the two environments are shown as a blue line. The order parameters for most of the residues have increased by a small amount in the URM. Significant increases are observed for residues Thr 7 to Ile 13, which are the loop region residues connecting beta-sheets I and II. In addition, the order parameters for residues Ile 36, Gln 40, Gln 41, and Arg 72 to Gly 76 have also increased significantly, which indicates that these residues are more rigid in URM than in UBK. Simorellis et al. observed that residues Leu 8, Glu 16, Gln 40, Gln 41, Leu 56, Leu 71, and Leu 73 became more rigid in RM.⁵² Our calculations agree with these observations. From the collectivity of the eigenmode plot, shown in Fig. 4, we can see the gap between global motion modes (the five largest lambda points) and internal motion modes (the remaining points) are larger in URM than in UBK. The separability between these global and internal motion modes is 7.68 and 5.39 in URM and in UBK, respectively. The larger separability indicates larger separation between protein global and internal fluctuations, which tells us that ubiquitin is more rigid in URM than in UBK.

Figure 3.

Comparison of LS model free S² order parameters for ubiquitin in URM and in UBK. The black line corresponds to the order parameters in UBK, $S_{\mathrm{UBK}}^2$, and the red line corresponds to the order parameters in URM, $S_{\text{URM}}^2$. The blue line corresponds to the difference between URM and UBK with positive values denoting larger order parameters in URM.

Figure 4.

Comparison of Eigenmode collectivity in URM and UBK systems. The red circles are the eigenvalues and the corresponding collectivity of the eigenmode in URM, while the black squares are those in UBK. κ is a measure of the relative number of N-H vectors that are significantly affected by a given mode (Ref. ⁴¹).

Backbone hydration structure

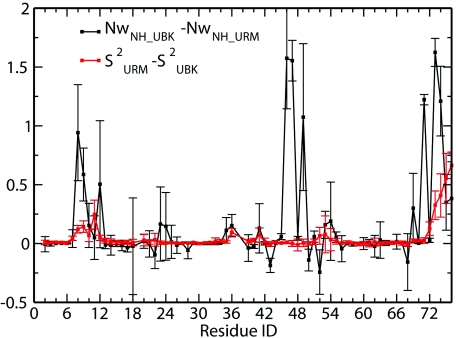
The LS model free S² order parameter calculations verified that ubiquitin becomes more rigid upon encapsulation, with residues Thr 7 to Ile 13, Ile 36, Gln 40, Gln 41, and Arg 72 to Gly 76 showing larger order parameter values. Ubiquitin's increased rigidity also results in a larger separation between global motion and internal motion. The regions with increased rigidity also show a decrease in water coordination and an increase in coordination to the AOT surfactant molecules. The N-H water coordination numbers are calculated and the difference for ubiquitin in URM and UBK systems is shown in Fig. 5. Water coordination number of N-H decreased significantly for those residues whose order parameters increased significantly upon encapsulation into a RM. This correlation between N-H dehydration and an increase in order parameters is unexpected, but it is the result of direct sidechain interactions with the AOT molecules. We also noticed that the residues with increased order parameters are also largely coordinated to AOT heavy atoms. In the simulations in high excess salt RM, where ubiquitin is preferentially located in the water pool, the order parameters are the same as those for ubiquitin in bulk. Ubiquitin is located off the center of the RM, but not close to the interface, its residues have no direct contact with surfactant molecules, and no residue backbone is highly dehydrated when compared to bulk. These results clearly show that dehydration of NH and strong interaction with surfactants result in the increase of order parameters for ubiquitin in RM.

Figure 5.

Comparison of N-H water coordination number and S². Black line shows N-H water coordination number difference for URM and UBK systems; red line shows N-H order parameter difference in URM and UBK systems.

Protein internal hydration

Many proteins, including ubiquitin, contain water molecules in the interior of their hydrophobic core.^{45, 55, 56} These waters are important to protein dynamics and conformational changes. Protein cold denaturation is also believed to involve water penetration of the protein core.⁵⁷ Based on coordination number calculations, we define penetrating water and solvating water (see Analysis), and the number of these two kinds of waters in the URM and UBK systems are shown in Table 2. There are, on average, two more water molecules penetrating in UBK than in URM, while there are twice as many solvating waters in UBK than in URM. The major difference in solvation waters comes from the location of ubiquitin in the URM system. We have already seen that ubiquitin locates at the interface of the RM, where its positively charged side faces RM interface, with the hydrophobic patch in contact with surfactants. There are very few waters between this positively charged side of ubiquitin and RM interface.

Table 2.

Number of penetrating and solvating waters for ubiquitin in URM and UBK environments.

	URM	UBK	URM	UBK
	penetrating	penetrating	solvating	solvating
Average	17.1	18.8	242.6	514.5
Std.Dev.	3.8	4.2	26.4	20.1

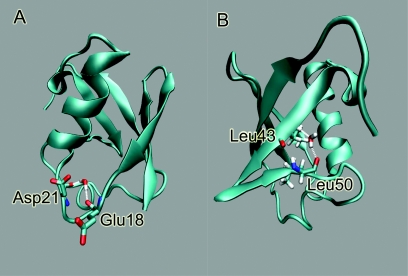
We define water pockets as those regions in the protein interior in which penetrating water molecules have long residence time (larger than 100 ps).^{50, 58} Two water pockets are identified in the URM and UBK systems (shown in Fig. 6). Pocket-U is located at the loop region near residues Glu 18 to Asp 22, and the water there has hydrogen bonds with Glu 18 and Asp 21 carbonyl oxygens; pocket-V is located between beta-sheet III and beta-sheet IV, and the water there makes hydrogen bonds with Leu 43 nitrogen and Leu 50 carbonyl oxygen. Pocket-U and pocket-V are named due to the shape of pocket region. The hydration of Pocket-V has been studied by Denisov et al.,^{59, 60} and water in this pocket is responsible for the ¹⁷O relaxation dispersion. The lifetime for a long-lived buried water molecule in ubiquitin has been estimated to be 60–90 ns.⁶⁰ In our calculations, the hydrogen bonds of water with ubiquitin polar atoms make the water stable there. The range of water residence time in pocket-V is about 0.6 to 2.0 ns; while it is 2.0 to 20.0 ns in pocket-U, for systems in bulk and RM. However, the residence time in water pockets in URM system is slightly longer than that in UBK. The excess chemical potential of water molecules, δμ_ex, in pocket-U is calculated using the Gaussian approximation model.⁴⁹ Table 3 shows the excess chemical potential for bulkwater and water in pocket-U. Bulk water refers to water molecules that do not bind or penetrate into ubiquitin. Water in pocket-U has higher binding energy but the distribution is narrower than bulkwater, so the excess chemical potential is lower than bulkwater both in UBK and URM. The calculated excess chemical potential of bulkwater and water in pocket-U are the same within thermal fluctuations in URM and UBK. The excess chemical potential difference of water penetrating into pocket-U is also the same in URM as in UBK. These results show that encapsulation does not affect the free energy of water penetration into ubiquitin. We did not calculate the chemical potential in the pocket-V since we did not have enough sampling of water on this region.

Figure 6.

Water Pockets in Ubiquitin: on the left is water pocket-U, which is located at the loop region of residues 18 to 22. Water molecules in this pocket form hydrogen bonds with the Glu 18 and Asp 21 carbonyl oxygens. On the right is water pocket V, which is located between beta-sheet III and beta-sheet IV. Water molecules in this pocket form hydrogen bonds with the Leu 43 nitrogen and the Leu 50 carbonyl oxygen.

Table 3.

Excess chemical potential for waters in pocket-U.

	Bulk	Pocket-U	Difference
System	(kcal∕mol)	(kcal∕mol)	(kcal∕mol)
URM	−9.6(.2)	−15.1(.1)	−5.5 (.2)
UBK	−9.2(.2)	−14.6(.1)	−5.5 (.3)

Interactions of ubiquitin with AOTs

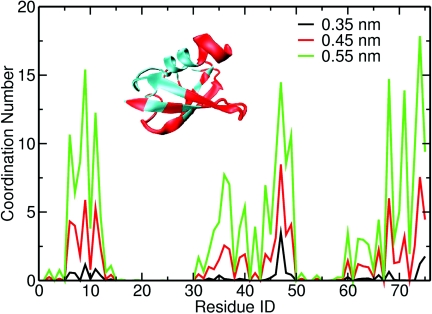
The location of a protein encapsulated in a RM depends on the protein, surfactant, and water pool conditions.^{61, 62, 63} In our simulations, ubiquitin is located at the interface of the RM with its hydrophobic patch in contact with surfactants. We calculated the ubiquitin sidechain coordination numbers to surfactant heavy atoms using different distance cutoffs between the protein and AOT atoms. We mapped the residues that have large AOT coordination numbers on the ubiquitin structure (shown in Fig. 7). When ubiquitin binds to other proteins, the binding occurs mainly through the I44 region, with residue G47 having the largest number of contacts.⁶⁴ Our simulation shows that there is a high correlation between residues that have large contact to surfactant heavy atoms and residues that have large contact number with ubiquitin-binding proteins in vivo. In the RM, ubiquitin rearranges itself in such a way that it interacts with RM through the hydrophobic patch, which is the same way as it interacts with ubiquitin binding domains.⁶⁵ Positively charged residues Lys 6, Arg 42, and Lys 48 near the hydrophobic patch make this side electrostatic positive. One possible reason for this binding mode is that AOT surfactants are negatively charged and they attract the positively charged ubiquitin side via electrostatic interaction. The residues that we see interact with the RM have been observed to disappear in low temperature ubiquitin∕AOT∕pentane experiments. Ubiquitin cold denaturation has been previously studied by the groups of Wand,⁶⁶ and Flynn.^{67, 68} Under low excess salt concentration, which are the condition of our self-assembly simulations, it is observed that denaturation is non-cooperative, multistate, with resonances corresponding to residues that make up the I44 face are lost, while resonances corresponding to the opposite face remained.^{66, 67, 68} In Fig. 7, we show the residues that have large surfactant heavy atom coordination. These residues overlap with the residues that lost resonance signals in Babu et al. cold denaturation NMR experiments.⁶⁶ Wand and co-workers and Flynn and co-workers disagree about the origin of the observed low temperature behavior of ubiquitin in RM. Flynn and co-workers have argued that the loss of resonances in the Ile44 region is due to interactions of ubiquitin with AOT headgroups.^{16, 68} The interaction between proteins and AOT RM has been previously shown to denature proteins.^{63, 69} Recent studies of ubiquitin in supercooled water failed to see cold denaturation of ubiquitin down to −32^○C in micro length emulsions.⁵⁷

Figure 7.

(a) Coordination number of ubiquitin side chains to surfactant heavy atoms. (b) Ubiquitin tertiary structure with residues that have large AOT heavy atoms coordination shown in red.

Location of ubiquitin within RM

To understand the energetics of ubiquitin positioning in the RM, we studied the location of ubiquitin inside the RM for three cases: low excess salt concentration (187 mM NaCl), at higher excess salt concentration (1.0, 1.5, 2.0, and 2.5 M NaCl) and in a RM composed by idealized neutral head group surfactants. We first conducted conventional MD simulations with ubiquitin initially placed at the center of the RM. In the low excess salt simulation, ubiquitin drifts toward the interface of the RM in about 10 ns and finally has direct contact with the surfactants. In the higher excess salt simulations, ubiquitin diffuses longer in the water bath of the RM before it reaches the AOT headgroups. In the simulation utilizing idealized neutral head group surfactants, ubiquitin drifts slowly and finally reaches the interface of the RM, where it remains for a long period of time. For this system we performed four different simulations and the migration process occurred between 20 and 80 ns of simulation time. In each case ubiquitin binds to the RM interface. These molecular dynamics simulations suggest that ubiquitin binds strongly at low salt and weakly under higher excess salt conditions. The interactions of ubiquitin with the AOT RM are better characterized by potential of mean force calculations, described next.

Potential of mean force calculations

We calculated the potential of mean force that describes the free energy of the position of ubiquitin in the RM, using the distance between the center of mass of ubiquitin and the center of mass of the RM as reaction coordinates (see methods). Figure s5 shows the schematic picture of ubiquitin in the RM.⁴⁰ The PMFs for three cases (187 mM, 1.0 M NaCl, and neutral surfactant RM) are shown in Fig. 8. In the RM with low excess salt, there is a strong bias toward the interface of the RM, with a free energy of 17 kcal∕mol, favoring the association of ubiquitin with the interface. The minimum of the PMF is located at about 1.48 nm, a distance at which ubiquitin starts to have direct contact with surfactant molecules. At higher excess salt concentration (1 M) the PMF is almost flat with slight decrease in free energy of less than 1 kcal∕mol, up to 0.9 nm, and after that it increases sharply. This is consistent with what we observed in the conventional MD simulations described above, in which ubiquitin diffuses widely inside the RM, without a strong bias toward the RM interior surface. In the system with idealized-neutral-head-group surfactants, the PMF is also flat, with a slight decrease up to 1.45 nm, when the PMF increases sharply. This also agrees with the conventional MD simulations in which ubiquitin drifts toward the interface of the RM, but the time it takes to reach the surface varies significantly since there is only a small bias force driving ubiquitin toward the interface of the RM. The difference between the minimum distance for low excess salt concentration and idealized neutral head group surfactants might come from the difference of orientation of ubiquitin inside the RM.

Figure 8.

Potential of mean force for ubiquitin in a RM with (a) low excess salt concentration (0.187 M NaCl), (b) at higher excess salt concentration (1 M NaCl) , and (c) in an idealized neutral head group surfactants. The reaction coordinate is the distance between center of mass of ubiquitin and center of mass of the RM.

Two kinds of forces exist in the protein-RM system that can drive the location of ubiquitin inside RM. One is the electrostatic attraction between positively charged ubiquitin sidechains and negatively charged AOT head groups. Model charged proteins with net dipole moments (modeled as hard spheres) are known to be driven to the interface of RM with a large bias.⁷⁰ The other force comes from the increase of water entropy. In the systems at low excess salt RM and with neutralized head group surfactants RM, interfacial waters have slower dynamics than those waters in the core region.^{71, 72, 73} By locating at the interface of the RM, ubiquitin shares hydration waters with the surfactant head groups and sodium ions and releases waters to the center of the RM that otherwise will hydrate ubiquitin. The released water will have larger translational and rotational entropy in the center of RM.²⁶ At low excess salt concentration, both forces apply so that there is a strong bias toward the interface of RM. While in the idealized neutral head group surfactants, the electrostatic attraction force is not present and only the entropy force acts so that the bias toward interface is small. At the high excess salt concentration, the electrostatic attraction force between ubiquitin and surfactant head groups is weakened due to screening. In addition, water molecules inside the RM water pool either hydrate ions, surfactant head groups or ubiquitin, such that there is no difference in the behavior of waters in different regions inside the RM. Overall, there is no strong bias for placing ubiquitin at the RM interface at high excess salt concentration.

CONCLUSIONS

We have conducted extensive molecular dynamics simulations on a self-assembled protein-RM system which is composed of AOT surfactants, water, a single folded ubiquitin, ions (Na+ and Cl-), and iso-octane. These simulations provided information about the location of the ubiquitin inside RM, the interaction between ubiquitin and surfactants, and the hydration structure and the protein dynamical changes of the encapsulated ubiquitin, when compared with ubiquitin in bulk water. These simulations provide an atomic level description of the structure and dynamics of the protein-RM system in the sub microsecond timescale, which we now describe.

The self-assembly process of the protein-RM system is demonstrated and verified by multiple, hundreds of nanoseconds long, molecular dynamics simulations. In these simulations ubiquitin is consistently contained into the largest RM formed. The positioning and orientation of the molecule is always the same: ubiquitin is located at the interface region of the RM, and the binding occurs through the hydrophobic patch formed by residues Leu 8, Ile 44, and Val 70, which is the same patch recognized by ubiquitin binding domains in vivo.⁶⁵ The side of ubiquitin facing the RM interface is positively charged, and the sidechains make direct interactions with the surfactants. The region of ubiquitin making contacts with the RM is partially dehydrated because of its location at the interface. This partial dehydration and the strong interactions with the surfactant result in a decrease of fast local backbone dynamics and make the protein more rigid when compared with ubiquitin in bulk water. The strength of the protein interactions with the RM interface can be controlled by changing the surfactant compositions and the RM water pool ionic conditions. At low excess salt conditions (0.187 M NaCl), which are the condition used for our studies of self-assembled systems, ubiquitin is located at the interface of the RM through the hydrophobic patch with a driving bias as large as 17 kcal∕mol. In an idealized RM, formed by surfactants with neutralized head groups, ubiquitin also prefers the interface region but with a much weaker driving bias, which is only 1 kcal∕mol. At higher excess salt conditions (1.0 to 2.5 M NaCl), where electrostatic interactions are screened significantly, ubiquitin samples widely the RM interior and exhibits fluctuations similar to those of the protein in bulk water. These results suggest that electrostatic interactions play a significant role in determining the interactions and location of the protein inside the RM. However, there are also weaker entropic forces associated with the surfactant and the protein hydration that provide a driving force for binding of the protein to the RM surface. Previous calculations²⁶ and experiments^{14, 17} on charged and neutral alpha helical peptides have shown that the peptides have a preference for the RM interface.

The behavior that we see in ubiquitin and alpha helical peptides may not be seen in other proteins or in RM formed with other surfactants. Depending on the surfactant type (cationic, anionic, or neutral) and the protein charge distribution and charge states, the location and orientation of the protein inside a RM may be different. Ubiquitin inside cationic RM is expected to bind through different face than in AOT RM. The interaction between the protein and the AOT RM has been previously shown to denature proteins.^{63, 69} In our calculations, the direct interactions between the protein and surfactants changed the protein dynamics. Under slightly varying conditions of pH and temperature and in a timescale appropriate for folding∕unfolding dynamics, the interactions between the protein and surfactant may lead to unfolding, as seen in the non-cooperative cold denaturation of ubiquitin in RM.^{66, 67, 68}

Our simulation studies presented here provide a detailed atomic description of the structure and dynamics of a protein-RM system. The results and findings presented can serve to guide future studies on protein-RM system. More significantly, the dependence of the recognition (binding) of a surface on local solvent conditions, surface charge, and protein charge distribution provide insights into the complexity of protein dynamics in a crowded cellular environment that goes beyond the availability of free volume, commonly invoked to explain crowding effects.^{2, 3, 4, 5} Our results suggest that interactions of the protein with the confining environment may be stronger than the entropic effects due to confinement.