Reexamining protein–protein and protein–solvent interactions from Kirkwood-Buff analysis of light scattering in multi-component solutions

Abstract

The classic analysis of Rayleigh light scattering (LS) is re-examined for multi-component protein solutions, within the context of Kirkwood-Buff (KB) theory as well as a more generalized canonical treatment. Significant differences arise when traditional treatments that approximate constant pressure and neglect concentration fluctuations in one or more (co)solvent∕co-solute species are compared with more rigorous treatments at constant volume and with all species free to fluctuate. For dilute solutions, it is shown that LS can be used to rigorously and unambiguously obtain values for the osmotic second virial coefficient (B₂₂), in contrast with recent arguments regarding protein interactions deduced from LS experiments. For more concentrated solutions, it is shown that conventional analysis over(under)-estimates the magnitude of B₂₂ for significantly repulsive(attractive) conditions, and that protein-protein KB integrals (G₂₂) are the more relevant quantity obtainable from LS. Published data for α–chymotrypsinogen A and a series of monoclonal antibodies at different pH and salt concentrations are re-analyzed using traditional and new treatments. The results illustrate that while traditional analysis may be sufficient if one is interested in only the sign of B₂₂ or G₂₂, the quantitative values can be significantly in error. A simple approach is illustrated for determining whether protein concentration (c₂) is sufficiently dilute for B₂₂ to apply, and for correcting B₂₂ values from traditional LS regression at higher c₂ values. The apparent molecular weight M_{2, app} obtained from LS is shown to generally not be equal to the true molecular weight, with the differences arising from a combination of protein-solute and protein-cosolute interactions that may, in principle, also be determined from LS.

INTRODUCTION

Light scattering (LS) from protein solutions has long been used to provide information regarding protein-protein interactions^{1, 2, 3, 4, 5, 6, 7} via the protein osmotic second virial coefficient (B₂₂). In keeping with common practice, the Scatchard notation for aqueous protein solutions is adopted here, with 1 denoting water, 2 denoting protein, and i = 3, 4, … denoting any co-solvent and co-solute species.⁸B₂₂ is formally related to protein–protein interactions in the limit of low protein concentration (c₂), averaged over the spatial degrees of freedom of the solvent and any co-solute or co-solvent species – i.e., the protein–protein potential of mean force W₂₂ in a grand-canonical ensemble⁹ via

$$B_{22}=-\frac{1}{2}\int (e^{-W_{22}∕k_{B}T}-1)4\pi r^{2}dr,$$ (1)

where k_B is the Boltzmann constant, T is the absolute temperature, and r denotes distance between centers-of-mass. Although one can derive a similar equation to Eq. 1 in any thermodynamic ensemble, the osmotic second virial coefficient is recovered only when the protein–protein potential of mean force comes from a grand-canonical ensemble.⁹ Otherwise the integral has a different thermodynamic meaning. For example, by using W₂₂ from a canonical ensemble (fixed temperature, composition, and volume) to solve the integral in Eq. 1, one obtains the trivial solution⁹ that the integral is independent of the magnitude or sign of the interactions described by W₂₂. The interested reader is referred to detailed discussions and derivations elsewhere (e.g., Refs. ^{9, 10}).

B₂₂ and other osmotic virial coefficients play central roles in both qualitative and quantitative models and theories relating colloidal protein-protein interactions to protein crystallization and fluid-fuid phase behavior,^{11, 12, 13, 14, 15, 16, 17, 18} protein aggregation,^{19, 20, 21, 22, 23, 24} and protein purification.^{25, 26, 27} In some cases, only the sign of B₂₂ is considered important, as a negative (positive) B₂₂ corresponds to net attractive (repulsive) protein-protein interactions relative to an ideal solution.^{9, 10, 28} More recent work highlights the importance of considering an equivalent hard-sphere (HS) or purely steric protein-protein interaction (i.e., $B_{22}^{HS}$) as a more appropriate reference point.^{24, 29, 30, 31} That is, systems with $B_{22}∕B_{22}^{HS}>1$ have non-steric interactions that are dominated by non-steric repulsions, while those with $B_{22}∕B_{22}^{HS}<1$ are dominated by attractive interactions.

Recent experimental comparisons between LS and alternative means to estimate B₂₂ have led some authors to conclude that LS fundamentally does not yield B₂₂ as an independent quantity – i.e., that the apparent virial coefficient (A₂) from traditional LS analysis is instead a convolution of B₂₂ with protein-cosolute and∕or (co)solvent virial coefficients.^{32, 33} This is potentially problematic, as LS is arguably the historic method of choice for determining B₂₂, and is the basis for much if not the majority of experimental B₂₂ values reported in the literature.^{34, 35, 36, 37}

The original treatments by Stockmayer and others form the basis of most non-trivial derivations to relate Rayleigh scattering to deviations from ideal solution for any solute-solvent system.^{38, 39, 40, 41} The approach proposed by Stockmayer has been the most widely used and accepted.^{42, 43, 44, 45, 46} For thermodynamic convenience and mathematical simplicity, Stockmayer's treatment and those of others make the simplifying assumption that fluctuations in pressure (p) and solvent (water) concentration are negligible within the scattering volume. That is, the scattering (sub)volume is treated as though it contains a constant number of water molecules, and it is implicitly assumed that one can neglect the differences between constant pressure and constant volume for the scattering region of the fluid. Corrections have also been applied to account for requirements of electroneutrality and resulting Donnan effects on A₂,⁴⁴ particularly for the case of protein solutions. As noted above, recent derivations^{32, 33} have been proposed that argue A₂ from LS contains contributions from other osmotic virial coefficients, or from Donnan contributions via constraints of electroneutrality.⁴⁴ Alternatively, Casassa and Eisenberg^{47, 48} corrected Stockmayer's treatment by imposing electroneutrality through the equilibration of protein with cosolutes within the scattering volume (a correction which was implicitly obtained herein). Nevertheless, in all of the above cases, fluctuations in pressure and solvent concentration are neglected, and fluctuations in the remaining species are related to LS intensity via thermodynamic transformations that express non-idealities in terms of activity coefficients,^{38, 39, 42, 44, 49, 50, 51} implying, as it is shown below, that information about interactions between solvent and all the other components is not recovered explicitly, but rather it is convoluted within A₂ and the apparent molecular weight.

This report examines the result of relaxing these assumptions, as well as utilizing Kirkwood-Buff (KB) solution theory⁵² to rigorously and more generally relate LS to protein-protein, protein-solvent, and protein-cosolute interactions. The results highlight errors or unnecessary approximations in alternative treatments, and also provide a new mathematical description of LS that in principle is valid at both low and high protein concentration, with a straightforward means to extract protein-protein KB integrals (G₂₂) from LS data. The remainder of the article is organized as follows. In Sec. 2, a general equation for Rayleigh scattering from multi-component solutions is developed in terms of KB integrals. Dilute and semi-dilute protein solutions are then considered in Sec. 3, including a comparison with a more general version of the traditional, non-KB approach that is strictly valid only for non-ionizable solutes. A more general expression is also derived in the canonical framework that does not assume c₂ → 0. Additionally, the supplementary material⁵³ provides a comparison with the simplest and the most traditional thermodynamic analysis with non-dissociable solutes to show equivalence between the two approaches as c₂ → 0 if fluctuations in pressure and solvent species are not neglected, and if protein-solvent and protein-cosolute interactions can be neglected. Finally Sec. 4 uses the working equations from the KB and more general canonical approaches, as well as the standard expression,⁵⁴ and analyzes published LS data for α–chymotrypsinogen A (aCgn) and a set of monoclonal antibodies (mAb)^{24, 31} to highlight differences in the resulting B₂₂ (or G₂₂) and apparent molecular weight values as a function of solvent pH and NaCl concentration for experimental systems.

KIRKWOOD-BUFF THEORY APPLIED TO RAYLEIGH SCATTERING FROM MULTICOMPONENT SOLUTIONS

Laser light scattering from multicomponent single-phase solutions due to Rayleigh scattering is described by the theory of Einstein,⁵⁵ with each species treated as a point scatter so long as its characteristic dimension is sufficiently small compared to the wavelength of the incident light.^{28, 38, 39, 56, 57} In the case of laser light scattering, light is scattered from a small but macroscopic volume V within a bulk solution, with time-averaged scattered intensity that is proportional to the magnitude of ensemble-averaged fluctuations in the dielectric constant, or equivalently fluctuations in refractive index (n),

$$R_{90}=\frac{4{\pi }^2{n}^2⟨{\left(\Delta n\right)}^2⟩V}{{\lambda }^4},$$ (2)

where R₉₀ is the Rayleigh ratio for a 90 degree scattering angle, and λ is the wavelength of incident light in vacuo. The brackets 〈⋅⋅⋅〉 denote an ensemble average. The fluctuations in refractive index within the scattering volume are expressed based on the total differential for n as a function of temperature (T), volume (V), and the number of molecules of each species (N_j, j = 1, 2, …). For fixed scattering volume, and assuming negligible fluctuations in temperature, this gives

$$\Delta n=\left(n-\overline{n}\right)\approx dn=\sum _j{\left(\frac{\partial n}{\partial N_j}\right)}_{T,V,N_{k\ne j}}d{N}_j.$$ (3)

Squaring Eq. 3 and ensemble averaging gives

$$\begin{array}{ccc}\hfill ⟨\Delta n^2⟩& =& \sum _i{\left(\frac{\partial n}{\partial N_i}\right)}_{T,V,N_{k\ne i}}^2\left(⟨N_i^2⟩-{⟨N_i⟩}^2\right)\hfill \\ & & +2\sum _{i<j}{\left(\frac{\partial n}{\partial N_i}\right)}_{T,V,N_{k\ne i}}{\left(\frac{\partial n}{\partial N_j}\right)}_{T,V,N_{k\ne j}}\hfill \\ & & \times (⟨N_i{N}_j⟩-⟨N_i⟩⟨N_j⟩).\hfill \end{array}$$ (4)

Because the scattering volume is open to exchange of all species and is constant volume and effectively constant temperature, the fluctuations in species concentrations are most easily and naturally expressed in terms of Kirkwood-Buff (KB) integrals (G_ij) in the grand canonical ensemble^{9, 52, 58}

$$⟨N_i{N}_j⟩-⟨N_i⟩⟨N_j⟩=⟨N_i⟩\left({\delta }_{ij}+\frac{⟨N_j⟩}{V}{G}_{ij}\right),$$ (5)

with δ_ij denoting the Kronecker delta function, the brackets denoting the average within the grand canonical ensemble for the scattering volume, and with G_ij defined by

$$G_{ij}=\int ({\overline{g}}_{ij}\left(r\right)-1)4\pi r^{2}dr,$$ (6)

where ${\overline{g}}_{ij}\left(r\right)$ is the molecular pair correlation function for component i with respect to component j. It gives the probability, relative to an ideal mixture, of finding an i − j pair of molecules at a distance r between centers-of-mass, averaged over the orientations of species i and j, and averaged over the possible positions and orientations of all other species in the mixture. The overbar indicates that the averaging must be done in an open system, i.e., with fixed chemical potential (μ) of each of components i and j, and not with fixed N_i or N_j.^{9, 58} This is equivalent to a weighted average over the canonical pair correlation functions g_ij(r; N_i, N_j) across all possible values of (N_i, N_j).⁹ That is, g_ij(r; N_i, N_j) is the pair correlation function in the closed ensemble at fixed (N_i, N_j). The overbar indicates an average over p(N_i, N_j)g_ij(r; N_i, N_j), with p(N_i, N_j) denoting the equilibrium probability of observing a particular set of (N_i, N_j) values within the open (i.e., grand canonical) ensemble.⁵⁸ The average values for each species are fixed by the bulk composition of the solution, within which the scattering volume is a small subsystem. Equations 5, 6 are general; they do not require assumptions of pairwise additivity, and inherently incorporate restrictions of electroneutrality for ionic solutions, provided that the system volume is open to exchange of all ionized species.

Combining Eqs. 2, 4, 5 gives upon rearrangement

$$\begin{array}{ccc}\hfill \frac{R_{90}}{K^{\prime }}& =& \sum _i{\left(\frac{\partial n}{\partial c_i}\right)}_{T,V,N_{k\ne i}}^2{c}_i(c_i{G}_{ii}^{\prime }+1)\hfill \\ \hfill & & +2\sum _{i<j}{\left(\frac{\partial n}{\partial c_i}\right)}_{T,V,N_{k\ne i}}{\left(\frac{\partial n}{\partial c_j}\right)}_{T,V,N_{k\ne j}}{c}_i{c}_j{G}_{ij}^{\prime },\hfill \end{array}$$ (7)

where c_i = N_i/(VN_A) is the concentration of component i on a mole∕volume basis, and the prime on each G_ij indicates that the KB integrals have units of volume∕mole. K′ is given by $4{\pi }^2{n}^2{N}_A^{-1}{\lambda }^{-4}$, with N_A denoting Avogadro's number. The prime is to distinguish this from the closely related quantity K that appears in traditional treatments of LS.

Experimentally, changes in n with bulk solvent and solute concentrations are more easily evaluated at fixed pressure (p), rather than at fixed V. Transforming the derivatives of refractive index from constant V to constant p gives

$$\begin{array}{ccc}\hfill {\left(\frac{\partial n}{\partial {\mathbf{n}}_{\mathbf{i}}}\right)}_{T,V,{\mathbf{n}}_{\mathbf{k}\ne \mathbf{i}}}& =& {\left(\frac{\partial n}{\partial {\mathbf{n}}_{\mathbf{i}}}\right)}_{T,p,{\mathbf{n}}_{\mathbf{k}\ne \mathbf{i}}}+{\left(\frac{\partial n}{\partial p}\right)}_{T,\left\{{\mathbf{n}}_{\mathbf{k}}\right\}}\frac{{\overline{v}}_i}{⟨V⟩{\kappa }_T},\hfill \end{array}$$ (8)

where {n_k} denotes the set of all mole numbers, ${\overline{v}}_i$ the partial molar volume of component i, κ_T the isothermal compressibility of the solution, and 〈V〉 the average volume of a solution with {n_k} at the T and p of interest.

Using Eq. 8 in Eq. 7 gives

$$\frac{R_{90}}{K^{\prime }}=\sum _i{\eta }_i^2{c}_i(c_i{G}_{ii}^{\prime }+1)+2\sum _{i<j}{\eta }_i{\eta }_j{c}_i{c}_j{G}_{ij}^{\prime },$$ (9)

with

$${\eta }_i=\left(1-c_i{\overline{v}}_i\right){\left(\frac{\partial n}{\partial c_i}\right)}_{T,p,c_{k\ne i}}+{\left(\frac{\partial n}{\partial p}\right)}_{T,\left\{{\mathbf{n}}_{\mathbf{k}}\right\}}\frac{{\overline{v}}_i}{{\kappa }_T}.$$ (10)

At dilute conditions of component i, the term $c_i{\overline{v}}_i$ in Eq. 10 can be neglected. Equations 9, 10 apply generally, and show that Rayleigh scattering as a function of solvent composition and solute concentrations can be described succinctly in terms of KB integrals, the dependence of n on the bulk concentrations of solvent and solute(s), the volumetric properties of the solution, and the dependence of n on pressure. The magnitude and sign of the difference between treating scattering as a constant pressure process instead of constant volume is then determined by the second term in Eq. 10, and this quantity is squared in the expression for Rayleigh scattering. In a sense, this indicates the magnitude of the errors introduced by neglecting pressure fluctuations, and thereby assuming one can replace η_i with $\left(1-c_i{\overline{v}}_i\right){\left(\partial n∕\partial c_i\right)}_{T,p,c_{k\ne i}}$.

RAYLEIGH SCATTERING IN DILUTE PROTEIN SOLUTIONS

Protein-protein and protein-solvent interactions from KB analysis

Consider a ϑ - component mixture of water (component 1), protein (component 2), and ϑ − 2 cosolute or cosolvent species (components 3, 4,…). Let R₀ be the scattering at 90 degrees from an equivalent solution at zero protein concentration, and let $R_{90}^{ex}=R_{90}-R_0$ denote the excess Rayleigh ratio. Assuming that c₂ is sufficiently small that G_ij (i, j ≠ 2) values are the same for the protein solution and the protein-free solution,⁵⁸ and converting to the more experimentally convenient concentration units of mass∕volume, $R_{90}^{ex}$ can be written with the aid of Eqs. 9, 10 as

$$\begin{array}{c}\hfill \frac{R_{90}^{ex}}{K^{\prime }{\left({\eta }_2^m\right)}^2}=M_{2,app}{c}_2^m+M_2{G}_{22}^m{\left(c_2^m\right)}^2,\end{array}$$ (11a)

$$\begin{array}{c}\hfill \frac{R_{90}^{ex}}{K^{\prime }{\left({\eta }_2^m\right)}^2}{|}_{c_2\to 0}=M_{2,app}{c}_2^m-2M_2{B}_{22}^m{\left(c_2^m\right)}^2,\end{array}$$ (11b)

with the apparent molecular weight (M_{2, app}) given by

$$M_{2,app}=M_2\left[1+2\sum _{i\ne 2}\left(\frac{{\eta }_i^m}{{\eta }_2^m}\right)c_i^m{G}_{2i}^m\right].$$ (12)

In the above expressions, M₂ is the protein molecular weight, $G_{2j}^m$ ($=G_{2j}^{\prime }∕M_2$) is G_2j in units of volume per mass-of-protein, and the superscript m denotes that concentrations and derivatives with respect to concentration are expressed on a w∕v basis. The summation in Eq. 12 can be either positive or negative, therefore the apparent molecular weight can be either larger or smaller than M₂. In the limit of c₂ → 0, $G_{22}^{\prime }$ can be replaced⁹ by −2B₂₂ in Eq. 11a, leading to Eq. 11b. For an ideal solution, $G_{22}^{\prime }$ and $G_{2i}^{\prime }$ are identically zero; yielding the classical ideal result $R_{90}^{ex}\propto M_2{c}_2^m$.^{38, 39, 42}

The results above clearly show that excess Rayleigh scattering is directly and unambiguously related to B₂₂ (or more generally to G₂₂) if one utilizes the KB-based analysis of the scattering data, and there is no fundamental convolution of B₂₂ or G₂₂ with other osmotic virial coefficients or KB integrals. Subsection 3B examines this further from the perspective of a more canonical treatment of Rayleigh scattering. Notably, there is no assumption regarding non-dissociable cosolutes or electroneutrality in Eq. 11. That is, scattering occurs in a grand canonical ensemble with the fluctuations of all species obeying the constraint of constant chemical potential for each species. The fluctuations within the system therefore cannot violate electroneutrality, as doing so would result in an effectively infinite chemical potential for one or more species within the scattering volume. As such, Eq. 11 holds for both ionizable and non-ionizable solutes.

Equation 11 also suggests it may be possible to assess protein-solvent∕cosolute interactions via the dependence of M_{2, app} on solvent composition. However, in the limit of $c_2^m\to 0$, the values of $c_{i\ne 2}^m$ are not independent. Thus, it may be difficult to determine independent values of G_2j(all j≠2) from light scattering alone. A similar conclusion holds in what follows in Subsection 3B. Finally, Eq. 11 is not limited to highly dilute protein solutions, in that $G_{2j}^{\prime }$ depends on $c_2^m$ at higher protein concentrations. The remainder of this report focuses on dilute or semi-dilute protein solutions, with a more detailed treatment of highly concentrated solutions left to a future report.

Revisiting the canonical treatment of Rayleigh scattering

In order to provide the relation between Rayleigh scattering and thermodynamic quantities such as activity coefficients, Eq. 4 can be expressed alternatively using an approach similar to that employed by Stockmayer³⁸ or Kirkwood and Goldberg,³⁹ but without making the simplifying assumption that one can neglect the differences between constant pressure and constant volume, and not neglecting fluctuations of any species in the mixture. By using the identity⁹

$$\frac{RT}{V}{\left(\frac{\partial c_i}{\partial {\mu }_j}\right)}_{T,V,{\mu }_{k\ne j}}=⟨c_i{c}_j⟩-⟨c_i⟩⟨c_j⟩.$$ (13)

Equation 4 can equivalently be written as

$$⟨{\left(\Delta n\right)}^2⟩=\frac{RT}{V}\sum _i\sum _j{\eta }_i{\eta }_j{\left(\frac{\partial c_i}{\partial {\mu }_j}\right)}_{T,V,{\mu }_{k\ne j}},$$ (14)

where η_i is defined in Eq. 10, μ_k is the chemical potential of the kth component in the solution, and R is the ideal gas constant. It is possible to express the derivatives in Eq. 14 in terms of derivatives at constant c_{k ≠ i} rather than constant μ_{k ≠ j}. To do so, one can begin with the set of differential equations

$$d{\mu }_k=\sum _i{a}_{ik}d{c}_i$$

with

$$a_{ik}={\left(\frac{\partial {\mu }_i}{\partial c_k}\right)}_{T,V,c_{j\ne k}}={\left(\frac{\partial {\mu }_k}{\partial c_i}\right)}_{T,V,c_{j\ne i}}=a_{ki}.$$ (15)

For neutral, non-dissociable cosolutes (components 3,4,…),^{38, 44} the solution to this set of simultaneous equations can be expressed as^{9, 38, 39}

$$\begin{array}{ccc}\hfill {\left(\frac{\partial c_i}{\partial {\mu }_j}\right)}_{T,V,{\mu }_{k\ne j}}& =& \frac{A_{ij}}{\left|A\right|}\hfill \\ \hfill a_{ij}& =& {\left(\frac{\partial {\mu }_i}{\partial c_j}\right)}_{T,V,c_{k\ne j}},\hfill \end{array}$$ (16)

where |A| represents the determinant of the matrix {a_ij}, and A_ij is the co-factor of the element a_ij in this determinant. Combining Eqs. 2, 14, 16 gives

$$\frac{R_{90}}{K^{\prime }}=RT\sum _i\sum _j{\eta }_i{\eta }_j\frac{A_{ij}}{\left|A\right|}.$$ (17)

For concreteness, consider a three-component mixture, using the same notation as in Subsection 3A. Equation 17 can then be rearranged to

$$\begin{array}{ccc}\hfill \frac{R_{90}}{K^{\prime }}& =& \frac{{\left[{\eta }_1\left(\frac{A_{21}}{A_{22}}\right)+{\eta }_2+{\eta }_3\left(\frac{A_{32}}{A_{22}}\right)\right]}^2}{\frac{1}{RT}\left[a_{12}\left(\frac{A_{21}}{A_{22}}\right)+a_{22}+a_{23}\left(\frac{A_{32}}{A_{22}}\right)\right]}\hfill \\ & & +\frac{{\left[{\eta }_3-{\eta }_1\left(\frac{a_{13}}{a_{11}}\right)\right]}^2}{\frac{1}{RT}\left[a_{33}-\frac{a_{13}^2}{a_{11}}\right]}+\frac{{\eta }_1^2}{a_{11}∕RT}.\hfill \end{array}$$ (18)

Defining R₀ and $R_{90}^{\mathit{ex}}$ as above, and making the same approximations as in Sec. 2 when subtracting contributions from the solvent background, gives

$$\frac{R_{90}^{\mathit{ex}}}{K^{\prime }}=\frac{{\left[{\eta }_1\left(\frac{A_{21}}{A_{22}}\right)+{\eta }_2+{\eta }_3\left(\frac{A_{32}}{A_{22}}\right)\right]}^2}{\frac{1}{RT}\left[a_{12}\left(\frac{A_{21}}{A_{22}}\right)+a_{22}+a_{23}\left(\frac{A_{32}}{A_{22}}\right)\right]}.$$ (19)

Note the term in brackets in the numerator of the right hand side of Eq. 19 is equivalent to applying a Legendre transform to η₂ in order to obtain (∂n∕∂c₂)_T,V,μj≠2. By doing so, one recoverers a similar term to that proposed by Casassa and Eisenberg^{47, 48} as a correction to Stockmayer's derivation, with the difference being that fluctuations in water concentration are not neglected in the present case. From a practical perspective, this would be equivalent to neglecting terms accounting for protein-solvent interactions, and assuming that fluctuations in protein concentration and co-solute concentration are coupled, but those involving water are not coupled (see also the further discussion below on this point).

Defining the protein activity coefficient (γ₂) using a molar reference state gives

$$RT\ln {\gamma }_2={\mu }_2^{ex}={\mu }_2-{\mu }_2^{id}$$ (20)

with

$${\mu }_2^{id}={\mu }_2^0+RT\ln c_2$$

and ${\mu }_2^0$ denoting the protein standard state chemical potential. Doing so allows one to express the denominator on the right hand side of Eq. 19 as

$$\begin{array}{ccc}& & \frac{1}{RT}\left[a_{12}\left(\frac{A_{21}}{A_{22}}\right)+a_{22}+a_{23}\left(\frac{A_{32}}{A_{22}}\right)\right]\hfill \\ & & =\frac{1}{c_2}+\frac{A_{21}}{A_{22}}{\left(\frac{\partial \ln {\gamma }_2}{\partial c_1}\right)}_{T,V,c_{k\ne 1}}+{\left(\frac{\partial \ln {\gamma }_2}{\partial c_2}\right)}_{T,V,c_{k\ne 2}}\hfill \\ & & +\frac{A_{32}}{A_{22}}{\left(\frac{\partial \ln {\gamma }_2}{\partial c_3}\right)}_{T,V,c_{k\ne 3}}.\hfill \end{array}$$ (21)

Equation 21 can be formally related (see Appendix A) to G₂₂, or to the osmotic second virial coefficient (B₂₂) when protein (component 2) is sufficiently dilute.

Combining Eqs. 19, 20, 21 and using KB theory (see also below) gives

$$\frac{R_{90}^{\mathit{ex}}}{K^{\prime }{\eta }_2^2}=\frac{{\left[1+\left(\frac{{\eta }_1}{{\eta }_2}\right)\left(\frac{c_1{G}_{12}^{\prime }}{1+c_2{G}_{22}^{\prime }}\right)+\left(\frac{{\eta }_3}{{\eta }_2}\right)\left(\frac{c_3{G}_{23}^{\prime }}{1+c_2{G}_{22}^{\prime }}\right)\right]}^2}{\frac{1}{c_2}-\frac{G_{22}^{\prime }}{1+c_2{G}_{22}^{\prime }}},$$ (22)

where the ratio A_2i/A₂₂ with i = 1, 3 was expressed with the aid of Eqs. 5, 13 in terms of KB integrals as

$$\begin{array}{ccc}\hfill \frac{A_{2i}}{A_{22}}& =& \frac{A_{2i}∕\left|A\right|}{A_{22}∕\left|A\right|}=\frac{{\left(\partial c_i∕\partial {\mu }_2\right)}_{T,V,{\mu }_{j\ne 2}}}{{\left(\partial c_2∕\partial {\mu }_2\right)}_{T,V,{\mu }_{j\ne 2}}}\hfill \\ & =& \frac{c_i{G}_{2i}^{\prime }}{1+c_2{G}_{22}^{\prime }}.\hfill \end{array}$$ (23)

Changing to w∕v units, multiplying the numerator and denominator by $c_2^m\left(1+c_2^m{G}_{22}^m\right)$, and rearranging Eq. 22 gives

$$\begin{array}{ccc}\hfill \frac{R_{90}^{\mathit{ex}}}{K^{\prime }{\left({\eta }_2^m\right)}^2}& =& M_2\left(1+2k_{13}\right)c_2^m+M_2{G}_{22}^m{\left(c_2^m\right)}^2\hfill \\ & & +\frac{M_2{c}_2^m{k}_{13}^2}{1+c_2^m{G}_{22}^m},\hfill \end{array}$$ (24)

where

$$k_{13}=\left(\frac{{\eta }_1^m}{{\eta }_2^m}\right)c_1^m{G}_{12}^m+\left(\frac{{\eta }_3^m}{{\eta }_2^m}\right)c_3^m{G}_{23}^m.$$ (25)

If k₁₃ is sufficiently small, Eq. 11 is recovered from Eq. 24. Alternatively, multiplying numerator and denominator by $c_2^m$ in Eq. 22, and converting to w∕v units, gives

$$\begin{array}{c}\hfill \frac{R_{90}^{\mathit{ex}}}{K^{\prime }{\left({\eta }_2^m\right)}^2}=\frac{c_2^m{M}_2{\left[1+\frac{k_{13}}{1+c_2^m{G}_{22}^m}\right]}^2}{1+\frac{c_2^m{G}_{22}^m}{1+c_2^m{G}_{22}^m}},\end{array}$$ (26a)

$$\begin{array}{c}\hfill \frac{R_{90}^{\mathit{ex}}}{K^{\prime }{\left({\eta }_2^m\right)}^2}=\frac{c_2^m{M}_{2,app}^{\prime }}{1+\frac{c_2^m{G}_{22}^m}{1+c_2^m{G}_{22}^m}},\end{array}$$ (26b)

with a somewhat different apparent molecular weight

$$M_{2,app}^{\prime }=M_2{\left(1+\frac{k_{13}}{1+c_2^m{G}_{22}^m}\right)}^2.$$

Equation 26 has the same functional form as that of the now standard expression for analysis of static light scattering,^{28, 54, 57}

$$\frac{R_{90}^{ex}}{K^{\prime }}\propto \frac{M_2{c}_2^m}{1+2A_2^m{c}_2^m}$$ (27)

if one defines

$$A_2^m=-\frac{1}{2}\left(\frac{G_{22}^m}{1+c_2^m{G}_{22}^m}\right).$$ (28)

Historically, A₂ in Eq. 27 is treated as being identical to B₂₂.^{18, 42, 59} Notably, A₂ > B₂₂ if one considers highly repulsive conditions (G₂₂ ≪ 0), and vice versa for highly attractive conditions (G₂₂ ≫ 0). Comparison of Eq. 27 with Eq. 26 also shows that the former erroneously replaces M_{2, app} with the molecular weight, M₂. While it is true that Eq. 26, 27 show that A₂ from LS is more complex than simply B₂₂, this is purely a consequence of not working at sufficiently low c₂, and is not due to convolution with other osmotic virial coefficients or KB integrals.³³ The same cannot be stated for M_{2, app}, as this clearly depends on all G_2j, independent of whether one uses Eq. 11 or 26 to show that M_{2, app} ≠ M₂.

A similar issue exists for other treatments^{42, 45} that neglect fluctuations in N₁, as well as additional consequences for those that incorrectly equate B₂₂ with a derivative of μ₂ or ${\mu }_2^{ex}$ with respect to c₂ without fixing μ_{k ≠ 2}.^{24, 32, 33, 44, 50, 51} When fluctuations in N₁ are neglected, one inherently changes the coupling of fluctuations in solvent with respect to fluctuations in all the other components. For example, if a protein molecule leaves the scattering volume but the system has a fixed number of water molecules, there would either be a large void or only co-solute molecules would be able to enter the system to fill that void; vice versa, adding a protein molecule to the system would result in preferentially “crowding” out co-solute molecules rather than water molecules if this constant-N₁ assumption holds. The supplementary material⁵³ provides additional, mathematical analysis of the consequences of assuming constant N₁, as well as if fluctuations in other solvent components or solutes are simultaneously neglected, akin to common treatments.^{28, 42} In addition, Appendix B shows that the same mathematical form as Eq. 27 can be obtained if one applies the classical approximations akin to that used by Stockmayer³⁸ (i.e., neglecting not only fluctuations in solvent concentration, but also in pressure), although B₂₂ or G₂₂ is not explicitly recovered.

EXPERIMENTAL VIRIAL COEFFICIENTS AND APPARENT MOLECULAR WEIGHTS

The preceding sections clearly show that B₂₂ and G₂₂ arise naturally, and without convolution by protein–solvent or protein–cosolute virial coefficients, if one properly accounts for fluctuations in all species simultaneously. Nevertheless, there are differences in the de novo mathematical forms presented herein if one considers the KB analysis (i.e., an open ensemble) (Eq. 11) or upon imposing a restriction of non-dissociable or unionized solutes (Eq. 24 or 26). Fundamentally, one might then expect differences in the results for experimental systems when comparing G₂₂ or B₂₂ values regressed from LS data using one form versus the other. Equation 11 would be expected to hold more generally than Eq. 24 or 26 for protein solutions, as proteins are necessarily ionized species in most practical instances, even if one can eliminate buffer salts from the solution via extensive dialysis.

In addition, because Eq. 27 is the traditional form used to regress LS data to obtain A₂ values, it remains an open question whether A₂ and B₂₂ or G₂₂ will differ significantly from a quantitative and qualitative perspective. The results below consider this question by comparing B₂₂ and A₂, as well as M_{2, app} values, obtained by regression of experimental SLS data as a function of $c_2^m$ for monoclonal antibodies (mAb) and α-chymotrypsinogen A (aCgn). The experimental details and the scattering data were published previously,^{24, 31} along with fitted A₂ values using the equivalent of Eq. 27. Those results are combined here with re-analysis of the same data using Eqs. 11, 26. Before doing so, however, it is useful to examine the implications of some of the standard assumptions when LS experiments are conducted.

Experimental implications

Two aspects of LS experiments that are related to the standard assumptions of classical LS analysis are revisited in this subsection. This first is regarding the assumption that the derivative of n with respect to protein concentration at constant V is equal to the same derivative at constant p. Equation 10 provides a rigorous relationship between ${\left(\partial n∕\partial c_i^m\right)}_{T,V,c_{k\ne i}^m}$ (=${\eta }_i^m$) and the more experimentally convenient ${(\partial n∕\partial c_i^m)}_{T,p,c_{k\ne i}^m}$. For water, the term (∂n∕∂p)_T,N∕κ_T is of order of 0.2. For proteins, typical values of (∂n∕∂c₂)_T,p,ck≠2 are of the order of 0.2 mL∕g, while typical values of partial specific volume are ≈0.75 mL∕g. Thus, both terms on the right hand side of Eq. 10 are expected to be quantitatively significant, and assuming that ${(\partial n∕\partial c_2^m)}_{T,p,c_{k\ne 2}^m}\approx {\eta }_2^m$ is likely a poor assumption when dealing with protein solutions.

Table 1 summarizes the values for solution conditions used here for aCgn and the four antibodies at different pH and cosolvent concentration. For illustrative proposes, the partial specific volume of protein $\left({\widehat{v}}_2\right)$ was assumed constant and equal to 0.75 mL∕g for all cares. In the case of the other thermodynamic quantities involved in Eq. 10, κ_T and (∂n∕∂p)_T,N were taken from Ref. 60 for aqueous solution of NaCl. The results in Table 1 show that typical values of ${\eta }_2^m$ are approximately twice the value of ${(\partial n∕\partial c_2^m)}_{T,p,c_{j\ne 2}^m}$ for all of the proteins and conditions, demonstrating a potentially large source of quantitative error in values of M_{2, app} and B₂₂ or G₂₂ fitted with the assumption of η₂≈(∂n∕∂c₂)_T,p,ck≠2.

Table 1.

Comparison of (∂n/∂c₂) under the assumption of constant volume or constant pressure.

		NaCl	${\left(\partial n∕\partial c_2^m\right)}_{T,p,c_{k\ne 2}^m}$	${\eta }_2^m$
Protein	pH	[mM]	[mL/g]	[mL/g]
aCgn	2.5 - 4.5	0	0.192	0.407
		100		0.410
		200		0.413
IgG1.1	6.5	54	0.181	0.398
	5.5		0.181	0.398
	4.5		0.183	0.400
	3.5		0.182	0.399
IgG1.2	6.5	54	0.183	0.400
	5.5		0.184	0.401
	4.5		0.184	0.401
	3.5		0.184	0.401
IgG1.3	6.5	54	0.182	0.399
	5.5		0.187	0.404
	4.5		0.183	0.400
	3.5		0.183	0.400
IgG1.4	6.5	54	0.180	0.397
	5.5		0.181	0.398
	4.5		0.181	0.398
	3.5		0.182	0.399

The second aspect which needs consideration is that LS experiments require the Rayleigh ratio of a reference (pure) liquid ($R_{90}^{\mathit{Ref}}$, e.g., toluene or benzene) in order to measure absolute values of $R_{90}^{\mathit{ex}}$.⁶¹ The relation between the excess Rayleigh ratio at 90° for a protein solution and that for the reference liquid is given by²⁸

$$R_{90}^{\mathit{ex}}=\frac{(I_{90}-I_{90}{|}_{c_2=0})}{I_{90}^{Ref}}{\left(\frac{n}{n_{\mathit{ref}}}\right)}^2{R}_{90}^{\mathit{Ref}},$$ (29)

where I₉₀ and I₉₀|_c2=0 are, respectively, the scattered intensities of the protein solution and the solution without protein. $I_{90}^{Ref}$ is the scattered intensity of the reference pure liquid, and n and n_ref are the refractive indexes of the solution and the reference liquid, respectively.

In the literature, one can find $R_{90}^{\mathit{Ref}}$ measured from several methods, though they are commonly classified as “high” or “low” values.⁶² “High” R₉₀ values correspond to those values (methods) which return the average molecular weight of a standard polymer when they are used in Eq. 29 for a dilute solution of the same polymer,^{63, 64, 65, 66, 67, 68} whereas “low” values do not correlate well with the expected M₂ values for standard–polymer solutions. Apparently, because it is now accepted that LS can be used to obtain the true molecular weight, “low” R₉₀ values are often omitted or neglected from later literature, and the use of “high” values has become standard. Thus, if the differences between (∂n/∂c)_T at fixed p versus V for the reference macromolecule-solvent system are similar to those for the protein-solvent system of interest, then the errors in approximating η₂≈(∂n∕∂c₂)_T,p,ck≠2 may be smaller than the statistical uncertainty in the fitted parameters.

This may explain the historical observations that utilizing (∂n∕∂c₂)_T,p,ck≠2 instead of η₂ yields at least physically reasonable magnitudes for M_{2, app}, although this can differ significantly from the known value of M₂ in either a positive or negative direction.^{24, 31, 69} It remains an open question of how valid this approximation is if one finds significant deviations of M_{2, app} from M₂, particularly if there is no evidence of oligomerization. Therefore, for parity with current practice, in Subsection 4B the reported experimental $R_{90}^{\mathit{ex}}$ values utilize the currently accepted values of $R_{90}^{\mathit{Ref}}$, and therefore also employ η₂≈(∂n∕∂c₂)_T,p,ck≠2. While doing so does not affect the comparison or conclusions below, it behooves the LS community to more carefully consider the historically accepted assumptions of constant pressure in LS analysis, and in this case its impact on the Rayleigh ratio of the reference liquid, and what is the correct value for the differential of n with respect to solute and∕or protein concentration.

Classical analysis vs. KB analysis

Using KB theory and a more general canonical treatment, two de novo expressions (Eq. 11 and each of the equivalent Eq. 24 or 26) have been derived to describe LS data. In addition, if one neglects the c₂ dependence of $M_{2,app}^{\prime }$ of Eq. 26b, this yields a third expression

$$\frac{R_{90}^{\mathit{ex}}}{K^{\prime }{\left({\eta }_2^m\right)}^2}=\frac{c_2^m{M}_{2,app}}{1+\frac{c_2^m{G}_{22}^m}{1+c_2^m{G}_{22}^m}}$$ (30)

that is reminiscent of the canonical expression for LS (Eq. 27, with $A_2^m$ held fixed) except that the denominator does not assume $A_2^m=-2G_{22}^m$. In Eq. 30, M_{2, app} = (1 + k₁₃)² ≈ M₂, and therefore this expression is expected to hold only when protein-solvent and protein-cosolute interactions are relatively weak. In what follows, the results from using each of the three expressions (Eq. 11, 26, or 30) with experimental data for protein solutions are compared with that from a canonical treatment. In the remainder of the report, Eq. 27 is used with $A_2^m$ as a constant, making it equivalent to the canonical expression that historically equates B₂₂ with $A_2^m$, factoring in the appropriate conversion between different conventions for the units of B₂₂.^{18, 42, 59} This provides a means to test not only whether the de novo expressions can provide reasonable fits to the experimental data, but also to assess differences in the resulting values of G₂₂ and M_{2, app} compared to A₂ and M₂ in the classical LS analysis.

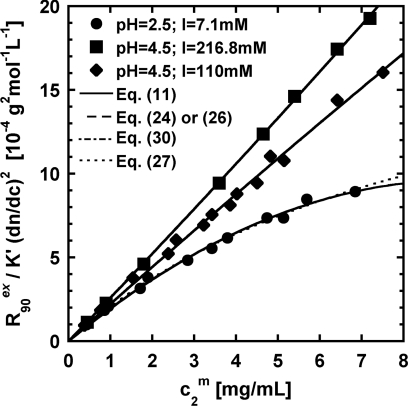
Figure 1 shows a comparison of illustrative fits for each de novo expression and the classical equation to representative LS data for aCgn at solvent conditions that span from attractive (upward curvature) to repulsive (downward curvature). For all the conditions, all the equations capture the qualitative behavior of $R_{90}^{\mathit{ex}}$ as a function of protein concentration, as expected since each of Eqs. 11, 26, 30, 27 produce the same sign for the curvature of $R_{90}^{ex}$ if one use a positive or negative value for G₂₂ or A₂. When protein–protein interactions are near ideal (i.e., linear $R_{90}^{\mathit{ex}}$ vs. $c_2^m$), no difference can be observed between these expressions. However, for large deviations, differences between the de novo equations (Eqs. 11), 26, 30), and the classical expression (Eq. 27 with constant $A_2^m$) become more evident. However, these differences are minor, and likely would not give one cause to conclude that one expression is inherently better able to capture the LS data per se. Rather, the comparison of the fitted parameter values reveals the differences more clearly.

Figure 1.

Representative LS data and fits for aCgn solutions at pH of 2.5 and 4.5, and different ionic strength. The symbols, solid lines, dashed lines, and dotted lines correspond to experimental data,³¹ and mathematical fits to Eqs. 11, 26, 27, 30 (using constant $A_2^m$), respectively. The fits to Eqs. 11, 24, 26, or 30 are indistinguishable on the scale of the plot.

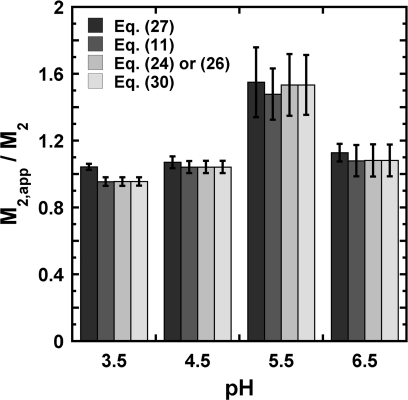
Figure 2, as well as Figs. S1 and S2 in the supplementary material,⁵³ summarize differences in M_{2, app} values obtained from regressing SLS data as a function of pH and I, using the classical analysis (Eq. 27 or B6) and the new expressions (Eqs. 11, 26, 30), for aCgn, and each antibody. These values are normalized by the true protein molecular weight M₂ derived from amino acid analysis. The true molecular weights for the five proteins are: 146.7, 146.9, 146.5, 143.0, and 25.7 kDa for IgG1.1, IgG1.2, IgG1.3, IgG1.4, and aCgn, respectively. For the four antibodies, LS data correspond to solutions at one cosolvent concentration ([NaCl] = 54 mM) and four different pH (3.5, 4.5, 5.5, and 6.5), whereas for aCgn the data correspond to solutions at three different cosolvent concentrations ([NaCl] = 0, 100, and 200 mM) and five different pH values (2.5, 3, 3.5, 4, and 4.5).

Figure 2.

Apparent protein molecular weight M_{2, app} for IgG1.3 in 54mM NaCl as a function of pH. The values are obtained from regressing experimental data to the working equations. For Eq. 26, $G_{22}^m$ and k₁₃ were regressed, and M_{2, app} calculated from the expression for $M_{2,app}^{\prime }$ defined in Eq. 26. Error bars are based on 95% confidence intervals for the fitted parameters. Analogous results are shown for IgG1.1, IgG1.2, and IgG1.4, as well as for aCgn, in the supplementary material.⁵³

Inspection of Fig. 2, and S1 and S2 in the supplementary material⁵³ show that the fitted M_{2, app} values are the same from Eqs. 11, 26, 27, 30 within 95% confidence intervals, across a wide range of conditions. Additionally, M_{22, app}/M₂ is not greatly different from 1 for most examples tested here. This suggests that |k₁₃| ≪ 1, as required for Eq. 24 or 26 to be equivalent to the more general expression (Eq. 11). In the case of IgG1.2 (Fig. S1b) and pH 5.5 in Fig. 2, protein dimerization was suspected,²⁴ consistent with M_{2, app} ≫ M₂. A more systematic and broader range of cosolute compositions may need to be tested to assess how large the deviations of M_{2, app} from M₂ may become for real systems.

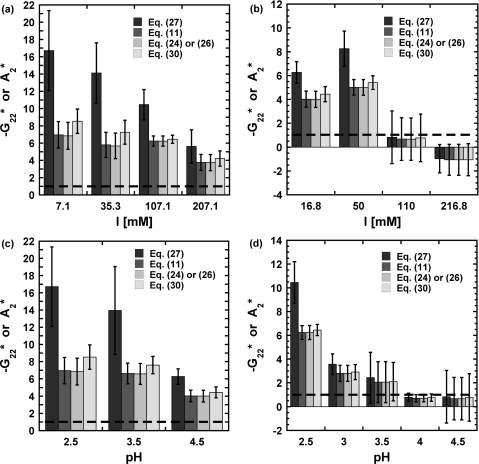
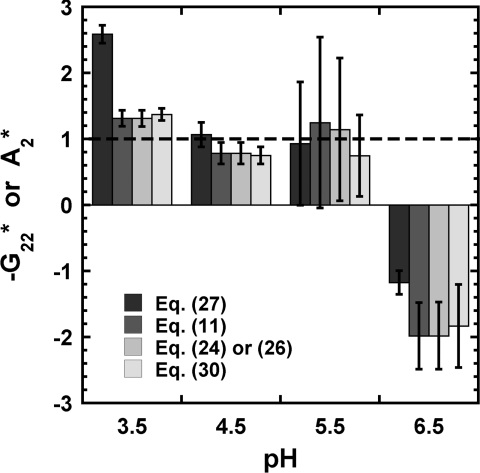
In terms of protein–protein interactions, Figs. 34, and S3 (see supplementary material⁵³) summarize the values of G₂₂ or A₂ obtained from regressing the experimental LS data for aCgn and each of mAb. These values are reported relative to the hard-sphere second virial coefficient ($-G_{22}^{*}=-G_{22}∕2B_2^{HS}$ and $A_2^{*}=A_2∕B_2^{HS}$) for easier comparison across different proteins; recall that G₂₂ = −2B₂₂ at low c₂.⁹ The estimated $B_2^{HS}$ was calculated as $B_2^{HS}=\left(2∕3\right)\pi {\sigma }_{HS}^3$, where the hard-sphere diameter (σ_HS) was taken as 10 nm for each of the four mAb^{70, 71, 72} and 4 nm for aCgn.³¹

Figure 3.

B₂₂ values for aCgn obtained from classical (Eq. 27) and KB (Eqs. 11, 24, 30 or 26) analysis at different pH and ionic strength (I): (a) pH = 2.5; (b) pH = 4.5; (c) low ionic strength ([NaCl] = 0 mM); (d) medium ionic strength ([NaCl] = 100 mM). Dashed line indicates value for ideal hard spheres. Error bars are based on 95% confidence intervals for the fitted parameters.

Figure 4.

B₂₂ values for IgG1.3 in 54 mM NaCl as a function of pH. The values are obtained from regressing experimental data to the working equations. Dashed line indicates value for ideal hard spheres. Error bars are based on 95% confidence intervals for the fitted parameters.

At low pH (⩽3.5), repulsive protein interactions are expected ($B_{22}>B_2^{HS}$, $G_{22}^{*}\ll 0$), since all the charged side chains have positive charges and the contribution from electrostatic interactions to the protein–protein interactions is significant at these relatively low ionic strength values. As pH increases, there are both repulsive and attractive protein–protein interactions because there are both positively and negatively charged side chains, and G₂₂ (A₂) is expected to increase (decrease). Similarly, at low ionic strength, electrostatic interactions are relatively unscreened, and become more screened with increasing I.⁷³ If one is concerned about only the sign of B₂₂, A₂, or G₂₂, then Eqs. 11, 24 or 26, 30, 27 provide equivalent results. That is, linear behavior for $R_{90}^{\mathit{ex}}$ gives A₂ = B₂₂ = G₂₂ = 0, and positive (negative) deviations from linearity requires A₂, B₂₂, or −G₂₂ to be negative (positive).

On the other hand, if one is concerned with the magnitude of protein–protein interactions, then Figs. 34, and S3 in the supplementary material⁵³ show that the classical LS treatment is in error. As Eq. 28 shows, the errors are most pronounced at high c₂ and∕or |G₂₂|. The now-standard expression to analyze LS (Eq. 27) implicitly assumes |c₂G₂₂| ≪ 1 by considering A₂ = B₂₂. However, within the experimentally accessible range of protein concentration, that product is not necessarily small. Thus, for very repulsive (attractive) conditions, G₂₂ ≪ 0 (≫0), the classical expression is no longer valid. This causes −G₂₂ or B₂₂ to be over (under) estimated under strongly repulsive (attractive) conditions. The main difference in deriving Eq. 11 or 26 is the assumption of non-dissociable solutes for Eq. 26, i.e., via the neglect of Donnan contributions in Eq. 26. The agreement between $G_{22}^{*}$ for fits to Eq. 11 vs. Eq. 26 or 30 in Figs. 34, and S2 (supplementary material⁵³) suggests that contributions from Donnan equilibria involving the proteins and the counterions are not significant for the present examples, within experimental uncertainty. As shown above, A₂ from traditional analysis is not equal to B₂₂ unless the magnitude of c₂B₂₂ (or c₂G₂₂) is small compared to 1. However, this cannot explain the difference in sign argued elsewhere.^{32, 33} The source of the discrepancies between B₂₂ obtained from different experimental methods^{33, 74} is not apparent at this point, but the analysis of LS provided here clearly shows that B₂₂ or G₂₂ is rigorously obtained from proper analysis of LS data.

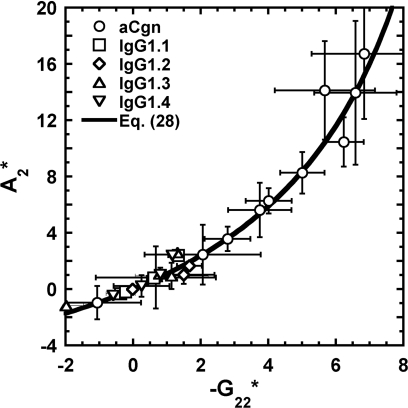
Furthermore, the fact that differences between A₂ and B₂₂ (or G₂₂) in Eq. 26, 27 are the artifact of a mathematical manipulation and the assumption of c₂ → 0 suggests A₂ may be corrected without a need to regress data retrospectively. Figure 5 shows $A_2^{*}$ values regressed from Eq. 27 vs. $-G_{22}^{*}$ values regressed from Eq. 11 for all the data analyzed here, along with a curve that represents Eq. 28 – i.e., the curve is not a fit to the data. The average protein concentration among all the LS data was used in Eq. 28 for Fig. 5. Together with the analysis provided in Sec. 3, this clearly demonstrates that A₂ regressed from Eq. 27 is not the osmotic second virial coefficient unless c₂ and∕or |G₂₂| are sufficiently small, but one can relate A₂ from classical analysis to G₂₂ via Eq. 28. However, the difference between A₂ and G₂₂ is not due to a convolution with other osmotic virial coefficients; it occurs because of the erroneous approximation of c₂ → 0 when analyzing LS data. For the data considered here, differences between A₂ and −G₂₂/2 are significant when $|G_{22}^m{c}_2^m|\ge 3\text{x}{10}^{-2}$, even if the average concentration is low (≈3 mg∕mL). Nevertheless, Eq. 28 may provide a way to recover accurate values of G₂₂ from previously determined A₂ values, and therefore also test whether the approximation A₂ ≈ B₂₂ is valid.

Figure 5.

Normalized osmotic virial coefficients obtained from Eq. 27 ($A_2^{*}$) and Eq. 11 ($-G_{22}^{*}$) for aCgn and each of the mAb's. Symbols corresponds to (○) aCgn; (□) IgG1.1; (◊) IgG1.2; (△) IgG1.3; (▽) IgG1.4; solid line corresponds to Eq. 28.

Interestingly, Asthagiri et al.⁴⁴ also found protein–protein interactions were over-estimated at repulsive conditions by comparing A₂ obtained from experimental LS data with those values obtained from molecular simulations. By acknowledging ionizable species in a derivation starting from Stockmayer approach,³⁸ they suggested that the A₂ parameter is the combination of a protein–protein interaction term and a Donnan effect term arising from a need to impose electroneutrality. Thus, for conditions dominated by electrostatic interactions (very high or low pH, and∕or low ionic strength), the Donnan term becomes important, leading to overestimated positive values of A₂. The analysis here provides an alternative explanation, without a need to invoke argument of electroneutrality, as the grand canonical ensemble inherently maintains electroneutrality by the imposition of constant chemical potential. The empirical observation that $G_{22}^{*}$ fit from Eqs. 11, 26 were equivalent in the present work argues that Donnan contributions to Eq. 26 could be neglected for the experimental data considered here, as Eq. 11 is not limited by such restrictions.

Strictly, if one considers the scenario of dissociable or ionizable species, particularly protein, the canonical treatment (Eq. 26) is no longer valid, since Eq. 21 (or Eq. A4) only applies to non-dissociable components. However, Eq. 11 can be used whether or not protein and∕or cosolutes dissociate or ionize if one acknowledges the concentration of some dissociated or ionized species is proportional to c₂. Nevertheless, special care must be taken in using the KB analysis for such situations, as G₂₂ may be a linear combination of the KB integrals for the interactions between protein and some of the dissociated components (e.g., counterions). This is a common issue in other types of experiments for measuring osmotic virial coefficients or KB integrals such as sedimentation equilibrium and classical osmometry experiments, since there is thermodynamic coupling between protein and some of the dissociated or ionized components in solution. This does not preclude the possibility that one would obtain significantly different results at very low ionic strength and∕or high protein charge if one used Eq. 26 instead of Eq. 11, as well as the importance of considering Donnan contributions when large strong electrostatic contributions are present. Correcting for additional factors such as Donnan equilibrium in deriving Eq. 26 or 30 is left to a future report, and instead Eq. 11 is recommended for use more generally.

SUMMARY AND CONCLUSIONS

Classic analysis of Rayleigh light scattering in terms of concentration fluctuations is revisited and three alternative versions of the final working equation are derived and compared with the traditional form. The new formulations are based on either KB solution theory, or on a more general canonical treatment applicable to solutions with non-dissociable solutes. The former is more general in that it is not restricted in terms of the nature of the solutes or solvents, or assumptions of independent cross fluctuations of charged species. The analysis shows that B₂₂ arises naturally and without convolution by other virial coefficients if one considers sufficiently dilute protein concentrations and∕or low |B₂₂| values – disputing recent arguments that are based on a less general analysis. However, comparison to the now-standard expression for regressing LS data shows that the standard analysis may significantly over(under)-estimate the magnitude of the osmotic second virial coefficient for strongly repulsive(attractive) protein-protein interactions. The KB integral G₂₂ is the more relevant quantity as one considers larger protein concentrations and∕or strong repulsions or attractions. Expressions are derived that in principle allow one to correct previous results, as well as to unambiguously determine whether one is sufficiently dilute to recover B₂₂ rather than G₂₂ from LS experiments. The analysis is applied to a number of experimental systems, illustrating that the magnitude of the errors from the traditional analysis can be significant (a factor of 2 or more) for estimating protein-protein virial coefficient or KB integral values; while the errors in assuming the apparent molecular weight from LS analysis is equal to the true molecular weight may be appreciably smaller but still measurable. The present work also lays a foundation for extending LS to model protein-protein and protein-solvent or protein-cosolute interactions in more concentrated solutions.

APPENDIX A: B₂₂ IN TERMS OF ACTIVITY COEFFICIENTS

In order to establish the relation between the osmotic second virial coefficient, B₂₂, and the activity coefficients, we can start from the definition of fluctuations in the concentration of protein for a multi component mixture in a grand-canonical ensemble. That is

$$⟨{\left(\Delta N_2\right)}^2⟩=kT{\left(\frac{\partial N_2}{\partial {\mu }_2}\right)}_{T,V,{\mu }_{k\ne 2}}=kT\frac{A_{22}}{\left|A\right|},$$ (A1)

where A₂₂ and |A| are defined in Eq. 16. In addition, these fluctuations can be expressed rigorously in terms of the KB integral, G₂₂, as⁹

$$\begin{array}{ccc}\hfill \frac{kT}{V}{\left(\frac{\partial N_2}{\partial {\mu }_2}\right)}_{T,V,{\mu }_{k\ne 2}}& =& c_2\left(1+c_2{G}_{22}\right)\hfill \\ & =& kT{\left(\frac{\partial c_2}{\partial {\mu }_2}\right)}_{T,V,{\mu }_{k\ne 2}}.\hfill \end{array}$$ (A2)

Combining Eqs. A1, A2, and defining the protein activity coefficient (γ₂) as Eq. 20, we can express G₂₂ as

$$\begin{array}{c}\hfill G_{22}=\frac{-\left[{\left(\frac{\partial \ln {\gamma }_2}{\partial c_2}\right)}_{T,V,c_{k\ne 2}}+{\sum }_{i\ne 2}\frac{A_{2i}}{A_{22}}{\left(\frac{\partial \ln {\gamma }_2}{\partial c_i}\right)}_{T,V,c_{k\ne i}}\right]}{1+c_2\left[{\left(\frac{\partial \ln {\gamma }_2}{\partial c_2}\right)}_{T,V,c_{k\ne 2}}+{\sum }_{i\ne 2}\frac{A_{2i}}{A_{22}}{\left(\frac{\partial \ln {\gamma }_2}{\partial c_i}\right)}_{T,V,c_{k\ne i}}\right]}.\end{array}$$ (A3)

Equation A3 is formally exact assuming non-dissociable species. In the limit of infinite dilution of protein (c₂ → 0) this becomes

$$\begin{array}{ccc}\hfill G_{22}& =& -\left[{\left(\frac{\partial \ln {\gamma }_2}{\partial c_2}\right)}_{T,V,c_{k\ne 2}}^{\left(\infty \right)}\right.\hfill \\ & & \left.+\sum _{i\ne 2}\frac{A_{2i}}{A_{22}}{\left(\frac{\partial \ln {\gamma }_2}{\partial c_i}\right)}_{T,V,c_{k\ne i}}^{\left(\infty \right)}\right],\hfill \end{array}$$ (A4)

where the superscript (∞) denotes that the derivatives are evaluated in the limit of low protein concentration. In addition, $G_{22}^{\left(\infty \right)}=-2B_{22}$,⁹ therefore

$$\begin{array}{ccc}\hfill B_{22}& =& \frac{1}{2}\left[{\left(\frac{\partial \ln {\gamma }_2}{\partial c_2}\right)}_{T,V,c_{k\ne 2}}^{\left(\infty \right)}+\sum _{i\ne 2}\frac{A_{2i}}{A_{22}}{\left(\frac{\partial \ln {\gamma }_2}{\partial c_i}\right)}_{T,V,c_{k\ne i}}^{\left(\infty \right)}\right].\hfill \end{array}$$ (A5)

Equations A3, A4, A5 give formal relations between protein–protein interactions in terms of G₂₂ and B₂₂ (i.e., an open ensemble), and the activity coefficients of the different component in the solution (i.e., a Helmholtz framework).

APPENDIX B: CONSTANT PRESSURE ASSUMPTION

Most of the theories²⁸, ³⁸, ³⁹, ⁴², ⁴⁴ which relate Rayleigh scattering to molecular interactions assume that the system is at constant pressure. In addition, fluctuations on N₁ (water), or in all solvent species, are often neglected. The impact of these approximations are illustrated here, for comparison to the results in Sections 2, 3. For concreteness, first consider a ternary mixture at constant T, p, and with μ_k of all the components but solvent (component 1) held fixed, i.e., constant (p, T, N₁, μ_{k ≠ 1}). In this ensemble, fluctuations in refractive index are due to fluctuations in V and N_{k ≠ 1}

$$\begin{array}{ccc}\hfill ⟨{\left(\Delta n\right)}^2⟩& =& {\left(\frac{\partial n}{\partial V}\right)}_{T,\mathbf{N}}^2⟨{\left(\Delta V\right)}^2⟩\hfill \\ & & +2\sum _{i=2}^3{\left(\frac{\partial n}{\partial V}\right)}_{T,\mathbf{N}}{\left(\frac{\partial n}{\partial N_i}\right)}_{T,V,N_{k\ne i}}⟨\Delta V\Delta N_i⟩\hfill \\ & & +\sum _{i=2}^3\sum _{j=2}^3{\left(\frac{\partial n}{\partial N_i}\right)}_{T,V,N_{k\ne i}}{\left(\frac{\partial n}{\partial N_j}\right)}_{T,V,N_{k\ne j}}⟨\Delta N_i\Delta N_j⟩,\hfill \end{array}$$ (B1)

where fluctuations in volume and number of molecules are expressed as

$$\begin{array}{ccc}\hfill \beta ⟨{\left(\Delta V\right)}^2⟩& =& -{\left(\frac{\partial V}{\partial p}\right)}_{T,N_1,{\mu }_{k\ne 1}}\hfill \\ & =& {\kappa }_{T}V-\sum _{i=2}^3{\overline{v}}_i{\left(\frac{\partial N_i}{\partial p}\right)}_{T,N_1,{\mu }_{k\ne 1}}\hfill \\ \hfill \beta ⟨\Delta V\Delta N_i⟩& =& {\left(\frac{\partial V}{\partial {\mu }_i}\right)}_{T,P,N_1,{\mu }_{k\ne 1,i}}\hfill \\ & =& -{\left(\frac{\partial N_i}{\partial p}\right)}_{T,N_1,{\mu }_{k\ne 1,i}}\hfill \\ & =& \sum _{j=2}^3{\overline{v}}_j{\left(\frac{\partial N_j}{\partial {\mu }_i}\right)}_{T,p,N_1,{\mu }_{k\ne 1,i}}\hfill \\ \hfill \beta ⟨\Delta N_i\Delta N_j⟩& =& {\left(\frac{\partial N_j}{\partial {\mu }_i}\right)}_{T,p,N_1,{\mu }_{k\ne 1,i}}\hfill \\ & =& {\left(\frac{\partial N_i}{\partial {\mu }_j}\right)}_{T,p,N_1,{\mu }_{k\ne 1,j}}.\hfill \end{array}$$

Replacing the above definitions in Eq. B2, and substituting derivatives at constant V for their equivalents derivatives at constant p, we obtain

$$\begin{array}{ccc}\hfill ⟨V⟩⟨{\left(\Delta n\right)}^2⟩& =& \mathit{k}T⟨V⟩\sum _{i=2}^3\sum _{j=2}^3{\xi }_i{\xi }_j{\left(\frac{\partial N_i}{\partial {\mu }_j}\right)}_{T,p,N_1,{\mu }_{k\ne j}}\hfill \\ & & -\frac{\mathit{k}T}{{\kappa }_T}{\left(\frac{\partial n}{\partial p}\right)}_{T,\mathbf{N}}^2,\hfill \end{array}$$ (B2)

where

$${\xi }_i={\left(\frac{\partial n}{\partial N_i}\right)}_{T,p,N_{k\ne i}}.$$

In a similar way to that for obtaining Eq. 16, the derivative of the number of molecules of the i’th component with respect the chemical potential of the j’th component can be written as

$${\left(\frac{\partial N_i}{\partial {\mu }_j}\right)}_{T,p,N_1,{\mu }_{k\ne j}}=\frac{{\Psi }_{ij}}{\left|\Psi \right|},$$ (B3)

where |Ψ| and Ψ_ij are the determinant and the ij–cofactor in the determinant, respectively, of the matrix formed by the elements

$${\psi }_{ij}={\psi }_{ji}={\left(\frac{\partial {\mu }_i}{\partial N_j}\right)}_{T,p,N_{k\ne j}}i,j=2,3.$$

With Eqs. B2, B3, Eq. 2 in mole/volume units becomes

$$\begin{array}{ccc}\hfill \frac{R_{90}}{K^{\prime }}& =& \frac{RT{\left[{\xi }_2-{\xi }_3\left(\frac{{\psi }_{23}}{{\psi }_{33}}\right)\right]}^2}{⟨V⟩\left[{\psi }_{22}-{\psi }_{23}\left(\frac{{\psi }_{23}}{{\psi }_{33}}\right)\right]}\hfill \\ & & +\frac{RT{\xi }_3^2}{⟨V⟩{\psi }_{33}}-\frac{RT}{{\kappa }_T}{\left(\frac{\partial n}{\partial p}\right)}_{T,\left\{{\mathbf{n}}_{\mathbf{k}}\right\}}^2.\hfill \end{array}$$ (B4)

One can then express $\left(R_{90}^{\mathit{ex}}\right)$ as

$$\frac{R_{90}^{\mathit{ex}}}{K^{\prime }{\xi }_2^2}=\frac{{\left[1-\left(\frac{{\xi }_3}{{\xi }_2}\right)\left(\frac{{\psi }_{23}}{{\psi }_{33}}\right)\right]}^2}{\frac{⟨V⟩}{RT}{\left(\frac{\partial {\mu }_2}{\partial {\mathbf{n}}_{\mathbf{2}}}\right)}_{T,p,{\mathbf{n}}_{\mathbf{1}},{\mu }_3}},$$ (B5)

where the denominator follows from

$$\begin{array}{ccc}\hfill {\left(\frac{\partial {\mu }_2}{\partial {\mathbf{n}}_{\mathbf{2}}}\right)}_{T,p,{\mathbf{n}}_{\mathbf{1}},{\mu }_3}& =& {\left(\frac{\partial {\mu }_2}{\partial {\mathbf{n}}_{\mathbf{2}}}\right)}_{T,p,{\mathbf{n}}_{\mathbf{j}\ne \mathbf{2}}}\hfill \\ & & +{\left(\frac{\partial {\mu }_2}{\partial {\mathbf{n}}_{\mathbf{3}}}\right)}_{T,p,{\mathbf{n}}_{\mathbf{j}\ne \mathbf{3}}}{\left(\frac{\partial {\mathbf{n}}_{\mathbf{3}}}{\partial {\mathbf{n}}_{\mathbf{2}}}\right)}_{T,p,{\mathbf{n}}_{\mathbf{1}},{\mu }_3}.\hfill \end{array}$$

Finally, by analogy with the derivation of Eq. 27 in Sec. 3, one can express Eq. B5 at low protein concentration as

$$\frac{R_{90}^{\mathit{ex}}}{K^{\prime }{\left({\xi }_2^m\right)}^2}=\frac{c_2^m{M}_{2,app}}{1+2c_2^m{A}_{2,app}^m},$$ (B6)

where

$$\begin{array}{ccc}\hfill M_{2,app}& =& M_2\left\{1+\frac{{\xi }_3}{{\xi }_2}{c}_3^m\left[\frac{G_{23}}{M_2}\right.\right.\hfill \\ \hfill & & {\left.\left.-\frac{M_1}{M_2}\left(\frac{G_{13}}{M_1}+\frac{G_{12}}{M_1}-\frac{1}{c_1^m}-\frac{G_{11}}{M_1}\right)\right]\right\}}^2,\hfill \end{array}$$ (B7)

$$A_{2,app}^m=-\frac{1}{2}\left[G_{22}^m+\frac{M_1}{M_2}\left(\frac{1}{c_1^m}+\frac{G_{11}}{M_1}-\frac{2G_{12}}{M_1}\right)\right].$$ (B8)