Differential expression analysis of digital gene expression data: RNA-tag filtering, comparison of t-type tests and their genome-wide co-expression based adjustments

Abstract

Deep sequencing techniques have shown a promising impact on biomedical studies. Based on a recently published two-sample Digital Gene Expression (DGE) data set, we compared three widely used t-type tests for the differential expression analysis. Both the ‘soft’ and ‘hard’ filtering strategies were considered. For the ‘hard’ filtering strategy, we also considered a genome-wide co-expression based adjustment for each t-type test. Our results suggest that excluding RNA-tags at an appropriate level of data variability can improve the control of false positives. Furthermore, the genome-wide co-expression based adjustments consistently provide comparably low levels of false positive control for different exclusion criteria.

1 Introduction

The genomic profiling technologies have been greatly advanced in the recent decades. In addition to the microarray technology (Schena et al., 1995; Lockhart et al., 1996), the deep sequencing technology such as RNA-seq or digital gene expression (DGE) has shown a promising impact on biomedical studies (Nagalakshmi et al., 2008; Wilhelm et al., 2008). The deep sequencing technology can directly measure the amount of molecules at a genomic level. Compared to the hybridization and image based microarray technology, this new technology can significantly reduce the noise in expression measurements and improve the detection range and accuracy (Marioni et al., 2008; ’t Hoen et al., 2008).

Microarrays have been widely used in two-sample experiments to detect genes with differential expression (Singh et al., 2002; Mootha et al., 2003). These genes can be useful biomarkers for biomedical research and clinical practice. In addition to the traditional two-sample t-test, many statistical methods have been proposed to improve the detection of differential expression (Cui and Churchill, 2003). Among these methods, the “soft” filtering based methods are the most successful and widely used (Cui et al., 2005). The essential idea is to penalize these genes with relatively small expression variances so that they will receive lower rank of differential expression. The SAM t-test (Tusher et al., 2001) and the moderated t-test (Smyth, 2004) are two of the most widely used “soft” filtering based methods.

Although a considerable amount of genes may be overlooked, it has been shown that this approach can generally improve the control of false positives. In the situation of analyzing data with a small sample size but a large number of variables, it is important to achieve a reasonable tradeoff between the screening coverage (the number of genes screened for the analysis of differential expression) and false positive control. Another approach is the “hard” filtering strategy: a certain amount of genes are excluded from the follow-up analysis based on a given criterion that is independent of the differential expression analysis (Singh et al., 2002; Mootha et al., 2003). For example, a gene may be considered non-expressed and excluded from the analysis if all of its expression observations are small (Mootha et al., 2003). It is also feasible to first perform a “hard” filtering and then conduct a “soft” filtering based analysis. Pounds and Cheng have pointed out that gene filtering may not always improve the analysis results (Pounds and Cheng, 2005).

Recently, there are several two-sample RNA-seq/DGE data sets collected for different biomedical studies (Marioni et al., 08; ’t Hoen et al., 2008). Our experience in analyzing microarray data is certainly useful for the analysis of RNA-seq/DGE data. Although these data represent the counts of different molecules, the widely used t-type tests can still be considered after an appropriate data transformation (e.g. log-transformation). However, the number of variables (RNA-tags) in this new type of genomics data is much larger than the number of genes in microarray data. The control of false positives is a more challenging task. It is necessary to understand how to efficiently balance the screening coverage and false positive control for the differential expression analysis of RNA-seq/DGE data.

Genes are not isolated during cellular and molecular processes. We expect to improve the detection of differential expression if the genome-wide interaction information can be efficiently incorporated into the analysis. We have recently proposed a method for genome-wide co-expression based prediction of differential expression and have shown its significant improvement over the univariate based testing approach (Lai, 2008). It is also our interest to understand the performance of this method in the differential expression analysis of RNA-seq/DGE data.

Since it is unknown which genes are truly differentially expressed or not in a study, the performance of false positive control has been widely used to compare different statistical methods (Wu, 2005). The traditional control of false positives is based on the family-wise error rate (FWER). However, it is well-known that this approach is too stringent to be used for the data with a small sample size but a large number of variables. Instead, the false discovery rate (FDR) has been widely used in microarray data analysis (Reiner et al., 2003). In this study, we will also use FDR to compare the ranking performance of different methods.

The evaluation of FDR requires the p-values computed for different variables (genes or RNA-tags). Since the underlying distributions are usually unknown for expression data and the sample sizes are usually small for genomics experiments, it is difficult to compute theoretical p-values. Instead, permutation based p-values have been widely used for the assessment of statistical significance in genomics studies (Dudoit et al., 2003). To address the control of false positives, we must be able to compute p-values at a “tiny” level. However, due to the issue of small sample sizes and/or the availability of computing power, the number of permutations is usually limited. Therefore, it is a common practice to pool permuted test scores from different variables so that “tiny” p-values can be computed (Storey and Tibshirani, 2003).

The rest of paper is organized as follows. We first introduce the data used in this study and provide the details of statistical and computational methods used in our analysis. Then, we present the analysis results to illustrate our data exploration and to compare different analysis strategies and methods. Finally, we give the conclusion and discussion for this study.

2 Methods

2.1 DGE/RNA-seq data

There is a recently published two-sample DGE/RNA-seq dataset: ’t Hoen et al. (2008) have collected data for a comparison between two mouse species. The dataset has been generated based on the Solexa/Illumina deep sequencing technology. Its GEO accession number is GSE10782 and it has a sample size 4 in each group, which allows us to perform 35 distinct permutations (see Permutation p-value for detail). Then, the level of adjusted p-values (FDRs) can be as low as 1=35 ≈ 3%. This makes our FDR based performance evaluation and comparison of different test statistics practically meaningful. The published dataset GSE10782 contains 844316 RNA-tags with observations. (There are about 2.0 × 10⁵ unique RNA-tags per subject. After combining data from 8 subjects, we obtain 844316 unique RNA-tags.) For this dataset, we first consider scaling and a modified log-transformation, then we perform the differential expression analysis.

2.2 Scaling, filtering and data transformation

The data set GSE10782 are first scaled according to ’t Hoen et al. (2008): the observations of different RNA-tags for a given subject are scaled by the ratio between the average over different total RNA-tag counts from different subjects and the total RNA-tag counts from the given subject. After this, different subjects will have the same total RNA-tag counts (not necessarily an integer after scaling).

We try to provide a simple although ad hoc criterion for excluding RNA-tags. For a given RNA-tag, let M and m be the maximum and minimum of its expression observations (counts of RNA-tags), respectively. If we assume the counts follow a Poisson distribution with parameter λ, then the population mean and variance are both λ. We are interested in these RNA-tags with sufficient variations in observations: the range should cover a given 2k-fold of standard deviation, or $M-m>2k\sigma =2k\sqrt{\lambda }$. If we assume that M + m ≈ 2μ = 2λ, then we simply require (M – m)²/(M + m) > 2k². RNA-tags with (M – m)²/(M + m) ≤ 2k² will be excluded from the differential expression analysis. k =1.65, 2, 3 and 4 are considered in this study.

Remark

If we consider the normal distribution approximation, then above criterion is equivalent to that the observations must cover approximately 90%, 95%, 99% and 100% of data distribution corresponding to k =1.65, 2, 3 and 4. Notice that the proportions 90%, 95% and 99% have been frequently used for constructing confidence intervals in practice.

After scaling, we consider a data transformation so that t-type test statistics can be efficiently used for data analysis. Since a count observation can be zero, we consider a simple modified log-transformation for each observation x: y = log(x+0.5). log-Transformation has been widely considered in practice to reduce data variance.

2.3 t-type test statistics

The Student’s t-test is a classical signal-to-noise ratio statistic. For a given RNA-tag, after the data transformation, let {y_ij: i = 1, 2; j = 1, 2, … n_i}be the expression observations. Then, the Student’s t-test is calculated as:

$$t=({\overline{y}}_2-{\overline{y}}_1)/(s_p\sqrt{n_1^{-1}+n_2^{-1}}),$$

where $s_p=\sqrt{{\sum }_{i=1}^2{\sum }_{j=1}^{n_i}{(y_{ij}-{\overline{y}}_i)}^2/(n_1+n_2-2)}$ and ${\overline{y}}_i={\sum }_{j=1}^{n_i}{y}_{ij}/n_i$.

The SAM t-test (Tusher et al., 2001) is a modified Student’s t-test:

$$t_{\text{SAM}}=({\overline{y}}_2-{\overline{y}}_1)/[(s_p+c)\sqrt{n_1^{-1}+n_2^{-1}}],$$

where c is an adjustment factor that can be estimated based on the procedure provided by Tusher et al. (2001). When c = 0, we have t_SAM = t. The SAM t-test has been widely used in practice. To our best knowledge, this is the first modified t-test that considers the variation of genome-wide expression variance in the analysis of differential expression.

The moderated t-test (Smyth, 2004) is another modified Student’s t-test:

$$t_{mod}=({\overline{y}}_2-{\overline{y}}_1)/(\stackrel{\sim }{s}\sqrt{n_1^{-1}+n_2^{-1}}),$$

where $\stackrel{\sim }{s}=\sqrt{(d_0{s}_0^2+(n_1+n_2-2)s_p^2)/(d_0+n_1+n_2-2)}$. d₀ and s₀ can be estimated by the procedure provided by Smyth (2004). When d₀ = 0, we have t_mod = t. The moderated t-test has also been widely used in practice. To our best knowledge, this test is representative of the (empirical) Bayesian approach to the analysis of differential expression.

2.4 Genome-wide co-expression based prediction of differential expression

We have recently proposed a method for genome-wide co-expression based prediction of differential expression (Lai, 2008). This method is a statistical framework in which the genome-wide co-expression information can be used to adjust the differential expression measures of individual genes. We have shown that this method can significantly improve the control of false positives and the detection of disease related genes with weak differential expression.

We describe briefly how this method is used in the current study. The co-expression between two RNA-tags can be measured by the traditional Pearson’s correlation coefficient. The differential expression of a RNA-tag can be measured by either the Student’s t-test, SAM t-test or the moderated t-test as reviewed above. For a given RNA-tag, there are a large number of co-expression measures between this RNA-tag and all other RNA-tags considered in the study. Furthermore, all the other RNA-tags have their own differential expression measures. Therefore, after adjusting the signs of co-expression and differential expression measures, we perform a local regression with the well-developed LOWESS technique between these two measures (co-expression measure as the predictor and differential expression measure as the response). The estimated local regression curve can be extended so that a differential expression measure can be predicted at correlation one (the co-expression measure between the given tag and itself). This predicted value is considered as the genome-wide co-expression based adjusted t-test for the original (unadjusted) t-test used for differential expression analysis. Based on our experience, if the co-expression is strong among differentially expressed genes (or RNA-tags) and/or strong among non-differentially expressed genes (or RNA-tags), then the genome-wide co-expression based adjusted t-test usually shows a clearly improved performance (compared to the original unadjusted t-test) in the detection of differential expression.

The above procedure is performed for all different RNA-tags considered in a reduced dataset and the list of predicted differential expression measures can be used to rank RNA-tags. We compare the performance of three t-type test statistics: the Student’s t-test, SAM t-test and the moderated t-test, as well as their related adjustments from the genome-wide co-expression based prediction of differential expression.

2.5 Permutation p-value

Since the underlying data distributions are unknown and the sample sizes are small, it is more appropriate to consider the permutation procedure (Dudoit et al., 2003) for computing the p-values for observed test scores. For each permutation, we randomly reassign n₁ and n₂ subjects to the first and the second sample groups, respectively, and then recalculate the test statistics. Since the sample sizes are small, we can enumerate all different permutations: the number is $\left(\begin{array}{c}n1+n2\\ n1\end{array}\right)$. However, since n₁ = n₂ = n and we are interested in two-tailed p-value, two permutations differed in a switch of sample labels will give the same absolute value of test scores. Therefore, we enumerate $\left(\begin{array}{c}2n\\ n\end{array}\right)/2$ distinct permutations.

The p-values of observed test scores can be computed based on the collection of permuted test scores. They must be evaluated at a “tiny” level so that the adjustment for multiple hypothesis testing can be effectively addressed. To gather enough number of permuted test scores, we choose to pool the permuted tests scores (Storey and Tibshirani, 2003) from different RNA-tags together (denoted as {S*}) and then compute the p-value of an observed test score S as {number of |S*| ≥ |S|}/{number of S*}.

2.6 False discovery rate

Since the family-wise error rate based adjustment for multiple hypothesis testing (e.g. Bonferroni adjustment) is usually too conservative, we choose the false discovery rate (FDR) based control procedure proposed by Benjamini and Hochberg (1995). For simplicity, we choose not to use the FDR estimation procedure proposed by Storey and Tibshirani (2003) since it requires an estimation of proportion of true null hypotheses.

The FDR control procedure proposed by Benjamini and Hochberg (1995) provides an estimated upper bound for the expected proportion of false positives among the claimed positives based on a given p-value as the threshold. Therefore, for each RNA-tag ranked according to its p-value, we can calculate the FDR for that RNA-tag. A curve can be generated when we connect the scatter-plot based on the pairs of FDR and rank from different RNA-tags. Each (adjusted or unadjusted) t-test has a curve to represent its performance in differential expression analysis. If a curve is relatively lower, then its associated t-test has a relatively better performance.

3 Results and Discussion

3.1 Data exploration

The expression range of digital gene expression (DGE) data is wide: most RNA-tags only have a few counts, while a few RNA-tags can have large counts. For the original dataset with 844316 unique RNA-tags, we observe a decreasing and log-log linear relationship between the range of expression measurements and its related number of RNA-tags (Figure 2b). This observation is consistent with the power-law observed in microarray data (Ueda et al., 2004). Then, we explore whether the majority of DGE data follows an approximately normal distribution after the log-transformation. Figure 2b shows that there is a huge number of RNA-tags with expression measurement range less than or equal to one. We perform the Shapiro-Wilk test of normality for each RNA-tag with expression measurement range larger than one. Figure 1a shows that the log-transformed data of most RNA-tags with low expression measurement range are not normally distributed. However, the log-transformed data of RNA-tags with high expression measurement range are more likely normally distributed. (Notice that 3.16, 31.62, 316.23 and 3162.28 in Figure 1a are actually 10^0.5, 10^1.5, 10^2.5 and 10^3.5.)

Figure 2.

(a, left): A graphic illustration of exclusion criterion: RNA-tags in the area below the black curve for a given k are excluded from the differential expression analysis; (b, right) The distributions of expression measurement range for different data sets.

Figure 1.

(a, histograms, left) Empirical p-value distributions for RNA-tags with different expression measurement ranges (p-values calculated based on the Shapiro-Wilk test of normality); (b, scatterplot, right) Comparison of FDR control based on the original dataset.

3.2 Soft filtering

For the “soft” filtering strategy, there is no pre-selection of RNA-tags and all the RNA-tags in the original data are used for differential expression analysis. RNA-tags with relatively low within-group variances are penalized to receive lower ranks. The SAM t-test (Tusher et al., 2001) and the moderated t-test (Smyth, 2004) are two representative test statistics based on this strategy. The SAM t-test simply adds an adjustment factor to the denominator of the traditional t-tests so that the test scores of RNA-tags with small within-group variances will be reduced. The moderated t-test considers a weighted average between the variance and an adjustment factor. Then, the test scores of RNA-tags with small within-group variances will be reduced but the test scores of RNA-tags with large within-group variances with be improved. Both methods “softly” filter out RNA-tags with small within-group variances unless their between-group differences are relatively large. Additionally, we also include the traditional Student’s t-test to observe the effect of “soft” filtering.

Figure 1b compares the false discovery rates (FDRs) from these three t-type test statistics. The best false positive control from the Student’s t-test can only be achieved at FDR≈0.6. The SAM t-test and the moderated t-test show a clearly improved false positive control. However, their performance is still not satisfactory: only 10 RNA-tags show FDR< 0.05; about 25 RNA-tags show FDR< 0.1 and about 65 RNA-tags show FDR< 0.2.

3.3 Hard filtering

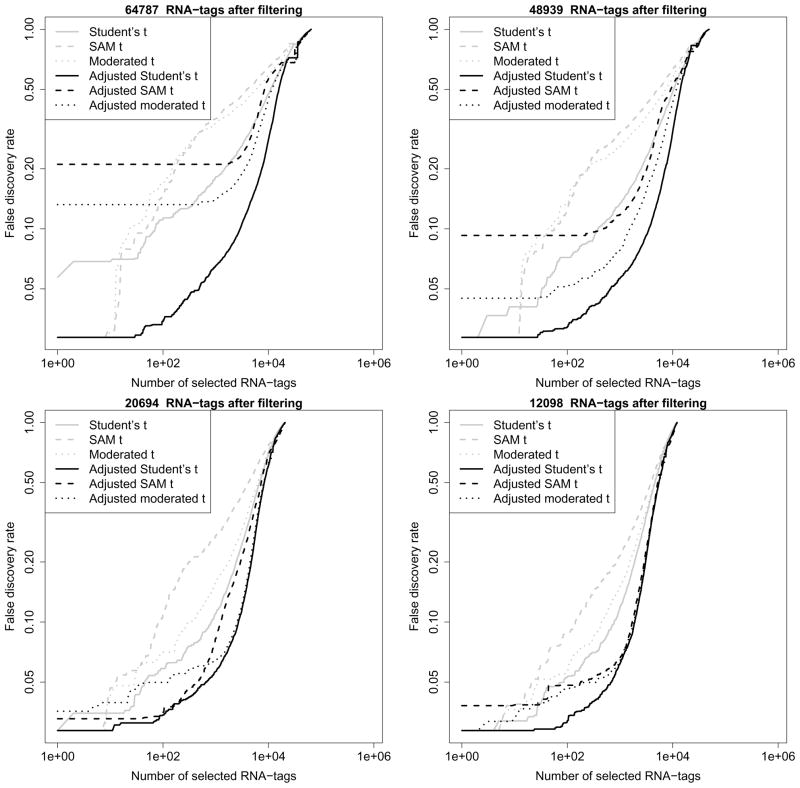
It is noticeable that the observations of most RNA-tags are of low variability (Figure 2b). Since these RNA-tags are usually not informative in the analysis of differential expression, we hypothesize that an appropriate filtering procedure can further improve the control of false positives. In Methods section, we provide a formula based on the range of expression measurements for excluding RNA-tags with low variability. Figure 2a demonstrates the exclusion region based on the range of expression observations. This filtering method is independent of the follow-up differential expression analysis since no sample group information is used in the formula. Based on four different threshold values, we extract four reduced datasets from the original data. Their numbers of RNA-tags are 12098, 20694, 48939 and 64787 (corresponding to the threshold values 1.65, 2, 3 and 4). Notice that a reduced dataset with a smaller number of RNA-tags is a subset of any one with a larger number of RNA-tags.

Figure 2b shows the distributions of the range of expression measurements of different subsets including the original one. Most of the included RNA-tags in the reduced datasets have larger expression measurements and wider range (10 ~ 10⁴) while most of the excluded RNA-tags have smaller expression measurements and narrower range (0 ~ 100). For the first two reduced datasets, all RNA-tags with expression measurement range less than 1 are excluded; for the last two reduced datasets, all RNA-tags with expression measurement range less than 10 are excluded. For each reduced dataset, we compare six different methods for the detection of differential expression: three t-type test statistics and our recently proposed genome-wide co-expression based adjustment (Lai, 2008) for each of these three t-type test statistics (see section Methods for details). Figure 3 shows the false discovery rates (FDRs) based on different test statistics.

Figure 3.

Comparison of FDR control based on the reduced datasets with (a, upper/left panel): k = 1.65, (b, upper/right): k = 2, (c, lower/left): k = 3, and (d, lower/right): k = 4.

When 64787 RNA-tags are included for differential expression analysis (Figure 3a), the traditional Student’s t-test shows a clear improvement: it provides a better control of false positives than the SAM and moderated t-tests do when the number of selected RNA-tags is more than 10. However, its FDRs all stay above 0.05 while two other t-tests can provide very significant FDRs for their several top ranked RNA-tags. A surprising observation is from the genome-wide co-expression based adjustments of these t-tests: compared to the unadjusted t-test, the adjusted one always shows a clearly improved false positive control at a relatively low FDR level. The genome-wide co-expression based adjustment of Student’s t-test shows the best false positive control: there are ~ 1000 RNA-tags with FDR~ 0.05.

When the number of included RNA-tags is decreased from 64787, 48939 to 20694 (Figure 3a–c), we observe that the false positive control is gradually improved for each of these six methods. The changes are clear for all the methods except the genome-wide co-expression based adjustment of Student’s t-test: only minor improvement can be observed for this method. When the number of included RNA-tags is further decreased to 12098 (Figure 3d), we cannot observe any clear improvement for all the methods: the genome-wide co-expression based adjustment of SAM t-test even shows a worse control of false positives. Overall, the genome-wide co-expression based adjustment of Student’s t-test always shows the best control of false positives regardless of different RNA-tag exclusion criteria.

3.4 Comparing different test statistics

Figure 4a compares the observed Student’s t-test vs. moderated t-test scores when no RNA-tags are excluded from the analysis (844316 RNA-tags). To reduce the figure complexity, we only compare top 20000 RNA-tags ranked by the absolute value of Student’s t-test. The moderated t-test shows a clearly shrinkage effect compared to the Student’s t-test: most scores of Student’s t-test are shrunken to the range of [−5; 5]. However, for these three t-type tests, their empirical and null distributions are almost identical (Figure 5a), which explains their unsatisfactory false positive control as shown in Figure 1. This is most likely due to the large number of noise RNA-tags not excluded from the analysis.

Figure 4.

Comparison of different test statistics based on (a, left): the original dataset, and (b/c, middle/right): a reduced dataset with 20694 RNA-tags. (a) and (b) are based on the original unadjusted t-tests.

Figure 5.

Comparison of distributions of test statistics based on (a, upper panel): the original dataset, and (b, middle and lower panels) a reduced dataset with 20694 RNA-tags. Shaded histograms represent the distributions of observed test statistics and solid curves represent the corresponding null distribution generated by the permutation procedure. The upper and middle panels are based on the original unadjusted t-tests.

Figure 4b compares the observed Student’s vs. moderated t-test scores when 20694 RNA-tags are included in the analysis. Although a clear shrinkage effect can still be observed from the moderated t-test, Figure 5b (middle panel) shows that this shrinkage actually worsen the separation between the empirical and null distributions. Therefore, the Student’s t-test performs better than the SAM and moderated t-tests (Figure 3c). This observation supports that our exclusion criterion can be used to exclude a considerable proportion of noise RNA-tags from the analysis.

Figure 4c compares the observed Student’s t-test vs. its genome-wide co-expression based adjusted scores when 20694 RNA-tags are included in the analysis. The pattern shows an interesting “S” shape. Based on some of our simulation studies (results not shown), the genome-wide co-expression based prediction of differential expression can generally reduce false but significant differential expression and improve true but insignificant differential expression. Figures 3a–d show that the genome-wide co-expression based adjusted tests always show certain improvement of false positive control over the unadjusted ones. Figure 5b (lower panel) confirms that this approach can further separate the empirical and null distributions. It is interesting to observe that the adjustment based on the Student’s t-test always performs the best and its performance is resistant to different exclusion criteria (Figure 3a–d).

4 Conclusions

In this study, we focused on the analysis methods for the detection of differential expression with digital gene expression (DGE) data. We first compared the “soft filtering” approach with the “hard filtering” approach. Although a few RNA-tags could still be detected with significant false discovery rates (FDRs) by the “soft filtering” approach, our results showed that the “hard filtering” followed by the traditional Student’s t-test was a more efficient approach: it was even better than the “soft followed by hard” approach. Furthermore, our results showed that the genome-wide co-expression based adjustment could always improve a univariate testing approach. After a specified “hard filtering”, the adjusted Student’s t-test always provided the best control of false positives, and its performance was surprisingly stable to different exclusion criteria for “hard filtering”. Due to our limit of computing power, we could not evaluate its performance for the original dataset with almost a million RNA-tags. This would be an interesting future research topic. If this method could still provide a satisfactory performance, then it would be an ideal choice for differential expression analysis: both full screening coverage and stringent false positive control could be simultaneously achieved.

A clear limitation of our study is that only one two-sample DGE data set with “reasonable” sample size could be found at the time of study. Some of our conclusion for this data set may not be reliably generalized to other similar data sets that may be available in a near future. However, we have applied the genome-wide co-expression based analysis of differential expression to several two-sample microarray gene expression data sets, and observed its improved performance over the traditional univariate approach (Lai, 2008). Since the DGE/RNA-seq data structure is basically similar to the microarray data structure, we expect that the improved performance from our genome-wide co-expression based analysis of differential expression will be generalized to other similar DGE/RNA-seq data. It is still necessary to confirm our conclusions with additional DGE/RNA-seq data when they are available.

The data scaling is a typical normalization procedure. It is based on the assumption that the existence of differential expression has a minor impact on the total RNA-tag count. However, if this assumption is not true, then we can obtain misleading results. Since it is unknown which RNA-tags are truly differentially expressed, it is difficult to validate this assumption. However, among 844316 RNA-tags, our results imply that only thousands of them are likely truly differentially expressed. It is reasonable to expect a minor impact on the total RNA-tag count from such a small proportion of differentially expressed RNA-tags.

Since many RNA-tags may belong to the same gene, one may consider mapping RNA-tags to the genome. This task has been well developed for many years. However, different RNA-tags from the same gene usually have different expression measurements. It is necessary to develop an efficient method for combining these different measurements so that a unique gene expression measurement can be obtained. When combining these different measurements, it is also necessary to consider possible alternative splicing events. Therefore, before an efficient method is available for this task, conducting a differential expression analysis at the RNA-tag level is a preferred choice at the current stage.

In this study, the p-values are evaluated based on the pooled permutation test scores. It has been recently shown that this approach may provide misleading results (Yang and Churchill, 2007). A major concern is that the null distributions of test statistic for different variables (RNA-tags) can be different. However, when the sample size is small and the number of variables is large, it is difficult to explore the difference of null distributions. This will be pursued in our future research.

Another interesting research topic is to develop a more efficient statistical test of differential expression for DGE/RNA-seq data although we have shown a satisfactory and stable performance from the genome-wide co-expression based adjustment of the Student’s t-test with transformed data. Since the data are based on the count of molecules, it is necessary to explore their unique distribution characteristics. This will help the development of a new statistical test for this new type of data. However, since scaling is necessary as a pre-processing step (’t Hoen et al., 2008), its impact on the change of data distributions must also be rigorously considered.

Biography

Yinglei Lai received his B.S. degrees in Information & Computation Sciences and Business Administration in 1999 from the University of Science and Technology of China, and his Ph.D. degree in Applied Mathematics in 2003 from the University of Southern California. After the postdoctoral training during 2003–2004 at Yale University School of Medicine, he joined The George Washington University as an Assistant Professor of Statistics. His research areas are statistical problems in the fields of bioinformatics, computational biology and statistical genetics.