A MATHEMATICAL MODEL OF FORCE TRANSMISSION FROM INTRAFASCICULARLY TERMINATING MUSCLE FIBERS

Abstract

Many long skeletal muscles are comprised of fibers that terminate intrafascicularly. Force from terminating fibers can be transmitted through shear within the endomysium that surrounds fibers or through tension within the endomysium that extends from fibers to the tendon; however, it is unclear which pathway dominates in force transmission from terminating fibers. The purpose of this work was to develop mathematical models to (i) compare the efficacy of lateral (through shear) and longitudinal (through tension) force transmission in intrafascicularly terminating fibers, and (ii) determine how force transmission is affected by variations in the structure and properties of fibers and the endomysium. The models demonstrated that even though the amount of force that can be transmitted from an intrafascicularly terminating fiber is dependent on fiber resting length (the unstretched length at which passive stress is zero), endomysium shear modulus, and fiber volume fraction (the fraction of the muscle cross-sectional area that is occupied by fibers), fibers that have values of resting length, shear modulus, and volume fraction within physiologic ranges can transmit nearly all of their peak isometric force laterally through shearing of the endomysium. By contrast, the models predicted only limited force transmission ability through tension within the endomysium that extends from the fiber to the tendon. Moreover, when fiber volume fraction decreases to unhealthy ranges (less than 50%), the force-transmitting potential of terminating fibers through shearing of the endomysium decreases significantly. The models presented here support the hypothesis that lateral force transmission through shearing of the endomysium is an effective mode of force transmission in terminating fibers.

1. INTRODUCTION

The majority of long muscles in vertebrates contain fibers that terminate without reaching a tendon (Barrett, 1962; e.g. Gans et al., 1989; Gaunt and Gans, 1990; Hijikata et al., 1993; Loeb et al., 1987; Ounjian et al., 1991; Paul, 2001). The force produced in a motor unit containing intrafascicularly terminating fibers is proportional to the total cross-sectional area of all fibers (Ounjian et al., 1991). Since these fibers do not insert into a tendon at one or both ends, how do they transmit force to the tendon?

Previous studies have suggested that force generated in intrafascicularly terminating fibers (herein called “terminating fibers”) is transmitted to the endomysium (Huijing, 1999; Monti et al., 1999; Purslow, 2002). Force is transmitted from the contractile proteins to the endomysium via costameres at Z-disks along the length of the fiber (Ervasti, 2003; Patel and Lieber, 1997; Bloch and Gonzalez-Serratos, 2003). Once force is transmitted to the endomysium there are two pathways through which it can be exerted onto the tendon: (i) laterally (in the direction transverse to the fiber) to the surrounding muscle tissue via shear within the endomysium that surrounds the fiber, or (ii) longitudinally through tension within the endomysium that extends from the fiber end to the tendon. Various experiments have established the existence of lateral force transmission within bundles of fibers (Street, 1983), within whole muscles (Huijing et al., 1998; Jaspers et al., 1999), and between muscles of the same compartment (Maas et al., 2001). Force transmission through shear has the advantage that shear stresses act over a large area (the entire surface of the fiber) compared to tensile stresses, which act over the small cross-sectional area of the endomysium. However, force transmission through tension has the advantage that the endomysium is stiffer in tension than in shear (estimates of the tensile and shear moduli of the endomysium are listed in Table 1). While it is clear that force can be transmitted both laterally and longitudinally within muscle, it is unclear which pathway dominates in force transmission from terminating fibers.

Table 1.

Range of model parameters available from the literature

Resting length of terminating fibers (cm)	4–20 human sartorius (Heron and Richmond, 1993) 4.5–6.3 cat tibialis anterior (Ounjian et al., 1991) 2–4 guinea pig sternomastoid (Young et al., 2000) 2–3 cat sartorius, tenuissimus, and semitendinosus (Loeb et al., 1987)
Fiber diametera (μm)	30 (Heron and Richmond, 1993) 50–80 (Ounjian et al., 1991) 50 (Young et al., 2000) 66 (Loeb et al., 1987)
L0/2r0 (ratio of fiber resting length to diameter, dimensionless)	800–4000 (Heron and Richmond, 1993) 560–1300 (Ounjian et al., 1991) 400–800 (Young et al., 2000) 303–454 (Loeb et al., 1987)
Fascicle length ( $L_0^{\text{fascicle}}$, cm)	50 (Heron and Richmond, 1993) 7.5 (Ounjian et al., 1991) 4–5b (Young et al., 2000) 7–11.5 (Loeb et al., 1987)
$L_0/L_0^{\text{fascicle}}$ (ratio of fiber resting length to fascicle length, dimensionless)	0.08–0.4 (Heron and Richmond, 1993) 0.6–0.84 (Ounjian et al., 1991) 0.4–1 (Young et al., 2000) 0.17–0.43 (Loeb et al., 1987)
Endomysium shear modulus (Gend, kPa)c	O(3.87) (Morrow et al., 2010) 5 (Trotter and Purslow, 1992; Trotter et al., 1995)
Endomysium tensile modulus (Cend, kPa)	O(2.6)d (Magid and Law, 1985) 40e (Friden and Lieber, 2003; Lieber et al., 2003)
Fiber Volume fraction (dimensionless)	38.5±13.6% for spastic muscle, 95.0±8.8% for healthy muscle (Lieber et al., 2003)

^aFiber diameters are approximate and are based on estimates from the images provided in the cited articles.

^bIn cases where muscle length was reported, muscle length is used in place of fascicle length.

^cA shear modulus has not been measured for the endomysium however Trotter and Purslow, 1992, and Trotter et al., 1995, used 5 kPa as a lower estimate. Morrow et al., 2010, measured 3.87 kPa as the along-fiber shear modulus of muscle. Previous work suggests that the along-fiber shear modulus of muscle is of the same order of magnitude as that of endomysium (Sharafi and Blemker, 2010).

^dMagid and Law, 1985, reported no significant difference between the tensile modulus of skinned fibers and those of a whole muscle in frog semitendinosus. It should therefore follow that the endomysium tensile modulus is of the same order of magnitude as the fiber (2.6±0.25 kPa).

^eC_end = 40 kPa was calculated based on the following: Friden and Lieber, 2003, reported an average tangent modulus of 28 kPa for single fibers. A tangent modulus of 40 kPa can be calculated based on the reported stress-versus-sarcomere-length plots for fiber bundles (Lieber et al., 2003). Based on a healthy fiber volume fraction of 95% the tangent modulus for the endomysium can be calculated as 268 kPa. In our model of the tensile behavior of endomysium (Appendix B), the tangent modulus is equal to E_tangent = 6.6C_end, which results in C_end ~ 40 kPa.

The purpose of this work was to (i) compare the effectiveness of lateral and tensile force transmission in terminating fibers, and (ii) determine how force transmission is affected by variations in the structure and properties of fibers and the endomysium. We developed mathematical models to achieve these goals because it would be virtually impossible to design an experiment capable of determining the force pathway for an individual terminating fiber under physiological conditions (i.e. within a muscle) and to independently explore the effects of variations in muscle microstructure properties. We created both analytical and finite element (FE) models of terminating fibers, and predicted the ability of terminating fibers to transmit force through both shear and tension within the endomysium. We used these models to analyze how the amount of force transmitted is affected by resting length, endomysium shear modulus, fiber volume fraction (the fraction of muscle cross-sectional area that is occupied by fibers), and fiber cross-sectional geometry.

2. METHODS

2.1. Analytical models

In order to compare the effectiveness of lateral and longitudinal force transmission in terminating fibers, we created two analytical models of force transmission. The first model predicts force transmitted solely through shear within endomysium, while the second model predicts force transmitted solely through tension within endomysium.

Both models assumed the terminating fiber is attached to a tendon at one end but terminates within the fascicle at the other end. In both the shear and the tensile models, the tensile stress-strain behavior of the fiber is given by (Blemker et al., 2005):

$${\sigma }_{\text{fiber}}=p_1{\sigma }_{\text{iso}}\left(e^{6.6(\lambda -1)}-1\right)+\lambda \alpha {\sigma }_{\text{iso}}\{\begin{array}{ll}9{(\lambda -0.4)}^2\hfill & \lambda \le 0.6\hfill \\ 1-4{(1-\lambda )}^2\hfill & 0.6<\lambda <1.4\hfill \\ 9{(\lambda -1.6)}^2\hfill & \lambda \ge 1.4\hfill \end{array},$$ (2.1.1)

where λ = l/L₀ is fiber stretch (λ<1 for a shortening fiber), l is final fiber length and L₀ is initial fiber length and is equal to fiber resting length, σ_iso = 300 kPa is the peak isometric stress, p₁σ_iso is the tensile modulus of the fiber, and α represents the activation level (α = 1 for maximal activation). In (2.1.1) the simplifying assumption has been made that optimal fiber length (the length at which the fiber generates its peak isometric stress) is equal to the resting or unstretched length of the fiber (λ = 1). Fiber force is equal to:

$$F_{\text{fiber}}=(A_0/\lambda ){\sigma }_{\text{fiber}},$$ (2.1.2)

where σ_fiber is given by equation (2.1.1), A₀ is the initial fiber cross-sectional area, and the following substitution was made for fiber area A, based on the assumption that muscle fibers are incompressible: A = A₀/λ.

2.1.1. Analytical shear model

The shear model (Fig. 1) simulates the transmission of force generated in the terminating fiber through shearing of the endomysium that encases it to the surrounding muscle tissue. The model assumes that the surrounding muscle tissue is held at a constant length and that its deformation in response to the contractile force of the terminating fiber is negligible.

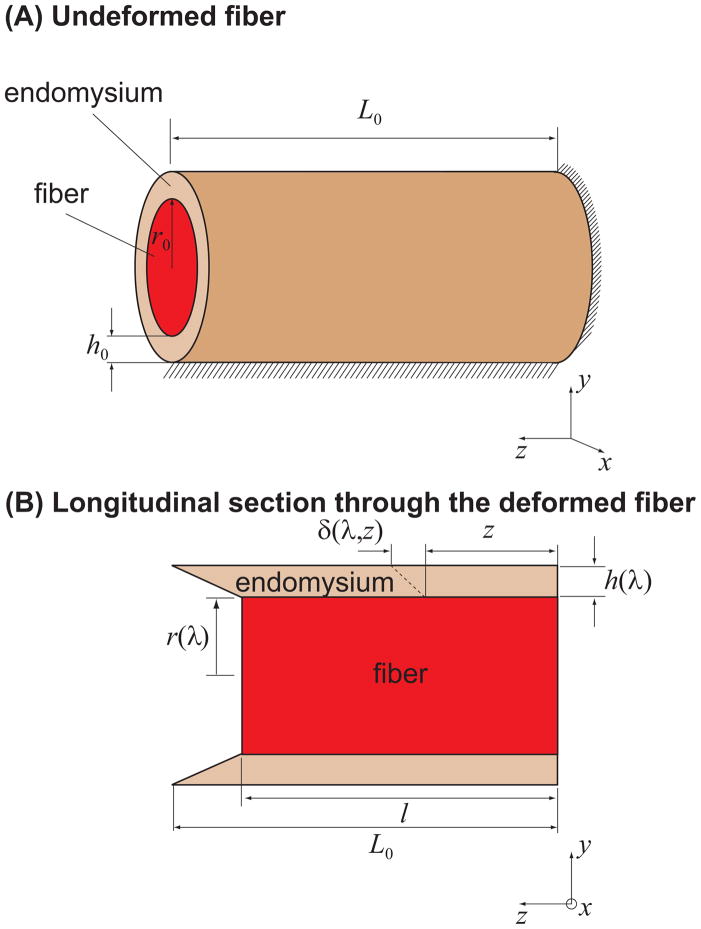
Figure 1.

Schematic of the analytical shear model in the undeformed configuration (A) and deformed configuration (B). The model assumes that the terminating fiber has a circular cross-section and is surrounded by an annular layer of endomysium (A) which transmits the force generated in the fiber to the surrounding muscle tissue. The surrounding muscle tissue is held at a constant length, and its presence was simulated by constraining the outer surface of the endomysium from moving in the fiber direction (z). This constraint was imposed based on the assumption that the surrounding muscle tissue is sufficiently stiff so that its deformation in response to the contractile force of the terminating fiber is negligible. One end of the fiber was constrained from moving in the z direction to represent an end attached to a tendon. L₀, r₀ and h₀ are fiber resting length, initial fiber radius and endomysium thickness, respectively (A). The thickness of endomysium, h₀, is shared by neighboring fibers, therefore fiber volume fraction was calculated based on half the thickness of the endomysium: $V_{\text{f}}=r_0^2/{\left(r_0+\frac{h_0}{2}\right)}^2=1/{(1+\kappa /2)}^2$. l is the fiber length at equilibrium, and l = λL₀ (B). r(λ) and h(λ) are the fiber radius and the endomysium thickness at fiber length l, respectively (B). δ(λ, z) is the displacement of a point on the periphery of the fiber at distance z from the fixed end of the fiber (B).

The following equation describes the shear response of the endomysium:

$${\sigma }_{\text{end}}=2G_{\text{end}}{\beta }_{\text{end}},$$ (2.1.1.1)

where G_end is the shear modulus and β_end is the shear strain. This relationship is based on previous studies that have shown the shear modulus of the endomysium remains constant over a physiological range of muscle lengths (Purslow and Trotter, 1994; Trotter and Purslow, 1992). The fiber shear strain was assumed to be negligible compared to the endomysium.

When the fiber is activated, it shortens and creates shear deformation within the endomysium (Fig. 1B). The final length of the fiber was obtained by determining the equilibrium between the active force generated in the fiber and the shear force within the endomysium that resists the shortening of the fiber, F_end = F_fiber (Appendix A):

$$\frac{2\left(\frac{G_{\text{end}}}{{\sigma }_{\text{iso}}}\right){\left(\frac{L_0}{r_0}\right)}^2\lambda (1-\lambda )}{-1+\sqrt{1+2\kappa (2-\kappa )\left(\frac{\lambda }{\lambda +1}\right)}}=p_1\left(\frac{e^{6.6(\lambda -1)}-1}{\lambda }\right)+\alpha \{\begin{array}{ll}9{(\lambda -0.4)}^2\hfill & \lambda \le 0.6\hfill \\ 1-4{(1-\lambda )}^2\hfill & 0.6<\lambda <1.4\hfill \\ 9{(\lambda -1.6)}^2\hfill & \lambda \ge 1.4\hfill \end{array},$$ (2.1.1.2)

where κ = h₀/r₀, h₀ is the initial thickness of the endomysium, and r₀ is the initial fiber radius (Fig. 1A).

We numerically solved equation (2.1.1.2) for λ, at α = 1 in MATLAB (MathWorks, Inc. Natick, MA). We subsequently calculated the force generated in the fiber using equation (2.1.2).

The goal of our analysis was to identify the range of values for fiber length, volume fraction, and endomysium moduli that are required for effective force transmission through shearing of the endomysium. To provide a full understanding how these parameters affect force transmission, we included values for fiber length, volume fraction, and endomysium moduli that were outside the range of values reported in the literature. Then, to assess the efficacy of lateral force transmission through shear in actual muscles, we compared these values to those reported in the literature (Table 1).

2.1.2. Analytical tensile model

The tensile model assumed that the active fiber force is transmitted via tension through the endomysium that extends from the terminating fiber end to the opposite tendon (Fig. 2). Both the fiber and endomysium were assumed to be initially at their unstretched lengths and the fascicle is held at a fixed length of $L_0^{\text{fascicle}}$

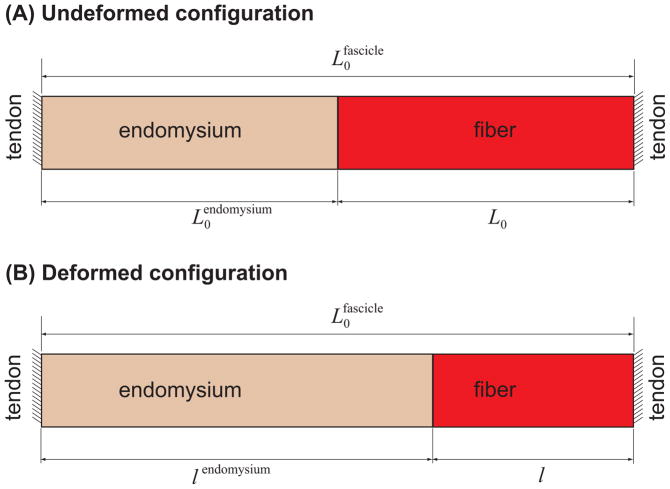
Figure 2.

Schematic of analytical tensile model, in the undeformed (A) and deformed (B) conditions. The fascicle is assumed to be held at a fixed length ( $L_0^{\text{fascicle}}$), and the force transmitted from the fiber is transmitted to the tendon at the other end by stretching the endomysium.

The fiber shortens when it is activated until its active force is balanced by the passive tensile force within the endomysium. We calculated the final length of the fiber by determining the equilibrium between the active fiber force and the tensile force within the endomysium in series with the fiber (Appendix B):

$$C_{\text{end}}\left(e^{6.6(1-\lambda )\left(\frac{L_0/L_0^{\text{fascicle}}}{1-L_0/L_0^{\text{fascicle}}}\right)}-1\right)=p_1{\sigma }_{\text{iso}}\left(e^{6.6(\lambda -1)}-1\right)+\lambda \alpha {\sigma }_{\text{iso}}\{\begin{array}{ll}9{(\lambda -0.4)}^2\hfill & \lambda \le 0.6\hfill \\ 1-4{(1-\lambda )}^2\hfill & 0.6<\lambda <1.4\hfill \\ 9{(\lambda -1.6)}^2\hfill & \lambda \ge 1.4\hfill \end{array},$$ (2.1.2.1)

where C_end is the tensile modulus of endomysium.

We numerically solved equation (2.1.2.1) for λ in MATLAB (MathWorks, Inc. Natick, MA) and subsequently calculated the force generated in the fiber using equation (2.1.2)..

Similar to the shear model, the goal of this analysis was to identify the range of values for fiber length–to–fascicle length ratio ( $L_0/L_0^{\text{fascicle}}$) and endomysium moduli (C_end) that are required for effective force transmission through tension within the endomysium. By comparing these values to those reported in the literature (Table 1) we assessed the effectiveness of force transmission through this pathway.

2.2. Finite element models

We created FE models of different fiber geometries in order to investigate the following simplifying assumptions made to create the analytical shear model: (i) shear strain is constant across the thickness of the endomysium, (ii) the fiber is rigid in shear, (iii) the fiber and endomysium cross-sections are circular, and (iv) the surrounding fibers can be represented by constraining the outer surface of the endomysium layer in the z direction. We created a set of FE models with a circular cross-section identical to the analytical model (Fig. 3A) in order to investigate the effects of nonuniform shear strains through the thickness of the endomysium, and shear deformations within the fiber. One end of the fiber and the outer surface of the endomysium were constrained from moving in the fiber direction (z). To determine the effect of the neighboring endomysium in the rest of the tissue, we created a model of a terminating fiber surrounded by a bundle of fibers (Fig. 2B) based on a histological cross-section obtained as previously described (Sharafi and Blemker, 2010).

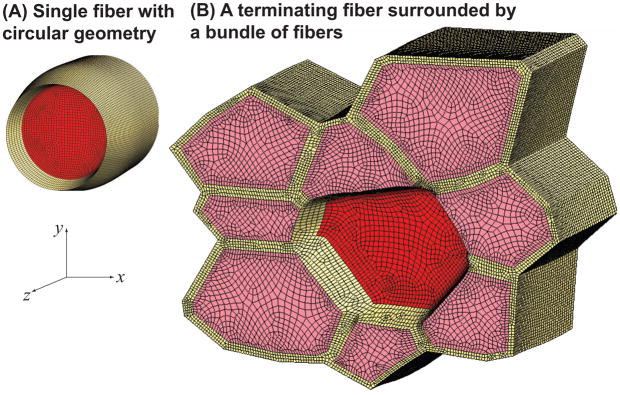
Figure 3.

Finite element models of a single fiber with a circular cross-section (A) and a terminating fiber (red) within a fiber bundle (B), both shown in the activated condition. The FE models with circular cross-section (A) have a fiber diameter of 80μm, a volume fraction of 75% and have lengths varying from 120μm (L₀/2r₀ = 1.5) and 1.6mm (L₀/2r₀ = 20) at 80μm increments. To create a model based on a histological cross-section (B), we obtained an image at 20X magnification that contained several fibers, and outlined the boundaries of nine adjacent fibers that formed a bundle. The resulting fiber polygons were scaled to create a fiber volume fraction of 75%. The cross-sectional geometry remains constant along the length of the fibers. Hexahedral meshes were created based on the outlines in Ansys 11 (Ansys, Inc. Canonsburg, PA). The model is 120μm long (L₀/2r₀ = 1.5). The terminating (middle) fiber has the same cross-sectional area as the fiber with the circular geometry ( $\frac{\pi }{4}{(80\mu \text{m})}^2$). The middle fiber was constrained in the z direction at one end. All other fibers were constrained in the z direction at both ends.

We used a hyperelastic, nearly incompressible, transversely isotropic constitutive model to represent the behavior of the fibers and the endomysium in the FE models (Blemker et al., 2005). The tensile and shear properties of both materials were defined via equations (2.1.1) (α = 0 for endomysium) and (2.1.1.1), and Table 2.

Table 2.

Material parameters used in all finite element simulations

	p1(dimensionless along-fiber tensile modulus)	G(shear modulus, kPa)
Fiber	0.1250	2.50
Endomysium	0.0125	1.25

The FE simulations were performed in the nonlinear FE solver, NIKE3D (Puso, 2006). Fiber activation, α, was increased from 0.0 to 1.0 incrementally throughout the simulation. The force was calculated at the constrained end of the fiber for the single fiber model and at the constrained end of all fibers for the bundle model, once α reached 1.0. To compare the FE results with the analytical shear model, we used the analytical model to calculate the force for the same fiber diameter (2r₀ = 80 μm), lengths (varying between 120μm and 1.6mm, and fiber volume fraction (75%) as the FE models. The parameters p₁ (for the fiber) and G_end were also chosen to be the same as the FE models (Table 2).

3. RESULTS

3.1. Analytical models

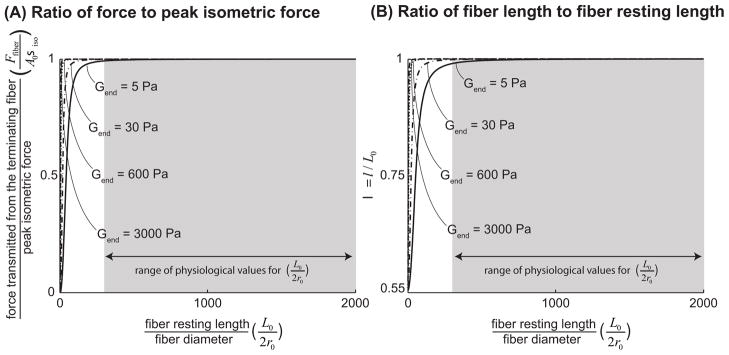
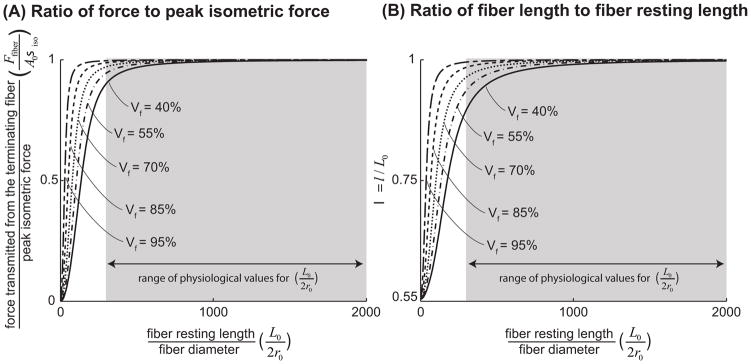
The analytical shear model predicted that force transmission increases with increasing fiber resting length and endomysium shear modulus (Fig. 4A). Similarly, as resting length increases and shear modulus increases, active terminating fibers remain closer to their optimal length (Fig. 4B). Most importantly, terminating fibers within physiological ranges of resting length, fiber volume fraction, and endomysium shear modulus can transmit virtually all their peak force through shearing of the endomysium. For example, a fiber that has a length to diameter ratio of L₀/2r₀ = 300, an endomysium shear modulus of 5Pa, and a volume fraction of 90% can transmit 99% of its peak isometric force through shearing of the endomysium. Since the values of L₀/2r₀ reported in the literature (Table 1) are higher than 300 and the endomysium shear modulus is orders of magnitude larger than 5Pa (Table 1), our model indicates that all terminating fibers would be capable of transmitting more than 99% of their peak isometric force through shear within the endomysium. The shear model also demonstrated that short terminating fibers in muscles with low fiber volume fractions (perhaps due to atrophy or disease) might have a diminished capacity for lateral force transmission (Fig. 5A). For example a fiber with a fiber volume fraction of 40% must have a much longer optimal fiber length than a fiber with a volume fraction of 95% to be able to transmit 99% of its peak force (L/2r₀ = 1000 for the 40% volume fraction versus L/2r₀ = 200 for the 95% volume fraction, assuming an endomysium shear modulus of 5Pa).

Figure 4.

The ratio of force transmitted laterally through shearing of the endomysium from a terminating fiber to peak isometric force that can be generated in a fiber of the same cross-sectional area, plotted against the ratio of fiber resting length to fiber diameter (A). λ, the ratio of fiber length at equilibrium to fiber resting length (B). We normalized the force transmitted from the fiber (equation 2.1.2), by the fiber’s peak isometric force, F_iso = Aσ_iso. The quantity plotted on the vertical axis (A) is therefore F_fiber/F_iso = σ_fiber(λ)/λσ_iso. From equation (2.1.1.2) it is clear that λ is a function of L₀/2r₀, the ratio of fiber resting length to initial fiber diameter, G_end, endomysium shear modulus and κ, and thereby V_f, fiber volume fraction. For values of λ smaller than one, F_fiber/F_iso is a monotonically increasing function of λ. In these plots fiber volume fraction (V_f) was held constant at 90% (Typical for a healthy muscle (Table 1)) and endomysium shear modulus (G_end) was varied from 5Pa which is lower than any estimates based on the literature (Table 1) to 3000Pa which is on the same order as the highest available estimates based on the literature (Table 1). The shaded region highlights the physiologically relevant range of values for L₀/2r₀ based on literature and cited in Table 1.

Figure 5.

The ratio of force transmitted laterally through shearing of the endomysium from a terminating fiber to peak isometric force that can be generated in a fiber of the same cross-sectional area, plotted against the ratio of fiber resting length to fiber diameter (L₀/2r₀ is varied by increments of 1) (A). λ, the ratio of fiber length at equilibrium to fiber resting length (B). Endomysium shear modulus was held constant at 5Pa and fiber volume fraction was varied from 95% to 40%. This ranged was chosen based on values reported in the literature for healthy and spastic muscle tissue (Table 1). The shaded region highlights the physiologically relevant range of values for L₀/2r₀ based on the literature and cited in Table 1.

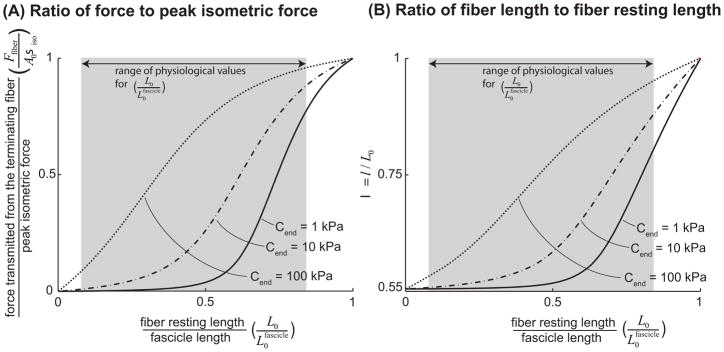
The tensile model predicts that force transmission through tension within the endomysium increases as the ratio of fiber resting length to fascicle length and the endomysium tensile modulus increase (Fig. 6A). However, the model predicted that, in contrast to force transmission via shear, for much of the range of physiological lengths and endomysium tensile moduli (Table 1), terminating fibers cannot transmit as much of their peak isometric force longitudinally through tension within the endomysium as they would through shear. For example, a fiber spanning half the length of a fascicle ( $L_0/L_0^{\text{fascicle}}=0.5$) with an endomysium tensile modulus of C_end = 40 kPa (the largest estimate based on the literature (Table 1)) can only transmit 55% of its peak force through tension within the endomysium. Since many fibers span less than half the fascicle length (Table 1) and may have endomysium tensile modulus smaller than 40kPa, they likely transmit less than 55% of their peak isometric force through tension within the endomysium.

Figure 6.

The ratio of force transmitted longitudinally through tension within the endomysium from a terminating fiber to peak isometric force that can be generated in a fiber of the same cross-sectional area, plotted against the ratio of fiber resting length to fascicle length (A). λ, the ratio of fiber length at equilibrium to fiber resting length (B). From equation (2.1.2.1) it is clear that λ is a function of $L_0/L_0^{\text{fascicle}}$, the ratio of fiber resting length to fascicle length, and C_end, endomysium tensile modulus. Endomysium tensile modulus (C_end) was varied from 1kPa to 100kPa. This range was chosen to encompass the range of estimates for the tensile modulus of the endomysium available in the literature (Table 1). The shaded region highlights the physiologically relevant range of values for $L_0/L_0^{\text{fascicle}}$ based on the literature, cited in Table 1.

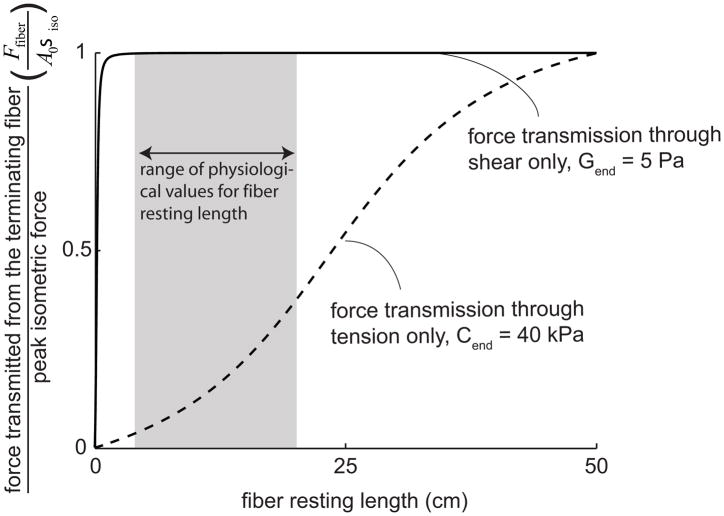
We compared the ratio of force to peak isometric force as a function of fiber length between the two modes of force transmission, for a fiber with a diameter of 30μm within a 50cm long fascicle (e.g. Heron and Richmond, 1993), an endomysium tensile modulus of 40kPa and shear modulus of 5Pa, and a fiber volume fraction of 90% (Fig. 7). In this case, lateral force transmission though shear is substantially more effective than longitudinal force transmission through tension.

Figure 7.

The ratio of force transmitted from a terminating fiber to peak isometric force when force is only transmitted laterally through shearing of the endomysium compared to when it is transmitted only longitudinally through tension in the endomysium. The fiber was assumed to have a diameter of 30μm and was within a 50cm long fascicle (e.g. human sartorius (Heron and Richmond, 1993)). We used a value of C_end = 40kPa for the tensile modulus of endomysium (the highest estimate based on the literature (Table 1)) and an endomysium shear modulus of 5Pa (the lowest estimate based on the literature (Table 1)). The shaded area highlights the range of lengths for intrafascicular terminating fibers reported for the human sartorius (Heron and Richmond, 1993).

3.2. Finite element models

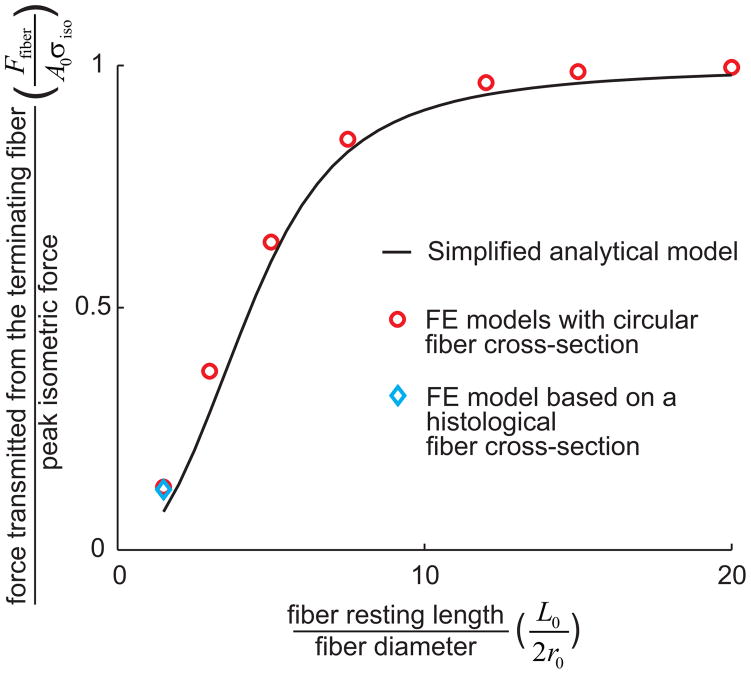
Comparisons of the analytical shear model with the FE models showed that the introduction of nonuniform shear strains through the thickness of the endomysium and fiber shear compliance resulted in only small differences in predicted force for fibers with higher resting lengths (Fig. 8). For a fiber with a resting length of 1.6mm (L₀/2r₀ = 20), the percentage of peak isometric force predicted by the circular FE model is 99.6% compared to 97.9% for the analytical model. For a fiber with a resting length of 120μm (L₀/2r₀ = 1.5), the percentage of peak isometric force is 13.0% for the FE model with circular cross-section, 12.5% for the FE model of the fiber bundle, and 7.8% for the analytical model. The analytical model underestimates the force transmitted from short fibers; however for a ratio of L₀/2r₀ = 20, the analytical model and the FE model of a single fiber with circular geometry showed good agreement, and the FE fiber bundle model and the circular fiber model were in perfect agreement.

Figure 8.

Comparison between the forces predicted by the analytical shear model ( ), FE models with a circular fiber cross-section ( ) for different fiber resting lengths lengths ranging from 120μm (L₀/2r₀ = 1.5) to 1.6mm (L₀/2r₀ = 20), and the FE model of a terminating fiber surrounded by a bundle of fibers created based on a histological cross-section ( ) with a resting length of 120μm (L₀/2r₀ = 1.5). In all models the fiber diameter is 80μm, and fiber volume fraction is 75%.

4. DISCUSSION

The mathematical models described here demonstrate that terminating fibers with volume fractions within a healthy range have the ability to transmit nearly all of their peak isometric force through shearing of the endomysium. By contrast, there is only limited force transmission ability through tension within the endomysium that extends from the fiber to the tendon.

Comparison of the shear and tensile models reveals that two key factors result in shearing of the endomysium is more effective than tension. First, shear forces transmit force to the endomysium over the entire surface of the fiber. By contrast, tensile forces transmit force on the small cross-sectional area of the endomysium. Second, since the endomysium is thin, a small displacement of the fiber results in large shear strains within the endomysium, and thereby a large shear force resisting the shortening of the terminating fiber (per equation 2.1.1.1). In comparison, the length of the endomysium extending from the fiber to the tendon is much larger (especially for small fiber length – to – fascicle length ratios), so large displacements still result in relatively small tensile strains, and thereby a smaller tensile resisting force resisting shorting of the fiber.

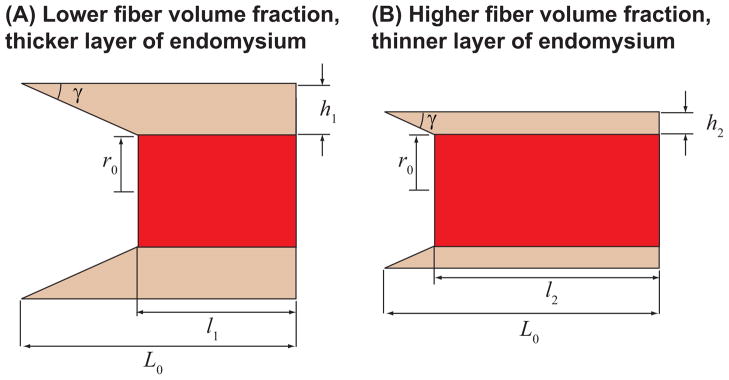
Analysis of the shear model showed that force transmission through shear becomes more effective as fibers become longer and as volume fraction of fibers increases (Figs. 4–5). The fiber length effect arises for two reasons: (i) longer fibers have larger surface areas to transmit shear stress, and (ii) for the given value of fiber stretch, longer fibers undergo a larger absolute length change and therefore results in larger shear strains within the endomysium, hence a larger shear resisting forces. The volume fraction effect arises for one key reason: fibers with larger volume fractions have thinner endomysium, and, for a given value of fiber stretch, the fiber with the thinner endomysium will undergo more shear deformation and provide larger shear resisting forces (Fig. 9). Fiber volume fraction can be diminished due to fatty infiltration and fibrosis in various myopathies (Chan and Liu, 2002) as well as injury (Nikolaou et al., 1987). Spastic muscles have been reported to have drastically decreased fiber volume fractions (from a mean of 95% for healthy fibers to 38.5%) (Lieber et al., 2004). The models presented here suggest that these pathological changes in microstructure properties may affect force transmission in muscles that have intrafascicularly terminating fibers.

Figure 9.

Explanation of the effects of fiber volume fraction. For the same shear angle γ in the endomysium, the fiber with the lower fiber volume fraction (A) will shorten more than the fiber with higher volume fraction (B) l₁ < l₂.

The analytical shear model employed several simplifying assumptions, including: (i) shear strain is constant across the thickness of the endomysium, (ii) the fiber is rigid in shear, (iii) the fiber and endomysium cross-sections are circular, and (iv) the surrounding muscle tissue can be represented by constraining the outer surface of the endomysium layer in the z direction. The FE models demonstrated that the effects of the simplifying assumptions are small except at very short lengths. The FE models displayed strain nonuniformity through the thickness of the endomysium (e.g., in the circular FE models, strains in the endomysium varied as much as 1.5 times). However, this nonuniformity was localized near the terminating end of the fiber and its effect on force predictions was negligible. For short fibers, the analytical model slightly underestimates the amount of force transmitted from the fiber, thus providing a conservative estimate. Comparison between the analytical and FE models was carried out for relatively short fiber lengths. For higher resting lengths the ratio of force to peak isometric force approaches one under all conditions. Therefore, if the models are in good agreement for relatively short fibers as demonstrated here, their predictions will be nearly identical at longer lengths.

Our models assumed that the muscle tissue surrounding the terminating fiber was held at a constant length. In Appendix C, we calculated the force transmitted from a terminating fiber within a muscle that undergoes length change. While the forces were slightly different for these cases, the models showed that shearing of endomysium is an effective pathway for force transmission, regardless of whether the surrounding muscle tissue was held at a constant length.

The model assumes that the deformation of the surrounding muscle tissue in response to the contractile force of the terminating fiber is negligible. If this were not the case, the terminating fiber should shorten more and its force would decrease. The stiffness of the surrounding muscle tissue depends on the amount of muscle tissue surrounding the terminating fiber, whether the surrounding fibers are active or passive, and what fraction of them are terminating intrafascicularly. A recently published study (Ramaswamy et al., 2011) showed that forces from a small number of active motor units can be transmitted very effectively through shear to the epimysium of the muscle. In this case where the rest of the muscle was passive, the fibers from the active motor unit were able to contract without considerable shortening. This suggests that assuming that the deformation of the tissue surrounding the terminating fiber is negligible is a reasonable assumption.

The models assumed that the cross-sectional area is constant along the entire length of the fiber. The majority of terminating fibers taper over a length of several millimeters (Trotter, 1990). Our analytical shear model suggests that these fibers can transmit nearly all their force through shearing of the endomysium as long as the untapered region of the fiber is at least ~1–2cm long. Additional force can be expected to be transmitted over the tapered length of the fiber. Furthermore, the tensile model demonstrates that these fibers will not be able to transmit much force longitudinally through tension within the endomysium in series with the tapered end of the fiber.

The models presented here provide new insights into the mechanics of force transmission for muscles that have terminating fibers. The models demonstrate that healthy terminating fibers have the ability to transmit all their force through shearing the endomysium, and substantially less force through tension of the endomysium. While we focused on terminating fibers, lateral force transmission between fibers is also important in spanning fibers, for example, in allowing force transmission in damaged fibers (Purslow, 2002). Furthermore, lateral force transmission has been demonstrated at higher levels of the muscle hierarchy, including within whole muscles (Huijing et al., 1998; Jaspers et al., 1999), and between muscles of the same compartment (Maas et al., 2001)). The models presented could be expanded to allow for further insights into lateral force transmission in the context of whole muscle and multiple muscle systems.