Hierarchical Commensurate and Power Prior Models for Adaptive Incorporation of Historical Information in Clinical Trials

Summary

Bayesian clinical trial designs offer the possibility of a substantially reduced sample size, increased statistical power, and reductions in cost and ethical hazard. However when prior and current information conflict, Bayesian methods can lead to higher than expected Type I error, as well as the possibility of a costlier and lengthier trial. This motivates an investigation of the feasibility of hierarchical Bayesian methods for incorporating historical data that are adaptively robust to prior information that reveals itself to be inconsistent with the accumulating experimental data. In this paper, we present several models that allow for the commensurability of the information in the historical and current data to determine how much historical information is used. A primary tool is elaborating the traditional power prior approach based upon a measure of commensurability for Gaussian data. We compare the frequentist performance of several methods using simulations, and close with an example of a colon cancer trial that illustrates a linear models extension of our adaptive borrowing approach. Our proposed methods produce more precise estimates of the model parameters, in particular conferring statistical significance to the observed reduction in tumor size for the experimental regimen as compared to the control regimen.

1. Introduction

Recent years have seen a dramatic increase in the use of Bayesian methods in the design, interim monitoring, and final analysis of clinical trials. By offering a formal statistical framework for incorporating all sources of knowledge (structural constraints, expert opinion, and both historical and experimental data), these methods offer the possibility of a substantially reduced sample size thanks to their more efficient use of information. This in turn typically leads to increases in statistical power and reductions in cost and ethical hazard, the latter since fewer patients need be exposed to the inferior treatment. On the other hand, the Bayesian approach carries some disadvantages when two or more sources of information conflict. In such cases, this can lead to higher than expected Type I error, as well as the possibility of a costlier and lengthier trial, since extra experimental information will be needed to resolve the conflict.

A commonly available (but often unincorporated) source of information in clinical trials is historical data. Such data may be available to the investigator based on previous studies in similar populations, or may simply be taken from the published summaries of other investigators. Even when no information related to a novel treatment is available, our understanding of the “standard care” group in a trial can almost always be augmented by existing information. Such borrowing of strength from historical data has long been encouraged in the case of medical device trials by the Center for Devices and Radiological Health (CDRH) at the U.S. Food and Drug Administration (FDA); (http://www.fda.gov/cdrh/osb/guidance/1601.html).

One specific challenge involves the problem of borrowing strength from a single historical study (be it in a control or a treatment group). As described by Irony (2008), simply fitting hierarchical models that borrow strength across levels in the usual way in such settings is overly sensitive to the hyperprior distribution on the variance parameters that control the amount of cross-study borrowing. That is, with only one historical study, there is no way to reliably estimate cross-study variability, and so this information must be imparted by the modeler – sometimes with drastic results for power and Type I error. This has led the FDA to preclude the use of historical information in such settings, even though this is clearly suboptimal in terms of cost and efficiency.

These issues motivate an investigation of the feasibility of hierarchical Bayesian borrowing of strength in such settings. The goal of such an approach is to determine a “sensible” amount of strength to borrow from the historical data that strikes a balance between increased cost-efficiency and long-run statistical integrity. Put another way, methods for incorporating historical data that are “adaptively robust” to prior knowledge that turns out to be inconsistent with the accumulating experimental data would be highly desirable. By contrast, we seek to utilize historical information given strong evidence of commensurability with the current.

In this paper, we propose various classes of commensurate priors as a solution to this problem. Section 2 introduces novel modifications to the traditional power prior approach which use a measure of commensurability among the historical and current data to guide the modeling. Then in Section 3 we propose several alternative hierarchical models for which borrowing depends upon some sensible measure of commensurability. Section 4 compares the frequentist performance of several of the proposed methods using simulation, while Section 5 offers an example from a colon cancer trial that illustrates the benefit of our proposed adaptive borrowing approach. Finally, Section 6 concludes and discusses our findings.

2. Hierarchical Power Priors

We begin with a review of power priors for general univariate models. Introduced by Ibrahim and Chen (2000), power priors offer a simple way to incorporate and downweight historical data, by raising the historical likelihood to a power α₀ ∈ [0, 1], and restandardizing the result to a proper distribution. These priors have been applied in a variety of contexts, including the sample size estimation problem by DeSantis (2007).

Let D denote data from the current study and L(θ|D) the general likelihood function of the current data, where θ is the parameter of interest. Adopting the notation of Ibrahim and Chen (2000), denote the historical data by D₀, and the historical likelihood by L(θ|D₀). The conditional power prior for parameter θ is defined as

$$\pi (\theta \mid D_0,{\alpha }_0)\propto L{(\theta \mid D_0)}^{{\alpha }_0}{\pi }_0(\theta ),$$ (1)

for initial prior π₀(θ) and power parameter α₀ ∈ [0, 1]. (Throughout the paper we generically denote priors by π and posteriors by q.) The power parameter controls the “degree of borrowing”: if α₀ = 0, (1) reduces to the initial prior (no borrowing), whereas if α₀ = 1, equation (1) returns the usual historical posterior (full borrowing).

In the case of normal historical data, $x_{0i}\stackrel{\mathit{iid}}{\sim }\mathit{Normal}(\theta ,{\sigma }_0^2),{\sigma }_0^2$ known, i = 1, …, n₀, under a flat initial prior, (1) yields a $\mathit{Normal}({\overline{x}}_0,{\sigma }_0^2/({\alpha }_0{n}_0))$ power prior distribution for θ. Hence α₀ plays the role of a relative precision parameter for the historical data. Since 0 ≤ α₀ ≤ 1, we might also think of α₀n₀ as the “effective” number of historical controls being incorporated into our analysis. Ibrahim and Chen (2000) introduced power priors to the broad statistical community, and illustrated their usefulness in a variety of settings; see also Ibrahim, Chen, and Sinha (2003), Chen and Ibrahim (2006), and Neelon, O’Malley, and Margolis (2008).

If we are willing to specify a particular value for α₀, the conditional posterior distribution for θ given D₀, D, and α₀ emerges as

$$q(\theta \mid D_0,D,{\alpha }_0)\propto {\pi }_0(\theta )L{(\theta \mid D_0)}^{{\alpha }_0}L(\theta \mid D)$$ (2)

Again in the case of known-variance normal observations, $x_i\stackrel{\mathit{iid}}{\sim }N(\theta ,{\sigma }^2)$, i = 1, …, n, this results in another normal distribution for the posterior of θ. We may be able to use the power parameter’s interpretation as “importance of each historical patient relative to each new patient” to select a value for α₀ (say, 1/2 or 1/3) for approximately Gaussian likelihoods.

More commonly, however, we are uncertain as to the degree to which our new data will agree with the historical data, and thus somewhat reluctant to prespecify the degree of borrowing. In such cases, we can enable the data to help determine probable values for α₀ by adopting the usual Bayesian solution of choosing a hyperprior π(α₀) for α₀.

2.1 Modified Power Priors

Ibrahim and Chen (2000) propose joint power priors consisting of the product of the conditional power prior in (1) and an independent proper prior on α₀. Duan, Ye, and Smith (2006, p.98) caution against this since it violates the Likelihood Principle (Birnbaum, 1962). Duan et al. (2006), Neuenschwander et al. (2009), and Pericchi (2009) modify the joint power prior to the product of the normalized conditional power prior (1) and an independent proper prior for α₀, producing the modified power prior (MPP)

$${\pi }^{\mathit{MPP}}(\theta ,{\alpha }_0\mid D_0)\propto \frac{L{(\theta \mid D_0)}^{{\alpha }_0}{\pi }_0(\theta )}{\int L{(\theta \mid D_0)}^{{\alpha }_0}{\pi }_0(\theta )d\theta }\pi ({\alpha }_0).$$ (3)

Modified power priors obey the Likelihood Principle and produce marginal posteriors for α₀ that are proportional to products of familiar probability distributions. If we specify π(α₀) as a Beta(a, b) distribution for fixed positive hyperparameters a and b, then the likely degree of borrowing from the historical data is controlled by a and b: (a = 10, b = 1) would strongly encourage borrowing, (a = 1, b = 10) would strongly discourage it, and (a = b = 1) would be agnostic on the subject, essentially letting the data determine the degree of borrowing.

2.2 Commensurate Power Priors

A problem with modified joint power priors is that they do not directly parametrize the commensurability of the historical and new data. For example, note that the full conditional posterior distribution for α₀, obtained by multiplying (3) by L(θ|D), is free of the current data D. Furthermore, Neelon and O’Malley (2010) caution against using Ibrahim-Chen and modified power priors since they both tend to overattenuate the impact of the historical data, forcing the use of fairly large α₀ (or in our case, fairly informative hyperpriors for α₀) in order to deliver sufficient borrowing. In fact, under a flat Beta(1, 1) prior on α₀, the marginal posterior for α₀ is flat for two identical datasets regardless of the sample sizes.

In this subsection, as a solution to the problems raised by the aforementioned authors we propose a novel adaptive modification to the basic power prior formulation that adjusts the power parameter prior conditionally through a measure of the degree to which the historical and current data are commensurate. Heretofore both the historical and current data depended on a common parameter θ. Now we assume different parameters in the historical and current group, θ₀ and θ, respectively, where θ ∈ ℜ and θ₀ ∈ ℜ are continuous location parameters. This dichotomous parameterization allows us to extend the hierarchical model to include a parameter that measures the evidence for commensurability between θ and θ₀. Suppose we pick a vague (or even flat) initial prior π₀(θ₀), but construct the prior for θ to be normal with mean θ₀ and precision τ, where τ parametrizes commensurability. We can use the information in τ to guide the prior on α₀. Specifying a vague prior for τ or log(τ) and normalizing with respect to θ₀ results in a power prior of the form,

$${\pi }^{\mathit{LCPP}}(\theta ,{\alpha }_0,\tau \mid D_0)\propto \int \frac{{[L({\theta }_0\mid D_0)]}^{{\alpha }_0}}{\int {[L({\theta }_0\mid D_0)]}^{{\alpha }_0}d{\theta }_0}d{\theta }_0\times N(\theta \mid {\theta }_0,\frac{1}{\tau })\times \mathit{Beta}({\alpha }_0\mid g(\tau ),1)\times \pi (\tau ),$$ (4)

where g(τ) > 0 is a function of the commensurability parameter that is small for τ close to zero and large for large values of τ. Since inference on θ₀ is not of primary interest in the current analysis, we integrate it out of the joint prior. Specifying τ as a normal precision parameter offers a clear interpretation of commensurability. When evidence for commensurability is weak, τ is forced towards zero, increasing the conditional prior variance of θ by $\frac{1}{\tau }$. Therefore, we refer to τ as the commensurability parameter, and to the prior in (4) as location commensurate power prior (LCPP), since borrowing strength from the historical study depends upon the evidence in the data for commensurability between the location parameters θ and θ₀. This extended power prior model requires the estimation of more parameters from the data (notably τ), but we can formulate the model such that the information gained is aimed directly at improving estimation of the crucial borrowing parameter α₀.

2.3 Single Arm Trial

Now let us turn our attention to the Gaussian case, where μ, μ₀ and σ², ${\sigma }_0^2$ parameterize the current and historical means and variances, respectively. Suppose a historical study suggests a true treatment benefit for a particular intervention, where one continuous response with mean μ can be collected for each subject. Investigators are interested in testing the point null hypothesis H₀: μ = 0 in a new single arm trial. Let x₀ = (x₀₁, …, x_0n0)′ denote the independent and identically distributed historical responses, and assume $x_{0i}\stackrel{\mathit{iid}}{\sim }\mathit{Normal}({\mu }_0,{\sigma }_0^2)$. If no initial information exists for μ₀, we would likely select π(μ₀) vprop; 1 and hence the historical posterior follows as $q_0({\mu }_0\mid {\mathbf{x}}_{\mathbf{0}},{\sigma }_0^2)=\mathit{Normal}({\overline{x}}_0,\frac{{\sigma }_0^2}{n_0})$. Next let x = (x₁, …, x_n)′ denote the vector of independent and identically distributed responses from the new study and assume $x_i\stackrel{\mathit{iid}}{\sim }\mathit{Normal}(\mu ,{\sigma }^2)$ and π₀(μ) vprop; 1. The power prior formulation requires that ${\sigma }_0^2$ be fixed and known, therefore, we replace ${\sigma }_0^2$ in the historical likelihood with its maximum likelihood estimate, ${\widehat{\sigma }}_0^2=(\frac{1}{n_0}){\sum }_{i=1}^{n_0}{(x_{0i}-{\overline{x}}_0)}^2$. We also assume the noninformative reference prior for σ², thus $q({\sigma }^2\mid {\mathbf{x}}_{\mathbf{0}},\mathbf{x})\propto {\mathrm{\Gamma }}^{-1}(\frac{n}{2},\frac{n}{2}[s^2+{(\overline{x}-\mu )}^2])$ for both power prior models. The conditional posterior for μ becomes

$$q(\mu \mid {\mathbf{x}}_{\mathbf{0}},\mathbf{x},{\alpha }_0,{\sigma }^2)=\mathit{Normal}\left(\frac{{\widehat{\sigma }}_0^{2}n\overline{x}+{\sigma }^2{\alpha }_0{n}_0{\overline{x}}_0}{n{\widehat{\sigma }}_0^2+{\sigma }^2{\alpha }_0{n}_0},\frac{{\sigma }^2{\widehat{\sigma }}_0^2}{n{\widehat{\sigma }}_0^2+{\sigma }^2{\alpha }_0{n}_0}\right).$$ (5)

The conditional posterior for the full (no) borrowing model is found by fixing α₀ = 1 (α₀ = 0) in (5), and thus has mean $\frac{n\overline{x}{\widehat{\sigma }}_0^2+n_0{\overline{x}}_0{\sigma }^2}{n_0{\sigma }^2+n{\widehat{\sigma }}_0^2}(\overline{x})$, and variance $\frac{{\sigma }^2{\widehat{\sigma }}_0^2}{n_0{\sigma }^2+n{\widehat{\sigma }}_0^2}(\frac{{\sigma }^2}{n})$. Suppose we assume α₀ ~ Beta(a, b), where α₀ ∈ [0, 1] and a, b > 0. The joint power prior and marginal posterior for α₀ under the MPP approach are

$${\pi }^{\mathit{MPP}}(\mu ,{\sigma }^2,{\alpha }_0\mid {\mathbf{x}}_0)\propto \mathit{Normal}\left(m\mid {\overline{x}}_0,\frac{{\widehat{\sigma }}_0^2}{{\alpha }_0{n}_0}\right)\times \mathit{Beta}({\alpha }_0\mid a,b)\times \frac{1}{{\sigma }^2}$$ (6)

and

$$q^{\mathit{MPP}}({\alpha }_0\mid {\mathbf{x}}_{\mathbf{0}},\mathbf{x})\propto \mathit{Normal}\left(\overline{x}-{\overline{x}}_0\mid 0,\frac{{\sigma }^2}{n}+\frac{{\widehat{\sigma }}_0^2}{{\alpha }_0{n}_0}\right)\times \mathit{Beta}({\alpha }_0\mid a,b).$$ (7)

Our location commensurate power prior (LCPP) follows as

$${\pi }^{\mathit{LCPP}}(\mu ,{\alpha }_0,\tau ,{\sigma }^2\mid {\mathbf{x}}_{\mathbf{0}})\propto N(\mu \mid {\overline{x}}_0,\frac{1}{\tau }+\frac{{\widehat{\sigma }}_0^2}{{\alpha }_0{n}_0})\times \mathit{Beta}({\alpha }_0\mid g(\tau ),1)\times \frac{1}{{\sigma }^2}\times \pi (\tau ).$$ (8)

Notice that, in addition to adding $\frac{1}{\tau }$ to the conditional prior variance of μ, the LCPP in (8) also inflates the estimated posterior variance of μ₀, $\frac{{\widehat{\sigma }}_0^2}{n_0}$, by a factor of $\frac{1}{{\alpha }_0}$. The posterior distribution is obtained from the product of the LCPP prior (8) and the normal likelihood for x. The full conditional posterior distribution for μ and marginal posterior distribution for α₀ and τ follow as

$$q^{\mathit{LCPP}}(\mu \mid {\mathbf{x}}_{\mathbf{0}},\mathbf{x},{\alpha }_0,\tau ,{\sigma }^2)\propto N\left(\mu \mid \frac{{\alpha }_0{n}_0\tau {\sigma }^2{\overline{x}}_0+nu\overline{x}}{{\alpha }_0{n}_0\tau {\sigma }^2+nu},\frac{u{\sigma }^2}{{\alpha }_0{n}_0\tau {\sigma }^2+nu}\right),$$ (9)

where $u={\alpha }_0{n}_0+{\widehat{\sigma }}_0^2\tau$, and

$$q^{\mathit{LCPP}}({\alpha }_0,\tau \mid {\mathbf{x}}_{\mathbf{0}},\mathbf{x},{\sigma }^2)\propto N\left(\overline{x}-{\overline{x}}_0\mid 0,\frac{{\sigma }^2}{n}+\frac{1}{\tau }+\frac{{\widehat{\sigma }}_0^2}{{\alpha }_0{n}_0}\right)\times \mathit{Beta}({\alpha }_0\mid g(\tau ),1)\times \pi (\tau ).$$ (10)

Information in the data pertaining to τ can be used to guide the Beta(g(τ), 1) prior on our power parameter, α₀. Since τ becomes extremely large (small) for highly commensurate (conflicting) data we work on the log-scale. In Section 4 we present simulated frequentist operating characteristics for the LCPP model using g^★ (log(τ)) = max (log(τ), 1). Thus as τ increases and g^★ (log(τ)) becomes large relative to the second beta hyperparameter (fixed at 1) the distribution of α₀ becomes increasingly peaked at 1 and the prior variance of μ tends towards $\frac{{\widehat{\sigma }}_0^2}{n_0}$, the approximate posterior variance of μ₀ given x₀. Thus, our model strongly encourages borrowing from the historical data when the data are commensurate. Alternatively, for τ ≤ 1 the distribution of α₀ becomes flat across the unit interval. Lastly, the LCPP model used in the simulation study below assumes a Cauchy(0, 30) prior on log(τ). The fat tails of Cauchy facilitate very large and small values of τ, which provide for a highly flexible model. Fúquene, Cook, and Pericchi (2009, p.820) endorse the use of robust priors in hierarchical models to prevent unbounded and undesirable shrinkages.

See Web Appendix A for further discussion on the power and commensurability parameters under the Ibrahim-Chen, MPP, and LCPP approaches. Web Figure 1 compares marginal posterior distributions for α₀ under the MPP and Ibrahim-Chen power prior models, while Web Figure 2 compares the marginal posterior and prior distributions for α₀ and log(τ) under the LCPP model.

2.4 Extension to Linear Models

Commensurate power priors are vastly more useful in clinical trials if they can be used in association with linear models. Ibrahim and Chen (2000) propose a framework for using power priors in GLMs. We formulate our own commensurate power prior linear model. Let us assume y₀ is a vector of n₀ responses from subjects in a previous investigation of an intervention that is to be used as a control in a current trial testing a newly developed intervention for which no reliable prior data exists. Let y be the vector of n responses from subjects in the current trial in both treatment and control arms. Suppose that both trials are designed to identically measure p−1 covariates of interest. Let X₀ be an n₀ × p design matrix and X be an n×p design matrix, both of full column rank p, such that the first columns of X₀ and X are vectors of 1s corresponding to the intercept. Now suppose $y_0\sim N_{n_0}(X_0{\beta }_0,{\sigma }_0^2)$ and y ~ N_n(Xβ + Zλ, σ²) where Z is an n × r design matrix containing variables relevant only to the current trial, as well as an indicator for the new treatment. Let D₀ = (y₀, X₀, n₀, p) and D = (y, X, Z, n, p, r).

We can design a commensurate power prior (CPP) model to adaptively borrow strength from the historical control group and identical covariates. Specifying our commensurate power prior as in (4) with the same priors on σ², α₀, and log(τ) as in the previous sub-section, a flat prior on λ, and integrating β₀ out of the joint prior leads to a full conditional prior on β that is normal with mean V⁻¹M and covariance (τV)⁻¹, where $M={\left(\frac{{\alpha }_0{X}_0^T{X}_0}{{\widehat{\sigma }}_0^2}+\tau I_p\right)}^{-1}\frac{{\alpha }_0{X}_0^T{X}_0{\widehat{\beta }}_0}{{\widehat{\sigma }}_0^2},V=I_p-\tau {\left(\frac{{\alpha }_0{X}_0^T{X}_0}{{\widehat{\sigma }}_0^2}+\tau I_p\right)}^{-1}$, and ${\widehat{\beta }}_0={(X_0^T{X}_0)}^{-1}{X}_0^T{y}_0$. The joint posterior follows by multiplying the joint prior by the likelihood of y and normalizing. The full conditional posteriors for λ and σ² and posterior for β given σ², α₀, and τ follow as,

$$q^{\mathit{CPP}}(\lambda \mid D_0,D,\beta ,{\sigma }^2)\propto N_r\left(\lambda \mid \widehat{\lambda },{\sigma }^2{(Z^{T}Z)}^{-1}\right),$$ (11)

$$q^{\mathit{CPP}}({\sigma }^2\mid D_0,D,\beta ,\lambda )\propto {\mathrm{\Gamma }}^{-1}\left({\sigma }^2\mid \frac{n}{2},\frac{{(y-X\beta -Z\lambda )}^T(y-X\beta -Z\lambda )}{2}\right),$$ (12)

$$q^{\mathit{CPP}}(\beta \mid D_0,D,{\sigma }^2,{\alpha }_0,\tau )\propto N_p\left(\beta \mid {\mathrm{\Lambda }}^{-1}\left(\tau M+\frac{X^T(I_n-w)y}{{\sigma }^2}\right),{\mathrm{\Lambda }}^{-1}\right),$$ (13)

where λ̂ = (Z^TZ)⁻¹Z^T(y − Xβ), $\mathrm{\Lambda }=\tau V+\frac{X^T(I_n-w)X}{{\sigma }^2}$, and w = Z(Z^TZ)⁻¹Z^T. Notice in (11) that the full conditional posterior mean for λ, λ̂, is a function of residuals (y − Xβ), whereas the conditional posterior mean of β in (13) is an average of the historical and concurrent data relative to the power and commensurability parameters, α₀ and τ. As τ and α₀ approach zero, the marginal posterior for β converges to a normal density with mean ${\left(\frac{X^{T}X-X^{T}Z{(Z^{T}Z)}^{-1}{Z}^{T}X}{{\sigma }^2}\right)}^{-1}(X^{T}y-X^{T}Z{(Z^{T}Z)}^{-1}{Z}^{T}y)$ and variance ${\left(\frac{X^{T}X-X^{T}Z{(Z^{T}Z)}^{-1}{Z}^{T}X}{{\sigma }^2}\right)}^{-1}$, recovering the result from a linear regression that ignores all of the historical data. In this case, λ̂ also converges to the no borrowing estimate of the treatment difference.

3. Commensurate Priors

Heretofore, we have considered posterior estimation of commensurability to be adjuvant for the purpose of facilitating more borrowing of strength in conjunction with a hierarchical power prior model. Yet, for Gaussian data, (8) reveals that both power and commensurability parameters inflate the conditional prior variance of μ given weak evidence for commensurability. In this section we consider hierarchical models that incorporate commensurate priors as the primary mechanism for weighting the influence of prior information relative to its consistency with data from the concurrent study.

Again let D₀ and D denote data from the historical and current studies and L(θ₀|D₀) and L(θ|D) the general likelihood functions, respectively, where θ is the parameter of interest. The dichotomous parameterization facilitates estimation of commensurability among the historical and current data in a hierarchical model by specifying the prior for θ to be “centered” at θ₀ and conditional on τ > 0, where τ parameterizes prior precision for θ given θ₀. Multiplying by the historical likelihood function results in a prior of the form,

$$\pi (\theta \mid D_0,\theta ,\tau )\propto L({\theta }_0\mid D_0)\pi (\theta \mid {\theta }_0,\tau ){\pi }_0(\theta ).$$ (14)

As τ approaches zero, π(θ|D₀, θ₀, τ) → π₀(θ), effectively ignoring the historical data. On the other hand, as τ → ∞, θ approaches θ₀ and π(θ|D₀, θ₀, τ) → L(θ|D₀)π₀(θ), recovering the result obtained from pooling the two datasets. If the historical study favors rejecting the current null, then decreasing τ reduces Type I error, while increasing τ increases power.

The posterior kernel is obtained by multiplying (14) by the current likelihood L(θ|D). Note that the full conditional posterior distribution for θ₀ would be independent of the current data, since the current likelihood would be nothing but a multiplicative constant. Therefore, θ₀ should be integrated out of the prior when the ∫ L(θ₀|D₀) π(θ|θ₀)dθ₀ is tractable. Specifying a vague prior for τ, π(τ), and adopting the joint prior π(θ, τ|D₀, θ₀) ∝ π(θ|D₀, θ₀, τ)π(τ) allows the model to utilize data from the current trial to help estimate τ.

Now let us return to the Gaussian case in the context of the simple trial outlined in Subsection 2.3. We again assume the noninformative reference prior for σ², thus $q({\sigma }^2\mid {\mathbf{x}}_0,\mathbf{x})\propto {\mathrm{\Gamma }}^{-1}(\frac{n}{2},\frac{n}{2}[s^2+{(\overline{x}-\mu )}^2])$. First let us construct a prior on μ such that borrowing strength from the historical study depends upon the evidence in the data for commensurability among location parameters μ and μ₀. We start by assuming the joint prior on μ and μ₀ is the product of the historical likelihood and a normal prior on μ with mean μ₀ and precision τ. Since posterior inference on the scale of the historical data is not of direct interest we again replace ${\sigma }_0^2$ in the historical likelihood with its maximum likelihood estimate. Integrating out the nuisance parameter, μ₀, leads to the location commensurate prior (LCP),

$${\pi }^{\mathit{LCP}}(\mu ,{\sigma }^2,\tau \mid {\mathbf{x}}_{\mathbf{0}})\propto N(\mu \mid {\overline{x}}_0,\frac{1}{\tau }+\frac{{\widehat{\sigma }}_0^2}{n_0})\times \frac{1}{{\sigma }^2}\times \pi (\tau ).$$ (15)

If evidence for commensurability is weak (ie, τ is close zero), the conditional prior variance of μ in (15) is increased by $\frac{1}{\tau }$. Assuming a vague prior on τ completes the prior specification. The posterior is proportional to the product of the joint prior in (15) and the current data likelihood. In Section 4 we present simulations to illustrate the frequentist operating characteristics of the LCP using an agnostic Uniform(−30, 30) prior on log(τ).

Suppose instead we want borrowing from the historical data to depend upon evidence for commensurability among both the location and scale parameters. We must now extend the hierarchical model to include a parameter, γ, that measures evidence of commensurability among σ² and ${\sigma }_0^2$ by specifying a prior on σ² that is “centered” at ${\sigma }_0^2$ and has precision γ. An obvious choice would be to assume an inverse gamma prior on σ², with mean ${\sigma }_0^2$ and precision γ. Assuming the reference initial prior on ${\sigma }_0^2$, multiplying by the historical likelihood, and integrating out μ₀ results in the conditional location-scale commensurate prior (LSCP),

$${\pi }^{\mathit{LSCP}}(\mu ,{\sigma }_0^2,{\sigma }^2\mid {\mathbf{x}}_{\mathbf{0}},\tau ,\gamma )\propto N\left(\mu \mid {\overline{x}}_0,\frac{1}{\tau }+\frac{{\sigma }_0^2}{n_0}\right){\mathrm{\Gamma }}^{-1}\left({\sigma }^2\mid {\alpha }^{★},{\beta }^{★}\right){\mathrm{\Gamma }}^{-1}\left({\sigma }_0^2\mid \frac{n_0-1}{2},\frac{n_0{\widehat{\sigma }}_0^2}{2}\right),$$ (16)

where ${\alpha }^{★}=\gamma {\sigma }_0^4+2$ and ${\beta }^{★}={\sigma }_0^2(\gamma {\sigma }_0^4+1)$. One can assume vague priors for the commensurability parameters, and proceed with posterior inference on μ and σ². Borrowing of strength that requires commensurate scales in addition to commensurate locations is more cautious and perhaps more appealing to skeptics.

Another option involves fixing values of τ and γ and using a mixture prior. Suppose we specify m distinct relationships of interest among the locations and scales of the historical and current data represented by fixed pairs of the commensurability parameters, (τ₁, γ₁), …, (τ_m, γ_m). Let ${\pi }^{\mathit{LCSP}}(\mu ,{\sigma }_0^2,{\sigma }^2\mid {\mathbf{x}}_{\mathbf{0}},{\tau }_j,{\gamma }_j)$ denote the conditional prior in (16) given τ and γ are fixed at τ_j and γ_j respectively. If we are also willing to specify fixed mixing proportions, ω_j ∈ (0, 1) where j = 1, …, m such that ${\sum }_{j=1}^m{\omega }_j=1$, we can formulate a LSCP for μ, ${\sigma }_0^2$, and σ² that is a convex combination of the m potential relationships of interest as

$${\pi }^{\mathit{LSCMP}}(\mu ,{\sigma }_0^2,{\sigma }^2\mid {\mathbf{x}}_{\mathbf{0}})=\sum _{j=1}^m{\omega }_j{\pi }^{\mathit{LSCP}}(\mu ,{\sigma }_0^2,{\sigma }^2\mid {\mathbf{x}}_{\mathbf{0}},{\tau }_j,{\gamma }_j).$$ (17)

We refer to this prior as the location-scale commensurate mixture prior (LSCMP). In contrast to the non-mixture commensurate and power priors, the LSCMP does not permit posterior estimation of commensurability, but instead facilitates measured, “partial borrowing”. The LSCMP featured in Section 4, an equal mixture of just two pairs of (τ, γ), corresponding to very high and low commensurability among the location and scale parameters, is shown to work rather well in our simulation study.

4. Simulation Results for a Single Arm Trial

In this section we investigate the Bayesian and frequentist operating characteristics of the models described in Sections 2 and 3 via simulation. For the power priors in Subsection 2.3, we used a MPP model with a Beta(1, 1) prior on α₀ and a LCPP assuming a Cauchy prior on log(τ) centered at zero with scale fixed at 30. Both power prior models use our noninformative reference prior on σ². Among the commensurate priors in Section 3, the simulations were run using a LCP model that assumes a vague, Uniform(−30, 30) prior on log(τ) and noninformative reference prior on σ², and a LSCMP model that is a mixture of (τ₁, γ₁) = (10⁶, 10) and (τ₂, γ₂) = (1/2, 1/2) with the mixing proportion fixed at 1/2. We also ran simulations on a model that ignores the historical data completely (by assuming the noninformative Jeffreys prior on μ and σ²) and, following Fúquene et al. (2009), a model that assumes a “robust” Cauchy prior on μ, centered at x̄₀ with scale parameter fixed at 1. We will refer to these as the “no borrowing” and “Cauchy” models.

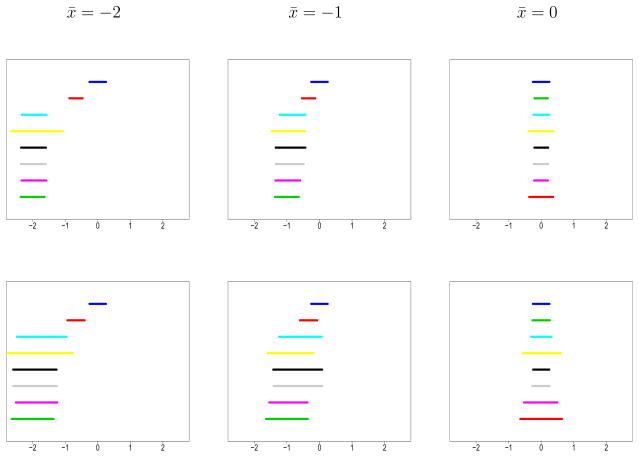
Figure 1 illustrates the adaptive movement capability of the commensurate prior methods. Each graph contains 95% posterior credible intervals for μ derived from all simulated models, generated with n₀ = 60 historical observations having x̄₀ = 0 and ${\widehat{\sigma }}_0^2=1$. The top interval corresponds to results from the analysis of the historical data alone, using noninformative Jeffreys priors on μ₀ and ${\sigma }_0^2$. The interval directly beneath it represents a pooled analysis using the full borrowing prior, and the bottom interval corresponds to the no borrowing analysis of the current data that ignores the historical data. Intervals in between from top to bottom correspond to the MPP, Cauchy, LCPP, LCP, and LSCMP.

Figure 1.

95% posterior credible intervals for μ for all simulated models where x̄₀ = 0, n₀ = 60, n = 30, and ${\widehat{\sigma }}_0^2=1$. Each graph contains results from eight different models: historical (top), full borrowing (second), MPP (third), Cauchy (fourth), LCPP (fifth), LCP (sixth), LSCMP (seventh), and no borrowing (bottom). Columns correspond to the current sample mean, x̄, while the top row shows results for σ̂² = 1 and the bottom row assumes σ̂² = 3.

Looking at graphs in the left column where the current data is the most inconsistent with the historical data, we see that intervals for the posteriors using commensurate priors and modified power priors are virtually identical to that for no borrowing. Conversely, the full borrowing prior, which contains no mechanism for acknowledging the obvious conflict, leads to a much tighter interval around the weighted average of the two sample means, $-\frac{2}{3}$. In fact, for Normal-Normal conjugate priors, increasing the sample sizes, n and n₀, always decreases the length of an equal-tail credible interval, leading to high Type I error. The Cauchy prior interval is properly centered at −2, but much wider, suggesting the procedure may be somewhat conservative. The center graphs demonstrates the adaptive shrinkage capabilities of the commensurate, MPP, and Cauchy models for intermediately commensurate datasets which lead to good Type I error behavior. The current and historical datasets have identical sufficient statistics in the third column. Intervals for the MPP, LCPP, LCP models have narrowed to mirror the pooled result. Notice that the LCPP has narrowed slightly more than the MPP, suggesting that the LCPP obtains more power. Intervals for the LSMCP are more reluctant to shrink towards the full borrowing result in the bottom right graph given the evidence for incommensurability among ${\sigma }_0^2$ and σ².

Next, to mimic the case of a single arm trial being run after a promising pilot study to test the null hypothesis that μ = 0, let μ₀ = 0.5 be the true mean of the historical data, and fix n₀ = 60 and ${\sigma }_0^2=1$. We can sample $x_{0i}\stackrel{\mathit{iid}}{\sim }N({\mu }_0,{\sigma }_0^2)$ and $x_i\stackrel{\mathit{iid}}{\sim }N({\mu }_0,{\sigma }^2)$ for some fixed true μ, σ², and n, and conduct a two-sided test of the null hypothesis μ = 0 using an equal-tail posterior credible interval. We repeated this entire process Nrep = 5000 times for current sample sizes of n = 15, 30, and 60 to compare frequentist Type I error and power properties across the various approaches.

Table 1 contains areas under the resulting power curves, where power was computed for true μ = 0, 0.05, 0.1, …, 0.5. All models are compared under two approaches to hypothesis testing. The first uses 95% posterior credible intervals to test the null, which for the adaptive methods maintain Type I error probability of 0.05 for the considered sample sizes only when μ₀ = μ = 0. The other approach is a “calibrated” one that controls Type I error at 0.05 for all considered sample sizes by using equal-tail posterior credible intervals with varying tail probabilities to test the null hypothesis. For discussion about controlling Type I error for Bayesians designs from a regulatory perspective see Pennello and Thompson (2008).

Table 1.

Area under the power curves: 95% posterior credible intervals (left); Controlled Type I error (right), for true μ = 0, 0.05, 0.1, …, 0.5 and μ₀ = 0.5.

	95% Posterior CI			Controlled Type I Error
	n = 15	n = 30	n = 60	n = 15	n = 30	n = 60
No borrowing	0.090	0.158	0.244	0.090	0.158	0.244
Cauchy	0.079	0.161	0.249	0.109	0.175	0.261
LSCMP	0.250	0.294	0.326	0.133	0.190	0.263
MPP	0.288	0.312	0.341	0.119	0.185	0.269
LCP	0.309	0.329	0.346	0.137	0.208	0.276
LCPP	0.344	0.351	0.362	0.122	0.196	0.278

Notice that the LSCMP, MPP, LCP, and LCPP models result in higher area than the no borrowing model for all cases. Therefore, the adaptive approaches always facilitate more power than an analysis that ignores the historical data, even when Type I error is controlled. Furthermore, the table suggests that the LCPP approach is always more powerful than the MPP, although the difference is slight for controlled Type I error. Furthermore, the LCPP is most powerful for the analysis using 95% credible intervals, while the LCP emerges as slightly better when Type I error is controlled. Our simulations also suggest that the calibrated analysis for the Cauchy model provides very slight gains in power over an analysis that ignores the historical data. The reader should note that the calibrated (controlled Type I error) analysis for the Cauchy model used equal-tail credible intervals corresponding to tail probabilities larger than 0.025. Type I error results for the full borrowing model were extremely poor and hence excluded.

Table 2 contains Type I error probabilities for all models and sample sizes given in Table 1. Comparing results in the left columns of the two tables for all models reveals that larger area under the power curve corresponds to higher Type I error probability when using 95% posterior credible intervals to test the null hypothesis. Results in the right column of Table 2 show that Type I error is controlled at 0.05 for all models and sample sizes under the “calibrated” approach.

Table 2.

Type I error probabilities: 95% posterior credible intervals (left); Controlled Type I error (right), for true μ = 0 and μ₀ = 0.5.

	95% Posterior CI			Controlled Type I Error
	n = 15	n = 30	n = 60	n = 15	n = 30	n = 60
No borrowing	0.050	0.050	0.050	0.050	0.050	0.050
Cauchy	0.025	0.035	0.046	0.050	0.050	0.050
LSCMP	0.175	0.168	0.126	0.050	0.050	0.050
MPP	0.247	0.177	0.130	0.050	0.050	0.050
LCP	0.266	0.209	0.148	0.050	0.050	0.050
LCPP	0.368	0.271	0.184	0.050	0.050	0.050

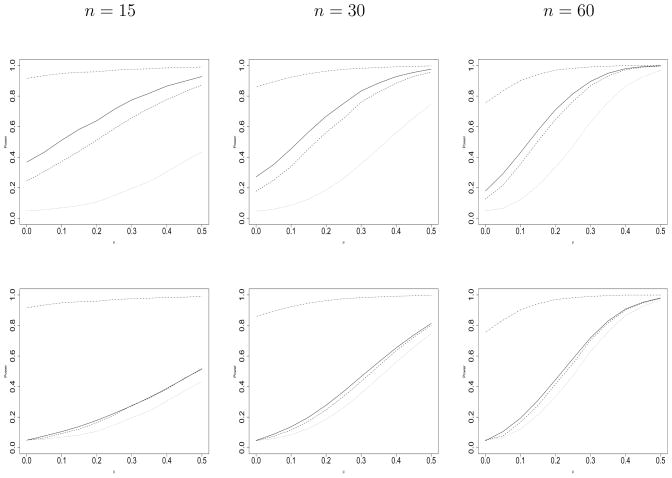
Lastly, power curves for the full borrowing (dot-dashed), LCPP (solid), MPP (dashed), and no borrowing (dotted) models are shown in Figure 2 to augment Table 1. The top row of plots corresponds to testing the null hypothesis that μ = 0 using the 95% posterior credible intervals, while the bottom row contains power curves for the analysis with controlled Type I error. The power curve for the LCPP is clearly above the MPP across the top row of plots, and either overlapping or slightly larger for the bottom row. This suggests that the LCPP approach obtains more power than the MPP approach. Notice the atrocious Type I error resulting from pooling the two datasets in the top row, which achieves a minimum of approximately 0.8 when n = 60. The ill-fated full borrowing prior has “unbounded influence” resulting in a dogmatic analysis of the current trial; Fúquene et al. (c.f. 2009, p.819).

Figure 2.

Power curves for the full borrowing, commensurate power prior, modified power prior, and no borrowing models where μ₀ = 0.5, n₀ = 60, and ${\sigma }^2={\sigma }_0^2=1$. Each graph shows results for the full borrowing (dot-dashed), LCPP (solid), MPP (dashed), and no borrowing (dotted) models. Columns correspond to the indicated current sample size n. The top row corresponds to hypothesis testing based on the respective 95% posterior credible intervals, while the bottom row contains results for hypothesis tests that use varying equal-tail posterior credible intervals such that the Type I Error is controlled at 0.05, except for the full borrowing model for which controlling Type I error at 0.05 is impossible for the considered scenarios.

5. Example Using Controlled Colorectal Cancer Trial Data

We consider data from two successive randomized colorectal cancer clinical trials originally reported by Saltz et al. (2000) and Goldberg et al. (2004). The initial trial randomized N₀ = 683 patients with previously untreated metastatic colorectal cancer between May 1996 and May 1998 to one of three regimens: Irinotecan alone; Irinotecan and bolus Fluorouracil plus Leucovorin (IFL); or a regimen of Fluorouracil and Leucovorin (5FU/LV) “standard therapy”. In an intent-to-treat analysis, IFL resulted in significantly longer progression free survival and overall survival than Irinotecan alone and 5FU/LV (Saltz et al., 2000).

The subsequent trial compared three drug combinations in N = 795 patients with previously untreated metastatic colorectal cancer, randomized between May 1999 and April 2001. Patients in the first drug group received the current “standard therapy,” the IFL regimen identical to that used in the historical study. The second group received Oxaliplatin and infused Fluorouracil plus Leucovorin (abbreviated FOLFOX), while the third group received Irinotecan and Oxaliplatin (abbreviated IROX); both of these latter two regimens were new as of the beginning of the second trial.

While both trials recorded many different patient characteristics and outcomes, in our analysis we concentrate on the trial’s measurements of tumor size, and how the FOLFOX regimen compared to the IFL regimen. Therefore, the historical dataset will consist of the IFL treatment arm from the initial study, while the current data will consist of patients randomized to IFL or FOLFOX in the subsequent trial. We omit data from the Irinotecan alone and 5FU/LV arms in the Saltz study and the IROX arm in the Goldberg study.

Both trials recorded two bi-dimensional measurements on each tumor for each patient at regular cycles. The trial reported by Saltz et al. measured patients every 6 weeks for the first 24 weeks and every 12 thereafter weeks after, while the trial reported by Goldberg et al. measured every 6 weeks for the first 42 weeks. We computed the sum of the longest diameter in cm (“ld sum”) for up to 9 tumors for each patient at each cycle, until the patient’s final follow-up visit; for 92% of the patients in our very ill study population, this was the final observation prior to the patient’s death. We then used the average change in ld sum from baseline to test for a significant treatment difference in ld sum reduction between the FOLFOX and control regimens. Our analysis will also incorporate baseline ld sum as a predictor as well as two important covariates identically measured at baseline: age in years, and aspartate aminotransferase (AST) in units/L.

We restricted our analysis to patients that had measurable tumors, at least two cycles of followup, and a nonzero ld sum at baseline, bringing the total sample size to 441: 171 historical and 270 current observations. Among the current patients, there are 129 controls (IFL) and 141 patients treated with the new regimen (FOLFOX). Suppose y₀ and y are vectors of lengths n₀ and n for the historical and concurrent responses such that

$$y_0\sim \mathit{Normal}(X_0{\beta }_0,{\sigma }_0^2),\text{and}y\sim \mathit{Normal}(X\beta +Z\lambda ,{\sigma }^2)$$ (18)

where X₀ and X are n₀ × 4 and n × 4 design matrices with columns corresponding to (1, ld sum at baseline, age, AST), and Z is the FOLFOX indicator function. Thus the β₀ and β parameters contain intercepts as well as regression coefficients for each of three baseline covariates, while λ represents change in average ld sum attributed to FOLFOX. Web Figure 3 contains histograms of the average change in ld tumor sum from baseline.

The “historical data” and “current data” columns of Table 3 summarize results from separate classical linear regression fits on the historical (y₀, X₀) and current (y, X) data alone. The “current data” values constitute the “no borrowing” analysis. Results from both datasets suggest that ld sum at baseline is highly significant while age and AST are not. Furthermore, while the estimated intercept corresponding to FOLFOX in the current data is negative, −0.413, the estimate is not precise enough to conclude a significant treatment difference at the 0.05 level.

Table 3.

Fits to colorectal cancer data: n₀ = 171 (left); n = 270 (right); LCPP (bottom).

	Historical data		Current data
	estimate	95% CI	estimate	95% CI
Intercept	0.88	(−1.98, 3.74)	−0.47	(−2.28, 1.34)
BL ld sum	−0.23	(−0.31, −0.15)	−0.40	(−0.45, −0.34)
Age	−0.02	(−0.07, 0.02)	0.01	(−0.01, 0.04)
AST	0	(−0.02, 0.02)	0.01	(−0.01, 0.02)
FOLFOX	–	–	−0.41	(−1.02, 0.19)

	LCPP
	estimate	95% Posterior CI
Intercept	0.180	(−1.11, 1.42)
BL ld sum	−0.39	(−0.44, −0.33)
Age	0	(−0.02, 0.02)
AST	0	(−0.01, 0.01)
FOLFOX	−0.46	(−0.82, −0.10)
α0	0.86	(0.44, 1.00)
log(τ)	16.53	(1.59, 82.00)

Information about β₀ appears to be relevant to β. Therefore, we implemented the commensurate power prior linear model presented in detail in Subsection 2.4 which borrows strength adaptively relative to the degree to which (y₀, X₀) is commensurate with (y, X). Point estimates (posterior medians) and 95% equal-tail Bayesian credible intervals are given in the bottom portion of Table 3. First, notice that the posterior for α₀ is peaked at 1. Therefore, our power prior linear model considers the historical and current data to be quite commensurate, increasing the precision of the parameter estimates. As a result, the 95% credible interval upper bound for λ is now less than zero, and so we can now conclude that FOLFOX resulted in a significant reduction in average ld sum when compared to the IFL regimen. This finding is consistent with those of Goldberg et al. (2004), who determined FOLFOX to have superior time to progression and response rate compared to IFL.

6. Discussion

In this paper, we have presented classes of hierarchical models using priors that facilitate adaptive borrowing from historical data when this is justified by its commensurability with the accumulating current data. Such adaptive borrowing is consistent with recent arguments on behalf of the ease and desirability of adaptivity in Bayesian clinical trials generally (Berry, 1993, 2006; Berry et al., 2010). The approach was shown to work well both with simulated and actual data, the latter based on two recent studies in colorectal cancer.

Before using the proposed linear model in the context of a new clinical trial, investigators must consider carefully the design (ie, randomized versus single-arm) of the historical study. Differences in patient populations between the historical and new study and other known/unknown confounding factors can be potential sources of bias when borrowing from the historical data. Furthermore, commensurate priors require extra care if the sampling distributions differ; estimating nuisance parameters like σ² becomes ever more challenging if, say, the two distributions were normal and Student’s t, respectively.

Future work looks toward extending our approach to non-Gaussian settings, especially those involving categorical and time-to-event data. We are also currently pursuing the use of commensurate priors for adaptive borrowing that allows the sample size or allocation ratio in the ongoing trial to be altered if this is warranted. For example, if historical and concurrent controls emerge as commensurate, we might randomize fewer patients to the control group, thus enhancing the efficiency of the ongoing trial.