Confined glassy dynamics at grain boundaries in colloidal crystals

Abstract

Grain boundary (GB) microstructure and dynamics dictate the macroscopic properties of polycrystalline materials. Although GBs have been investigated extensively in conventional materials, it is only recently that molecular dynamics simulations have shown that GBs exhibit features similar to those of glass-forming liquids. However, current simulation techniques to probe GBs are limited to temperatures and driving forces much higher than those typically encountered in atomic experiments. Further, the short spatial and temporal scales in atomic systems preclude direct experimental access to GB dynamics. Here, we have used confocal microscopy to investigate the dynamics of high misorientation angle GBs in a three-dimensional colloidal polycrystal, with single-particle resolution, in the zero-driving force limit. We show quantitatively that glassy behavior is inherent to GBs as exemplified by the slowing down of particle dynamics due to transient cages formed by their nearest neighbors, non-Gaussian probability distribution of particle displacements and string-like cooperative rearrangements of particles. Remarkably, geometric confinement of the GB region by adjacent crystallites decreases with the misorientation angle and results in an increase in the size of cooperatively rearranging regions and hence the fragility of the glassy GBs.

Grain boundaries (GBs)—thin interfaces that separate adjacent regions with different crystallographic orientation in polycrystals (1)—are central to our understanding of deformation and fracture mechanisms (2), melting kinetics (3), and transport properties (4) in a wide class of natural and man-made materials. An active area of materials research is to elucidate the spatio-temporal evolution of GBs and dynamics of their constituent atoms to better understand processes for enhancing material performance, which include Hall–Petch strengthening (5, 6) and GB engineering (7). Dislocation GBs resulting from small mismatches in grain orientation are reasonably well-understood (8). However, high misorientation angle grain boundaries (HAGBs), which play a crucial role in plastic deformation and grain growth, continue to pose a challenge (9). Observations of GB embrittlement at low temperatures (10) and with impurity doping (11, 12) have led to suggestions that HAGBs might share similarities with glass-forming liquids. Recent molecular dynamics (MD) simulations of polycrystalline metals, at high temperatures and under external stresses, have indeed provided substantial support for the glassy behavior of HAGBs (13, 14). On the other hand, an amorphous HAGB would imply that its interfacial energy is insensitive to the grain misorientation angle (9, 15, 16). Nevertheless, GB mobility and diffusion, which have a strong dependence on the interfacial energy, are found to vary with the misorientation angle (17, 18). Also, given that GBs are only a few particle diameters wide at low temperatures, it is natural to expect confinement effects to play a key role in the dynamics. Conventional simulation approaches cannot access the dynamics of GBs in the low temperature zero-driving force limit (19, 20). Direct evidence for the amorphous nature of HAGBs is beset by experimental limitations (20, 21) and consequently, a unified microscopic picture incorporating the above observations is still lacking.

Colloids are suitable model systems to probe statistical mechanical phenomena and their large size, typically a micron, allows detailed studies of dynamics down to the single particle level using optical techniques (3, 22–26). In this report, we have investigated the dynamics of GBs, sans external perturbations, in a 3-D colloidal polycrystal made of temperature-sensitive diameter tunable colloids. Our confocal microscopy experiments show that HAGBs have dynamical features that are remarkably similar to those of glasses. Analogous to glasses, we have observed strongly sublinear time dependence of the mean squared displacement due to transient caging of particles, non-Gaussian probability distribution of particle displacements and string-like collective motion of particles at GBs. In spite of their amorphous character, we find that the HAGB structure and dynamics systematically depend on the misorientation angle. This dependence stems from the misorientation angle-dependent size of cooperatively rearranging regions (CRRs), and hence the fragility, which decreases with the spatial extent of confinement of the GB region by neighboring crystallites. The spatial extent of confinement, set by the width of the GB region, is found to increase with the misorientation angle.

We used fluorescently labeled poly N-isopropylacryl amide (PNIPAM-AAc) microgel spheres with a diameter of 600 nm at 299 K. Above the lower critical solution temperature of 306 K, the particles shrink to ≈300 nm. Samples with volume fraction ϕ > 70% at 299 K were loaded in wedge-shaped cells. Thermal annealing of the sample resulted in a random hexagonally close packed colloidal polycrystal with a broad range of misorientation angles (Materials and Methods). The GB planes are perpendicular to the walls of our cell and our studies are confined to tilt boundaries (8).

Results and Discussion

Each experiment consisted of studying the dynamics of GB colloids in a horizontal plane for a fixed misorientation angle Θ and temperature T. Because GB colloids possess a lower coordination compared to their crystalline counterparts, we used a method based on local bond-order parameters to identify them. For each particle j and at each time step, we calculated the extent of the particle’s local orientational order using the 2-D Halperin–Nelson bond-order parameter, ψ₆(j) = (1/N)Σ_k exp(6iθ_jk) (27). Here N is the number of nearest neighbors and θ_jk is the angle between the j - k bond and a reference axis. A particle k is a nearest neighbor of j if it lies within 1.4σ, where σ is the lattice spacing. Typically, a particle with ψ₆ > 0.7 is considered to be crystal-like (28). Dense amorphous regions can possess a high degree of local orientational order and ψ₆ alone is insufficient to label GB colloids (29). To unambiguously determine crystal-like and amorphous-like particles, we set a cut-off on the number of ordered nearest neighbors N_∘ for particle j (30). A particle k is an ordered nearest neighbor of particle j if the complex inner product ψ₆(j)ψ₆(k)^∗ exceeds a value 0.5. Particles are termed amorphous-like if N_∘ < 4. The above procedure is similar in spirit to the Steinhardt bond-order parameter approach for identifying crystal-like clusters in 3-D (31). Further, we found that a colloid at the crystal-GB interface spends only a fraction of the time as amorphous-like (SI Text). Particles that have spent at least 50% of the time as amorphous-like were identified as GB colloids (Fig. S1 and Movie S1).

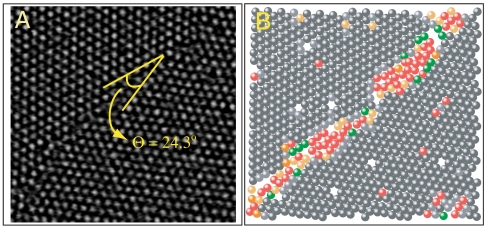
In Fig. 1B we have color-coded particles, based on the number of ordered nearest neighbors, by performing the aforementioned analysis on an image shown in Fig. 1A. Here Θ = 24.3°, which we identify as a HAGB as per convention [nominally Θ > 12° (8)]. A simple-minded approach toward understanding the structure of GBs is to extend the model for dislocation GBs to HAGBs solely on geometric arguments (8). Any GB can be thought of as a planar array of misfit dislocations with the dislocation density depending on Θ. Dislocation GBs (Θ < 12°) consist of a periodic array of discrete dislocation cores (Fig. S2). With increasing Θ, the dislocation density increases and the dislocation cores begin to overlap leading to a continuous amorphous interface (Fig. 1B).

Fig. 1.

GB in a colloidal polycrystal. (A) Image of HAGB. (B) Bond-order analysis of A. The dark and light gray particles are crystal-like with ordered nearest neighbors ≥4, and the green to red colors correspond to < 4 ordered nearest neighbors.

To gain insights into the local order of HAGBs seen in our colloid experiments, in Fig. S3 we have plotted the radial pair-correlation function, 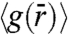. An underlying feature of the 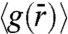for the three Θs investigated is the presence of a split-second peak (SI Text). This feature of 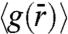has been observed in metallic (32) and colloidal glasses (22), random close packed granular media (33) and in computer simulations of HAGBs (13). Also, with decreasing Θ, we find that the splitting of the second peak becomes more pronounced. This enhancement in splitting is indicative of a higher degree of particle localization. In addition, for HAGBs we find that the spatial and time averaged width of the GB interface extracted from the images decreases systematically from 2.1 to 1.8 to 1.5σ for Θ corresponding to 24.3°, 18.4°, and 17.6°, respectively (34).

Misorientation Angle-Dependent HAGB Dynamics.

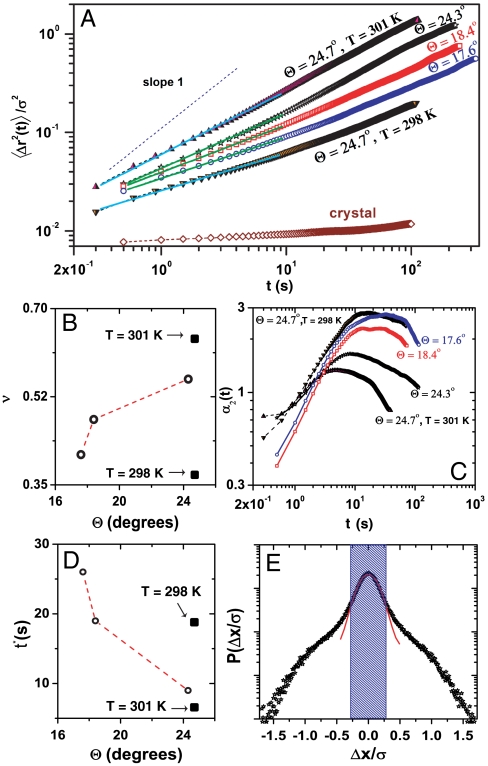
There are prominent dynamical signatures associated with glasses and we seek them in the GB dynamics (35). In glass forming systems, particles are trapped in transient cages formed by neighboring particles at short times. At long times, thermally activated reconfiguration of the cage allows the trapped particle to escape. This process is captured by the mean-squared displacement (MSD), 〈Δr²(t)〉 ∝ t^ν, of the particles which at short to intermediate times shows subdiffusive behavior, ν < 1, indicative of trapping. The MSD approaches diffusive scaling (ν = 1), also known as α-relaxation, at long times due to cage breaking. In Fig. 2A we show 〈Δr²(t)〉/σ² for three Θ values (hollow symbols). For HAGBs, ν progressively increases with Θ at intermediate times (Fig. 2B, ○) which reflects the increasing mobility of the GB colloids with Θ. In addition, we find that the diffusion of GB colloids is anisotropic with diffusion along GBs faster as compared to diffusion perpendicular to them (Fig. S4). Experiments on hard-sphere colloidal glasses and computer simulations of molecular and polymeric fluids have shown that spatial confinement has a profound effect on glass formation (36, 37) and can, in many cases, enhance the tendency of forming the glassy state (38–40). Keeping in mind that with decreasing Θ the GB width decreases, we attribute the observed slowing down of particle dynamics in HAGBs with decreasing Θ to enhanced confinement of the amorphous phase by the adjacent crystalline phases. To lend further support to the confinement argument, we exploit the size-tunable nature of PNIPAM-AAc colloids and study the GB dynamics for fixed Θ, as a function of temperature. As we approach the melting temperature (≈306 K), the GB width increases due to particle deswelling and we expect reduced confinement and hence higher GB colloid mobility. Starting from T = 298 K, as we reach T = 301 K, we find that the GB width increases from 1.75 to 1.95σ for Θ = 24.7°. As expected, 〈Δr²(t)〉_301 K > 〈Δr²(t)〉_298 K  (Fig. 2A, ▴ and ▾, respectively) with ν_301 K > ν_298 K (Fig. 2B, ▪).

Fig. 2.

Misorientation angle-dependent dynamics at GBs. (A) MSDs, rescaled by σ², for HAGBs. The hollow symbols are for different Θ and T = 299 K and the solid symbols are for the same Θ and different T. The brown hollow diamonds correspond to the crystal MSD at T = 299 K. The intermediate time exponent, ν, is obtained from linear fits to the data and is shown by green and cyan lines. (B) Intermediate time exponent ν, as a function of Θ at T = 299 K (○) and for Θ = 24.7° at different T (▪). (C) Non-Gaussian parameter α₂(Δt) for HAGBs. (D) Cage breaking time t^∗ obtained from polynomial fits to α₂(Δt). (E) Probability distribution of particle displacements over Δt = t^∗, for Θ = 24.3° at T = 299 K. The red line is the Gaussian fit. Particles outside the shaded region are the top 10% most mobile particles.

For glasses, the particle dynamics in the vicinity of the cage breaking time is expected to be non-Gaussian. To better quantify the cage-breaking dynamics, we plot the non-Gaussian parameter, in two-dimensions, defined as α₂(Δt) = (〈Δr⁴〉/2〈Δr²〉²) - 1, which quantifies the deviation from Gaussian nature (Fig. 2C). For diffusive behavior, α₂(t) = 0. For glasses, α₂(t) has a maximum at time t^∗ corresponding to the cage breaking time. For the GB colloids, Fig. 2C shows that α₂(t) is large and goes through a maximum for all Θs studied. Further, we find that with decreasing Θ and t, both t^∗ and the peak value of α₂(t) increase systematically (Fig. 2 C and D) and confirms the confinement induced slowing down of GB colloid dynamics. In Fig. 2E, we plot the probability distribution of particle displacements at t^∗ for Θ = 24.3°. We find that while 90% of GB colloids display diffusive dynamics, the top 10% most mobile GB colloids are non-Gaussian, characterized by the tails of P(Δx/σ), similar to that seen in hard-sphere colloidal glasses (35).

String-Like Cooperative Motion at HAGBs.

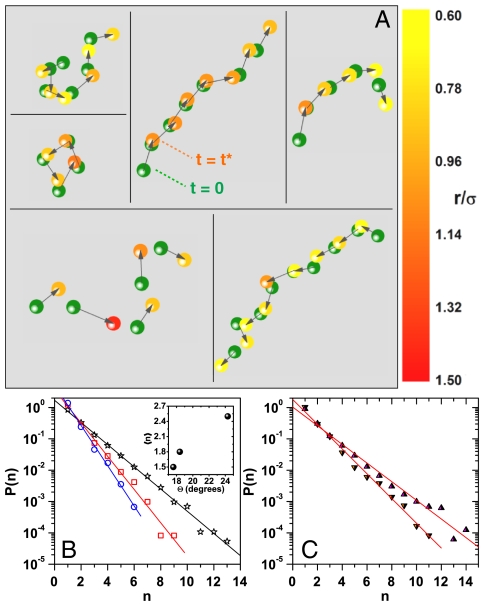
To unambiguously prove that GBs are dynamically similar to glasses, we check for signatures of cooperative particle dynamics. Cooperative motion of particles in the glassy state provides a pathway for structural relaxation and is, perhaps, the most striking feature of glass formers (41). In particular, MD simulations of atomic crystals (14) and experiments on 2-D vibrated granular media (42) have demonstrated the string-like cooperative displacements of the most mobile particles at GBs. To quantify the dynamics of CRRs in our experiments, we have first analyzed the displacements of GB colloids occurring over a time interval Δt = t^∗. We then identify the top 10% GB colloids undergoing the largest displacements as the most mobile particles and find that they are spatially clustered, as shown in Fig. 3A (green circles show the positions of the most mobile particles at time t = 0). Following ref. 41, two mobile particles i and j are considered to be a part of the same CRR if , where δ = 1.0σ. Physically, two mobile particles belong to the same CRR if over t^∗, one particle makes a hop and its position is occupied by the other, with a position of uncertainty less than δ. From the positions of the most mobile particles at t^∗ (Fig. 3A and Movie S2) it is evident that these particles indeed undergo cooperative rearrangements in a string-like manner (also see SI Text and Fig. S5 for van Hove correlation analysis).

Fig. 3.

String-like cooperative motion at GBs. (A) Snapshots of typical particle strings observed for Θ = 24.3°. Particles are drawn to 50% of their actual size. Particle positions at t = 0 (green circles) are linked to their positions at t = t^∗ (color-coded circles) by arrows. The length of the arrows and the particle color code are based on the magnitude of their displacement. Occasionally, we also see closed loops (Middle). (B) P(n) versus n for Θ = 24.3° (☆), Θ = 18.4° (□), and Θ = 17.6° (○). Inset, 〈n〉 versus Θ at T = 299 K. (C) P(n) versus n for Θ = 24.7° at T = 298 K (▾) and T = 301 K (▴). The straight lines in B and C are linear fits to the data.

In Fig. 3B, we have plotted the probability distribution of string lengths P(n) versus n, where n is the number of particles belonging to a string, for the three HAGBs. We find that P(n) falls exponentially with n as seen in MD simulations (14). A similar dependence of P(n) on n has also been observed in the equilibrium polymerization of linear polymers (43). Interestingly, we find that the maximum string length n_max and 〈n〉 systematically increases with Θ (Fig. 3B, Inset) and this trend is not altered for different choices of δ (SI Text, Fig. S6 A and B). Also a similar trend in n_max and 〈n〉 with Θ is seen when the CRR cluster size is defined to be the number of most mobile nearest neighbor particles that lie within a distance of 1.4σ from each other (Fig. S6 C, D and E). As per the Adam–Gibbs (44) hypothesis, which predicts an increase in the size of CRRs with supercooling, one would expect the string length to decrease with Θ in our experiments. However, this hypothesis is not applicable in the present context because geometric confinement is known to alter the very nature of the glass transition. Theory (45) and simulations (40) of polymeric glass-forming fluids have shown a decrease in the fragility (46)—which characterizes the deviation from Arrhenius-like/strong glass behavior of the structural relaxation time—with confinement. This decrease in fragility has been experimentally seen in intercalated polymer films (47). Further, the decrease in the fragility is accompanied by a decrease in the size of the CRRs, as seen in experiments on bulk polymeric glass formers (48) and simulations on confined polymeric glasses (40). In light of these studies, the increase in n_max and 〈n〉 with Θ, seen in our experiments, is ascribed to the increase in the fragility of the glassy GB region. Experiments carried out at different temperatures agree with the confinement scenario, 〈n〉_298 K < 〈n〉_301 K (Fig. 3C). Our results illustrate that the behavior of HAGBs is strikingly similar to that of confined glasses and point to the crucial role played by misorientation angle-dependent fragility in the dynamics of GBs.

Conclusions

Our model colloidal system has allowed us to investigate directly and with detail the dynamics of GB colloids in a 3-D polycrystal. We have shown conclusively that GBs display features that are hallmarks of glasses. In addition, our experiments highlight the pivotal role of misorientation angle-dependent GB confinement in determining the dynamical properties of HAGBs. Notably, thermally induced changes in confinement by only a fraction of the particle diameter can also alter the behavior of HAGBs (Fig. 3C). Although a consensus on the behavior of confined glasses is yet to emerge, our experiments illustrate that the glassy GB region, with a misorientation angle-dependent fragility (Fig. 3B), is a prototypical system where the rich physics of confined glasses can be directly applied. It is also tempting to speculate that the aging behavior ubiquitous in glassy systems may be relevant in the context of GBs. Our experiments not only offer a unique perspective on the current understanding of HAGBs but also reiterate that colloids are an ideal test bed for addressing fundamental and technological problems such as GB diffusion mechanisms and GB migration under shear.

Materials and Methods

PNIPAM-AAc colloids of diameter of 600 nm (polydispersity < 5%) were synthesized using the procedure described in ref. 49. The particles are negatively charged and interact via screened Coulomb repulsions. All chemicals used in the synthesis were procured from Sigma-Aldrich and had a purity in excess of 98%. The synthesis product was purified using dialysis membranes (Spectrapor molecular weight 10,000, VWR Lab Products) to remove the unreacted monomer. The purified suspension was concentrated to a ϕ ≈ 70% at 299 K. The fluorophor rhodamine 6G (99%, Sigma-Aldrich) was added to the suspension for confocal imaging. Samples were loaded into wedge-shaped cells, designed using a method analogous to ref. 50. The particles self-assembled into a random hexagonal close packed structure. Confocal imaging was done for a typical sample thickness of ≈23 μm, which is large enough to avoid confinement effects (51). All measurements were made 8 to 10 crystalline layers from the bottom of the cell to avoid wall effects (52). A Visitech VT-eye fast laser confocal scanner coupled to a Leica DMI 6,000B optical microscope was used for confocal imaging. The samples were imaged using a Leica objective (Plan Apochromat 100X NA 1.4, oil immersion) with a laser excitation centered at 514 nm. The field of view was 20  × 20 μm and a two-dimensional slice consisted of ≈1,200 particles. Images were captured at 2 frames per second (fps) for experiments probing the effect of misorientation angle on the dynamics, and at 3.3 fps for experiments probing the effect of temperature. An objective heater was used to facilitate local heating of the sample for experiments performed at 301 K. For these experiments, the temperature was increased from 298 K in steps of 0.2 K, with a waiting time of 30 min per step, to ensure sample equilibration. Particles were tracked using standard algorithms (53) and the uncertainty in determining particle positions, as obtained from the micron to pixel ratio (54), was found to be 0.029 μm. In addition, codes were developed in house to quantify GB dynamics.