Neural and computational mechanisms of postponed decisions

Abstract

We consider the mechanisms that enable decisions to be postponed for a period after the evidence has been provided. Using an information theoretic approach, we show that information about the forthcoming action becomes available from the activity of neurons in the medial premotor cortex in a sequential decision-making task after the second stimulus is applied, providing the information for a decision about whether the first or second stimulus is higher in vibrotactile frequency. The information then decays in a 3-s delay period in which the neuronal activity declines before the behavioral response can be made. The information then increases again when the behavioral response is required. We model this neuronal activity using an attractor decision-making network in which information reflecting the decision is maintained at a low level during the delay period, and is then selectively restored by a nonspecific input when the response is required. One mechanism for the short-term memory is synaptic facilitation, which can implement a mechanism for postponed decisions that can be correct even when there is little neuronal firing during the delay period before the postponed decision. Another mechanism is graded firing rates by different neurons in the delay period, with restoration by the nonspecific input of the low-rate activity from the higher-rate neurons still firing in the delay period. These mechanisms can account for the decision making and for the memory of the decision before a response can be made, which are evident in the activity of neurons in the medial premotor cortex.

An important aspect of decision making is that actions must often be delayed after the information for the decision has been provided. We examine the mechanisms that underlie this in a well-known paradigm because research in decision-making is the comparison of two vibrotactile stimuli (f₁, f₂) applied to the fingertips with a fixed delay period between them (1–8). To perform this cognitive task, the subject needs to store in working memory the information about the first stimulus, f₁, and to compare it with the second stimulus, f₂, to make the decision of whether f₁ < f₂ or f₁ > f₂, and report it immediately after the f₂ stimulus is released. Romo and coworkers (1–8) have analyzed neuronal activity in this paradigm. They have found that the activity of one type of neuron in a number of cortical areas is correlated with f₁ during its presentation [in the primary somatosensory cortex (S1), the secondary somatosensory cortex (S2), the ventral premotor cortex (VPC), the prefrontal cortex (PFC), and the medial premotor cortex (MPC)] and also during the delay period (in all of the previous brain areas except for the S1). During the presentation of f₂ they have identified three different types of neurons: neurons with firing correlated with f₁; neurons with firing correlated with f₂; and neurons with firing correlated with the sign of the difference between f₁ and f₂, which we denote (f₁ > f₂) and (f₂ > f₁) and which reflect which of these decisions is taken.

To extend the analysis of the mechanisms underlying decisions, which sometimes cannot be made immediately after the evidence is provided, Lemus et al. (3) introduced an additional delay between the second stimulus and the subject's response. This unique operation requires the subject to store in working memory the decision during the second delay period. The authors recorded the activity of neurons in the MPC, and found some neurons that reflected the decision throughout the delay period before the response could be made [e.g., figure 2B in Lemus et al. (3)]. To understand further the information about the decision carried by the neurons, Lemus et al. (3) made use of a linear regression model between the firing rates and the frequencies of the f₁ and f₂ stimuli: rates (t) = a₀(t) + a₁(t) f₁ + a₂(t) f₂. They analyzed the significance of a₁, a₂, or a₁−a₂ (1–8) to understand the role of the neuron: if a₁ is significant, the neuron encodes f₁; similarly, a₂ relevant implies the neuron encodes f₂; in the particular case in which a₁ = −a₂, the neuron is called a differential neuron, and it encodes the decision motor report. Lemus et al. (3) found neurons that in the postponed response delay period had firing rates that were correlated with the frequency of the f₁ stimuli and/or the f₂ stimuli, as well as with the motor response. They suggested that the neurons that reflect the sensory stimuli in the postponed response delay period enable the subject to revise the report and thus allow for a change in the initial decision.

In this paper, we use a different approach to the linear regression model to analyze the nature of the activity in the postponed response delay period. We measure the mutual information (MI) between the neuronal activity and the postponed response, which takes into account the variability of the firing (9–12), and apply this to understanding neuronal activity in the MPC recorded in the same paradigm as Lemus et al. (3). We wished to measure the information in the firing rates during the delay period. To do so, we computed the MI between the variables “firing rate” and “category of response” (i.e., f₁ < f₂ or f₁ > f₂) throughout the 3-s delay period in which the response is being postponed. For the population of neurons with significant information during the second stimulus (f₂), when the evidence required to make the decision is available, many of the neurons have low information during the delay period after f₂ before the postponed response can be made, but recover the information when the response must be made, as illustrated in Fig. 1B. We propose here that the information can be recovered by a nonspecific input applied at the time of the response, and demonstrate this with two models. In one model, synaptic facilitation (SF) (13–15) occurring in the postponed response delay period allows the memory to be maintained with little firing, and little information from the firing, in the delay period. In a second model, graded firing rates in the attractor decision-making network (16) in the delay period allow the faster-firing neurons to maintain sufficient firing and information in the delay period so that the nonspecific recall cue can activate these and the lower-firing neurons in the same attractor network to their full information value when the behavioral response is required at the end of the delay period.

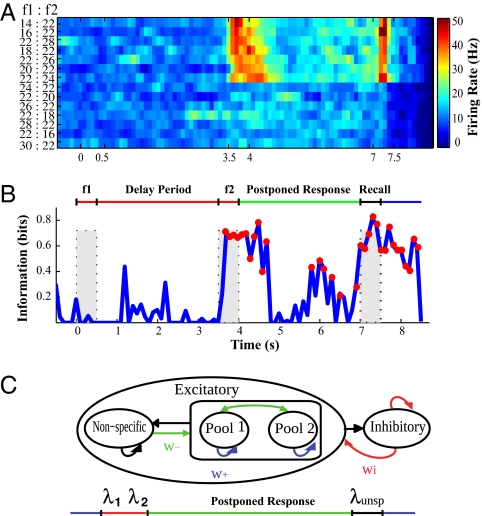
Fig. 1.

Response of a single decision-making neuron recorded in the MPC during the vibrotactile discrimination task with a postponed decision report (1). (A) Color map of the firing rate in bins of 200 ms moving in steps of 100 ms. Each square is colored according to its firing rate. (Right) Color map with firing rate scale in hertz. Each row is the mean activity for a specific pair of stimuli [f₁:f₂]. (Left) Labels indicate the pairs of vibrotactile frequencies [f₁: f₂] for each trial type. The trials are organized into two blocks: first with f₁ < f₂, and then f₁ > f₂; this makes the decision-making pattern of neuron firing clear: the neuron fires for decisions when f₁ < f₂, for a short time after f₂, and close to the time of the response. Only correct trials were included in the analysis. The time scale beneath the map shows the periods of stimulation and for reporting the decision. The f₁ period is 0.0–0.5 s. The delay period between the stimuli is 0.5–3.5 s. The f₂ period is 3.5–4.0 s. The postponed response delay period is 4.0–7.0 s. The behavioral response can be started at a signal given at the time of 7.0 s. (B) The MI between the activity shown in A and the category of the response with a surrogate correction (200 surrogates) (28). The red circles indicate the values that are significant at P < 0.05, tested with a first-order Monte Carlo method. The shaded rectangles show the stimulation periods f₁ and f₂, and the report period. (C) Architecture of the spiking integrate-and-fire attractor network model of decision making and of activity in the subsequent delay period. The model consists of two different neuronal populations: excitatory and inhibitory (interneurons). There are two types of excitatory population: selective (pool 1 and pool 2 for each of the two decisions) and nonselective. The recurrent arrows indicate recurrent connections between the different neurons in a pool, and the other arrows show the different connections between the groups. The selective pools first receive λ₁ = 250 Hz and λ₂ = 150 Hz during the red period. The inputs are then removed during a delay of 3 s in which the same unspecific input λ = 204 Hz (0.255 Hz for each of 800 synapses onto each neuron) is injected to both selective pools. For nonselective and inhibitory neurons, λ_unsp = 0.

Results

Information in the Neuronal Activity of Medial Premotor Cortex Neurons.

The activity of a single MPC neuron in the postponed response delay task is illustrated in Fig. 1 A and B. The monkeys (Macaca mulatta) were trained to discriminate in frequency between two consecutive mechanical vibrations (f₁ and f₂) delivered to one fingertip (1–8). The monkeys were asked to report the results of the decision about which vibrotactile stimulus, f₁ or f₂, had a higher flutter frequency after a fixed delay period (3 s) between the end of f₂ and the cue that triggered the beginning of the motor report. Sequential decision tasks with a delayed response require information about f₁, temporally stored in working memory, to be compared with the current information from f₂ to form a decision of whether f₂ > f₁ or f₂ < f₁. After the discrimination, the subject must keep the decision or response in working memory for 3 s, and then report the outcome by pressing one of two push buttons (one for each option: f₂ > f₁, f₂ < f₁) after the postponed response delay (Fig. 1B). Fig. 1A shows that the neuron fired during the f₂ period on trials in which f₂ > f₁, had a lower firing rate in the postponed response delay period (4–7 s), and then increased its rate when the signal was given that the behavioral response could be made (7.0–7.5 s). Fig. 1B, the MI analysis for the same neuron, shows that there was information in the firing rate about the response made at the end of each trial during and just after the f₂ period when the decision could be made, and that the information decreased during the postponed response delay period and increased again when the signal for the behavioral response was given.

The single-cell mutual information for the whole set of MPC neurons is shown in Fig. 2 Top. It is clear that some neurons do have low information in the postponed response delay period. These neurons also tend to have low information in the f₂ and response periods. Other neurons have higher amounts of information in the delay period, and these neurons tend to have higher information in the f₂ and response periods. (The neurons are ordered according to how much information they have in the f₂ period.) We confirmed that some of these neurons maintain their firing in the delay period even after a strict Holm–Bonferroni correction for multiple tests (17) described in SI Text, Fig. S1, and Table S1.

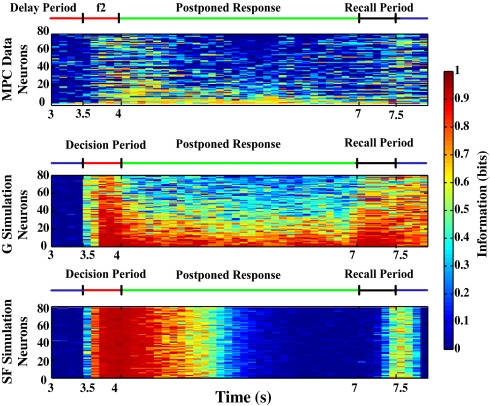
Fig. 2.

Mutual information analyses as a function of time. (Top) Eighty neurons from the medial premotor cortex. Each row corresponds to a different neuron. (All neurons in the dataset are included for which there were five or more trials for each condition.) The times when the f₂ stimuli are applied (the delay period and the behavioral response period) are indicated (Fig. 1). In particular, the f₂ period is 3.5–4.0 s. The postponed response delay period is 4.0–7.0 s. The behavioral response can be started at signal given at 7.0 s. The mutual information shown is that between the firing rate in a 200-ms window (sliding every 100 ms) and the response made by the monkey. The calibration bar shows the information value for a single neuron. (Middle) Eighty neurons in pool 1 of the graded firing rate simulation. Each row is a single neuron. The rows are sorted by the amount of information during the decision period, 3.5–4.0 s, which corresponds to the f₂ period for the MPC neurons. The delay period is 4–7 s. The equal external inputs are applied at t = 7.0–7.5 s, labeled recall period. The mutual information shown is that between the firing rate in a 200-ms sliding window and the firing in the decision period. (Bottom) SF simulation (conventions as in Middle).

More tellingly, we performed a multiple-cell information analysis, which tests how the information about the decision increases with the number of neurons in the sample (10, 18) (Figs. S2 and S3). We found that with 18 neurons taken at random from those with low single-cell information content in a 600-ms window in the delay period (5.2–5.8 s), the average information per neuron was 0.06 bits, and the total information provided was 0.51 bits, with a 90% correct prediction of the decision (Fig. S2). (These 18 neurons had low information even during f₂, on average 0.4 bits/neuron, and we needed 14 such neurons selected at random to reach 1 bit of information.) If we consider 16 randomly selected neurons from those with the higher information values shown in Fig. 3, then the multiple-cell information analysis showed that the average amount of information for each cell was 0.56 bits in the same 600-ms window in the delay period, and that with subsets of cells chosen at random from the 16 cells the information reached 1 bit and 100% correct with four to six cells (Fig. S3). The implication is that with just six MPC cells chosen at random from the set with higher information values in the delay period shown in Fig. 2, the animal could do the task perfectly, with 100% correct.

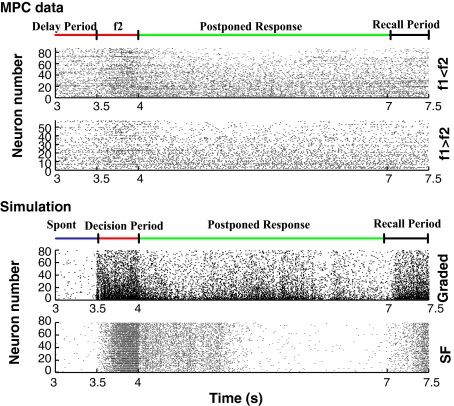
Fig. 3.

Rastergrams to illustrate the firing for the MPC neurons (Upper rastergrams), the graded simulations, and the SF simulations. For the MPC neurons, the Upper set of rasters is for neurons with firing to f₁ < f₂, and the Lower set of rasters is for neurons with firing to f₁ > f₂. One trial is shown for each neuron, and the trial selected is one in which that neuron by its high firing rate encodes the decision. For the graded simulation, each row is the firing for a different neuron, and all of the data are from one simulation trial, to show how the rates for the different neurons remain graded throughout the trial, including when there is some fluctuation of average firing rate in the delay period. For the synaptic facilitation simulations, one trial is also shown. The times correspond to those in Fig. 1. The recall period for the MPC data was when the behavioral response could be initiated, and for the simulations was when the unspecific input was applied to produce recall.

Overall, the single- and multiple-cell information analyses show that some neurons do contain little information in the delay period about which report will be made at the end of the postponed response delay period, whereas other neurons do maintain significant information in the delay period, with four to six such MPC neurons being sufficient to account for the correct behavioral response at the end of the delay period.

We now consider two models that examine the basis of the recovery of the information at the end of the postponed response delay period when the behavioral response must be made. The models have in common the fact that a nonspecific external input applied at the time when the response can be made after the delay allows the information to be recovered in the neuronal firing, as shown in Fig. 2 Top.

Synaptic Facilitation Model.

To explain the mechanism underlying the appearance of information about the decision during and just after f₂, then its disappearance for some neurons in the postponed response delay period, and finally its reappearance at the response time, we made an integrate-and-fire attractor network model (13, 14, 19) of the decision-making neurons (Fig. 1C) that is able to reproduce that pattern of activity by incorporating SF. There are two decision populations, or pools, of neurons, with pool 1 activated by stimulus f₁ via the λ₁ inputs and winning the competition if f₁ > f₂, and pool 2 activated by stimulus f₂ via the λ₂ inputs and winning the competition if f₁ < f₂. The global inhibition produced by the inhibitory neurons, together with the different λ₁ and λ₂ inputs to pools 1 and 2, provide the basis for the competition, which is influenced by the randomness of the spiking times of the neurons to produce probabilistic choice (10, 20). We also implemented short-term SF (Methods) in which the calcium-mediated SF makes the residual calcium level grow (21). Each neuron that spikes increases the residual calcium level, u, in the presynaptic terminals, which in turn increases the release probability. The time constant for this process was 2 s. Details of the implementation and operation of the simulation are in SI Text.

The results of the SF simulations are illustrated in Fig. 2 Bottom and Fig. 3 Lower. After a period of spontaneous activity before t = 3.5 s, the decision cues λ₁ and λ₂ are applied at t = 3.5–4.0 s. If λ₁ > λ₂, pool 1 corresponding to a decision that f₁ > f₂ wins, and its firing rate and the MI between the firing and the behavioral response increases. In the delay period from 4 to 7 s, the decision cues are no longer present, and the firing rate and the MI decrease to close to zero (Figs. 2 and 3). During this delay period, the synaptic facilitation between the neurons in pool 1 that occurred during f₂ in decision pool 1 remains, gradually decaying (Fig. S4). When a nonspecific external input (λ_unsp) is applied at t = 7.0–7.5 s to both pools 1 and 2 to reflect the moment when the subject receives the stimulus to give its behavioral response, then because of the altered synaptic calcium levels, the firing rate of one of the selective pools increases to the attractor activity level (Fig. 3), as does its information about the response to be made (Fig. 4), whereas the firing of the other selective pool remains with low activity, although a little higher than the spontaneous firing rate. In this way, the SF model recalls the selective firing for the correct response even though there was no firing in the delay period (Figs. 2–4).

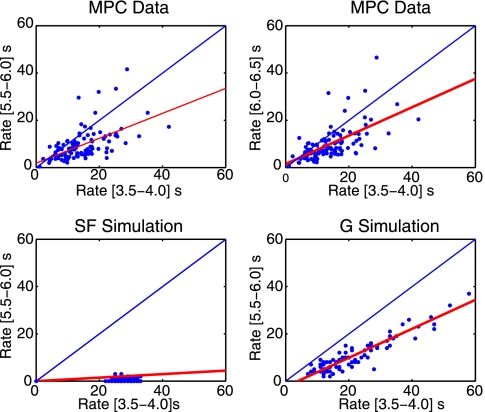
Fig. 4.

The firing rate during the delay period (ordinate) vs. the firing rate in the decision period (abscissa). Each point represents one neuron. (Upper) MPC neurons. Scatterplots show the rates for two different 0.5-s time windows in the delay period. (Lower Left) SF simulations. (Lower Right) Graded (G) firing rate simulations. The blue line shows where an equal response would lie. Red lines show linear fits to the data.

It has been shown that as the postponed response delay period increases, the performance of the subjects decreases (3). We found that the performance of the SF model decreases in a similar way over periods of up to 3 s (Table S2). However, it is a prediction of the SF model that performance will decay as the short-term memory period increases much beyond the time constant of the synaptic facilitation, 2 s. We therefore examine a firing rate model in the next section that can maintain the memory over much longer periods than this. Further, it is a property of the SF model that it can perform the delay task with no firing and no firing rate information in the delay period, because the memory is held in the facilitated synaptic weights (Figs. 2–4); however, this was not found for the MPC neurons, the majority of which do have some firing during the delay period (Figs. 3 and 4), and retain some information in their firing rates in the delay period (Fig. 2). Moreover, the MPC neurons have a distribution of firing rates and of the single-cell information in the delay period, with some neurons maintaining their firing rates and firing rate-related information in the delay period well, and others less so (Figs. 2–4). We therefore analyzed a different model of the delay-related firing, which has a graded distribution of firing rates.

Graded Firing Rate Attractor Network Model of the Activity in the Delay Period After the Decision.

An integrate-and-fire decision-making network was implemented in the way just described, but without any synaptic facilitation, and with graded firing rates. The gradation to the firing rates was implemented by replacing the equal and strong synaptic weights (w+) that connect the neurons within each specific decision-making pool with an exponentially graded set of synaptic weights. The graded synaptic weights had the same average value (w+ = 2.1), but some were considerably stronger, and the distribution decreased exponentially to a value of 1, as described elsewhere (16) and in SI Text. Graded firing rate distributions are not usually examined in these attractor decision-making networks because the mean field analysis used to set the network parameters requires the same value for the weights within a pool. However, because neurons in the brain typically have graded firing rate distributions, frequently close to exponential (10, 22), we have investigated the properties of decision-making networks with graded firing rate representations (16). Here, we investigate the activity of a similar network in a short-term memory period after a decision, and analyze whether the firing rate distribution in the delay period is similar to that found for MPC neurons in that some neurons encode little information in their firing rates, and others more information. For these graded simulations, there was a predecision cue period of spontaneous firing; the decision cues were applied at 3.5–4.0 s, and in this period the decision was made; there was a 3-s delay period from 4 to 7 s, and then a nonspecific input was applied equally to the two decision pools (1 and 2) from 7.0 to 7.5 s, to investigate whether just pool 1, which had reached the decision during 3.5–4.0 s, could be restored to its high and selective activity with respect to pool 2 when the behavioral response was required.

The performance of the graded firing rate network for neurons in the winning pool (pool 1) is illustrated by rastergrams in Fig. 3. Some neurons continue firing in the delay period, whereas others decrease their rates considerably, to only slightly above the spontaneous rate shown in the spontaneous period. This pattern is qualitatively similar to that found for the MPC neurons (Fig. 3, Upper). Fig. 4 shows that the firing rates for these simulations are indeed graded in the delay period, and that, as is expected, the firing rates in the delay period are monotonically related to the firing rate in the decision period (3.5–4.0 s). Fig. 4 also shows that the MPC neurons have graded rates in the delay period, as well as in the f₂ decision period. Fig. 2 shows that the graded firing rate simulations have graded information conveyed by the different neurons, with some with relatively high firing rate information, and others with much lower firing rate information, in the delay period. This is qualitatively similar to the MPC neurons’ information measures throughout the task, although as the MPC neurons are noisier from trial to trial than the graded simulation, the actual magnitude of the information is less for the MPC neurons than for the graded simulations.

Of particular interest and theoretical significance is that the graded simulations recover the information when the external stimulus is applied nonselectively (i.e., equally) to pools 1 and 2 at t = 7.0–7.5 s. The concept here is that with low inputs during the delay period, the neurons overall have less activity than in the decision period when the decision cues are applied. However, the correct decision pools can maintain the identity of the decision by having just some neurons firing at a sufficient rate to keep the attractor active by the feedback of the firing rates through the graded synaptic weights. The neurons with the low weights in the graded distribution may have very little firing in the delay period, and indeed may be firing at a rate insufficient to maintain the attractor themselves in the delay period (as shown by further simulations). However, when the nonselective external signal is applied at t = 7.0–7.5 s equally to neurons in pools 1 and 2, the neurons in pool 1 that are already active are stimulated into higher firing, which has the effect of recruiting through the intrapool recurrent synaptic connections the other lower-firing neurons in pool 1, and also, by competition through the inhibitory interneurons, keeping the neurons in pool 2 at low activity. This results in the recovery of information during t = 7.0–7.7 s, illustrated in Fig. 2, which models what is shown for the MPC neurons in Fig. 2. (The actual process at the time of the application of the external stimulus at t = 7.0–7.5 s can also be viewed as a decision-making process in which λ₁ = λ₂, but there is a bias to λ₁ from the greater activity left in pool 1 than in pool 2 at the end of the delay period.)

In summary, the graded firing rate model of decision making has properties that capture many of the properties of the MPC neurons (Figs. 2–4). These properties include the maintenance of low but significant information in the delay period, which is graded according to the graded firing rates, and the restoration of the information when it needs to be recalled, by a nonselective external input in the case of the network. This operation is different from that of the synaptic facilitation model, which can hold the memory in the synaptic facilitation with no firing rate or information evident in the delay period (Figs. 2–4), and which has only a limited short-term memory period.

Discussion

In this paper we have shown using mutual information analyses that though some MPC neurons lose their information about the decision in a subsequent delay period before the behavioral response can be made, some neurons maintain that information, although at a lower level and with lower firing rates than during the decision period (f₂) (Figs. 2–4). We have shown previously that an integrate-and-fire decision-making attractor network can account for the decision-making itself in this task (14), and show here that the same network can also account for the memory of the decision in the subsequent delay period before the behavioral response can be made. This use of the same network to make the decision and to hold the decision in a short-term memory is a good and evolutionarily efficient property of this model of decision making (10, 20).

The two mechanisms we model for the details of how these processes are implemented have different advantages. The SF mechanism is energy efficient, for it can, as we show here, maintain the evidence of a previous decision even with no neuronal firing (Figs. 2–4); however, it is limited by the maximum duration of its short-term memory, set by the time constant of the synaptic facilitation, which is ∼1–2 s (13, 23). The SF model can be made to have, as in the MPC (Figs. 2–4) and many other brain areas (3, 10, 24, 25), some continuing firing in the delay period by increasing the nonspecific inputs to the neurons in the delay period. In the MPC, in which some neurons have low single-cell information levels at some point in the delay, the multiple-cell information shows that a group of as few as seven neurons in the group with most single-cell loss of information never fall below 0.42 bits, allowing 90% correct performance in the delay period (SI Text). The graded firing model of decision making and subsequent short-term memory for the decision described here shows that low levels of firing in some neurons in an attractor population with graded firing rates can enable the attractor to be maintained, and later restored, even when some of the neurons in the graded representation have low activity in the delay period, and correspondingly low MI values. (In the graded firing rate simulations analyzed, we took the parameters—in particular the inputs being applied equally to pools 1 and 2 in the delay period—down to levels that just enabled the attractor to be maintained.) Because neurons in the MPC and in many other cortical areas (10) have graded representations, ours is an accurate model of the neurophysiological mechanism. And by using firing rates, the graded firing rate model can maintain its firing rates for potentially long periods, of tens of seconds.

In practice, it could well be that the cortex uses both mechanisms described here in the same network. That is, the level of firing that is required in a small proportion of neurons in the graded firing rate attractor population may be sufficient to produce some synaptic facilitation, and thus synaptic facilitation may be involved in the cortex in these types of networks. In this mixed scenario, however, the mechanism relies more on the graded nature of the firing rate representations, and for the attractors to be maintained by low firing rates of at least some neurons, especially when the memory must be for more than a few seconds.

A synaptic facilitation mechanism has been proposed previously to help with the memory of f₁ during the delay between the stimuli f₁ and f₂ in a sequential decision-making task (14), but has not been suggested before for implementing the memory in a postponed decision task. We have shown here that synaptic facilitation provides a possible mechanism for remembering the decision during the delay period before the decision can be reported.

In this paper we used MI to quantify the relationship between the firing of the MPC decision-making neurons during different parts of the task, and the decision taken when f₂ is applied. MI analysis is useful because it takes into account the variability of the firing from trial to trial, and at different times within a trial. The MI analysis shows that the information about the response is not significant until the end of the second stimulus (by which time f₁ and f₂ have been presented; Fig. 2). Immediately after f₂, the analysis shows an association between the firing rates and the later response of the monkey. Then for some neurons (Fig. 2), the information becomes low during the delay period only to come back again at the response time. At the report time the MI becomes significant as a consequence of the large difference in the firing rates of the two selective populations. The multiple-cell information analysis is helpful in showing that if a population of neurons with low single-cell information values in the delay period are considered together, then because the information from the different neurons adds (Fig. S2), there is in fact some information provided even by these neurons in the delay period. The MI analysis also highlights that it is the high firing rate neurons that encode much information, as the information measure reflects the difference in the firing rates—that is, the number of spikes in a short time window between the two populations being considered (10, 26).

The relative contribution of the two mechanisms, synaptic facilitation vs. restoration of firing in the whole set from the firing in a subset with graded activity, could be investigated experimentally by using longer delay periods before the behavioral response can be made. The synaptic facilitation mechanism with its time constant of 2 s would predict very poor performance (by the neurons and behaviorally) if the delay period is increased to 5 s. In contrast, the mechanism that involves restoration of firing in the whole set of neurons from the firing remaining in a subset could in principle restore the firing in all of the neurons in the appropriate decision pool after much longer periods.

Finally, we note that in the first delay period, between f₁ and f₂, a sensory representation of f₁ must be stored. In the postponed response delay period, the result of the decision must be stored, and we show in this paper that it is natural for the decision-making network to also store the results of the decision, for it is an attractor decision-making mechanism that we analyze. The networks that implement these memories must be different, and are shown to be different by the fact that different neuronal populations are engaged by these two processes (1–8).

Methods

Discrimination Task.

Stimuli were delivered to the skin of the distal segment of one digit of the right, restrained hand of a monkey via a computer-controlled stimulator (2-mm round tip; BME Systems). The initial indentation was 500 μm. Vibrotactile stimuli were trains of mechanical sinusoids. Stimulation amplitudes were adjusted to produce equal subjective effects (3). On each trial, two vibrotactile stimuli (f₁ and f₂) were delivered consecutively, separated by a fixed interstimulus delay period of 3 s. The monkey was asked to report discrimination of the two stimuli after a fixed delay period of 3 s between the end of f₂ and a cue signal (provided at 7 s; Fig. 1) that triggered the beginning of the motor report. In the correct trials, the animal was rewarded with a drop of liquid. Discrimination was reported by pressing one of two push buttons (see refs. 1–8 for more information).

Model.

The decision-making model is illustrated in Fig. 1C and is described in detail in SI Text. In the SF version, to implement a short-term memory trace that did not depend on maintained firing rates, we used calcium-mediated SF (13–15). All of the presynaptic spikes that arrive at the presynaptic terminals increase the accumulation of intracellular calcium, which increases release probability. These dynamics are influenced by the parameter u (which reflects the residual calcium level) as described in SI Text and elsewhere (13). The time constant of the synaptic facilitation is adjusted by the parameter τ_F. The values for the baseline utilization factor U (0.15) and for τ_F (2 s) are similar to values reported experimentally and used elsewhere (13, 23).

The graded firing rate model was implemented by setting the synaptic weights of the intrapool synaptic connections to an exponentially graded set of synaptic weights, as described in SI Text and elsewhere (16). No synaptic facilitation was used.

Information Theoretic Analysis.

We calculated the single-cell MI between the neuronal firing rate measured in a 200-ms time window slid along the time axis in units of 100 ms, and the behavioral response. The MI was calculated as

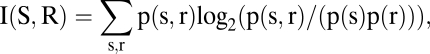where p(s), p(r) are the marginal distributions of the variables, and p(s, r) is the joint distribution (11). Because the MI estimate is subject to statistical errors, which can lead to an overestimate of the information, we corrected the information estimates using a first-order Monte Carlo method described in SI Text (10, 27). This method also leads to a test of the statistical significance of the corrected MI between firing rates and category (28), as described in SI Text.